Prasanna

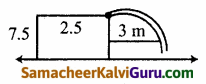
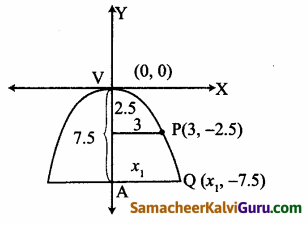
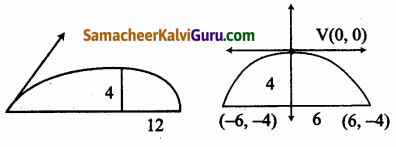
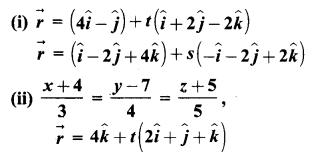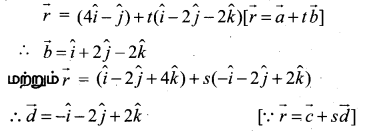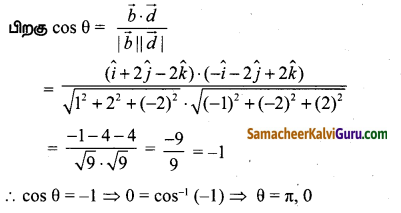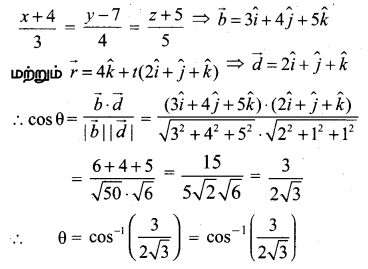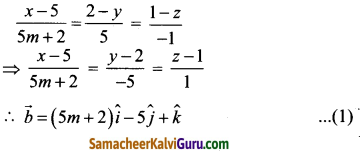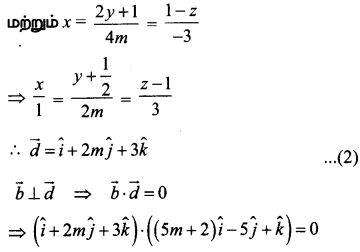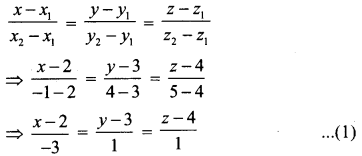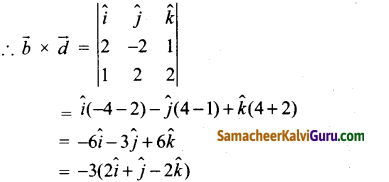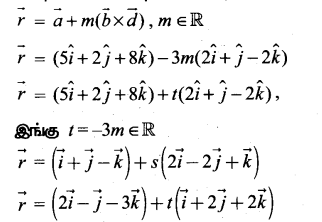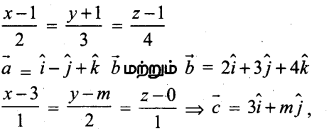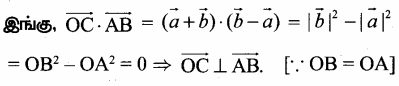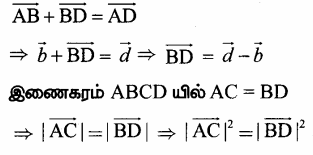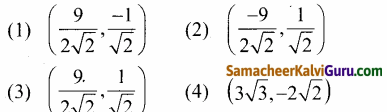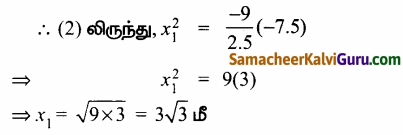Tamilnadu State Board New Syllabus Samacheer Kalvi 9th Maths Guide Pdf Chapter 2 மெய்யெண்கள் Ex 2.3 Textbook Questions and Answers, Notes.

TN Board 9th Maths Solutions Chapter 2 மெய்யெண்கள் Ex 2.3

கேள்வி 1.
கீழ்க்கண்ட விகிதமுறா எண்களை எண்கோட்டில் குறிக்கவும்

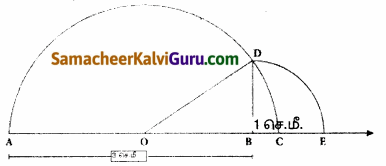
(i) \(\sqrt{3}\)
(ii) \(\sqrt{4.7}\)
(iii) \(\sqrt{6.5}\)
தீர்வு
(i) \(\sqrt{3}\)

• ஒரு நேர்கோடு வரைந்து அதில் A என்ற புள்ளியைக் குறிக்கவும்.
• AB = 1.732 செ.மீ. எனுமாறு B என்ற புள்ளியைக் குறிக்கவும்
• BC = 1 என்ற அலகுக்கு ஒரு கோடு வரைந்து அதை ‘C’ எனக் குறிக்கவும்.
• AC இக்கு மையக் குத்துக்கோடு வரைந்து அதன் மையப் புள்ளியை O எனக் குறிக்கவும்.
• O ஐ மையமாகவும் OC = OA ஐ ஆரமாகவும் கொண்டு அரை வட்டம் வரையவும்.
• BD இக்குச் செங்குத்தாக B இல் AB என்ற கோடு வரையவும்.
• இப்போது, BD = \(\sqrt{3}\) இதை எண்கோட்டில் BE = BD = \(\sqrt{3}\) எனக் குறிக்கலாம்.

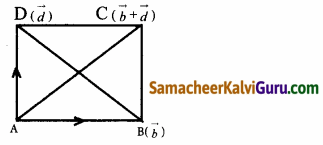
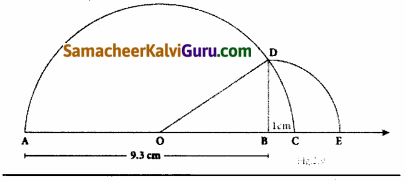
(ii) \(\sqrt{4.7}\)

• ஒரு நேர்கோடு வரைந்து அதில் A என்ற புள்ளியைக் குறிக்கவும்.
• AB = 4.7 செ.மீ. எனுமாறு B என்ற புள்ளியைக் குறிக்கவும்
• BC = 1 என்ற அலகுக்கு ஒரு கோடு வரைந்து அதை C எனக் குறிக்கவும்.
• AC இக்கு மையக் குத்துக்கோடு வரைந்து அதன் மையப் புள்ளியை O எனக் குறிக்கவும்.
• O மையமாகவும் OC = OA ஐ ஆரமாகவும் கொண்டு அரை வட்டம் வரையவும்.
• BD இக்குச் செங்குத்தாக B இல் AB என்ற கோடு வரையவும்.
• இப்போது, BD = \(\sqrt{4.7}\) இதை எண்கோட்டில் BE = BD = \(\sqrt{4.7}\) எனக் குறிக்கலாம்.
  

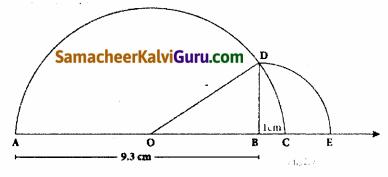
(iii) \(\sqrt{6.5}\)

• ஒரு நேர்கோடு வரைந்து அதில் A என்ற புள்ளியைக் குறிக்கவும்.
• AB = 6.5 செ.மீ. எனுமாறு B என்ற புள்ளியைக் குறிக்கவும்
• BC = 1 என்ற அலகுக்கு ஒரு கோடு வரைந்து அதை ‘C’ எனக் குறிக்கவும்.
• AC இக்கு மையக் குத்துக்கோடு வரைந்து அதன் மையப் புள்ளியை O எனக் குறிக்கவும்.
• O ஐ மையமாகவும் OC = OA ஐ ஆரமாகவும் கொண்டு அரை வட்டம் வரையவும்.
• BD இக்குச் செங்குத்தாக B இல் AB என்ற கோடு வரையவும்.
  இப்போது, BD = \(\sqrt{6.5}\) இதை எண்கோட்டில் BE = BD = \(\sqrt{6.5}\) எனக் குறிக்கலாம்.
  

கேள்வி 2.
கீழ்க்காணும் எண்களுக்கு இடையே உள்ள எவையேனும் இரு விகிதமுறா எண்களைக் காண்க.
(i) 0.3010011000111 மற்றும் 0.3020020002
விடை:
0.3010011000111 மற்றும் 0.3020020002 இடையேயுள்ள இரு விகிதமுறா எண்கள்
0.301202200222 3.301303300333

(ii) \(\frac{6}{7}\) மற்றும் \(\frac{12}{13}\)
விடை:
\(\frac{6}{7}\) = 0.8571428571
\(\frac{12}{13}\) = 0.9230769231
\(\frac{6}{7}\) மற்றும் \(\frac{12}{13}\) உமற்றும் 2 க்கு இடையேயுள்ள இரு விகித முறா எண்க ள்
0.8616611666111 0.8717711777111

(iii) \(\sqrt{2}\) மற்றும் \(\sqrt{3}\)
விடை:
\(\sqrt{2}\) = 1.414….
\(\sqrt{3}\) = 1.732……
\(\sqrt{2}\) மற்றும் \(\sqrt{3}\) இடையேயுள்ள இரு விகிதமுறா எண்க ள் 1.515511555….1.616611666…..

கேள்வி 3.
2.2360679 மற்றும் 2.236505500 இவ்வெண்களுக்கிடையே எவையேனும் இரு விகிதமுறு எண்களை எழுதுக.
விடை:
2.2360679 மற்றும் 2.236505500 இடையேயுள்ள இரு விகிதமுறு எண்கள் 2.2362 மற்றும் 2.2363

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 6 வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள் Ex 6.4 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 6 வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள் Ex 6.4

கேள்வி 1.
\(\hat{4} \hat{i}+3 \hat{j}-7 \hat{k}\) என்ற வெக்டரை நிலை வெக்டராகக் கொண்ட புள்ளி வழிச் செல்வதும் \(2 \hat{i}-6 \hat{j}+7 \hat{k}\) என்ற வெக்டருக்கு இணையானதுமான நேர்க்கோட்டின் துணை அலகு அல்லாத வெக்டர் சமன்பாடு மற்றும் கார்டீசியன் சமன்பாடுகளைக் காண்க.
தீர்வு:
\(\vec{a}=4 \hat{i}+3 \hat{j}-7 \hat{k}\) மற்றும் \(\vec{b}=2 \hat{i}-6 \hat{j}+7 \hat{k}\) என்க.
ஒரு புள்ளி \((\vec{a})\) வழிச் செல்லும் மற்றும் வெக்டர் \((\vec{b})\) க்கு இணையான கோட்டின் வெக்டர் சமன்பாட்டின் துணையலகு இல்லாத வடிவம்
\((\vec{r}-\vec{a}) \times \vec{b}=\vec{0}\)
⇒ \([\vec{r}-(4 \hat{i}+3 \hat{j}-7 \hat{k})] \times(2 \hat{i}-6 \hat{j}+7 \hat{k})=\vec{0}\)
அதனுடைய கார்டீசியன் சமன்பாடு
\(\frac{x-x_{1}}{b_{1}}=\frac{y-y_{1}}{b_{2}}=\frac{z-z_{1}}{b_{3}}\)
⇒ \(\frac{x-4}{2}=\frac{y-3}{-6}=\frac{z+7}{7}\)
[∵ (x₁, y₁, z₁), (4, 3, -7) மற்றும் (b₁, b₂, b₃), (2,-6, 7)]

கேள்வி 2.
(-2, 3, 4) என்ற புள்ளி வழியாகச் செல்லும் \(\frac{x-1}{-4}=\frac{y+3}{5}=\frac{8-z}{6}\) என்ற கோட்டிற்கு இணையானதுமான நேர்க்கோட்டின் துணை அலகு வெக்டர், சமன்பாடு மற்றும் கார்டீசியன் சமன்பாடுகளைக் காண்க.
தீர்வு:
\(\vec{a}=-2 \hat{i}+3 \hat{j}+4 \hat{k}\) மற்றும் \(\vec{b}=-4 \hat{i}+5 \hat{j}-6 \hat{k}\)
என்க.
ஒரு புள்ளி \((\vec{a})\) வழிச்செல்லும் \(\vec{b}\) க்கு இணையான நேர்க்கோட்டின் வெக்டர் சமன்பாட்டின் துணையலகு வடிவம்
\(\vec{r}=\vec{a}+t \vec{b}\) இங்கு t ∈ ℝ
∴ \(\vec{r}=-2 \hat{i}+3 \hat{j}+4 \hat{k}+t(-4 \hat{i}+5 \hat{j}-6 \hat{k})\), t ∈ ℝ
அதனுடைய கார்டீசியன் சமன்பாடு
\(\frac{x-x_{1}}{b_{1}}=\frac{y-y_{1}}{b_{2}}=\frac{z-z_{1}}{b_{3}}\)
⇒ \(\frac{x+2}{-4}=\frac{y-3}{5}=\frac{z-4}{-6}\)
[∵ (x₁, y₁, z₁), (-2, 3, 4), (b₁, b₂, b₃), (4, 5,-6)]

கேள்வி 3.
(6, 7, 4) மற்றும் (8,4,9) என்ற புள்ளிகள் வழியாகச் செல்லும் நேர்க்கோடு xz மற்றும் yz தளங்களை வெட்டும் புள்ளிகளைக் காண்க.
தீர்வு:
(x₁, y₁, z₁), (6, 7, 4) மற்றும் (x₂, y₂, z₂), (8, 4, 9) என்க .
இரண்டு புள்ளிகள் வழிச்செல்லும் நேர்க்கோட்டின் கார்டீசியன் சமன்பாடு

∴ கோட்டின் மீதுள்ள புள்ளி (2s + 6,-3s +7,5s +4). ……….(2)
(1) மற்றும் x z தளத்தின் வெட்டுப்புள்ளி காண, y = 0, என (2)ல் பிரதியிடு
∴ -3s + 7 = 0 ⇒ -3s = – 7 ⇒ s = \(\frac{7}{3}\),
s = \(\frac{7}{3}\) என (2) -ல் பிரதியிட வெட்டுப் புள்ளியானது

(1) மற்றும் yz தளத்தின் வெட்டுபுள்ளி காண, x = 0. என (2)ல் பிரதியிடு
∴ 2s + 6 = 0
⇒ 2s = -6
⇒ s = -3.
∴ (2) → (2 (-3) + 6,-3 (-3) + 7, 5 (-3) + 4)
= (0, 16, -11)

கேள்வி 4.
(5, 6, 7) மற்றும் (7, 9, 13) என்ற புள்ளிகள் வழியாகச் செல்லும் நேர்க்கோட்டின் திசைக் கொசைன்களைக் காண்க. மேலும், கொடுக்கப்பட்ட இவ்விரு புள்ளிகள் வழியாகச் செல்லும் நேர்க்கோட்டின் துணை அலகு வெக்டர் சமன்பாடு , மற்றும் கார்டீசியன் சமன்பாடுகளைக் காண்க.
தீர்வு:
\(\vec{b}=5 \hat{i}+6 \hat{j}+7 \hat{k}\) மற்றும் \(\vec{a}=7 \hat{i}+9 \hat{j}+13 \hat{k}\) என்க.
இரண்டு புள்ளிகள் \(\vec{a}\) மற்றும் \(\vec{b}\) வழிச்செல்லும் நேர்க்கோட்டின் வெக்டர் சமன்பாட்டின் துணையலகு வடிவம்

இரண்டு புள்ளிகள் வழிச்செல்லும் கார்டீசியன் சமன்பாட்டின் நேர்க்கோட்டு வடிவம்

இது திசை விகிதங்கள் 2, 3, 6 உடைய நேர்க்கோடு ஆகையால் அதனுடைய திசைக் கொசைன்கள்

கேள்வி 5.
பின்வரும் கோடுகளுக்கு இடைப்பட்ட குறுங்கோணம் காண்க.

(iii) 2x = 3y = -z மற்றும் 6x = -y – 4z
தீர்வு:
(i) கொடுக்கப்பட்ட கோடுகளானது

θ என்பது கொடுக்கப்பட்ட கோடுகளுக்கு இடையேயான கோணம் என்க.

(ii) கொடுக்கப்பட்ட கோடுகளானது

(iii) கொடுக்கப்பட்ட கோடுகளானது 2x = 3y = -z மற்றும் 6x = -y – 4z
2x = 3y = -z ⇒ \(\frac{x-0}{\frac{1}{2}}=\frac{y-0}{-1}=\frac{z-0}{-1}\)

∴ \(\vec{b} \perp \vec{d}\)
∴ \(\vec{b}\) மற்றும் \(\vec{d}\) க்கு இடையேயான கோணம் \(\frac{\pi}{2}\)

கேள்வி 6.
A(7, 2, 1), B(6, 0, 3), மற்றும் C(4, 2, 4) என்ப ன ∆ABC -ன் உச்சிகள் எனில், ∠ABC-ஐக் காண்க.
தீர்வு:

AB -ன் திசை விகிதங்கள்
(6 – 7, 0 – 2, 3 – 1) = (-1, -2, 2)
[∵ (x₂ – x₁), (y₂ – y₁), (z₂ – z₁)]
மேலும் BC ன் திசை விகிதங்கள்
(4 – 6, 2 – 0, 4 – 3) = (- 2, 2, 1)
திசை விகிதங்களின் பெருக்கல் பலன்
(-1) (- 2) + (- 2) (2) + 2 (1)
= (2 – 4 + 2)
[∵ இரண்டு கோடுகள் ⊥^r எனில் திசை விகிதங்கள் d₁b₁ + d₂b₂ + d₃b₃ = 0]
= 4 – 4 = 0
எனவே AB ⊥ BC
∠ABC = \(\frac{\pi}{2}\)

கேள்வி 7.
(2, 1, 4) மற்றும் (a – 1, 4, -1) என்ற புள்ளிகளை இணைக்கும் நேர்க்கோடு (0, 2, -1) மற்றும் (5, 3, -2) , என்ற புள்ளிகளை இணைக்கும் நேர்க்கோட்டுக்கு இணை எனில் a மற்றும் b -ன் மதிப்புகளைக் காண்க.
தீர்வு:
(2, 1, 4) மற்றும் (a – 1, 4 – 1) என்ற இரு புள்ளிகள் வழிச் செல்லும் நேர்க்கோட்டின் கார்டீசியன் வடிவம்

அதே போல் இரண்டு புள்ளிகள் (0, 2, b – 1) மற்றும் (5, 3, -2) வழிச்செல்லும் நேர்க்கோட்டின் கார்டீசியன் வடிவம்

(1) மற்றும் (2)ன் திசைக் கொசைன்கள் சமம் எனில் அவை இணை
∴ கோடு (1)ன் திசை விகிதங்கள் a – 3, 3, -5 (3) கோடு (2)ன் திசை விகிதங்கள் -5, -1, b + 1 (4) திசை விகிதங்கள் சமம் எனில் (4) ஐ -3 ஆல் பெருக்க.
∴ (4) → +15, 3, -3b – 3
(3) → a – 3, 3, -5
∴ a – 3 = + 15 ⇒ a= 15 + 3 = 18 ⇒ a = 18
-3b – 3 = -5 ⇒ -3b = -5 + 3 = -2
⇒ b = \(\frac{-2}{-3}=\frac{2}{3}\)
∴ a = 18 மற்றும் b = \(\frac{2}{3}\)

கேள்வி 8.
\(\frac{x-5}{5 m+2}=\frac{2-y}{5}=\frac{1-z}{-1}\) மற்றும் x = \(\frac{2 y+1}{4 m}=\frac{1-z}{-3}\) என்ற நேர்க்கோடுகள் ஒன்றுக்கொன்று செங்குத்தானவை எனில், m-ன் மதிப்பைக் காண்க.
தீர்வு:
கொடுக்கப்பட்ட கோடுகள்


⇒ (5m + 2) 1 + 2m (-5) + 3(1) = 0
⇒ 5m + 2 – 10m + 3 = 0
⇒ 5 – 5m = 0
⇒ 5 = 5m
⇒ m = 1.

கேள்வி 9.
(2, 3, 4), (-1, 4, 5) மற்றும் (8, 1, 2) என்ற புள்ளிகள் ஒரு கோடமைப் புள்ளிகள் எனக் காட்டுக.
தீர்வு:
A (2, 3, 4), B (-1, 4, 5) மற்றும் C (8, 1, 2) புள்ளிகள் என்க.
A மற்றும் B யை இணைக்கும் கோட்டின் சமன்பாடு

புள்ளி C (8, 1, 2) வை கோடு (1)ல் பிரதியிட கிடைப்பது,
\(\frac{8-2}{-3}=\frac{1-3}{1}=\frac{2-4}{1}\) ⇒ -2 = -2 = -2
A மற்றும் B யை இணைக்கும் கோட்டை புள்ளி C பூர்த்தி செய்வதால், மூன்று புள்ளிகளும் ஒரு நேர்க்கோட்டு அமைவன.
எனவே . கொடுக்கப்பட்ட புள்ளிகள் ஒரு நேர்க்கோட்டு அமைவன.

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 6 வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள் Ex 6.5 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 6 வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள் Ex 6.5

கேள்வி 1.
(5, 2, 8) என்ற புள்ளி வழிச் செல்லும் \(\vec{r}=(\hat{i}+\hat{j}-\hat{k})+s(2 \hat{i}-2 \hat{j}+\hat{k})\) மற்றும் \(\vec{r}=(2 \hat{i}-\hat{j}-3 \hat{k})+t(\hat{i}+2 \hat{j}+2 \hat{k})\) ஆகிய கோடுகளுக்குச் செங்குத்தானதுமான நேர்க்கோட்டின் துணையலகு வெக்டர் சமன்பாடு மற்றும் கார்டீசியன் சமன்பாடுகளைக் காண்க.
தீர்வு:
கொடுக்கப்பட்ட புள்ளிகள் \(\vec{a}=5 \hat{i}+2 \hat{j}+8 \hat{k}\)
கொடுக்கப்பட்ட கோடுகள்

தேவையான கோடு \(\vec{b}\) மற்றும் \(\vec{d}\) செங்குத்து ஆதலால் அது \(\vec{b} \times \vec{d}\) க்கு இணை

∴ தேவையான நேர்க்கோட்டின் சமன்பாடு

நேர்க்கோடு மற்றும் செங்குத்து வழி செல்லும் நேர்க்கோட்டின் கார்டீசியன் சமன்பாடு (5, 2, 8).
\(\frac{x-x_{1}}{b_{1}}=\frac{y-y_{1}}{b_{2}}=\frac{z-z_{1}}{b_{3}}\)
\(\frac{x-5}{2}=\frac{y-2}{1}=\frac{z-8}{-2}\)

கேள்வி 2.
\(\vec{r}=(6 \hat{i}+\hat{j}+2 \hat{k})+s(\hat{i}+2 \hat{j}-3 \hat{k})\) மற்றும் \(\vec{r}=(3 \hat{i}+2 \hat{j}-2 \hat{k})+t(2 \hat{i}+4 \hat{j}-5 \hat{k})\) என்பன ஒரு தளம் அமையாக் கோடுகள் எனக்காட்டுக. மேலும், அக்கோடுகளுக்கு இடைப்பட் மீச்சிறு தூரத்தைக் காண்க.
தீர்வு:
கொடுக்கப்பட்ட கோடுகள்
\(\vec{r}=(6 \hat{i}+\hat{j}+2 \hat{k})+s(\hat{i}+2 \hat{j}-3 \hat{k})\)
\(\vec{a}=6 \hat{i}+\hat{j}+2 \hat{k}, \vec{b}=\hat{i}+2 \hat{j}-3 \hat{k}\)
மற்றும் \(\vec{r}=(3 \hat{i}+2 \hat{j}-2 \hat{k})+t(2 \hat{i}+4 \hat{j}-5 \hat{k})\)
\(\vec{c}=3 \hat{i}+2 \hat{j}-2 \hat{k}\), மற்றும் \(\vec{d}=2 \hat{i}+4 \hat{j}-5 \hat{k}\)
ஆதலால் \(\vec{b} \neq \vec{d}\), இணை இல்லை மற்றும் வெட்டுவதில்லை.
எனவே இரு கோடுகளும் ஒரு தளம் அமையா கோடுகள்.
ஒரு தளம் அமையா கோடுகளுக்கு இடைப்பட்ட குறைந்தபட்ச தூரம்.

கேள்வி 3.
\(\frac{x-1}{2}=\frac{y+1}{3}=\frac{z-1}{4}\) மற்று \(\frac{x-3}{1}=\frac{y-m}{2}\) = z என்ற கோடுகள் ஒரு புள்ளியில் வெட்டிக் கொள்ளும் எனில், m-ன் மதிப்பைக் காண்க.
தீர்வு:
கொடுக்கப்பட்ட கோடுகள்

கேள்வி 4.
\(\frac{x-3}{3}=\frac{y-3}{-1}\), z – 1 = 0 மற்றும் \(\frac{x-6}{2}=\frac{z-1}{3}\), y – 2 = 0 என்ற கோடுகள் ஒரு புள்ளியில் வெட்டிக் கொள்ளும் எனக்காட்டுக. மேலும், அவை வெட்டும் புள்ளியைக் காண்க.
தீர்வு:
கொடுக்கப்பட்ட கோடுகள் = \(\frac{x-3}{3}=\frac{y-3}{-1}\) (1)
மற்றும் z – 1 = 0 ⇒ z = 1
மற்றும் \(\frac{x-6}{2}=\frac{z-1}{3}\) …………. (2)
மற்றும் 2 = 0 ⇒ y = 2
y = 2 மற்றும் z = 1 என (1)ல் பிரதியிட கிடைப்பது
\(\frac{x-3}{3}=\frac{2-3}{-1}=\frac{-1}{-1}\) = 1 ⇒ x – 3 = 3 = x = 6 (6,2, 1) வெட்டுப்புள்ளி (6, 2, 1), (1) மற்றும் (2)ஐ பூர்த்தி செய்கிறதா என்பதை சோதிக்க.
(1) → \(\frac{6-6}{2}=\frac{1-1}{3}\) ⇒ 0 = 0
(2) → \(\frac{6-3}{3}=\frac{1-3}{-1}\) ⇒ -1 = 1
எனவே கொடுக்கப்பட்ட கோடுகள் ஒன்றையொன்று வெட்டுகின்றன மற்றும் வெட்டும் புள்ளி (6, 2, 1).

கேள்வி 5.
x +1 = 2y = -12z மற்றும் x = y + 2 = 6z – 6 என்ற கோடுகள் ஒரு தளம் அமையாக் கோடுகள் எனக் காட்டி, அவற்றிற்கு இடைப்பட்ட மீச்சிறு தூரத்தையும் காண்க.
தீர்வு:
கொடுக்கப்பட்ட கோடுகள் x + 1 = 2y = -12z


\((\vec{c}-\vec{a}) \cdot(\vec{b} \times \vec{a})=0\) ஆதலால் கொடுக்கப்பட்ட கோடுகள் ஒரு தளம் அமையா

ஒரு தளம் அமையா கோடுகளுக்கு இடைப்பட்ட குறைந்தபட்ச தூரம்

கேள்வி 6.
(-1, 2, 1) என்ற புள்ளி வழிச் செல்வதும் \(\vec{r}=(2 \hat{i}+3 \hat{j}-\hat{k})+t(\hat{i}-2 \hat{j}+\hat{k})\) என்ற நேர்க் கோட்டிற்கு இணையானதுமான நேர்க்கோட்டின் துணையலகு வெக்டர் சமன்பாட்டைக் காண்க. மேலும் இக்கோடுகளுக்கு இடைப்பட்ட மீச்சிறு தூரத்தையும் காண்க.
தீர்வு:
கொடுக்கப்பட்ட புள்ளி \(\vec{a}=-\hat{i}+2 \hat{j}+\hat{k}\)
மற்றும் இணை வெக்டர் \(\vec{b}=\hat{i}-2 \hat{j}+\hat{k}\)
∴ \(\vec{a}\) வழிச் செல்லும் \(\vec{b}\) க்கு இணையான நேர்க்கோட்டின் வெக்டர் சமன்பாட்டின் துணையலகு வடிவம்

∴ இணைக்கோடுகளுக்கு இடையேயான தூரம்
d = \(\frac{|(\vec{c}-\vec{a}) \times \vec{b}|}{|\vec{b}|}=\frac{\sqrt{83}}{\sqrt{6}}\) அலகுகள்

கேள்வி 7.
(5, 4, 2) என்ற புள்ளியிலிருந்து \(\frac{x+1}{2}=\frac{y-3}{3}=\frac{z-1}{-1}\) என்ற நேர்க்கோட்டிற்கு வரையப்படும் செங்குத்துக் கோட்டின் அடியைக் காண்க. மேலும், இச்செங்குத்துக் கோட்டின் சமன்பாட்டைக் காண்க.
தீர்வு:
கொடுக்கப்பட்ட கோட்டின் சமன்பாடு
\(\frac{x+1}{2}=\frac{y-3}{3}=\frac{z-1}{-1}\) = A என்பது (-1, 3, 1)
மற்றும் \(\vec{b}=2 \hat{i}+3 \hat{j}-\hat{k}\)
\(\frac{x+1}{2}=\frac{y-3}{3}=\frac{z-1}{-1}\) = t என்க

D யிலிருந்து நேர்கோட்டிற்கு வரையப்படும் செங்குத்து கோட்டின் அடி F எனில் அதனுடைய வடிவம்
(2t – 1, 3t + 3, -t+ 1) …………(1)
⇒ \(\overrightarrow{\mathrm{OF}}=(2 t-1) \hat{i}+(3 t+3) \hat{j}+(-t+1) \hat{k}\)
கொடுக்கப்பட்ட புள்ளி D(5, 4, 2)
⇒ \(\vec{OD}=5 \hat{i}+4 \hat{j}+2 \hat{k}\)
∴ \(\vec{DF}=\vec{OF}-\vec{OD}\)
= \((2 t-1-5) \hat{i}+(3 t+3-4) \hat{j}+(-t+1-2) \hat{k}\) …………….. (2)
\(\vec{b} \perp \vec{DF}\) ஆதலால் நம்மிடம் \(\vec{b} \cdot \vec{DF}\) = 0
⇒2(2t – 6) +3(3t – 1) – 1 (-t – 1) = 0
⇒ 4t 12 + 9t – 3 + t + 1 = 0
⇒ 14t – 14 = 0
⇒ 14t = 14
⇒ t = 1
(1)லிருந்து F ஆனது (2(1) – 1, 3(1) + 3, –1 + 1 )
= (1, 6, 0)
∴ செங்குத்தின் அடிப்பகுதி (1, 6, 0)
∴ செங்குத்து DF ன் சமன்பாடு என்பது (5, 4, 2) மற்றும் (1, 6, 0) புள்ளிகள் வழிச்செல்லும் கோட்டின் சமன்பாடு. அதனுடைய கார்டீசியன் சமன்பாடு என்பது

தேவையான செங்குத்து கோட்டின் சமன்பாடாகும்.

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 6 வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள் Ex 6.1 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 6 வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள் Ex 6.1

கேள்வி 1.
ஒரு வட்டத்தின் மையத்திலிருந்து அவ் வட்டத்தின் ஒரு நாணின் மையப்புள்ளிக்கு வரையப்படும் கோடு அந்நாணிற்கு செங்குத்தாகும் என வெக்டர் முறையில் நிறுவுக.
தீர்வு :

வட்டத்தின் மீதுள்ள புள்ளிகள் A மற்றும் Bயின் நிலை வெக்டர் முறையே \(\vec{a}\) மற்றும் \(\vec{b}\) என்க. வட்டத்தின் மையம் O ஆதலால்
|\(\overrightarrow{\mathrm{OA}}\)| = |\(\overrightarrow{\mathrm{OB}}\)| ⇒ |\(\vec{a}\)| = |\(\vec{b}\)|
மேலும், ABன் மையப்புள்ளி D.

= \(\) = 0
⇒ \(\overrightarrow{\mathrm{OD}}\) . \(\overrightarrow{\mathrm{AB}}\) = 0 ⇒ \(\overrightarrow{\mathrm{OD}}\) ⊥ \(\overrightarrow{\mathrm{AB}}\)
ஆகையால், ஒரு வட்டத்தின் மையத்திலிருந்து அவ்வட்டத்தின் ஒரு நாணின் மையப்புள்ளிக்கு வரையப்படும் கோடு அந்நாணிற்கு
செங்குத்தாகும்.

கேள்வி 2.
ஓர் இருசமப்பக்க முக்கோணத்தின் அடிப் பக்கத்திற்கு வரையப்படும் நடுக்கோடு , அப்பக்கத்திற்கு செங்குத்தாகும் என வெக்டர்
முறையில் நிறுவுக.
தீர்வு:

AB = AC உடன் ABC ஒரு இருசமபக்க முக்கோணம் மற்றும் D என்பது BC யின் நடுப்புள்ளி.
A ஆதியாகக் கொண்டு B மற்றும் C யின் நிலை
வெக்டர் \(\vec{b}\) மற்றும் \(\vec{c}\) என்க.


ஆகையால் △ABC-ல் நடுக்கோடு AD அடிப்பக்கம் BC க்கு செங்குத்து △ABC.

கேள்வி 3.
வெக்டர் முறையில், ஓர் அரைவட்டத்தில் அமையும் கோணம் ஒரு செங்கோணம் என நிறுவுக.
தீர்வு :

O என்பது அரைவட்டத்தின் மையப்புள்ளி மற்றும் AA’ என்பது விட்டம் என்க. அரைவட்டத்தின் சுற்றளவிலுள்ள ஏதேனும் ஒரு புள்ளி P என்க. O வை ஆதியாக கொண்டு A மற்றும் P யின் நிலை வெக்டர் முறையே \(\vec{a}\) மற்றும் \(\vec{r}\) என்க.
பிறகு, A’ன் நிலை வெக்டர் என்பது – \(\vec{a}\) இங்கு \(\overrightarrow{\mathrm{AP}}\) = (P யின் நிலை வெக்டர்) – (Aயின் நிலை வெக்டர்) = \(\vec{r}\) – \(\vec{a}\)
மற்றும் \(\overrightarrow{\mathrm{AP}}\) = (P யின் நிலை வெக்டர்) – (A யின் நிலை வெக்டர்)

ஆகையால் அரைவட்டத்தின் அமையும் ஒரு கோணம் செங்கோணம் ஆகும்.

கேள்வி 4.
ஒரு சாய்சதுரத்தின் மூலை விட்டங்கள் ஒன்றையொன்று செங்குத்தாக இருசமக்கூறிடும் என வெக்டர் முறையில் நிறுவுக.
தீர்வு:

OACB என்பது ஒரு சாய்சதுரம் என்க. O வை ஆதியாகக் கொண்டு, A மற்றும் B யின் நிலை வெக்டர் முறையே \(\vec{a}\) மற்றும் \(\vec{b}\) என்க.

ஆகையால் C யின் நிலை வெக்டர் \(\vec{a}\) + \(\vec{b}\).
∴ OC ன் நடுப்புள்ளியின் நிலை வெக்டர் என்பது \(\frac{\vec{a}+\vec{b}}{2}\)
அதை போல AB யின் நடுப்புள்ளியின் நிலைவெக்டர் என்பது \(\frac{\vec{a}+\vec{b}}{2}\)
ஆகையால் OC மற்றும் ABயின் நடுப்புள்ளி ஒன்றேயாகும்.

ஆகையால் ஒரு சாய்சதுரத்தின் மூலை விட்டங்கள் ஒன்றையொன்று செங்குத்தாக இரு சமக்கூறிடும்.

Question 5.
ஓர் இணைகரத்தின் மூலை விட்டங்கள் சமம் எனில், அந்த இணைகரம் ஒரு செவ்வகமாகும் என வெக்டர் முறையில் நிறுவுக.
தீர்வு:

மூலைவிட்டங்கள் AC மற்றும் BD சமம் எனுமாறு இணைகரம் ABCD என்க. A யை ஆதி என்க. B மற்றும் Dன் நிலை வெக்டர் \(\vec{b}\) மற்றும் \(\vec{a}\) என்க.
பிறகு \(\overrightarrow{\mathrm{AB}}\) = \(\vec{b}\) மற்றும் \(\overrightarrow{\mathrm{AD}}\) = \(\vec{d}\).
△ABCயில் வெக்டர்களின் கூடுதலுக்கான முக்கோண விதியை பயன்படுத்த கிடைப்பது

கேள்வி 6.
வெக்டர் முறையில், AC மற்றும் BD ஆகியவற்றை மூலை விட்டங்களாகக் கொண்ட நாற்கரம் ABCD-ன் பரப்பு \(\frac{1}{2}|\overrightarrow{\mathbf{A C}} \times \overrightarrow{\mathbf{B D}}|\) என நிறுவுக.
தீர்வு :

நாற்கரம் ABCDயின் வெக்டர் பரப்பு = △ABCயின் வெக்டர் பரப்பு + △ACDயின் வெக்டர் பரப்பு

∴ நாற்கரம் ABCDயின் பரப்பு
= \(\frac{1}{2}|\overrightarrow{\mathrm{AC}} \times \overrightarrow{\mathrm{BD}}|\)

கேள்வி 7.
ஒரே அடிப்பக்கத்தின் மீதமைந்த இரு இணைகோடுகளுக்கு இடைப்பட்ட இணை கரங்களின் பரப்பளவுகள் சமமானவை என
வெக்டர் முறையில் நிறுவுக.
தீர்வு:

ABCD என்பது கொடுக்கப்பட்ட இணைகரம் மற்றும் அதே அடிப்பக்கம் AB மற்றும் அதே இணைகோடுகள் AB மற்றும் DCக்கு இடையே அமைந்த புதிய இணைகரம் ABC’ D’.
∴ இணைகரம் ABCD யின் வெக்டர் பரப்பு

= இணைகரம் ABC’D’யின் பரப்பு
∴ இணைகரம் ABCDயின் பரப்பு = இணைகரம் ABC’D’ ன் வெக்டர் பரப்பு
ஆகையால் ஒரே அடிப்பக்கத்தின் மீதமைந்த இரு இணைகோடுகளுக்கு இடைப்பட்ட இணைகரங்களின் பரப்பளவுகள் சமமானவை.

கேள்வி 8.
△ABC-ன் நடுக்கோட்டு மையம் G எனில், வெக்டர் முறையில் நிறுவுக. (△GAB-ன் பரப்பு) = (△GBC-ன் பரப்பு) = (△GCA-ன் பரப்பு ) = – \(\frac{1}{3}\)(△ABC-ன் பரப்பு) என நிறுவுக.
தீர்வு :

△ABCயின் உச்சி புள்ளிகளின் நிலை
வெக்டர்கள் முறையே \(\vec{a}\), \(\vec{b}\) மற்றும் \(\vec{c}\) என்க.
△ABCயின் நடுக்கோட்டு மையம் G ஆதலால்

[ ∵ குறுக்கும் பெருக்கல் பங்கீட்டுடையது]



(1), (2) மற்றும் (3) லிருந்து,
△GABயின் = △GAC யின் பரப்பு = △GBC யின் பரப்பு

எனவே நிரூபிக்கப்பட்டது.

கேள்வி 9.
வெக்டர் முறையில் cos(α – β) = cos α cos β + sin α sin β என நிறுவுக.
தீர்வு :

\(\hat{a}\) = \(\overrightarrow{\mathrm{OA}}\) மற்றும் \(\hat{b}\) = \(\overrightarrow{\mathrm{OB}}\) என்பன அலகு வெக்டர்கள் என்க மற்றும் அவைகள் கோணங்கள் α, β, நவை x-அச்சின் மிகையுடன் ஏற்படுத்துகின்றன. AL மற்றும் BM ⊥^r லிருந்து x-அச்சு எனுமாறு வரைக.


[△விதியை பயன்படுத்தி கூட்டு]

(3) மற்றும் (4)லிருந்து,
cos (α – β) = cos α cos β + sin α sin β.

கேள்வி 10.
sin(α + β) = sin α cos β + cos α sin β என வெக்டர் முறையில் நிறுவுக.
தீர்வு :

\(\hat{a}\) = \(\overrightarrow{\mathrm{OA}}\) மற்றும் \(\hat{b}\) = \(\overrightarrow{\mathrm{OB}}\) என்பன அலகு வெக்டர்கள் என்க மற்றும் அவைகள் கோணங்கள் α, βவை x-அச்சின் மிகையுடன் ஏற்படுத்துகின்றன. AL மற்றும் BM ⊥^r லிருந்து x-அச்சு எனுமாறு வரைக.
AL மற்றும் BM ⊥^r லிருந்து x,க்கு எனுமாறு வரைக.
எனவே |\(\overrightarrow{\mathrm{OL}}\)| = |\(\overrightarrow{\mathrm{OA}}\)|cos α
⇒ \(\overrightarrow{\mathrm{OL}}\) =|\(\overrightarrow{\mathrm{OL}}\)|\(\hat{i}\) = cosα\(\hat{i}\)


(3) மற்றும் (4) ஐ பயன்படுத்த,
sin(α + β) = sin α cos β + cos α sin β

கேள்வி 11.
ஒரு துகள் (1, 2, 3) எனும் புள்ளியிலிருந்து (5, 4, 1) எனும் புள்ளிக்கு 8\(\hat{\boldsymbol{i}}\) + 2\(\hat{\boldsymbol{j}}\) – 6\(\hat{\boldsymbol{k}}\) மற்றும் 6\(\hat{\boldsymbol{i}}\) + 2\(\hat{\boldsymbol{j}}\) – 2\(\hat{\boldsymbol{k}}\) என்ற மாறாத விசைகளின் செயல்பாட்டினால் நகர்த்தப்பட்டால், அவ்விசைகள் செய்த மொத்த வேலையைக் காண்க.
தீர்வு:
\(\overrightarrow{\mathrm{F}}\) மற்றும் \(\overrightarrow{\mathrm{F}_{2}}\), என்பன விசைகள் மற்றும் \(\vec{d}\) என்பது இடப்பெயர்ச்சி வெக்டர் என்க.
∴ விளைவு விசை \(\overrightarrow{\mathrm{F}}\) = \(\overrightarrow{\mathrm{F}}_{1}\) + \(\overrightarrow{\mathrm{F}}_{2}\)

மற்றும் \(\vec{d}\) = இடம் பெயர்ந்த புள்ளி – புள்ளியிலிருந்து இடப்பெயர்வு

செய்த வேலை (w) = \(\overrightarrow{\mathrm{F}}\).\(\overrightarrow{\mathrm{d}}\)

= 56 + 8 + 16
= 80 அலகுகள்

கேள்வி 12.
முறையே 5\(\sqrt{2}\) மற்றும் 10\(\sqrt{2}\) அலகுகள் எண்ண ளவு கொண்ட 3\(\hat{\boldsymbol{i}}\) + 4\(\hat{\boldsymbol{j}}\) + 5\(\hat{\boldsymbol{k}}\) மற்றும் 10\(\hat{\boldsymbol{i}}\) + 6\(\hat{\boldsymbol{j}}\) – 8\(\hat{\boldsymbol{k}}\) என்ற வெக்டர்களின் திசைகளில் அமைந்த விசைகள், ஒரு துகளை 4\(\hat{\boldsymbol{i}}\) – 3\(\hat{\boldsymbol{j}}\) – 2\(\hat{\boldsymbol{k}}\) என்ற வெக்டரை நிலைவெக்டராகக் கொண்ட புள்ளியிலிருந்து 6\(\hat{\boldsymbol{i}}\) + \(\hat{\boldsymbol{j}}\) – 3\(\hat{\boldsymbol{k}}\) என்ற வெக்டரை நிலைவெக்டராகக் கொண்ட புள்ளிக்கு நகர்த்துகிறது எனில், அவ்விசைகள் செய்த வேலையைக் காண்க.
தீர்வு:
\(\overrightarrow{\mathrm{F}_{1}}\) மற்றும் \(\overrightarrow{\mathrm{F}_{2}}\), கொடுக்கப்பட்ட இரு விசைகள் என்க.

கேள்வி 13.
3\(\hat{\boldsymbol{i}}\) + 4\(\hat{\boldsymbol{j}}\) – 5\(\hat{\boldsymbol{k}}\) என்னும் விசை 4\(\hat{\boldsymbol{i}}\) + 2\(\hat{\boldsymbol{j}}\) – 3\(\hat{\boldsymbol{k}}\) என்ற வெக்டரை நிலைவெக்டராகக் கொண்ட புள்ளி வழியாகக் செயல்படுகிறது எனில், 2\(\hat{\boldsymbol{i}}\) – 3\(\hat{\boldsymbol{j}}\) + 4\(\hat{\boldsymbol{k}}\) என்ற வெக்டரை நிலைவெக்டராகக் கொண்ட புள்ளியைப் பொறுத்து அவ்விசையின் முறுக்குத் திறனின் எண்ணளவு மற்றும் திசைக்கொசைன்களைக் காண்க.
தீர்வு:
கொடுக்கப்பட்ட \(\overrightarrow{\mathrm{F}}\) = 3\(\hat{\boldsymbol{i}}\) + 4\(\hat{\boldsymbol{j}}\) – 5\(\hat{\boldsymbol{k}}\)

∴ முறுக்குத் திறனின் எண்ணளவு

ஆகையால், திசைக் கொசைன்கள்

கேள்வி 14.
8\(\hat{\boldsymbol{i}}\) – 6\(\hat{\boldsymbol{j}}\) – 4\(\hat{\boldsymbol{k}}\) என்ற வெக்டரை நிலை வெக்டராகக் கொண்ட புள்ளியில் செயல்படும் -3\(\hat{\boldsymbol{i}}\) + 6\(\hat{\boldsymbol{j}}\) – 3\(\hat{\boldsymbol{k}}\), 4\(\hat{\boldsymbol{i}}\) – 10\(\hat{\boldsymbol{j}}\) + 12\(\hat{\boldsymbol{k}}\) மற்றும் 4\(\hat{\boldsymbol{i}}\) + 7\(\hat{\boldsymbol{j}}\) விசைகளின் திருப்புத் திறனை 18\(\hat{\boldsymbol{i}}\) + 3\(\hat{\boldsymbol{j}}\) – 9\(\hat{\boldsymbol{k}}\) என்ற வெக்டரை நிலை வெக்டராகக் கொண்ட புள்ளியைப் பொறுத்துக் காண்க.
தீர்வு:
விளைவு விசை \(\overrightarrow{\mathrm{F}}\) = \(\overrightarrow{\mathrm{F}}_{1}\) + \(\overrightarrow{\mathrm{F}}_{2}\) + \(\overrightarrow{\mathrm{F}}_{3}\)
\(\overrightarrow{\mathrm{F}}\) = (-3\(\hat{\boldsymbol{i}}\)+ 6\(\hat{\boldsymbol{j}}\) – 3\(\hat{\boldsymbol{k}}\)) + (4\(\hat{\boldsymbol{i}}\) – 10\(\hat{\boldsymbol{j}}\) + 12\(\hat{\boldsymbol{k}}\)) + (4\(\hat{\boldsymbol{i}}\) + 7\(\hat{\boldsymbol{j}}\))
= 5\(\hat{\boldsymbol{i}}\) + 3\(\hat{\boldsymbol{j}}\) + 9\(\hat{\boldsymbol{k}}\)
\(\overrightarrow{\mathrm{r}}\) = (விசை செயல்படுகிற புள்ளி) – (புள்ளியை பொறுத்து செயல்படுகிற விசை)
= (8\(\hat{\boldsymbol{i}}\) – 6\(\hat{\boldsymbol{j}}\) – 4\(\hat{\boldsymbol{k}}\)) – (18\(\hat{\boldsymbol{i}}\) + 3\(\hat{\boldsymbol{j}}\) – 9\(\hat{\boldsymbol{k}}\))
= -10\(\hat{\boldsymbol{i}}\) – 9\(\hat{\boldsymbol{j}}\) + 5\(\hat{\boldsymbol{k}}\)
திருப்புத்திறன் (\(\overrightarrow{\mathrm{t}}\)) = \(\overrightarrow{\mathrm{r}}\) × \(\overrightarrow{\mathrm{F}}\)

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 6 வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள் Ex 6.6 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 6 வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள் Ex 6.6

கேள்வி 1.
ஆதிப்புள்ளியில் இருந்து 7 அலகுகள் தொலைவில் உள்ளதும், செங்குத்தின் திசை விகிதங்கள் 3, -4, 5 கொண்டதுமான தளத்தின் துணையலகு வெக்டர், மற்றும் கார்டீசியன் சமன்பாடுகளைக் காண்க.
தீர்வு:
கொடுக்கப்பட்ட p = 7

[∵ 3, -4, 5] திசைவிகிதங்கள் ஆதிப்புள்ளியிலிருந்து தளத்திற்கு உள்ள தூரம் p மற்றும் தளத்திற்குச் செங்குத்தான ஓரலகு வெக்டர் \(\hat{d}\) எனில், தளத்திற்கு சமன்பாடு \(\vec{r} \cdot \hat{d}=p\).
தேவையான தளத்தின் சமன்பாடு
\(r \cdot\left(\frac{3 \hat{i}-4 \hat{j}+5 \hat{k}}{5 \sqrt{2}}\right)=7\)

கேள்வி 2.
12x + 3y – 4z = 65 என்ற தளத்தின் செங்குத்தின் திசைக் கொசைன்களைக் காண்க. மேலும், தளத்தின் துணைணையலகு அல்லாத வெக்டர் சமன்பாடு மற்றும் ஆதியில் இருந்து தளத்திற்கு வரையப்படும் செங்குத்தின் நீளம் காண்க.
தீர்வு:
கொடுக்கப்பட்ட தளத்தின் கார்டீசியன் சமன்பாடு
12x + 3y – 4z = 65.
அதனுடைய வெக்டர் சமன்பாட்டின் துணையலகு வடிவம்

எனவே தளம் 12x + 3y – 4z = 65 -ன் செங்குத்தின்
திசைக் கொசைன்கள் \(\frac{12}{13}, \frac{3}{13}, \frac{-4}{13}\)
மேலும் தளத்தின் துணையலகு இல்லாத வெக்டர் வடிவ சமன்பாடு
\(\vec{r} \cdot\left(\frac{12 \hat{i}+3 \hat{j}-4 \hat{k}}{13}\right)=\frac{65}{13}\) [(1)லிருந்து][13–ஆல் வகுக்க]
⇒ \(\vec{r} \cdot \hat{d}=p \Rightarrow p=\frac{65}{13}=5\)

கேள்வி 3.
\(2 \hat{i}+6 \hat{j}+3 \hat{k}\) என்ற நிலை வெக்டரை கொண்ட புள்ளி வழியாகச் செல்வதும் \(\hat{i}+3 \hat{j}+5 \hat{k}\) என்ற வெக்டருக்குச் செங்குத்தானதுமான தளத்தின் வெக்டர் மற்றும் கார்டீசியன் சமன்பாடுகளைக் காண்க.
தீர்வு:
கொடுக்கப்பட்ட \(\vec{a}=2 \hat{i}+6 \hat{j}+3 \hat{k}\)
\(\vec{n}=\hat{i}+3 \hat{j}+5 \hat{k}\)
புள்ளி \((\vec{a})\) வழிச் செல்லும் மற்றும் வெக்டர் \((\vec{n})\) க்கு செங்குத்தான தளத்தின் வெக்டர் வடிவ சமன்பாடு
\(\vec{r} \cdot \vec{n}=\vec{a} \cdot \vec{n}\)
= \(\vec{r} \cdot(\hat{i}+3 \hat{j}+5 \hat{k})\)
= \((2 \hat{i}+6 \hat{j}+3 \hat{k}) \cdot(\hat{i}+3 \hat{j}+5 \hat{k})\) = 2 + 18 + 15
⇒ \(\vec{r} \cdot(\hat{i}+3 \hat{j}+5 \hat{k})\) = 35
அதனுடைய கார்டீசியன்
a(x – x₁) + b(y – y₁) + c(z – z₁) = 0
1(x – 2) + 3(1 – 6) + 5(z – 3) = 0
[∵ (x₁, y₁, z₁) = (2, 6, 3) மற்றும் a, b, c = 1, 3, 5]
⇒ – 2 + 3y – 18 + 5z – 15 = 0
⇒ x + 3y + 5z – 35 = 0
⇒ x + 3y + 5z = 35

கேள்வி 4.
(-1,1,2) என்ற புள்ளி வழியாகச் செல்வதும் ஆய அச்சுகளுடன் சமகோணத்தை ஏற்படுத்தும் எண்ணளவு 3\(\sqrt{3}\) கொண்ட செங்கோட்டைக் கொண்டதுமான தளத்தின் வெக்டர் மற்றும் கார்டீசியன் சமன்பாடுகளைக் காண்க.
தீர்வு:
தளம்,\(\vec{a}=\hat{i}+\hat{j}+2 \hat{k}\) என்ற புள்ளி வழிச் செல்கிறது.
கொடுக்கப்பட்ட \(|\vec{n}|=3 \sqrt{3}\) மற்றும் α என்பது செங்குத்து ஆய அச்சுகளுடன் ஏற்படுத்தும் கோணம் என்க.
∴ cos²α + cos²α + cos²α = 1 ⇒ 3cos²α = 1
⇒ cos²α = \(\frac{1}{3}\) ⇒ cosα = \(\frac{1}{\sqrt{3}}\)
∴ \(\vec{n}=3 \sqrt{3}\left(\frac{1}{\sqrt{3}} \hat{i}+\frac{1}{\sqrt{3}} \hat{j}+\frac{1}{\sqrt{3}} \hat{k}\right)=3 \hat{i}+3 \hat{j}+3 \hat{k}\)
∴ தேவையான தளத்தின் சமன்பாடானது

என்பது தேவையான தளத்தின் சமன்பாடு

கேள்வி 5.
\(\vec{r} \cdot(6 \hat{i}+4 \hat{j}-3 \hat{k})\) = 12 என்ற தளம் ஆய அச்சுகளுடன் ஏற்படுத்தும் வெட்டுத் துண்டுகளைக் காண்க.
தீர்வு:
தளத்தின் சமன்பாட்டிற்கான வெக்டர் வடிவம் என்பது
\(\vec{r} \cdot(6 \hat{i}+4 \hat{j}-3 \hat{k})\) = 1
\(\vec{r}=x \hat{i}+y \hat{j}+z \hat{k}\) என்க
⇒ \((x \hat{i}+y \hat{j}+z \hat{k}) \cdot(6 \hat{i}+4 \hat{j}-3 \hat{k})\) = 12
⇒ 6x + 4y – 3z = 0
12 ஆல் வகுக்க கிடைப்பது \(\frac{6 x}{12}+\frac{4 y}{12}-\frac{3 z}{12}\) = 1
[∵\(\frac{x}{a}+\frac{y}{b}+\frac{z}{c}\) = 1 என்பது தளத்தின் வெட்டுத்துண்டு வடிவச் சமன்பாடு]
⇒ \(\frac{x}{2}+\frac{y}{3}+\frac{z}{-4}\) = 1
∴ தளத்தின் x- வெட்டுத்துண்டு 2,yவெட்டுத்துண்டு 3 மற்றும் z- வெட்டுத்துண்டு -4.

கேள்வி 6.
ஒரு தளம் ஆய அச்சுக்களை ளை முறையே A,B,C என்ற புள்ளிகளில் வெட்டுவதால் உருவாகும் முக்கோணம் ABC-ன் மை மையக்கோட்டுச் சந்தி (u, v, w) எனில் தளத்தின் சமன்பாட்டைக் காண்க.
தீர்வு:
தளம் ஆய அச்சுக்களுடன் ஏற்படுத்தும் வெட்டுத்
துண்டுகள் முறையே a, b, c என்க.
∴ தளத்தின் வெட்டுத்துண்டு வடிவச் சமன்பாடு

கொடுக்கப்பட்ட ∆ABC யின் மையக்கோட்டுச் சந்தி (u, v, w)
∴ (u, v, w) = \(\left(\frac{a+0+0}{3}, \frac{0+b+0}{3}, \frac{0+0+c}{3}\right)\)
⇒ (u, v, w) = \(\left(\frac{a}{3}, \frac{b}{3}, \frac{c}{3}\right)\)
ஒத்த ஆயத் தொலைவுகளை சமப்படுத்த கிடைப்பது
⇒ u = \(\frac{a}{3}\) ⇒ a = 3u
v = \(\frac{b}{3}\) ⇒ b = 3v
w = \(\frac{c}{3}\) ⇒ c = 3w
∴ (1) லிருந்து
\(\frac{x}{3 u}+\frac{y}{3 v}+\frac{z}{3 w}=1 \Rightarrow \quad \frac{x}{u}+\frac{y}{v}+\frac{z}{w}=3\)
என்பது தேவையான தளத்தின் சமன்பாடாகும்.

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 5 இரு பரிமாண பகுமுறை வடிவியல் – II Ex 5.6 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 5 இரு பரிமாண பகுமுறை வடிவியல் – II Ex 5.6

I. கொடுக்கப்பட்ட நான்கு விடைகளிலிருந்து சரியான அல்லது மிகப் பொருத்தமான
விடையைத் தேர்ந்தெடுக்க.

கேள்வி 1.
(1, 5) மற்றும் (4,1) என்ற புள்ளிகள் வழிச் செல்வதும் -அச்சைத் தொட்டுச் செல்வதுமான வட்டத்தின் சமன்பாடு x² + y² – 5x – 6y + 9 + λ (4x + 3y = 19) = 0 எனில், λ – ன் மதிப்பு
(1) 0, –\(\frac{40}{9}\)
(2) 0
(3) \(\frac{40}{9}\)
(4) –\(\frac{40}{9}\)
விடை:
(1) 0, –\(\frac{40}{9}\)

கேள்வி 2.
செவ்வகல நீளம் 8 அலகுகள் மற்றும் துணையச்சின் நீளம் குவியங்களுக்கிடையே உள்ள தூரத்தில் பாதி உள்ள அதிபரவளையத்தின் மையத்தொலைத் தகவு
(1) \(\frac{4}{3}\)
(2) \(\frac{4}{\sqrt{3}}\)
(3) \(\frac{2}{\sqrt{3}}\)
(4) \(\frac{40}{9}\)
விடை:
(3) \(\frac{2}{\sqrt{3}}\)
குறிப்பு:

கேள்வி 3.
வட்டம் x² + y² = 4x + 8y + 5 நேர்க்கோடு 3x – 4y = m-ஐ இரு வெவ்வேறு புள்ளிகளில் வெட்டுகின்றது எனில்
(1) 15 < m < 65
(2) 35 < m < 85
(3) -85 < m < -35
(4) -35 < m < 15
விடை:
(4) -35 < m < 15

கேள்வி 4.
x- அச்சை (1,0) என்ற புள்ளியில் தட்டுச் செல்வதும் (2,3) என்ற புள்ளிவழிச் செல்வதுமான வட்டத்தின் விட்டம்
(1) \(\frac{6}{5}\)
(2) \(\frac{5}{3}\)
(3) \(\frac{10}{3}\)
(4) \(\frac{3}{5}\)
விடை:
(3) \(\frac{10}{3}\)
குறிப்பு:
வட்டம் X- அச்சு (1, 0), என்ற புள்ளியில் தொட்டுச் செல்வதால் அதனுடைய சமன்பாடு (x – 1)² + (y – a)² = a²
இது (2, 3) வழி செல்கிறது
⇒ (2 – 1)² + (3 – a)² = a²
⇒ 1 + 9 + a² – 6a = a²
⇒ 10 – 6a = 0 ⇒ 6a = 10 ⇒ a = \(\frac{10}{6}\)
∴ a = \(\frac{5}{3}\)
∴ ஆரம் = \(\frac{5}{3}\)
⇒ விட்டம் = \(\frac{10}{3}\)

கேள்வி 5.
3x² + by² + 4bx – 6by + b² = 0 என்ற வட்டத்தின் ஆரம்
(1) 1
(2) 3
(3) \(\sqrt{10}\)
(4) \(\sqrt{11}\)
விடை:
(3) \(\sqrt{10}\)
குறிப்பு:
x² – ன் கெழு =y -ன் கெழு ⇒ b = 3
சமன்பாடு 3x² + 3y² + 12x – 18y + 9 = 0
÷3, x² + y² + 4x – 6y + 3 = 0
-g = -2, -f= 3, மற்றும் c = 3
r = \(\sqrt{g^{2}+f^{2}-c}\) = \(\sqrt{4+9-3}\)
= \(\sqrt{13-3}\) = \(\sqrt{10}\)

கேள்வி 6.
x² – 8x – 12 = 0 மற்றும் y² – 14y + 45 = 0 என்ற கோடுகளால் அடைபடும் சதுரத்தின் உள்ளே வரையப்படும் மிகப்பெரிய வட்டத்தின் ஆரம்
(1) (4, 7)
(2) (7, 4)
(3) (9, 4)
(4) (4, 9)
விடை:
(1) (4, 7)
குறிப்பு : x² – 8x + 12 = 0 தீர்க்க கிடைப்பது
(x – 6)(x – 2) = 0
ஆகையால் y² – 14y + 45 = 0, கிடைப்பது (y – 9)(y – 5) = 0.
ஆகையால் விட்டத்தின் முனைபுள்ளிகள் (6, 9) மற்றும் (2, 5)
∴ (6, 9) மற்றும் (2, 5)ன் மையப்புள்ளி
= \(\left(\frac{6+2}{2}, \frac{9+5}{2}\right)\) = (4, 7)

கேள்வி 7.
நேர்க்கோடு 2x + 4y = 3 -க்கு இணையாக x² + y² – 2x 2y + 1 = 0 என்ற வட்டத்தின் செங்கோட்டுச் சமன்பாடு
(1) x + 2y = 3
(2) x + 2y + 3 = 0
(3) 2x + 4y + 3 = 0
(4) x – 2y + 3 = 0
விடை:
(1) x + 2y = 3
குறிப்பு:
x² + y² – 2x – 2y + 1 = 0
2g = -2, 2f = -2 ⇒ -g = 1 மற்றும் –f = 1
∴ மையம் என்பது (1, 1)
ஒரு வட்டத்திற்கான செங்கோட்டிற்கு இணையான கோடு (1, 1) வழிச் செல்கிறது. அதன் சமன்பாடு 2x + 4y + k = 0
(1, 1)ஐ பிரதியிட, 2(1) + 4(1) + k = 0 ⇒ k = -6
2x + 4y – 6 = 0 ⇒ x + 2y = 3

கேள்வி 8.
P(x, y) என்ற புள்ளி குவியங்கள் F₁(3, 0) மற்றும் F₂(-3, 0) கொண்ட கூம்பு வளைவு 16x² + 25y² = 400 – ன் மீதுள்ள புள்ளி எனில் PF¹ + PF² -ன் மதிப்பு (1) 8
(2) 6
(3) 10
(4) 12
விடை:
(3) 10
குறிப்பு:
16x² + 25x² = 400
⇒ \(\frac{x^{2}}{25}\) + \(\frac{y^{2}}{16}\) = 1
⇒ a² = 25
⇒ a = 5
குவி பண்பின்படி, PF₁ + PF₂ = 2a = 2(5) = 10

கேள்வி 9.
x + y = 6 மற்றும் x + 2y = 4 என்ற நேர்க்கோடுகளை விட்டங்களாகக் கொண்டு (6,2) புள்ளிவழிச் செல்லும் வட்டத்தின் ஆரம்
(1) 10
(2) \(2 \sqrt{5}\)
(3) 6
(4) 4
விடை:
(2) \(2 \sqrt{5}\)
குறிப்பு:
மையம் என்பது விட்டங்களின் வெட்டு புள்ளி

∴ x – 2 = 6 ⇒ x = 8 ⇒ மையம் (8,-2)
r = (8, -2) மற்றும் (6, 2) க்கு இடையேயான தூரம்

கேள்வி 10.
\(\frac{x^{2}}{a^{2}}\) – \(\frac{y^{2}}{b^{2}}\) = 1 மற்றும் \(\frac{x^{2}}{a^{2}}\) – \(\frac{y^{2}}{b^{2}}\) = -1 என்ற அதியர் வளையங்களின் குவியங்கள் ஒரு நாற்கரத்தின் முனைகள் எனில் அந்த நாற்கரத்தின் பரப்பு
(1) 4(a² + b²)
(2) 2(a² + b²)
(3) a² + b²
(4) \(\frac{1}{2}\)(a² + b²)
விடை:
(2) 2(a² + b²)

கேள்வி 11.
y² = 4x என்ற பரவளையத்தின் செவ்வகல முனை களில் வரையப்பட்ட செங்குத்துக் கோடுகள் (x – 3)² + (y + 2)² = r², என்ற வட்டத்தின் தொடுகோடுகள் எனில் ரீ-ன் மதிப்பு
(1) 2
(2) 3
(3) 1
(4) 4
விடை:
(1) 2

கேள்வி 12.
x + y = k என்ற நேர்க்கோடு பரவளையம் y² = 12x-இன் செங்கோட்டுச் சமன்பாடாக உள்ளது எனில் – ன் மதிப்பு
(1) 3
(2) -1
(3) 1
(4) 9
விடை:
(4) 91
குறிப்பு :
2y\(\frac{d y}{d x}\) = 12 ⇒ \(\frac{d y}{d x}\) = \(\frac{6}{y}\)
செங்கோட்டின் சாய்வு = \(\frac{-y}{6}\)
செங்கோட்டின் சாய்வு x + y = k என்பது \(\frac{-1}{1}\)
\(\frac{-y}{6}\) = -1
⇒ y = 6
y = 6 என y² = 12xல் பிரதியிட
⇒ 36 = 12x
⇒ x = 3
∴ x + y = k
⇒ 3 + 6 = k
⇒ k = 9

கேள்வி 13.
நீள்வட்டம் E₁ : \(\frac{x^{2}}{9}\) + \(\frac{y^{2}}{4}\) = 1 செவ்வகம் R-க்குள்
செவ்வகத்தின் பக்கங்கள் நீள்வட்டத்தின் அச்சுகளுக்கு இணையாக இருக்குமாறு அமைந்துள்ளன. அந்த செவ்வகத்தின் சுற்று வட்டமாக அமைந்த மற்றொரு நீள்வட்டம் E₂(0, 4) என்ற புள்ளி வழியாகச் செல்கிறது எனில் அந்த நீள்வட்டத்தின் மையத்தொலைத் தகவு
(1) \(\frac{\sqrt{2}}{2}\)
(2) \(\frac{\sqrt{3}}{2}\)
(3) \(\frac{1}{2}\)
(4) \(\frac{3}{4}\)
விடை:
(3) \(\frac{1}{2}\)

கேள்வி 14.
2x – y = 1 என்ற கோட்டிற்கு இணையாக \(\frac{x^{2}}{9}\) – \(\frac{y^{2}}{4}\) = 1 திங்க கொடு என்ற நீள்வட்டத்திற்கு தொடு கோடுகள் வரையப்பட்டால் தொடுபுள்ளிகளில் ஒன்று

விடை:
(3) \(\left(\frac{9}{2 \sqrt{2}}, \frac{1}{\sqrt{2}}\right)\)
குறிப்பு:
\(\frac{x^{2}}{9}\) – \(\frac{y^{2}}{4}\) = 1, a² = 9, b² = 4
தொடுகோடு 2x – y – 1 = 0 க்கு, இணை ஆதலால் தொடுகோட்டின் சமன்பாடு 2x – y + k = 0
⇒ y = 2k + k.
m = 2, c = k
தொடுகோட்டின் சமன்பாடு என்பது
y = mx ± \(\sqrt{a^{2} m^{2}-b^{2}}\)
y = 2x ± \(\sqrt{9(4)-4}\)
= \(\sqrt{32}\) = 4\(\sqrt{2}\)
ஆகையால் தொடுகோடுகள் ஆனது
-2x + y + 4\(\sqrt{2}\) = 0, அல்லது
-2x + y – 4\(\sqrt{2}\) = 0
2x – 4 – 4\(\sqrt{2}\) = 0 அல்லது
2x – y + 4\(\sqrt{2}\) = 0
∴ c = -4\(\sqrt{2}\)
தொடுபுள்ளி என்பது \(\left(\frac{-a^{2} m}{c}, \frac{-b^{2}}{c}\right)\)

கேள்வி 15.
\(\frac{x^{2}}{16}\) + \(\frac{y^{2}}{9}\) = 1 என்ற நீள்வட்டத்தின் குவியங்கள் வழியாகவும் (0, 3) என்ற புள்ளியை மையமாகவும் கொண்ட நீள்வட்டத்தின் சமன்பாடு
(1) x² + y² – 6y – 7 = 0
(2) x² + y² – 6y + 7 = 0
(3) x² + y² – 6y – 5 = 0
(4) x² + y² – 6y + 5 = 0
விடை:
(1) x² + y² – 6y – 7 = 0
குறிப்பு:
a² = 16, b² = 9

(0, 3) மையம் உடைய வட்டத்தின் சமன்பாடு என்பது
(x – 0)² + (y – 3)² = r²
⇒ x² + (y – 3)² = r² …(1)
(\(\sqrt{7}\), 0) வழி செல்கிறது
7 + (-3)² = r²
⇒ r² = 7 + 9 = 16
∴ (1) → x² + (y – 3)² = 16
⇒ x² + y² – 6y + 9 = 16
⇒ x² + y² – 6y + 9 – 16 = 0
⇒ x² + y² – 6y – 7 = 0

கேள்வி 16.
C என்ற வட்டத்தின் மையம் (1, 1) மற்றும் ஆரம் 1 அலகு என்க. T என்ற வட்டத்தின் மையம் (0, y) ஆகவும் ஆதிப்புள்ளி வழியாகவும் உள்ளது. மேலும் C என்ற வட்டத்தை வெளிப்புறமாகத் தொட்டுச் செல்கிறது எனில் வட்டம் -ன் ஆரம்
(1) \(\frac{\sqrt{3}}{\sqrt{2}}\)
(2) \(\frac{\sqrt{3}}{2}\)
(3) \(\frac{1}{2}\)
(4) \(\frac{1}{4}\)
விடை:
(4) \(\frac{1}{4}\)
குறிப்பு:
வட்டம் Cக்கு மையம் C₁(1, 1), r₁ = 1
வட்டம் T க்கு மையம் C₂(0, y) மற்றும், r₂ = y
∴ r₂ = இடையே உள்ள தூரம் (0, 4) மற்றும் (0, 0)க்கு
= \(\sqrt{(0-0)^{2}+(y-0)^{2}}\) = y
வட்டங்கள் வெளிப்புறமாகத் தொட்டுச் செல்வதால்
C₁C₂ = r₁ + r₂

கேள்வி 17.
மையம் ஆதிப்புள்ளியாகவும் நெட்டச்சு x- அச்சாகவும் உள்ள நீள்வட்டத்தைக் கருத்தில் கொள்க. அதன் மையத்தொலைத் தகவு \(\frac{3}{5}\) மற்றும் குவியங்களுக்கிடையே உள்ள தூரம் 6 எனில் அந்த நீள்வட்டத்தின் உள்ளே நெட்டச்சு மற்றும் குற்றச்சுகளை மூலைவிட்டங்களாகக் கொண்டு வரையப்படும் நாற்கரத்தின் பரப்பு
(1) 8
(2) 32
(3) 80
(4) 40
விடை:
(4) 40
குறிப்பு:
கொடுக்கப்பட்ட e = \(\frac{3}{57}\) 2ae = 6
∴ 2a\(\left(\frac{3}{5}\right)\) = 6 ⇒ a = 5
b² = a²(1 – e²) = 25\(\left(1-\frac{9}{25}\right)\) = 16
∴ b = 4
நீள்வட்டத்தின் உள்ளே நெட்டச்சு மற்றும் குற்றச்சுகளை மூலைவிட்டங்களாக கொண்டு வரையப்படும் நாற்கரத்தின் பரப்பு 2ab = 2(5)(4) = 4

கேள்வி 18.
\(\frac{x^{2}}{a^{2}}\) + \(\frac{y^{2}}{b^{2}}\) = 1 என்ற நீள்வட்டத்தினுள் வரையப்படும் மிகப்பெரிய செவ்வகத்தின் பரப்பு
(1) 2ab
(2) ab
(3) \(\sqrt{a b}\)
(4) \(\frac{a}{b}\)
விடை:
(1) 2ab

கேள்வி 19.
நீள்வட்டத்தின் அரைக்குற்றச்சு OB, F மற்றும் F’ மற்றும் FBF’ ஒரு செங்கோணம் எனில் அந்த நீள்வட்டத்தின் மையத்தொலைத் தகவு காண்க.
(1) \(\frac{1}{\sqrt{2}}\)
(2) \(\frac{1}{2}\)
(3) \(\frac{1}{4}\)
(4) \(\frac{1}{\sqrt{3}}\)
விடை:
(1) \(\frac{1}{\sqrt{2}}\)
குறிப்பு:
BEF செங்கோண முக்கோணம் ஆதலால்
EF² = BF² + BF²

(2ac)² = (ae –0)² + (0 – b)² + (0 + ae)² + (b – 0)² 4a²e² = 2a²e² + 2b²
⇒ 2a²e² – 2b² = 0
⇒ a²e² = b²
b² = a²(1 – e²) … (1)
⇒ b² = a² – a²e² = a² – b²
⇒ 2b² = a²

கேள்வி 20.
(x – 3)² + (y – 4)² = \(\frac{y^{2}}{9}\), என்ற நீளவட்டத்தின் மையத்தொலைத் தகவு
(1) \(\frac{\sqrt{3}}{2}\)
(2) \(\frac{1}{3}\)
(3) \(\frac{1}{3 \sqrt{2}}\)
(4) \(\frac{1}{\sqrt{3}}\)
விடை:
(2) \(\frac{1}{3}\)

கேள்வி 21.
P என்ற புள்ளியிலிருந்து y² = 4x என்ற பரவளையத்திற்கு வரையப்படும் இரு தொடுகோடுகளுக்கிடையேயான கோணம் செங்கோணம் எனில் P-ன் நியமப்பாதை
(1) 2x + 1 = 0
(2) x = -1
(3) 2x – 1 = 0
(4) x = 1
விடை:
(2) x = -11
குறிப்பு:
P என்ற புள்ளியிலிருந்து y² = 4x என்ற பரவளையத்திற்கு வரையப்படு தொடு கோடுகளுக்கிடையேயான கோணம் செங்கோணம் எனில் P -ன் நியமப்பாதை இயக்குவரை ஆகும்.
4a = 4 ⇒ a = 1
∴ இயக்குவரையின் சமன்பாடு என்பது
x = -1.

கேள்வி 22.
(1, -2) என்ற புள்ளி வழியாகவும் (3, 0) என்ற புள்ளியில் x அச்சைத் தொட்டுச் செல்வதுமான வட்டம் பின்வரும் புள்ளிகளில் எந்தப் புள்ளி வழியாகச் செல்லும்?
(1) (-5, 2)
(2) (2, -5)
(3) (5, -2)
(4) (-2, 5)
விடை:
(3) (5, -2)
குறிப்பு:
x-அச்சை (3, 0) என்ற புள்ளியில் வட்டம் தொட்டு செல்வதால் வட்டத்தின் மையமானது (3, k) மற்றும் r = 3.

∴ அதனுடைய சமன்பாடு
(x – 3)² + (y – k)² = 3²
இது (1, -2) வழிச் செல்கிறது
⇒ (1 – 3)² + (-2 – k)² = 9
⇒ 4 + (k + 2)² = 9
⇒ (k + 2)² = 5
⇒ k + 2 = \(\sqrt{5}\)
k = \(\sqrt{5}\) – 2
சமன்பாடு என்பது (x – 3)² + (y – \(\sqrt{5}\) + 2)² = 9.
[∴ (5 – 3)² + (-2 – \(\sqrt{5}\))² + 2 = 9
2² + (-\(\sqrt{5}\))² = 9 ⇒ 4 + 5 = 9
(5,-2) மட்டும் இந்த சமன்பாட்டை நிறைவு செய்கிறது.

கேள்வி 23.
(-2, 0) – இலிருந்து ஒரு நகரும் புள்ளிக்கான தூரம் அந்தப் புள்ளிக்கும் நேர்க்கோடு x = \(\frac{2}{3}\) க்கும் இடையேயான தூரத்தைப் போல் மடங்கு உள்ளது எனில் அந்தப் புள்ளியின் நியமப்பாதை
(1) பரவளையம்
(2) அதிபரவளையம்
(3) நீள்வட்டம்
(4) வட்டம்
விடை:
(3) நீள்வட்டம்
குறிப்பு:
A(-2, 0), P(x₁, y₁) மற்றும் PM = ⊥^r
x = –\(\frac{9}{2}\) லிருந்து நிக்கான செங்குத்து தூரம்
∴ AP = \(\frac{2}{3}\)[PM] ⇒ \(\frac{AP}{PM}\) = \(\frac{2}{3}\)
\(\frac{2}{3}\) = e [∵ e = \(\frac{AP}{PM}\)]
e = \(\frac{2}{3}\) < 1
ஆதலால் P(x₁ , y₁) – ன் நியமப்பாதை நீள்வட்டம் ஆகும்.

கேள்வி 24.
x² – (a + b)x – 4 = 0 என்ற சமன்பாட்டின் மூலங்களின் மதிப்புகள் m-ன் மதிப்புகளாக இருக்கும் போது.y = mx + 2\(\sqrt{5}\) என்ற நேர்க்கோடு 16x – 9y² = 144 என்ற அதிபரவளையத்தைத் தொட்டுச் செல்கின்றது எனில் (a+b)-ன் மதிப்பு
(1) 2
(2) 4
(3) 0
(4) -2
விடை:
(3) 0
குறிப்பு:

a² = 9, b² = 16
நிபந்தனை c² = a²m² – b²
⇒ (2\(\sqrt{5}\))² = 9m² – 16
⇒ 20 = 9m² – 16
⇒ 9m² = 36 ⇒ m² = 4
⇒ m = 2, -2
∴ a = 2, b = -2
[∵ x² – (a + b)x – 4 = 0-ன் மூலங்கள் a மற்றும் b]
∴ a + b = 2 – 2 = 0

கேள்வி 25.
x² + y² – 8x – 4y + c = 0 என்ற வட்டத்தின் விட்டத்தின் ஒரு முனை (11, 2) எனில் அதன் மறுமுனை (1) (-5, 2)
(2) (2,-5)
(3) (5, -2)
(4) (-2, 5)
கொடுக்கப்பட்ட அனைத்து விடைகளும் தவறானது
விடை: ★
[★ சரியான விடை (-3, 2)]
குறிப்பு:
வட்டத்தின் சமன்பாடு x² + y² – 8x – 4y + c = 0

2g = -8 ⇒ g = -4
2f = -4 ⇒ f = -2
∴ மையம் (-g, -f) = (4, 2)
(x, y) என்பது மறு முனை என்க. (x, y) மற்றும் (11, 2)இன் நடுப்புள்ளி மையம் ஆகும்.

∴ (-3, 2) என்பது மறுமுனை

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 5 இரு பரிமாண பகுமுறை வடிவியல் – II Ex 5.5 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 5 இரு பரிமாண பகுமுறை வடிவியல் – II Ex 5.5

கேள்வி 1.
ஒரு பாலம் பரவளைய வளைவில் உள்ளது. மையத்தில் 10மீ உயரமும், அடிப்பகுதியில் 30மீ அகலமும் உள்ளது. மையத்திலிருந்து இருபுறமும் 6 மீ தூரத்தில் பாலத்தின் உயரத்தைக் காண்க.
தீர்வு:
பரவளையம் பாலம் கீழ் நோக்கி திறப்புடைய பரவளையம் என்க. அதனுடைய சமன்பாடு x² = -4ay …..(1)
ஆதலால் 10 மீ உயர மையம் (0,0) மற்றும் AD = 30 மீ.

∴ (15, -10) என்ற புள்ளி A ஆனது IV ஆம் கால்பகுதியில் உள்ள து. A(15, -10), (1)ல் அமைந்துள்ளது.
15² = -4a(-10)
⇒ \(\frac{225}{10}\) = 4a ⇒ 4a = \(\frac{45}{2}\)
(1) லிருந்து x² = –\(\frac{45}{2}\)y …(2)
x = 6 மீ,பாலத்தின் உயரத்தை காண, B(6, -y₁), (2)ல் அமைந்துள்ளது.
6² = –\(\frac{45}{2}\)(-y₁)

∴ இருபுறமும் பாலத்தின் உயரம் = 10 – 1.6 = 8.4 மீ

கேள்வி 2.
ஒரு நான்கு வழிச்சாலைக்கான மலைவழியே செல்லும் சுரங்கப்பாதையின் முகப்பு ஒரு நீள்வட்டவடிவமாக உள்ளது. நெடுஞ்சாலையின் மொத்த அகலம் (முகப்பு அல்ல) 16மீ. சாலையின் விளிம்பில் சுரங்கப்பாதையின் உயரம், 4மீ உயரமுள்ள சரக்கு வாகனம் செல்வதற்குத் தேவையான அளவிற்கும் முகப்பின் அதிகபட்ச உயரம் 5மீ ஆகவும் இருக்க வேண்டுமெனில் சுரங்கப்பாதையின் திறப்பின் அகலம் என்னவாக இருக்க வேண்டும்?
தீர்வு:
சுரங்க பாதையின் குறுக்கு வெட்டு நீள் வட்ட வடிவில் உள்ளது என்க.

கொடுக்கப்பட்ட AA’ = 16 மீ ⇒ OA = 8 மீ மற்றும் OB = 5மீ
∴ நீள்வட்டத்தின் சமன்பாட்டு வடிவம் \(\frac{x^{2}}{5^{2}}\) + \(\frac{y^{2}}{8^{2}}\) = 1 … (1) திறப்பின் அகலம் 2h என்க. 4 மீ உயரம் என்ற தூரத்தில், C(4, h) என்ற புள்ளி நீள்வட்டத்தில் உள்ளது.
∴ (1) லிருந்து,

⇒ y = \(\frac{24}{5}\)
⇒ y = 4.8
∴ சுரங்கப்பாதையின் திறப்பின் 2y = 2(4.8) = 9.6 மீ.

கேள்வி 3.
ஒரு நீரூற்றில், ஆதியிலிருந்து 0.5மீ கிடை மட்டத் தூரத்தில் நீரின் அதிகபட்ச உயரம் 4மீ, நீரின் பாதை ஒரு பரவளையம் எனில் ஆதியிலிருந்து 0.75மீ கிடைமட்டத் தூரத்தில் நீரின் உயரத்தைக் காண்க.
தீர்வு:
பரவளையத்தின் சமன்பாடு
(x – h)² = -4a(y – k).
இங்கு முனை (0.5, 4)
பரவளையத்தின் சமன்பாடு (x – 0.5)² = -4a(y – 4) … (1)
O(0, 0) பரவளையத்தின் மீதுள்ள புள்ளி
(0 – 0.5)² = -4a (0 – 4)
⇒ \(\frac{1}{4}\) = 16a ⇒ a = \(\frac{1}{64}\)
∴ (1) லிருந்து (x – 0.5)² = -4 × \(\frac{1}{64}\)(y – 4)
மேலும் D(0.75, y₁) பரவளையத்தின் மீதுள்ள ஒருபுள்ளி

⇒ 1 = -y₁ + 4
⇒ y₁ = -1 + 4 = 3 மீ
0.75 மீ கிடைமட்டத் தூரத்தில் நீரின் உயரம் 3 மீ.

கேள்வி 4.
பொறியாளர் ஒருவர் குறுக்கு வெட்டு பரவளையமாக உள்ள ஒரு துணைக்கோள் ஏற்பியை வடிவமைக்கின்றார். ஏற்பி அதன் மேல் பக்கத்தில் 5மீ அகலமும், முனையிலிருந்து குவியம் 1.2 மீ தூரத்திலும் உள்ளது.
(a) முனையை ஆதியாகவும், x-அச்சு பரவளையத்தின் சமச்சீர் அச்சாகவும் கொண்டு ஆய அச்சுகளைப் பொருத்தி பரவளையத்தின் சமன்பாடு காண்க.
(b) முனையிலிருந்து செயற்கைக்கோள் ஏற்பியின் ஆழம் காண்க.
தீர்வு:
துணைக்கோள் ஏற்பியின் குறுக்கு வெட்டு பரவளையம் வலது பக்க திறப்புடையது.

அதனுடைய சமன்பாடு y² = 4ax
முனையிலிருந்து குவியம் 1.2 மீ தூரத்தில் உள்ள தால் OA = 1.2 மீ மற்றும் BC = 2.5 மீ ஏற்பியின் அகலம் 5மீ.
படத்திலிருந்து, a = 1.2மீ
∴ y² = 4(1.2)x
(a) ⇒ y² = 4.8 …(1)
(b) (x₁, , 2.5) (1)-ன் மீது அமைந்துள்ளதால்
(2.5)² = 4.8(x₁)
x₁ = \(\frac{2.5 \times 2.5}{4.8}\)
x₁ = 1.3 மீ
∴ முனையிலிருந்து செயற்கைக்கோள் ஏற்பியின் ஆழம் 1.3 மீ.

கேள்வி 5.
ஒரு தொங்கு பாலத்தின் 60மீ சாலைப்பகுதிக்கு பரவளைய கம்பி வடம் படத்தில் உள்ளவாறு பொறுத்தப்பட்டுள்ளது. செங்குத்துக் கம்பி வடங்கள் சாலைப்பகுதியில் ஒவ்வொன்றுக்கும் 6மீ இடைவெளி இருக்குமாறு அமைக்கப் பட்டுள்ளது. முனையிலிருந்து முதல் இரண்டு செங்குத்து கம்பி வடங்களுக்கான நீளத்தைக் காண்க.

தீர்வு:
பரவளையத்தின் சமன்பாடு x² = 4ay என்க… (1)

(30, 16), (1)-ன் மீதுள்ள புள்ளி ஆதலால் கிடைப்பது, 30² = 4 × a × 16
⇒ a = \(\frac{30 \times 30}{4 \times 16}\) = \(\frac{225}{16}\)
∴ (1)லிருந்து x² = \(\frac{4 \times 225}{16}\) y = \(\frac{225}{4}\)y
AC = h e மற்றும் BD = 1 மீ என்க.
∴ A(6, h)பரவளையத்தின் மீதுள்ள புள்ளி

∴ AD = 3 + h = 3 + 0.64 = 3.64 மீ
மேலும் (12, l) பரவளையத்தின் மீதுள்ள புள்ளி
[ ∵ ON = 6 + 6 = 12]

∴ BN = 3 + l = 3 + 2.56 = 5.56 மீ.
எனவே முதல் இரண்டு செங்குத்து கம்பி வடங்களுக்கான நீளம் 3.64 மீ மற்றும் 5.56 மீ.

கேள்வி 6.
ஒரு அணு உலை குளிரூட்டும் தூணின் குறுக்கு வெட்டு அதிபரவளைய வடிவில் உள்ளது. மேலும் அதன் சமன்பாடு \(\frac{x^{2}}{30^{2}}\) – \(\frac{y^{2}}{44^{2}}\) = 1. தூண் 150மீ உயரமுடையது. மேலும் அதிபரவளையத்தின் மையத்திலிருந்து தூணின் மேல்பகுதிக்கான தூரம் மையத்திலிருந்து அடிப்பகுதிக்கு உள்ள தூரத்தில் பாதியாக உள்ளது. தூணின் மேற்பகுதி மற்றும் அடிப்பகுதியின் விட்டங்களைக் காண்க.

தீர்வு:
அணு உலை குளிரூட்டும் தூணின் குறுக்கு வெட்டு அதிபரவளைய வடிவில் உள்ளது.

கொடுக்கப்பட்ட OC = \(\frac{1}{2}\)OD மற்றும் CD = 150 மீ அதனுடைய சமன்பாடு OC = 50 மீ மற்றும் OD = 100 மீ
\(\frac{x^{2}}{30^{2}}\) – \(\frac{y^{2}}{44^{2}}\) = 1 …. (1)
தூணின் உச்சியின் ஆரம் l என்க.
∴ A(l, 50) அதிபரவளையத்தின் மீதுள்ள புள்ளி

l = \(\frac{1998}{44}\) = 45.40 மீ
தூணின் உச்சியின் ஆரம் 45.40 மீ. தூணின் அடிப்பகுதியின் ஆரம் h என்க.
∴ B(h, 100) அதிபரவளையத்தின் மீதுள்ள ஒரு புள்ளி
∴ (1) லிருந்து

தூணின் அடிப்பகுதியின் ஆரம் 74.48 மீ.

கேள்வி 7.
1.2 மீ நீளமுள்ள தடி அதன் முனைகள் எப்போதும் ஆய அச்சுகளைத் தொட்டுச் செல்லுமாறு நகருகின்றது. தடியின் x-அச்சு முனையிலிருந்து 0.3மீ தூரத்தில் உள்ள ஒரு புள்ளி P-ன் நியமப்பாதை ஒரு நீள்வட்டம் என நிறுவுக, மேலும் அதன் மையத்தொலைத்தகவும் காண்க.
தீர்வு:
AB என்பது தடி என்க மற்றும் P(x₁, y₁) தடியின் மீதுள்ள புள்ளி AP= 0.3 மீ.
வரைக PD ⊥ x- அச்சு மற்றும் PC ⊥ y-அச்சு.


16 ஆல் வகுக்க கிடைப்பது,

கேள்வி 8.
தரைமட்டத்திலிருந்து 7.5மீ உயரத்தில் , தரைக்கு இணையாகப் பொருத்தப்பட்ட ஒரு ! குழாயிலிருந்து வெளியேறும் நீர் தரையைத் தொடும் பாதை ஒரு பரவளையத்தை ஏற்படுத்துகிறது. மேலும் இந்தப் பரவளையப் பாதையின் முனை குழாயின் வாயில் அமைகிறது. குழாய் மட்டத்திற்கு 2.5மீ கீழே ! நீரின் பாய்வானது குழாயின் முனை வழியாகச் செல்லும் நிலைகுத்துக் கோட்டிற்கு 3மீ தூரத்தில் உள்ளது. எனில் குத்துக் கோட்டிலிருந்து எவ்வளவு தூரத்திற்கு அப்பால் நீரானது தரையில் விழும் என்பதைக் காண்க.
தீர்வு:
கொடுக்கப்பட்ட தகவலை கொண்டு பரவளையம் கீழ் நோக்கி திறப்படையது என எடுத்துக் கொள்ளலாம்.

∴ அதனுடைய சமன்பாடு x² = -4ay … (1)
விழும் பாதையில் உள்ள புள்ளி P என்க, குழாயிலிருந்து 2.5 மீ கீழே குழாயின் முனை வழியாகச் செல்லும் செங்குத்து கோட்டிற்கு 3மீ தூரத்தில் உள்ளது.

∴ P(3, -2.5)
∴ (1) லிருந்து 3² = -4a(- 2.5)
⇒ \(\frac{9}{2.5}\) = 4a
∴ (1) லிருந்து, x² = –\(\frac{9}{2.5}\) … (2)
குத்துக் கோட்டிலிருந்து x₁ தூரத்திற்கு அப்பால் நீரானது தரையில் விழும் என்க. ஆனால் குழாயின் உயரமானது தரையிலிருந்து 7.5 மீ.
∴ (x₁, -7.5) அமைகிறது … (2)

குத்துக்கோட்டிலிருந்து 3\(\sqrt{3}\)மீ தூரத்திற்கு அப்பால் நீரானது தரையில் விழும்.

கேள்வி 9.
ஒரு ராக்கெட் வெடியானது கொளுத்தும் போது அது ஒரு பரவளையப் பாதையில் செல்கிறது. அதன் உச்ச உயரம் 4மீ-ஐ எட்டும் போது அது கொளுத்தப்பட்ட இடத்திலிருந்து கிடைமட்டத் தூரம் 6மீ தொலைவிலுள்ளது. இறுதியாக கிடைமட்டமாக 12மீ தொலைவில் தரையை வந்தடைகிறது. எனில் புறப்பட்ட இடத்தில் தரையுடன் ஏற்படுத்தப்படும் எறிகோணம் காண்க.
தீர்வு:
ஆதியில் முனையை கொண்டால் பரவளையம் கீழ் நோக்கிய திறப்புடையது.

அதனுடைய சமன்பாடு x² = -4ay
இது (6,-4) வழிச் செல்கிறது
∴ 36 = -4a(4) ⇒ 4a = \(\frac{36}{4}\) = 9
∴ (1) லிருந்து, x² = -9y
(-6,-4)ல் சாய்வைக் காண
(1) ஐஸ் பொறுத்து வகையிட கிடைப்பது
2x = -9\(\frac{d y}{d x}\)
⇒ \(\frac{d y}{d x}\) = \(\frac{-2 x}{9}\)

∴ தரையுடன் ஏற்படுத்தும் எறிகோணம்
tan^-1\(\left(\frac{4}{3}\right)\)

கேள்வி 10.
A, B என்ற இரு புள்ளிகள் 10கி.மீ இடைவெளியில் உள்ளன. இந்தப் புள்ளிகளில் வெவ்வேறு நேரங்களில் கேட்கப்பட்ட வெடிச்சத்தத்திலிருந்து வெடிச்சத்தம் உண்டான இடம் A என்ற புள்ளி B என்ற புள்ளியைவிட 6 கி.மீ அருகாமையில் உள்ளது என நிர்ணயிக்கப்பட்டது. வெடிச்சத்தம் உண்டான இடம் ஒரு குறிப்பிட்ட வளைவரைக்கு உட்பட்டது என நிரூபித்து அதன் சமன்பாட்டைக் காண்க.
தீர்வு:
வெடிச்சத்தம் உண்டான இடம் P(x, y) என்க.
கொடுக்கப்பட்ட PB – PA = 6

தூரத்திற்கான சமன்பாட்டை பயன்படுத்த,

இருபுறமும் வர்க்கப்படுத்த கிடைப்பது

மீண்டும் வர்க்கப்படுத்த,
x⁴ + y⁴ + 49 + 2x⁴y⁴ + 14y⁴ + 14x² = (x² – 10x + 25 + y⁴) (x² + 10x + 25 + y⁴)

⇒ 14y² + 14x² = -50x² + 50y² + 625 – 49
⇒ 64x² – 36y² = 576
÷ 4 கிடைப்பது,
16x² – 9y² = 144
÷ 144,
\(\frac{x^{2}}{9}\) – \(\frac{y^{2}}{16}\) = 1
எனவே வெடிச்சத்தம் உண்டான இடம் அதிபரவளையத்திற்கு உட்பட்டது. அதன் சமன்பாடு \(\frac{x^{2}}{9}\) – \(\frac{y^{2}}{16}\) = 1.