Samacheer Kalvi 12th Maths Guide Chapter 6 வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள் Ex 6.1

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 6 வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள் Ex 6.1 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 6 வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள் Ex 6.1

கேள்வி 1.
ஒரு வட்டத்தின் மையத்திலிருந்து அவ் வட்டத்தின் ஒரு நாணின் மையப்புள்ளிக்கு வரையப்படும் கோடு அந்நாணிற்கு செங்குத்தாகும் என வெக்டர் முறையில் நிறுவுக.
தீர்வு :

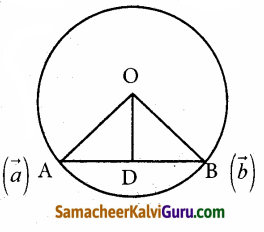
வட்டத்தின் மீதுள்ள புள்ளிகள் A மற்றும் Bயின் நிலை வெக்டர் முறையே \(\vec{a}\) மற்றும் \(\vec{b}\) என்க. வட்டத்தின் மையம் O ஆதலால்
|\(\overrightarrow{\mathrm{OA}}\)| = |\(\overrightarrow{\mathrm{OB}}\)| ⇒ |\(\vec{a}\)| = |\(\vec{b}\)|
மேலும், ABன் மையப்புள்ளி D.

= \(\) = 0
⇒ \(\overrightarrow{\mathrm{OD}}\) . \(\overrightarrow{\mathrm{AB}}\) = 0 ⇒ \(\overrightarrow{\mathrm{OD}}\) ⊥ \(\overrightarrow{\mathrm{AB}}\)
ஆகையால், ஒரு வட்டத்தின் மையத்திலிருந்து அவ்வட்டத்தின் ஒரு நாணின் மையப்புள்ளிக்கு வரையப்படும் கோடு அந்நாணிற்கு
செங்குத்தாகும்.

கேள்வி 2.
ஓர் இருசமப்பக்க முக்கோணத்தின் அடிப் பக்கத்திற்கு வரையப்படும் நடுக்கோடு , அப்பக்கத்திற்கு செங்குத்தாகும் என வெக்டர்
முறையில் நிறுவுக.
தீர்வு:

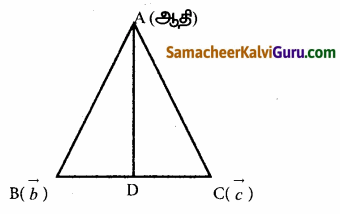
AB = AC உடன் ABC ஒரு இருசமபக்க முக்கோணம் மற்றும் D என்பது BC யின் நடுப்புள்ளி.
A ஆதியாகக் கொண்டு B மற்றும் C யின் நிலை
வெக்டர் \(\vec{b}\) மற்றும் \(\vec{c}\) என்க.


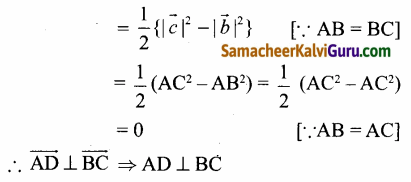
ஆகையால் △ABC-ல் நடுக்கோடு AD அடிப்பக்கம் BC க்கு செங்குத்து △ABC.

கேள்வி 3.
வெக்டர் முறையில், ஓர் அரைவட்டத்தில் அமையும் கோணம் ஒரு செங்கோணம் என நிறுவுக.
தீர்வு :

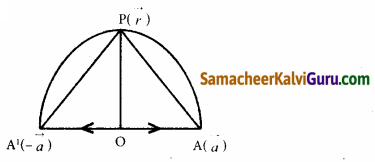
O என்பது அரைவட்டத்தின் மையப்புள்ளி மற்றும் AA’ என்பது விட்டம் என்க. அரைவட்டத்தின் சுற்றளவிலுள்ள ஏதேனும் ஒரு புள்ளி P என்க. O வை ஆதியாக கொண்டு A மற்றும் P யின் நிலை வெக்டர் முறையே \(\vec{a}\) மற்றும் \(\vec{r}\) என்க.
பிறகு, A’ன் நிலை வெக்டர் என்பது – \(\vec{a}\) இங்கு \(\overrightarrow{\mathrm{AP}}\) = (P யின் நிலை வெக்டர்) – (Aயின் நிலை வெக்டர்) = \(\vec{r}\) – \(\vec{a}\)
மற்றும் \(\overrightarrow{\mathrm{AP}}\) = (P யின் நிலை வெக்டர்) – (A யின் நிலை வெக்டர்)

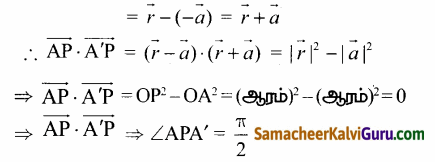
ஆகையால் அரைவட்டத்தின் அமையும் ஒரு கோணம் செங்கோணம் ஆகும்.

கேள்வி 4.
ஒரு சாய்சதுரத்தின் மூலை விட்டங்கள் ஒன்றையொன்று செங்குத்தாக இருசமக்கூறிடும் என வெக்டர் முறையில் நிறுவுக.
தீர்வு:

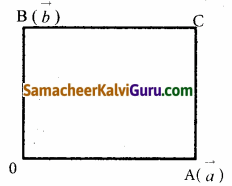
OACB என்பது ஒரு சாய்சதுரம் என்க. O வை ஆதியாகக் கொண்டு, A மற்றும் B யின் நிலை வெக்டர் முறையே \(\vec{a}\) மற்றும் \(\vec{b}\) என்க.

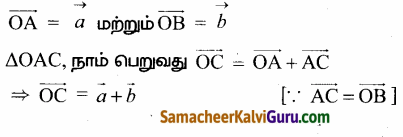
ஆகையால் C யின் நிலை வெக்டர் \(\vec{a}\) + \(\vec{b}\).
∴ OC ன் நடுப்புள்ளியின் நிலை வெக்டர் என்பது \(\frac{\vec{a}+\vec{b}}{2}\)
அதை போல AB யின் நடுப்புள்ளியின் நிலைவெக்டர் என்பது \(\frac{\vec{a}+\vec{b}}{2}\)
ஆகையால் OC மற்றும் ABயின் நடுப்புள்ளி ஒன்றேயாகும்.

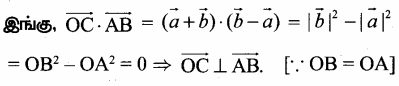
ஆகையால் ஒரு சாய்சதுரத்தின் மூலை விட்டங்கள் ஒன்றையொன்று செங்குத்தாக இரு சமக்கூறிடும்.

Question 5.
ஓர் இணைகரத்தின் மூலை விட்டங்கள் சமம் எனில், அந்த இணைகரம் ஒரு செவ்வகமாகும் என வெக்டர் முறையில் நிறுவுக.
தீர்வு:

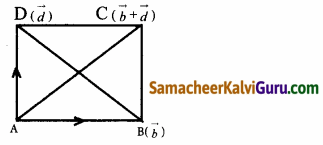
மூலைவிட்டங்கள் AC மற்றும் BD சமம் எனுமாறு இணைகரம் ABCD என்க. A யை ஆதி என்க. B மற்றும் Dன் நிலை வெக்டர் \(\vec{b}\) மற்றும் \(\vec{a}\) என்க.
பிறகு \(\overrightarrow{\mathrm{AB}}\) = \(\vec{b}\) மற்றும் \(\overrightarrow{\mathrm{AD}}\) = \(\vec{d}\).
△ABCயில் வெக்டர்களின் கூடுதலுக்கான முக்கோண விதியை பயன்படுத்த கிடைப்பது

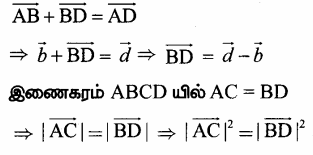
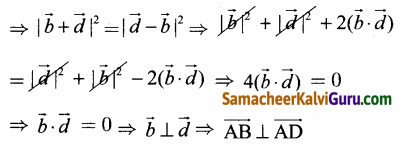
கேள்வி 6.
வெக்டர் முறையில், AC மற்றும் BD ஆகியவற்றை மூலை விட்டங்களாகக் கொண்ட நாற்கரம் ABCD-ன் பரப்பு \(\frac{1}{2}|\overrightarrow{\mathbf{A C}} \times \overrightarrow{\mathbf{B D}}|\) என நிறுவுக.
தீர்வு :

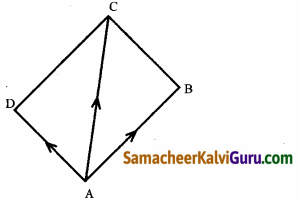
நாற்கரம் ABCDயின் வெக்டர் பரப்பு = △ABCயின் வெக்டர் பரப்பு + △ACDயின் வெக்டர் பரப்பு

∴ நாற்கரம் ABCDயின் பரப்பு
= \(\frac{1}{2}|\overrightarrow{\mathrm{AC}} \times \overrightarrow{\mathrm{BD}}|\)

கேள்வி 7.
ஒரே அடிப்பக்கத்தின் மீதமைந்த இரு இணைகோடுகளுக்கு இடைப்பட்ட இணை கரங்களின் பரப்பளவுகள் சமமானவை என
வெக்டர் முறையில் நிறுவுக.
தீர்வு:

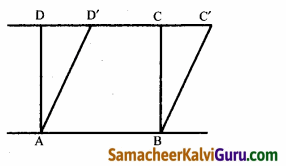
ABCD என்பது கொடுக்கப்பட்ட இணைகரம் மற்றும் அதே அடிப்பக்கம் AB மற்றும் அதே இணைகோடுகள் AB மற்றும் DCக்கு இடையே அமைந்த புதிய இணைகரம் ABC’ D’.
∴ இணைகரம் ABCD யின் வெக்டர் பரப்பு

= இணைகரம் ABC’D’யின் பரப்பு
∴ இணைகரம் ABCDயின் பரப்பு = இணைகரம் ABC’D’ ன் வெக்டர் பரப்பு
ஆகையால் ஒரே அடிப்பக்கத்தின் மீதமைந்த இரு இணைகோடுகளுக்கு இடைப்பட்ட இணைகரங்களின் பரப்பளவுகள் சமமானவை.

கேள்வி 8.
△ABC-ன் நடுக்கோட்டு மையம் G எனில், வெக்டர் முறையில் நிறுவுக. (△GAB-ன் பரப்பு) = (△GBC-ன் பரப்பு) = (△GCA-ன் பரப்பு ) = – \(\frac{1}{3}\)(△ABC-ன் பரப்பு) என நிறுவுக.
தீர்வு :

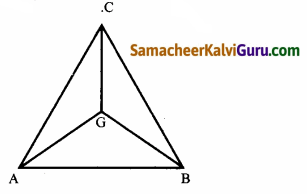
△ABCயின் உச்சி புள்ளிகளின் நிலை
வெக்டர்கள் முறையே \(\vec{a}\), \(\vec{b}\) மற்றும் \(\vec{c}\) என்க.
△ABCயின் நடுக்கோட்டு மையம் G ஆதலால்

[ ∵ குறுக்கும் பெருக்கல் பங்கீட்டுடையது]



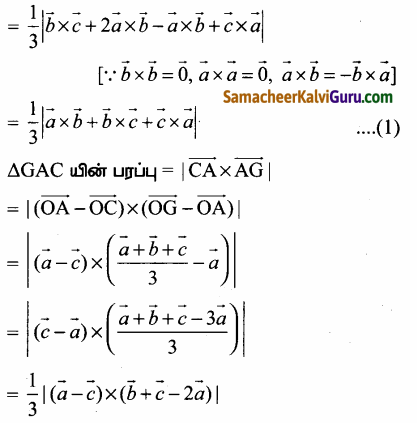
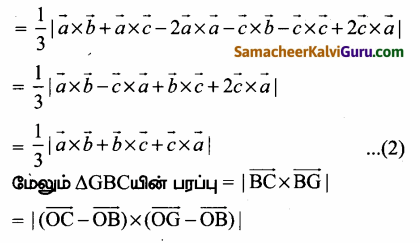
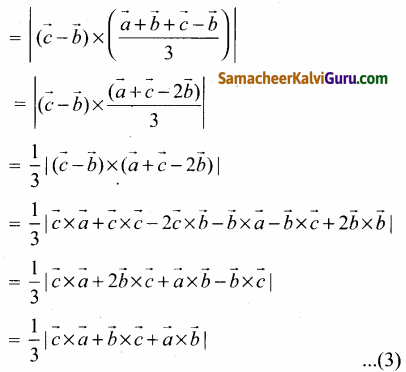
(1), (2) மற்றும் (3) லிருந்து,
△GABயின் = △GAC யின் பரப்பு = △GBC யின் பரப்பு

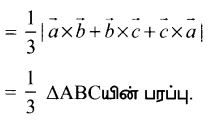
எனவே நிரூபிக்கப்பட்டது.

கேள்வி 9.
வெக்டர் முறையில் cos(α – β) = cos α cos β + sin α sin β என நிறுவுக.
தீர்வு :

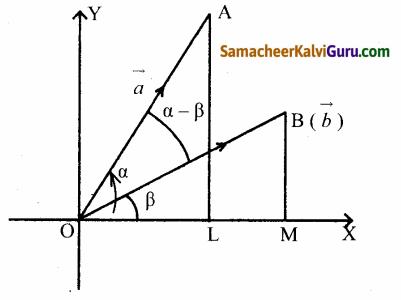
\(\hat{a}\) = \(\overrightarrow{\mathrm{OA}}\) மற்றும் \(\hat{b}\) = \(\overrightarrow{\mathrm{OB}}\) என்பன அலகு வெக்டர்கள் என்க மற்றும் அவைகள் கோணங்கள் α, β, நவை x-அச்சின் மிகையுடன் ஏற்படுத்துகின்றன. AL மற்றும் BM ⊥^r லிருந்து x-அச்சு எனுமாறு வரைக.


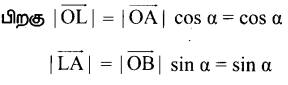
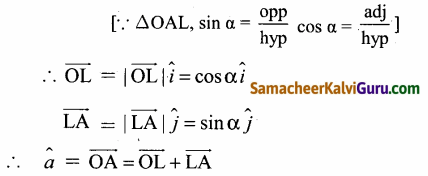
[△விதியை பயன்படுத்தி கூட்டு]

(3) மற்றும் (4)லிருந்து,
cos (α – β) = cos α cos β + sin α sin β.

கேள்வி 10.
sin(α + β) = sin α cos β + cos α sin β என வெக்டர் முறையில் நிறுவுக.
தீர்வு :

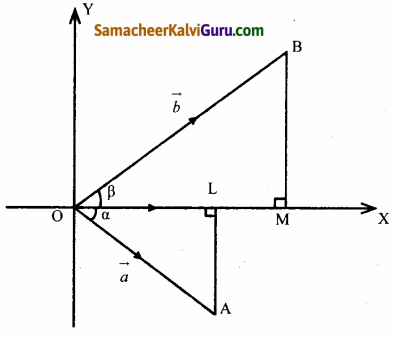
\(\hat{a}\) = \(\overrightarrow{\mathrm{OA}}\) மற்றும் \(\hat{b}\) = \(\overrightarrow{\mathrm{OB}}\) என்பன அலகு வெக்டர்கள் என்க மற்றும் அவைகள் கோணங்கள் α, βவை x-அச்சின் மிகையுடன் ஏற்படுத்துகின்றன. AL மற்றும் BM ⊥^r லிருந்து x-அச்சு எனுமாறு வரைக.
AL மற்றும் BM ⊥^r லிருந்து x,க்கு எனுமாறு வரைக.
எனவே |\(\overrightarrow{\mathrm{OL}}\)| = |\(\overrightarrow{\mathrm{OA}}\)|cos α
⇒ \(\overrightarrow{\mathrm{OL}}\) =|\(\overrightarrow{\mathrm{OL}}\)|\(\hat{i}\) = cosα\(\hat{i}\)


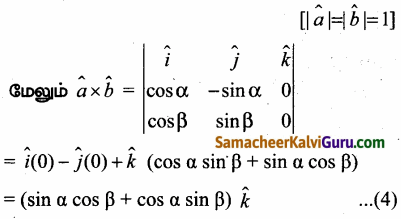
(3) மற்றும் (4) ஐ பயன்படுத்த,
sin(α + β) = sin α cos β + cos α sin β

கேள்வி 11.
ஒரு துகள் (1, 2, 3) எனும் புள்ளியிலிருந்து (5, 4, 1) எனும் புள்ளிக்கு 8\(\hat{\boldsymbol{i}}\) + 2\(\hat{\boldsymbol{j}}\) – 6\(\hat{\boldsymbol{k}}\) மற்றும் 6\(\hat{\boldsymbol{i}}\) + 2\(\hat{\boldsymbol{j}}\) – 2\(\hat{\boldsymbol{k}}\) என்ற மாறாத விசைகளின் செயல்பாட்டினால் நகர்த்தப்பட்டால், அவ்விசைகள் செய்த மொத்த வேலையைக் காண்க.
தீர்வு:
\(\overrightarrow{\mathrm{F}}\) மற்றும் \(\overrightarrow{\mathrm{F}_{2}}\), என்பன விசைகள் மற்றும் \(\vec{d}\) என்பது இடப்பெயர்ச்சி வெக்டர் என்க.
∴ விளைவு விசை \(\overrightarrow{\mathrm{F}}\) = \(\overrightarrow{\mathrm{F}}_{1}\) + \(\overrightarrow{\mathrm{F}}_{2}\)

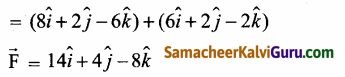
மற்றும் \(\vec{d}\) = இடம் பெயர்ந்த புள்ளி – புள்ளியிலிருந்து இடப்பெயர்வு

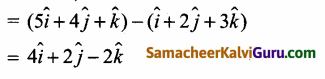
செய்த வேலை (w) = \(\overrightarrow{\mathrm{F}}\).\(\overrightarrow{\mathrm{d}}\)

= 56 + 8 + 16
= 80 அலகுகள்

கேள்வி 12.
முறையே 5\(\sqrt{2}\) மற்றும் 10\(\sqrt{2}\) அலகுகள் எண்ண ளவு கொண்ட 3\(\hat{\boldsymbol{i}}\) + 4\(\hat{\boldsymbol{j}}\) + 5\(\hat{\boldsymbol{k}}\) மற்றும் 10\(\hat{\boldsymbol{i}}\) + 6\(\hat{\boldsymbol{j}}\) – 8\(\hat{\boldsymbol{k}}\) என்ற வெக்டர்களின் திசைகளில் அமைந்த விசைகள், ஒரு துகளை 4\(\hat{\boldsymbol{i}}\) – 3\(\hat{\boldsymbol{j}}\) – 2\(\hat{\boldsymbol{k}}\) என்ற வெக்டரை நிலைவெக்டராகக் கொண்ட புள்ளியிலிருந்து 6\(\hat{\boldsymbol{i}}\) + \(\hat{\boldsymbol{j}}\) – 3\(\hat{\boldsymbol{k}}\) என்ற வெக்டரை நிலைவெக்டராகக் கொண்ட புள்ளிக்கு நகர்த்துகிறது எனில், அவ்விசைகள் செய்த வேலையைக் காண்க.
தீர்வு:
\(\overrightarrow{\mathrm{F}_{1}}\) மற்றும் \(\overrightarrow{\mathrm{F}_{2}}\), கொடுக்கப்பட்ட இரு விசைகள் என்க.

கேள்வி 13.
3\(\hat{\boldsymbol{i}}\) + 4\(\hat{\boldsymbol{j}}\) – 5\(\hat{\boldsymbol{k}}\) என்னும் விசை 4\(\hat{\boldsymbol{i}}\) + 2\(\hat{\boldsymbol{j}}\) – 3\(\hat{\boldsymbol{k}}\) என்ற வெக்டரை நிலைவெக்டராகக் கொண்ட புள்ளி வழியாகக் செயல்படுகிறது எனில், 2\(\hat{\boldsymbol{i}}\) – 3\(\hat{\boldsymbol{j}}\) + 4\(\hat{\boldsymbol{k}}\) என்ற வெக்டரை நிலைவெக்டராகக் கொண்ட புள்ளியைப் பொறுத்து அவ்விசையின் முறுக்குத் திறனின் எண்ணளவு மற்றும் திசைக்கொசைன்களைக் காண்க.
தீர்வு:
கொடுக்கப்பட்ட \(\overrightarrow{\mathrm{F}}\) = 3\(\hat{\boldsymbol{i}}\) + 4\(\hat{\boldsymbol{j}}\) – 5\(\hat{\boldsymbol{k}}\)

∴ முறுக்குத் திறனின் எண்ணளவு

ஆகையால், திசைக் கொசைன்கள்

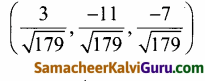
கேள்வி 14.
8\(\hat{\boldsymbol{i}}\) – 6\(\hat{\boldsymbol{j}}\) – 4\(\hat{\boldsymbol{k}}\) என்ற வெக்டரை நிலை வெக்டராகக் கொண்ட புள்ளியில் செயல்படும் -3\(\hat{\boldsymbol{i}}\) + 6\(\hat{\boldsymbol{j}}\) – 3\(\hat{\boldsymbol{k}}\), 4\(\hat{\boldsymbol{i}}\) – 10\(\hat{\boldsymbol{j}}\) + 12\(\hat{\boldsymbol{k}}\) மற்றும் 4\(\hat{\boldsymbol{i}}\) + 7\(\hat{\boldsymbol{j}}\) விசைகளின் திருப்புத் திறனை 18\(\hat{\boldsymbol{i}}\) + 3\(\hat{\boldsymbol{j}}\) – 9\(\hat{\boldsymbol{k}}\) என்ற வெக்டரை நிலை வெக்டராகக் கொண்ட புள்ளியைப் பொறுத்துக் காண்க.
தீர்வு:
விளைவு விசை \(\overrightarrow{\mathrm{F}}\) = \(\overrightarrow{\mathrm{F}}_{1}\) + \(\overrightarrow{\mathrm{F}}_{2}\) + \(\overrightarrow{\mathrm{F}}_{3}\)
\(\overrightarrow{\mathrm{F}}\) = (-3\(\hat{\boldsymbol{i}}\)+ 6\(\hat{\boldsymbol{j}}\) – 3\(\hat{\boldsymbol{k}}\)) + (4\(\hat{\boldsymbol{i}}\) – 10\(\hat{\boldsymbol{j}}\) + 12\(\hat{\boldsymbol{k}}\)) + (4\(\hat{\boldsymbol{i}}\) + 7\(\hat{\boldsymbol{j}}\))
= 5\(\hat{\boldsymbol{i}}\) + 3\(\hat{\boldsymbol{j}}\) + 9\(\hat{\boldsymbol{k}}\)
\(\overrightarrow{\mathrm{r}}\) = (விசை செயல்படுகிற புள்ளி) – (புள்ளியை பொறுத்து செயல்படுகிற விசை)
= (8\(\hat{\boldsymbol{i}}\) – 6\(\hat{\boldsymbol{j}}\) – 4\(\hat{\boldsymbol{k}}\)) – (18\(\hat{\boldsymbol{i}}\) + 3\(\hat{\boldsymbol{j}}\) – 9\(\hat{\boldsymbol{k}}\))
= -10\(\hat{\boldsymbol{i}}\) – 9\(\hat{\boldsymbol{j}}\) + 5\(\hat{\boldsymbol{k}}\)
திருப்புத்திறன் (\(\overrightarrow{\mathrm{t}}\)) = \(\overrightarrow{\mathrm{r}}\) × \(\overrightarrow{\mathrm{F}}\)