Samacheer Kalvi 12th Maths Guide Chapter 6 வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள் Ex 6.4

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 6 வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள் Ex 6.4 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 6 வெக்டர் இயற்கணிதத்தின் பயன்பாடுகள் Ex 6.4

கேள்வி 1.
\(\hat{4} \hat{i}+3 \hat{j}-7 \hat{k}\) என்ற வெக்டரை நிலை வெக்டராகக் கொண்ட புள்ளி வழிச் செல்வதும் \(2 \hat{i}-6 \hat{j}+7 \hat{k}\) என்ற வெக்டருக்கு இணையானதுமான நேர்க்கோட்டின் துணை அலகு அல்லாத வெக்டர் சமன்பாடு மற்றும் கார்டீசியன் சமன்பாடுகளைக் காண்க.
தீர்வு:
\(\vec{a}=4 \hat{i}+3 \hat{j}-7 \hat{k}\) மற்றும் \(\vec{b}=2 \hat{i}-6 \hat{j}+7 \hat{k}\) என்க.
ஒரு புள்ளி \((\vec{a})\) வழிச் செல்லும் மற்றும் வெக்டர் \((\vec{b})\) க்கு இணையான கோட்டின் வெக்டர் சமன்பாட்டின் துணையலகு இல்லாத வடிவம்
\((\vec{r}-\vec{a}) \times \vec{b}=\vec{0}\)
⇒ \([\vec{r}-(4 \hat{i}+3 \hat{j}-7 \hat{k})] \times(2 \hat{i}-6 \hat{j}+7 \hat{k})=\vec{0}\)
அதனுடைய கார்டீசியன் சமன்பாடு
\(\frac{x-x_{1}}{b_{1}}=\frac{y-y_{1}}{b_{2}}=\frac{z-z_{1}}{b_{3}}\)
⇒ \(\frac{x-4}{2}=\frac{y-3}{-6}=\frac{z+7}{7}\)
[∵ (x₁, y₁, z₁), (4, 3, -7) மற்றும் (b₁, b₂, b₃), (2,-6, 7)]

கேள்வி 2.
(-2, 3, 4) என்ற புள்ளி வழியாகச் செல்லும் \(\frac{x-1}{-4}=\frac{y+3}{5}=\frac{8-z}{6}\) என்ற கோட்டிற்கு இணையானதுமான நேர்க்கோட்டின் துணை அலகு வெக்டர், சமன்பாடு மற்றும் கார்டீசியன் சமன்பாடுகளைக் காண்க.
தீர்வு:
\(\vec{a}=-2 \hat{i}+3 \hat{j}+4 \hat{k}\) மற்றும் \(\vec{b}=-4 \hat{i}+5 \hat{j}-6 \hat{k}\)
என்க.
ஒரு புள்ளி \((\vec{a})\) வழிச்செல்லும் \(\vec{b}\) க்கு இணையான நேர்க்கோட்டின் வெக்டர் சமன்பாட்டின் துணையலகு வடிவம்
\(\vec{r}=\vec{a}+t \vec{b}\) இங்கு t ∈ ℝ
∴ \(\vec{r}=-2 \hat{i}+3 \hat{j}+4 \hat{k}+t(-4 \hat{i}+5 \hat{j}-6 \hat{k})\), t ∈ ℝ
அதனுடைய கார்டீசியன் சமன்பாடு
\(\frac{x-x_{1}}{b_{1}}=\frac{y-y_{1}}{b_{2}}=\frac{z-z_{1}}{b_{3}}\)
⇒ \(\frac{x+2}{-4}=\frac{y-3}{5}=\frac{z-4}{-6}\)
[∵ (x₁, y₁, z₁), (-2, 3, 4), (b₁, b₂, b₃), (4, 5,-6)]

கேள்வி 3.
(6, 7, 4) மற்றும் (8,4,9) என்ற புள்ளிகள் வழியாகச் செல்லும் நேர்க்கோடு xz மற்றும் yz தளங்களை வெட்டும் புள்ளிகளைக் காண்க.
தீர்வு:
(x₁, y₁, z₁), (6, 7, 4) மற்றும் (x₂, y₂, z₂), (8, 4, 9) என்க .
இரண்டு புள்ளிகள் வழிச்செல்லும் நேர்க்கோட்டின் கார்டீசியன் சமன்பாடு

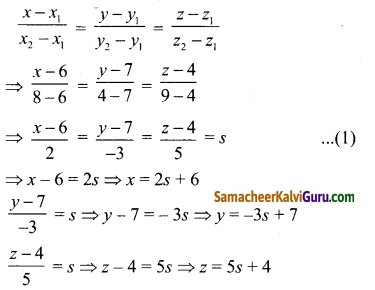
∴ கோட்டின் மீதுள்ள புள்ளி (2s + 6,-3s +7,5s +4). ……….(2)
(1) மற்றும் x z தளத்தின் வெட்டுப்புள்ளி காண, y = 0, என (2)ல் பிரதியிடு
∴ -3s + 7 = 0 ⇒ -3s = – 7 ⇒ s = \(\frac{7}{3}\),
s = \(\frac{7}{3}\) என (2) -ல் பிரதியிட வெட்டுப் புள்ளியானது

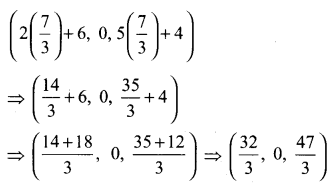
(1) மற்றும் yz தளத்தின் வெட்டுபுள்ளி காண, x = 0. என (2)ல் பிரதியிடு
∴ 2s + 6 = 0
⇒ 2s = -6
⇒ s = -3.
∴ (2) → (2 (-3) + 6,-3 (-3) + 7, 5 (-3) + 4)
= (0, 16, -11)

கேள்வி 4.
(5, 6, 7) மற்றும் (7, 9, 13) என்ற புள்ளிகள் வழியாகச் செல்லும் நேர்க்கோட்டின் திசைக் கொசைன்களைக் காண்க. மேலும், கொடுக்கப்பட்ட இவ்விரு புள்ளிகள் வழியாகச் செல்லும் நேர்க்கோட்டின் துணை அலகு வெக்டர் சமன்பாடு , மற்றும் கார்டீசியன் சமன்பாடுகளைக் காண்க.
தீர்வு:
\(\vec{b}=5 \hat{i}+6 \hat{j}+7 \hat{k}\) மற்றும் \(\vec{a}=7 \hat{i}+9 \hat{j}+13 \hat{k}\) என்க.
இரண்டு புள்ளிகள் \(\vec{a}\) மற்றும் \(\vec{b}\) வழிச்செல்லும் நேர்க்கோட்டின் வெக்டர் சமன்பாட்டின் துணையலகு வடிவம்

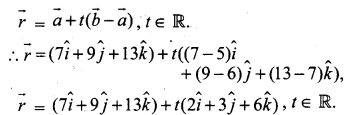
இரண்டு புள்ளிகள் வழிச்செல்லும் கார்டீசியன் சமன்பாட்டின் நேர்க்கோட்டு வடிவம்

இது திசை விகிதங்கள் 2, 3, 6 உடைய நேர்க்கோடு ஆகையால் அதனுடைய திசைக் கொசைன்கள்

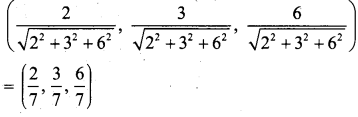
கேள்வி 5.
பின்வரும் கோடுகளுக்கு இடைப்பட்ட குறுங்கோணம் காண்க.

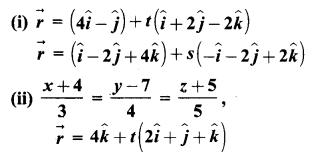
(iii) 2x = 3y = -z மற்றும் 6x = -y – 4z
தீர்வு:
(i) கொடுக்கப்பட்ட கோடுகளானது

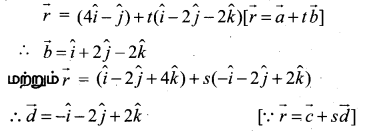
θ என்பது கொடுக்கப்பட்ட கோடுகளுக்கு இடையேயான கோணம் என்க.

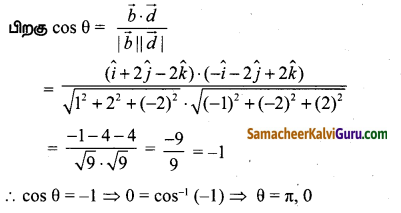
(ii) கொடுக்கப்பட்ட கோடுகளானது

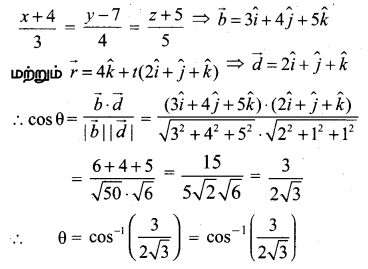
(iii) கொடுக்கப்பட்ட கோடுகளானது 2x = 3y = -z மற்றும் 6x = -y – 4z
2x = 3y = -z ⇒ \(\frac{x-0}{\frac{1}{2}}=\frac{y-0}{-1}=\frac{z-0}{-1}\)

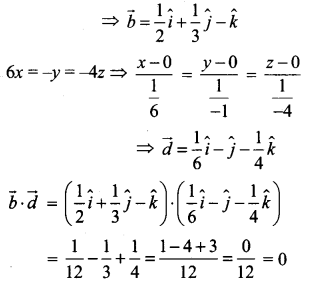
∴ \(\vec{b} \perp \vec{d}\)
∴ \(\vec{b}\) மற்றும் \(\vec{d}\) க்கு இடையேயான கோணம் \(\frac{\pi}{2}\)

கேள்வி 6.
A(7, 2, 1), B(6, 0, 3), மற்றும் C(4, 2, 4) என்ப ன ∆ABC -ன் உச்சிகள் எனில், ∠ABC-ஐக் காண்க.
தீர்வு:

AB -ன் திசை விகிதங்கள்
(6 – 7, 0 – 2, 3 – 1) = (-1, -2, 2)
[∵ (x₂ – x₁), (y₂ – y₁), (z₂ – z₁)]
மேலும் BC ன் திசை விகிதங்கள்
(4 – 6, 2 – 0, 4 – 3) = (- 2, 2, 1)
திசை விகிதங்களின் பெருக்கல் பலன்
(-1) (- 2) + (- 2) (2) + 2 (1)
= (2 – 4 + 2)
[∵ இரண்டு கோடுகள் ⊥^r எனில் திசை விகிதங்கள் d₁b₁ + d₂b₂ + d₃b₃ = 0]
= 4 – 4 = 0
எனவே AB ⊥ BC
∠ABC = \(\frac{\pi}{2}\)

கேள்வி 7.
(2, 1, 4) மற்றும் (a – 1, 4, -1) என்ற புள்ளிகளை இணைக்கும் நேர்க்கோடு (0, 2, -1) மற்றும் (5, 3, -2) , என்ற புள்ளிகளை இணைக்கும் நேர்க்கோட்டுக்கு இணை எனில் a மற்றும் b -ன் மதிப்புகளைக் காண்க.
தீர்வு:
(2, 1, 4) மற்றும் (a – 1, 4 – 1) என்ற இரு புள்ளிகள் வழிச் செல்லும் நேர்க்கோட்டின் கார்டீசியன் வடிவம்

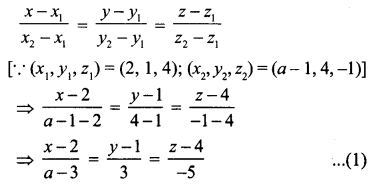
அதே போல் இரண்டு புள்ளிகள் (0, 2, b – 1) மற்றும் (5, 3, -2) வழிச்செல்லும் நேர்க்கோட்டின் கார்டீசியன் வடிவம்

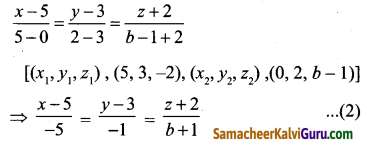
(1) மற்றும் (2)ன் திசைக் கொசைன்கள் சமம் எனில் அவை இணை
∴ கோடு (1)ன் திசை விகிதங்கள் a – 3, 3, -5 (3) கோடு (2)ன் திசை விகிதங்கள் -5, -1, b + 1 (4) திசை விகிதங்கள் சமம் எனில் (4) ஐ -3 ஆல் பெருக்க.
∴ (4) → +15, 3, -3b – 3
(3) → a – 3, 3, -5
∴ a – 3 = + 15 ⇒ a= 15 + 3 = 18 ⇒ a = 18
-3b – 3 = -5 ⇒ -3b = -5 + 3 = -2
⇒ b = \(\frac{-2}{-3}=\frac{2}{3}\)
∴ a = 18 மற்றும் b = \(\frac{2}{3}\)

கேள்வி 8.
\(\frac{x-5}{5 m+2}=\frac{2-y}{5}=\frac{1-z}{-1}\) மற்றும் x = \(\frac{2 y+1}{4 m}=\frac{1-z}{-3}\) என்ற நேர்க்கோடுகள் ஒன்றுக்கொன்று செங்குத்தானவை எனில், m-ன் மதிப்பைக் காண்க.
தீர்வு:
கொடுக்கப்பட்ட கோடுகள்


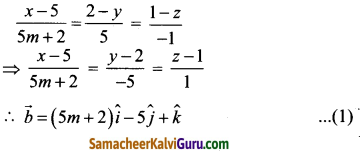
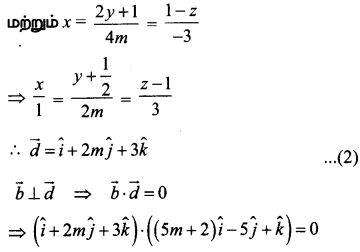
⇒ (5m + 2) 1 + 2m (-5) + 3(1) = 0
⇒ 5m + 2 – 10m + 3 = 0
⇒ 5 – 5m = 0
⇒ 5 = 5m
⇒ m = 1.

கேள்வி 9.
(2, 3, 4), (-1, 4, 5) மற்றும் (8, 1, 2) என்ற புள்ளிகள் ஒரு கோடமைப் புள்ளிகள் எனக் காட்டுக.
தீர்வு:
A (2, 3, 4), B (-1, 4, 5) மற்றும் C (8, 1, 2) புள்ளிகள் என்க.
A மற்றும் B யை இணைக்கும் கோட்டின் சமன்பாடு

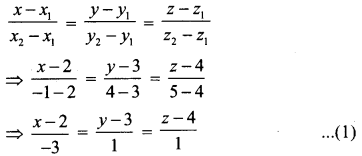
புள்ளி C (8, 1, 2) வை கோடு (1)ல் பிரதியிட கிடைப்பது,
\(\frac{8-2}{-3}=\frac{1-3}{1}=\frac{2-4}{1}\) ⇒ -2 = -2 = -2
A மற்றும் B யை இணைக்கும் கோட்டை புள்ளி C பூர்த்தி செய்வதால், மூன்று புள்ளிகளும் ஒரு நேர்க்கோட்டு அமைவன.
எனவே . கொடுக்கப்பட்ட புள்ளிகள் ஒரு நேர்க்கோட்டு அமைவன.