Samacheer Kalvi 12th Maths Guide Chapter 5 இரு பரிமாண பகுமுறை வடிவியல் – II Ex 5.5

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 5 இரு பரிமாண பகுமுறை வடிவியல் – II Ex 5.5 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 5 இரு பரிமாண பகுமுறை வடிவியல் – II Ex 5.5

கேள்வி 1.
ஒரு பாலம் பரவளைய வளைவில் உள்ளது. மையத்தில் 10மீ உயரமும், அடிப்பகுதியில் 30மீ அகலமும் உள்ளது. மையத்திலிருந்து இருபுறமும் 6 மீ தூரத்தில் பாலத்தின் உயரத்தைக் காண்க.
தீர்வு:
பரவளையம் பாலம் கீழ் நோக்கி திறப்புடைய பரவளையம் என்க. அதனுடைய சமன்பாடு x² = -4ay …..(1)
ஆதலால் 10 மீ உயர மையம் (0,0) மற்றும் AD = 30 மீ.

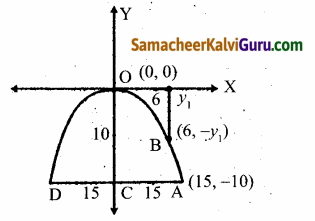
∴ (15, -10) என்ற புள்ளி A ஆனது IV ஆம் கால்பகுதியில் உள்ள து. A(15, -10), (1)ல் அமைந்துள்ளது.
15² = -4a(-10)
⇒ \(\frac{225}{10}\) = 4a ⇒ 4a = \(\frac{45}{2}\)
(1) லிருந்து x² = –\(\frac{45}{2}\)y …(2)
x = 6 மீ,பாலத்தின் உயரத்தை காண, B(6, -y₁), (2)ல் அமைந்துள்ளது.
6² = –\(\frac{45}{2}\)(-y₁)

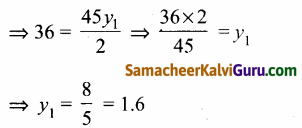
∴ இருபுறமும் பாலத்தின் உயரம் = 10 – 1.6 = 8.4 மீ

கேள்வி 2.
ஒரு நான்கு வழிச்சாலைக்கான மலைவழியே செல்லும் சுரங்கப்பாதையின் முகப்பு ஒரு நீள்வட்டவடிவமாக உள்ளது. நெடுஞ்சாலையின் மொத்த அகலம் (முகப்பு அல்ல) 16மீ. சாலையின் விளிம்பில் சுரங்கப்பாதையின் உயரம், 4மீ உயரமுள்ள சரக்கு வாகனம் செல்வதற்குத் தேவையான அளவிற்கும் முகப்பின் அதிகபட்ச உயரம் 5மீ ஆகவும் இருக்க வேண்டுமெனில் சுரங்கப்பாதையின் திறப்பின் அகலம் என்னவாக இருக்க வேண்டும்?
தீர்வு:
சுரங்க பாதையின் குறுக்கு வெட்டு நீள் வட்ட வடிவில் உள்ளது என்க.

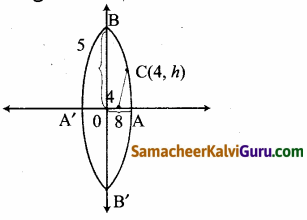
கொடுக்கப்பட்ட AA’ = 16 மீ ⇒ OA = 8 மீ மற்றும் OB = 5மீ
∴ நீள்வட்டத்தின் சமன்பாட்டு வடிவம் \(\frac{x^{2}}{5^{2}}\) + \(\frac{y^{2}}{8^{2}}\) = 1 … (1) திறப்பின் அகலம் 2h என்க. 4 மீ உயரம் என்ற தூரத்தில், C(4, h) என்ற புள்ளி நீள்வட்டத்தில் உள்ளது.
∴ (1) லிருந்து,

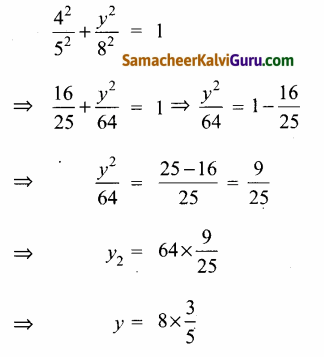
⇒ y = \(\frac{24}{5}\)
⇒ y = 4.8
∴ சுரங்கப்பாதையின் திறப்பின் 2y = 2(4.8) = 9.6 மீ.

கேள்வி 3.
ஒரு நீரூற்றில், ஆதியிலிருந்து 0.5மீ கிடை மட்டத் தூரத்தில் நீரின் அதிகபட்ச உயரம் 4மீ, நீரின் பாதை ஒரு பரவளையம் எனில் ஆதியிலிருந்து 0.75மீ கிடைமட்டத் தூரத்தில் நீரின் உயரத்தைக் காண்க.
தீர்வு:
பரவளையத்தின் சமன்பாடு
(x – h)² = -4a(y – k).
இங்கு முனை (0.5, 4)
பரவளையத்தின் சமன்பாடு (x – 0.5)² = -4a(y – 4) … (1)
O(0, 0) பரவளையத்தின் மீதுள்ள புள்ளி
(0 – 0.5)² = -4a (0 – 4)
⇒ \(\frac{1}{4}\) = 16a ⇒ a = \(\frac{1}{64}\)
∴ (1) லிருந்து (x – 0.5)² = -4 × \(\frac{1}{64}\)(y – 4)
மேலும் D(0.75, y₁) பரவளையத்தின் மீதுள்ள ஒருபுள்ளி

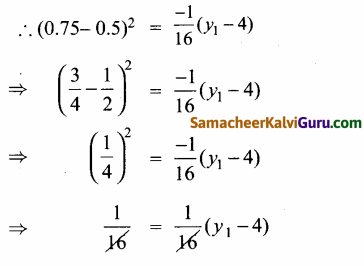
⇒ 1 = -y₁ + 4
⇒ y₁ = -1 + 4 = 3 மீ
0.75 மீ கிடைமட்டத் தூரத்தில் நீரின் உயரம் 3 மீ.

கேள்வி 4.
பொறியாளர் ஒருவர் குறுக்கு வெட்டு பரவளையமாக உள்ள ஒரு துணைக்கோள் ஏற்பியை வடிவமைக்கின்றார். ஏற்பி அதன் மேல் பக்கத்தில் 5மீ அகலமும், முனையிலிருந்து குவியம் 1.2 மீ தூரத்திலும் உள்ளது.
(a) முனையை ஆதியாகவும், x-அச்சு பரவளையத்தின் சமச்சீர் அச்சாகவும் கொண்டு ஆய அச்சுகளைப் பொருத்தி பரவளையத்தின் சமன்பாடு காண்க.
(b) முனையிலிருந்து செயற்கைக்கோள் ஏற்பியின் ஆழம் காண்க.
தீர்வு:
துணைக்கோள் ஏற்பியின் குறுக்கு வெட்டு பரவளையம் வலது பக்க திறப்புடையது.

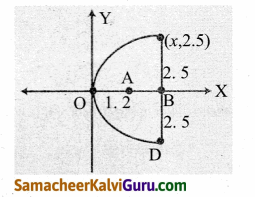
அதனுடைய சமன்பாடு y² = 4ax
முனையிலிருந்து குவியம் 1.2 மீ தூரத்தில் உள்ள தால் OA = 1.2 மீ மற்றும் BC = 2.5 மீ ஏற்பியின் அகலம் 5மீ.
படத்திலிருந்து, a = 1.2மீ
∴ y² = 4(1.2)x
(a) ⇒ y² = 4.8 …(1)
(b) (x₁, , 2.5) (1)-ன் மீது அமைந்துள்ளதால்
(2.5)² = 4.8(x₁)
x₁ = \(\frac{2.5 \times 2.5}{4.8}\)
x₁ = 1.3 மீ
∴ முனையிலிருந்து செயற்கைக்கோள் ஏற்பியின் ஆழம் 1.3 மீ.

கேள்வி 5.
ஒரு தொங்கு பாலத்தின் 60மீ சாலைப்பகுதிக்கு பரவளைய கம்பி வடம் படத்தில் உள்ளவாறு பொறுத்தப்பட்டுள்ளது. செங்குத்துக் கம்பி வடங்கள் சாலைப்பகுதியில் ஒவ்வொன்றுக்கும் 6மீ இடைவெளி இருக்குமாறு அமைக்கப் பட்டுள்ளது. முனையிலிருந்து முதல் இரண்டு செங்குத்து கம்பி வடங்களுக்கான நீளத்தைக் காண்க.

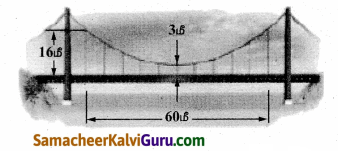
தீர்வு:
பரவளையத்தின் சமன்பாடு x² = 4ay என்க… (1)

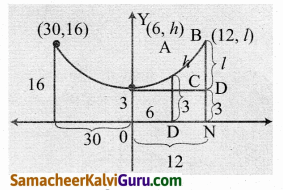
(30, 16), (1)-ன் மீதுள்ள புள்ளி ஆதலால் கிடைப்பது, 30² = 4 × a × 16
⇒ a = \(\frac{30 \times 30}{4 \times 16}\) = \(\frac{225}{16}\)
∴ (1)லிருந்து x² = \(\frac{4 \times 225}{16}\) y = \(\frac{225}{4}\)y
AC = h e மற்றும் BD = 1 மீ என்க.
∴ A(6, h)பரவளையத்தின் மீதுள்ள புள்ளி

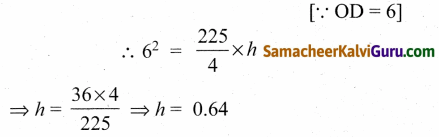
∴ AD = 3 + h = 3 + 0.64 = 3.64 மீ
மேலும் (12, l) பரவளையத்தின் மீதுள்ள புள்ளி
[ ∵ ON = 6 + 6 = 12]

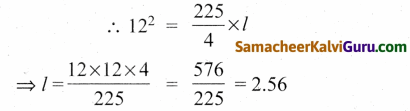
∴ BN = 3 + l = 3 + 2.56 = 5.56 மீ.
எனவே முதல் இரண்டு செங்குத்து கம்பி வடங்களுக்கான நீளம் 3.64 மீ மற்றும் 5.56 மீ.

கேள்வி 6.
ஒரு அணு உலை குளிரூட்டும் தூணின் குறுக்கு வெட்டு அதிபரவளைய வடிவில் உள்ளது. மேலும் அதன் சமன்பாடு \(\frac{x^{2}}{30^{2}}\) – \(\frac{y^{2}}{44^{2}}\) = 1. தூண் 150மீ உயரமுடையது. மேலும் அதிபரவளையத்தின் மையத்திலிருந்து தூணின் மேல்பகுதிக்கான தூரம் மையத்திலிருந்து அடிப்பகுதிக்கு உள்ள தூரத்தில் பாதியாக உள்ளது. தூணின் மேற்பகுதி மற்றும் அடிப்பகுதியின் விட்டங்களைக் காண்க.

தீர்வு:
அணு உலை குளிரூட்டும் தூணின் குறுக்கு வெட்டு அதிபரவளைய வடிவில் உள்ளது.

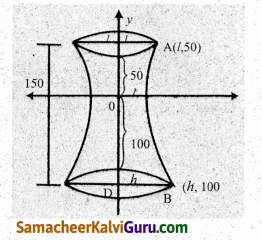
கொடுக்கப்பட்ட OC = \(\frac{1}{2}\)OD மற்றும் CD = 150 மீ அதனுடைய சமன்பாடு OC = 50 மீ மற்றும் OD = 100 மீ
\(\frac{x^{2}}{30^{2}}\) – \(\frac{y^{2}}{44^{2}}\) = 1 …. (1)
தூணின் உச்சியின் ஆரம் l என்க.
∴ A(l, 50) அதிபரவளையத்தின் மீதுள்ள புள்ளி

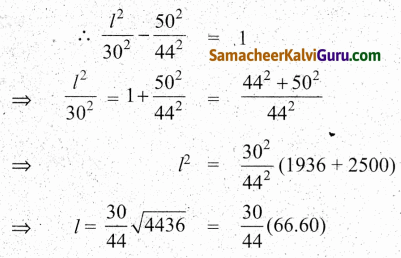
l = \(\frac{1998}{44}\) = 45.40 மீ
தூணின் உச்சியின் ஆரம் 45.40 மீ. தூணின் அடிப்பகுதியின் ஆரம் h என்க.
∴ B(h, 100) அதிபரவளையத்தின் மீதுள்ள ஒரு புள்ளி
∴ (1) லிருந்து

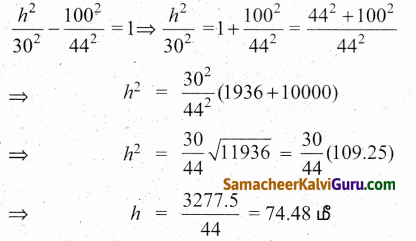
தூணின் அடிப்பகுதியின் ஆரம் 74.48 மீ.

கேள்வி 7.
1.2 மீ நீளமுள்ள தடி அதன் முனைகள் எப்போதும் ஆய அச்சுகளைத் தொட்டுச் செல்லுமாறு நகருகின்றது. தடியின் x-அச்சு முனையிலிருந்து 0.3மீ தூரத்தில் உள்ள ஒரு புள்ளி P-ன் நியமப்பாதை ஒரு நீள்வட்டம் என நிறுவுக, மேலும் அதன் மையத்தொலைத்தகவும் காண்க.
தீர்வு:
AB என்பது தடி என்க மற்றும் P(x₁, y₁) தடியின் மீதுள்ள புள்ளி AP= 0.3 மீ.
வரைக PD ⊥ x- அச்சு மற்றும் PC ⊥ y-அச்சு.


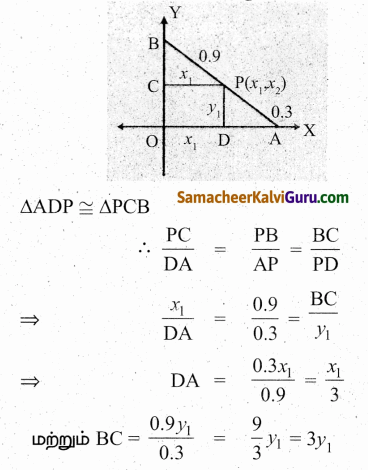
16 ஆல் வகுக்க கிடைப்பது,

கேள்வி 8.
தரைமட்டத்திலிருந்து 7.5மீ உயரத்தில் , தரைக்கு இணையாகப் பொருத்தப்பட்ட ஒரு ! குழாயிலிருந்து வெளியேறும் நீர் தரையைத் தொடும் பாதை ஒரு பரவளையத்தை ஏற்படுத்துகிறது. மேலும் இந்தப் பரவளையப் பாதையின் முனை குழாயின் வாயில் அமைகிறது. குழாய் மட்டத்திற்கு 2.5மீ கீழே ! நீரின் பாய்வானது குழாயின் முனை வழியாகச் செல்லும் நிலைகுத்துக் கோட்டிற்கு 3மீ தூரத்தில் உள்ளது. எனில் குத்துக் கோட்டிலிருந்து எவ்வளவு தூரத்திற்கு அப்பால் நீரானது தரையில் விழும் என்பதைக் காண்க.
தீர்வு:
கொடுக்கப்பட்ட தகவலை கொண்டு பரவளையம் கீழ் நோக்கி திறப்படையது என எடுத்துக் கொள்ளலாம்.

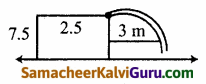
∴ அதனுடைய சமன்பாடு x² = -4ay … (1)
விழும் பாதையில் உள்ள புள்ளி P என்க, குழாயிலிருந்து 2.5 மீ கீழே குழாயின் முனை வழியாகச் செல்லும் செங்குத்து கோட்டிற்கு 3மீ தூரத்தில் உள்ளது.

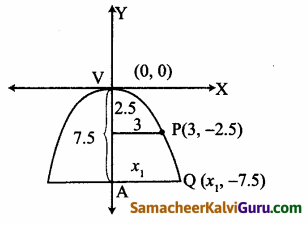
∴ P(3, -2.5)
∴ (1) லிருந்து 3² = -4a(- 2.5)
⇒ \(\frac{9}{2.5}\) = 4a
∴ (1) லிருந்து, x² = –\(\frac{9}{2.5}\) … (2)
குத்துக் கோட்டிலிருந்து x₁ தூரத்திற்கு அப்பால் நீரானது தரையில் விழும் என்க. ஆனால் குழாயின் உயரமானது தரையிலிருந்து 7.5 மீ.
∴ (x₁, -7.5) அமைகிறது … (2)

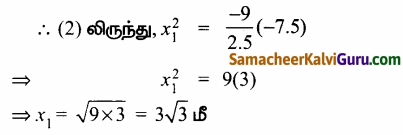
குத்துக்கோட்டிலிருந்து 3\(\sqrt{3}\)மீ தூரத்திற்கு அப்பால் நீரானது தரையில் விழும்.

கேள்வி 9.
ஒரு ராக்கெட் வெடியானது கொளுத்தும் போது அது ஒரு பரவளையப் பாதையில் செல்கிறது. அதன் உச்ச உயரம் 4மீ-ஐ எட்டும் போது அது கொளுத்தப்பட்ட இடத்திலிருந்து கிடைமட்டத் தூரம் 6மீ தொலைவிலுள்ளது. இறுதியாக கிடைமட்டமாக 12மீ தொலைவில் தரையை வந்தடைகிறது. எனில் புறப்பட்ட இடத்தில் தரையுடன் ஏற்படுத்தப்படும் எறிகோணம் காண்க.
தீர்வு:
ஆதியில் முனையை கொண்டால் பரவளையம் கீழ் நோக்கிய திறப்புடையது.

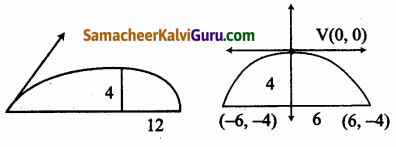
அதனுடைய சமன்பாடு x² = -4ay
இது (6,-4) வழிச் செல்கிறது
∴ 36 = -4a(4) ⇒ 4a = \(\frac{36}{4}\) = 9
∴ (1) லிருந்து, x² = -9y
(-6,-4)ல் சாய்வைக் காண
(1) ஐஸ் பொறுத்து வகையிட கிடைப்பது
2x = -9\(\frac{d y}{d x}\)
⇒ \(\frac{d y}{d x}\) = \(\frac{-2 x}{9}\)

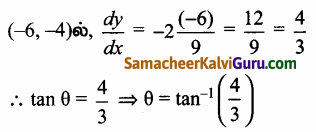
∴ தரையுடன் ஏற்படுத்தும் எறிகோணம்
tan^-1\(\left(\frac{4}{3}\right)\)

கேள்வி 10.
A, B என்ற இரு புள்ளிகள் 10கி.மீ இடைவெளியில் உள்ளன. இந்தப் புள்ளிகளில் வெவ்வேறு நேரங்களில் கேட்கப்பட்ட வெடிச்சத்தத்திலிருந்து வெடிச்சத்தம் உண்டான இடம் A என்ற புள்ளி B என்ற புள்ளியைவிட 6 கி.மீ அருகாமையில் உள்ளது என நிர்ணயிக்கப்பட்டது. வெடிச்சத்தம் உண்டான இடம் ஒரு குறிப்பிட்ட வளைவரைக்கு உட்பட்டது என நிரூபித்து அதன் சமன்பாட்டைக் காண்க.
தீர்வு:
வெடிச்சத்தம் உண்டான இடம் P(x, y) என்க.
கொடுக்கப்பட்ட PB – PA = 6

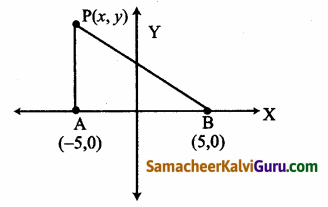
தூரத்திற்கான சமன்பாட்டை பயன்படுத்த,

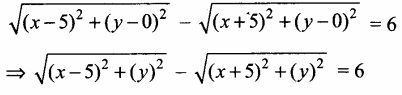
இருபுறமும் வர்க்கப்படுத்த கிடைப்பது

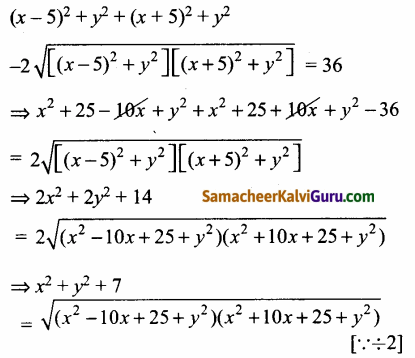
மீண்டும் வர்க்கப்படுத்த,
x⁴ + y⁴ + 49 + 2x⁴y⁴ + 14y⁴ + 14x² = (x² – 10x + 25 + y⁴) (x² + 10x + 25 + y⁴)

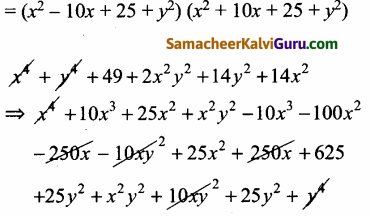
⇒ 14y² + 14x² = -50x² + 50y² + 625 – 49
⇒ 64x² – 36y² = 576
÷ 4 கிடைப்பது,
16x² – 9y² = 144
÷ 144,
\(\frac{x^{2}}{9}\) – \(\frac{y^{2}}{16}\) = 1
எனவே வெடிச்சத்தம் உண்டான இடம் அதிபரவளையத்திற்கு உட்பட்டது. அதன் சமன்பாடு \(\frac{x^{2}}{9}\) – \(\frac{y^{2}}{16}\) = 1.