Prasanna

Students of 12th can get the pdf links of Tamilnadu State Board Economics Solutions here. You can Download Samacheer Kalvi 12th Economics Book Solutions Chapter 12 Introduction to Statistical Methods and Econometrics Questions and Answers, Notes Pdf, Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Economics Solutions Chapter 12 Introduction to Statistical Methods and Econometrics

It is very important to put the textbook aside while preparing for the exams. So, if you follow Samacheer Kalvi 12th Economics Textbook Solutions you can cover all the topics in Chapter 12 Introduction to Statistical Methods and Econometrics Questions and Answers. This helps to improve your communication skills.

Samacheer Kalvi 12th Economics Introduction to Statistical Methods and Econometrics Text Book Back Questions and Answers

Part – A
Multiple Choice Questions.

Question 1.
The word ‘statistics’ is used as ………………………
(a) Singular
(b) Plural
(c) Singular and Plural
(d) None of above
Answer:
(c) Singular and Plural

Question 2.
Who stated that statistics as a science of estimates and probabilities?
(a) Horace Secrist
(b) R. A Fisher
(c) Ya-Lun-Chou
(d) Boddington
Answer:
(d) Boddington

Question 3.
Sources of secondary data are …………………………..
(a) Published sources
(b) Unpublished sources
(c) Neither published nor unpublished sources
(d) Both (a) and (b)
Answer:
(d) Both (a) and (b)

Question 4.
The data collected by questionnaires are …………………………..
(a) Primary data
(b) Secondary data
(c) Published data
(d) Grouped data
Answer:
(a) Primary data

Question 5.
A measure of the strength of the linear relationship that exists between two variables is called …………………………..
(a) Slope
(b) Intercept
(c) Correlation coefficient
(d) Regression equation
Answer:
(c) Correlation coefficient

Question 6.
If both variables X and Y increase or decrease simultaneously, then the coefficient of correlation will be …………………………..
(a) Positive
(b) Negative
(c) Zero
(d) One
Answer:
(a) Positive

Question 7.
If the points on the scatter diagram indicate that as one variable increases the other variable tends to decrease the value of r will be …………………………..
(a) Perfect positive
(b) Perfect negative
(c) Negative
(d) Zero
Answer:
(c) Negative

Question 8.
The value of the coefficient of correlation r lies between …………………………..
(a) 0 and 1
(b) – 1 and 0
(c) – 1 and + 1
(d) – 0.5 and + 0.5
Answer:
(c) – 1 and + 1

Question 9.
The term regression was used by …………………………..
(a) Newton
(b) Pearson
(c) Spearman
(d) Galton
Answer:
(d) Galton

Question 10.
The purpose of simple linear regression analysis is to …………………………..
(a) Predict one variable from another variable
(b) Replace points on a scatter diagram by a straight-line
(c) Measure the degree to which two variables are linearly associated
(d) Obtain the expected value of the independent random variable for a given value of the dependent variable
Answer:
(a) Predict one variable from another variable

Question 11.
A process by which we estimate the value of dependent variable on the basis of one or more independent variables is called …………………………..
(a) Correlation
(b) Regression
(c) Residual
(d) Slope
Answer:
(b) Regression

Question 12.
If Y = 2 – 0.2X, then the value of Y intercept is equal to …………………………..
(a) -0.2
(b) 2
(c) 0.2X
(d) All of the above
Answer:
(b) 2

Question 13.
In the regression equation Y = β₀ + β₁ X, the Y is called …………………………..
(a) Independent variable
(b) Dependent variable
(c) Continuous variable
(d) None of the above
Answer:
(b) Dependent variable

Question 14.
In the regression equation X = β₀ + β₁ X, the X is called …………………………..
(a) Independent variable
(b) Dependent variable
(c) Continuous variable
(d) None of the above
Answer:
(a) Independent variable

Question 15.
Econometrics is the integration of …………………………..
(a) Economics and Statistics
(b) Economics and Mathematics
(c) Economics, Mathematics and Statistics
(d) None of the above
Answer:
(c) Economics, Mathematics and Statistics

Question 16.
Econometric is the word coined by …………………………..
(a) Francis Galton
(b) Ragnar Frish
(c) Karl Person
(d) Spearsman
Answer:
(b) Ragnar Frish

Question 17.
The raw materials of Econometrics are ……………………………
(a) Data
(b) Goods
(c) Statistics
(d) Mathematics
Answer:
(a) Data

Question 18.
The term Uiin regression equation is …………………………..
(a) Residuals
(b) Standard error
(c) Stochastic error term
(d) None
Answer:
(c) Stochastic error term

Question 19.
The term Uiis introduced for the representation of …………………………..
(a) Omitted Variable
(b) Standard error
(c) Bias
(d) Discrete Variable
Answer:
(a) Omitted Variable

Question 20.
Econometrics is the amalgamation of …………………………..
(a) 3 subjects
(b) 4 subjects
(c) 2 subjects
(d) 5 subjects
Answer:
(a) 3 subjects

Part – B
Answer The Following Questions In One or Two Sentences.

Question 21.
What is Statistics?
Answer:

1. The term‘Statistics’is used in two senses: as singular and plural.
2. In singular form it simply means statistical methods.
3. Statistics when used in singular form helps in the collection, presentation, classification and interpretation of data to make it easily comprehensible.
4. In its plural form it denotes collection of numerical figures and facts.
5. In the narrow sense it has been defined as the science of counting and science of averages.

Question 22.
What are the kinds of Statistics?
Answer:
Types of Statistics:
1. There are two major types of statistics named as Descriptive Statistics and Inferential Statistics.

2. Descriptive Statistics:
The branch of statistics devoted to the summarization and description of data is called Descriptive Statistics.

3. Inferential Statistics:
The branch of statistics concerned with using sample data to make an inference about a population of data is called Inferential Statistics.

Question 23.
What do you mean by Inferential Statistics?
Answer:
Inferential Statistics:

1. The branch of statistics concerned with using sample data to make an inference about a population of data is called Inferential Statistics.
2. It draws conclusion for the population based on the sample result.
3. It uses hypotheses, testing and predicting on the basis of the outcome.
4. It tries to understand the population beyond the sample.

Question 24.
What are the kinds of data?
Answer:

Question 25.
Define Correlation?
Answer:
Correlation is a statistical device that helps to analyse the covariation of two or more variables. Sir Francis Galton, is responsible for the calculation of correlation coefficient.

Question 26.
Define Regression?
Answer:

1. The term ‘Regression’ was first coined and used in 1877 by Francis Galton while studying the relationship between the height of fathers and sons.
2. The average height of children bom of parents of a given height tended to move or “regress” toward the average height in the population as a whole.
3. Gabon’s law of universal regression was confirmed by his friend Karl Pearson, who collected more than a thousand records of heights of members of family groups.
4. The literal meaning of the word “regression” is “Stepping back towards the average”.

Question 27.
What is Econometrics?
Answer:
Origin Of Econometrics:

1. Economists tried to support their ideas with facts and figures in ancient times.
2. Irving Fisher is the first person, developed mathematical equation in the quantity theory of money with help of data.
3. Ragnar Frisch, a Norwegian economist and statistician named the integration of three subjects such that mathematics, statistical methods and economics as Econometrics” in 1926.

Part – C
Answer The Following Questions In One Paragraph.

Question 28.
What are the functions of Statistics?
Answer:
Functions of Statistics:

1. Statistics presents facts in a definite form.
2. It simplifies mass of figures.
3. It facilitates comparison.
4. It helps in formulating and testing.
5. It helps in prediction.
6. It helps in the formulation of suitable policies.

(I) Statistics are an aggregate of facts:
For example, numbers in a calendar pertaining to a year will not be called statistics, but to be included in statistics it should contain a series of figures with relationships for a prolonged period.

(II) Statistics are numerically enumerated, estimated and expressed.

(III) Statistical collection should be systematic with a predetermined purpose:
The purpose of collection of statistics should be determined beforehand in order to get accurate information.

(IV) Should be capable of being used as a technique for drawing comparison:
It should be capable of drawing comparison between two different sets of data by tools such as averages, ratios, rates, coefficients etc.

Question 29.
Find the Standard Deviation of the following data:
14, 22, 9, 15, 20, 17, 12, 11


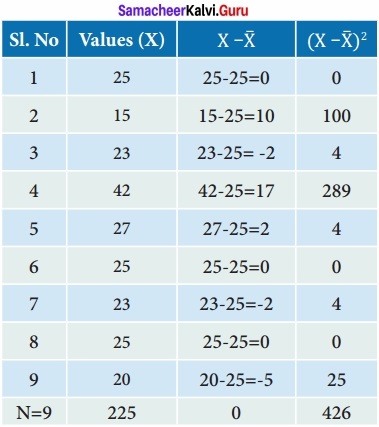
∴ σ = 4.18

Question 30.
State and explain the different kinds of Correlation?
Answer:

Type I:
Based on the direction of change of variables:
Correlation is classified into two types as Positive correlation and Negative Correlation based on the direction of change of the variables.

Positive Correlation:
The correlation is said to be positive if the values of two variables move in the same direction.

Ex 1:
If income and Expenditure of a Household may be increasing or decreasing simultaneously. If so, there is positive correlation. Ex. Y = a + bx

Negative Correlation:
The Correlation is said to be negative when the values of variables move in the opposite directions. Ex. Y = a – bx

Ex 1:
Price and demand for a commodity move in the opposite direction.

Type II:
Based upon the number of variables studied
There are three types based upon the number of variables studied as

1. Simple Correlation
2. Multiple Correlation
3. Partial Correlation

Simple Correlation:
If only two variables are taken for study then it is said to be simple correlation. Ex. Y = a + bx

Multiple Correlations:
If three or more than three variables are studied simultaneously, then it is termed as multiple correlation.

Ex: Determinants of Quantity demanded
Qd = f (P, Pc, Ps, t, y)
Where Qd stands for Quantity demanded, f stands for function.
P is the price of the goods,
P_c is the price of competitive goods
P_s is the price of substituting goods
t is the taste and preference
y is the income.

Partial Correlation:
If there are more than two variables but only two variables are considered keeping the other variables constant, then the correlation is said to be Partial Correlation.

Type III: Based upon the constancy of the ratio of change between the variables

Correlation is divided into two types as linear correlation and Non – Linear correlation based upon the Constancy of the ratio of change between the variables.

Linear Correlation:
Correlation is said to be linear when the amount of change in one variable tends to bear a constant ratio to the amount of change in the other.
Ex. Y = a + bx

Non Linear:
The correlation would be non-linear if the amount of change in one variable does not bear a constant ratio to the amount of change in the other variables.
Ex. Y = a + bx²

Question 31.
Mention the uses of Regression Analysis?
Answer:
Use of Regression Analysis:

1. Regression means going back and it is a mathematical measure showing the average relationship between two variables.
2. Both the variables may be random variables.
3. It indicates the cause and effect relationship between the variables and establishes functional relationship.
4. Besides verification it is used for the prediction of one value, in relation to the other given value.
5. Regression coefficient is an absolute figure. If we know the value of the independent variable, we can find the value of the dependent variable.
6. In regression there is no such spurious regression.
7. It has wider application, as it studies linear and nonlinear relationship between the variables.
8. It is widely used for further mathematical treatment.

Question 32.
Specify the objectives of econometrics?
Answer:
Objectives of Econometrics:
The general objective of Econometrics is to give empirical content to economic theory. The specific objectives are as follows:

1. It helps to explain the behaviour of a forthcoming period that is forecasting economic phenomena.
2. It helps to prove the old and established relationships among the variables or between the variables
3. It helps to establish new theories and new relationships.
4. It helps to test the hypotheses and estimation of the parameter.

Question 33.
Differentiate the economic model with econometric model?
Answer:
Economic Model:

1. Economic model is the theoretical construct that represents the complex economic process.
2. Economic model is based on mathematical modeling.
3. Economic model is focused on establishing the logical relationships between the variables in the model.
4. Economic model is applied in stating the theoretical relationship into mathematical equations.
5. Economic model believes that outcome is certain and exact. So disturbance term is not required.
6. Economic model is deterministic in nature.
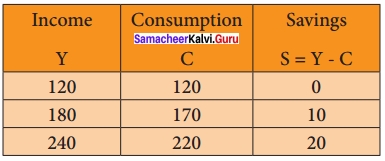
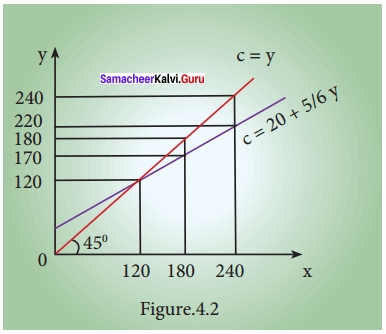
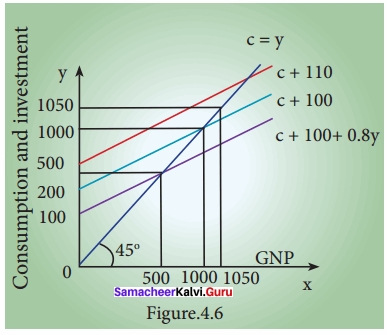
7. The Keynesian consumption function: C = a + by is the economic model

Econometric Model:

1. Econometric model is the statistical concept that represents the numerical estimate of the variables involved in economic process.
2. Econometric model is based on statistical modeling.
3. Econometric model is focused on estimating the magnitude and direction of relationship between the variables.
4. Econometric model is applied in stating the empirical extent of the economic model.
5. Econometric model believes that outcome is certain but not exact. So disturbance term plays the vital role.
6. Econometric model is stochastic in nature.
7. The Keynesian consumption function: C = a + by + µ is the econometric model

Question 34.
Discuss the important statistical organizations (offices) in India?
Answer:

1. Official Statistics are statistics published by government agencies or other public bodies such as international organizations.
2. They provide quantitative or qualitative information on all major areas of citizens’ lives.
3. Official Statistics make information on economic and social development accessible to the public, allowing the impact of government policies to be assessed, thus improving accountability.
4. The Ministry of Statistics and Programme Implementation (MOSPI) came into existence as an Independent Ministry in 1999 after the merging of the Department of Statistics and the Department of Programme Implementation.
5. The Ministry has two wings, Statistics and Programme Implementation.

National Sample Survey Organisation (NSSO):

1. The National Sample Survey Organisation, now known as National Sample Survey Office, is an organization under the Ministry of Statistic of the Government of India.
2. It is the largest organisation in India, conducting regular socio-economic surveys.
3. It was established in 1950. NSSO has four divisions:
   1. Survey Design and Research Division (SDRD)
   2. Field Operations Division (FOD)
   3. Data Processing Division (DPD)
   4. Co-ordination and Publication Division (CPD)

The Programme Implementation Wing has three Divisions, namely,

1. Twenty Point Programme
2. Infrastructure Monitoring and Project Monitoring
3. Member of Parliament Local Area Development Scheme.

Besides these three wings, there is National Statistical Commission created through a Resolution of Government of India (MOSPI) and one autonomous Institute, viz., Indian Statistical Institute declared as an institute of National importance by an Act of Parliament.

Part – D
Answer The Following Questions.

Question 35.
Elucidate the nature and scope of Statistics?
Nature of Statistics:

1. Different Statisticians and Economists differ in views about the nature of statistics, some call it a science and some say it is an art.
2. Tipett on the other hand considers Statistics both as a science as well as an art.

Scope of Statistics:
Statistics is applied in every sphere of human activity – social as well as physical – like Biology, Commerce, Education, Planning, Business Management, Information Technology, etc.

Statistics and Economics:

1. Statistical data and techniques are immensely useful in solving many economic problems
2. Such as fluctuation in wages, prices, production, distribution of income and wealth and so on.

Statistics and Firms:
Statistics is widely used in many firms to find whether the product is conforming to specifications or not.

Statistics and Commerce:

1. Statistics are life blood of successful commerce.
2. Market survey plays an important role to exhibit the present conditions and to forecast the likely changes in future.

Statistics and Education:

1. Statistics is necessary for the formulation of policies to start new course, according to the changing environment.
2. There are many educational institutions owned by public and private engaged in research and development work to test the past knowledge and evolve new knowledge.
3. These are possible only through statistics.

Statistics and Planning:
1. Statistics is indispensable in planning. In the modem world, which can be termed as the “world of planning”, almost all the organisations in the government are seeking the help of planning for efficient working, for the formulation of policy decisions and execution of the same.

2. In order to achieve the above goals, various advanced statistical techniques are used for processing, analyzing and interpreting data.

3. In India, statistics play an important role in planning, both at the central and state government levels, but the quality of data highly unscientific.

Statistics and Medicine:

1. In Medical sciences, statistical tools are widely used. In order to test the efficiency of a new drug or to compare the efficiency of two drugs or two medicines, t – test for the two samples is used.
2. More and more applications of statistics are at present used in clinical investigation.

Statistics and Modern applications:

1. Recent developments in the fields of computer and information technology have enabled statistics to integrate their models and thus make statistics a part of decision making procedures of many organisations.
2. There are many software packages available for solving simulation problems.

Question 36.
Calculate the Karl Pearson Correlation Co-efficient for the following data?
Answer:

Question 37.
Find the regression equation Y on X and X on Y for the following data?
Answer:



= \(\frac { 16810 }{ 17250-225 } \) = 1.01
X on Y
X – \(\bar { X } \) = b_Xy (Y – \(\bar { Y } \) )
X – 43.5 = 1.01 (Y – 64.5)
X – 43.5 = 1.01 Y – 65.145 [64.5 × 1.01]
X – 43.5 = 1.01 Y – 65.145
X – 43.5 = 0.01 Y – [65.145 – 43.5]
X = 0.01 Y – 21.645

Question 38.
Describe the application of Econometrics in Economics?
Answer:
Origin Of Econometrics:

• Economists tried to support their ideas with facts and figures in ancient times.
• Irving Fisher is the first person, developed mathematical equation in the quantity theory of money with help of data.
• Ragnar Frisch, a Norwegian economist and statistician named the integration of three subjects such that mathematics, statistical methods and economics as Econometrics” in 1926. Ragnar Anton Kittil Frisch Noble Memorial Prize in 1969.
• The term econometrics is formed from two words of Greek origin, ‘oukovouia’ meaning economy and ‘uetpov’ meaning measure. Econometrics emerged as an independent discipline studying economics phenomena.
• Econometrics may be considered as the integration of economics, Statistics and Mathematics.
• Econometrics is an amalgamation of three subjects which can be easily understood by following Venn diagram and picture representation.
• Economics + Mathematics = Mathematical Economics
• Mathematical Economics + Statistical Data & Its Technique = Econometrics
• {Economics + Statistics + Mathematics} + Empirical Data = Econometrics

Definitions:

• In the words of Arthur S. Goldberger, “Econometrics may be defined as the social science in which the tools of economic theory, mathematics and statistical inference are applied to the analysis of economic phenomena”.
• Gerhard Tinbergen points out that “Econometrics, as a result of certain outlook on the role of economics, consists of application of mathematical statistics to economic data to lend empirical support to the models constructed by mathematical economics and to obtain numerical results”.
• H Theil“Econometrics is concerned with the empirical determination of economic laws”
• In the words of Ragnar Frisch “The mutual penetration of quantitative econometric theory and statistical observation is the essence of econometrics”.
• Econometrics means economic measurement. Econometrics deals with the measurement of economic relationships.

Objectives Of Econometrics:
The general objective of Econometrics is to give empirical content to economic theory. The specific objectives are as follows:

1. It helps to explain the behaviour of a forthcoming period that is forecasting economic phenomena.
2. It helps to prove the old and established relationships among the variables or between the variables
3. It helps to establish new theories and new relationships.
4. It helps to test the hypotheses and estimation of the parameter.

Samacheer Kalvi 12th Economics Introduction to Statistical Methods and Econometrics Additional Questions and Answers

Part – A
I. Multiple Choice Questions.

Question 1.
The term statistics originated in the Latin word known as ………………………….
(a) Statistik
(b) Status
(c) Statisque
(d) Statistics
Answer:
(b) Status

Question 2.
The fundamental principles of statistics were developed by the biologist ………………………….
(a) Ronald Fisher
(b) Gottfried Achenwall
(c) R.A. Fisher
(d) GR Neison
Answer:
(a) Ronald Fisher

Question 3.
The first book to have statistics as its title was ………………………….
(a) Contributions to vital statistics
(b) Principles of statistics
(c) Statistics principles
(d) Statistics probabilities
Answer:
(a) Contributions to vital statistics

Question 4.
The subjects of statistics can be attributed to ………………………….
(a) Francis GP. Neison
(b) Ronald Fisher
(c) Gottfried Achenwall
(d) R.A. Fisher
Answer:
(d) R.A. Fisher

Question 5.
To prepare a systematic study of birth and death related data is called ………………………….
(a) Principles of statistics
(b) Contributions of vital statistics
(c) Subject of statistics
(d) Statistics evolution
Answer:
(b) Contributions of vital statistics

Question 6.
Who is the father of statistics?
(a) Gottfried Achenwall
(b) Francis GP. Neison
(c) Ronald Fisher
(d) R.A. Fisher
Answer:
(d) R.A. Fisher

Question 7.
…………………………. form helps in the collection, presentation, classificationandinterpretation of data make it easily comprehensible.
(a) Singular form
(b) Plural form
(c) Collection form
(d) Presentation form
Answer:
(a) Singular form

Question 8.
Statistics is applied in every sphere of ………………………….
(a) Physical activity
(b) Human activity
(c) Maths activity
(d) Statistics activity
Answer:
(b) Human activity

Question 9.
Statistical data and techniques are immensely useful in solving many …………………………. problems.
(a) Statistical
(b) Technical
(c) Economic
(d) Maths
Answer:
(c) Economic

Question 10.
Statistics are life blood of successful ………………………….
(a) Maths
(b) Datas
(c) Calculations
(d) Commerce
Answer:
(d) Commerce

Question 11.
In the modem world, which can be termed as the “World of planning”?
(a) Statistics
(b) Datas
(c) Numerical data
(d) Five year plan
Answer:
(a) Statistics

Question 12.
Since 2007, 29^th June every year is celebrated as …………………………
(a) Economic day
(b) Datas day
(c) Statistics day
(d) Planning day
Answer:
(c) Statistics day

Question 13.
In India, statistics play an important role of planning, both at the central and ……………………….. government levels.
(a) State
(b) Local
(c) District
(d) National
Answer:
(a) State

Question 14.
Statistical tools are widely used in …………………………..
(a) Statistical science
(b) Technical science
(c) Medical science
(d) Engineering science
Answer:
(c) Medical science

Question 15.
The branch of statistics devoted to the summerization and description of data is called ………………………… statistics.
(a) Descriptive
(b) Inferential
(c) Qualitative
(d) Quantitative
Answer:
(a) Descriptive

Question 16.
The branch of statistics concerned with using sample data is called ……………………… statistics.
(a) Descriptive
(b) Qualitative
(c) Descriptive
(d) Inferential
Answer:
(d) Inferential

Question 17.
…………………………. are those that can be quantified in definite units of measurement
(a) Quantitative
(b) Qualitative
(c) Descriptive
(d) Inferential
Answer:
(a) Quantitative

Question 18.
……………………….. is called a measure of central tendency or an average or a measure of location.
(a) Arithmetic mean
(b) Mean
(c) Cental value
(d) Geometric mean
Answer:
(c) Cental value

Question 19.
…………………….. is one of the methods of Absolute measure of dispersion.
(a) Standard Deviation
(b) Arithmetic mean
(c) Mean
(d) Median
Answer:
(a) Standard Deviation

Question 20.
…………………… is a statistical device that helps to analyse the covariation of two or more variables.
(a) Deviation
(b) Standard deviation
(c) Correlation
(d) Median
Answer:
(c) Correlation

Question 21.
………………………. Method is very simple and non-mathematical method.
(a) Scatter Diagram
(b) Graphic
(c) Karl Pearson’s
(d) Actual mean
Answer:
(a) Scatter Diagram

Question 22.
The literal meaning of the word “Regression” is stepping back towards the …………………………….
(a) Standard deviation
(b) Mean deviation
(c) Average
(d) Median
Answer:
(c) Average

Question 23.
…………………………. may be considered as the integration of economics, statistics and mathematics.
(a) Mathematical economics
(b) Statistical economics
(c) Technic economics
(d) Econometrics
Answer:
(d) Econometrics

Question 24.
The Central statistical office is one of the two – wings of the …………………………
(a) State statistical organisation
(b) National statistical organisation
(c) District statistical organisation
(d) World statistical organisation
Answer:
(b) National statistical organisation

II. Match The Following And Choose The Correct Answer By Using Codes Given Below.

Question 1.
A. Galton – (i) Principle of statistics
B. Ragnar Frisch – (ii) Regression
C. P.C. Mohalanobis – (iii) Econometrics
D. Ronald Fisher – (iv) Modem Statistics
Codes:
(a) A (i) B (ii) C (iii) D (iv)
(b) A (ii) B (iii) C (iv) D(i)
(c) A (iii) B (iv) C (i) D (ii)
(d) A (iv) B (i) C (ii) D (iii)
Answer:
(b) A (ii) B (iii) C (iv) D(i)

Question 2.
A. Statistics – (i) Solving economic problems
B. Statistical data – (ii) Successful commerce
C. Statistical tools – (iii) World of planning
D. Statistics life blood – (iv) Medical science
Codes:
(a) A (i) B (ii) C (iii) D (iv)
(b) A (ii) B (iv) C (i) D (iii)
(c) A (iii) B (i) C (iv) D (ii)
(d) A (iv) B (iii) C (ii) D(i)
Answer:
(c) A (iii) B (i) C (iv) D (ii)

Question 3.
A. Types of statistics – (i) Central value
B. Statistics data categories – (ii) Primary data
C. Collection of data – (iii) Central value
D. Measure of central tendency – (iv) Descriptive statistics
Codes:
(a) A (i) B (ii) C (ii) D (iv)
(b) A (iv) B (iii) C (ii) D(i)
(c) A (iii) B (i) C (iv) D (ii)
(d) A (ii) B (iv) C (i) D (iii)
Answer:
(b) A (iv) B (iii) C (ii) D(i)

Question 4.
A. Karl Pearson – (i) Regression
B. Measures of dispersion – (ii) Standard Deviation
C. Sir. Francis Galton – (iii) Absolute
D. Stepping back towards the average – (iv) Correlation
Codes:
(a) A (i) B (ii) C (iii) D (iv)
(b) A (iii) B (iv) C (i) D (ii)
(c) A (iv) B (i) C (ii) D (iii)
(d) A (ii) B (iii) C (iv) D(i)
Answer:
(d) A (ii) B (iii) C (iv) D(i)

Question 5.
A. NSSO – (i) 1999
B. MOSPI – (ii) 1877
C. Francis Galton – (iii) 1890 – 1962
D. R.A. Fisher – (iv) 1950
Codes:
(a) A (i) B (ii) C (iii) D (iv)
(b) A (iii) B (iv) C (i) D (ii)
(c) A (iv) B (i) C (ii) D (iii)
(d) A (ii) B (iii) C (iv) D (i)
Answer:
(c) A (iv) B (i) C (ii) D (iii)

Question 6.
A. Francis GP. Neison – (i) England
B. Gottfried Achenwall – (ii) Contributions to vital statistics
C. Ronald Fisher – (iii) P.C. Mahalanobis
D. Modem statistics – (iv) Statistik
Codes:
(a) A (i) B (ii) C (iii) D (iv)
(b) A (iii) B (i) C (iv) D (ii)
(c) A (ii) B (iv) C (i) D (iii)
(d) A (iv) B (iii) C (ii) D(i)
Answer:
(c) A (ii) B (iv) C (i) D (iii)

III. Choose The Correct Statement:

Question 1.
(i) Statistics is indispensable planning.
(ii) In the modem world, it can be termed as the “World of planning”.

(a) Both (i) and (ii) are true
(b) Both (i) and (ii) are false
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(a) Both (i) and (ii) are true

Question 2.
(i) Statistical data and techniques are immensely useful in solving many economic problems.
(ii) Fluctuation in Inflation, Deflation.

(a) Both (i) and (ii) are true
(b) Both (i) and (ii) are false
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(c) (i) is true but (ii) is false

Question 3.
(i) Quantitative data are those that can be quantified in definite units of measurement.
(ii) These refer to characteristics in successive measurements yield quantifiable observations.

(a) Both (i) and (ii) are true
(b) Both (i) and (ii) are false
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(a) Both (i) and (ii) are true

Question 4.
(i) Karl Pearson introduced the concept of Standard deviation.
(ii) Standard Deviation is one of the methods of Relative measure of dispersion.

(a) Both (i) and (ii) are true
(b) Both (i) and (ii) are false
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(c) (i) is true but (ii) is false

Question 5.
(i) The term econometrics is formed from two words of Greek origin, ‘Oukovovia’ meaning economy and ‘vetpov’ meaning measure.
(ii) Econometrics may be considered as integration of economics, statistics and mathematics.

(a) Both (i) and (ii) are true
(b) Both (i) and (ii) are false
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(a) Both (i) and (ii) are true

IV. Which of The Following Is Correctly Matched.

Question 1.
(a) Gottfried Achenwall – Statistics
(b) GP. Neison – Contributions to vital statistics
(c) Ronald Fisher – Movemental contribution
(d) Modem statistics – Ronald Fisher
Answer:
(b) GP. Neison – Contributions to vital statistics

Question 2.
(a) Quantitative data – Gender, community
(b) Qualitative data – Age, income
(c) Nominal data – Classification of students
(d) Rank data – Collection of data
Answer:
(c) Nominal data – Classification of students

Question 3.
(a) Central value – Measure of central tendency
(b) Dispersion – Average
(c) Standard Deviation – Ronald Fisher
(d) Sir Francis Galton – Graphic Method
Answer:
(a) Central value – Measure of central tendency

Question 4.
(a) Francis Galton – Stepping back towards the average
(b) Irving Fisher – Data
(c) Ragner Frisch – Technique
(d) Econometrics – Economy + Metrics
Answer:
(a) Francis Galton – Stepping back towards the average

Question 5.
(a) Arthur S. Gold Berger – Maths
(b) Gerherd Tinbergen – Social
(c) H. Theil – Economic laws
(d) Ragnar Frisch – Statistics
Answer:
(c) H. Theil – Economic laws

V. Which of The Following is Not Correctly Matched.

Question 1.
(a) Statistic Regression – Y₁ = β₀ + β₁X₁
(b) Econometrics Regression – Y₁ = β₀ + β₁X₁ + U₁
(c) Regression lines – X on Y ⇒ X = a + by
(d) Actual Mean Method = \(\frac { \Sigma X }{ N } \)
Answer:
(d) Actual Mean Method = \(\frac { \Sigma X }{ N } \)

Question 2.
(a) SDRD – Survey Design and Research Division
(b) FOD – Field Operations Division
(c) DPD – Division Processing Data
(d) CPD – Co – Operation and Publication Division
Answer:
(c) DPD – Division Processing Data

Question 3.
(a) NSO – National Statistical Office
(b) CSO – Cental Statistical Office
(c) NSSO – National Sample Survey Organisation
(d) NAD – National Arithematic Division
Answer:
(d) NAD – National Arithematic Division

Question 4.
(a) NAD – National Accounts Division
(b) SSD – Social Stastistics Division
(c) ESD – Economic Social Division
(d) TD – Training Division
Answer:
(c) ESD – Economic Social Division

Question 5.

Answer:

VI. Pick The Odd One Out.

Question 1.
Functions of Statistics
(a) Statistics presents facts in a definite form
(b) It simplifies mass of figures
(c) It helps firms
(d) It helps in formulating and testing
Answer:
(c) It helps firms

Question 2.
Based upon the number of variables studied as
(a) Simple correlation
(b) Multiple correlation
(c) Partial correlation
(d) Linear correlation
Answer:
(d) Linear correlation

Question 3.
Methods of studying correlation
(a) Scatter diagram method
(b) Graphic method
(c) Maths method
(d) Method of least squares
Answer:
(c) Maths method

Question 4.
NSSO divisions are
(a) Survey Design and Research Division [SDRD]
(b) Fashion Operation Division [FOD]
(c) Data Processing Division [DPD]
(d) Co – ordination and Publication Division [CPD]
Answer:
(b) Fashion Operation Division [FOD]

Question 5.
CSO Director Generals are
(a) National Accounts Division [NAD]
(b) Sample Statistics Division [SSD]
(c) Economic Statistics Division [ESD]
(d) Co – ordination and Publication Division [CPD]
Answer:
(b) Sample Statistics Division [SSD]

VII. Assertion and Reason.

Question 1.
Assertion (A): The monumental contribution to the subject of statistics can be attributed to R.A. Fisher was able to apply statistics to a variety.
Reason (R): Fields such as Biometry, Genetics, Psychology, Education, Agriculture and others.

(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’

Question 2.
Assertion (A): In singular form it simply means simple method.
Reason (R): Singular forms help in the collection, presentation, classification and interpretation of data.

(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(d) ‘A’ is false but ‘R’ is true

Question 3.
Assertion (A): Statistics is indispensable in planning.
Reason (R): In the modem world, which can be termed as the “World of Planning” almost all organisations.

(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’

Question 4.
Assertion (A): Quantitative data are those that can be quantified in definite units of measurement.
Reason (R): These refer to characteristics of a subject or an object.

(a) Both ‘A’ and ‘R’ are tme and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are tme but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(c) ‘A’ is true but ‘R’ is false

Question 5.
Assertion (A): Ronald Fisher introduced the concept of Standard Deviation.
Reason (R): Standard Deviation is one of the methods of Absolute measure of dispersion.

(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(d) ‘A’ is false but ‘R’ is true

Part – B
Answer The Following Questions In One or Two Sentences.

Question 1.
Write five averages?
Answer:

1. There are five averages.
2. Among them mean, median and mode are called simple averages and the other two averages geometric mean and harmonic mean are called special averages.

Question 2.
Write meaning of averages?
Answer:

1. “A measure of central tendency is a typical value around which other figures congregate.”
2. “An average stands for the whole group of which it forms a part yet represents the whole.”
3. “One of the most widely used set of summary figures is known as measures of location.”

Question 3.
Write the kinds of dispersion?
Answer:
There are two kinds of measures of dispersion, namely

1. Absolute measure of dispersion
2. Relative measure of dispersion

Question 4.
Explain the calculation of standard deviation individual series?
Answer:
Calculation of Standard deviation-individual Series:
There are two methods of calculating Standard deviation in an individual series.
(a) Deviations taken from Actual mean
(b) Deviation taken from Assumed mean
Standard Deviation =
Where, \(\bar { X } \) = mean value of distribution
n = number of observations

Question 5.
Write the four methods of studying correlation?
Answer:
Methods of Studying Correlation:
The various methods of ascertaining whether two variables are correlated or not are:

1. Scatter diagram Method
2. Graphic Method
3. Karl Pearson’s Co-efficient of correlation and
4. Method of Least Squares.

Question 6.
Explain the advantages of Scatter diagram method?
Answer:
Advantages of Scatter Diagram method:

1. It is very simple and non- mathematical method
2. It is not influenced by the size of extreme item.
3. It is the first step in resting the relationship between two variables.

Question 7.
Write the two regression lines?
Answer:
Two Regression lines:
X on Y => X = a + by
Y on X => Y = a + bx

Question 8.
Write flow chart of Anatomy/Methodology of Econometrics?
Answer:
Flow Chart of Anatomy / Methodology of Econometrics:
Anatomy of Econometric Modeling

Question 9.
Explain the statistics and econometrics regression equations?
Answer:
Statistics Regression:
Yi = β₀ + β₁X₁
Econometrics Regression:
Yi = β₀ + β₁X_i + U_i
(with more than 2 variables) or
Y = β₀ + β₁X₁ + β₂X₂ + β₃X₃ + U_i

1. Systematic Part: β₀ + β₁X₁ or explained part and Random Part: U_f unexplained part in a regression.
2. U_i represents the role of omitted variables in specifying a regression relationship of Y on X.
3. Hence, the U_i cannot and should not be ignored.

Part – C
Answer The Following Questions In One Paragraph.

Question 1.
Explain the sources of collection of data?
Answer:
Sources of Collection of data:
Based on the data sources, data could be seen as of two types, viz., secondary data and primary data. The two can be defined as under:

(I) Primary data:

1. Those data which do not already exist in any form, and thus have to be collected for the first time from the primary source(s).
2. By their very nature, these data are fresh and first-time collected covering the whole population or a sample drawn from it.

(II) Secondary data:

1. They already exist in some form: published or unpublished in an identifiable secondary source.
2. They are, generally, available from published source(s), though not necessarily in the form actually required, e.g. Data from CSO, NSSO, RBI….

Question 2.
Briefly explain the kinds of measures of dispersion?
Answer:
There are two kinds of measures of dispersion, namely

1. Absolute measure of dispersion
2. Relative measure of dispersion

Absolute measure of dispersion indicates the amount of variation in a set of values in terms of units of observations. Relative measures of dispersion are free from the units of measurements of the observations. They are pure numbers. They are used to compare the variation in two or more sets, which are having different units of measurements of observations. Standard Deviation is one of the methods of Absolute measure of dispersion.

Karl Pearson introduced the concept of standard deviation in 1893. Standard deviation is also called Root- Mean Square Deviation. The reason is that it is the square – root of the mean of the squared deviation from the arithmetic mean. It provides accurate result. Square of standard deviation is called Variance.

Question 3.
Briefly explain the calculation of standard deviation individual series steps?
Answer:
Steps:

1. Find out the actual mean of given data ( \(\bar { X } \) )
2. Find out the deviation of each value from the mean (x = X – \(\bar { X } \) )
3. Square the deviations and take the total of squared deviations Σx²
4. Divided the total Σx² by the number of observation ( \(\frac { \Sigma x^{ 2 } }{ n } \) )
5. The square root of ( \(\frac { \Sigma x^{ 2 } }{ n } \) ) is standard deviation.

\(\frac { \Sigma x^{ 2 } }{ n } \) = Variance = \(\frac { \Sigma (x-\bar { x } )^{ 2 } }{ n } \)
When the sample size is less than 30, variance = \(\frac { \Sigma (x-\bar { x } )^{ 2 } }{ n-1 } \)
When n = number of observations.

Question 4.
Calculate the standard deviation from the following data by Actual Mean Method?
125, 15, 23, 42, 27, 25, 23, 25 and 20
Solution:
Deviations from actual mean.

\(\bar { X } \) = \(\frac{225}{9}\) = 25

σ = 6.88

Question 5.
Calculate the standard deviation for the following data by assumed mean method?
[43, 48, 65, 57, 31, 60, 37, 48, 78, 59]
Solution:
Deviation from assumed mean

Question 6.
Write the assumptions of the Linear Regression Model?
Answer:
Assumptions of the Linear Regression Model:
The Linear regression model is based on certain assumptions

1. Some of them refer to the distribution of the random variable .
2. Some of them refer to the relationship between U_i and the explanatory variables (x₁, x₂, x₃ given in the above example).
3. Some of them refer to the relationship between U_i the explanatory variables themselves.

Part – D
Answer The Following Questions In About A Page.

Question 1.
Explain the Scatter Diagram Method. Advantages and Disadvantages with diagram?
Answer:
Scatter Diagram Method:

1. Scatter diagram is a graph of observed plotted points where each point represents the values of X and Y as a coordinate.
2. It portrays the relationship between these two variables graphically.

Advantages of Scatter Diagram method:

1. It is very simple and non- mathematical method
2. It is not influenced by the size of extreme item.
3. It is the first step in resting the relationship between two variables.

Disadvantages of Scatter diagram method:

1. It cannot establish the exact degree of correlation between the variables, but provides direction of correlation and depicts it is high or low.

Question 2.
Briefly explain Karl Pearson’s co-effecient of correlation?
Answer:
Karl Pearson’s Coefficient of Correlation:

1. Karl Pearson’s Method is popularly known as Pearson’s coefficient of correlation denoted by the symbol V.
2. The coefficient of correlation V measures the degree of linear relationship between two variables say X and Y.
3. The Formula for computing Karl Pearson’s Coefficient of correlation is:

(I)

‘r’ is caluculated by Direct Method without taking deviation of terms either from actual mean or assumed mean.

(II) r is calculated by taking the Deviation from actual mean.

(III) ‘r’ is caluculated by taking assumed mean

Where dx refers to deviations ofx series from assumed mean (x – \(\bar { x } \) ), dy refers to deviations of y series from an assumed mean of (y – \(\bar { y } \) )
Σdxdy = Sum of product of the deviations x and y series from their assumed means.
Σdx² = Sum of the squares of the deviation of x series from an assumed mean
Σdy² = Sum of the squares of the deviations of y series from an assumed mean
Σdx = Sum of the deviation of x series from an assumed mean of x
Σdy = Sum of the deviation of y series from an assumed mean of y

Question 3.
Explain the procedure for computing the correlation co – effecient for direct and deviation from actual mean method steps?
Answer:
Procedure for Computing the Correlation Coefficient: (For Direct and Deviation from actual mean method).

1. Step – 1 Calculate the mean of two series ‘X’ ‘Y’
2. Step – 2 Calculate the deviations ‘X’ and Y in two series from their respective mean.
3. Step – 3 Square each deviations of ‘X’ and ‘ Y’ then obtain the sum of the Squared deviation
4. Step – 4 Multiply each deviation under X with each deviation under Y and obtain the product of ‘xy’. Then obtain the sum of the product of X, Y. Then obtain the sum of the product of x, y is Σxy.
5. Step – 5 Substitute the value in the formula.

Question 4.
State the formula of Karl Pearson’s co – effecient of correlation upgrouped data?

1. Direct Method:
(I)

(II) Assumed Mean Deviation Method

2. Indirect Method:
dx = (x – \(\bar { x } \) ) and dy = (y – \(\bar { y } \) )
r is free from origin
r is free from unit of measurement -1 ≤ r ≤ + 1

Question 5.
Calculate Karl Pearson’s Coefficient of correlation from the following data and interpret its value:

Solution: Let us take Price as X and supply as Y
Computation of Pearson’s Correlation Coefficient:



Price of the product and supply for the product is positively correlated. When price of the product increases then the supply for the product also increases.

Question 6.
Estimate the coefficient of correlation with actualmean method for the following data?

Solution:


Applying in Formula

r = 0.327, The Car is getting old in years the cost of maintainance is also increasing. The age of Car and its maintainance are positively correlated.

Question 7.
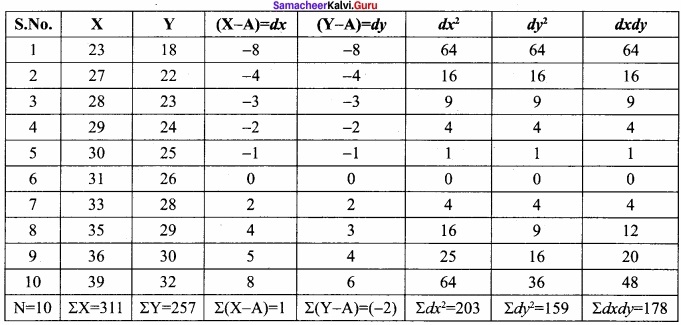
Find the Karl Pearson coefficient of Correlation between X and Y from the following data:

Solution:
Formula for Assumed Mean Deviation method.



Take the assumed values A = 16 & B = 27 therefore dx = X – A ⇒ X – 16 and
dy = Y – A ⇒ Y = 27

There exists a positive high correlation between X and Y.

Question 8.
Explain the difference between correlation and regression?
Answer:
Difference between Correlation and Regression:
Correlation:

1. Correlation is the relationship between two or more variables, which vary with the other in the same or the opposite direction.
2. Both the variables X and Y are random variables.
3. It finds out the degree of relationship between two variables and not the cause and effect relationship.
4. It is used for testing and verifying the relation between two variables and gives limited information.
5. The coefficient of correlation is a relative measure. The range of relationship lies between -1 and +1.
6. There may be spurious correlation between two variables.
7. It has limited application, because it is confined only to linear relationship between the variables.
8. It is not very useful for further mathematical treatment.

Regression:

1. Regression means going back and it is a mathematical measure showing the average relationship between two variables.
2. Both the variables may be random variables.
3. It indicates the cause and effect relationship between the variables and establishes functional relationship.
4. Besides verification it is used for the prediction of one value, in relation to the other given value.
5. Regression coefficient is an absolute figure. If we know the value of the independent variable, we can find the value of the dependent variable.
6. In regression there is no such spurious regression.
7. It has wider application, as it studies linear and nonlinear relationship between the variables.
8. It is widely used for further mathematical treatment.

Question 9.
Explain Fit the Regression equation on [X on Y]?
Answer:
Fit regression equation X on Y and Y on X for the following data.
\(\bar { X } \) = 12, \(\bar { Y } \) = 10, σy = 0.2, σx = 0.1 and r = 0.85
Solution:
The regression X on Y is
(X – \(\bar { X } \) ) r = r × \(\frac{σx}{σy}\) × (X – \(\bar { X } \) )
Given \(\bar { X } \) = 12, \(\bar { Y } \) = 10
r = 0.85, σx = 0.1 and σy = 0.2
Then substituting the values in formula
(X – 12) = 0.85 × (0.1/0.2) × (Y – 10)
(X – 12) = 0.85 × (0.5) × (Y – 10)
X = 0.425 × (Y – 10) + 12
X = 0.425 Y – 4.25 + 12
X = 0.425 Y + 7.75
Y on X
Y = 0.425 Y + 7.75

Question 10.
Explain Fit the Regression equation on [Y on X]?
Answer:
The regression Y on X is
(Y – \(\bar { Y } \) ) r = r × \(\frac{σx}{σy}\) × (X – \(\bar { X } \) )
Given \(\bar { X } \) = 12, \(\bar { Y } \) = 10
r = 0.85, σx = 0.1 and σy = 0.2
Then substituting the values in formula
(Y – 10) = 0.85 × (0.2/0.1) × (X – 12)
(Y – 10) = 0.85 × (2) × (X – 12)
Y = 1.7 × (X – 12) + 10
Y = 1.7 X – 20.4 + 10
Y = 1.7 X – 10.4
Y on X
Y = 1.7 X – 10.4

Question 11.
Briefly explain Methodology of Econometrics?
Answer:
Methodology of Econometrics:
Broadly speaking, traditional or classical econometric methodology consists of the following steps.

1. Statement of the theory or hypothesis
2. Specification of the mathematical model of the theory
3. Specification of the econometric model of the theory
4. Obtaining the data
5. Estimation of the parameters of the econometric model
6. Hypothesis testing
7. Forecasting or prediction
8. Using the model for control or policy purposes.

Question 12.
Explain the explanatory variables Assumptions?
Answer:
The explanatory variables are called assumptions.
Assumptions:

1. “U” is a random real variable. That is “U” may assume positive, negative or zero values. Hence the mean of the “U” will be zero.
2. The variance of “U” is constant for all values of “U”
3. The “U” has a normal distribution.
4. The Covariances of any U. with any other U are equal to zero
5. “U” is independent of explanatory variable (s)
6. Explanatory variables are measured without error.
7. The explanatory variables are not perfectly linearly correlated.
8. The variables are correctly aggregated.
9. The relationship is correctly identified and specified.
10. Parameters are linear.

Question 13.
Explain the flow chart of statistics and programme Implementation of the Ministry wings?
Answer:
The Ministry has two wings, Statistics and Programme Implementation

Share this Tamilnadu State Board 12th Economics Solutions Chapter 12 Introduction to Statistical Methods and Econometrics Questions and Answers with your friends to help them to overcome the grammar issues in exams. Keep visiting this site frequently to get the latest information on different subjects. Clarify your doubts by posting the comments and get the answers in an easy manner.

Students of 12th can get the pdf links of Tamilnadu State Board Economics Solutions here. You can Download Samacheer Kalvi 12th Economics Book Solutions Chapter 10 Environmental Economics Questions and Answers, Notes Pdf, Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Economics Solutions Chapter 10 Environmental Economics

It is very important to put the textbook aside while preparing for the exams. So, if you follow Samacheer Kalvi 12th Economics Textbook Solutions you can cover all the topics in Chapter 10 Environmental Economics Questions and Answers. This helps to improve your communication skills.

Samacheer Kalvi 12th Economics Environmental Economics Text Book Back Questions and Answers

Part – A
Multiple Choice Questions.

Question 1.
The term environment has been derived from a French word …………………………
(a) Environ
(b) Environs
(c) Environia
(d) Envir
Answer:
(c) Environia

Question 2.
The word biotic means environment
(a) Living
(b) Non – living
(c) Physical
(d) None of the the above
Answer:
(a) Living

Question 3.
Ecosystem is smallest unit of …………………………
(a) Ionosphere
(b) Lithosphere
(c) Biosphere
(d) Mesosphere
Answer:
(c) Biosphere

Question 4.
Who developed Material Balance Models?
(a) Thomas and Picardy
(b) Non – market goods
(c) Joan Robinson and J.M. Keynes
(d) Joseph Stiglitz and Edward Chamberlin
Answer:
(d) Joseph Stiglitz and Edward Chamberlin

Question 5.
Environmental goods are …………………………
(a) Market goods
(b) Non – market goods
(c) Both
(d) None of the above
Answer:
(b) Non – market goods

Question 6.
In a pure public good, consumption is …………………………
(a) Rival
(b) Non – rival
(c) Both
(d) None of the the above
Answer:
(a) Rival

Question 7.
One of the most important market failures is caused by …………………………
(a) Positive externalities
(b) Negative externalities
(c) Both
(d) None of the above
Answer:
(b) Negative externalities

Question 8.
The common source of outdoor air pollution is caused by combustion processes from the following …………………………
(a) Heating and cooking
(b) Traditional stoves
(c) Motor vehicles
(d) All the above
Answer:
(b) Traditional stoves

Question 9.
The major contributor of Carbon monoxide is …………………………
(a) Automobiles
(b) Industrial process
(c) Stationary fuel combustion
(d) None of the above
Answer:
(a) Automobiles

Question 10.
Which one of the following causes of global warming?
(a) Earth gravitation force
(b) Oxygen
(c) Centripetal force
(d) Increasing temperature
Answer:
(d) Increasing temperature

Question 11.
Which of the following is responsible for protecting humans from harmful ultraviolet rays?
(a) UY – A
(b) UV – C
(c) Ozone layer
(d) None of the above
Answer:
(c) Ozone layer

Question 12.
Global warming also refers to as …………………………
(a) Ecological change
(b) Climate Change
(c) Atmosphere change
(d) None of the above
Answer:
(d) None of the above

Question 13.
Which of the following is the anticipated effect of Global warming?
(a) Rising sea levels
(b) Changing precipitation
(c) Expansion of deserts
(d) All of the above
Answer:
(b) Changing precipitation

Question 14.
The process of nutrient enrichment is termed as …………………………
(a) Eutrophication
(b) Limiting nutrients
(c) Enrichment
(d) Schistosomiasis
Answer:
(b) Limiting nutrients

Question 15.
Primary cause of Soil pollution is …………………………
(a) Pest control measures
(b) Land reclamation
(c) Agricultural runoff
(d) Chemical fertilizer
Answer:
(d) Chemical fertilizer

Question 16.
Which of the following is main cause for deforestation?
(a) Timber harvesting industry
(b) Natural afforestation
(c) Soil stabilization
(d) Climate stabilization
Answer:
(a) Timber harvesting industry

Question 17.
Electronic waste is commonly referred as …………………………
(a) Solid waste
(b) Composite waste
(c) E – waste
(d) Hospital waste
Answer:
(c) E – waste

Question 18.
Acid rain is one of the consequences of ………………………… Air pollution.
(a) Water Pollution
(b) Land pollution
(c) Noise pollution
(d) Soil Pollution
Answer:
(a) Water Pollution

Question 19.
Sustainable Development Goals and targets are to be achieved by …………………………
(a) 2020
(b) 2025
(c) 2030
(d)2050
Answer:
(c) 2030

Question 20.
Alkali soils are predominantly located in the ………………………… plains?
(a) Indus – Ganga
(b) North – Indian
(c) Gangetic plains
(d) All the above
Answer:
(d) All the above

Part – B
Answer The Following Questions In One or Two Sentences.

Question 21.
State the meaning of environment?
Answer:

1. Meaning of Environmental Economics is a different branch of economics that recognizes the value of both the environment and economic activity and makes choices based on those values.
2. The goal is to balance the economic activity and the environmental impacts by taking into account all the costs and benefits.
3. In short, Environmental Economics is an area of economics that studies the financial impact of environmental issues and policies.
4. Environmental Economics involves theoretical and empirical studies of the economic effects of national or local environmental policies around the world.

Question 22.
What do you mean by ecosystem?
Answer:

1. An ecosystem includes all living things (plants, animals and organisms) in a given area, interacting with each other, and also with their non-living environments (weather, earth, sun, soil, climate, atmosphere).
2. Ecosystems are the foundations of the Biosphere and they determine the health of the entire earth system.

Question 23.
Mention the countries where per capita carbondioxide emission is the highest in the world?
Answer:

1. United States of America – (USA)
2. Europian Union – (EU)
3. Japan
4. Russian Federation
5. United Arab Emirates (UAE)
6. Saudi Arabia
7. China.

Question 24.
What are environmental goods? Give examples?
Answer:
1. Environmental goods are typically non-market goods, including clear air, clean water, landscape, green transport infrastructure (footpaths, cycle ways, greenways, etc.), public parks, urban parks, rivers, mountains, forests, and beaches.

2. Concerns with environmental goods focus on the effects that the exploitation of ecological systems have on the economy, the well – being of humans and other species, and on the environment.

Question 25.
What are the remedial measures to control noise pollution?
Answer:
Remedial measures to control Noise Pollution

1. Use of noise barriers
2. Newer roadway for surface transport
3. Traffic control
4. Regulating times for heavy vehicles
5. Installations of noise barriers in the work place
6. Regulation of Loudspeakers

Question 26.
Define Global warming?
Answer:
1. Global warming is the current increase in temperature of the Earth’s surface (both land and water) as well as its atmosphere. Average temperatures around the world have risen by 0.75°C (1.4°F) over the last 100 years. About two thirds of this increase has occurred since 1975.

Carbon dioxide, methane, Chlorofluoro Carbon, nitrous oxides are the green house gases warming the earth’s surface. So it is also called green house effect. The CO₂ is the most important of the green house gases contributing to 50% of global warming.

2. Global warming adversely affects agriculture, horticulture and eco system.

Question 27.
Specify the meaning of seed ball?
Answer:

1. A seed ball (or seed bomb) is a seed that has been wrapped in soil materials, usually a mixture of clay and compost, and then dried.
2. Essentially, the seed is ‘pre-planted’ and can be sown by depositing the seed ball anywhere suitable for the species, keeping the seed safely until the proper germination window arises.
3. Seed balls are an easy and sustainable way to cultivate plants that provide a larger window of time when the sowing can occur.

Part – C
Answer The Following Questions In One Paragraph.

Question 28.
Brief the linkage between economy and environment?
Answer:
Linkage between Economy and Environment:

1. Man’s life is interconnected with various other living and non-living things.
2. The life also depends on social, political, ethical, philosophical and other aspects of economic system.
3. In fact, the life of human beings is shaped by his living environment.
4. The relationship between the economy and the environment is generally explained in the form of a “Material Balance Model”.
5. The model considers the total economic process as a physically balanced flow between inputs and outputs.
6. Inputs are bestowed with physical property of energy which is received from the environment.
7. The interdependence of economics and environment.

Economy – Environmental Interlinkages Material Balance Model

Question 29.
Specify the meaning of material balance principle?
Answer:

1. The relationship between the economy and the environment is generally explained in the form of a “Material Balance Model” developed by AlenKneese and R.V. Ayres.
2. The model considers the total economic process as a physically balanced flow between inputs and outputs.
3. Inputs are bestowed with physical property of energy which is received from the environment.

1. The interdependence of economics and environment.

2. The first law of thermodynamics, i.e. the law of conservation of matter and energy, emphasizes that in any production system “what goes in must come out”. This is known as the Material Balance Approach or Material Balance Principle.

3. Moreover, all resources extracted from the environment eventually become unwanted wastes and pollutants. Production of output by firms from inputs resulting in discharge of solid, liquid and gaseous wastes. Similarly, waste results from consumption activities by households.

4. In its simple form the Material Balance Approach can be put in form equation.
M = G – R_C – R_P + R^r_P + R^r_c = R^d_c + R^d_c

Question 30.
Explain different types of air pollution?
Answer:
Types of Air pollution:
1. Indoor Air Pollution:
It refers to toxic contaminants that we encounter in our daily lives in our homes, schools and workplaces. For example, cooking and heating with solid fuels on open fires or traditional stoves results in high levels of indoor air pollution.

2. Outdoor Air Pollution:
It refers to ambient air. The common sources of outdoor air pollution are caused by combustion processes from motor vehicles, solid fuel burning and industry.

Question 31.
What are the causes of water pollution?
Answer:
Causes of Water Pollution:
Water pollution is caused due to several reasons. Here are the few major causes of water
pollution:

(I) Discharge of sewage and waste water:

1. Sewage, garbage and liquid waste of households, agricultural runoff and effluents from factories are discharged into lakes and rivers.
2. These wastes contain harmful chemicals and toxins which make the water poisonous for aquatic animals and plants.

(II) Dumping of solid wastes:
The dumping of solid wastes and litters in water bodies cause huge problems.

(III) Discharge of industrial wastes:
Industrial waste contains pollutants like asbestos, lead, mercury, grease oil and petrochemicals, which are extremely harmful to both people and environment.

(IV) Oil Spill:

1. Sea water gets polluted due to oil spilled from ships and tankers while travelling.
2. The spilled oil does not dissolve in water and forms a thick sludge polluting the water.

(V) Acid rain:

1. Acid rain is pollution of water caused by air pollution.
2. When the acidic particles caused by air pollution in the atmosphere mix with water vapor, it results in acid rain.

(VI) Global warming:
Due to global warming, there is an increase in water temperature as a result aquatic plants and animals are affected.

(VII) Eutrophication:

1. Eutrophication is an increased level of nutrients in water bodies.
2. This results in bloom of algae in water.
3. It also depletes the oxygen in water which negatively affects fish and other aquatic animal population.

Question 32.
State the meaning of e – waste?
Answer:
1. Electronic waste which is commonly referred as “e-waste” is the new byproduct of the Info Tech society.

2. It is a physical waste in the form of old discarded, end of life electronics.

3. It includes a broad and growing range of electronic devices from large household appliances such as refrigerators, air conditioners, cellular phones, computers and other electronic goods”.

4. Similarly, e-waste can be defined as the result when consumer, business and household devices are disposed or sent for re-cycling (example, television, computers, audio-equipments, VCR, DVD, telephone, Fax, Xerox machines, wireless devices, video games, other household electronic equipments).

Question 33.
What is land pollution? Mention the causes of land pollution?
Answer:
1. The land pollution is defined as, “the degradation of land because of the disposal of waste on the land”. Any substance (solid, liquid or gaseous) that is discharged, emitted or deposited in the environment in such a way that it alters the environment causes land pollution.

Causes of Land Pollution:

(I) Deforestation and soil erosion:

1. Deforestation carried out to create dry lands is one of the major concerns.
2. Land that is once converted into a dry or barren land, can never be made fertile again, whatever the magnitude of measures to convert it.

(II) Agricultural activities:

1. With growing human and pet animal population, demand for food has increased considerably.
2. Farmers often use highly toxic fertilizers and pesticides to get rid off insects, fungi and bacteria from their crops.
3. However the overuse of these chemicals, results in contamination and poisoning of land.

(III) Mining activities:
During extraction and mining activities, several land spaces are created beneath the surface.

(IV) Landfills:

1. Each household produces tones of garbage each year due to changing economic lifestyle of the people.
2. Garbage like plastic, paper, cloth, wood and hospital waste get accumulated.
3. Items that cannot be recycled become a part of the landfills that cause land pollution.

(V) Industrialization:

1. Due to increasing consumerism more industries were developed which led to deforestation.
2. Research and development paved the way for modem fertilizers and chemicals that were highly toxic and led to soil contamination.

(VI) Construction activities:

1. Due to urbanization, large amount of construction activities are taking place.
2. This has resulted in large waste articles like wood, metal, bricks, plastic.
3. These are dumped at the outskirts of urban areas that lead to land pollution.

(VII) Nuclear waste:

1. The leftover radioactive materials, harmful and toxic chemicals affect human health.
2. They are dumped beneath the earth to avoid any casualty.

Question 33.
Write a note on
(a) Climate change and
(b) Acid rain.
Answer:
(a) Climate Change:
1. The climate change refers to seasonal changes over a long period with respect to the growing accumulation of greenhouse gases in the atmosphere.

2. Recent studies have shown that human activities since the beginning of the industrial revolution, have contributed to an increase in the concentration of carbon dioxide in the atmosphere by as much as 40%, from about 280 parts per million in the pre-industrial period, to 402 parts per million in 2016, which in turn has led to global warming.

3. Several parts of the world have already experienced the warming of coastal waters, high temperatures, a marked change in rainfall patterns, and an increased intensity and frequency of storms. Sea levels and temperatures are expected to be rising.

(b) Acid Rain:

1. Acid rain is one of the consequences of air pollution.
2. It occurs when emissions from factories, cars or heating boilers contact with the water in the atmosphere.
3. These emissions contain nitrogen oxides, sulphur dioxide and sulphur trioxide which when mixed with water becomes sulfurous acid, nitric acid and sulfuric acid.
4. This process also occurs by nature through volcanic eruptions.
5. It can have harmful effects on plants, aquatic animals and infrastructure.

Part – D
Answer The Following Questions In About A Page.

Question 35.
Briefly explain the relationship between GDP growth and the quality of environment?
Answer:
GDP Growth:

1. Ross domestic product is the money value of final goods and services produced in the domestic territory of a country during an accounting year.
2. GDP can determined in 3 ways in all of which should in principle give the same result.
3. The real Economic GDP growth rate expressed as percentage that shows the rate of change in a countries GDP.
4. The Four supply Factors are natural resources capital goods, human resources and technology.
5. GDP is a monetary measure of the market value of all the final goods and services.
6. The contribution of the nature to GDP as well as depletion of natural resources are not accounted in the present system of National Income.

Quality of Environment:

1. Environmental quality is a set of properties and characteristics of the environment either generalized or local as they impinge on human beings and other organisms.
2. It is measure of condition of an environment relative to one or more species any human need or purpose.
3. Environmental quality has been continuously declining due to capitalistic mode of functioning.
4. Environment is a pure public good that can be consumed simultaneously by everyone and from which no one can be excluded.
5. A pure public good is one for which consumption is non-revival and from which it is impossible to exclude a consumer.
6. The environment directly affects health status and plays a major role in quality of life lived and good health disparties.

Question 36.
Explain the concepts of externality and its classification?
Answer:

Externalities refer to external effects or spillover effects resulting from the act of production or consumption on the third parties. Externalities arise due to interdependence between economic units.

Positive Consumption Externality:
When some residents of a locality hire a private security agency to patrol their area, the other residents of the area also benefit from better security without bearing cost.

Negative Consumption Externality:
A person smoking cigarette gets may gives satisfaction to that person, but this act causes hardship (dissatisfaction) to the non – smokers who are driven to passive smoking.

Positive Production Externality:

1. The ideal location for beehives is orchards (first growing fields).
2. While bees make honey, they also help in the pollination of apple blossoms.
3. The benefits accrue to both producers (honey as well as apple). This is called reciprocal untraded interdependency.
4. Suppose training is given for the workers in a company. If those trained workers leave the. company to join some other company, the later company gets the benefit of skilled workers without incurring the cost of training.

Negative Production Externality:

Question 37.
Explain the importance of sustainable development and its goals?
Answer:
Sustainable Development Goals (SDGs):
1. It is crucial to harmonize three core elements such as economic growth, social inclusion and environmental protection.

2. A set of 17 goals for the World’s future can be achieved before 2030 with three unanimous principles fixed by United Nations such as Universality, Integration and Transformation.

1. End Poverty in all its forms everywhere
2. End hunger, achieve food security and improved nutrition and promote sustainable agriculture
3. Ensure healthy lives and promote well-being for all at all ages
4. Ensure inclusive and quality education for all and promote lifelong learning
5. Achieve gender equality and empower women.and girls
6. Ensure access to water and sanitation for all
7. Ensure access to affordable, reliable, sustainable and modem energy for all.
8. Promote inclusive and sustainable economic growth, employment and decent work for all.
9. Build resilient infrastructure, promote sustainable industrialization and foster innovation.
10. Reduce inequality within and among countries
11. Make cities inclusive, safe, resilient and sustainable
12. Ensure sustainable consumption and production pattern
13. Take urgent action to combat climate change and its impacts
14. Conserve and sustainably use the oceans, seas and marine resources
15. Sustainably manage forests, combat desertification, halt and reverse land degradation, halt biodiversity loss
16. Promote just, peaceful and inclusive societies
17. Revitalize the global partnership for sustainable development.

Samacheer Kalvi 12th Economics Environmental Economics Additional Questions and Answers

Part – A
I. Multiple Choice Questions.

Question 1.
“All the conditions, circumstances, and influences surrounding and affecting the development of an organism or group of organisms” is called ………………………..
(a) Environment
(b) Economics
(c) Eco system
(d) Biosphere
Answer:
(a) Environment

Question 2.
The relationship between the Economy and the environment is generally explained in the form of a …………………….. model.
(a) Material Economic
(b) Material Eco
(c) Material balance
(d) Material Environment
Answer:
(c) Material balance

Question 3.
…………………….. Economics involves theoretical and empirical studies of the Economic effects.
(a) Biosphere
(b) Political
(c) Environment
(d) Philosphical
Answer:
(c) Environment

Question 4.
Environmental externalities are called ……………………..
(a) Externality
(b) Economic externalities
(c) Nagative externalities
(d) Positive externalities
Answer:
(d) Positive externalities

Question 5.
…………………….. is of contaminants environment.
(a) Pollution
(b) Air Pollution
(c) Water pollution
(d) Noise Pollution
Answer:
(a) Pollution

Question 6.
Vehicles smoke happens to release high amounts of ……………………..
(a) Carbon – di – oxide
(b) Carbon – monoxide
(c) Carbon
(d) Oxygen
Answer:
(b) Carbon – monoxide

Question 7.
…………………….. it creates several respiratory and heart ailments along with cancer.
(a) Water pollution
(b) Noise pollution
(c) Air pollution
(d) Land pollution
Answer:
(c) Air pollution

Question 8.
…………………….. is an increase in water temperature as a result aquatic plants and animals are affected.
(a) Oil spill
(b) Acid rain
(c) Global warming
(d) Eutrophication
Answer:
(c) Global warming

Question 9.
…………………….. is unwanted or excessive sound that can have deleterious effects on human health and environmental quality.
(a) Air pollution
(b) Water pollution
(c) Noise pollution
(d) Land pollution
Answer:
(c) Noise pollution

Question 10.
…………………….. adversely affects agriculture, horticulture and eco system.
(a) Climate change
(b) Global warming
(c) Land pollution
(d) Acid rain
Answer:
(b) Global warming

Question 11.
Soil pollution is another form of …………………….. pollution.
(a) Land
(b) Fertilizer
(c) Chemical
(d) Medicinal
Answer:
(a) Land

Question 12.
…………………….. is the supplier of the forms of resources.
(a) Farmers
(b) Environment
(c) Chemicals
(d) Fertilizers
Answer:
(b) Environment

Question 13.
…………………….. is led to land pollution.
(a) Forestation
(b) Forest
(c) Fertilizers
(d) Deforestation
Answer:
(d) Deforestation

Question 14.
Acid rain is one of the consequences of …………………….. pollution.
(a) Land
(b) Air
(c) Water
(d) Soil
Answer:
(a) Land

Question 15.
Atmospheric noise or static is caused by lighting discharges in ……………………..
(a) Thunder storms
(b) Flood
(c) Land slide
(d) Drought
Answer:
(a) Thunder storms

Question 16.
Polluted water is harmful for ……………………..
(a) Industries
(b) Agriculture
(c) Land pollution
(d) Soil pollution
Answer:
(b) Agriculture

Question 17.
Electronic waste is commonly referred as …………………….. is the new by product of the Info Tech society.
(a) E – waste
(b) Plastic waster
(c) Waste
(d) Rubber waste
Answer:
(a) E – waste

Question 18.
…………………….. is the current increase in temperature of the Earth’s surface as well as its atmosphere.
(a) Globe warming
(b) Global warming
(c) Globe spoiled
(d) Temperature warming
Answer:
(b) Global warming

Question 19.
…………………….. is an increased level of nutrients in water bodies.
(a) Eutrophication
(b) Global warming
(c) Acid rain
(d) Oil spill
Answer:
(a) Eutrophication

Question 20.
…………………….. is the supplier of all forms of resources like renewable and non – renewable.
(a) Environment
(b) Environmental goods
(c) Environmental quality
(d) Environmental wastes
Answer:
(a) Environment

Question 21.
Heavy machineries located inside big factories and industrial plants also emit pollutants into the ……………………..
(a) Land
(b) Soil
(c) Air
(d) Water
Answer:
(c) Air

Question 22.
…………………….. causes great damage to human beings, animals and crops.
(a) Natural
(b) Factories
(c) Acid rain
(d) Global warming
Answer:
(c) Acid rain

Question 23.
…………………….. is development that meets the needs of the present without compromising the ability of future generations to meet their own needs.
(a) Alternative approach
(b) Environmental protection
(c) Economic growth
(d) Sustainable development
Answer:
(d) Sustainable development

Question 24.
…………………….. is a system of agricultural production which relies on animal manure, organic waste, crop rotation, legumes and biological pest control.
(a) Organic farming
(b) Land forming
(c) Land pollution
(d) Soil pollution
Answer:
(a) Organic farming

II. Match The following And Choose The Correct Answer By Using Codes Given Below.

Question 1.
A. Causes of air pollution – (i) Solid waste
B. Types of water pollution – (ii) Vehicle exhaust smoke
C. Types of land pollution – (iii) Deforestation
D. Causes of land pollution (iv) Ground water pollution
Codes:
(a) A (i) B (ii) C (iii) D (iv)
(b) A (iv) B (iii) c (ii) D(i)
(c) A (ii) B (iv) C (i) D (iii)
(d) A (iii) B(i) C (iv) D (ii)
Answer:
(c) A (ii) B (iv) C (i) D (iii)

Question 2.
A. Organic farming – (i) Global warming
B. Effects of noise pollution – (ii) Animal manure
C. Effects of water pollution – (iii) Hearing loss
D. Effects of air pollution – (iv) Death of aquatic animals
Codes:
(a) A (i) B (ii) C (iii) D (iv)
(b) A (iv) B (i) C (ii) D (iii)
(c) A (iii) B (iv) C (i) D (ii)
(d) A (ii) B (iii) C (iv) D(i)
Answer:
(d) A (ii) B (iii) C (iv) D(i)

Question 3.
A. World commision – (i) Seawater
B. Organic farming – (ii) Environment and Development
C. Oil spill – (iii) Nutrients in water
D. Eutrophication – (iv) Animal husbandry
Codes:
(a) A (i) B (ii) C (iii) D (iv)
(b) A (ii) B (iv) C(i) D (iii)
(c) A (iii) B (i) C (iv) D (ii)
(d) A (iv) B (iii) C (ii) D (i)
Answer:
(b) A (ii) B (iv) C(i) D (iii)

Question 4.
A. Alkali soil – (i) High noise
B. Cardio vascular – (ii) Indo gangetic
C. Solid waste – (iii) Toxic chemicals
D. Skin cancer (iv) Rubbish
Codes:
(a) A (ii) B (i) C (iv) D (iii)
(b) A (i) B (ii) C (iii) D (iv)
(c) A (iii) B (iv) C (ii) D(i)
(d) A (iv) B (iii) C(i) D (ii)
Answer:
(a) A (ii) B (i) C (iv) D (iii)

Question 5.
A. Remedies of land pollution – (i) Sulphur dioxide
B. Acid rain – (ii) Degradation of land
C. Land pollution – (iii) Fossil fuel
D. Power plants – (iv) Usage of plastic
Codes:
(a) A (i) B (ii) C (iii) D (iv)
(b) A (ii) B (iii) C(iv) D (i)
(c) A (iv) B (i) C (ii) D (iii)
(d) A (iii) B (iv) C(i) D(ii)
Answer:
(c) A (iv) B (i) C (ii) D (iii)

III. State Whether The Statements Are True or False.

Question 1.
(i) Environmental economics is a different branch of economics that recognizes the value of both the environment and economic activity.
(ii) Environmental Economics involves theoretical and empirical studies of the economic effects.

(a) Both (i) and (ii) are true
(b) Both (i) and (ii) are false
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(a) Both (i) and (ii) are true

Question 2.
(i) The relationship between the economy and the environment is generally explained in the form of a “Material Balance Model”.
(ii) This model developed by Alenkneese and R.V. Ayres.

(a) Both (i) and (ii) are true
(b) Both (i) and (ii) are false
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(a) Both (i) and (ii) are true

Question 3.
(i) Beneficial externalities are called “Positive externalities”.
(ii) Beneficial externalities are called “Negative externalities”.

(a) Both (i) and (ii) are true
(b) (i) is true but (ii) is false
(c) Both (i) and (ii) are false
(d) (i) is false but (ii) is true
Answer:
(b) (i) is true but (ii) is false

Question 4.
(i) Surface water includes natural water found on the earth’s surface, like rivers, lakes, lagoons and oceans.
(ii) Hazardous substances coming into contact with this surface water, dissolving or mixing physically with the water can be called surface of land pollution.

(a) Both (i) and (ii) are true
(b) Both (i) and (ii) are false
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(c) (i) is true but (ii) is false

Question 5.
(i) Noise pollution is unwanted or excessive sound that can have deleterious effects on human health and environmental quality.
(ii) Noise pollution is also comes from highway, railway and airplane traffic and from outdoor construction activities.
(a) Both (i) and (ii) are true
(b) Both (i) and (ii) are false
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(a) Both (i) and (ii) are true

IV. Which Of The Following Is Correctly Matched:

Question 1.
(a) Types of noise pollution – Death of aquatic animals
(b) Effects of water pollution – Factory mechinery
(c) Types of water pollution – Respiratory and heart problems
(d) Causes of air pollution – Vehicle exhaust smoke
Answer:
(d) Causes of air pollution – Vehicle exhaust smoke

Question 2.
(a) Environmental goods – Human beings
(b) Types of pollution – Transport
(c) Human health – Land pollution
(d) Microbiological pollution – Water pollution
Answer:
(d) Microbiological pollution – Water pollution

Question 3.
(a) Global warming – Affects industry
(b) Acid rain – Usage of pesticides
(c) Electronic waste – e – waste
(d) SDGs – Poverty increased
Answer:
(c) Electronic waste – e – waste

Question 4.
(a) Crackers – Big industry
(b) Soil pollution – Damaged river
(c) Farmers – Use highly toxic fertilizers
(d) Deforestation – Due to urbanisation
Answer:
(c) Farmers – Use highly toxic fertilizers

Question 5.
(a) Seed ball – Providing oxygen
(b) E – waste – Sustainable development
(c) Fertilizers used – Water pollution
(d) Oil spill – Sea water polluted
Answer:
(d) Oil spill – Sea water polluted

V. Which Of The Following Is Not Correctly Matched.

Question 1.
(a) Acid rain – Sulphur dioxide
(b) Agro – Eco system
(c) Negative production – Factory emission
(d) Ozone layer – Major cause of death
Answer:
(d) Ozone layer – Major cause of death

Question 2.
(a) Fossil fuel – Power plants
(b) Forest – Replenish soil
(c) Environmental goods – Pre – planted
(d) Agriculture – Fertilizer
Answer:
(c) Environmental goods – Pre – planted

Question 3.
(a) Sustainable development – Monitors
(b) Oil spill – Seawater
(c) Water – Land pollution
(d) Tree – Lungs of the Earth
Answer:
(c) Water – Land pollution

Question 4.
(a) Natural pollution – Aquatic and Human illness
(b) Global warming – Increasing temperature
(c) Discharge of sewage – Outdoor air pollution
(d) Organic farming – Deforestation
Answer:
(d) Organic farming – Deforestation

Question 5.
(a) Acid rain – Land pollution
(b) Soil – Soil contamination
(c) Heavy industries – Land pollution
(d) Environmental goods – Environmental quality
Answer:
(c) Heavy industries – Land pollution

VI. Pick The Odd One Out.

Question 1.
Types of Noise pollution
(a) Atmospheric noise pollution
(b) Industrial noise pollution
(c) Man made noise pollution
(d) Acid rain pollution
Answer:
(d) Acid rain pollution

Question 2.
Causes of Noise pollution
(a) Construction
(b) Motor vehicles
(c) Crackers
(d) Factory machinery
Answer:
(a) Construction

Question 3.
Types of Land pollution
(a) Solid waste
(b) Cardiovascular effects
(c) Pesticides and fertilizers
(d) Deforestation
Answer:
(b) Cardiovascular effects

Question 4.
Causes of Land Pollution
(a) Deforestation and soil erosin
(b) Agriculture activities spoiled
(c) Fertilizer spoiled
(d) Mining activities spoiled
Answer:
(c) Fertilizer spoiled

Question 5.
Organic farming
(a) Manure
(b) Biofertilizers
(c) Crop rotation
(d) Solid waste
Answer:
(d) Solid waste

VII. Assertion And Reason.

Question 1.
Assertion (A): The natural pollution causes both aquatic and human illness.
Reason (R): Pollution is damage to eco system and aesthetics of our surrounding.

(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’

Question 2.
Assertion (A): Vehicles smoke happens to release high amounts of carbon monoxide.
Reason (R): Chemicals like carbon-di-oxide are released during the burning process.

(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(c) ‘A’ is true but ‘R’ is false

Question 3.
Assertion (A): Sewage, garbage and liquid waste of households, agriculture runoff and effluents from factories are discharged into lakes and rivers.
Reason (R): These wastes contain useful chemicals and toxins.

(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(c) ‘A’ is true but ‘R’ is false

Question 4.
Assertion (A): Remedial measures to control air pollution is growing more plants and trees.
Reason (R): Remedial measures to control air pollution is establishment of industries in the town and cities.

(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(c) ‘A’ is true but ‘R’ is false

Question 5.
Assertion (A): Soil pollution is another form of water pollution.
Reason (R): The upper layer of the soil is damaged is caused by the over use of chemical fertilizers and pesticides.

(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(d) ‘A’ is false but ‘R’ is true

Part – B
Answer The Following Questions In One or Two Sentences.

Question 1.
Define “Solid wastes”?
Answer:
Solid Wastes:

1. Non-liquid, non-soluble materials, ranging from municipal garbage to industrial wastes that contain complex, and hazardous, substances.
2. Solid wastes include sewage sludge, agricultural refuse, demolition wastes, and mining residues.

Question 2.
What is organic farming?
Answer:

1. Organic farming is a system of agricultural production which relies on animal manure, organic waste, crop rotation, legumes and biological pest control.
2. It avoids use of synthetic fertilizer, pesticides and livestock additives.
3. Organic inputs have certain benefits, such as enriching soil for microbes.

Question 3.
Define “Sustainable Development”?
Answer:

1. Sustainable Development is development that meets the needs of the present generation without compromising the ability of future generations to meet their own needs.
2. “The alternative approach (to sustainable development) is to focus on natural capital assets and suggest that they should not decline through time.”

Question 4.
Define “Noise pollution”?
Answer:

1. Noise pollution is unwanted or excessive sound that can have deleterious effects on human health and environmental quality.
2. Noise pollution is commonly generated by many factories.
3. It also comes from highway, railway and airplane traffic and from outdoor construction ’ activities.

Question 5.
Define “Deforestation”?
Answer:

1. Humans depend on trees for many things including life.
2. Trees absorb carbon dioxide from the air and release Oxygen, which is needed for life.
3. Forest helps replenish soils and help retain nutrients being washed away.
4. Deforestation is led to land pollution.

Question 6.
What are the types of pollution?
Answer:
Types of Pollution:

1. Air pollution
2. Water pollution
3. Noise pollution
4. Land pollution.

Part – C
Answer The Following Questions In One Paragraph.

Question 1.
Write note on “Remedial Measures to control land pollution?
Answer:
Remedial measures to control Land Pollution:

1. Making people aware about the concept of a Reduce, Recycle and Reuse
2. Buying biodegradable products
3. Minimizing the usage of pesticides
4. Shifting cultivation
5. Disposing unwanted garbage properly either by burning or by burying under the soil.
6. Minimizing the usage of plastics.

Question 2.
Mention the Remedial Measures to control water pollution?
Answer:
Remedial measures to control Water Pollution:

1. Comprehensive water management plan.
2. Construction of proper storm drains and settling ponds.
3. Maintenance of drain line.
4. Effluent and sewage treatment plant.
5. Regular monitoring of water and waste water.
6. Stringent actions towards illegal dumping of waste into the water bodies.

Question 3.
Explain the types of Noise pollution?
Answer:
Types of Noise Pollution:
(I) Atmospheric Noise:
Atmospheric noise or static is caused by lighting discharges in thunderstorms and other natural electrical disturbances occurring in the atmosphere.

(II) Industrial Noise:

1. Industrial noise refers to noise that is created in the factories.
2. When sound becomes noise it becomes unwanted.
3. Heavy industries like ship building, iron and steel have long been associated with Noise Induced Hearing Loss (NIHL).

(III) Man made Noise:
The main sources of man-made noise pollution are ships, aircraft, seismic exploration, marine construction, drilling and motor boats.

Part – D
Answer The Following Questions In About A Page.

Question 1.
What are the effects of Land pollution?
Answer:
Effects of Land Pollution:
(I) Soil pollution:

1. Soil pollution is another form of land pollution, where the upper layer of the soil is damaged.
2. This is caused by the overuse of chemical fertilizers, and pesticides.
3. This leads to loss of fertile land.
4. Pesticides kill not only pests and also human beings.

(II) Health Impact:

1. The land when contaminated with toxic chemicals and pesticides lead to problem of skin cancer and human respiratory system.
2. The toxic chemicals can reach our body through foods and vegetables.

(III) Cause for Air pollution:

1. Landfills and waste dumping lead to air pollution.
2. The abnormal toxic substances spread in the atmosphere cause transmit respiratory diseases among the masses.

(IV) Effect on wildlife:

1. The animal kingdom has suffered mostly in the past decades.
2. They face a serious threat with regards to loss of habitat and natural environment.
3. The constant human activity on land is leaving it polluted, forcing these species to move farther away.
4. Sometimes several species are pushed to the verge of extinction or disappear due to no conducive environment.

Question 2.
Briefly explain effects of Noise pollution?
Answer:
Effects of Noise Pollution:
(a) Hearing Loss:

1. Chronic exposure to noise may cause noise-induced hearing loss.
2. Older people are exposed to significant occupational noise and thereby reduced hearing sensitivity.

(b) Damage Physiological and Psychological health:

1. Unwanted noise can damage physiological and psychological health.
2. For example, annoyance and aggression, hypertension, and high stress levels.

(c) Cardiovascular effects:
High noise levels can contribute to cardiovascular problems and exposure to blood pressure.

(d) Detrimental effect on animals and aquatic life:
Noise can have a detrimental effect on animals, increasing the risk of death.

(e) Effects on wildlife and aquatic animals:
It creates hormone imbalance, chronic stress, panic and escape behavior and injury.

Question 3.
Explain the causes of Air pollution?
Answer:
Causes of Air Pollution:
(I) Vehicle exhaust smoke:

1. Vehicles smoke happens to release high amounts of Carbon monoxide.
2. Millions of vehicles are operated every day in cities, each one leaving behind its own carbon footprint on the environment.

(II) Fossil fuel based power plants:

1. Fossil fuels also present a wider scale problem when they are burned for energy in power plants.
2. Chemicals like sulphur dioxide are released during the burning process, which travel straight into the atmosphere.
3. These types of pollutants react with water molecules to yield something known as acid rain.

(III) Exhaust from Industrial Plants and Factories:
Heavy machineries located inside big factories and industrial plants also emit pollutants into the air.

(IV) Construction and Agricultural activities:

1. Potential impacts arising from the construction debris would include dust particles and gaseous emissions from the construction sites.
2. Likewise, using of ammonia for agriculture is a frequent byproduct that happens to be one of the most dangerous gases affecting air.

(V) Natural Causes:

1. Earth is one of the biggest polluters itself, through volcanoes, forest fires, and dust storms.
2. They are nature-borne events that dump massive amounts of air pollution into the atmosphere.

(VI) Household activities:
Household activities like cooking, heating and lighting, use of various forms of mosquito repellents, pesticides and chemicals for cleaning at home and use of artificial fragrances are some of the sources that contribute to air pollution.

Question 4.
Explain different sources of E – waste?
Answer:

Share this Tamilnadu State Board 12th Economics Solutions Chapter 10 Environmental Economics Questions and Answers with your friends to help them to overcome the grammar issues in exams. Keep visiting this site frequently to get the latest information on different subjects. Clarify your doubts by posting the comments and get the answers in an easy manner.

Students of 12th can get the pdf links of Tamilnadu State Board Economics Solutions here. You can Download Samacheer Kalvi 12th Economics Book Solutions Chapter 7 International Economics Questions and Answers, Notes Pdf, Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Economics Solutions Chapter 7 International Economics

It is very important to put the textbook aside while preparing for the exams. So, if you follow Samacheer Kalvi 12th Economics Textbook Solutions you can cover all the topics in Chapter 7 International Economics Questions and Answers. This helps to improve your communication skills.

Samacheer Kalvi 12th Economics International Economics Text Book Back Questions and Answers

Part – A
Multiple Choice Questions.

Question 1.
Trade between two countries is known as ………………………. trade
(a) External
(b) Internal
(c) Inter – regional
(d) Home
Answer:
(a) External

Question 2.
Which of the following factors influence trade?
(a) The stage of development of a product
(b) The relative price of factors of productions
(c) Government
(d) All of the above.
Answer:
(d) All of the above.

Question 3.
International trade differs from domestic trade because of ……………………….
(a) Trade restrictions
(b) Immobility of factors
(c) Different government policies
(d) All the above
Answer:
(d) All the above

Question 4.
In general, a primary reason why nations conduct international trade is because ……………………….
(a) Some nations prefer to produce one thing while others produce another
(b) Resources are not equally distributed among all trading nations
(c) Trade enhances opportunities to accumulate profits
(d) Interest rates are not identical in all trading nations
Answer:
(b) Resources are not equally distributed among all trading nations

Question 5.
Which of the following is a modem theory of international trade?
(a) Absolute cost
(b) Comparative cost
(c) Factor endowment theory
(d) None of these
Answer:
(c) Factor endowment theory

Question 6.
Exchange rates are determined in ……………………….
(a) Money market
(b) Foreign exchange market
(c) Stock market
(d) Capital market
Answer:
(b) Foreign exchange market

Question 7.
Exchange rate for currencies is determined by supply and demand under the system of ……………………….
(a) Fixed exchange rate
(b) Flexible exchange rate
(c) Constant
(d) Government regulated
Answer:
(b) Flexible exchange rate

Question 8.
Net export equals ……………………….
(a) Export × Import
(b) Export + Import
(c) Export – Import
(d) Exports of services only
Answer:
(c) Export – Import

Question 9.
Who among the following enunciated the concept of single factoral terms of trade?
(a) Jacob Viner
(b) G.S.Donens
(c) Taussig
(d) J.S.Mill
Answer:
(a) Jacob Viner

Question 10.
Terms of Trade of a country show ……………………….
(a) Ratio of goods exported and imported
(b) Ratio of import duties
(c) Ratio of prices of exports and imports
(d) Both (a) and (c)
Answer:
(c) Ratio of prices of exports and imports

Question 11.
Favourable trade means value of exports are ………………………. Than that of imports.
(a) More
(b) Less
(c) More or Less
(d) Not more than
Answer:
(a) More

Question 12.
If there is an imbalance in the trade balance (more imports than exports), it can be reduced by ……………………….
(a) Decreasing customs duties
(b) Increasing export duties
(c) Stimulating exports
(d) Stimulating imports
Answer:
(c) Stimulating exports

Question 13.
BOP includes ……………………….
(a) Visible items only
(b) Invisible items only
(c) Both visible and invisible items
(d) Merchandise trade only
Answer:
(c) Both visible and invisible items

Question 14.
Components of balance of payments of a country includes ……………………….
(a) Current account
(b) Official account
(c) Capital account
(d) All of above
Answer:
(d) All of above

Question 15.
In the case of BOT ……………………….
(a) Transactions of goods are recorded.
(b) Transactions of both goods and services are recorded.
(c) Both capital and financial accounts are included.
(d) All of these
Answer:
(a) Transactions of goods are recorded.

Question 16.
Tourism and travel are classified in which of balance of payments accounts?
(a) Merchandise trade account
(b) Services account
(c) Unilateral transfers account
(d) Capital account
Answer:
(b) Services account

Question 17.
Cyclical disequilibrium in BOP occurs because of ……………………….
(a) Different paths of business cycle.
(b) The income elasticity of demand or price elasticity of demand is different.
(c) Long – run changes in an economy
(d) Both (a) and (b)
Answer:
(d) Both (a) and (b)

Question 18.
Which of the following is not an example of foreign direct investment?
(a) The construction of a new auto assembly plant overseas
(b) The acquisition of an existing steel mill overseas
(c) The purchase of bonds or stock issued by a textile company overseas
(d) The creation of a wholly owned business firm overseas
Answer:
(c) The purchase of bonds or stock issued by a textile company overseas

Question 19.
Foreign direct investments not permitted in India ……………………….
(a) Banking
(b) Automic energy
(c) Pharmaceutical
(d) Insurance
Answer:
(b) Automic energy

Question 20.
Benefits of FDI include, theoretically ……………………….
(a) Boost in Economic Growth
(b) Increase in the import and export of goods and services
(c) Increased employment and skill levels
(d) All of these
Answer:
(d) All of these

Part – B
Answer The Following Questions Each Question Carries 2 Marks.

Question 21.
What is International Economics?
Answer:

1. International Economics is that branch of economics which is concerned with the exchange of goods and services between two or more countries. Hence the subject matter is mainly related to foreign trade.
2. International Economics is a specialized field of Economics which deals with the economic interdependence among countries and studies the effects of such interdependence and the factors that affect it.

Question 22.
Define international trade?
Answer:
International Trade refers to the trade or exchange of goods and services between two or more countries. In other words, it is a trade among different countries or trade across political boundaries. It is also called as ‘external trade’ or ‘foreign trade’ or ‘inter-regional trade’.

Question 23.
State any two merits of trade?
Answer:

1. Trade is one of the powerful forces of economic integration.
2. The term ‘trade’ means exchange of goods, wares or merchandise among people.

Question 24.
What is the main difference between Adam Smith and Ricardo with regard to the emergence of foreign trade?
Answer:
Adam Smith Foreign Trade:

1. According to Adam Smith the basis of International trade was absolute cost advantage.
2. Trade between two countries would be mutually beneficial when one country produces a commodity at an absolute cost advantage.
3. Adam Smith argued that all nations can be benefitted when there is free trade and specialisation interms of their absolute cost advantage.

Ricardo Foreign Trade:

1. Ricardo demonstrates that the basis of trade is the comparative cost difference.
2. Trade can take place even if the absolute cost difference is absent but there is comparative cost difference.
3. According to Ricardo a country can gain from trade when it produces at relatively lower costs.

Question 25.
Define Terms of Trade?
Answer:
Terms of Trade:

1. The gains from international trade depend upon the terms of trade which refers to the ratio of export prices to import prices.
2. It is the rate at which the goods of one country are exchanged for goods of another country’.
3. It is expressed as the relation between export prices and import prices.
4. Terms of trade improves when average price of exports is higher than average price of imports.

Question 26.
What do you mean by balance of payments?
Answer:
Balance of Payments (BOP):

1. BoP is a systematic record of a country’s economic and financial transactions with the rest of the world over a period of time.

2. When a payment is received from a foreign country, it is a credit transaction while a payment to a foreign country is a debit transaction.

3. The principal items shown on the credit side are exports of goods and services, transfer receipts in the form of gift etc., from foreigners, borrowing from abroad, foreign direct investment and official sale of reserve assets including gold to foreign countries and international agencies.

4. The principal items on the debit side include imports of goods and serv ices, transfer payments to foreigners, lending to foreign countries, investments by residents in foreign countries and official purchase of reserve assets or gold from foreign countries and international agencies.

Question 27.
What is meant by Exchange Rate?
Meaning of Foreign Exchange (FOREX):

1. FOREX refers to foreign currencies. The mechanism through which payments are effected between two countries having different currency systems is called FOREX system. It covers methods of payment, rules and regulations of payment and the institutions facilitating such payments.

2. “FOREX is the system or process of converting one national currency into another, and of transferring money from one country to another”.

Part – C
Answer The Following Questions Each Question Carries 3 Marks.

Question 28.
Describe the subject matter of International Economics?
Answer:
Subject Matter of International Economics:
The subject matter of International Economics includes large number of segments which are classified into the following parts.

1. Pure Theory of Trade:
This component explains the causes for foreign trade, composition, direction and volume of trade, determination of the terms of trade and exchange rate, issues related to balance of trade and balance of payments.

2. Policy Issues:
Under this part, policy issues such as free trade vs. protection, methods of regulating trade, capital and technology flows, use of taxation, subsidies and dumping, exchange control and convertibility, foreign aid, external borrowings and foreign direct investment, measures of correcting disequilibrium in the balance of payments etc are covered.

3. International Cartels and Trade Blocs:
This part deals with the economic integration in the form of international cartels, customs unions, monetary unions, trade blocs, economic unions and the like. It also discusses the operation of Multi National Corporations (MNCs).

4. International Financial and Trade Regulatory Institutions:
The financial institutions like International Monetary Fund IMF, IBRD, WTO etc which influence international economic transactions and relations shall also be the part of international economics.

Question 29.
Compare the Classical Theory of international trade with Modern Theory of International trade?
Answer:
Classical Theory of International Trade:

1. The classical theory explains the phenomenon of international trade on the basis of labour theory of value.
2. It presents a one factor (labour) model.
3. It attributes the differences in the comparative costs to differences in the productive efficiency of workers in the two countries.

Modern Theory of International Trade:

1. The modem theory explains the phenomenon of international trade on the basis of general theory of value.
2. It presents a multi – factor (labour and capital) model.
3. It attributes the differences in comparative costs to the differences in factor endowments in the two countries.

Question 30.
Explain the Net Barter Terms of Trade and Gross Barter Terms of Trade?
Answer:
1. Net Barter Terms of Trade:
This type was developed by Taussig in 1927.The ratio between the prices of exports and of imports is called the “net barter terms of trade’. It is named by Viner as the ‘commodity terms of trade’.
It is expressed as:
T_n = (P _x /P_m ) × 100
Where,
T_n = Net Barter Terms of Trade
P_x = Index number of export prices
P_m = Index number of import prices
This is used to measure the gain from international trade. If ‘Tn’ is greater than 100, then it is a favourable terms of trade which will mean that for a rupee of export, more of imports can be received by a country.

2. Gross Barter Terms of Trade:
This was developed by Taussig in 1927 as an improvement over the net terms of trade. It is an index of relationship between total physical quantity of imports and the total physical quantity of exports.
T = (Q_m/Q_x) × 100
Where,
Q_m = Index of import quantities
Q_x = Index of export quantities
If for a given quantity of export, more quantity of import can be consumed by a country, then one can say that terms of trade are favourable.

Question 31.
Distinguish between Balance of Trade and Balance of Payments?
Answer:
Balance of Trade:

1. Balance of Trade refers to the total value of a country’s exports of commodities and total value of imports of commodities.
2. Only export and import of commodities are included in the statement of Balance of Trade of a country.
3. The Balance of Trade between the values of goods exchanged between two countries.
4. Balance of Trade is a merchandise items or visible items only.

Balance of Payments:

1. Balance of payments is a systematic record of a country’s economic and financial transactions with the rest of the world over a period of time.
2. The principal items shown on the credit side are exports of goods and services, transfer receipts in the form of gift, etc.
3. The Balance of payments between the values of goods and services changed between two countries.
4. Balance of payments is a both visible and non – visible items.

Question 32.
What are import quotas?
Answer:
Import Control: Imports may be controlled by

1. Imposing or enhancing import duties
2. Restricting imports through import quotas
3. Licensing and even prohibiting altogether the import of certain non-essential items. But this would encourage smuggling.

Question 33.
Write a brief note on flexible exchange rate?
Answer:
Flexible Exchange Rates: Under the flexible exchange rate (also known as floating exchange rate) system, exchange rates are freely determined in an open market by market forces of
demand and supply

Question 34.
State the objectives of Foreign Direct Investment.
Answer:
Objectives of FDI:
FDI has the following objectives.

1. Sales Expansion
2. Acquisition of resources
3. Diversification
4. Minimization of competitive risk.
   • FDI may help to increase the investment level and thereby the income and employment in the host country.
   • Direct foreign investment may facilitate transfer of technology to the recipient country.
   • FDI may also bring revenue to the government of host country when it taxes profits of foreign firms or gets royalties from concession agreements.
   • A part of profit from direct foreign investment may be ploughed back into the expansion, modernization or development of related industries.
   • It may kindle a managerial revolution in the recipient country through professional management and sophisticated management techniques.
   • Foreign capital may enable the country to increase its exports and reduce import requirements. And thereby ease BoP disequilibrium.
   • Foreign investment may also help increase competition and break domestic monopolies.
   • If FDI adds more value to output in the recipient country than the return on capital from foreign investment, then the social returns are greater than the private returns on foreign investment.
   • By bringing capital and foreign exchange FDI may help in filling the savings gap and the foreign exchange gap in order to achieve the goal of national economic development.
   • Foreign investments may stimulate domestic enterprise to invest in ancillary industries in collaboration with foreign enterprises.

Part – D
Answer The Following Questions Each Question Carries 5 Marks.

Question 35.
Discuss the differences between Internal Trade and International Trade?
Answer:
Internal Trade:

1. Trade takes place between different individuals and firms within the same nation.
2. Labour and capital move freely from one region to another.
3. There will be free flow of goods and services since there are no restrictions.
4. There is only one common currency.
5. The physical and geographical conditions of a country are more or less similar.
6. Trade and financial regulations are more or less the same.
7. There is no difference in political affiliations, customs and habits of the people and government policies.

International Trade:

1. Trade takes place between different individuals and firms in different countries.
2. Labour and capital do not move easily from one nation to another.
3. Goods and services do not easily move from one country to another since there are a number of restrictions like tariff and quota.
4. There are different currencies.
5. There are differences in physical and geographical conditions of the two countries.
6. Trade and financial regulations such as interest rate, trade laws differ between countries.
7. Differences are pronounced in political affiliations, habits and customs of the people and government policies

Question 36.
Explain briefly the Comparative Cost Theory?
Answer:
Ricardo’s Theory of Comparative Cost Advantage:

1. David Ricardo, the British economist in his ‘Principles of Political Economy and Taxation’ published in 1817, formulated a systematic theory called ‘Comparative Cost Theory’.

2. Ricardo demonstrates that the basis of trade is the comparative cost difference. In other words, trade can take place even if the absolute cost difference is absent but there is comparative cost difference.

3. According to Ricardo, a country can gain from trade when it produces at relatively lower costs. Even when a country enjoys absolute advantage in both goods, the country would specialize in the production and export of those goods which are relatively more advantageous.

Assumptions:

1. There are only two nations and two commodities (2 × 2 model)
2. Labour is the only element of cost of production.
3. All labourers are of equal efficiency.
4. Labour is perfectly mobile within the country but perfectly immobile between countries, (v) Production is subject
5. To the law of constant returns.
6. Foreign trade is free from all barriers.
7. No change in technology.
8. No transport cost.
9. Perfect competition.
10. Full employment.
11. No government intervention.

Illustration:
Ricardo’s theory of comparative cost can be explained with a hypothetical example of production costs of cloth and wheat in America and India.

It is evident from the example that India has an absolute advantage in production of both cloth and wheat.

However, India should concentrate on the production of wheat in which she enjoys a comparative cost advantage. (80/120 < 90/100). For America the comparative cost disadvantage is lesser in cloth production. Hence America will specialize in the production of cloth and export it to India in exchange for wheat. (Any exchange ratio between 0.88 units and 1.2 units of cloth against one unit of wheat represents gain for both the nations).

With trade, India can get 1 unit of cloth and 1 unit of wheat by using its 160 labour units. In the absence of trade, for getting this benefit, India will have to use 170 units of labour. America also gains from this trade. With trade, America can get 1 unit of cloth and one unit of wheat by using its 200 units of labour. Otherwise, America will have to use 220 units of labour for getting 1 unit of cloth and 1 unit of wheat.

Question 37.
Discuss the Modern Theory of International Trade?
Answer:
Modern Theory of International Trade:
Introduction:
The modem theory of international trade was developed by Swedish economist Eli Heckscher and his student Bertil Ohlin in 1919. This model was based on the Ricardian theory of international trade. This theory says that the basis for international trade is the difference in factor endowments. It is otherwise called as ‘Factor Endowment Theory’.

The Theory:
The classical theory argued that the basis for foreign trade was comparative cost difference and it considered only labour factor. But the modem theory of international trade explains the causes for such comparative cost difference. This theory attributes international differences in comparative costs to:

1. Difference in the endowments of factors of production between countries, and
2. Differences in the factor proportions required in production.

Assumptions:

1. There are two countries, two commodities and two factors. (2 × 2 × 2 model)
2. Countries differ in factor endowments.
3. Commodities are categorized in terms of factor intensity.
4. Countries use same production technology.
5. Countries have identical demand conditions.
6. There is perfect competition in both product and factor markets in both the countries

Explanation:
According to Heckscher – Ohlin, “a capital – abundant country will export the capital – intensive goods, while the labour-abundant country will export the labour – intensive goods”. A factor is regarded abundant or scare in relation to the quantum of other factors. A country can be regarded as richly endowed with capital only if the ratio of capital to other factors is higher than other countries

Illustration:

In the above example, even though India has more capital in absolute terms, America is more richly endowed with capital because the ratio of capital in India is 0.8 which is less than that in America where it is 1.25. The following diagram illustrates the pattern of word trade.

Limitations:

1. Factor endowment of a country may change over time.
2. The efficiency of the same factor (say labour) may differ in the two countries. For example, America may be labour scarce in terms of number of workers. But in terms of efficiency, the total labour may be larger.

Question 38.
Explain the types of Terms of Trade given by Viner?
Answer:
Terms of Trade related to the Interchange between Productive Resources:

1. The Single Factoral Terms of Trade:
Viner has devised another concept called “the single factoral terms of trade” as an improvement upon the commodity terms of trade. It represents the ratio of export – price index to the import – price index adjusted for changes in the productivity of a country’s factors in the production of exports. Symbolically, it can be stated as
T_f = (P_x / P_m ) F_x
Where, T_f stands for single factoral terms of trade index. F_x stands for productivity in exports (which is measured as the index of cost in terms of quantity of factors of production used per unit of export).

2. Double Factoral Terms of Trade:
Viner constructed another index called “Double factoral terms of Trade”. It is expressed as
T_ff = (P_x / P_m )(F_x / F_m)
which takes into account the productivity in country’s exports, as well as the productivity of foreign factors.
Here, F_m represents import index (which is measured as the index of cost in terms of quantity of factors of production employed per unit of imports).

Question 39.
Bring out the components of balance of payments account?
Answer:
Components of BOPs:
The credit and debit items are shown vertically in the BOP account of a country. Horizontally, they are divided into three categories, i.e.

1. The current account,
2. The capital account and
3. The official settlements account or official reserve assets account.

1. The Current Account:
It includes all international trade transactions of goods and services, international service transactions (i.e. tourism, transportation and royalty fees) and international unilateral transfers (i.e. gifts and foreign aid).

2. The Capital Account:
Financial transactions consisting of direct investment and purchases of interest-bearing financial instruments, non-interest bearing demand deposits and gold fall under the capital account.

3. The Official Reserve Assets Account:
Official reserve transactions consist of movements of international reserves by governments and dfficial agencies to accommodate imbalances arising from the current and capital accounts.

The official reserve assets of a country include its gold stock, holdings of its convertible foreign currencies and Special Drawing Rights (SDRs) and its net position in the International Monetary Fund (IMF).
Balance of payment (BOP) Account Chart
Credit (Receipts) – Debit (Payments) = Balance [Deficit (-), Surplus (+)]
Deficit if Debit > Credit

Question 40.
Discuss the various types of disequilibrium in the balance of payments?
Answer:
Types BOP Disequilibrium:
There are three main types of BOP Disequilibrium, which are discussed below.

1. Cyclical Disequilibrium,
2. Secular Disequilibrium,
3. Structural Disequilibrium.

1. Cyclical Disequilibrium:
Cyclical disequilibrium occurs because of two reasons. First, two countries may be passing through different phases of business cycle. Secondly, the elasticities of demand may differ between countries.

2. Secular Disequilibrium:
The secular or long-run disequilibrium in BOP occurs because of long – run and deep seated changes in an economy as it advances from one stage of growth to another. In the initial stages of development, domestic investment exceeds domestic savings and imports exceed exports, as it happens in India since 1951.

3. Structural Disequilibrium:
Structural changes in the economy may also cause balance of payments disequilibrium. Such structural changes include development of alternative sources of supply, development of better substitutes, exhaustion of productive resources or changes in transport routes and costs.

Question 41.
How the Rate of Exchange is determined? Illustrate?
Answer:
Determinants of Exchange Rates:
Exchange rates are determined by numerous factors and they are related to the trading relationship between two countries.
Factors determining Exchange Rate:

1. Differentials in Inflation
2. Differential in Interest Rates
3. Current Account Deficits
4. Public Debt
5. Terms of Trade
6. Political and Economic Stability
7. Recession
8. Speculation

1. Differentials in Inflation:

1. Inflation and exchange rates are inversely related.
2. A country with a consistently lower inflation rate exhibits a rising currency value, as its purchasing power increases relative to other currencies.

2. Differentials in Interest Rates:

1. There is a high degree of correlation between interest rates, inflation and exchange rates.
2. Central banks can influence over both inflation and exchange rates by manipulating interest rates.
3. Higher interest rates attract foreign capital and cause the exchange rate to rise and vice versa.

3. Current Account Deficits:

1. A deficit in the current account implies excess of payments over receipts.
2. The country resorts to borrowing capital from foreign sources to make up the deficit.
3. Excess demand for foreign currency lowers a country’s exchange rate.

4. Public Debt:

1. Large public debts are driving out foreign investors, because it leads to inflation.
2. As a result, exchange rate will be lower.

5. Terms of Trade:

1. A country’s terms of trade also determines the exchange rate.
2. If the price of a country’s exports rises by a greater rate than that of its imports, its terms ‘ of trade will improve.
3. Favorable terms of trade imply greater demand for the country’s exports and thus BoP becomes favorable.

6. Political and Economic Stability:
If a nation’s political climate is stable and economic performance is good, its currency value will be appreciated by attracting more foreign capital.

7. Recession:

1. Interest rates are low during the recession phase.
2. This will decrease inflow of foreign capital.
3. As a result, a currency will be depreciated against other currencies, thereby lowering the exchange rate.

8. Speculation:

1. If a country’s currency value is expected to rise, investors will demand more of that currency in order to make a profit in the near future.
2. This results in appreciation of the exchange rate.
3. Beside the above determinants, relative dominance in the global politics and the power to announce economic sanctions over other countries also determine exchange rates.

Question 42.
Explain the relationship between Foreign Direct Investment and economic development?
Answer:
Foreign Direct Investment (FDI) and Trade:

1. FDI is an important factor in global economy.
2. Foreign trade and FDI are closely related. In developing countries like India
3. FDI in the natural resource sector, including plantations, increases trade volume.
4. Foreign production by FDI is useful to substitute foreign trade.
5. FDI is also influenced by the income generated from the trade and regional integration schemes.
6. FDI is helpful to accelerate the economic growth by facilitating essential imports needed for carrying out development programmes like capital goods, technical know-how, raw materials and other inputs and even scarce consumer goods.
7. FDI may be required to fill the trade gap.
8. FDI is encouraged by the factors such as foreign exchange shortage, desire to create employment and acceleration of the pace of economic development.
9. Many developing countries strongly prefer foreign investment to imports.
10. However, the real impact of FDI on different sections of an economy.

Samacheer Kalvi 12th Economics International Economics Addtional Questions and Answers

Part – I
Multiple Choice Questions.

Question 1.
Foreign trade means ………………………..
(a) Trade between nations of the world
(b) Trade among different states
(c) Trade among two states
(d) Trade with one nation
Answer:
(a) Trade between nations of the world

Question 2.
Balance of Trade means
(a) Import and export of invisible items only
(b) Import and export of both visible and invisible items
(c) Import of visible items only
(d) Import and export of visible items only
Answer:
(d) Import and export of visible items only

Question 3.
International trade is regulated at present by ………………………..
(a) IBRD
(b) WTO
(c) OMF
(d) GATT
Answer:
(b) WTO

Question 4.
The exports of India are broadly classified into ……………………….. categories.
(a) Two
(b) Three
(c) Four
(d) Five
Answer:
(c) Four

Question 5.
The New Export – Import policy gives a further push to ………………………..
(a) Liberalisation
(b) Mixed system
(c) Capitalism
(d) Socialism
Answer:
(a) Liberalisation

Question 6.
The World Trade organisation is a ………………………..
(a) Promote of private foreign investment
(b) Promoter of International monetary co-operation
(c) Lateral trade agreement
(d) New trade body to settle trade disputes between nations
Answer:
(d) New trade body to settle trade disputes between nations

Question 7.
To promote ……………………….. stability is one of the aims of IMF.
(a) Exchange
(b) Money
(c) Investment
(d) Finance
Answer:
(a) Exchange

Question 8.
The New Export Import policy was implemented in ………………………..
(a) 1990 – 1995
(b) 1991 – 1996
(c) 1992 – 1997
(d) 1993 – 1998
Answer:
(c) 1992 – 1997

Question 9.
The role of WTO is to regulate trade among the nations of the ………………………..
(a) Trade
(b) Organisation
(c) World
(d) Regulation
Answer:
(c) World

Question 10.
The WTO was setup in the year ………………………..
(a) 1995
(b)1885
(c) 1875
(d) 1865
Answer:
(a) 1995

Question 11.
……………………….. means value of imports is in excess of the value exports.
(a) Balance of Trade
(b) Unfavourable balance of trade
(c) Favourable balance of trade
(d) Export trade
Answer:
(b) Unfavourable balance of trade

Question 12.
……………………….. items means the imports and exports of services and other foreign transfer transactions.
(a) Invisible
(b) Visible
(c) Exports
(d) Imports
Answer:
(a) Invisible

Question 13.
Foreign trade increases worker’s welfare atleast ……………………….. ways.
(a) Two
(b) Three
(c) Four
(d) Five
Answer:
(c) Four

Question 14.
……………………….. trade refers to the trade or exchange of goods and services between two or more countries.
(a) Internal
(b) External
(c) International
(d) Domestic
Answer:
(c) International

Question 15.
If trade is done on large scale it is called ………………………..
(a) Whole sale trade
(b) State trade
(c) Central trade
(d) World trade
Answer:
(a) Whole sale trade

Question 16.
The relationship between value of exports and value of imports is known as ………………………..
(a) EXIM
(b) Foreign exchange
(c) Trade
(d) Terms of trade
Answer:
(d) Terms of trade

Question 17.
If the value of exports is greater than value of imports then it is known as ……………………….. terms of trade.
(a) Unfavourable
(b) Favourable
(c) Moderate
(d) Low
Answer:
(b) Favourable

Question 18.
Imports of India may be divided into ……………………….. parts.
(a) Two
(b) Three
(c) Four
(d) Five
Answer:
(b) Three

Question 19.
……………………….. means imports and exports of commodities.
(a) EXIM
(b) Visible items
(c) Non visible items
(d) Foreign exchange
Answer:
(b) Visible items

Question 20.
……………………….. means exports and imports may be exactly equal.
(a) Balance of trade
(b) Balance of payments
(c) Balanced balance of Trade
(d) Balanced balance of payments
Answer:
(c) Balanced balance of Trade

Question 21.
A special branch of Economics which primarily deals with the basics of ……………………….. trade.
(a) Internal
(b) External
(c) International
(d) Foreign trade
Answer:
(c) International

Question 22.
FDI objective is called ………………………..
(a) Sales expansion
(b) Export expansion
(c) Import expansion
(d) EXIM expansion
Answer:
(a) Sales expansion

Question 23.
The currency of another country is called ………………………..
(a) Money transfer
(b) Money exchange
(c) Foreign exchange
(d) Foreign transfer
Answer:
(c) Foreign exchange

Question 24.
Abundance in the availability of a factor in a country is called ………………………..
(a) Endowment policy
(b) Comparative cost
(c) Absolute cost
(d) Factor Endowment
Answer:
(d) Factor Endowment

Question 25.
Foreign Investment mostly takes the form of ………………………..
(a) Indirect investment
(b) Direct investment
(c) IMF investment
(d) World bank investment
Answer:
(b) Direct investment

II. Match the following and choose the correct answer by using codes given below:

Question 1.
A. Internal Trade – (i) International trade
B. Modem Theory – (ii) Labour
C. Classical Theory – (iii) Geographical boundaries
D. Modem Theory – (iv) Eli Heckscher
Codes:
(a) A (ii) B (iii) C (iv) D (i )
(b) A (iii) B (i) C (ii) D (iv)
(c) A (iv) B (ii) C (i) D (iii)
(d) A (i) B (iv) C (iii) D (ii)
Answer:
(b) A (iii) B (i) C (ii) D (iv)

Question 2.
A. Export – (i) Disequillibrium
B. Secular – (ii) Surplus goods
C. Delibrate measure – (iii) Foreign loans
D. Monetary measures – (iv) Exchange control
Codes:
(a) A (ii) B (i) C (iii) D (iv)
(b) A (i) B (ii) C (iv) D (iii)
(c) A (iii) B (iv) C (ii) D (i)
(d) A (iv) B (iii) C (i) D (ii)
Answer:
(a) A (ii) B (i) C (iii) D (iv)

Question 3.
A. Adam Smith – (i) Foreign Exchange
B. Eli Heckscher – (ii) Absolute cost advantage
C. Movement of goods – (iii) Modem theory of International trade
D. FOREX – (iv) Visible trade
Codes:
(a) A (i) B (ii) C (iii) D (iv)
(b) A (ii) B (iii) C (iv) D (i)
(c) A (iv) B (i) C (ii) D (iii)
(d) A (iii) B (iv) C (i) D (ii)
Answer:
(b) A (ii) B (iii) C (iv) D (i)

Question 4.
A. Term of trade – (i) Official reserve
B. FDI – (ii) Exchange rate
C. Gold stock – (iii) Income terms of trade
D. G.S; Dorrance – (iv) Global economy
Codes:
(a) A (i) B (ii) C (iii) D (iv)
(b) A (iv) B (iii) C (ii) D (i)
(c) A (ii) B (iv) C (i) D (iii)
(d) A (iii) B (i) C (iv) D (ii)
Answer:
(c) A (ii) B (iv) C (i) D (iii)

Question 5.
A. Net Barter Terms of Trade – (i) T_f = (P_x / P_m)F_s
B. Gross Barter Terms of Trade – (ii) T_n = (P_s / P_m) × 100
C. Income Terms of Trade – (iii) T_g = (Q_m / Q_s) × 100
D. Single Factoral Terms of Trade – (iv) T_s = (P_s / P_m)Q_s
Codes:
(a) A (i) B (ii) C (iii) D (iv)
(b) A (iv) B (iv) C (i) D (ii)
(c) A (iv) B (i) C (ii) D (iii)
(d) A (ii) B (iii) C (iv) D (i)
Answer:
(d) A (ii) B (iii) C (iv) D (i)

III. State whether the statements are true or false.

Question 1.
(i) Trade is one of the powerful forces of economic integration.
(ii) Price of a commodity is measured by the amount of labour required to produce it.

(a) Both (i) and (ii) are false
(b) Both (i) and (ii) are true
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(b) Both (i) and (ii) are true

Question 2.
(i) International Economics is a specialized field of economics.
(ii) Inflation and exchange rates are direct relationship.

(a) Both (i) and (ii) are true
(b) Both (i) and (ii) are false
(c) (i) is false but (ii) is true
(d) (i) is true but (ii) is false .
Answer:
(d) (i) is true but (ii) is false.

Question 3.
(i) Movement of goods are called “Visible Trade”.
(ii) Only export and import of commodities are included in the statement of balance of trade of the country.

(a) Both (i) and (ii) are false
(b) Both (i) and (ii) are true
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(b) Both (i) and (ii) are true

Question 4.
(i) The Income terms of trade was given by Taussig.
(ii) Gross Barter Terms of trade was developed by G.S. Dorrance.

(a) Both (i) and (ii) are false
(b) Both (i) and (ii) are true
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(a) Both (i) and (ii) are false

Question 5.
(i) Viner constructed another index called “Double Factoral terms of Trade”.
(ii) Viner has devised another concept called the “Single factoral terms of trade”.

(a) Both (i) and (ii) are false
(b) Both (i) and (ii) are true
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(b) Both (i) and (ii) are true

IV. Which of the following is correctly matched.

Question 1.
(a) David Ricardo – Factor Endowment Theory
(b) Eli Heckscher – British Economist
(c) Marshall – Swedish Economist
(d) Adam Smith – Theory of Absolute cost advantage
Answer:
(d) Adam Smith – Theory of Absolute cost advantage

Question 2.
(a) T_N = (P_x / P_m) x 100 – Net Barter Term of Trade
(b) T = (Q_m / Q_x) x 100 – Income Terms of Trade
(c) T_y = (P_x / P_m) Q_x – Gross Barter Terms of Trade
(d) T_ff = (P_x / P_m)(F_x / F_m) – Single Factoral Terms of Trade
Answer:
(a) T_N = (P_x / P_m) x 100 – Net Barter Term of Trade

Question 3.
(a) SDR – Special Drawing Rights
(b) IMF – India Monetary Fund
(c) BOP – Balance of Price
(d) BOT – Balance of Technology
Answer:
(a) SDR – Special Drawing Rights

Question 4.
(a) NER – Normal Exchange Rate
(b) RER – Real Exchange Ratio
(c) NEER – Normal Effective Exchange Rate
(d) REER – Real Effective Exchange Rate
Answer:
(d) REER – Real Effective Exchange Rate

Question 5.
(a) FDI – Foreign Direct Investment
(b) FOREX – Foreign Export
(c) UDC – Under Development Consumption
(d) MNC – Multi National Country
Answer:
(a) FDI – Foreign Direct Investment

V. Which of the following is not correctly matched.

Question 1.
(a) P₂ – Price level in India
(b) P_f – Price level in abroad (say VS)
(c) e – Nominal exchange rate is flexible
(d) P_x – Price index of exports
Answer:
(c) e – Nominal exchange rate is flexible

Question 2.
(a) Internal Trade – Trade with in Nation
(b) External Trade – Trade between two countries
(c) Balance of Trade – Visible Trade
(d) Income Terms of Trade – Adam smith
Answer:
(d) Income Terms of Trade – Adam smith

Question 3.
(a) FOREX – Foreign Exchange
(b) WTO – World Trade Organisation
(c) FDI – Foreign Direct Investment
(d) IBRD – india Bank Recruitment Development
Answer:
(d) IBRD – india Bank Recruitment Development

Question 4.
(a) Cartels – Economic Integration
(b) Scarce factor – Imports
(c) Factor endowment theory – Ohlin and Ricardo
(d) Labour cost – Unrealistic
Answer:
(c) Factor endowment theory – Ohlin and Ricardo

Question 5.
(a) Intra – regional trade – Internal trade
(b) World Bank – IMF
(c) Types of Exchange Rate – Fixed exchange rate system
(d) Equillibrium Exchange Rate – David Ricardo
Answer:
(d) Equillibrium Exchange Rate – David Ricardo

VI. Pick the odd one out.

Question 1.
The major sectors benefied from FDi in India are ………………….
(a) Financial Sector
(b) Insurance
(c) Telecommunication
(d) Agriculture
Answer:
(d) Agriculture

Question 2.
Determinants of Exchange Rates
(a) Differentials in Inflation
(b) Differntials in Interest Rates
(c) Current Account Deficits
(d) Public people
Answer:
(d) Public people

Question 3.
Types of Exchange Rates
(a) REAL
(b) NEER
(c) Nominal exchange rate
(d) Real exchange rate
Answer:
(a) REAL

Question 4.
Export promotion is ………………….
(a) Reduction of duties
(b) Import Incentives
(c) Export subsidies
(d) Export Incentives
Answer:
(b) Import Incentives

Question 5.
Monetary measures is ………………………
(a) Monetary contraction
(b) Devaluation
(c) Tourism Development
(d) Exchange control
Answer:
(c) Tourism Development

VII. Assertion and Reason.

Question 1.
Assertion (A): David Ricardo was formulated as an explicit and precise theory.
Reason (R): David Ricardo developed the theory of absolute cost advantage.

(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(c) ‘A’ is true but ‘R’ is false

Question 2.
Assertion (A): Gains from International trade.
Reason (R): International trade also known as domestic trade.
(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(c) ‘A’ is true but ‘R’ is false

Question 3.
Assertion (A): FDI is an Domestic Economy.
Reason (R): FDI is an Global Economy.

(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(d) ‘A’ is false but ‘R’ is true

Question 4.
Assertion (A): Exchange control means the state intervention.
Reason (R): Exchange control means the forex market.

(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’

Question 5.
Assertion (A): Price of a commodity is measured by the amount of labour required to produce it.
Reason (R): Trade is one of the Demerit.

(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(c) ‘A’ is true but ‘R’ is false

Part – B
Answer The Following Questions In One or Two Sentences.

Question 1.
Define “Domestic Trade”?
Answer:

1. It refers to the exchange of goods and services within the political and geographical boundaries of a nation.
2. It is a trade within a country.
3. This is also known as ‘domestic trade’ or ‘home trade’ or ‘intra-regional trade’.

Question 2.
State Ricardo’s Theory of comparative cost advantage criticisms?
Answer:
Criticisms:

1. Labour cost is a small portion of the total cost. Hence, theory based on labour cost is unrealistic.
2. Labourers in different countries are not equal in efficiency.

Question 3.
Write Factor endowment model?
Answer:
Factor endowment model:

1. Developed by Heckscher and Ohlin
2. Countries with a relative factor abundance can specialise and trade
3. Abundance of skilled labour → specialisation → export → exchange for goods are services produced by countries with abundance of unskilled labour
4. Exports embody the abundant factor
5. Imports embody the scarce factor

Question 4.
Write Modern Theory of International Trade differences in comparative costs?
Answer:
Modem Theory of International Trade theory attributes international differences in comparative costs to:

1. Difference in the endowments of factors of production between countries, and
2. Differences in the factor proportions required in production.

Question 5.
Write Modern Theory of International Trade Limitations?
Answer:
Limitations:

1. Factor endowment of a country may change over time.
2. The efficiency of the same factor (say labour) may differ in the two countries. For example, America may be labour scarce in terms of number of workers. But in terms of efficiency, the total labour may be larger.

Question 6.
Define “Visible Trade”?
Answer:
Visible Trade:
Only export and import of commodities are included in the statement of Balance of Trade of a country. Movements of goods (export and imports of commodities) are also known as ‘visible trade’,

Question 7.
Define “Balance of Payments Disequillibrium”?
Answer:
Balance of Payments Disequilibrium:
The BoP is said to be balanced when the receipts (R) and payments (P) are just equal, i.e.,
R / P = 1

Question 8.
Write favourable and unfavourable balance of payments and equations?
Answer:
Favourable BoP:
When receipts exceed payments, the BoP is said to be favourable. That is,
R / P > 1.

Unfavourable BOP:
When receipts are less than payments, the BoP is said to be unfavourable or adverse. That is,
R / P < 1.

Part – C
Answer The Following Questions In One Paragraph.

Question 1.
Write Adam Smith’s theory of Absolute Cost Advantage Assumptions?
Answer:
Assumptions:

1. There are two countries and two commodities (2 x 2 model).
2. Labour is the only factor of production.
3. Labour units are homogeneous.
4. The cost or price of a commodity is measured by the amount of labour required to produce it.
5. There is no transport cost.

Question 2.
Write Ricardo’s Theory of Comparative Cost Advantage Assumptions/
Answer:
Assumptions:

1. There are only two nations and two commodities (2 × 2 model)
2. Labour is the only element of cost of production.
3. All labourer s are of equal efficiency.
4. Labour is perfectly mobile within the country but perfectly immobile between countries.
5. Production is subject to the law of constant returns.
6. Foreign trade is free from all barriers.
7. No change in technology.
8. No transport cost.
9. Perfect competition.
10. Full employment.
11. No government intervention.

Question 3.
What are International Specialization gains?
Answer:
International specialization offers the following gains.

1. Better utilization of resources.
2. Concentration in the production of goods in which it has a comparative advantage.
3. Saving in time.
4. Perfection of skills in production.
5. Improvement in the techniques of production.
6. Increased production.
7. Higher standard of living in the trading countries.

Question 4.
Write favourable and unfavourable balance of Trade?
Answer:
Favourable BOT:
When the total value of commodity exports of a country exceeds the total value of commodity imports of that country, it is said that the country has a ‘favourable’ balance of trade.

Unfavourable BOT:
If total value of commodity exports of a country is less than the total . value of commodity imports of that country, that country is said to have an ‘unfavourable’ balance of trade.

Part – D
Answer The Following Questions In About A page.

Question 1.
Explain the Adam Smith’s Theory of Absolute Cost Advantage Theory and Assumptions with diagram?
Answer:
Adam Smith’s Theory of Absolute Cost Advantage:
Adam Smith argued that all nations can be benefitted when there is free trade and specialisation in terms of their absolute cost advantage.

The Theory:

1. According to Adam Smith, the basis of international trade was absolute cost advantage.

2. Trade between two countries would be mutually beneficial when one country produces a commodity at an absolute cost advantage over the other country which in turn produces another commodity at an absolute cost advantage over the first country.

Assumptions:

1. There are two countries and two commodities (2 × 2 model).
2. Labour is the only factor of production.
3. Labour units are homogeneous.
4. The cost or price of a commodity is measured by the amount of labour required to produce it.
5. There is no transport cost.

Illustration:

Absolute cost advantage theory can be illustrated with the help of the following example.

1. From the illustration, it is clear that India has an absolute advantage in the production of wheat over China and China has an absolute advantage in the production of cloth over India.
2. Therefore, India should specialize in the production of wheat and import cloth from China.
3. China should specialize in the production of cloth and import wheat from India.
4. This kind of trade would be mutually beneficial to both India and China.

Question 2.
Briefly explain the gains from International Trade Categories?
Answer:
Gains from International Trade:

1. International trade helps a country to export its surplus goods to other countries and secure a better market for it.
2. Similarly, international trade helps a country to import the goods which cannot be produced at all or can be produced at a higher cost.
3. The gains from international trade may be categorized under four heads.

I. Efficient Production:

1. International trade enables each participatory country to specialize in the production of goods in which it has absolute or comparative advantages.
2. International specialization offers the following gains.
   1. Better utilization of resources.
   2. Concentration in the production of goods in which it has a comparative advantage.
   3. Saving in time.
   4. Perfection of skills in production.
   5. Improvement in the techniques of production.
   6. Increased production.
   7. Higher standard of living in the trading countries.

II. Equalization of Prices between Countries:
International trade may help to equalize prices in all the trading countries.

1. Prices of goods are equalized between the countries (However, in reality it has not happened).
2. The difference is only with regard to the cost of transportation.
3. Prices of factors of production are also equalized (However, in reality it has not happened).

III. Equitable Distribution of Scarce Materials:
International trade may help the trading countries to have equitable distribution of scarce resources.

IV. General Advantages of International Trade:

1. Availability of variety of goods for consumption.
2. Generation of more employment opportunities.
3. Industrialization of backward nations.
4. Improvement in relationship among countries (However, in reality it has not happened).
5. Division of labour and specialisation.
6. Expansion in transport facilities.

Question 3.
Describe the Types of Terms of Trades?
Answer:
Types of Terms of Trade:
The different concepts of terms of trade were classified by Gerald M.Meier into the following three categories:
Terms of Trade related to the Ratio of Exchange between Commodities:

1. Net Barter Terms of Trade:

1. This type was developed by Taussig in 1927.
2. The ratio between the prices of exports and of imports is called the “net barter terms of trade’.
3. It is named by Viner as the ‘commodity terms of trade’.

It is expressed as:
T_n = (P_x / P_m ) × 100
Where,
T_n = Net Barter Terms of Trade
P_x = Index number of export prices
P_m = Index number of import prices
This is used to measure the gain from international trade.
If ‘T_n’ is greater than 100, then it is a favourable terms of trade which will mean that for a rupee of export, more of imports can be received by a country.

2. Gross Barter Terms of Trade:

1. This was developed by Taussig in 1927 as an improvement over the net terms of trade.
2. It is an index of relationship between total physical quantity of imports and the total physical quantity of exports.

T = (Q_m / Q_x) × 100 Where,
Q_m = Index of import quantities .
Q_x = Index of export quantities
If for a given quantity of export, more quantity of import can be consumed by a country, then one can say that terms of trade are favourable.

3. Income Terms of Trade:

1. The income terms of trade was given by G.S.Dorrance in 1948.
2. It is the index of the value of exports divided by the price index for imports multiplied by quantity index of experts.
3. In other words, it is the net barter terms of trade of a country multiplied by its exports – volume index.

T = (P_x / P_m) Q
Where,
P_x = Price index of exports
P_m = Price index of imports
Q_x = Quantity index of exports

Question 4.
Briefly explain causes for Balance of payments disequillibrium?
Answer:
Causes for BoP Disequilibrium:
The following are the major causes producing disequilibrium in the balance of payments of a country.

(I) Cyclical Fluctuation:

1. Cyclical disequilibrium in different countries is caused by their cyclical fluctuations, their phases and magnitude.
2. World trade shrinks during depression while trade flourishes during prosperity.

(II) Structural Changes:

1. Structural disequilibrium is caused by the structural changes brought by huge development and investment programmes in the developing economies.
2. Such economies may have high propensity to import for want of capital for rapid industrialization, while export may not be boosted up to that extent.

(III) Development Expenditure:

1. Development disequilibrium is caused by rapid economic development which results in income and price effects.
2. The less developed countries in the early stage of development are not self sufficient.
3. Income, savings and investment are abysmally low.
4. They depend upon developed countries for import of commodities, capital and technology.
5. Export potential is low and import intensity is high.
6. So the LDCs suffer from adverse BoP.

(IV) Consumerism:

1. Balance of payments position of a country is adversely affected by a huge increase in consumption.
2. This increases the need for imports and decreases the capacity to export.

(V) Demonstration Effect:

1. Deficit in the balance of payments of developing countries is also caused by demonstration effect which influences the people in UDCs to imitate western styled goods.
2. This will raise the propensity to import causing adverse balance of payments.
3. This is good for the developed countries.

(VI) Borrowing:

1. International borrowing and investment may cause a deficit in the balance of payments.
2. When the international borrowing is heavy, a country’s balance of payments will be adverse since it repays loans with interest.
3. Servicing of debt is a huge burden. That is why the UDCs are forced to borrow more, (viz) Technological Backwardness:
4. Due to technological backwardness, the people (Indians) are unable to use the energy (Solar) available with them.
5. As a result they import huge petroleum products from foreign countries, increasing the trade deficit.

(VII) Technological Backwardness:

1. Due to technological backwardness, the people (Indians) are unable to use the energy (Solar) available with them.
2. As a result they import huge petroleum products from foreign countries, increasing the trade deficit.

(VIII) Global Politics:

1. The rich countries (e.g. USA) need to sell their weapons to promote their economy and generate employment.

2. Hence, wars between countries (for example Iran and Irag, Pakistan and India) are stimulated In order to win the wars, the poor countries are forced to buy the weapons from weapon – rich countries, using their export earnings and creating trade deficit.

3. Thus UDCs are trapped forever.

Share this Tamilnadu State Board 12th Economics Solutions Chapter 7 International Economics Questions and Answers with your friends to help them to overcome the grammar issues in exams. Keep visiting this site frequently to get the latest information on different subjects. Clarify your doubts by posting the comments and get the answers in an easy manner.

Students of 12th can get the pdf links of Tamilnadu State Board Economics Solutions here. You can Download Samacheer Kalvi 12th Economics Book Solutions Chapter 9 Fiscal Economics Questions and Answers, Notes Pdf, Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Economics Solutions Chapter 9 Fiscal Economics

It is very important to put the textbook aside while preparing for the exams. So, if you follow Samacheer Kalvi 12th Economics Textbook Solutions you can cover all the topics in Chapter 9 Fiscal Economics Questions and Answers. This helps to improve your communication skills.

Samacheer Kalvi 12th Economics Fiscal Economics Text Book Back Questions and Answers

Part – A
Multiple Choice Questions.

Question 1.
The modem state is ……………………..
(a) Laissez – faire state
(b) Aristocratic state
(c) Welfare state
(d) Police state
Answer:
(c) Welfare state

Question 2.
One of the following is NOT a feature of private finance.
(a) Balancing of income and expenditure
(b) Secrecy
(c) Saving some part of income
(d) Publicity
Answer:
(d) Publicity

Question 3.
The tax possesses the following characteristics.
(a) Compulsory
(b) No quid pro quo
(c) Failure to pay is offence
(d) All the above
Answer:
(d) All the above

Question 4.
Which of the following canons of taxation was not listed by Adam smith?
(a) Canon of equality
(b) Canon of certainty
(c) Canon of convenience
(d) Canon of simplicity
Answer:
(d) Canon of simplicity

Question 5.
Consider the following statements and identify the correct ones.
i. Central government does not have exclusive power to impose tax which is not mentioned in state or concurrent list.
ii. The Constitution also provides for transferring certain tax revenues from union list to states.
(a) i only
(b) ii only
(c) both
(d) none
Answer:
(b) ii only

Question 6.
GST is equivalence of ……………………..
(a) Sales tax
(b) Corporation tax
(c) Income tax
(d) Local tax
Answer:
(a) Sales tax

Question 7.
The direct tax has the following merits except
(a) equity
(b) convenient
(c) certainty
(d) civic consciousness
Answer:
(b) convenient

Question 8.
Which of the following is a direct tax?
(a) Excise duty
(b) Income tax
(c) Customs duty
(d) Service tax
Answer:
(b) Income tax

Question 9.
Which of the following is not a tax under Union list?
(a) Personal Income Tax
(b) Corporation Tax
(c) Agricultural Income Tax
(d) Excise duty
Answer:
(c) Agricultural Income Tax

Question 10.
“Revenue Receipts” of the Government do not include
(a) Interest
(b) Profits and dividents
(c) Recoveries and loans
(d) Rent from property
Answer:
(d) Rent from property

Question 11.
The difference between revenue expenditure and revenue receipts is
(a) Revenue deficit
(b) Fiscal deficit
(c) Budget deficit
(d) Primary deficit
Answer:
(a) Revenue deficit

Question 12.
The difference between total expenditure and total receipts including loans and other liabilities is called …………………………….
(a) Fiscal deficit
(b) Budget deficit
(c) Primary deficit
(d) Revenue deficit
Answer:
(a) Fiscal deficit

Question 13.
The primary purpose of deficit financing is
(a) Economic development
(b) Economic stability
(c) Economic equality
(d) Employment generation
Answer:
(a) Economic development

Question 14.
Deficit budget means
(a) An excess of government’s revenue over expenditure
(b) An excess of government’s current expenditure over its current revenue
(c) An excess of government’s total expenditure over its total revenue
(d) None of above
Answer:
(c) An excess of government’s total expenditure over its total revenue

Question 15.
Methods of repayment of public debt is
(a) Conversion
(b) Sinking fund
(c) Funded debt
(d) All these
Answer:
(d) All these

Question 16.
Conversion of public debt means exchange of ……………………………
(a) New bonds for the old ones
(b) Low interest bonds for higher interest bonds
(c) Long term bonds for short term bonds
(d) All the above
Answer:
(b) Low interest bonds for higher interest bonds

Question 17.
The word budget has been derived from the French word “bougette” which means
(a) A small bag
(b) An empty box
(c) A box with papers
(d) None of the above
Answer:
(a) A small bag

Question 18.
Which one of the following deficits does not consider borrowing as a receipt?
(a) Revenue deficit
(b) Budgetary deficit
(c) Fiscal deficit
(d) Primary deficit
Answer:
(c) Fiscal deficit

Question 19.
Finance Commission determines
(a) The finances of Government of India
(b) The resources transfer to the states
(c) The resources transfer to the various departments
(d) None of the above
Answer:
(b) The resources transfer to the states

Question 20.
Consider the following statements and identify the right ones.
i. The finance commission is appointed by the President
ii. The tenure of Finance commission is five years

(a) i only
(b) ii only
(c) Both
(d) None
Answer:
(c) Both

Part – B
Two Mark Questions.

Question 21.
Define public finance?
Answer:
“Public finance is one of those subjects that lie on the border line between Economics and Politics. It is concerned with income and expenditure of public authorities and with the adjustment of one to the other”. – Huge Dalton “Public finance is an investigation into the nature and principles of the state revenue and expenditure”. – Adam Smith

Question 22.
What is public revenue?
Answer:
Public Revenue:
Public revenue deals with the methods of raising public revenue such as tax and non-tax, the principles of taxation, rates of taxation, impact, incidence and shifting of taxes and their effects.

Question 23.
Differentiate tax and fee?
Answer:
Tax:

• A tax is a compulsory payment made to the government.
• People on whom a tax is imposed must pay the tax.
• There is no quid pro quo between a taxpayer and public authorities. This means that the tax payer cannot claim any specific benefit against the payment of a tax.

Fee:

• Fees are another important source of revenue for the government.
• A fee is charged by public authorities for rendering a service to the citizens.
• The government provides certain services and charges certain fees for them. For example, fees are charged for issuing of passports, driving licenses, etc.

Question 24.
Write a short note on zero based budget/
Answer:
Zero Base Budget:
1. The Government of India presented Zero-Base-Budgeting (ZBB first) in 1987-88.

2. It involves fresh evaluation of expenditure in the Government budget, assuming it as a new item.

3. The review has been made to provide justification or otherwise for the project as a whole in the light of the socio economic objectives which have been already set up for this project and as well as in view of the priorities of the society.

Question 25.
Give two examples for direct tax?
Answer:
Equity:
Direct taxes are progressive i.e. rate of tax varies according to tax base. For example, income tax satisfies the canon of equity.

Certainity:
Canon of certainty can be ensured by direct taxes. For example, an income tax payer knows when and at what rate he has to pay income tax.

Question 26.
What are the components of GST?
Answer:
Components of GST:
The component of GST are of 3 types. They are: CGST, SGST & IGST.

1. CGST: Collected by the Central Government on an intra – state sale (e.g. Within state/ union territory)
2. SGST: Collected by the State Government on an intra – state sale {e.g. Within state/ union territory)
3. IGST: Collected by the Central Government for inter – state sale {e.g. Maharashtra to Tamil Nadu)

Question 27.
What do you mean by public debt?
Answer:

1. The state has to supplement the traditional revenue sources with borrowing from individuals, and institutions within and outside the country.
2. The amount of borrowing is huge in the under developed countries to finance development activities.
3. The debt burden is a big problem and most of the countries are in debt trap.

Part – C
Three Mark Questions.

Question 28.
Describe canons of Taxation?
Answer:
According to Adam Smith, there are four canons or maxims of taxation. They are as follows:
Canons of Taxation:

1. Economical
2. Equitable
3. Convenient
4. Certain
5. (Efficient and Flexible)

1. Canon of Ability:

1. The Government should impose tax in such a way that the people have to pay taxes according to their ability.
2. In such case a rich person should pay more tax compared to a middle class person or a poor person.

2. Canon of Certainty:

1. The Government must ensure that there is no uncertainty regarding the rate of tax or the time of payment.
2. If the Government collects taxes arbitrarily, then these will adversely affect the efficiency of the people and their working ability too.

3. Canon of Convenience:

1. The method of tax collection and the timing of the tax payment should suit the convenience of the people.
2. The Government should make convenient arrangement for all the tax payers to pay the taxes without difficulty.

4. Canon of Economy:

1. The Government has to spend money for collecting taxes, for example, salaries are given to the persons who are responsible for collecting taxes.
2. The taxes, where collection costs are more are considered as bad taxes.
3. Hence, according to Smith, the Government should impose only those taxes whose collection costs are very less and cheap.

Question 29.
Mention any three similarities between public finance and private finance?
Answer:
Similarities:
1. Rationality:

1. Both public finance and private finance are based on rationality.
2. Maximization of welfare and least cost factor combination underlie both.

2. Limit to borrowing:

1. Both have to apply restraint with regard to borrowing.
2. The Government also cannot live beyond its means.
3. There is a limit to deficit financing by the state also.

3. Resource utilisation:

1. Both the private and public sectors have limited resources at their disposal.
2. So both attempt to make optimum use of resources.

Question 30.
What are the functions of a modern state?
Answer:
Functions of Modern State:

1. The modem state is a welfare state and not just police state.

2. The state assumes greater roles by creating economic and social overheads, ensuring stability both internally and externally, conserving resources for sustainable development and so on.

(I) Defence:
The primary function of the Government is to protect the people from external aggression and internal disorder.
The government has to maintain adequate police and military forces and render protective services.

(II) Judiciary:
Rendering justice and settlement of disputes are the concern of the government.
It should provide adequate judicial structure to render justice to all classes of citizens.

(III) Enterprises:
The regulation and control of private enterprise fall under the purview of the modem State. Ownership of certain enterprises and operating them successfully are the responsibilities of the government.

(IV) Social Welfare:
It is the duty of the state to make provisions for education, social security, social insurance, health and sanitation for the betterment of the people in the country.

(V) Infrastructure:
Modem States have to build the base for the economic development of the country by creating social and economic infrastructure.

(VI) Macro – economic policy:
The Government has to administer fiscal policy and monetary policy to achieve macro¬economic goals.

(VII) Social Justice:
During the process of growth of an economy, certain sections of the society gain at the cost of others.
The Government needs to intervene with fiscal measures to redistribute income.

(VIII) Control of Monopoly:

1. Concentration of economic power is another evil to be corrected by the Government.
2. So, the state intervenes through control of monopolies and restrictive trade practices to curb concentration of economic power.

Question 31.
State any three characteristics of taxation?
Answer:
Characteristics of Tax:
1. A tax is a compulsory payment made to the government. People on whom a tax is imposed must pay the tax. Refusal to pay the tax is a punishable offence.

2. There is no quid pro quo between a taxpayer and public authorities. This means that the tax payer cannot claim any specific benefit against the payment of a tax.

3. Every tax involves some sacrifice on part of the tax payer.

4. A tax is not levied as a fine or penalty for breaking law.

Question 32.
Point out any three differences between direct tax and indirect tax?
Answer:
Direct Tax:

1. Progressive
2. Falls on the same person.
3. Cannot be shifted.

Indirect Tax:

1. Regressive
2. Falls on different persons.
3. Can be shifted

Question 33.
What is primary deficit?
Answer:
Primary Deficit:

1. Primary deficit is equal to fiscal deficit minus interest payments.
2. It shows the real burden of the government and it does not include the interest burden on loans taken in the past.
3. Thus, primary deficit reflects borrowing requirement of the government exclusive of interest payments.
   Primary Deficit (PD) = Fiscal deficit (PD) – Interest Payment (IP)

Question 34.
Mention any three methods of redemption of public debt?
Answer:
Methods of Redemption of Public Debt:
The process of repaying a public debt is called redemption. The Government sells securities to the public and at the time of maturity, the person who holds the security surrenders it to the Government. The following methods are adopted for debt redemption.

(I) Sinking Fund:

1. Under this method, the Government establishes a separate fund known as “Sinking Fund”.
2. The Government credits every year a fixed amount of money to this fund.
3. By the time the debt matures, the fund accumulates enough amount to pay off the principal along with interest.
4. This method was first introduced in England by Walpol.

(II) Conversion:

1. Conversion of loans is another method of redemption of public debt.
2. It means that an old loan is converted into a new loan.
3. Under this system’a high interest public debt is converted into a low interest public debt.
4. Dalton felt that debt conversion actually relaxes the debt burden.

(III) Budgetary Surplus:

1. When the Government presents surplus budget, it can be utilised for repaying the debt.
2. Surplus occurs when public revenue exceeds the public expenditure.
3. However, this method is rarely possible.

Part – D
Five Mark Questions.

Question 35.
Explain the scope of public finance?
Answer:
Scope of Public Finance:
The subject ‘Public Finance’ includes five major sub-divisions, viz., Public Revenue, Public Expenditure, Public Debt, Financial Administration and Fiscal Policy.

(I) Public Revenue:
Public revenue deals with the methods of raising public revenue such as tax and non-tax, the principles of taxation, rates of taxation, impact, incidence and shifting of taxes and their effects.

(II) Public Expenditure:
This part studies the fundamental principles that govern the Government expenditure, effects of public expenditure and control of public expenditure.

(III) Public Debt:

1. Public debt deals with the methods of raising loans from internal and external sources.
2. The burden, effects and redemption of public debt fall under this head.

(IV) Financial Administration:

1. This part deals with the study of the different aspects of public budget.
2. The budget is the Annual master financial plan of the Government.
3. The various objectives and steps in preparing a public budget, passing or sanctioning, allocation evaluation and auditing fall within financial administration.

(V) Fiscal Policy:
Taxes, subsidies, public debt and public expenditure are the instruments of fiscal policy.

Question 36.
Bring out the merits of indirect taxes over direct taxes?
Answer:
Merits of Direct Taxes:
(I) Equity:

1. Direct taxes are progressive i.e. rate of tax varies according to tax base.
2. For example, income tax satisfies the canon of equity.

(II) Certainity:

1. Canon of certainty can be ensured by direct taxes.
2. For example, an income tax payer knows when and at what rate he has to pay income tax.

(III) Elasticity:

1. Direct taxes also satisfy the canon of elasticity.
2. Income tax is income elastic in nature. As income level increases, the tax revenue to the Government also increases automatically.

(IV) Economy:

1. The cost of collection of direct taxes is relatively low.
2. The tax payers pay the tax directly to the state.

Merits of Indirect Taxes:

(I) Wider Coverage:

1. All the consumers, whether they are rich or poor, have to pay indirect taxes.
2. For this reason, it is said that indirect taxes can cover more people than direct taxes.
3. For example, in India everybody pays indirect tax as against just 2 percent paying income tax.

(I) Equitable:
The indirect tax satisfies the canon of equity when higher tax is imposed on luxuries used by rich people.

(II) Economical:

1. Cost of collection is less as producers and retailers collect tax and pay to the Government.
2. The traders act as honorary tax collectors.

(IV) Checks harmful consumption:

1. The Government imposes indirect taxes on those commodities which are harmful to health
2. e.g. tobacco, liquor etc.
3. They are known as sin taxes.

(V) Convenient:

1. Indirect taxes are levied on commodities and services.
2. Whenever consumers make purchase, they pay tax along with the price.
3. They do not feel the pinch of paying tax.

Question 37.
Explain the methods of debt redemption?
Answer:
Methods of Redemption of Public Debt:
The process of repaying a public debt is called redemption. The Government sells securities to the public and at the time of maturity, the person who holds the security surrenders it to the Government. The following methods are adopted for debt redemption.

(I) Sinking Fund:

1. Under this method, the Government establishes a separate fund known as “Sinking Fund”.
2. The Government credits every year a fixed amount of money to this fund.
3. By the time the debt matures, the fund accumulates enough amount to pay off the principal along with interest.
4. This method was first introduced in England by Walpol.

(II) Conversion:

1. Conversion of loans is another method of redemption of public debt.
2. It means that an old loan is converted into a new loan.
3. Under this system a high interest public debt is converted into a low interest public debt.
4. Dalton felt that debt conversion actually relaxes the debt burden.

(III) Budgetary Surplus:

1. When the Government presents surplus budget, it can be utilised for repaying the debt.
2. Surplus occurs when public revenue exceeds the public expenditure.
3. However, this method is rarely possible.

(IV) Terminal Annuity:

1. In this method, Government pays off the public debt on the basis of terminal annuity in equal annual instalments.
2. This is the easiest way of paying off the public debt.

(V) Repudiation:

1. It is the easiest way for the Government to get rid of the burden of payment of a loan.
2. In such cases, the Government does not recognise its obligation to repay the loan.
3. It is certainly not paying off a loan but destroying it.
4. However, in normal case the Government does not do so; if done it will lose its credibility, (vz) Reduction in Rate of Interest:
5. Another method of debt redemption is the compulsory reduction in the rate of interest, during the time of financial crisis.

(VII) Capital Levy:

1. When the Government imposes levy on the capital assets owned by an individual or any . institution, it is called capital levy.
2. This levy is imposed on capital assets above a minimum limit on a progressive scale.
3. The fund so collected can be used by the Government for paying off war time debt obligations.
4. This is the most controversial method of debt repayment.

Question 38.
State and explain instruments of fiscal policy?
Answer:
Fiscal Instruments:
Fiscal Policy is implemented through fiscal instruments also called ‘fiscal tools’ or fiscal levers: Government expenditure, taxation and borrowing are the fiscal tools.
(I) Taxation:

1. Taxes transfer income from the people to the Government.
2. Taxes are either direct or indirect.
3. An increase in tax reduces disposable income.
4. So taxation should be raised to control inflation.
5. During depression, taxes are to be reduced.

(II) Public Expenditure:

1. Public expenditure raises wages and salaries of the employees and thereby the aggregate demand for goods and services.
2. Hence public expenditure is raised to fight recession and reduced to control inflation.

(III) Public debt:

1. When Government borrows by floating a loan, there is transfer of funds from the public to the Government.
2. At the time of interest payment and repayment of public debt, funds are transferred from Government to public.

Question 39.
Explain the principles of federal finance?
Answer:
Principles of Federal Finance:
In the case of federal system of finance, the following main principles must be applied:

1. Principle of Independence.
2. Principle of Equity.
3. Principle of Uniformity.
4. Principle of Adequacy.
5. Principle of Fiscal Access.
6. Principle of Integration and coordination.
7. Principle of Efficiency.
8. Principle of Administrative Economy.
9. Principle of Accountability.

1. Principle of Independence:
(i) Under the system of federal finance, a Government should be autonomous and free about the internal financial matters concerned.

(ii) It means each Government should have separate sources of revenue, authority to levy taxes, to borrow money and to meet the expenditure.

3. The Government should normally enjoy autonomy in fiscal matters.

2. Principle of Equity:
From the point of view of equity, the resources should be distributed among the different states so that each state receives a fair share of revenue.

3. Principle of Uniformity:
In a federal system, each state should contribute equal tax payments for federal finance.

4. Principle of Adequacy of Resources:

1. The principle of adequacy means that the resources of each Government i.e. Central and State should be adequate to carry out its functions effectively.
2. Here adequacy must be decided with reference to both current as well as future needs.
3. Besides, the resources should be elastic in order to meet the growing needs and unforeseen expenditure like war, floods etc.

5. Principle of Fiscal Access:
(i) In a federal system, there should be possibility for the Central and State Governments to develop new source of revenue within their prescribed fields to meet the growing financial needs.

(ii) In nutshell, the resources should grow with the increase in the responsibilities of the . Government.

6. Principle of Integration and coordination:

1. The financial system as a whole should be well integrated.
2. There should be perfect coordination among different layers of the financial system of the country.
3. Then only the federal system will survive.
4. This should be done in such a way to promote the overall economic development of the country.

7. Principle of Efficiency:

1. The financial system should be well organized and efficiently administered.
2. Double taxation should be avoided.

8. Principle of Administrative Economy:

1. Economy is the important criterion of any federal financial system.
2. That is, the cost of collection should be at the minimum level and the major portion of revenue should be made available for the other expenditure outlays of the Governments.

9. Principle of Accountability:
Each Government should be accountable to its own legislature for its financial decisions i.e. the Central to the Parliament and the State to the Assembly.

Question 40.
Describe the various types of deficit in budget?
Answer:
The Indian Government budget, budget deficit is of four major types.

1. Revenue Deficit
2. Budget Deficit
3. Fiscal Deficit, and
4. Primary Deficit

(I) Revenue Deficit:
It refers to the excess of the government revenue expenditure over revenue receipts. It does not consider capital receipts and capital expenditure. Revenue deficit implies that the government is living beyond its means to conduct day-to-day operations.
Revenue Deficit (RD) = Total Revenue Expenditure (RE) – Total Revenue Receipts (RR) When RE – RR > 0

(II) Budget Deficit:
Budget deficit is the difference between total receipts and total expenditure (both revenue and capital)
Budget Deficit = Total Expenditure – Total Revenue

(III) Fiscal Deficit:
Fiscal deficit (FD) = Budget deficit + Government’s market borrowings and liabilities

(IV) Primary Deficit:
Primary deficit is equal to fiscal deficit minus interest payments. It shows the real burden of the government and it does not include the interest burden on loans taken in the past. Thus, primary deficit reflects borrowing requirement of the government exclusive of interest payments.
Primary Deficit (PD) = Fiscal deficit (PD) – Interest Payment (IP)

Question 41.
What are the reasons for the recent growth in public expenditure?
Answer:
Causes for the Increase in Government Expenditure:
The modem state is a welfare state. In a welfare state, the government has to perform several functions viz Social, economic and political. These activities are the cause for increasing public expenditure.

(I) Population Growth:
1. During the past 67 years of planning, the population of India has increased from 36.1 crore in 1951, to 121 crore in 2011.

2. The growth in population requires massive investment in health and education, law and order, etc.

3. Young population requires increasing expenditure on education & youth services, whereas the aging population requires transfer payments like old age pension, social security & health facilities.

(II) Defence Expenditure:

1. There has been enormous increase in defence expenditure in India during planning period.
2. The defence expenditure has been increasing tremendously due to modernisation of defence equipment.
3. The defence expenditure of the government was ? 10,874 crores in 1990-91 which increased significantly to ? 2,95,511 crores in 2018-19.

(III) Government Subsidies:
1. The Government of India has been providing subsidies on a number of items such as food, fertilizers, interest on priority sector lending, exports, education, etc.

2. Because of the massive amounts of subsidies, the public expenditure has increased manifold.

(IV) Debt Servicing:
The government has been borrowing heavily both from the internal and external sources, As a result, the government has to make huge amounts of repayment towards debt servicing.

(V) Development Projects:
1. The government has been undertaking various development projects such as irrigation, iron and steel, heavy machinery, power, telecommunications, etc.

2. The development projects involve huge investment.

(VI) Urbanisation:

1. There has been an increase in urbanization.
2. In 1950 – 51 about 17% of the population was urban based.
3. Now the urban population has increased to about 43%.
4. There are more than 54 cities above one million population.
5. The increase in urbanization requires heavy expenditure on law and order, education and civic amenities.

(VII) Industrialisation:

1. Setting up of basic and heavy industries involves a huge capital and long gestation period.
2. It is the government which starts such industries in a planned economy.
3. The under developed countries need a strong of infrastructure like transport, communication, power, fuel, etc.

(VIII) Increase in grants in aid to state and union territories:
There has been tremendous increase in grant-in-aid to state and union territories to meet natural disasters.

Samacheer Kalvi 12th Economics Fiscal Economics Addtional Questions and Answers

I. Multiple Choice Questions.

Question 1.
“Public finance is one of those subjects that lie on the border line between Economics and ……………………….
(a) Finance
(b) Investment
(c) Politics
(d) Money
Answer:
(c) Politics

Question 2.
Tax revenue deals with the ……………………….
(a) Fees
(b) Revenue
(c) Kinds of taxes
(d) Non – tax revenue
Answer:
(c) Kinds of taxes

Question 3.
The compulsory charge levied by the government is ……………………….
(a) Tax
(b) Loan
(c) Licence
(d) Gifts and grants
Answer:
(a) Tax

Question 4.
In ZBB every year is considered as a ……………………….
(a) Academic year
(b) New year
(c) Financial year
(d) Base year
Answer:
(b) New year

Question 5.
………………………. means different sources of government income.
(a) Public finance
(b) Public revenue
(c) Public expenditure
(d) Public credit
Answer:
(b) Public revenue

Question 6.
Public debt deals with the methods of raising loans from Internal and ………………………. sources.
(a) International
(b) National
(c) External
(d) State level
Answer:
(c) External

Question 7.
Taxes, subsidies, public debt and public expenditure are the instruments of ……………………….
(a) Public Revenue
(b) Public Expenditure
(c) Public debt
(d) Fiscal policy
Answer:
(d) Fiscal policy

Question 8.
………………………. deals with study of income, expenditure, borrowing and financial administration of the government.
(a) Public Finance
(b) Public Revenue
(c) Public Expenditure
(d) Public Debt
Answer:
(a) Public Finance

Question 9.
Both Public Finance and Finance are based on rationality.
(a) Private
(b) Resource
(c) Maximization
(d) Private
Answer:
(d) Private

Question 10.
The modem state is a state.
(a) Revenue
(b) Defence
(c) Government
(d) Welfare
Answer:
(d) Welfare

Question 11.
………………………. is the duty of the state to make provisions for education, social security, social insurance, health and sanitation.
(a) Social Welfare
(b) Infrastructure
(c) Social Justice
(d) Macro Economic Policy
Answer:
(a) Social Welfare

Question 12.
…………………………… refers to Government spending incurred by central, state, local government of a country.
(a) Public Finance
(b) Public Expenditure
(c) Public Revenue
(d) Social Welfare
Answer:
(b) Public Expenditure

Question 13.
Adam Smith classified public expenditure on the basis of Production Functions, Commercial Functions and ………………………………. Functions.
(a) Defence
(b) Growth
(c) Development
(d) Government
Answer:
(c) Development

Question 14.
…………………….. such as irrigation, iron and steel, heavy machinery, power, tele communications, etc.
(a) Development projects
(b) Investment projects
(c) Finance project
(d) Monetary projects
Answer:
(a) Development projects

Question 15.
The increase in ………………………… requires heavy expenditure on law and order, education and civic amentities.
(a) Development project
(b) Industrialization
(c) Urbanisation
(d) Public revenue
Answer:
(c) Urbanisation

Question 16.
Heavy Industries involves a huge …………………………. and long gestation period.
(a) Capital
(b) Investment
(c) Revenue
(d) Finance
Answer:
(a) Capital

Question 17.
Welfare activities are undertaken by …………………………..
(a) Modem governments
(b) Capitalist governments
(c) Mixed governments
(d) Socialist governments
Answer:
(a) Modem governments

Question 18.
Borrowing by the government from the public is called ……………………..
(a) Public Revenue
(b) Public expenditure
(c) Public debt
(d) Public finance
Answer:
(c) Public debt

Question 19.
Budget is prepared and submitted …………………………
(a) Every year
(b) Twice in a year
(c) Thrice in a year
(d) Five in a year
Answer:
(a) Every year

Question 20.
Sources of Public Revenue is Tax Revenue and …………………….
(a) Taxes
(b) Non – Tax Revenue
(c) Direct Tax
(d) Indirect Tax
Answer:
(b) Non – Tax Revenue

Question 21.
Income Tax is an example of ………………………….
(a) Proportional Tax
(b) Direct Tax
(c) Indirect Tax
(d) Regressive Tax
Answer:
(b) Direct Tax

Question 22.
………………………… is referred to as a tax charged on a person who purchases the goods and services and it is paid indirectly to the government.
(a) Direct Tax
(b) Indirect Tax
(c) Progressive Tax
(d) Regressive Tax
Answer:
(b) Indirect Tax

Question 23.
……………………….. is an Indirect tax levied on the supply of goods and services.
(a) Direct Tax
(b) Regressive Tax
(c) GST
(d) Progressive Tax
Answer:
(c) GST

Question 24.
………………………… institutions like UTI, LIC, GIC, etc. also buy the Government bonds.
(a) Financial
(b) Non – Financial
(c) Government
(d) Private
Answer:
(a) Financial

Question 25.
The main sources of …………………………… are IMF, World Bank, IDA and ADB, etc.
(a) Internal public debt
(b) External public debt
(c) International debt
(d) World public debt
Answer:
(b) External public debt

II. Match the following and choose the correct answer by using codes given below:

Question 1.
A. Modern state – (i) Indirect tax
B. Gift tax – (ii) Welfare state
C. Corporate tax – (iii) Direct tax
D. Sales tax – (iv) Tax of the central government
Codes:
(a) A (ii) B (iii) C (iv) D (i)
(b) A (iii) B (ii) C (i) D (iv)
(c) A (iv) B (i) C (ii) D (iii)
(d) A (i) B (iv) C (iii) D (ii)
Answer:
(a) A (ii) B (iii) C (iv) D (i)

Question 2.
A. Gifts and grants – (i) Canon of equity
B. Ability to pay – (ii) State government tax
C. Income tax – (iii) Non tax revenue
D. Stamp duties Codes – (iv) Progressive tax
Codes:
(a) A (i) B (ii) C (iii) D (iv)
(b) A (iii) B (i) C (iv) D (ii)
(c) A (iv) B (ii) C (i) D (iv)
(d) A (i) B (iv) C (iii) D (ii)
Answer:
(b) A (iii) B (i) C (iv) D (ii)

Question 3.
A. Components of budget – (i) Macro Economic Policy
B. Causes for public debt – (ii) Revenue Receipts
C. Fiscal policy – (iii) Tax on animals
D. Municipality revenue – (iv) War and preparation of war
Codes:
(a) A (i) B (ii) C (iii) D (iv)
(b) A (ii) B (iv) C(i) D (iii)
(c) A (iv) B (iii) C (ii) D (i)
(d) A (iii) B (i) C (iv) D (ii)
Answer:
(b) A (ii) B (iv) C(i) D (iii)

Question 4.
A. Adam Smith – (i) Progressive tax
B. Best tax system – (ii) Fiscal policy
C. Rebate and subsidies – (iii) Regressive tax
D. Tax rate decreases – (iv) Canons of taxation
Codes:
(a) A (i) B (ii) C (iii) D (iv)
(b) A (ii) B (iv) C (i) D (iii)
(c) A (iii) B (iv) C (ii) D (i)
(d) A (iv) B (i) C (ii) D (iii)
Answer:
(d) A (iv) B (i) C (ii) D (iii)

Question 5.
A. Government Accounts Maintained – (i) Committees of Parliament
B. The estimates committee – (ii) Consolidated Fund
C. Budgetary deficit – (iii) Source of Revenue
D. Federal finance – (iv) Government Deficit
Codes:
(a) A (i) B (ii) C (iii) D (iv)
(b) A (iii) B (iv) C (ii) D (i)
(c) A (ii) B (i) C (iv) D (iii)
(d) A (iv) B (iii) C (i) D (ii)
Answer:
(c) A (ii) B (i) C (iv) D (iii)

III. State whether the statements are true or false.

Question 1.
(i) The difference between Revenue expenditure and Revenue Receipt is Revenue deficit.
(ii) The primary purpose of deficit financing is Economic Development.

(a) Both (i) and (ii) are true
(b) Both (i) and (ii) are false
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(a) Both (i) and (ii) are true

Question 2.
(i) GST is equivalence of sales tax.
(ii) The modem state is police state.

(a) Both (i) and (ii) are true
(b) Both (i) and (ii) are false
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(c) (i) is true but (ii) is false

Question 3.
(i) The word budget has been derived from the French word “bougette” means a small bag.
(ii) Finance commission determines the resources transfer to the various departments.

(a) Both (i) and (ii) are frue
(b) Both (i) and (ii) are false
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(c) (i) is true but (ii) is false

Question 4.
(i) Bougett refers to a small purse.
(ii) Budget estimates are prepared by public finance.

(a) Both (i) and (ii) are tme
(b) Both (i) and (ii) are false
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(b) Both (i) and (ii) are false

Question 5.
(i) Public revenue occupies an important place in the study of public finance.
(ii) Public finance is concerned with the Income and expenditure of public authorities.

(a) Both (i) and (ii) are tme
(b) Both (i) and (ii) are false
(c) (i) is tme but (ii) is false
(d) (i) is false but (ii) is tme
Answer:
(a) Both (i) and (ii) are tme

IV. Which of the following is correctly matched.

Question 1.
(a) Ministry of finance – Central budget every year
(b) Types of budget – Credit budget
(c) Public debt – Agriculture
(d) Federal finance – Employment
Answer:
(a) Ministry of finance – Central budget every year

Question 2.
(a) Canons of taxation – Adam Smith
(b) Indirect tax – Modem state
(c) Compulsory payment – Indirect tax
(d) Proportional tax – Direct tax
Answer:
(a) Canons of taxation – Adam Smith

Question 3.
(a) Wealth tax – Indirect tax
(b) Sales tax – Direct tax
(c) Progressive tax – Health tax
(d) Corporate tax – Tax of the Central Government
Answer:
(d) Corporate tax – Tax of the Central Government

Question 4.
(a) Gifts and grants – Non tax Revenue
(b) Gift tax – Indirect tax
(c) Tax evasion – Capital receipts
(d) Loans from RBI – Deficit budget
Answer:
(a) Gifts and grants – Non tax Revenue

Question 5.
(a) Stamp duties – Tax of the Central Government
(b) Interest on debts – Revenue expenditure
(c) Land tax collected – Direct tax
(d) Income tax – Expenditure
Answer:
(b) Interest on debts – Revenue expenditure

V. Which of the following is not correctly matched:

Question 1.
(a) Canons of Taxation – Adam Smith
(b) SGST – State and Union Territory
(c) Compulsory payment – Tax
(d) Modem state – Technology
Answer:
(d) Modem state – Technology

Question 2.
(a) Income tax – Direct tax
(b) Sales tax – Indirect tax
(c) Proportional tax – Village tax
(d) GST – Goods and Services tax
Answer:
(c) Proportional tax – Village tax

Question 3.
(a) Components of budget – Capital Receipts
(b) State sources – Land and building tax
(c) Redemption of public debt – Sinking fund
(d) Fiscal policy – Micro economic policy
Answer:
(d) Fiscal policy – Micro economic policy

Question 4.
(a) Fiscal Deficit – Budget deficit
(b) Primary Deficit – Fiscal deficit
(c) Revenue Deficit – Total revenue receipt
(d) Deficit budget – Private Revenue
Answer:
(d) Deficit budget – Private Revenue

Question 5.
(a) Public debt – Fiscal instmment
(b) Economic growth – Fiscal policy
(c) Transfer wealth – Internal public debt
(d) Loans from other countries – External revenue
Answer:
(d) Loans from other countries – External revenue

VI. Pick the odd one out.

Question 1.
Causes for increase in public debt
(a) War and preparation of war
(b) Social obligations
(c) Economic development and deficit
(d) Unemployment problem
Answer:
(d) Unemployment problem

Question 2.
Methods of Redemption of public debt
(a) Sinking Fund
(b) Budgetary Surplus
(c) Depression
(d) Terminal Annuity
Answer:
(d) Terminal Annuity

Question 3.
Types of Budget
(a) Revenue budget
(b) Capital budget
(c) Union budget
(d) Supplementary budget
Answer:
(c) Union budget

Question 4.
Central financial relationship union sources are
(a) Corporation tax
(b) Foreign loans
(c) Transport
(d) Railways
Answer:
(c) Transport

Question 5.
Principles of Federal finance
(a) Principles of Integration
(b) Principle of Equity
(c) Principle of Efficiency
(d) Principle of Accountability
Answer:
(a) Principles of Integration

VII. Assertion and Reason.

Question 1.
Assertion (A): Public finance is a study of the financial aspects of government.
Reason (R): Public finance is concerned with the revenue and expenditure of public authorities and with adjustment of the one to the other.

(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’

Question 2.
Assertion (A): Fiscal Economics is a new one. The old and popular term of the subject is ‘Public Finance’.
Reason (R): Public Finance is related financing the central activities only.

(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(c) ‘A’ is true but ‘R’ is false

Question 3.
Assertion (A): The modem state is a police state.
Reason (R): Functions of a government is called Defence, judiciary, enterprises and so on.

(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(d) ‘A’ is false but ‘R’ is true

Question 4.
Assertion (A): Sources of Public Revenue is called Tax Revenue and Non tax Revenue.
Reason (R): Some of the tax revenue sources are Income tax, Corporate tax, Sales tax, Surcharge andCess.

(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’

Question 5.
Assertion (A): Canons of Taxation are Economical, Equitable, Convenient, Certain Efficient and Flexible.
Reason (R): Adam Smiths four canons of taxation are Canon of Ability, Canon of Certainty, Canon of Convenience, Canon of Economy.

(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’

Part – B
Answer The Following Questions In One or Two Sentences.

Question 1.
What do you mean by Public Finance?
Answer:

1. Public finance is a study of the financial aspects of Government.
2. It is concerned with the revenue and expenditure of the public authorities and with adjustment of the one to the other.

Question 2.
What do you mean by Public Expenditure?
Answer:
Public expenditure refers to Government spending incurred by Central, State and Local governments of a country.

Question 3.
Define “Public Expenditure”?
Answer:
Public expenditure can be defined as, “The expenditure incurred by public authorities like central, state and local governments to satisfy the collective social wants of the people is known as public expenditure”.

Question 4.
Define “Public Revenue”?
Answer:

1. Public revenue occupies an important place in the study of public finance.
2. The Government has to perform several functions for the welfare of the people.
3. They involve substantial amount of public expenditure which can be financed only through public revenue.
4. The amount of public revenue to be raised depends on the necessity of public expenditure and the people’s ability to pay.

Question 5.
What are the classification of Public Revenue?
Answer:
Public revenue can be classified into two types.

1. Tax Revenue
2. Non – Tax Revenue

Question 6.
What do you mean by Tax Revenue?
Answer:

1. Tax is a compulsory payment by the citizens to the government to meet the public expenditure.
2. It is legally imposed by the government on the tax payer and in no case tax payer can refuse to pay taxes to the government.

Question 7.
Define “Tax Revenue”?
Answer:
1. “A Tax is a compulsory payment made by a person or a firm to a government without reference to any benefit the payer may derive from the government.” – Anatol Murad

2. “A Tax is a compulsory contribution imposed by public authority, irrespective of the exact amount of service rendered to the tax payer in return and not imposed as a penalty for any legal offence.” – Dalton

Question 8.
Write some of the tax revenue sources?
Answer:
Some of the tax revenue sources are

1. Income tax
2. Corporate tax
3. Sales tax
4. Surcharge and
5. Cess

Part – C
Answer The Following Questions In One Paragraph.

Question 1.
What are the similarities of Public and Private Finance?
Answer:
(I) Rationality:

1. Both public finance and private finance are based on rationality.
2. Maximization of welfare and least cost factor combination underlie both.

(II) Limit to borrowing:

1. Both have to apply restraint with regard to borrowing.
2. The Government also cannot live beyond its means.
3. There is a limit to deficit financing by the state also.

(III) Resource utilisation:

1. Both the private and public sectors have limited resources at their disposal.
2. So both attempt to make optimum use of resources.

(IV) Administration:

1. The effectiveness of measures of the Government as well as private depends on the administrative machinery.
2. If the administrative machinery is inefficient and corrupt it will result in wastages and losses.

Question 2.
What do you mean by Public Revenue?
Answer:

1. The income of the government through all sources is called public income or public revenue.
2. According to Dalton, the term “Public Income” has two senses — wide and narrow.
3. In its wider sense it includes all the incomes or receipts which a public authority may secure during any period of time.
4. In its narrow sense, it includes only those sources of income of the public authority which are ordinarily known as “revenue resources.”
5. To avoid ambiguity, the former is termed “public receipts” and the latter “public revenue.”
6. In a narrow sense, it includes only those sources of income of the Government which are described as “revenue resources”.
7. In broad sense, it includes loans raised by the Government also.

Question 3.
Bringout the merits and demerits of Direct taxes?
Answer:
Merits of Direct Taxes:
(I) Equity:

1. Direct taxes are progressive i.e. rate of tax varies according to tax base.
2. For example, income tax satisfies the canon of equity.

(II) Certainity:

1. Canon of certainty can be ensured by direct taxes.
2. For example, an income tax payer knows when and at what rate he has to pay income tax.

(III) Elasticity:

1. Direct taxes also satisfy the canon of elasticity.
2. Income tax is income elastic in nature.
3. As income level increases, the tax revenue to the Government also increases automatically.

(IV) Economy:

1. The cost of collection of direct taxes is relatively low.
2. The tax payers pay the tax directly to the state.

Demerits of Direct Taxes:

(I) Unpopular:

1. Direct taxes are generally unpopular.
2. It is inconvenient and less flexible.

(II) Productivity affected:

1. According to many economists direct tax may adversely affect productivity.
2. Citizens are not willing to earn more income because in that case they have to pay more taxes.

(III) Inconvenient:
The tax payers find it inconvenient to maintain accounts, submit returns and pay tax in lump sum.

(IV) Tax Evasion:

1. The burden of direct tax is so heavy that tax-payers always try to evade taxes.
2. This ultimately leads to the generation of black money, which is harmful to the economy.

Question 4.
What are the several types of Indirect taxes?
Answer:
There are several types of Indirect Taxes, such as:
1. Excise Duty:
Payable by the manufacturer who shifts the tax burden to retailers and wholesalers.

2. Sales Tax:
Paid by a shopkeeper or retailer, who then shifts the tax burden to customers by charging sales tax on goods and services.

3. Custom Duty:
Import duties levied on goods from outside the country, ultimately paid for by consumers and retailers.

4. Entertainment Tax:
Liability is on the cinema theatre owners, who transfer the burden to cinema goers.

5. Service Tax:
Charged on services like telephone bill, insurance premium such as food bill in a restaurant etc.

Part – D
Answer The Following Questions In About A Page.

Question 1.
What are the Dissimilarities of Public and Private finance?
Answer:
Dissimilarities:
(I) Income and Expenditure adjustment:

1. The government adjusts the income to the expenditure while individuals adjust their expenditure to the income.
2. Private finance involves stitching coat according to cloth available whereas public finance decides the cloth according to the need for the coat.

(II) Borrowing:

1. The government can borrow from internal and external sources; it can borrow from the people by issuing bonds.
2. However, an individual cannot borrow from himself.

(III) Right to print currency:

1. The government can print currency.
2. This involves the creation, distribution and monitoring of currency.
3. The private sector cannot create currency.

(IV) Present vs. future decisions:

1. The public finance is more involved with future planning and making long-term decisions.
2. These investments could include building of schools, hospitals and infrastructure.
3. The private finance makes financial decisions on projects with a short term vision.

(V) Objective:

1. The public sector’s main objective is to provide social benefit in the economy.
2. The private sector aims to maximize personal benefit i.e. Profit.

(VI) Coercion to get revenue:

1. The sources of income of a private individual is relatively limited while those of the Government is wide.
2. The Government can use its power and authority.

(VII) Ability to make huge and deliberate changes:

1. The public finance has the ability to make big decisions on income.
2. For example, it can effectively and deliberately adjust the revenue.
3. But individuals cannot make such massive decisions.

Question 2.
Briefly explain classification of Public expenditure?
Answer:
Classification of public expenditure are as follows:
(I) Classification on the Basis of Benefit:
Cohn and Plehn have classified the public expenditure on the basis of benefit into four classes:

(a) Public expenditure benefiting the entire society, e.g., the expenditure on general administration, defence, education, public health, transport.

(b) Public expenditure conferring a special benefit on certain people and at the same time common benefit on the entire community, e.g., administration of justice etc.

(c) Public expenditure directly benefiting particular group of persons and indirectly the entire society, e.g., social security, public welfare, pension, unemployment relief etc.

(d) Public expenditure conferring a special benefit on some individuals, e.g., subsidy granted to a particular industry.

(II) Classification on the Basis of Function:
Adam Smith classified public expenditure on the basis of functions of government in the following main groups:

(a) Protection Functions:
This group includes public expenditure incurred on the security of the citizens, to protect from external invasion and internal disorder, e.g., defence, police, courts etc.

(b) Commercial Functions:
This group includes public expenditure incurred on the development of trade and commerce, e.g., development of means of transport and communication etc.

(c) Development Functions:
This group includes public expenditure incurred for the development infrastructure and industry.

Question 3.
Explain the sources of Non-Tax Revenue?
Answer:
The sources of non-tax revenue are:
(I) Fees:

1. Fees are another important source of revenue for the government.
2. A fee is charged by public authorities for rendering a service to the citizens.
3. Unlike tax, there is no compulsion involved in case of fees.
4. The government provides certain services and charges certain fees for them.
5. For example, fees are charged for issuing of passports, driving licenses, etc.

(II) Fine:

1. A fine is a penalty imposed on an individual for violation of law.
2. For example, violation of traffic rules, payment of income tax after the stipulated time etc.

(III) Earnings from Public Enterprises:

1. The Government also gets revenue by way of surplus from public enterprises.
2. Some of the public sector enterprises do make a good amount of profits.
3. The profits or dividends which the government gets can be utilized for public expenditure.

(IV) Special assessment of betterment levy:
1. It is a kind of special charge levied on certain members of the community who are beneficiaries of certain government activities or public projects.

2. For example, due to a public park or due to the construction of a road, people in that locality may experience an appreciation in the value of their property or land.

(V) Gifts, Grants and Aids:

1. A grant from one government to another is an important source of revenue in the modem days.
2. The government at the Centre provides grants to State governments and the State governments provide grants to the local government to carry out their functions.
3. Grants from foreign countries are known as Foreign Aid.
4. Developing countries receive military aid, food aid, technological aid, etc. from other countries.

(VI) Escheats:
It refers to the claim of the state to the property of persons who die without legal heirs or documented will.

Question 4.
Bringout the Demerits of Indirect taxes?
Answer:
Demerits of Indirect Taxes:
(I) Higher Cost of Collection:

1. The cost of collection of indirect taxes is higher than the direct taxes.
2. The Government has to spend huge money to collect indirect taxes.

(II) Inelastic:

1. Indirect taxes are less elastic compared to direct taxes.
2. As indirect taxes are generally proportional.

(III) Regressive:
Indirect taxes are sometimes unjust and regressive in nature since both rich and poor persons have to pay same amount as taxes irrespective of their income level.

(IV) Uncertainly:

1. The rise in indirect taxes increase the price and reduces the demand for goods.
2. Therefore, the Government is uncertain about the expected revenue collection.
3. So Dalton says under indirect taxes 2 + 2 is not 4 but 3 or even less than 3.

(V) No civic Consciousness:
As the tax is hidden in price, the consumers are not aware of paying tax.

Share this Tamilnadu State Board 12th Economics Solutions Chapter 9 Fiscal Economics Questions and Answers with your friends to help them to overcome the grammar issues in exams. Keep visiting this site frequently to get the latest information on different subjects. Clarify your doubts by posting the comments and get the answers in an easy manner.

Students of 12th can get the pdf links of Tamilnadu State Board Economics Solutions here. You can Download Samacheer Kalvi 12th Economics Book Solutions Chapter 6 Banking Questions and Answers, Notes Pdf, Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Economics Solutions Chapter 6 Banking

It is very important to put the textbook aside while preparing for the exams. So, if you follow Samacheer Kalvi 12th Economics Textbook Solutions you can cover all the topics in Chapter 6 Banking Questions and Answers. This helps to improve your communication skills.

Samacheer Kalvi 12th Economics Banking Text Book Back Questions and Answers

Part – A
Multiple Choice Questions.

Question 1.
A Bank is a …………………………
(a) Financial institution
(b) Corporate
(c) An Industry
(d) Service institutions
Answer:
(a) Financial institution

Question 2.
A Commercial Bank is an institution that provides services …………………………
(a) Accepting deposits
(b) Providing loans
(c) Both a and b
(d) None of the above
Answer:
(c) Both a and b

Question 3.
The Functions of commercial banks are broadly classified into …………………………
(a) Primary Functions
(b) Secondary functions
(c) Other functions
(d) a, b, and c
Answer:
(d) a, b, and c

Question 4.
Bank credit refers to …………………………
(a) Bank Loans
(b) Advances
(c) Bank loans and advances
(d) Borrowings
Answer:
(c) Bank loans and advances

Question 5.
Credit creation means …………………………
(a) Multiplication of loans and advances
(b) Revenue
(c) Expenditure
(d) Debt
Answer:
(a) Multiplication of loans and advances

Question 6.
NBFI does not have …………………………
(a) Banking license
(b) Government approval
(c) Money ministry approval
Answer:
(a) Banking license

Question 7.
Central bank is …………………………….. authority of any country.
(a) Monetary
(b) Fiscal
(c) Wage
(d) National Income
Answer:
(a) Monetary

Question 8.
Who will act as the banker to the Government of India?
(a) SBI
(b) NABARD
(c) ICICI
(d) RBI
Answer:
(d) RBI

Question 9.
Lender of the last resort is one of the functions of …………………………
(a) Central Bank
(b) Commercial banks
(c) Land Development Banks
(d) Co – operative banks
Answer:
(a) Central Bank

Question 10.
Bank Rate means …………………………
(a) Re – discounting the first class securities
(b) Interest rate
(c) Exchange rate
(d) Growth rate
Answer:
(a) Re – discounting the first class securities

Question 11.
Repo Rate means …………………………
(a) Rate at which the Commercial Banks are willing to lend to RBI
(b) Rate at which the RBI is willing to lend to commercial banks
(c) Exchange rate of the foreign bank
(d) Growth rate of the economy
Answer:
(b) Rate at which the RBI is willing to lend to commercial banks

Question 12.
Moral suasion refers …………………………
(a) Optimization
(b) Maximization
(c) Persuasion
(d) Minimization
Answer:
(c) Persuasion

Question 13.
ARDC started functioning from …………………………
(a) June 3, 1963
(b) July 3, 1963
(c) June 1, 1963
(d) July 1, 1963
Answer:
(d) July 1, 1963

Question 14.
NABARD was set up in …………………………
(a) July 1962
(b) July 1972
(c) July 1982
(d) July 1992
Answer:
(c) July 1982

Question 15.
EXIM bank was established in …………………………
(a) June 1982
(b) April 1982
(c) May 1982
(d) March 1982
Answer:
(d) March 1982

Question 16.
The State Financial Corporation Act was passed by …………………………
(a) Government of India
(b) Government of Tamilnadu
(c) Government of Union Territories
(d) Local Government.
Answer:
(a) Government of India

Question 17.
Monetary policy is formulated by …………………………
(a) Co – operative banks
(b) Commercial banks
(c) Central Bank
(d) Foreign banks
Answer:
(c) Central Bank

Question 18.
Online Banking is also known as …………………………
(a) E – Banking
(b) Internet Banking
(c) RTGS
(d) NEFT
Answer:
(b) Internet Banking

Question 19.
Expansions of ATM.
(a) Automated Teller Machine
(b) Adjustment Teller Machine
(c) Automatic Teller mechanism
(d) Any Time Money
Answer:
(a) Automated Teller Machine

Question 20.
2016 Demonetization of currency includes denominations of …………………………
(a) ₹ 500 and ₹ 1000
(b) ₹ 1000 and ₹ 2000
(c) ₹ 200 and ₹ 500
(d) All the above
Answer:
(a) ₹ 500 and ₹ 1000

Part – B
Answer The Following Questions In One or Two Sentences.

Question 21.
Define Commercial banks?
Answer:
Commercial bank refers to a bank, or a division of a large bank, which more specifically deals with deposit and loan services provided to corporations or large/middle-sized business – as opposed to individual members of the public/small business.

Question 22.
What is credit creation?
Answer:

1. Credit Creation means the multiplication of loans and advances.
2. Commercial banks receive deposits from the public and use these deposits to give loans.
3. However, loans offered are many times more than the deposits received by banks.
4. This function of banks is known as ‘Credit Creation’.

Question 23.
Define Central bank?
Answer:

1. A central bank, reserve bank, or monetary authority is an institution that manages a state’s currency, money supply, and interest rates.
2. Central banks also usually oversee the commercial banking system of their respective countries.

Question 24.
Distinguish between CRR and SLR?
Answer:
CRR:

1. The Central Bank controls credit by changing the Cash Reserves Ratio.
2. Commercial Banks have excessive cash reserves on the basis of which they are creating too much of credit, this will be harmful for the larger interest of the economy.
3. So it will raise the cash reserve ratio which the Commercial Banks are required to maintain with the Central Bank.

SLR:

1. Statutory Liquidity Ratio (SLR) is the amount which a bank has to maintain in the form of cash, gold or approved securities.
2. The quantum is specified as some percentage of the total demand and time liabilities.
3. The liabilities of the bank which are payable on demand anytime, and those liabilities which are accruing in one month’s time due to maturity.

Question 25.
Write the meaning of Open market operations?
Answer:

1. In narrow sense, the Central Bank starts the purchase and sale of Government securities in the money market.
2. In Broad Sense, the Central Bank purchases and sells not only Government securities but also other proper eligible securities like bills and securities of private concerns.
3. When the banks and the private individuals purchase these securities they have to make payments for these securities to the Central Bank.

Question 26.
What is rationing of credit?
Answer:

1. This is the oldest method of credit control. Rationing of credit as an instrument of credit control was first used by the Bank of England by the end of the 18th Century.
2. It aims to control and regulate the purposes for which credit is granted by commercial banks.
3. It is generally of two types.

Question 27.
Mention the functions of agriculture credit department?
Answer:
Functions of Agriculture Credit Department:

1. To maintain an expert staff to study all questions on agricultural credit;
2. To provide expert advice to Central and State Government, State Co – operative Banks and other banking activities.
3. To finance the rural sector through eligible institutions engaged in the business of agricultural credit and to co-ordinate their activities.

Part – C
Answer The Following Questions In One Paragraph.

Question 28.
Write the mechanism of credit creation by commercial banks?
Answer:
Mechanism / Technique of Credit Creation by Commercial Banks:

1. Bank credit refers to bank loans and advances.
2. Money is said to be created when the banks, through their lending activities, make a net addition to the total supply of money in the economy.
3. Money is said to be destroyed when the loans are repaid by the borrowers to the banks and consequently the credit already created by the banks is wiped out in the process.
4. Banks have the power to expand or contract demand deposits and they exercise this power through granting more or less loans and advances and acquiring other assets.
5. This power of commercial bank to create deposits through expanding their loans and advances is known as credit creation.

Question 29.
Give a brief note on NBFI?
Answer:
Non – Banking Financial Institution (NBFI):

1. A non – banking financial institution (NBFI) or non-bank financial company (NBFC) is a financial institution that does not have a full banking license or is not supervised by the central bank.

2. The NBFIs do not carry on pure banking business, but they will carry on other financial transactions. They receive deposits and give loans. They mobilize people’s savings and use the funds to finance expenditure on investment activities. In short, they are institutions which undertake borrowing and lending. They operate in both the money and the capital markets.

3. NBFIs can be broadly classified into two categories. Viz.., (1) Stock Exchange; and (2) Other Financial institutions. Under the latter category comes Finance Companies, Finance Corporations, ChitFunds, Building Societies, Issue Houses, Investment Trusts and Unit Trusts and Insurance Companies.

Question 30.
Bring out the methods of credit control?
Answer:
Methods of Credit Control:
I. Quantitative or General Methods:

1. Bank Rate Policy:
The bank rate is the rate at which the Central Bank of a country is prepared to re – discount the first class securities.

2. Open Market Operations:

1. In narrow sense, the Central Bank starts the purchase and sale of Government securities in the money market.
2. In Broad Sense, the Central Bank purchases and sells not only Government securities but also other proper eligible securities like bills and securities of private concerns.

3. Variable Reserve Ratio:
(I) Cash Reserves Ratio:

1. Under this system the Central Bank controls credit by changing the Cash Reserves Ratio.
2. For example, if the Commercial Banks have excessive cash reserves on the basis of which they are creating too much of credit,this will be harmful for the larger interest of the economy.
3. So it will raise the cash reserve ratio which the Commercial Banks are required to maintain with the Central Bank.

(II) Statutory Liquidity Ratio:

1. Statutory Liquidity Ratio (SLR) is the amount which a bank has to maintain securities.
2. The quantum is specified as some percentage of the total demand and time liabilities (i.ethe liabilities of the bank which are payable on demand anytime, and those liabilities which are accruing in one month’s time due to maturity) of a bank.

Question 31.
What are the functions of NABARD?
Answer:
Functions of NABARD:
NABARD has inherited its apex role from RBI i.e, it is performing all the functions performed
by RBI with regard to agricultural credit.

1. NABARD acts as a refinancing institution for all kinds of production and investment credit to agriculture, small-scale industries, cottage and village industries, handicrafts and rural crafts and real artisans and other allied economic activities with a view to promoting integrated rural development.

2. NABARD gives long-term loans (upto 20 Years) to State Government to enable them to subscribe to the share capital of co – operative credit societies.

3. NABARD gives long-term loans to any institution approved by the Central Government or contribute to the share capital or invests in securities of any institution concerned with agriculture and rural development.

4. NABARD has the responsibility of co – ordinating the activities of Central and State Governments, the Planning Commission (now NITI Aayog) and other all India and State level institutions entrusted with the development of small scale industries, village and cottage industries, rural crafts, industries in the tiny and decentralized sectors, etc.

5. It maintains a Research and Development Fund to promote research in agriculture and rural development

Question 32.
Specify the functions of IFCI?
Answer:

1. Long – term loans; both in rupees and foreign currencies.
2. Underwriting of equity, preference and debenture issues.
3. Subscribing to equity, preference and debenture issues.
4. Guaranteeing the deferred payments in respect of machinery imported from abroad or purchased in India; and
5. Guaranteeing of loans raised in foreign currency from foreign financial institutions.

Question 33.
Distinguish between money market and capital market?
Answer:
Money Market:

1. Money market is the mechanism through which short term funds are loaned and. borrowed. It designates financial institutions which handle the purchase, sale and transfer of short term credit instruments.
2. Commercial banks, acceptance houses, Non Banking Financial Institutions and the Central Bank are the institutions catering to the requirements of short term funds in the money Market.

Capital Market:

1. Capital Market is a part of financial system which is concerned with raising capital by dealing in shares, bonds and other long term investments.
2. The market where investment instruments like bonds, equities and mortgages are traded is known as the capital market.

Question 33.
Mention the objectives of demonetizations?
Answer:
Objectives of Demonetisation:

1. Removing Black Money from the country.
2. Stopping of Corruption.
3. Stopping Terror Funds.
4. Curbing Fake Notes.

Demonitisation is the act of stripping a currency unit of its status as legal tender. It occurs whenever there is a change of national currency. The current form or forms of money is pulled from circulation, often to bereplaced with new coins or notes.

Part – D
Answer The Following Questions In About A Page.

Question 34.
Explain the role of Commercial Banks in economic development?
Answer:
Role of Commercial Banks in Economic Development of a Country Role of Commercial Banks:

1. Capital Formation
2. Creation of Credit
3. Channelizing the funds
4. Encouraging Rights Type of Industries
5. Banks Monetize Debt
6. Finance to Government
7. Employment Generation
8. Bank Promote Entrepreneurship

1. Capital Formation:

1. Banks play an important role in capital formation, which is essential for the economic development of a country.
2. They mobilize the small savings of the people scattered over a wide area through their network of branches all over the country and make it available for productive purposes.

2. Creation of Credit:

1. Banks create credit for the purpose of providing more funds for development projects.
2. Credit creation leads to increased production, employment, sales and prices and thereby they bring about faster economic development.

3. Channelizing the Funds towards Productive Investment:

1. Banks invest the savings mobilized by them for productive purposes.
2. Capital formation is not the only function of commercial banks.

4. Encouraging Right Type of Industries:

1. Many banks help in the development of the right type of industries by extending loan to right type of persons.
2. In this way, they help not only for industrialization of the country but also for the economic development of the country.
3. They grant loans and advances to manufacturers whose products are in great demand.

5. Banks Monetize Debt:

1. Commercial banks transform the loan to be repaid after a certain period into cash, which can be immediately used for business activities.
2. Manufacturers and wholesale traders cannot increase their sales without selling goods on credit basis.

6. Finance to Government:

1. Government is acting as the promoter of industries in underdeveloped countries for which finance is needed for it.
2. Banks provide long – term credit to Government by investing their funds in Government securities and short-term finance by purchasing Treasury Bills.

7. Employment Generation:

1. After the nationalization of big banks, banking industry has grown to a great extent.
2. Bank’s branches are opened frequently, which leads to the creation of new employment opportunities.

8. Banks Promote Entrepreneurship:

• In recent days, banks have assumed the role of developing entrepreneurship particularly in developing countries like India by inducing new entrepreneurs to take up the well- formulated projects and provision of counseling services like technical and managerial guidance.

Question 36.
Elucidate the functions of Commercial Banks?
Answer:
The functions of commercial banks are broadly classified into primary functions and secondary functions.


Functions of Commercial Banks

(a) Primary Functions:
1. Accepting Deposits:
It implies that commercial banks are mainly dependent on public deposits.
There are two types of deposits

(I) Demand Deposits:
It refers to deposits that can be withdrawn by individuals without any prior notice to the bank. In other words, the owners of these deposits are allowed to withdraw money anytime by writing a withdrawal slip or a cheque at the bank counter or from ATM centres using debit card.

(II) Time Deposits:
It refers to deposits that are made for certain committed period of time. Banks pay higher interest on time deposits. These deposits can be withdrawn only after a specific time period by providing a written notice to the?bank.

2. Advancing Loans:

(a) It refers to granting loans to individuals and businesses. Commercial banks grant loans in the form of overdraft, cash credit, and discounting bills of exchange.

(b) Secondary Functions:
The secondary functions can be classified under three heads, namely, agency functions, general utility functions, and other functions.

1. Agency Functions:
It implies that commercial banks act as agents of customers by performing various functions.

(I) Collecting Cheques:
Banks collect cheques and bills of exchange on the behalf of their customers through clearing house facilities provided by the central bank.

(II) Collecting Income:
Commercial banks collect dividends, pension, salaries, rents, and interests on investments on behalf of their customers. A credit voucher is sent to customers for information when any income is collected by the bank.

(III) Paying Expenses:
Commercial banks make the payments of various obligations of customers, such as telephone bills, insurance premium, school fees, and rents.

2. General Utility Functions:
It implies that commercial banks provide some utility services to customers by performing various functions.

(I) Providing Locker Facilities:
Commercial banks provide locker facilities to its customers for safe custody of jewellery, shares, debentures, and other valuable items. This minimizes the risk of loss due to theft at homes. Banks are not responsible for the items in the lockers.

(II) Issuing Traveler’s Cheques:
Banks issue traveler’s cheques to individuals for traveling outside the country. Traveler’s cheques are the safe and easy way to protect money while traveling.

(III) Dealing in Foreign Exchange:
Commercial banks help in providing foreign exchange to businessmen dealing in exports and imports. However, commercial banks need to take the permission of the Central Bank for dealing in foreign exchange.

3. Transferring Funds:
It refers to transferring of funds from one bank to another. Funds are transferred by means of draft, telephonic transfer, and electronic transfer.

4. Letter of Credit:
Commercial banks issue letters of credit to their customers to certify their creditworthiness.

(I) Underwriting Securities:
Commercial banks also undertake the task of underwriting securities. As public has full faith in the credit worthiness of banks, public do not hesitate in buying the securities underwritten by banks.

(II) Electronic Banking:
It includes services, such as debit cards, credit cards, and Internet banking.

(c) Other Functions:

(I) Money Supply:
It refers to one of the important functions of commercial banks that help in increasing money supply.

(II) Credit Creation:
Credit Creation means the multiplication of loans and advances. Commercial banks receive deposits from the public and use these deposits to give loans.

Question 37.
Describe the functions of Reserve Bank of India?
Answer:
Functions of Central Bank (Reserve Bank of India):
The Reserve Bank of India (RBI) is India’s central banking institution, which controls the monetary policy of the Indian rupee.

1. Monetary Authority:
It controls the supply of money in the economy to stabilize exchange rate, maintain healthy balance of payment, attain financial stability, control inflation, strengthen banking system.

2. The issuer of currency:
The objective is to maintain the currency and credit system of the country. It is the sole authority to issue currency. It also takes action to control the circulation of fake currency.

3. The issuer of Banking License:
As per Sec 22 of Banking Regulation Act, every bank has to obtain a banking license from RBI to conduct banking business in India.

4. Banker to the Government:
It acts as banker both to the central and the state governments. It provides short-term credit. It manages all new issues of government loans, servicing the government debt outstanding and nurturing the market for government securities. It advises the government on banking and financial subjects.

5. Banker’s Bank:
RBI is the bank of all banks in India as it provides loan to banks, accept the deposit of banks, and rediscount the bills of banks.

6. Lender of last resort:
The banks can borrow from the RBI by keeping eligible securities as collateral at the time of need or crisis, when there is no other source.

7. Act as clearing house:
For settlement of banking transactions, RBI manages 14 clearing houses. It facilitates the exchange of instruments and processing of payment instructions.

8. Custodian of foreign exchange reserves:
It acts as a custodian of FOREX. It administers and enforces the provision of Foreign Exchange Management Act (FEMA), 1999. RBI buys and sells foreign currency to maintain the exchange rate of Indian rupee v/s foreign currencies.

9. Regulator of Economy:
It controls the money supply in the system, monitors different key indicators like GDP, Inflation, etc.

10. Managing Government securities:
RBI administers investments in institutions when they invest specified minimum proportions of their total assets/liabilities in government securities.

11. Regulator and Supervisor of Payment and Settlement Systems:
The Payment and Settlement Systems Act of 2007 (PSS Act) gives RBI oversight authority for the payment and settlement systems in the country. RBI focuses on the development and functioning of safe, secure and efficient payment and settlement mechanisms.

12. Developmental Role:
This role includes the development of the quality banking system in India and ensuring that credit is available to the productive sectors of the economy. It provides a wide range of promotional functions to support national objectives.

It also includes establishing institutions designed to build the country’s financial infrastructure. It also helps in expanding access to affordable financial services and promoting financial education and literacy.

13. Publisher of monetary data and other data:
RBI maintains and provides all essential banking and other economic data, formulating and critically evaluating the economic policies in India. RBI collects, collates and publishes data regularly.

14. Exchange manager and controller:
RBI represents India as a member of the International Monetary Fund [IMF], Most of the commercial banks are authorized dealers of RBI.

15. Banking Ombudsman Scheme:
RBI introduced the Banking Ombudsman Scheme in 1995. Under this scheme, the complainants can file their complaints in any form, including online and can also appeal to the Ombudsman against the awards and the other decisions of the Banks.

16. Banking Codes and Standards Board of India:
To measure the performance of banks against Codes and standards based on established global practices, the RBI has set up the Banking Codes and Standards Board of India (BCSBI).

Question 38.
What are the objectives of Monetary Policy? Explain?
The specific objectives of monetary policy are Objectives of monetary policy:

1. Neutrality of Money
2. Stability of Exchange Rates
3. Price Stability
4. Full Employment
5. Economic Growth
6. Equilibrium in the Balance of Payments

1. Neutrality of Money:

1. Economists like Wicksteed, Hayek and Robertson are the chief exponents of neutral money.
2. They hold the view that monetary authority should aim at neutrality of money in the economy.
3. Monetary changes could be the root cause of all economic fluctuations.
4. According to neutralists, the monetary change causes distortion and disturbances in the proper operation of the economic system of the country.

2. Exchange Rate Stability:

1. Exchange rate stability was the traditional objective of monetary authority.
2. This was the main objective under Gold Standard among different countries.
3. When there was disequilibrium in the balance of payments of the country, it was automatically corrected by movements.

3. Price Stability:

1. Economists like Crustave Cassel and Keynes suggested price stabilization as a main objective of monetary policy.
2. Price stability is considered the most genuine objective of monetary policy.
3. Stable prices repose public confidence.
4. It promotes business activity and ensures equitable distribution of income and wealth.

4. Full Employment:

1. During world depression, the problem of unemployment had increased rapidly.
2. It was regarded as socially dangerous, economically wasteful and morally deplorable.
3. Thus, full employment was considered as the main goal of monetary policy.

5. Economic Growth:

1. Economic growth is the process whereby the real per capita income of a country increases over a long period of time.
2. It implies an increase in the total physical or real output, production of goods for the satisfaction of human wants.
3. Monetary policy should promote sustained and continuous economic growth by maintaining equilibrium between the total demand for money and total production capacity and further creating favourable conditions for saving and investment.

6. Equilibrium in the Balance of Payments:

• Equilibrium in the balance of payments is another objective of monetary policy which emerged significant in the post war years.

Samacheer Kalvi 12th Economics Banking Additional Questions and Answers

Part – A
I. Multiple Choice Questions.

Question 1.
Reserve Bank of India was nationalised in …………………………
(a) 1947
(b) 1948
(c) 1949
(d)1950
Answer:
(c) 1949

Question 2.
Overdraft is a facility offered by commercial banks to …………………………
(a) Exporters
(b) Importers
(c) Farmers
(d) Businessmen
Answer:
(d) Businessmen

Question 3.
Current account deposites are operated by …………………………
(a) Agriculturists
(b) Business mens
(c) Goverment servants
(d) Labourers
Answer:
(b) Business mens

Question 4.
Primary functions of the commercial bank is …………………………
(a) Accepting deposits from the public
(b) Making loans and advances to public
(c) Discounting bills of exchange
(d) Inter bank borrowing
Answer:
(a) Accepting deposits from the public

Question 5.
The first bank in India was established in …………………………
(a) 1670
(b) 1770
(c) 1870
(d) 1872
Answer:
(b) 1770

Question 6.
The coins are issued by …………………………
(a) Ministry of Finance
(b) RBI
(c) Central Bank
(d) State Bank
Answer:
(a) Ministry of Finance

Question 7.
The amount of cash kept by commercial banks to meet the day to day transactions is known as …………………………
(a) Bank cash
(b) Commercial bank cash
(c) Reserve cash
(d) Cheque
Answer:
(c) Reserve cash

Question 8.
In India, Central bank is known as –
(a) SBI
(b) RBI
(c) Commercial bank
(d) IDBI
Answer:
(b) RBI

Question 9.
Open Market operations enable the ………………………… to reduce the money supply in the economy.
(o) Commercial bank
(b) SBI
(c) ICICI
(d) RBI
Answer:
(d) RBI

Question 10.
………………………… Bank Finance the Import and Export trade.
(a) Industrial Bank
(b) Exim Bank
(c) Co – operative Bank
(d) RBI
Answer:
(b) Exim Bank

Question 11.
Commercial Banks create credit in favour of the …………………………
(a) Consumers
(b) Business men
(c) Customers
(d) Agriculturists
Answer:
(c) Customers

Question 12.
………………………… is a non profit making financial institution of the country.
(a) Central Bank
(b) Commercial Bank
(c) Co – operative Bank
(d) Industrial Bank
Answer:

Question 13.
Extending banking facilities to the rural and semi urban areas is the promotional activity of the …………………………
(a) Co – operative Bank
(b) Commercial Bank
(c) RBI
(d) State Bank
Answer:
(a) Co – operative Bank

Question 14.
The qualitative credit control methods are also called …………………………
(a) Selective cash control
(b) Selective expenditure control
(c) Selective credit control
(d) Selective money control
Answer:
(c) Selective credit control

Question 15.
Withdraw money more than deposit is called …………………………
(a) Cash credit
(b) Discounting bill
(c) Current account
(d) Over draft
Answer:
(d) Over draft

Question 16.
………………………… help in proper allocation of funds among different regions of the economy.
(a) Central banks
(b) Co – operative banks
(c) Commercial banks
(d) Agriculture banks
Answer:
(c) Commercial banks

Question 17.
Lowering the Bank rate off sets ……………………….. tendencies.
(a) Deflationary
(b) Inflationary
(c) Stagflationary
(d) Hyper inflationary
Answer:
(a) Deflationary

Question 18.
The main aim of the Central bank is …………………………
(a) Full employment
(b) Economic stability
(c) Balance of payment
(d) International capital movement
Answer:
(b) Economic stability

Question 19.
………………………… Bank regulates the credit and currency according to the economic situation of the country.
(a) State
(b) Commercial
(c) RBI
(d) Agriculture
Answer:
(b) Economic stability

Question 20.
………………………… credit control method mean the Regulation and control of the supply of the credit among its possible users.
(a) Quantitative
(b) Qualitative
(c) General
(d) Possible
Answer:
(b) Qualitative

Question 21.
The issue of paper money is the most important function of a …………………………
(a) Commercial Bank
(b) Central Bank
(c) ICICI Bank
(d) State Bank
Answer:
(b) Central Bank

Question 22.
………………………… stimulate saving and investment.
(a) Credit
(b) Bank
(c) Debit
(d) Cheque
Answer:
(b) Bank

Question 23.
The commercial banks only deal in foreign exchange under the directions of the …………………………
(a) State bank
(b) Central bank
(c) Commercial bank
(d) Co – operative bank
Answer:
(b) Central bank

Question 24.
Fixed Deposits are otherwise known as …………………………
(a) Bank Deposits
(b) Customer’s Deposits
(c) Time Deposits
(d) Money Deposits
Answer:
(c) Time Deposits

Question 25.
The rate of interest of every Central bank is known as …………………………
(a) Interest rate
(b) Credit rate
(c) Debit rate
(d) Bank rate
Answer:
(d) Bank rate

II. Match the following and choose the correct answer by using codes given below.

Question 1.
A. Saving Deposits – (i) Official minimum rate
B. Cash credit – (ii) Cheque facilities
C. Bank rate – (iii) Facility to business man
D. Over draft – (iv) Collateral security
Codes:
(a) A (ii) B (iv) C (i) D (iii)
(b) A (i) B (ii) C (iii) D (iv)
(c) A (iii) B (i) C (iv) D (ii)
(d) A (iv) B (iii) C (ii) D (i)
Answer:
(a) A (ii) B (iv) C (i) D (iii)

Question 2.
A. Transfer of funds – (i) Buying and selling
B. Commercial bank – (ii) Clearing
C. Open market operation – (iii) Interest not given
D. Demand deposits – (iv) Profit making
Codes:
(a) A (ii) B (iv) C (i) D (iii)
(b) A (i) B (iii) C (ii) D (iv)
(c) A (iii) B (ii) C (iv) D (i)
(d) A (iv) B (i) C (iii) D (ii)
Answer:
(a) A (ii) B (iv) C (i) D (iii)

Question 3.
A. NBFI – (i) Monetary policy
B. Per Capita Income – (ii) Minimum amount of fund
C. Inflation – (iii) Economic growth
D. RTGS – (iv) Non – bank Financial Institution
Codes:
(a) A (iii) B (ii) C (iv) D (i)
(b) A (iv) B (iii) C (i) D (ii)
(c) A (ii) B (i) C (iii) D (iv)
(d) A (i) B (iv) C (ii) D (iii)
Answer:
(b) A (iv) B (iii) C (i) D (ii)

Question 4.
A. UTI – (i) Quantitative credit control
B. Open market operation – (ii) Mutual fund
C. Bank – (iii) Automatic Teller mechine
D. ATM – (iv) Financial Institution
Codes:
(a) A (i) B (ii) C (iii) D (iv)
(b) A (iii) B (iv) C (ii) D (i)
(c) A (iv) B (iii) C (i) D (ii)
(d) A (ii) B (i) C (iv) D (iii)
Answer:
(d) A (ii) B (i) C (iv) D (iii)

Question 5.
A. NABARD – (i) Internet banking
B. SFC – (ii) Short term seasonal credit
C. Rationing of credit – (iii) State level institution
D. Online banking – (iv) Qualitative credit control of RBI
Codes:
(a) A (i) B (ii) C (iii) D (iv)
(b) A (iii) B (iv) C (i) D (ii)
(c) A (ii) B (iii) C (iv) D (i)
(d) A (iv) B (i) C (ii) D (iii)
Answer:
(c) A (ii) B (iii) C (iv) D (i)

III. State whether the statements are true or false.

Question 1.
(i) Business men operates the current account deposits.
(ii) State Bank organization established EXIM Bank

(a) Both (i) and (ii) are true
(b) Both (i) and (ii) are false
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(c) (i) is true but (ii) is false

Question 2.
(i) The Central bank of a country acts as the banker, fiscal agent and advisor to the government.
(ii) The banks expand their loans resulting in the expansion of investment employment production and prices.

(a) Both (i) and (ii) are true
(b) Both (i) and (ii) are false
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(a) Both (i) and (ii) are true

Question 3.
(i) NABARD provides agriculture finance to medium and long term basis.
(ii) Bank observed that credit is the lubricant of all commerce and trade.

(a) Both (i) and (ii) are true
(b) Both (i) and (ii) are false
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(a) Both (i) and (ii) are true

Question 4.
(i) State Bank is the financial advisor to the government.
(ii) Central Bank possesses the monopoly of note issue.

(a) Both (i) and (ii) are true
(b) Both (i) and (ii) are false
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(d) (i) is false but (ii) is true

Question 5.
(i) For maintaining saving deposits, cheque facilities can be enjoyed.
(ii) Fixed Deposits are otherwise known as time deposits.

(a) Both (i) and (ii) are true
(b) Both (i) and (ii) are false
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(a) Both (i) and (ii) are true

IV. Which of the following is correctly matched.

Question 1.
(a) EXIM Bank – Export and Import
(b) NABARD – Industrial finance
(c) Bank – Excess money
(d) Fixed Deposits – Bank saving
Answer:
(a) EXIM Bank – Export and Import

Question 2.
(a) CRR – Current Reserve Ratio
(b) Saving deposits – Cheque facilities
(c) Bank rate policy – High interest
(d) Adviser to government – SBI
Answer:
(b) Saving deposits – Cheque facilities

Question 3.
(a) ICICI Bank – Three tier Export Bank
(b) NABARD – Agriculture Finance
(c) IDBI – Co – operative Bank
(d) IFCI – State Bank
Answer:
(b) NABARD – Agriculture Finance

Question 4.
(a) South African Reserve Bank – 1921
(b) The Central bank of China – 1934
(c) The Reserve Bank of Newzealand – 1928
(d) The Reserve Bank of India – 1935
Answer:
(d) The Reserve Bank of India – 1935

Question 5.
(a) Forex cards – Smart card
(b) Paper currency – Legal tender
(c) Medium of Exchange – Functions of money
(d) CRR – Credit Reserve Ratio
Answer:
(c) Medium of Exchange – Functions of money

V. Which of the following is not correctly matched.

Question 1.
(a) RBI – Reserv e Bank of India
(b) SBI – State Bank of India
(c) IMF – International Monetary Fund
(d) ATM – Any Time Money
Answer:
(d) ATM – Any Time Money

Question 2.
(a) Qualitative credit control of RBI – Rationing of credit
(b) Agricultural credit department – To finance the rural sector
(c) NABARD – Short term seasonal credit
(d) UTI – Mutual fund
Answer:
(d) UTI – Mutual fund

Question 3.
(a) RBI – Central Bank of SBI
(b) ARDC – The agricultural refinance development corporation
(c) Bank Crdit – Bank loans and advances
(d) Moral suasion – Persuasion
Answer:
(a) RBI – Central Bank of SBI

Question 4.
(a) Traveler’s cheques – Group of people
(b) Credit creation – Multiplication of loans and advances
(c) Primary deposits – Passive deposits
(d) Bank – Financial Institution
Answer:
(a) Traveler’s cheques – Group of people

Question 5.
(a) RBI – Monetary authority
(b) Bank rate – Re – discounting
(c) Recession – Monetary policy
(d) Keynes – Economic growth
Answer:
(d) Keynes – Economic growth

Question 6.
(a) RTGS – Real Time Gross Settlement
(b) NEFT – National Electronic Fund Transfer
(c) ATM – Any Time Money
(d) SIDCO – Small Industrial Development Corporation
Answer:
(c) ATM – Any Time Money

VI. Pick the odd one out.

Question 1.
1. Commercial Bank Secondary Functions
(a) Agency functions
(b) General utility services
(c) Transfer of bank
(d) Credit creation
Answer:
(c) Transfer of bank

Question 2.
Functions of Central Bank
(a) Monetary Authority
(b) The issuer of currency
(c) Banker to the foreign level
(d) Banker’s Bank
Answer:
(c) Banker to the foreign level

Question 3.
The frequent methods of credit control under Selective method is called ……………………..
(a) Rationing of credit
(b) Direct Action of Industries
(c) Method of publicity
(d) Moral persuasion
Answer:
(b) Direct Action of Industries

Question 4.
Functions of ICICI is called ……………………..
(a) Assistance to Industries
(b) Merchant banking
(c) Credit bank operation
(d) Project promotion
Answer:
(c) Credit bank operation

Question 5.
The main objectives of Demonetisation ……………………..
(a) Removing black money from the country
(b) Stopping of corruption
(c) Stopping Terror Funds
(d) Fake notes given
Answer:
(d) Fake notes given

VII. Assertion and Reason.

Question 1.
Assertion (A): Commercial banks provide some utility services to the customers.
Reason (R): Credit creation leads to increased production, employment, sales and prices.

(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’

Question 2.
Assertion (A): Bank rate means re – discounting the first class securities.
Reason (R): Credit creation means not given loans and advances.

(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(c) ‘A’ is true but ‘R’ is false

Question 3.
Assertion (A): Bank is service institution.
Reason (R): Commercial Bank is an institutions that provides accepting deposits and providing loans to the public.

(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(d) ‘A’ is false but ‘R’ is true

Question 4.
Assertion (A): Credit creation leads to increase in production.
Reason (R): Credit creation means the multiplication of loans and advances.

(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’

Question 5.
Assertion (A): The objectives of demonetization is called issuing currency notes.
Reason (R): Black money accepted.

(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(c) ‘A’ is true but ‘R’ is false

Question 6.
Assertion (A): Primary deposits are also called as passive deposits.
Reason (R): Passive deposits are also called as time deposits.

(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(c) ‘A’ is true but ‘R’ is false

Part – B
Answer The Following Questions In One or Two Sentences.

Question 1.
What is meaning of primary deposite and derived deposit?
Answer:

1. The modem banks create deposits in two ways. They are primary deposit and derived deposit.
2. When a customer gives cash to the bank and the bank creates a book debt in his name called a deposit, it is known as a “primary deposit”.
3. But when such a deposit is created, without there being any prior payment of equivalent cash to the bank, it is called a ‘derived deposit’.

Question 2.
What are the functions of primary deposits?
Answer:
Primary Deposits:

1. It is out of these primary deposits that the bank makes loans and advances to its customers.
2. The initiative is taken by the customers themselves. In this case, the role of the bank is passive.
3. So these deposits are also called “Passive deposits”.

Question 3.
What are the credit control measures?
Answer:

Question 4.
Define RBI Rural credit?
Answer:
Reserve Bank of India and Rural Credit:
In a developing econorqy like India, the Central bank of the country cannot confine itself to the monetary regulation only, and it is expected that it should take part in development function in all sectors especially in the agriculture and industry.

Question 5.
Write RBI granting Regional Rural Banks concessions?
Answer:
The RBI has been granting many concessions to RRBs:

1. 1. They are allowed to maintain cash reserve ratio at 3 per cent and statutory liquidity ratio at 25 per cent; and
   2. They also provide refinance facilities through NABARD.

Question 6.
Define Three Tier co – operative credit structure?
Answer:

Part – C
Answer The Following Questions In One Paragraph.

Question 1.
What are the functions of RBI agricultural credit?
Answer:
Role of RBI in agricultural credit:

1. RBI has been playing a very vital role in the provision of agricultural finance in the country.
2. The Bank’s responsibility in this field had been increased due to the predominance of agriculture in the Indian economy and the inadequacy of the formal agencies to cater to the huge requirements of the sector.
3. In order to fulfill this important role effectively, the RBI set up a separate Agriculture Credit Department.
4. However, the volume of informal loans has not declined sufficiently.

Question 2.
What are the ARDC – objectives?
Answer:
Objectives of the ARDC:

1. To provide necessary funds by way of refinance to eligible institutions such as the Central Land Development Banks, State Co – operative Banks, and Scheduled banks.
2. To subscribe to the debentures floated by the Central Land Development banks, State Co-operative Banks, and Scheduled banks, provided they were approved by the RBI.

Question 3.
Describe the functions of IDBI?
Answer:
Functions of IDBI:

1. The functions of IDBI fall into two groups
   1. Assistance to other financial institutions; and –
   2. Direct assistance to industrial concerns either on its own or in participation with other institutions.
2. The IDBI can provide refinance in respect of term loans to industrial concerns given by the IFC, the SFCs, other financial institutions notified by the Government, scheduled banks and state cooperative banks.
3. A special feature of the IDBI is the provision for the creation of a special fund known as the Development Assistance Fund.
4. The fund is intended to provide assistance to industries which require heavy investments with low anticipated rate of return.
5. Such industries may not be able to get assistance in the normal course.
6. The financing of exports was also undertaken by the IDBI till the establishment of EXIM BANK in March, 1982.

Question 4.
Difference between NEFT and RTGS?
Answer:
NEFT:

1. National electronic Fund Transfer
2. Transactions happens in batches hence slow
3. Timings: 8:00 am to 6:30 pm (12:30 pm on Saturday)
4. No minimum limit

RTGS:

1. Real Time Gross Settlement
2. Transactions happens in real time hence fast
3. Timings : 9:00 am to 4:30 pm (1:30 pm on Saturday)
4. Minimum amount for RTGS transfer is ₹ 2 lakhs

Question 5.
What is E – Banking?
Answer:

1. Online banking, also known as internet banking, is an electronic payment system that enables customers of a bank or other financial institution to conduct a range of financial transactions through the financial institution’s website.
2. The online banking system typically connects to or be part of the core banking system operated by a bank and is in contrast to branch banking which was the traditional way customers accessed banking services.

Part – D
Answer The Following Questions In One Page.

Question 1.
Describe the frequent methods of selective method credit control?
Answer:
Qualitative or Selective Method of Credit Control:

1. The qualitative or the selective methods are directed towards the diversion of credit into particular uses or channels in the economy.
2. Their objective is mainly to control and regulate the flow of credit into particular industries or businesses.
3. The following are the frequent methods of credit control under selective method:
4. Rationing of Credit:
   1. Direct Action
   2. Moral Persuasion
   3. Method of Publicity
   4. Regulation of Consumer’s Credit
   5. Regulating the Marginal Requirements on Security Loans
   6. Rationing of Credit:

1. Rationing of Credit:

• This is the oldest method of credit control.
• Rationing of credit as an instrument of credit control was first used by the Bank of England by the end of the 18th Century.
• It aims to control and regulate the purposes for which credit is granted by commercial banks. It is generally of two types.

(I) The variable portfolio ceiling:
It refers to the system by which the central bank fixes ceiling or maximum amount of loans and advances for every commercial bank.

(II) The variable capital asset ratio:
It refers to the system by which the central bank fixes the ratio which the capital of the commercial bank should have to the total assets of the bank.

2. Direct Action:
Direct action against the erring banks can take the following forms.

• The central bank may refuse to altogether grant discounting facilities to such banks.
• The central bank may refuse to sanction further financial accommodation to a bank whose existing borrowing are found to be in excess of its capital and reserves.
• The central bank may start charging penal rate of interest on money borrowed by a bank beyond the prescribed limit.

3. Moral Suasion:

• This method is frequently adopted by the Central Bank to exercise control over the Commercial Banks.
• Under this method Central Bank gives advice, then requests and persuades the Commercial Banks to co-operate with the Central Bank in implementing its credit policies.

4. Publicity:

• Central Bank in order to make their policies successful, take the course of the medium of publicity.
• A policy can be effectively successful only when an effective public opinion is created in its favour.

5. Regulation of Consumer’s Credit:

• The down payment is raised and the number of installments reduced for the credit sale, (vz) Changes in the Marginal Requirements on Security Loans:
• This system is mostly followed in U.S.A.
• Under this system, the Board of Governors of the Federal Reserve System has been given the power to prescribe margin requirements for the purpose of preventing an excessive use of credit for stock exchange speculation.

Question 2.
Describe the Merger of Banks?
Answer:
Merger of Banks:

1. Union Cabinet decided to merge all the remaining five associate banks of State Bank Group with State Bank of India in 2017.

2. After the Parliament passed the merger Bill, the subsidiary banks have ceased to exist.

3. Five associates and the Bharatiya Mahila Bank have become the part of State Bank of India (SBI) beginning April 1, 2017.

4. This has placed State Bank of India among the top 50 banks in the world.

5. The five associate banks that were merged are State Bank of Bikaner and Jaipur (SBBJ), State Bank of Hyderabad (SBH), State Bank of Mysore (SBM), State Bank of Patiala (SBP) and State Bank of Travancore (SBT).

6. The other two Associate Banks namely State Bank of Indore and State Bank of Saurashtra had already been merged with State Bank of India.

7. After the merger, the total customer base of SBI increased to 37 crore with a branch network of around 24,000 and around 60,000 ATMs across the country.

Question 3.
Briefly describe the ATM?
Answer:
ATM (Automated Teller Machine):

1. ATMs transformed the bank tech system when they were first introduced in 1967.
2. The next revolution in ATMs is likely to involve contactless payments.
3. Much like Apple Pay or Google Wallet, soon we will be able to conduct contactless ATM transactions using a smartphone.
4. Some ATM innovations are already available overseas.
5. For example, biometric authentication is already used in India, and its recognition is in place at Qatar National Bank ATMs.
6. These technologies can help overall bank security by protecting against ATM hacks.

Question 4.
Explain the State Industrial Development Corporations?
Answer:
State Industrial Development Corporations (SIDCOs):

• The Industrial Development Corporations have been set up by the state governments and they are wholly owned by them.
• These institutions are not merely financing agencies; they are entrusted with the responsibility of accelerating the industrialization of their states.

SIDCO (Small Industrial Development Corporation):

• SIDCOs provide financial assistance to industrial concerns by way of loans guarantees and underwriting of or direct subscriptions to shares and debentures.
• In addition to these, they undertake various promotional activities, such as conducting techno-economic surveys, project identification, preparation of feasibility studies and selection and training of entrepreneurs.
• They also promote joint sector projects in association with private promoter in such type of projects.
• SIDCOs take 26 percent, private co-promoter takes 25 percent of the equity, and the rest is offered to the investing public.
• SIDCOs undertake the development of industrial areas by providing all infrastructural facilities and initiation of new growth centers.
• They also administer various State government incentive schemes.
• SIDCOs get refinance facilities form IDBI.
• They also borrow through bonds and accept deposits.

Share this Tamilnadu State Board 12th Economics Solutions Chapter 6 Banking Questions and Answers with your friends to help them to overcome the grammar issues in exams. Keep visiting this site frequently to get the latest information on different subjects. Clarify your doubts by posting the comments and get the answers in an easy manner.

Students of 12th can get the pdf links of Tamilnadu State Board Economics Solutions here. You can Download Samacheer Kalvi 12th Economics Book Solutions Chapter 3 Theories of Employment and Income Questions and Answers, Notes Pdf, Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Economics Solutions Chapter 3 Theories of Employment and Income

It is very important to put the textbook aside while preparing for the exams. So, if you follow Samacheer Kalvi 12th Economics Textbook Solutions you can cover all the topics in Chapter 3 Theories of Employment and Income Questions and Answers. This helps to improve your communication skills.

Samacheer Kalvi 12th Economics Theories of Employment and Income Text Book Back Questions and Answers

Part – A
Multiple Choice Questions.

Question 1.
Every able bodied person who is willing to work at the prevailing wage rate is employed called as –
(a) Full employment
(b) Under employment
(c) Unemployment
(d) Employment opportunity
Answer:
(a) Full employment

Question 2.
Structural unemployment is a feature in a –
(a) Static society
(b) Socialist society
(c) Dynamic society
(d) Mixed economy
Answer:
(c) Dynamic society

Question 3.
In disguised unemployment, the marginal productivity of labour is –
(a) Zero
(b) One
(c) Two
(d) Positive
Answer:
(a) Zero

Question 4.
The main concention of the Classical Economic Theory is –
(a) Under employment
(b) Economy is always in the state of equilibrium
(c) Demand creates its supply
(d) Imperfect competition
Answer:
(b) Economy is always in the state of equilibrium

Question 5.
J.B. Say is a –
(a) Neo Classical Economist
(b) Classical Economist
(c) Modem Economist
(d) New Economist
Answer:
(b) Classical Economist

Question 6.
According to Keynes, which type of unemployment prevails in capitalist economy?
(a) Full employment
(b) Voluntary unemployment
(c) Involuntary unemployment
(d) Under employment
Answer:
(d) Under employment

Question 7.
The core of the classical theory of employment is –
(a) Law of Diminishing Return
(b) Law of Demand
(c) Law of Markets
(d) Law of Consumption
Answer:
(c) Law of Markets

Question 8.
Keynes attributes unemployment to –
(a) A lack of effective supply
(b) A lock of effective demand
(c) Alack of both
(d) None of the above
Answer:
(b) A lock of effective demand

Question 9.
…………………… Flexibility brings equality between saving and investment.
(a) Demand
(b) Supply
(c) Capital
(d) Interest
Answer:
(d) Interest

Question 10.
……………………. theory is a turning point in the development of modem economic theory.
(a) Keynes’
(b) Say’s
(c) Classical
(d) Employment.
Answer:
(a) Keynes’

Question 11.
The basic concept used in Keynes Theory of Employment and Income is –
(a) Aggregate demand
(b) Aggregate supply
(c) Effective demand
(d) Marginal Propensity Consume
Answer:
(c) Effective demand

Question 12.
The component of aggregate demand is –
(a) Personal demand
(b) Government expenditure
(c) Only export
(d) Omli import
Answer:
(b) Government expenditure

Question 13.
Aggregate supply is equal to –
(a) C +1 + G
(b) C + S + G + (x – m)
(c) C + S + T + (x-m)
(d) C + S + T + Rf
Answer:
(d) C + S + T + Rf

Question 14.
Keynes theory pursues to replace laissez faire by –
(a) No government intervention
(b) Maximum intervention
(c) State intervention in certain situation
(d) Private sector intervention
Answer:
(c) State intervention in certain situation

Question 15.
In Keynes theory of employment and income, ……………………… is the basic cause of economic depression.
(a) Less production
(b) More demand
(c) Inelastic supply
(d) Less aggregate demand in relation to productive capacity.
Answer:
(d) Less aggregate demand in relation to productive capacity.

Question 16.
Classical theory advocates –
(a) Balanced budget
(b) Unbalanced budget
(c) Surplus budget
(d) Deficit budget
Answer:
(a) Balanced budget

Question 17.
Keynes theory emphasized on ……………………….. equilibrium.
(a) Very short run
(b) Short run
(c) Very long run
(d) Long run
Answer:
(b) Short run

Question 18.
According to classical theory, rate of interest is a reward for –
(a) Investment
(b) Demand
(c) Capital
(d) Saving
Answer:
(d) Saving

Question 19.
In Keynes theory, the demand for and supply of money are determined by –
(a) Rate of interest
(b) Effective demand
(c) Aggregate demand
(d) Aggregate supply
Answer:
(a) Rate of interest

Question 20.
Say’s law stressed the operation of ……………………… in the economy.
(a) Induced price mechanism
(b) Automatic price mechanism
(c) Induced demand
(d) Induced investment
Answer:
(b) Automatic price mechanism

Part – B
Answer The Following Questions In One or Two Sentences.

Question 21.
Define full employment?
Answer:
Full employment refers to a situation in which every able bodied person who is willing to work at the prevailing wage rate, is employed. In other words full employment means that persons who are willing to work and able to work must have employment or a job.

Question 22.
What is the main feature of rural unemployment?
Answer:

1. India’s rural economy has both unemployment and underemployment.
2. The major feature of rural unemployment is the existence of unemployment in the form of disguised unemployment and seasonal unemployment.
3. In agriculture and agro based industries like sugar, production activities are carried out only in some seasons.

Question 23.
Give short note on frictional unemployment?
Answer:
Frictional Unemployment (Temporary Unemployment):

1. Frictional unemployment arises due to imbalance between supply of labour and demand for labour.
2. This is because of immobility of labour, lack of necessary skills, break down of machinery, shortage of raw materials etc.
3. The persons who lose jobs and in search of jobs are also included under frictional unemployment.

Question 24.
Give reasons for labour retrenchment at present situation?
Answer:

1. Modem technology being capital intensive requires less labourers and contributes to ’ technological unemployment.
2. Now a days, invention and innovations lead to the adoption of new techniques there by the existing workers are retrenched.
3. Labour saving devices are responsible for technological unemployment.

Question 25.
List out the assumptions of Say’s law?
Answer:
The Say’s Law of market is based on the following assumptions:

1. No single buyer or seller of commodity or an input can affect price.
2. Full employment.
3. People are motivated by self interest and self – interest determines economic decisions.
4. The laissez faire policy is essential for an automatic and self adjusting process of full employment equilibrium. Market forces determine everything right.
5. There will be a perfect competition in labour and product market.
6. There is wage-price flexibility.
7. Money acts only as a medium of exchange.
8. Long – run analysis.
9. There is no possibility for over production or unemployment.

Question 26.
What is effective demand?
Answer:

1. The starting point of Keynes theory of employment and income is the principle of effective demand.
2. Effective demand denotes money actually spent by the people on products of industry.
3. The money which entrepreneurs receive is paid in the form of rent, wages, interest and profit.
4. Therefore effective demand equals national income.

Question 27.
What are the components of aggregate supply?
Answer:
Aggregate demand has the following four components:

1. Consumption demand
2. Investment demand
3. Government expenditure and
4. Net Export (export – import)

Part – C
Answer The Following Questions In A Paragraph.

Question 28.
Explain the following in short:

1. Seasonal unemployment
2. Frictional unemployment
3. Educated unemployment

Answer:
Seasonal Unemployment:

1. This type of unemployment occurs during certain seasons of the year.
2. In agriculture and agro based industries like sugar,production activities are carried out only in some seasons.
3. These industries offer employment only during that season in a year. Therefore people may remain unemployed during the off season.
4. Seasonal unemployment happens from demand side also; for example ice cream industry, holiday resorts etc.

Frictional Unemployment (Temporary Unemployment):

1. Frictional unemployment arises due to imbalance between supply of labour and demand for labour.
2. This is because of immobility of labour, lack of necessary skills, break down of machinery, shortage of raw materials etc.
3. The persons who lose jobs and in search of jobs are also included under frictional unemployment.

Educated Unemployment:

1. Sometimes educated people are underemployed or unemployed when qualification does not match the job.
2. Faulty education system, lack of employable skills, mass student turnout and preference for white collar jobs are highly responsible for educated unemployment in India.

Question 29.
According to classical theory of employment, how wage reduction solves the problem of unemployment? Diagrammatically explain?
Answer:
The classical theory of employment assumes that the economy operates at the level of full employment without inflation in the long period. It also assumes that wages and prices of goods are flexible and the competitive market exists in the economy (laissez – faire economy). According to the classical theory of employment, full employment condition can be achieved by cutting down the wage rate. Unemployment would be eliminated when wages are determined by the mechanism of economy itself. The following figure shows the relationship between wage rate and employment:

In the figure, when the wage rate is OW, then the employment is ON. As the wage rate is reduced to OW¹, then the employment has increased to ON¹. Prof. Pigou has taken this theory as base for developing the solution of unemployment problem.

Question 30.
Write short note on the implications of Say’s law?
Answer:
Implications of Say’s Law:

1. There is no possibility for over production or unemployment.
2. If there exist unutilized resources in the economy, it is profitable to employ them up to the point of full employment. This is true under the condition that factors are willing to accept rewards on a par with their productivity.
3. As automatic price mechanism operates in the economy, there is no need for government intervention. (However, J.M. Keynes emphasized the role of the State)
4. Interest flexibility brings about equality between saving and investment.
5. Money performs only the medium of exchange function in the economy, as people will not hold idle money.

Question 31.
Explain Keynes’ theory in the form of flow chart?
Answer:

Question 32.
What do you mean by aggregate demand? Mention its components?
Answer:

1. The aggregate demand is the amount of money which entrepreneurs expect to get by selling the output produced by the number of labourers employed.
2. Therefore, it is the expected income or revenue from the sale of output at different levels of employment.
3. Aggregate demand has the following four components:
   1. Consumption demand
   2. InvestmenTdemand
   3. Government expenditure and
   4. Net Export (export – import)

Question 33.
Explain about aggregate supply with the help of diagram?
Answer:

1. Aggregate supply function is an increasing function of the level of employment.
2. Aggregate supply refers to the value of total output of goods and services produced in an economy in a year.
3. In other words, aggregate supply is equal to the value of national product, i.e., national income.
4. Aggregate Supply = C + S + T + Rf = Aggregate income generated in the economy.
5. The following figure shows the shape of the two aggregate supply curves drawn for the assumption of fixed money wages and variable wages.

Aggregate Supply Curve

1. Z curve is linear where money wages remains fixed; Z₁ curve is non – linear since wage rate increases with employment.
2. When full employment level of Nf is reached it is impossible to increase output by employing more men.
3. So aggregate supply curve becomes inelastic (Vertical straight line).
4. The slope of the aggregate supply curve depends on the relation between the employment and productivity.
5. Based upon this relation, the aggregate supply curve can be expected to slope upwards.
6. In reality the aggregate supply curve will be like Z₁
7. Therefore, the aggregate supply depends on the relationship between price and wages.

Question 34.
Write any five differences between classism and Keynesianism?
Answer:
Comparison of Classicism and Keynesianism
Keynesianism:

1. Short – run equilibrium Saving is a vice
2. The function of money is a medium of exchange on the one side and a store of value on the other side.
3. Macro approach to national problems
4. State intervention is advocated

Classicism:

1. Long – run equilibrium
2. Saving is a social virtue
3. The function of money is to act as a medium of exchange.
4. Micro foundation to macro problems
5. Champions of Laissez – fair policy

Part – D
Answer The Following Questions In One Page.

Question 35.
Describe the types of unemployment?
Answer:
The following are the types of unemployment.
Types of unemployment:

1. Cyclical Unemployment
2. Frictional Unemployment
3. Technical Unemployment
4. Disguised Unemployment
5. Seasonal Unemployment
6. Educated Unemployment
7. Structural Unemployment

1. Cyclical Unemployment:

1. This unemployment exists during the downturn phase of trade cycle in the economy.
2. In a business cycle during the period of recession and depression, income and output fall leading to widespread unemployment.
3. It is caused by deficiency of effective demand.
4. Cyclical unemployment can be cured by public investment or expansionary monetary policy.

2. Seasonal Unemployment:

1. This type of unemployment occurs during certain seasons of the year.
2. In agriculture and agro based industries like sugar, production activities are carried out only in some seasons.
3. These industries offer employment only during that season in a year. Therefore people may remain unemployed during the off season.
4. Seasonal unemployment happens from demand side also; for example ice cream industry, holiday resorts etc.

3. Frictional Unemployment (Temporary Unemployment):

1. Frictional unemployment arises due to imbalance between supply of labour and demand for labour.
2. This is because of immobility of labour, lack of necessary skills, break down of machinery, shortage of raw materials etc.
3. The persons who lose jobs and in search of jobs are also included under frictional unemployment.

4. Educated Unemployment:

1. Sometimes educated people are underemployed or unemployed when qualification does not match the job.
2. Faulty education system, lack of employable skills, mass student turnout and preference for white collar jobs are highly responsible for educated unemployment in India.

5. Technical Unemployment:

1. Modem technology being capital intensive requires less labourers and contributes to technological unemployment.
2. Now a days, invention and innovations lead to the adoption of new techniques there by the existing workers are retrenched.
3. Labour saving devices are responsible for technological unemployment.

6. Structural Unemployment:

1. Structural unemployment is due to drastic change in the structure of the society.
2. Lack of demand for the product or shift in demand to other products cause this type of unemployment.
3. For example rise in demand for mobile phones has adversely affected the demand for cameras, tape recorders etc.
4. So this kind of unemployment results from massive and deep rooted changes in economic structure.

7. Disguised Unemployment:

1. Disguised unemployment occurs when more people are than what is actually required.
2. Even if some workers are withdrawn, production does not suffer.
3. This type of unemployment is found in agriculture.
4. A person is said to be disguisedly by unemployed if his contribution to output is less than what he can produce by working for normal hours per day.
5. In this situation, marginal productivity of labour is zero or less or negative.

Question 36.
Critically explain Say’s law of market?
Answer:
Criticisms of Say’s Law:
The following are the criticisms against Say’s law:

1. According to Keynes, supply does not create its demand. It is not applicable where demand does not increase as much as production increases.
2. Automatic adjustment process will not remove unemployment. Unemployment can be removed by increase in the rate of investment.
3. Money is not neutral. Individuals hold money for unforeseen contingencies while businessmen keep cash reserve for future activities.
4. Say’s law is based on the proposition that supply creates its own demand and there is no over production. Keynes said that over production is possible.
5. Keynes regards full employment as a special case because there is under – employment in capitalist economies.
6. The need for state intervention arises in the case of general over production and mass unemployment.

Question 37.
Narrate the equilibrium between ADF and ASF with diagram? Equilibrium between ADF and ASF?
Answer:

• Under the Keynes theory of employment, a simple two sector economy consisting of the household sector and the business sector is taken to understand the equilibrium between ADF and ASF.
• All the decisions concerning consumption expenditure are taken by the individual households, while the business firms take decisions concerning investment.
• It is also assumed that consumption function is linear and planned investment is autonomous.
• There are two approaches to determination of the equilibrium level of income in Keynesian theory. These are:
  1. Aggregate demand – Aggregate supply approach
  2. Saving – Investment approach –
• In this chapter, out of these two, aggregate demand and aggregate supply approach is alone explained to understand the determination of equilibrium level of income and employment.
• The concept of effective demand is more clearly shown in the figure.
• In the figure, the aggregate demand and aggregate supply reach equilibrium at point E. The employment level is N0 at that point.
• At ON₁ employment, the aggregate supply is N, Rr But they are able to produce M₁ N₁ The expected level of profit is M₁, R₁
• To attain this level of profit, entrepreneurs will employ more labourers.
• The tendency to employ more labour will stop once they reach point E.
• At all levels of employment beyond, ON₀, the aggregate demand curve is below the aggregate supply curve indicating loss to the producers.
• Hence they will never employ more than ON₀ labour.
• Thus effective demand concept becomes a crucial point in determining the equilibrium level of output in the capitalist economy or a free market economy in the Keynesian system.
• It is important to note that the equilibrium level of employment need not be the full employment level (N₁) from the Figure, it is understood that the difference between N₀ – N₀ is the level of unemployment.
• Thus the concept of effective demand becomes significant in explaining the under employment equilibrium.

Question 38.
Explain the differences between classical theory and Keynes theory?
Answer:
Keynesianism:

1. Short – run equilibrium
2. Saving is a vice
3. The function of money is a medium of exchange on the one side and a store of value on the other side.
4. Macro approach to national problems
5. State intervention is advocated.
6. Applicable to all situations – full employment and less than full employment.
7. Capitalism has inherent contradictions
8. Budgeting should be adjusted to the requirements of economy.
9. The equality between saving and investment is advanced through changes in income.
10. Rate of interest is determined by the demand for and supply of money.
11. Rate of interest is a flow.
12. Demand creates its own supply.
13. Rate of interest is a reward for parting with liquidity.

Classicism:

1. Long – run equilibrium
2. Saving is a social virtue.
3. The function of money is to act as a medium of exchange
4. Micro foundation to macro problems
5. Champions of Laissez – fair policy
6. Applicable only to the full employment situation.
7. Capitalism is well and good.
8. Balanced budget
9. The equality between saving and investment is achieved through changes of rate of interest.
10. Rate of interest is determined by saving and investment.
11. Rate of interest is a stock.
12. Supply creates its own demand.
13. Rate of interest is a reward for saving.

Samacheer Kalvi 12th Economics Theories of Employment and Income Addtional Questions and Answers

Part – A
I. Multiple Choice Questions.

Question 1.
Who is one of the greatest and most influential economist?
(a) J.M. Keynes
(b) Adam Smith
(c) Marshall
(d) Simon Kuznets
Answer:
(a) J.M. Keynes

Question 2.
Keynes book “The General theory of Employment, Interest and Money” published in –
(a) 1926
(b) 1936
(c) 1946
(d) 1956
Answer:
(b) 1936

Question 3.
The total stock of money circulating in an Economy is called –
(a) Money
(b) Capital
(c) Money Supply
(d) Finance
Answer:
(c) Money Supply

Question 4.
The …………………… function depends upon Income of the people and marginal propensity to consume?
(a) demand
(b) consumption
(c) supply
(d) marginal
Answer:
(b) consumption

Question 5.
Every economy in the world aims at attaining the level of –
(a) full employment
(b) under employment
(c) un employment
(d) employment opportunity
Answer:
(a) full employment

Question 6.
…………………… is an increasing function of the level of employment –
(a) Aggregate supply function
(b) Aggregate demand function
(c) Aggregate consumption function
(d) Aggregate consumption expenditure
Answer:
(a) Aggregate supply function

Question 7.
Effective demand signifies the money spent on consumption of goods and services and on –
(a) capital
(b) investment
(c) profit
(d) finance
Answer:
(b) investment

Question 8.
Who has given importance to the concept of liquidity preference?
(a) Kuznet
(b) Marshall
(c) Keynes
(d) Adam Smith
Answer:
(c) Keynes

Question 9.
…………………….. was a French Economist and an Industrialist?
(a) J.B. Say
(b) Keynes
(c) Adam Smith
(d) David Ricardo
Answer:
(a) J.B. Say

Question 10.
Frictional unemployment another name is called –
(a) Educated unemployment
(b) Seasonal unemployment
(c) Temporary unemployment
(d) Technical unemployment
Answer:
(c) Temporary unemployment

Question 11.
Discussed unemployment is mostly found in –
(a) agriculture
(b) sericulture
(c) industry
(d) architecture
Answer:
(a) agriculture

Question 12.
The main reason for massive unemployment is poor –
(a) economic planning
(b) educational planning
(c) military planning
(d) man power planning
Answer:
(d) man power planning

Question 13.
The Employment Assurance Scheme was launched in the year –
(a) 1983
(b) 1993
(c) 2003
(d) 2013
Answer:
(b) 1993

Question 14.
Cyclical unemployment is caused by …………………………. cycles.
(a) business
(b) money
(c) trade
(d) finance
Answer:
(c) trade

Question 15.
The problem of rural unemployment can be solved only by ………………………….. agriculture.
(a) modernising
(b) agro based
(c) innovative
(d) new method followed
Answer:
(a) modernising

Question 16.
Unemployment is classified as voluntary unemployment and –
(a) involuntary unemployment
(b) cyclical unemployment
(c) rural unemployment
(d) seasonal unemployment
Answer:
(b) cyclical unemployment

Question 17.
Existence of Joint Family System in India promotes –
(a) educational unemployment
(b) disguised unemployment
(c) seasonal unemployment
(d) voluntary unemployment
Answer:
(b) disguised unemployment

Question 18.
Educated and skilled persons who may not accept casual work. This is called ………………………. unemployment.
(a) closed
(b) open
(c) seasonal
(d) disguised unemployment
Answer:
(b) open

Question 19.
………………………. law of market was the basis for assuming the situation of full employment.
(a) J.B. Say
(b) Keynes
(c) Marshall
(d) Lemer
Answer:
(a) J.B. Say

Question 20.
The aggregate effective demand would increase the level of –
(a) unemployment
(b) employment
(c) cyclical unemployment
(d) open unemployment
Answer:
(b) employment

Question 21.
…………………. refers to the labour force of a country.
(a) Employment
(b) Unemployment
(c) Full employment
(d) Open employment
Answer:
(c) Full employment

Question 22.
…………………. means that persons who are willing to work and able to work must have employment or a job?
(a) Full employment
(b) Unemployment
(c) Educational unemployment
(d) Seasonal unemployment
Answer:
(a) Full employment

Question 23.
………………….. is the principle of effective demand?
(a) Profit
(b) Income
(c) Money
(d) Interest
Answer:
(a) Profit

Question 24.
When goods are produced by firms in the economy, they pay reward to the factors of the production is called –
(a) J.M. Keynes
(b) Adam Smith
(c) J.B. Say
(d) Ricardo
Answer:
(c) J.B. Say

Question 25.
…………………….. defines “Full employment as that level of employment at which any further increase in spending would resort in an inflationary spiral of wages and prices”
(a) Lemer
(b) J.M. Keynes
(c) J.B. Say
(d) Adam Smith
Answer:
(a) Lemer

II. Match the following and choose the correct answer by using codes given below

Question 1.
A. Full employment – (i) Qualified job
B. Educated unemployment – (ii) Deficiency of effective demand
C. Cyclical unemployment – (iii) During season of the year
D. Seasonal unemployment – (iv) Learner
Codes:
(a) A (i) B (ii) C (iii) D (iv)
(b) A (ii) B (iv) C (i) D (iii)
(c) A (iv) B (i) C (ii) D (iii)
(d) A (iii) B (iv) C (i) D (ii)
Answer:
(c) A (iv) B (i) C (ii) D (iii)

Question 2.
A. Public Investment – (i) Temporary unemployment
B. Production activities only in Some seasons – (ii) Deficiency of effective demand
C. Frictional unemployment – (iii) During season of the year
D. Educated unemployment – (iv) Learner
Codes:
(a) A (ii) B (ii) C (iii) D (iv)
(b) A (iii) B (ii) C (iv) D (i)
(c) A (i) B (iii) C (ii) D (iv)
(d) A (iv) B (i) C (iii) D (ii)
Answer:
(a) A (ii) B (ii) C (iii) D (iv)

Question 3.
A. ED – (i) Income of the people
B. ADF – (ii) Y = C + I = Output = Employment
C. ASF – (iii) C + I + G + (X – M)
D. CF – (iv) C + S + T + Rf = Aggregate Income generated in the economy
Codes:
(a) A (i) B (ii) C (iii) D (iv)
(b) A (iii) B (i) C (iv) D (i)
(c) A (iv) B (ii) C (i) D (iii)
(d) A (iv) B (iii) C (iv) D (i)
Answer:
(d) A (iv) B (iii) C (iv) D (i)

Question 4.
A. Keynes concept – (i) Aggregate spending
B. Demand – (ii) Liquidity preference
C. Aggregate supply – (iii) To spend on domestic output
D. Aggregate demand – (iv) The value of national product
Codes:
(a) A (i) B (ii) C (iii) D (iv)
(b) A (ii) B (i) C (iv) D (iii)
(c) A (iii) B (iv) C (ii) D (i)
(d) A (iv) B (iii) C (i) D (ii)
Answer:
(b) A (ii) B (i) C (iv) D (iii)

Question 5.
A. Keynesianism – (i) Long run – equilibrium
B. Classicism – (ii) Short run – equilibrium
C. Keynesianism – (iii) State intervention is advocated
D. Classicism – (iv) Saving is a vice
Codes:
(a) A (ii) B (i) C (iv) D (iii)
(b) A (i) B (ii) C (iii) D (iv)
(c) A (iii) B (iv) C (ii) D(i)
(d) A (iv) B (iii) C (i) D (ii)
Answer:
(a) A (ii) B (i) C (iv) D (iii)

III. State whether the statements are true or false

Question 1.
(i) The function of money is a medium of exchange on the one side and a store of value on the other side is called Keynesianism.
(ii) Macro approach to national problems.

(a) Both (i) and (ii) are true
(b) Both (i) and (ii) are false
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(a) Both (i) and (ii) are true

Question 2.
(i) Aggregate demand has the four components are consumption demand, investment demand, Government expenditure and Net export.
(ii) Aggregate demand refers to the required amount of labourers and materials to produce the neccessary output.

(a) Both (i) and (ii) are true
(b) Both (i) and (ii) are false
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(c) (i) is true but (ii) is false

Question 3.
(i) Keynesian theory is – Aggregate demand – Aggregate supply approach. Saving – Investment approach.
(ii) This approach explained the determination level of Income and employment.

(a) Both (i) and (ii) are true
(b) Both (i) and (ii) are false
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(a) Both (i) and (ii) are true

Question 4.
(i) Effective demand denotes money actually spent by the people on products of Industry and agriculture.
(ii) Effective demand equals to State Income.

(a) Both (i) and (ii) are true
(b) Both (i) and (ii) are false
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(b) Both (i) and (ii) are false

Question 5.
(i) “Supply creates its own Demand”.
(ii) The aggregate demand and aggregate supply reach equilibrium at point ‘E’.

(a) Both (i) and (ii) are true
(b) Both (i) and (ii) are false
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(a) Both (i) and (ii) are true

IV. Which of the following is correctly matched

Question 1.
(a) Seasonal unemployment – Type of unemployment
(b) Technical unemployment – Some season only
(c) Cyclical unemployment – Public capital
(d) Full employment – Not willing to job
Answer:
(a) Seasonal unemployment – Type of unemployment

Question 2.
(a) Frictional unemployment – Permanant
(b) Educated unemployment – White collar jobs
(c) Structural unemployment – In search job
(d) Disguised unemployment – Found in industry
Answer:
(b) Educated unemployment – White collar jobs

Question 3.
(a) Keynes – A general theory
(b) Aggregate supply – A level of money
(c) Keynesianism – Champions of Laissez – Faire
(d) Effective demand – Classical Economy
Answer:
(a) Keynes – A general theory

Question 4.
(a) Effective demand – Income Effective
(b) Aggregate demand – Money demand
(c) Say’s law – Supply creates own demand
(d) Aggregate supply – Money supply
Answer:
(c) Say’s law – Supply creates own demand

Question 5.
(a) J.B. Say – Industrialist
(b) Adam Smith – Classical Economist
(c) David Ricardo – Capitalist Economist
(d) Lemer – Socialist
Answer:
(a) J.B. Say – Industrialist

V. Which of the following is not correctly matched

Question 1.
(a) Say’s law of Market – Classical theory of Employment
(b) Adam Smith – Wealth of nations
(c) Keynes – The General theory of Employment, Interest and Money
(d) A.C. Pigou – French Economist
Answer:
(d) A.C. Pigou – French Economist

Question 2.
(a) Full Employment – Willing to work and able to work
(b) Unemployment – Cannot find suitable job
(c) Underemployment – Not fully utilized
(d) Disguised unemployment – More people not working
Answer:
(d) Disguised unemployment – More people not working

Question 3.
(a) Keynes – Liquidity preference
(b) Aggregate demand – Consumption demand
(c) Consumption function – Money supply
(d) Marginal effeciency of capital – Investment level
Answer:
(c) Consumption function – Money supply

Question 4.
(a) Effective demand – Y = C + I = Output = Employment
(b) Aggregate supply – C + S + T + Rf = Aggregate Income
(c) Aggregate demand – C + I + G + (X – M)
(d) Aggregate private saving – C + S + T
Answer:
(d) Aggregate private saving – C + S + T

Question 5.
(a) Keynesianism – Capitalism has inherant contradictions
(b) Classism – Capitalism well and good
(c) Keynesian theory – Saving – Investment approach
(d) Frictional – Full employment
Answer:
(d) Frictional – Full employment

VI. Pick the odd one out

Question 1.
Types of unemployment
(a) Cyclical unemployment
(b) Seasonal unemployment
(c) Frictional unemployment
(d) nature unemployment
Answer:
(d) nature unemployment

Question 2.
Classical theory was developed by –
(a) David Ricardo
(b) Adam Smith
(c) J.S. Mill
(d) J.B. Say
Answer:
(b) Adam Smith

Question 3.
The Say’s law of Market Assumptions are –
(a) No single buyer
(b) Full employment
(c) Money is not neutral
(d) Wage flexibility
Answer:
(c) Money is not neutral

Question 4.
Keynesianism is called –
(a) Short run equilibrium
(b) saving is social virtue
(c) Macro approach to national problems
(d) State intervention is advocated
Answer:
(b) Saving is social virtue

Question 5.
Classicism is called –
(a) Capatalism is well and good
(b) Balanced Budget
(c) savinf is vice
(d) Micro foundation to Macro problems
Answer:
(c) Saving is vice

VII. Assertion and Reason

Question 1.
Assertion (A): Modem technology being capital intensive requires less labourers, and contributes to technological unemployment.
Reason (R): Now – a – days invention and innovations lead to the adoption of new techniques there by the existing workers are retrenched.

(a) Both ‘A’ and ‘R’ are tme and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are tme but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is tme but ‘R’ is false
(d) ‘A’ is false but ‘R’ is tme .
Answer:
(a) Both ‘A’ and ‘R’ are tme and ‘R’ is the correct explanation to ‘A’

Question 2.
Assertion (A): According to say, “when goods are produced by firms in the Economy”.
Reason (R): There was no single theory which could be labeled as classical theory of employment.

(a) Both ‘A’ and ‘R’ are tme and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(c) ‘A’ is true but ‘R’ is false

Question 3.
Assertion (A): Keynes book “The General theory of Employment, Interest and Money” published in 1916.
Reason (R): A turning point in the development of modem economic theory – Keynes.

(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(d) ‘A’ is false but ‘R’ is true

Question 4.
Assertion (A): Aggregate supply function is increasing function of the level of employment.
Reason (R): Aggregate supply is only state product.

(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(c) ‘A’ is true but ‘R’ is false

Question 5.
Assertion (A): Keynesianism is Macro approach to national problems.
Reason (R): Keynesianism is state intervention is advocated.

(a) Both ‘A’ and ‘R’ are tme and ‘R’ is the correct explanation to ‘A’
(.b) Both ‘A’ and ‘R’ are tme but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is tme but ‘R’ is false
(d) ‘A’ is false but ‘R’ is tme
Answer:
(d) ‘A’ is false but ‘R’ is tme

Part – B
Answer The Following Questions In One or Two Sentences

Question 1.
Write two approaches of the equilibrium level of Income in Keynesian theory?
Answer:
There are two approaches te determination of the equilibrium level of income in Keynesian theory. These are:

1. Aggregate demand – Aggregate supply approach
2. Saving – Investment approach

Question 2.
Define “Unemployment”?
Answer:
Unemployment:
When there are people, who are willing to work and able to work but cannot find suitable jobs.

Question 3.
Define “Marginal propensity to consume”?
Answer:
Marginal Propensity to Consume is the additional consumption due to an additional unit of income.

Question 4.
Write the types of unemployment?
Answer:
Types of unemployment:

1. Cyclical Unemployment
2. Frictional Unemployment
3. Technical Unemployment
4. Disguised Unemployment
5. Seasonal Unemployment
6. Educated Unemployment
7. Structural Unemployment

Part – C
Answer The Following Questions In One Paragraph.

Question 1.
Explain the Aggregate Demand Function with Diagram?
Answer:

1. In the Keynesian model, output is determined mainly by aggregate demand.
2. The aggregate demand is the amount of money which entrepreneurs expect to get by selling the output produced by the number of labourers employed.
3. Therefore, it is the expected income or revenue from the sale of output at different levels of employment.
   • Aggregate demand has the following four components:
     • Consumption demand
     • Investment demand
     • Government expenditure and
     • Net Export (export – import)
4. The desired or planned demand (spending) is the amount that households, firms, the governments and the foreign purchasers would like to spend on domestic output.
5. In other words, desired demand in the economy is the sum total of desired private consumption expenditure, desired investment expenditure, desired government spending and desired net exports (difference between exports and imports).
6. Thus, the desired spending is called aggregate spending (demand), and can be expressed as:
   AD = C + I + G + (X – M)
7. The diagram explains that aggregate demand price increases or decreases with an increase or decrease in the volume of employment.
8. Aggregate demand curve increases at an increasing rate in the beginning and then increases at a decreasing rate.
9. This shows that as income increases owing to increase in employment, expenditure of the economy increases at a decreasing rate.

Question 2.
Aggregate Supply Function meaning and components?
Answer:

1. Aggregate supply function is an increasing function of the level of employment.
2. Aggregate supply refers to the value of total output of goods and services produced in an economy in a year.
3. In other words, aggregate supply is equal to the value of national product, i.e., national income.

The components of aggregate supply are:

1. Aggregate (desired) consumption expenditure (C)
2. Aggregate (desired) private savings (S)
3. Net tax payments (T) (Total tax payment to be received by the government minus transfer payments, subsidy and interest payments to be incurred by the government) and (iv) Personal (desired) transfer payments to the foreigners (Rf) (e.g. Donations to international relief efforts)

Question 3.
Describe the features of classicism?
Answer:

1. Long – run equilibrium
2. Saving is a social virtue.
3. The function of money is to act as a medium of exchange
4. Micro foundation to macro problems
5. Champions of Laissez-fair policy
6. Applicable only to the full employment situation.
7. Capitalism is well and good.
8. Balanced budget
9. The equality between saving and investment is achieved through changes of rate of interest.
10. Rate of interest is determined by saving and investment.
11. Rate of interest is a stock.
12. Supply creates its own demand.
13. Rate of interest is a reward for saving.

Part – D
Answer The Following Questions In One Page.

Question 1.
Describe the Say’s Law of Market?
Answer:

1. Say’s law of markets is the core of the classical theory of employment.
2. J.B.Say (1776 – 1832) was a French Economist and an industrialist.
3. He was influenced by the writings of Adam Smith and David Ricardo.
4. J.B. Say enunciated the proposition that “Supply creates its own demand”.
5. Hence there cannot be general over production or the problem of unemployment in the economy.
6. According to Say, “When goods are produced by firms in the economy, they pay reward to the factors of production.
7. The households after receiving rewards of the factors of production spend the amount on the purchase of goods and services produced by them.
8. Therefore, each product produced in the economy creates demand equal to its value in the market.
9. In short, this classical theory explains that “A person receives his income from production which is spent on the purchase of goods and services produced by others.
10. For the economy as a whole, therefore, total production equals total income.

Question 2.
Explain the features of Keynesianism?
Answer:

1. Short – run equilibrium
2. Saving is a vice
3. The function of money is a medium of exchange on the one side and a store of value on the other side.
4. Macro approach to national problems
5. State intervention is advocated.
6. Applicable to all situations – full employment and less than full employment.
7. Capitalism has inherent contradictions.
8. Budgeting should be adjusted to the requirements of economy.
9. The equality between saving and investment is advanced through changes in income.
10. Rate of interest is determined by the demand for and supply of money.
11. Rate of interest is a flow.
12. Demand creates its own supply.
13. Rate of interest is a reward for parting with liquidity.

Question 3.
Describe the Effective demand?
Answer:

1. The starting point of Keynes theory of employment and income is the principle of effective demand.
2. Effective demand denotes money actually spent by the people on products of industry.
3. The money which entrepreneurs receive is paid in the form of rent, wages, interest and profit.
4. Therefore effective demand equals national income.
5. An increase in the aggregate effective demand would increase the level of employment.
6. A decline in total effective demand would lead to unemployment.
7. Therefore, total employment of a country can be determined with the help of total demand ‘ of a country.
8. According to the Keynes theory of employment, “Effective demand signifies the money spent on consumption of goods and services and on investment.
9. The total expenditure is equal to the national income, which is equivalent to the national output”.
10. The relationship between employment and output of an economy depends upon the level of effective demand which is determined by the forces of aggregate supply and aggregate demand.
    ED = Y = C + I = Output = Employment
11. Effective demand determines the level of employment in the economy.
12. When effective demand increases, employment will increase.
13. When effective demand decreases, the level employment will decline.
14. The effective demand will be determined by two determinants namely consumption and investment expenditures.
15. The consumption function depends upon income of the people and marginal propensity to consume.
16. According to Keynes, if income increases, consumption will also increase but by less than the increase in income.

Share this Tamilnadu State Board 12th Economics Solutions Chapter 3 Theories of Employment and Income Questions and Answers with your friends to help them to overcome the grammar issues in exams. Keep visiting this site frequently to get the latest information on different subjects. Clarify your doubts by posting the comments and get the answers in an easy manner.

Students of 12th can get the pdf links of Tamilnadu State Board Economics Solutions here. You can Download Samacheer Kalvi 12th Economics Book Solutions Chapter 4 Consumption and Investment Functions Questions and Answers, Notes Pdf, Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Economics Solutions Chapter 4 Consumption and Investment Functions

It is very important to put the textbook aside while preparing for the exams. So, if you follow Samacheer Kalvi 12th Economics Textbook Solutions you can cover all the topics in Chapter 4 Consumption and Investment Functions Questions and Answers. This helps to improve your communication skills.

Samacheer Kalvi 12th Economics Consumption and Investment Functions Text Book Back Questions and Answers

Part – A
Multiple Choice Questions.

Question 1.
The average propensity to consume is measured by –
(a) C / Y
(b) C × Y
(c) Y / C
(d) C + Y
Answer:
(a) C / Y

Question 2.
An increase in the marginal propensity to consume will:
(a) Lead to consumption function becoming steeper
(b) Shift the consumption function upwards
(c) Shift the consumption function downwards
(d) Shift savings function upwards
Answer:
(a) Lead to consumption function becoming steeper.

Question 3.
If the Keynesian consumption function is C = 10 + 0.8 Y then, if disposable income is Rs 1000, what is amount of total consumption?
(a) ₹ 0.8
(b) ₹ 800
(c) ₹ 810
(d) ₹ 0.81
Answer:
(c) ₹ 810

Question 4.
If the Keynesian consumption function is C = 10 + 0.8 Y then, when disposable income is Rs 100, what is the marginal propensity to consume?
(a) ₹ 0.8
(b) ₹ 800
(c) ₹ 810
(d) ₹ 0.81
Answer:
(a) ₹ 0.8

Question 5.
If the Keynesian consumption function is C = 10 + 0.8 Y then, and disposable income is ₹ 100, what is the average propensity to consume?
(a) ₹ 0.8
(b) ₹ 800
(c) ₹ 810
(d) ₹ 0.9
Answer:
(d) ₹ 0.9

Question 6.
As national income increases –
(a) The APC falls and gets nearer in value to the MPC.
(b) The APC increases and diverges in value from the MPC.
(c) The APC stays constant
(d) The APC always approaches infinity.
Answer:
(a) The APC falls and gets nearer in value to the MPC.

Question 7.
As increase in consumption at any given level of income is likely to lead –
(a) Higher aggregate demand
(b) An increase in exports
(c) A fall in taxation revenue
(d) A decrease in import spending
Answer:
(a) Higher aggregate demand

Question 8.
Lower interest rates are likely to:
(a) Decrease in consumption
(b) increase cost of borrowing
(c) Encourage saving
(d) increase borrowing and spending
Answer:
(d) increase borrowing and spending

Question 9.
The MPC is equal to:
(a) Total spending / total consumption
(b) Total consumption / total income
(c) Change in consumption / change in income
(d) None of the above
Answer:
(c) Change in consumption / change in income

Question 10.
The relationship between total spending on consumption and the total income is the –
(a) Consumption function
(b) Savings function
(c) Investment function
(d) aggregate demand function
Answer:
(a) Consumption function

Question 11.
The sum of the MPC and MPS is –
(a) 1
(b) 2
(c) 0.1
(d) 1.1
Answer:
(a) 1

Question 12.
As income increases, consumption will –
(a) fall
(b) not change
(c) fluctuate
(d) increase
Answer:
(d) increase

Question 13.
When investment is assumed autonomous the slope of the AD schedule is determined by the –
(a) marginal propensity to invest
(b) disposable income
(c) marginal propensity to consume
(d) average propensity to consume
Answer:
(c) marginal propensity to consume

Question 14.
The multiplier tells us how much changes after a shift in –
(a) Consumption, income
(b) investment, output
(c) savings, investment
(d) output, aggregate demand
Answer:
(d) output, aggregate demand

Question 15.
The multiplier is calculated as –
(a) 1 / (1 – MPC)
(b) 1 / MPS
(c) 1 / MPC
(d) a and b
Answer:
(d) a and b

Question 16.
It the MPC is 0.5, the multiplier is –
(a) 2
(b) 1/2
(c) 0.2
(d) 20
Answer:
(a) 2

Question 17.
In an open economy import ………………………. the value of the multiplier
(a) Reduces
(b) increase
(c) does not change
(d) changes
Answer:
(a) Reduces

Question 18.
According to Keynes, investment is a function of the MEC and –
(a) Demand
(b) Supply
(c) Income
(d) Rate of interest
Answer:
(d) Rate of interest

Question 19.
The term super multiplier was first used by –
(a) J.R.Hicks
(b) R.G.D. Allen
(c) Kahn
(d) Keynes
Answer:
(a) J.R.Hicks

Question 20.
The term MEC was introduced by –
(a) Adam Smith
(b) J.M. Keynes
(c) Ricardo
(d) Malthus
Answer:
(b) J.M. Keynes

Part – B
Answer The Following Questions In One or Two Sentences

Question 21.
What is consumption function?
Answer:
Meaning of Consumption Function:

1. The consumption function or propensity to consume refers to income consumption relationship. It is a “functional relationship between two aggregates viz., total consumption and gross national income.”

2. Symbolically, the relationship is represented as C = f (Y)
Where,
C = Consumption; Y = Income; f = Function

3. Thus the consumption function indicates a functional relationship between C and Y, where C is the dependent variable and Y is the independent variable, i.e., C is determined by Y. This relationship is based on the ceteris paribus (other things being same) assumption, as only income consumption relationship is considered and all possible influences on consumption are held constant.

Question 22.
What do you mean by propensity to consume?
Answer:

1. The consumption function or propensity to consume refers to income consumption relationship. It is a “functional relationship between two aggregates viz., total consumption and gross national income.”

2. Symbolically, the relationship is represented as C = f(Y) Where, C = Consumption; Y = Income; f = Function

3. Thus the consumption function indicates a functional relationship between C and Y, where C is the dependent variable and Y is the independent variable, i.e., C is determined by Y. This relationship is based on the ceteris paribus (other things being same) assumption, as only income consumption relationship is considered and all possible influences on consumption are held constant.

Question 23.
Define average propensity to consume (APC)?
Answer:
Average Propensity to Consume:

1. The average propensity to consume is the ratio of consumption expenditure to any particular level of income.” Algebraically it may be expressed as under:
Where, C = Consumption; Y = Income
APC = \(\frac{C}{Y}\)
Where, C = Consumption; Y = Income.

Question 24.
Define marginal propensity to consume (MPC)?
Answer:
Marginal Propensity to Consume:

1. The marginal propensity to consume may be defined as the ratio of the change in the consumption to the change in income. Algebraically it may be expressed as under:
MPC = \(\frac { \Delta C }{ \Delta Y } \)
Where, ∆C = Change in Consumption; ∆Y = Change in Income
MPC is positive but less than unity, 0 < \(\frac { \Delta C }{ \Delta Y } \) < 1.

Question 25.
What do you mean by propensity to save?
Answer:

1. Thus the consumption function measures not only the amount spent on consumption but also the amount saved.
2. This is because the propensity to save is merely the propensity not to consume.
3. The 45° line may therefore be regarded as a zero – saving line, and the shape and position of the C curve indicate the division of income between consumption and saving.

Question 26.
Define average propensity to save (APS)?
Answer:
Average Propensity to Save (APS):

1. The average propensity to save is the ratio of saving to income.
2. APS is the quotient obtained by dividing the total saving by the total income. In other words, it is the ratio of total savings to total income. It can be expressed algebraically in the form of equation as under
3. APS = \(\frac{S}{Y}\) Where, S = Saving; Y = Income

Question 27.
Define Marginal Propensity to Save (MPS)?
Answer:
Marginal Propensity to Save (MPS):

1. Marginal Propensity to Save is the ratio of change in saving to a change in income.

2. MPS is obtained by dividing change in savings by change in income. It can be expressed algebraically as MPS = \(\frac { \Delta S }{ \Delta Y } \)
∆S = Change in Saving; ∆Y = Change in Income
Since MPC + MPS = 1
MPS = 1 – MPC and MPC = 1 – MPS.

Question 28.
Define Multiplier?
Answer:

1. The multiplier is defined as the ratio of the change in national income to change in investment.
2. If AI stands for increase in investment and AY stands for resultant increase in income, the multiplier K =AY/AI.
3. Since AY results from AI, the multiplier is called investment multiplier.

Question 29.
Define Accelerator?
Answer:

1. “The accelerator coefficient is the ratio between induced investment and an initial change in consumption.”
2. Assuming the expenditure of ₹50 crores on consumption goods, if industries lead to an investment of ₹100 crores in investment goods industries, we can say that the accelerator is 2.
3. Accelerator = \(\frac { 100 }{ \Delta Y } \) = 2

Part – C
Answer The Following Questions In One Paragraph.

Question 30.
State the propositions of Keynes’s Psychological Law of Consumption?
Answer:
Propositions of the Law:
This law has three propositions:
1. When income increases, consumption expenditure also increases but by a smaller amount. The reason is that as income increases, we wants are satisfied side by side, so that the need to spend more on consumer goods diminishes. So, the consumption expenditure increases with increase in income but less than proportionately.

2. The increased income will be divided in some proportion between consumption expenditure and saving. This follows from the first proposition because when the whole • of increased income is not spent on consumption, the remaining is saved. In this way, consumption and saving move together.

3. Increase in income always leads to an increase in both consumption and saving. This means that increased income is unlikely to lead to fall in either consumption or saving. Thus with increased income both consumption and saving increase.

Question 31.
Differentiate autonomous and induced investment?
Answer:
Autonomous Investment:

1. Independent
2. Income inelastic
3. Welfare motive

Induced Investment:

1. Planned
2. Income elastic
3. Profit Motive

Question 32.
Explain any three subjective and objective factors influencing the consumption function?
Answer:
Subjective Factors:

1. The motive of precaution: To build up a reserve against unforeseen contingencies. e.g. Accidents, sickness. ,
2. The motive of foresight: The desire to provide for anticipated future needs. e.g. Old age.
3. The motive of calculation: The desire to enjoy interest and appreciation. Consumption and Investment Functions.

Objective Factors:
1. Income Distribution:
If there is large disparity between rich and poor, the consumption is low because the rich people have low propensity to consume and high propensity to save.

2. Price level:
Price level plays an important role in determining the consumption function. When the price falls, real income goes up; people will consume more and propensity to save of the
society increases.

3. Wage level:
Wage level plays an important role in determining the consumption function and there is positive relationship between wage and consumption. Consumption expenditure increases with the rise in wages. Similar is the effect with regard to windfall gains.

Question 33.
Mention the differences between accelerator and multiplier effect?
Answer:
Accelerator Effect Multiplier Effect:

1. Accelerator is the numerical value of the relation between an increase in consumption and the resulting increasing in Investment. Multiplier is the ration of the change in national income to change in Investment.

2. Accelerator (β) = \(\frac { \Delta I }{ \Delta C } \)
ΔI = Change in Investment
ΔC = Change in consumption demand Multiplier (K) = \(\frac { \Delta I }{ \Delta C } \)
ΔI = Increase in Investment ΔY = Increase in Income ΔY results from ΔI

3. Accelerator Effects are –

1. Increase in consumer demand.
2. Films get close to fill capacity.
3. Film invest to meet rising demand. Multiplier Effects are

Multiplier Effect:
1. Multiplier is the ration of the change in national income to change in Investment.

2. Multiplier:
Multiplier (K) = \(\frac { \Delta Y }{ \Delta I } \)
ΔI = Increase in Investment
ΔY = Increase in Income
ΔY results from ΔI

Multiplier Effects are:

1. Positive Multiplier an initial increases is an injection (or a decrease in a leakage) leads to a greater final increase in real GDP.
2. Negative Multiplier an initial increases in an injection (or an increase in a leakage) leads to a greater final decrease in real GDP.

Question 34.
State the concept of super multiplier?
Answer:
Super Multiplier: (k and β interaction):

1. The super multiplier is greater than simple multiplier which includes only autonomous investment and no induced investment, while super multiplier includes induced investment.
2. In order to measure the total effect of initial investment on income, Hicks has combined the k and β mathematically and given it the name of the Super Multiplier.
3. The super multiplier is worked out by combining both induced consumption and induced investment.

Question 35.
Specify the limitations of the multiplier?
Answer:

1. There is change in autonomous investment.
2. There is no induced investment
3. The marginal propensity to consume is constant.
4. Consumption is a function of current income.
5. There are no time lags in the multiplier process.
6. Consumer goods are available in response to effective demand for them.
7. There is a closed economy unaffected by foreign influences.
8. There are no changes in prices.
9. There is less than full employment level in the economy.

Part – D
Answer The Following Questions In About A Page.

Question 36.
Explain Keynes psychological law of consumption function with diagram?
The three propositions of the law:

Proposition (1):
Income increases by ₹ 60 crores and the increase in consumption is by ₹ 50 crores.

Proposition (2):
The increased income of ₹ 60 crores in each case is divided in some proportion between consumption and saving respectively, (i.e., ₹ 50 crores and ₹ 10 crores).

Proposition (3):
As income increases consumption as well as saving increase. Neither consumption nor saving has fallen. Diagrammatically, the three propositions are explained in figure. Here, income is measured horizontally and consumption and saving are measured on the vertical axis. C is the consumption function curve and 45° line represents income consumption equality.

Proposition (1):
When income increases from 120 to 180 consumption also increases from 120 to 170 but the increase in consumption is less than the increase in income, 10 is saved.

Proposition (2):
When income increases to 180 and 240, it is divided in some proportion between consumption by 170 and 220 and saving by 10 and 20 respectively.

Proposition (3):
Increases in income to 180 and 240 lead to increased consumption 170 and 220 and increased saving 20 and 10 than before. It is clear from the widening area below the C curve and the saving gap between 45° line and C curve.

Question 37.
Briefly explain the subjective and objective factors of consumption function?
Answer:
Subjective Factors:

1. The motive of precaution: To build up a reserve against unforeseen contingencies. e.g. Accidents, sickness
2. The motive of foresight: The desire to provide for anticipated future needs, e.g. Old age
3. The motive of calculation: The desire to enjoy interest and appreciation.
4. The motive of improvement: The desire to enjoy for improving standard of living.
5. The motive of financial independence.
6. The motive of enterprise (desire to do forward trading).
7. The motive of pride.(desire to bequeath a fortune)
8. The motive of avarice.(purely miserly instinct)

Objective Factors:
1. Income Distribution:
If there is large disparity between rich and poor, the consumption is low because the rich people have low propensity to consume and high propensity to save.

2. Price level:

1. Price level plays an important role in determining the consumption function.
2. When the price falls, real income goes up; people will consume more and propensity to save of the society increases.

3. Wage level:

1. Wage level plays an important role in determining the consumption function and there is positive relationship between wage and consumption.
2. Consumption expenditure increases with the rise in wages.
3. Similar is the effect with regard to windfall gains.

4. Interest rate:

1. Rate of interest plays an important role in determining the consumption function.
2. Higher rate of interest will encourage people to save more money and reduces consumption.

5. Fiscal Policy:
When government reduces the tax the disposable income rises and the propensity to consume of community increases.

6. Consumer credit:

1. The availability of consumer credit at easy installments will encourage households to buy consumer durables like automobiles, fridge, computer.
2. This pushes up consumption.

7. Demographic factors:

1. Ceteris paribus, the larger the size of the family, the grater is the consumption.
2. Besides size of family, stage in family life cycle, place of residence and occupation affect the consumption function.

8. Duesenberry hypothesis:
Duesenberry has made two observations regarding the factors affecting consumption.

1. The consumption expenditure depends not only on his current income but also past income and standard of living.
2. Consumption is influenced by demonstration effect. The consumption standards of low income groups are influenced by the consumption standards of high income groups.

9. Windfall Gains or losses:
Unexpected changes in the stock market leading to gains or losses tend to shift the consumption function upward or downward.

Question 38.
Illustrate the working of Multiplier?
Answer:
Working of Multiplier:

1. Suppose the Government undertakes investment expenditure equal to ₹ 100 crore on some public works, by way of wages, price of materials etc.
2. Thus income of labourers and suppliers of materials increases by ₹ 100 crore. Suppose the MPC is 0.8 that is 80 %.
3. A sum of ₹ 80 crores is spent on consumption (A sum of ₹ 20 Crores is saved).
4. As a result, suppliers of goods get an income of ₹ 80 crores.
5. They intum spend ₹ 64 crores (80% of ₹ 80 cr).
6. In this manner consumption expenditure and increase in income act in a chain like maimer.

The final result is ∆Y = 100 + 100 × 4/5 + 100 × [4/5]² + 100 × [4/5]³ or,
∆Y = 100 + 100 × 0.8 + 100 × (0.8)² + 100 × (0.8)³
= 100 + 80 + 64 + 51.2… = 500 .
that is 100 × 1/1 – 4/5
100 × 1/1/5
100 × 5 = ₹ 500 crores
For instance if C = 100 + 0.8Y, I = 100,
Then Y = 100 + 0.8Y + 100
0.2Y = 200
Y = 200/0.2 = 1000 → Point B
If I is increased to 110, then
0.2Y = 210
Y = 210/0.2 = 1050 → Point D
For ₹ 10 increase in I, Y has increased by ₹ 50.
This is due to multiplier effect.
At point A, Y = C = 500
C = 100 + 0.8 (500) = 500; S = 0
At point B, Y = 1000
C = 100 + 0.8 (1000) = 900; S = 100 = I At point D, Y = 1050
C = 100 + 0.8 (1050) = 940; S = 110 = I
When I is increased by 10, Y increases by 50.
This is multiplier effect (K = 5)
K = \(\frac{1}{0.2}\) = 5

Question 39.
Explain the operation of the Accelerator?
Answer:
Operation of the Acceleration Principle:

1. Let us consider a simple example. The operation of the accelerator may be illustrated as follows.
2. Let us suppose that in order to produce 1000 consumer goods, 100 machines are required.
3. Also suppose that working life of a machine is 10 years.
4. This means that every year 10 machines have to be replaced in order to maintain the constant flow of 1000 consumer goods. This might be called replacement demand.
5. Suppose that demand for consumer goods rises by 10 percent (i.e. from 1000 to 1100).
6. This results in increase in demand for 10 more machines.
7. So that total demand for machines is 20. (10 for replacement and 10 for meeting increased demand).
8. It may be noted here a 10 percent increase in demand for consumer goods causes a 100 percent increase in demand for machines (from 10 to 20).
9. So we can conclude even a mild change in demand for consumer goods will lead to wide change in investment.

Diagrammatic illustration:
Operation of Accelerator.

1. SS is the saving curve. II is the investment curve. At point E₁ the economy is in equilibrium with OY₁ income. Saving and investment are equal at OY₁ Now, investment is increased from OI₂ to OI₄.
2. This increases income from OY₁ to OY₃, the equilibrium point being E₃ If the increase in investment by I₂ I₄ is purely exogenous, then the increase in income by Y₁ Y₃ would have been due to the multiplier effect.
3. But in this diagram it is assumed that exogenous investment is only by I, I3 and induced investment is by I₃I₄.
4. Therefore, increase in income by Y₁ Y₂ is due to the multiplier effect and the increase in income by Y₂ Y₃ is due to the accelerator effect.

Question 40.
What are the differences between MEC and MEI?
Answer:
Marginal Efficiency of Capital (MEC):

1. It is based on a given supply price for capital.
2. It represents the rate of return on all successive units of capital without regard to existing capital.
3. The capital stock is taken on the X axis of diagram.
4. It is a “stock” concept.
5. It determines the optimum capital stock in an economy at each level of interest rate.

Marginal Efficiency of Investment (MEI):

1. It is based on the induced change in the price due to change in the demand for capital.
2. It shows the rate of return on just those units of capital over and above the existing capital stock.
3. The amount of investment is taken on the X – axis of diagram.
4. It is a “flow” concept.
5. It determines the net investment of the economy at each interest rate given the capital stock.

Samacheer Kalvi 12th Economics Consumption and Investment Functions Additional Questions and Answers

part – A
I. Multiple Choice Questions.

Question 1.
Price level plays an important role in determining the ……………………
(a) Consumption function
(b) Income function
(c) Finance function
(d) Price function
Answer:
(a) Consumption function

Question 2.
The progressive tax system increases the ……………………….. of the people by altering the income distribution in favour of poor?
(a) price level
(b) wage level
(c) propensity to consume
(d) Fiscal policy
Answer:
(c) propensity to consume

Question 3.
…………………….. means purchase of stocks and shares, debentures, government bonds and equities?
(a) Consumption
(b) Investment
(c) Finance
(d) Saving
Answer:
(b) Investment

Question 4.
…………………… is influenced by demonstration effect.
(a) Investment
(b) Interest
(c) Expenditure
(d) Consumption
Answer:
(d) Consumption

Question 5.
Additional investment that is independent of income is called ……………………
(a) Autonomous Investment
(b) Autonomous Consumption
(c) Average Investment
(d) Marginal Investment
Answer:
(a) Autonomous Investment

Question 6.
Induced investment is motivated?
(a) Investment
(b) Capital
(c) Saving
(d) Profit
Answer:
(d) Profit

Question 7.
MEI is the expected rate of return on investment as additional units of ……………………
(a) Saving
(b) Investment
(c) Consumption
(d) Expenditure
Answer:
(b) Investment

Question 8.
Dynamic multiplier is also known as ……………………
(a) Sequence multiplier
(b) Static multiplier
(c) Double multiplier
(d) Single multiplier
Answer:
(a) Sequence multiplier

Question 9.
The combined effect of interaction of multiplier and accelerator is called ……………………
(a) Super accelerator
(b) Super multiplier
(c) Accelerator
(d) Multiplier
Answer:
(b) Super multiplier

Question 10.
The tendency to initiate Superior consumption pattern is called ……………………
(a) Accelerator effect
(b) Multiplier effect
(c) Super Multiplier effect
(d) Demonstration effect
Answer:
(d) Demonstration effect

Question 11.
The multiplier is the reciprocal of one minus ……………………
(a) MPC
(b) MPS
(c) Multiplier
(d) Accelerator
Answer:
(a) MPC

Question 12.
The concept of multiplier was first developed by ……………………
(a) J.M. Keynes
(b) David Ricardo
(c) R.F. Khan
(d) J.B. Say
Answer:
(c) R.F. Khan

Question 13.
…………………… the larger size of the family, the greater is the consumption?
(a) Demographic factors
(b) Income Distribution
(c) Duesenberry hypothesis
(d) Wage level
Answer:
(b) Income Distribution

Question 14.
MPS is the ratio of change in saving to a change in ……………………
(a) profit
(b) money
(c) finance
(d) income
Answer:
(d) income

Question 15.
Consumption function is called the relationship between ……………………….. and Income?
(a) Money
(b) Consumption
(c) Finance
(d) Investment
Answer:
(b) Consumption

Question 16.
Consumer’s surplus is useful to the Finance Minister in formulating ……………………….. policies?
(a) Surplus
(b) Consumption
(c) Taxation
(d) Income
Answer:
(c) Taxation

Question 17.
Consumer surplus is called potential price – ……………………………. price?
(a) real
(b) actual
(c) normal
(d) high
Answer:
(b) actual

Question 18.
Dynamic multiplier is also known as ………………………. Multiplier.
(a) Sequence
(b) Static
(c) Timeless
(d) Logical
Answer:
(a) Sequence

Question 19.
Static Multiplier is otherwise known as …………………………… Multiplier.
(a) Dynamic
(b) Leakage
(c) Simultaneous
(d) Multi effect
Answer:
(c) Simultaneous

Question 20.
The propensity to consume refers to the portion of Income spent on ……………………….
(a) Income
(b) Profit
(c) Expenditure
(d) Consumption
Answer:
(d) Consumption

Question 21.
………………………. redefined it as investment multiplier.
(a) R.K. Khan
(b) David Ricardo
(c) J.M. Keynes
(d) Marshall
Answer:
(c) J.M. Keynes

Question 22.
Accelerator Model was made by ……………………
(a) J.M. Keynes
(b) J.M. Clark
(c) R.F. Khan
(d) Marshall
Answer:
(b) J.M. Clark

Question 23.
The multiplier tells us …………………………. changes after a shift in ……………………
(a) income
(b) investment
(c) aggregate demand
(d) savings
Answer:
(c) aggregate demand

Question 24.
The simple accelerated model was made by J.M. Clark in ……………………
(a) 1915
(b) 1916
(c) 1914
(d) 1917
Answer:
(d) 1917

II. Match the following and choose the correct answer by using codes given below

Question 1.
A. Consumption function – (i) Consmption increased
B. Induced Investment – (ii) Borrowings
C. Income Increases – (iii) Subjective and objective
D. Autonomous consumption – (iv) Profit motive
Codes:
(a) A (iii) B (iv) C (i) D (ii)
(b) A (iv) B (i) C (ii) D (iii)
(c) A (i) B (ii) C (iii) D (iv)
(d) A (ii) B (iii) C (iv) D (i)
Answer:
(a) A (iii) B (iv) C (i) D (ii)

Question 2.
A. MPS – measured – (i) K = 1/MPS
B. Multiplier developed by – (ii) MEC
C. Investment depends on – (iii) ∆S/∆Y
D. Value of multiplier – (iv) R.F. Khan
Codes:
(a) A (i) B (ii) C (iv) D (iii)
(b) A (ii) B (iii) C (i) D (iv)
(c) A (iii) B (iv) C (ii) D (i)
(d) A (iv) B (i) C (iii) D (ii)
Answer:
(c) A (iii) B (iv) C (ii) D (i)

Question 3.
A. Reduced Investment – (i) 1930
B. Keynes employment dependes on – (ii) Highest interest rate
C. Fall in investment – (iii) Zero
D. Long fun autonomous consumption will – (iv) Investment
Codes:
(a) A (i) B (iii) C (iv) D (ii)
(b) A (ii) B (iv) C (i) D (iii)
(c) A (iii) B (i) C (ii) D (iv)
(d) A (iv) B (ii) C (iii) D (i)
Answer:
(b) A (ii) B (iv) C (i) D (iii)

Question 4.
A. MPS – (i) AC/AY
B. MPC – (ii) C/Y
C. APS – (iii) S/Y
D. APC – (iv) AS/AY
Codes:
(a) A (iv) B (i) C (iii) D (ii)
(b) A (i) B (ii) C (iv) D (iii)
(c) A (ii) B (iii) C (i) D (iv)
(d) A (iii) B (iv) C (ii) D (i)
Answer:
(a) A (iv) B (i) C (iii) D (ii)

Question 5.
A. Investment means – (i) Expenditure on capital formation
B. Uses of multiplier – (ii) Consumption forgone
C. Saving is – (iii) Achieve full employment
D. Autonomous investment – (iv) Stocks and shares
Codes:
(a) A (ii) B (i) C (iv) D (iii)
(b) A (iii) B (ii) C (iii) D (iv)
(c) A (iv) B (iii) C (ii) D (i)
(d) A (i) B (iv) C (i) D (ii)
Answer:
(c) A (iv) B (iii) C (ii) D (i)

III. State whether the statements are true or false.

Question 1.
(i) Keynes propounded the fundamental psychological law of consumption.
(ii) J.M. Keynes has divided factors influencing the consumption function.

(a) Both (i) and (ii) are true
(b) Both (i) and (ii) are false
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(a) Both (i) and (ii) are true

Question 2.
(i) The kinds of multiplier is called Tax Multiplier, Employment Multiplier, Foreign trade Multiplier, Investment Multiplier.
(ii) Investment means money collecting.

(a) Both (i) and (ii) are true
(b) Both (i) and (ii) are false
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(d) (i) is false but (ii) is true

Question 3.
(i) The term investment means purchase of stocks and shares, debentures, government bonds and equities.
(ii) The term Investment means expenditure on capital formation.

(a) Both (i) and (ii) are true
(b) Both (i) and (ii) are false
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(c) (i) is true but (ii) is false

Question 4.
(i) Leakages of multiplier is payment only.
(ii) Leakages of multiplier limitation is called full employment situation.

(a) Both (i) and (ii) are true
(b) Both (i) and (ii) are false
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(d) (i) is false but (ii) is true

Question 5.
(i) The types of Investment is called Autonomous Investment, Induced Investment.
(ii) Induced Investment is the expenditure on fixed assets and stocks.

(a) Both (i) and (ii) are true
(b) Both 0) and (if) are false
(c) (i) is true but (ii) is false
(d) (i) is false but (ii) is true
Answer:
(a) Both (i) and (ii) are true

IV. Which of the following is correctly matched:

Question 1.
(a) J.M. Clark – Ceteris Paribus
(b) J.M. Keynes – Psychological law of consumption
(c) R.F. Khan – Accelerator model
(d) Duesenberry – Laissez – faire
Answer:
(b) J.M. Keynes – Psychological law of consumption

Question 2.
(a) Induced Investment – Profit motive
(b) MEC – Autonomous Investment
(c) MEI – Technology
(d) MPC – Accelerator
Answer:
(a) Induced Investment – Profit motive

Question 3.
(a) Dynamic Multiplier – Employment
(b) Static Multiplier – Wealth
(c) Accelerator Model – J.M. Clark
(d) Leakage Multiplier – Investment goods
Answer:
(c) Accelerator Model – J.M. Clark

Question 4.
(a) Afltalion – 1909
(b) Hawtrey – 1914
(c) Bickerdike – 1915
(d) J.M. Clark – 1916
Answer:
(a) Afltalion – 1909

Question 5.
(a) Aggregate Income – C
(b) Consumption expenditure – I_A
(c) Autonomous Investment – Y
(d) Induced Private Investment – I_P
Answer:
(d) Induced Private Investment – I_P

V. Which of the following is not correctly matched

Question 1.
(a) Static multiplier – Simultaneous multiplier
(b) Dynamic multiplier – Sequence multiplier
(c) Leakage multiplier – Timeless multiplier
(d) Kinds of multiplier – Tax multiplier
Answer:
(c) Leakage multiplier – Timeless multiplier

Question 2.
(a) Ratio of the consumption – APC expenditure to Income
(b) Ratio of change in consumption – MPC to change in Income
(c) Ratio of the saving to Income – APS
(d) Ratio of change in saving to change in Income – PSM change in Income
Answer:
(d) Ratio of change in saving to change in Income – PSM change in Income

Question 3.
(a) Demonstration Effect – Superior consumption pattern
(b) Subjective factors – Psychological feeling
(c) Objective factors – Real and Measurable
(d) Super multiplier – Investment demand
Answer:
(d) Super multiplier – Investment demand

Question 4.
(a) Average propensity to consume – C/Y
(b) Marginal propensity to consume – AC/AY
(c) Average propensity to consume – S/Y
(d) Marginal propensity to save – AY/AS
Answer:
(d) Marginal propensity to save – AY/AS

Question 5.
(a) The motive of precaution – Accidents, Sickness
{b) The motive of foresight – Old age
(c) The motive of improvement – Improve standard of living
(d) The motive of calculation – Money collecting
Answer:
(d) The motive of calculation – Money collecting

VI. Pick the odd one out.

Question 1.
(a) ∆C – Change in consumption
(b) ∆Y – Change in expenditure
(c) ∆S – Change in saving 4
(d) ∆Y – Change in income
Answer:
(b) ∆Y – Change in expenditure

Question 2.
(a) APC – Algebraically Propensity to Consume
(b) MPC – Marginal Propensity to Consume
(c) APS – Average Propensity to Consume
(d) MPS – Marginal Propensity to Save
Answer:
(a) APC – Algebraically Propensity to Consume

Question 3.
Keynes’s Law is based on the Assumptions.
(a) Ceteris paribus
(b) Existence of Normal conditions
(c) Existence of a Laissez – Faire
(d) Existence of a Technical attributes
Answer:
(d) Existence of a Technical attributes

Question 4.
Investment means
(a) Purchase of stocks and shares
(b) Debentures
(c) Government bonds and equities
(d) Bank amount
Answer:
(d) Bank amount

Question 5.
MEC – Short Run Factors
(a) Supply for the product
(b) Liquid Assets
(c) Sudden changes in Income
(d) Current rate of Investment
Answer:
(a) Supply for the product

VII. Assertion and Reason.

1. Assertion (A): Keynes Law of propositions – when Income increases, consumption expenditure also increases but by a smaller amount.
Reason (R): Keynes Law of propositions – Increase in Income always lead to an increase in both consumption and saving.

(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’

Question 2.
Assertion (A): J.M. Keynes has influencing consumption function into subjective factors are the Internal factors related to psychological feelings.
Reason (R): J.M. Keynes has influencing consumption function into objective factors are Internal factors are not measurable.

(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(c) ‘A’ is true but ‘R’ is false

Question 3.
Assertion (A): Autonomous Investment is the expenditure on capital formation.
Reason (R): Autonomous Investment is Independent of the change in Income, rate of Interest or rate of profit.

(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’

Question 4.
Assertion (A): MEC – depends on the Demand yield from a capital asset.
Reason (R): MEC – depends on the Supply price of a capital asset.

(a) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(d) ‘A’ is false but ‘R’ is true

Question 5.
Assertion (A): Keynes theory of the Multiplier Assumption is change in autonomous Investment.
Reason (R): Keynes theory of the Multiplier Assumption is no Induced Investment.

(а) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’
(b) Both ‘A’ and ‘R’ are true but ‘R’ is not the correct explanation to ‘A’
(c) ‘A’ is true but ‘R’ is false
(d) ‘A’ is false but ‘R’ is true
Answer:
(а) Both ‘A’ and ‘R’ are true and ‘R’ is the correct explanation to ‘A’

Part – B
Answer The Following Questions In One or Two Sentences.

Question 1.
Write “Propensity to consume” Equations?
Answer:
(i) The Average Propensity to Consume = \(\frac{c}{y}\)
(ii) The Marginal Propensity to Consume = \(\frac{∆c}{∆y}\)
(iii) The Average Propensity to Save = \(\frac{x}{y}\)
(iv) The Marginal Propensity to Save = \(\frac{∆s}{∆y}\)

Question 2.
Define “Ceteris paribus”?
Answer:
Ceteris paribus (constant extraneous variables):
The other variables such as income distribution, tastes, habits, social customs, price movements, population growth, etc. do not change and consumption depends on income alone.

Question 2.
Define “Laissez-Faire” – Capitalist Economy?
Answer:
Existence of a Laissez – faire Capitalist Economy:
The law operates in a rich capitalist economy where there is no government intervention. People should be free to spend increased income. In the case of regulation of private enterprise and consumption expenditures by the State, the law breaks down.

Question 3.
What do you mean “Windfall Gains” or “Losses”?
Answer:
Windfall Gains or losses:
Unexpected changes in the stock market leading to gains or losses tend to shift the consumption function upward or downward.

Question 4.
Define “Autonomous consumption”?
Answer:
Autonomous Consumption:
Autonomous consumption is the minimum level of consumption or spending that must take place even if a consumer has no disposable income, such as spending for . basic necessities.

Part – C
Answer the Following Questions In One Paragraph.

Question 1.
Explain the Keynes Psychological Law’ of consumption assumptions?
Answer:
Keynes’s Law is based on the following assumptions:
1. Ceteris paribus (constant extraneous variables):
The other variables such as income distribution, tastes, habits, social customs, price movements, population growth, etc. do not change and consumption depends on income alone.

2. Existence of Normal Conditions:

1. The law holds good under normal conditions.
2. If, however, the economy is faced with abnormal and extraordinary circumstances like war, revolution or hyperinflation, the law will not operate.
3. People may spend the whole of increased income on consumption.

3. Existence of a Laissez – faire Capitalist Economy:

1. The law operates in a rich capitalist economy where there is no government intervention.
2. People should be free to spend increased income.
3. In the case of regulation of private enterprise and consumption expenditures by the State, the law breaks down.

Question 2.
Explain the Marginal Efficiency of capital?
Answer:
Marginal Efficiency of Capital:

1. MEC was first introduced by J.M Keynes in 1936 as an important determinant of autonomous investment.
2. The MEC is the expected profitability of an additional capital asset.
3. It may be defined as the highest rate of return over cost expected from the additional unit of capital asset.
4. Meaning of Marginal Efficiency of Capital (MEC) is the rate of discount which makes the discounted present value of expected income stream equal to the cost of capital.

MEC depends on two factors:

1. The prospective yield from a capital asset.
2. The supply price of a capital asset.

Factors Affecting MEC:

Question 3.
Explain the uses of multiplier?
Answer:
Uses of multiplier

1. Multiplier highlights the importance of investment in income and employment theory
2. The process throws light on the different stages of trade cycle.
3. It also helps in bringing the equality between S and I.
4. It helps in formulating Government policies.
5. It helps to reduce unemployment and achieve full employment.

Question 4.
Write the Accelerator Assumptions?
Answer:
Assumptions:

1. Absence of excess capacity in consumer goods industries.
2. Constant capital – output ratio
3. Increase in demand is assumed to be permanent
4. Supply of funds and other inputs is quite elastic
5. Capital goods are perfectly divisible in any required size.

Question 5.
Write the “Leverage Effect” and Equation Explanation?
Answer:
Leverage Effect:
The combined effect of the multiplier and the accelerator is also called the leverage effect which may lead the economy to very high or low level of income propagation.
Symbolically
Y = C + I_A + I_P
Y = Aggregate income
C = Consumption expenditure
T = autonomous investment; I_P = induced private investment

Part – D
Answer The Following Questions In One Page.

Question 1.
Briefly explain the Leakages of Multiplier?
Answer:
Leakages of multiplier:

1. The multiplier assumes that those who earn income are likely to spend a proportion of their additional income on consumption.
2. But in practice, people tend to spend their additional income on other items. Such expenses are known as leakages.

Payment towards past debts:
If a portion of the additional income is used for repayment of old loan, the MPC is reduced and as a result the value of multiplier is cut.

Purchase of existing wealth:

1. If income is used in purchase of existing wealth such as land, building and shares money is circulated among people and never enters into the consumption stream.
2. As a result the value of multiplier is affected.

Import of goods and services:

1. Income spent on imports of goods or services flows out of the country and has little chance to return to income stream in the country.
2. Thus imports reduce the value of multiplier.

Non availability of consumer goods:

1. The multiplier theory assumes instantaneous supply of consumer goods following demand.
2. But there is often a time lag.
3. During this gap (D > S) inflation is likely to rise.
4. This reduces the consumption expenditure and there by multiplier value.

Full employment situation:

1. Under conditions of full employment, resources are almost fully employed.
2. So, additional investment will lead to inflation only, rather than generation of additional real income.

Question 2.
Explain Marginal Propensity to Consume [MPC] and Multiplier with diagram and Diagrammatic explanation?
Answer:
Marginal propensity to consume and multiplier.
The propensity to consume refers to the portion of income spent on consumption.
The MPC refers to the relation between change in consumption (C) and change in income (Y).

Symbolically MPC = ∆C/∆Y
The value of multiplier depends on MPC
Multiplier (K) = 1/1 – MPC
The multiplier is the reciprocal of one minus marginal propensity to consume.
Since marginal propensity to save is 1 – MPC. (MPC + MPS = 1).
Multiplier is 1/ MPS.
The multiplier is therefore defined as reciprocal of MPS.
Multiplier is inversely related to MPS and directly with MPC.
Numerically if MPC is 0.75, MPS is 0.25 and k is 4.
Using formula k = 1/1 – MPC
1/1 – 0.75 = 1/0.25 = 4
Taking the following values, we can explain the functioning of multiplier.

C = 100 + 0.8 y; 1 = 100 1 = 10
Y = C + I
Y = 100 + 0.8y = 100 + (1000) = 900;
S = 100 = I
After I is raised by 10, now I = 110
Y = 100 + 0.8y + 110
0.2y = 210
Y = \(\frac{210}{0.2}\) = 1050
Here C = 100 = 0.8 (1050) = 940; S = 110 = 1
Diagrammatic Explanation.
At 45° line y = C + S
It implies the variables in axis and axis are equal.
The MPC is assumed to be at 0.8 (C = 100 + 0.8y)
The aggregate demand (C + I) curve intersects 45° line at point E.
The original national income is 500.
(C = 100 + 0.8y = 100 + 0.8 (500) = 500)
When I is 100, y = 1000, C = 900;
S = 100 = I
The new aggregate demand curve is C+F = 100 + 0.8y + 100 + 10
Y = \(\frac{210}{0.2}\) = 1050
C = 940; S = 110 = 1

Question 3.
Explain about Marginal Efficiency of Capital [MEC] short run factors and long run factors?
Answer:
(a) Short – Run Factors

1. Demand for the product:

1. If the market for a particular good is expected to grow and its costs are likely to fall, the rate of return from investment will be high.
2. If entrepreneurs expect a fall in demand for goods and a rise in cost, the investment will decline.

2. Liquid assets:

1. If the entrepreneurs are holding large volume of working capital, they can take advantage of the investment opportunities that come in their way.
2. The MEC will be high.

3. Sudden changes in income:

1. The MEC is also influenced by sudden changes in income of the entrepreneurs.
2. If the business community gets windfall profits, or tax concession the MEC will be high and hence investment in the country will go up.
3. On the other hand, MEC falls with the decrease in income.

4. Current rate of investment:

1. Another factor which influences MEC is the current rate of investment in a particular industry.
2. If in a particular industry, much investment has already taken place and the rate of investment currently going on in that industry is also very large, then the marginal efficiency of capital will be low.

5. Waves of optimism and pessimism:

1. The marginal efficiency of capital is also affected by waves of optimism and pessimism in the business cycle.
2. If businessmen are optimistic about future, the MEC will be likely to be high.
3. During periods of pessimism the MEC is under estimated and so will be low.

(b) Long – Run Factors
The long run factors which influence the marginal efficiency of capital are as follows:

1. Rate of growth of population:

1. Marginal efficiency of capital is also influenced by the rate of growth of population.
2. If population is growing at a rapid speed, it is usually believed that the demand of various types of goods will increase.
3. So a rapid rise in the growth of population will increase the marginal efficiency of capital and a slowing down in its rate of growth will discourage investment and thus reduce marginal efficiency of capital.

2. Technological progress:

1. If investment and technological development take place in the industry, the prospects of increase in the net yield brightens up.
2. For example, the development of automobiles in the 20th century has greatly stimulated the rubber industry, the steel and oil industry etc.
3. So we can say that inventions and technological improvements encourage investment in various projects and increase marginal efficiency of capital.

3. Monetary and Fiscal policies:
Cheap money policy and liberal tax policy pave the way for greater profit margin and so MEC is likely to be high.

4. Political environment:
Political stability, smooth administration, maintenance of law and order help to improve MEC.

5. Resource availability:
Cheap and abundant supply of natural resources, efficient labour and stock of capital enhance the MEC.

Share this Tamilnadu State Board 12th Economics Solutions Chapter 4 Consumption and Investment Functions Questions and Answers with your friends to help them to overcome the grammar issues in exams. Keep visiting this site frequently to get the latest information on different subjects. Clarify your doubts by posting the comments and get the answers in an easy manner.