Prasanna

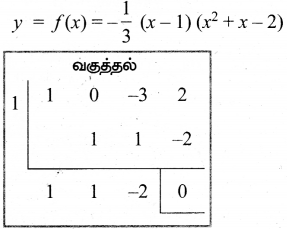
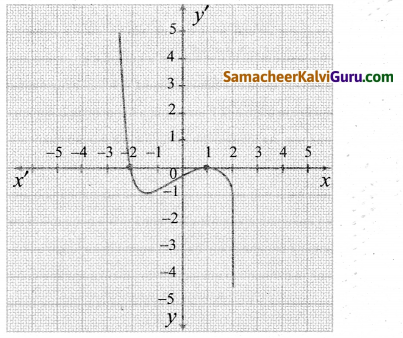
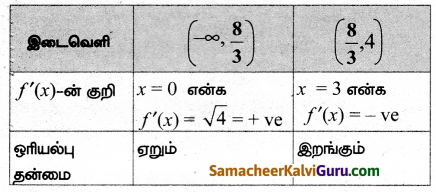
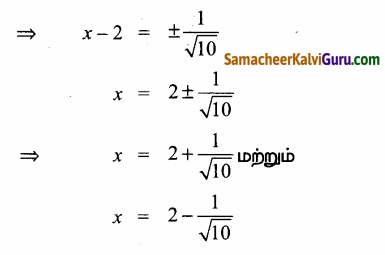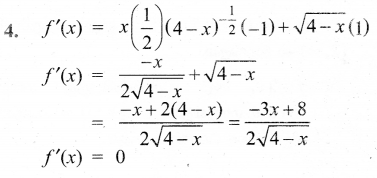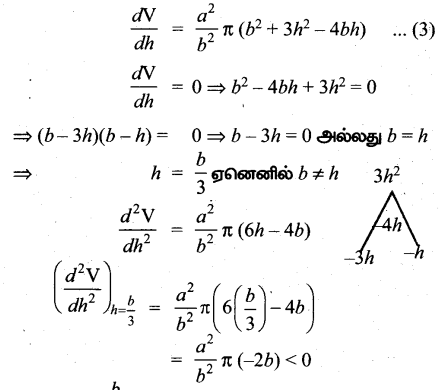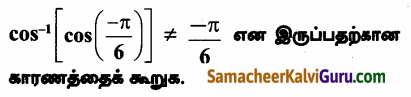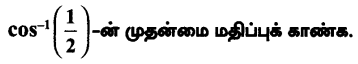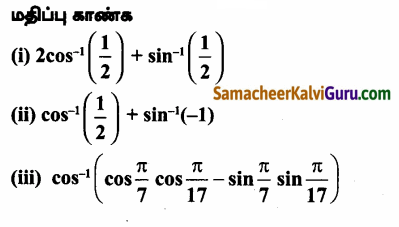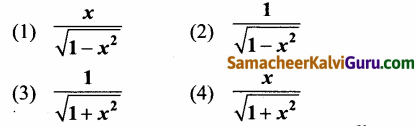Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 5 இரு பரிமாண பகுமுறை வடிவியல் – II Ex 5.2 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 5 இரு பரிமாண பகுமுறை வடிவியல் – II Ex 5.2

கேள்வி 1.
பின்வரும் ஒவ்வொன்றிற்கும் பரவளையத்தின் சமன்பாடு காண்க:
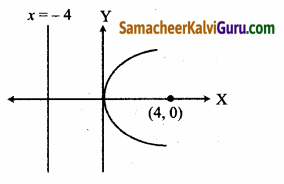
(i) குவியம் (4, 0) மற்றும் இயக்குவரை x = -4.
(ii) y-அச்சுக்கு சமச்சீரானது மற்றும் (2, -3) வழிச்செல்வது.
(iii) முனை (1,- 2) மற்றும் குவியம் (4, -2).
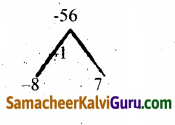
(iv) செவ்வகலத்தின் முனைகள் (4, -8) மற்றும் (4, 8).
தீர்வு:
(i) கொடுக்கப்பட்ட குவியம் (4, 0) மற்றும் இயக்குவரை x = 4. (4, 0) குவியம் மற்றும் இயக்குவரை x = 4, ஆதலால் பரவளயைத்தின் வடிவம் y² = 4ax.

மேலும் a = 4
∴ பரவளையத்தின் சமன்பாடு y² = 4(4)x
⇒ y² = 16x

(ii) பரவளையம் (2,-3) வழி செல்கிறது மற்றும் சமச்சீர் அச்சு y- அச்சு ஆகும்.

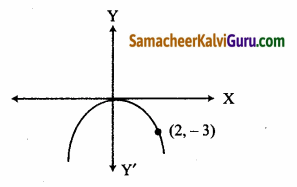
பரவளையம் (2, -3) வழிச் செல்வதன் காரணமாக அது கீழ்நோக்கி திறப்புடையது.
∴ அதனுடைய சமன்பாடு x² = -4ay ….(1)
(2, -3) என்ற புள்ளியை பிரதியிட கிடைப்பது,
2² = -4a(-3)
⇒ 4 = 12a

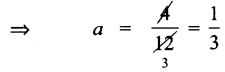
(1) லிருந்து
∴ x² = -4\(\left(\frac{1}{3}\right)\)
⇒ 3x² = -4y

(iii) முனை (1, -2) மற்றும் குவியம் (4, -2).
பரவளையம் வலது புறம் திறப்புடையது.

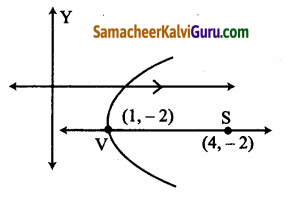
a = (1, -2) மற்றும் (4, -2) க்கு இடைபட்ட தூரம்
a = \(\sqrt{(1-4)^{2}+(-2+2)^{2}}\)
a = \(\sqrt{(-3)^{2}}\) = 3
பரவளையத்தின் சமன்பாடு
(y – k)² = 4a (x – h)
(y + 2)² = 4(3) (x – 1)
[∵ (h, k) (1, -2)]
⇒ (y + 2)² = 12 (x – 1)

(iv) செவ்வகலத்தின் முனை புள்ளிகள் (4,-8) மற்றும் (4, 8).
குவியம் (4, -8) மற்றும் (4, 8)ன் மையப்புள்ளி

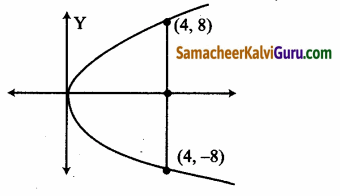
∴ குவியம் = \(\left(\frac{4+4}{2}, \frac{-8+8}{2}\right)\) = (4, 0)
∴ a = 4 மற்றும் உச்சிப்புள்ளி (0, 0)
பரவளையத்தின் சமன்பாடு y² = 4ax
⇒ y² = 4(4)x
⇒ y² = 16x

கேள்வி 2.
பின்வரும் ஒவ்வொன்றிற்குமான நீள்வட்டத்தின் சமன்பாடு காண்க :
(i) குவியங்கள் (±3, 0), மற்றும் e = \(\frac{1}{2}\),
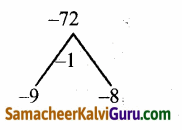
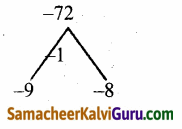
(ii) குவியங்கள் (0, ±4) மற்றும் நெட்டச்சின் முனைகள் (0, ±5).
(iii) செவ்வகல நீளம் 8, e = \(\frac{3}{5}\) மற்றும் நெட்டச்சு x-அச்சு.
(iv) செவ்வகல நீளம் 4, குவியங்களுக் கிடையேயான தூரம் 4\(\sqrt{2}\) மற்றும் நெட்டச்சு )- அச்சு.
தீர்வு:
(i) குவியங்கள் (±3, 0), e = \(\frac{1}{2}\)
ஆதலால் (±ae, 0) குவியங்கள்
⇒ ae = 3
⇒ a . \(\frac{1}{2}\) = 3 ⇒ a = 6
மையம் (0, 0)
மற்றும் b² = a²(1 – e²)
b² = 36\(\left(1-\frac{1}{4}\right)\)
⇒ b² = 36\(\left(\frac{3}{4}\right)\)
⇒ b² = 27
∴ நீள்வட்டத்தின் சமன்பாடு \(\frac{x^{2}}{a^{2}}\) + \(\frac{y^{2}}{b^{2}}\) = 1
⇒ \(\frac{x^{2}}{36}\) + \(\frac{y^{2}}{27}\) = 1

(ii) குவியங்கள் (0, ±4) மற்றும் நெட்டச்சின்
முனைப்புள்ளிகள் (0, ±5)
குவியங்க ள் (0, ±be) ⇒ be = 4
நெட்டச்சின் முனை புள்ளிகள் (0, ±5)
⇒ b = 5
∴ 5(e) = 4
⇒ e = \(\frac{4}{5}\)
மேலும், a² = b² (1 – e²)
⇒ a² = 25\(\left(1-\frac{16}{25}\right)\) = \(\left(\frac{25-16}{25}\right)\)
⇒ a² = 9
நீள்வட்டத்தின் சமன்பாடு \(\frac{x^{2}}{a^{2}}\) + \(\frac{y^{2}}{b^{2}}\) = 1
⇒ \(\frac{x^{2}}{9}\) + \(\frac{y^{2}}{25}\) = 1

(iii) நீள் வட்டத்தின் சமன்பாடு = 8, e = \(\frac{3}{5}\) மற்றும் நெட்டச்சு x-அச்சு
கொடுக்கப்பட்ட \(\frac{2 b^{2}}{a}\) = 8, e = \(\frac{3}{5}\)
b² = 4a
b² = a²(1 – e²)
4a = a²\(\left(1-\frac{9}{25}\right)\)
4 = a\(\left(\frac{25-9}{25}\right)\)
100 = a(16)
a = \(\frac{100}{16}\) = \(\frac{25}{4}\) ⇒ a² = \(\frac{625}{16}\)
b² = 4 × \(\frac{25}{4}\) = 25
நெட்டச்சு X-அச்சு ஆதலால் நீள்வட்டத்தின் சமன்பாடு

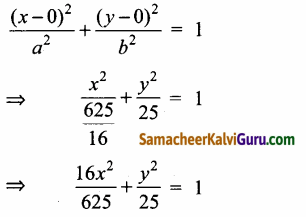
(iv) செவ்வகத்தின் நீளம் = 4, குவியங்களுக்கு இடைப்பட்ட தூரம் = 4\(4 \sqrt{2}\) நெட்டச்ச y- அச்சு.
கொடுக்கப்பட்ட \(\frac{2 b^{2}}{a}\) = 4 மற்றும் குவியங்களுக்கு இடைப்பட்ட தூரம்
= 2ae = 4\(\sqrt{2}\)
⇒ ae = 2\(\sqrt{2}\)
⇒ a²e² = 8 … (1)
\(\frac{2 b^{2}}{a}\) = 4 ⇒ b² = 2a ….(2)
b² = a²(1 – e²)
என அறிவோம்.
⇒ b² = a² – a²e²
⇒ 2a = a² – 8
[(1) மற்றும் (2)ஐ பயன்படுத்தி)
⇒ a² – 2a – 8 = 0
காரணிபடுத்த கிடைப்பது
(a – 4)(a + 2) = 0
⇒ a = 4 அல்ல து -2
a = 4
[∵ a = -2 சாத்தியமில்லை]
⇒ ae = 16
∴ (2)லிருந்து, b² = 2(4) = 8
ஆகையால் நீள்வட்டத்தின் சமன்பாடு
\(\frac{x^{2}}{8}\) + \(\frac{y^{2}}{16}\) = 1
[∵ நெட்டச்சு y -அச்சு]

கேள்வி 3.
பின்வரும் ஒவ்வொன்றிற்குமான அதிபர வளையத்தின் சமன்பாடு காண்க:
(i) குவியங்கள் (±2, 0), e = \(\frac{3}{2}\)
(ii) மையம் (2, 1), ஒரு குவியம் (8, 1) மற்றும் இதற்கொத்த இயக்குவரை x = 4.
(iii) (5, -2) வழிச்செல்வது மற்றும் குற்றச்சின் நீளம் 8 அலகுகள், நெட்டச்சு x அச்சு:
தீர்வு:
(i) கொடுக்கப்பட்ட குவியங்கள் (±2, 0)
⇒ ae = 2 மற்றும் மையம் (0, 0)

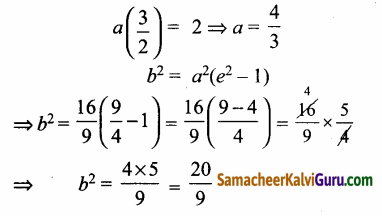
∴ அதிபரவளையத்தின் சமன்பாடு \(\frac{x^{2}}{a^{2}}\) – \(\frac{y^{2}}{b^{2}}\) = 1

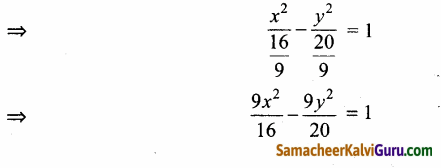
(ii) ae = மையம் மற்றும் குவியத்திற்கு
இடைப்பட்ட தூரம்
ae = \(\sqrt{(8-2)^{2}-(1-1)^{2}}\) = \(\sqrt{6^{2}}\) = 6 … (1)
மேலும் \(\frac{a}{e}\) = மையம் மற்றும் இயக்கு வரைக்கு இடைப்பட்ட தூரம்
\(\frac{a}{e}\) = \(\sqrt{(4-2)^{2}+(1-1)^{2}}\) = \(\sqrt{2^{2}}\) = 2
[∵ (4, 1) இயக்குவரை மீது அமைந்துள்ள புள்ளி]

⇒ a² = 12
(1) → a²e² = 36
12(e²) = 36
⇒ e² = 3
⇒ e = \(\sqrt{3}\)
மேலும், b² = a² (e² – 1) = 12(3 – 1) = 12(2) = 24
∴அதிபரவளையத்தின் சமன்பாடு

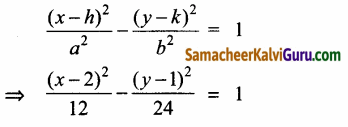
(iii) (5, -2)வழிச் செல்வது மற்றும் குற்றச்சின் நீளம் 8 அலகுகள் நெட்டச்சு x-அச்சு.
2a = 8 ⇒ a = 4
நெட்டச்சு x-அச்சு ஆதலால் மையம் (0, 0)
அதிபரவளையத்தின் சமன்பாடு
\(\frac{x^{2}}{16}\) – \(\frac{y^{2}}{b^{2}}\) = 1
(5,-2) பரவளையத்தின் வழிச் செல்கிறது, ஆதலால்,

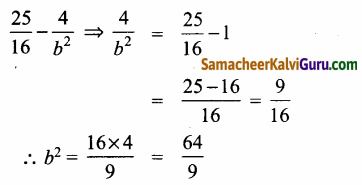
∴ அதிபரவளையத்தின் சமன்பாடு

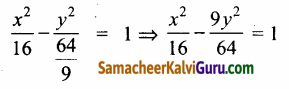
கேள்வி 4.
பின்வருவனவற்றிற்கான முனை, குவியம், இயக்குவரையின் சமன்பாடு மற்றும் செவ்வகல நீளம் காண்க:
(i) y² = 16x
(ii) x² = 24y
(iii) y² = -8x
(iv) x² + 8y + 17 = 0
(v) y² – 4y – 8x + 12 = 0
தீர்வு:
(i) y² = 16x
கொடுக்கப்பட்ட பரவளையம் வலது பக்க திறப்புடையது மற்றும்
4a = 16 ⇒ a = 4.
(a) முனை (0, 0)
⇒ h = 0, k = 0
(b) குவியம் (h + a, 0 + k)
⇒ (0 + 4, 0 + 0) = (4, 0)
(c) இயக்குவரையின் சமன்பாடு.x = h – a
⇒ x = 0 – 4 ⇒ x = -4
(d) செவ்வகலத்தின் நீளம் 4a = 16.

(ii) x = 24y
கொடுக்கப்பட்ட பரவளையம் மேல்புறம் திறப்புடையது மற்றும் 4a = 24 ⇒ a = 6.
(a) முனை (0, 0)
⇒ h = 0, k = 0
(b) குவியம் (0 + h, a + k)
⇒ (0 + 0, 6 + 0) = (0, 6)
(c) இயக்குவரையின் சமன்பாடு y = k – a
⇒ y = 0 – 6 ⇒ y = -6
(d) இயக்குவரையின் நீளம் 4a = 24.

(iii) y² = -8x
கொடுக்கப்பட்ட பரவளையம் இடது புறம் திறப்புடையது மற்றும் 4a = 8 ⇒ a = 2.
(a) முனை (0, 0)
⇒ h = 0, k = 0
(b) குவியம் (h – a, 0 + k)
⇒ (0 – 2, 0 +0) ⇒ (-2, 0)
(c) இயக்குவரையின் சமன்பாடு x = h + a
⇒ x = 0 + 2 ⇒ x = 2
(d) செவ்வகத்தின் நீளம் 4a = 8.

(iv) x² – 2x + 8y + 17 = 0
x² – 2x = -8y – 17
இருபுறமும் 1 ஐ கூட்ட கிடைப்பது
x² – 2x + 1 = -8y – 17 + 1
⇒ (x – 1)² = -8y – 16 = -8(y + 2)
⇒ (x – 1)² = -8(y + 2)
இது கீழ்நோக்கி திறப்புடைய பரவளையம், செவ்வ கலம் 4a = 8 ⇒ a = 2.
(a) முனை (1,-2)
⇒ h = 1, k = -2
(b) குவியம் (0 + h, -a + k)
⇒ (0 + 1, -2 – 2)
⇒ (1, -4)
(c) இயக்குவரையின் சமன்பாடு y = k + a
⇒ y = -2 + 2 ⇒ y = 0
(d) செவ்வகலத்தின் நீளம் 4a = 8 அலகுகள்.

(v) y² – 4y – 8x + 12 = 0
y² -4y = 8x – 12
இருபுறமும் 4 ஐ கூட்ட கிடைப்பது
y² – 4y + 4 = 8x – 12 + 4 = 8x – 8
⇒ (y – 2) = 8(x – 1)
இது வலதுபுற திறப்புடைய பரவளையம் மற்றும் செவ்வகலம் 4a = 8 ⇒ a = 2.
(a) முனை (1, 2) ⇒ h = 1, k = 2
(b) குவியம் (h + a, 0 + k)
= (1 + 2, 0 + 2)
= (3, 2)
(c) இயக்குவரையின் சமன்பாடு x = h – a
⇒ x = 1 – 2
⇒ x = -1
(d) செவ்வகலத்தின் நீளம் 4a = 8 அலகுகள்.

கேள்வி 5.
பின்வரும் சமன்பாடுகளின் கூம்பு வளைவின் வகையைக் கண்டறிந்து அவற்றின் மையம், குவியங்கள், முனைகள் மற்றும் இயக்குவரைகள் காண்க:

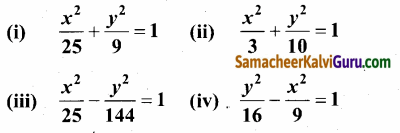
தீர்வு:
(i) \(\frac{x^{2}}{25}\) + \(\frac{y^{2}}{9}\) = 1
இது நீள்வட்டத்தின் சமன்பாடு
a² = 25 மற்றும் b² = 9 மற்றும் c² = a² + b²
⇒ c² = 25 + 9 = 16 ⇒ c = 4
(a) மையம் (0, 0) ⇒ h = 0, k = 0
(b) குவியங்க ள் (h – c, k), (h + c, k)
⇒ (0 – 4, 0), (0 + 4, 0)
⇒ (-4, 0) மற்றும் (4, 0)
(c) முனைகள் (h – a, k) மற்றும் (h + a, k)
⇒ (0 – 5, 0) மற்றும் (0 + 5, 0)
⇒ (-5, 0) மற்றும் (5, 0)
(d) இயக்குவரைகள் x = ±\(\frac{a}{e}\)

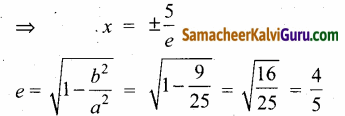
∴கொடுக்கப்பட்ட சமன்பாடு 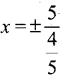⇒ x = ±\(\frac{25}{4}\)

(ii) \(\frac{x^{2}}{3}\) + \(\frac{y^{2}}{10}\) = 1
கொடுக்கப்பட்ட சமன்பாடு \(\frac{x^{2}}{3}\) + \(\frac{y^{2}}{10}\) = 1

(c) குவியங்கள் (h, k – c)(h, k + c)

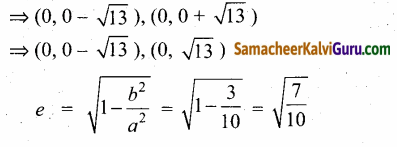
இயக்குவரைகள் y = ± \(\frac{a}{e}\)

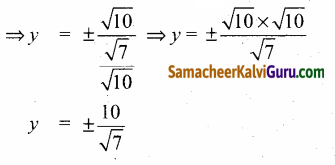
(iii)
\(\frac{x^{2}}{25}\) + \(\frac{y^{2}}{144}\) = 1
கொடுக்கப்பட்ட சமன்பாடு : \(\frac{x^{2}}{25}\) + \(\frac{y^{2}}{144}\) = 1
இது அதிபரவளையத்தின் சமன்பாடாகும்.
∴ a² = 25 மற்றும் b² = 144
⇒ c² = a² + b² ⇒ 25 + 144 = 169 ⇒ c = 13

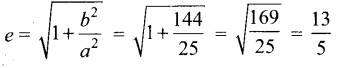
(a) மையம் (0, 0) ⇒ h = 0, k = 0
(b) குவியங்க ள் (h + c, k), (h – c, k)
⇒ (0 + 13, 0), (0 – 13, 0)
⇒ (13, 0), (-13, 0)
(c) முனைகள் (h + a, k) மற்றும் (h- a, k)
⇒ (0 + 5, 0), (0 – 5, 0) ⇒ (5, 0), (-5, 0)
(d) இயக்குவரையின் சமன்பாடுகள்

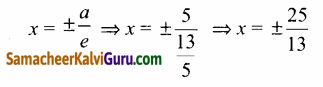
(iv) \(\frac{y^{2}}{16}\) + \(\frac{x^{2}}{9}\) = 1
கொடுக்கப்பட்ட சமன்பாடு \(\frac{y^{2}}{16}\) + \(\frac{x^{2}}{9}\) = 1
இது துணையச்சு y-அச்சுக்கு அதிபர வளையத்தின் சமன்பாடாகும்.
∴ a² = 16, b² = 9, c² = a² + b²
⇒ c² = 16 + 9 = 25 ⇒ c = 5

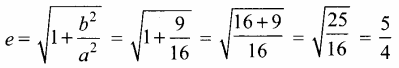
(a) மையம் (0, 0)
⇒ h = 0, k = 0
(b) முனைகள் (h, k + a), (h, k – a)
⇒ (0, 0 + 4), (0, 0 – 4) ⇒ (0, 4) (0, -4)
(c) குவியங்க ள் (h, k + c), (h, k – c)
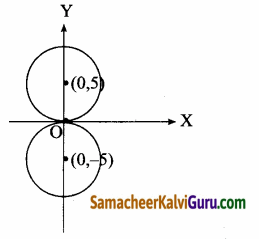
⇒ (0, 0 + 5), (0, 0 – 5) ⇒ (0, 5) (0,-5)
(d) இயக்குவரையின் சமன்பாடுகள் y = +\(\frac{a}{e}\)

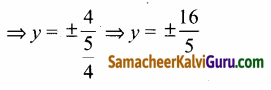
கேள்வி 6.
\(\frac{x^{2}}{a^{2}}\) – \(\frac{y^{2}}{b^{2}}\) = 1 என்ற அதிபரவளையத்தின் செவ்வகல நீளம் \(\frac{2 b^{2}}{a}\) என நிறுவுக.
தீர்வு:
அதிபரவளையத்தின் செவ்வகலம் LL’ S(ae, 0) வழிச் செல்கிறது.

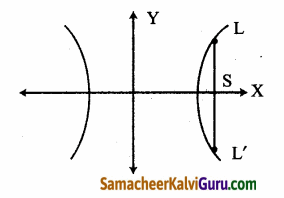
∴ L = (ae, y₁)
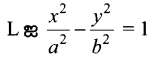ல் பிரதியிட கிடைப்பது,

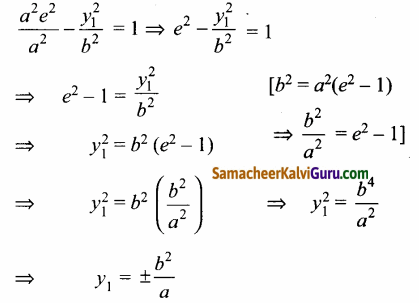
கேள்வி 7.
அதிபரவளையத்தின் மீதுள்ளள்ள புள்ளி P-இலிருந்து அதன் குவியத்தூரங்களின் வித்தியாசத்தின் மட்டு மதிப்பு குறுக்கச்சின்
நீளத்திற்குச் சமம் என நிறுவுக.
தீர்வு:
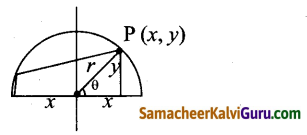
P(x, y) அதிபரவளையத்தின் மீதுள்ள ஏதேனும் ஒரு புள்ளி என்க.
\(\frac{x^{2}}{a^{2}}\) + \(\frac{y^{2}}{b^{2}}\) = 1

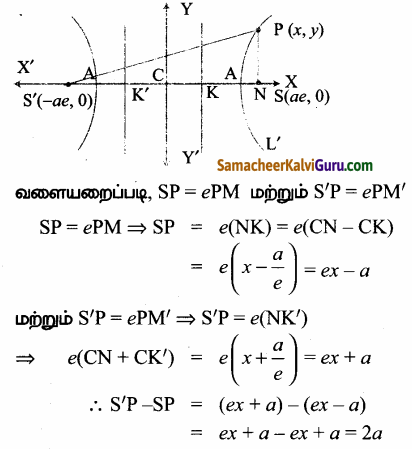
= துணையச்சின் நீளம்.
ஆகையால், அதிபரவளையத்தின் மீதுள்ள புள்ளி P-இலிருந்து அதன் குவியத்தூரங்களின் வித்தியாசத்தின் மட்டு மதிப்பு குறுக்கச்சின் நீளத்திற்குச் சமம்.

கேள்வி 8.
பின்வரும் சமன்பாடுகளின் கூம்பு வளைவின் வகையைக் கண்டறிந்து அவற்றின் மையம், குவியங்கள், முனைகள் மற்றும் இயக்குவரைகளைக் காண்க:

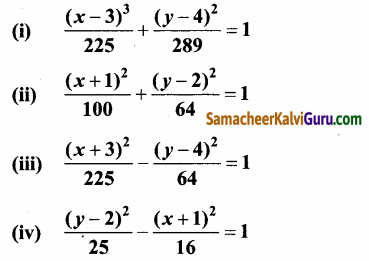
(v) 18x² + 12y² – 144x + 48y + 120 = 0
(vi) 9x² – y² – 36x – 6y + 18 = 0
தீர்வு:
(i) \(\frac{(x-3)^{2}}{225}\) + \(\frac{(y-4)^{2}}{289}\) = 1
கொடுக்கப்பட்ட சமன்பாடு \(\frac{(x-3)^{2}}{225}\) + \(\frac{(y-4)^{2}}{289}\) = 1
இது நீள்வட்டத்தின் சமன்பாடு a² = 289, b² = 225 மற்றும் c² = a² + b² ⇒ 289 – 225 = 64
⇒ c = 8.

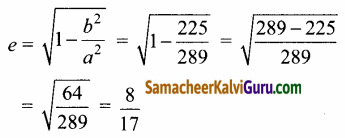
(a) மையம் (3, 4) ⇒ h = 3, k = 4
(b) குவியங்க ள் (h, k + c), (h, k – c)
⇒ (3, 4 + 8), (3, 4 – 8) ⇒ (3, 12), (3, -4)
(c) முனைகள் (h, k – a), (h, k + a)
⇒ (3, 4 – 17), (3, 4 + 17) ⇒ (3, -13), (3, 21)
(d) இயக்குவரைகளின் சமன்பாடுகள்

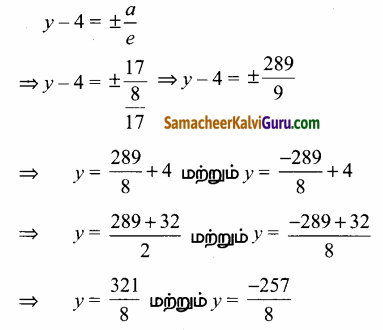
(ii) \(\frac{(x+1)^{2}}{100}\) + \(\frac{(y-2)^{2}}{64}\) = 1
கொடுக்கப்பட்ட சமன்பாடு \(\frac{(x+1)^{2}}{100}\) + \(\frac{(y-2)^{2}}{64}\) = 1
இது நீள்வட்டத்தின் சமன்பாடு
∴a² = 100, b² = 64
c² = a² – b²
⇒ c² = 100 – 64 = 36
∴ c = 6

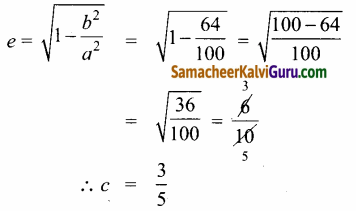
(a) மையம் (-1, 2) ⇒ h = -1, k = 2
(b) குவியங்க ள் (h – c, k), (h + c, k)
⇒ (-1 – 6, 2), (-1 + 6, -2) ⇒ (-7, 2), (5, 2)
(c) முனைகள் (h – a, k) மற்றும் (h + a, k)
⇒ (-1 – 10, 2), (-1 + 10, 2) ⇒ (-11, 2), (9, 2)
(d) இயக்குவரைகளின் சமன்பாடுகள்

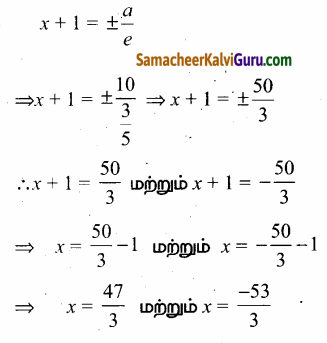
(iii) \(\frac{(x+3)^{2}}{225}\) – \(\frac{(y-4)^{2}}{64}\) = 1
கொடுக்கப்பட்ட சமன்பாடு \(\frac{(x+3)^{2}}{225}\) – \(\frac{(y-4)^{2}}{64}\) = 1
இது அதிபரவளையத்தின் சமன்பாடு
∴a² = 225, b² = 64
⇒ c² = a² + b² = 225 + 64 = 289
⇒ c = 17

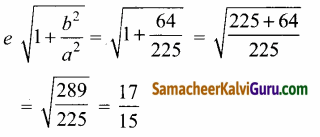
(a) மையம் (-3, 4)
⇒ h = -3, k = 4
(b) குவியங்கள் (h + c, k), (h – c, k)
⇒ (-3 + 17, 4), (-3 – 17, 4)
⇒ (14, 4) (-20, 4)
(c) முனைகள் (h + a, k) மற்றும் (h – a, k)
= (-3 + 15, 4), (-3 – 15, 4)
⇒ (12, 4) (-18, 4)
(d) இயக்குவரைகளின் சமன்பாடுகள்

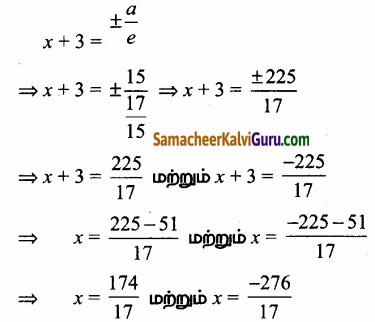
(iv) \(\frac{(y-2)^{2}}{25}\) – \(\frac{(x+1)^{2}}{16}\) = 1
கொடுக்கப்பட்ட சமன்பாடு \(\frac{(y-2)^{2}}{25}\) – \(\frac{(x+1)^{2}}{16}\) = 1
துணையச்சு y-அச்சுக்கு இணையான அதிபரவளையத்தின் சமன்பாடு.
∴a² = 25, b² = 16
⇒ c² = a² + b² = 25 + 16 = 41
⇒ c = \(\sqrt{41}\)

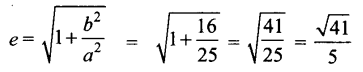
(a) மையம் (-1, 2) ⇒ h = -1, k = 2
(b) குவியங்க ள் (h, k + c), (h, k – c)
= (-1, 2 + \(\sqrt{41}\)), (-1, 2 – \(\sqrt{41}\))
(c) முனைகள் (h, k + a), (h, k – a)
= (-1, 2 + 5), (-1, 2 – 5)
= (-1, 7), (-1, -3)
(d) இயக்குவரைகளின் சமன்பாடுகள்
y – 2 = ±\(\frac{5}{\frac{\sqrt{41}}{5}}\)
⇒ y – 2 = ±\(\frac{25}{\sqrt{41}}\)
⇒ y = 2 + \(\frac{25}{\sqrt{41}}\) மற்றும்
y = 2 – \(\frac{25}{\sqrt{41}}\)

(v) 18x² + 12y² – 144x + 48y + 120 = 0
கொடுக்கப்பட்ட சமன்பாடு
18x² + 12y² – 144x + 48y + 120 = 0
18x² – 144x + 12y² + 48y = -120
⇒ 18(x² – 8x) + 12(y⇒ + 4y) = -120
⇒ 18(x² – 8x + 16 – 16) + 12(y² + 4y + 4 – 4) = -120
18(x – 4)² – 288 + 12 (y + 2)² – 48 = -120
⇒ 18(x – 4)² + 12(y + 2)² = -120 + 288 + 48
⇒ 18(x – 4)² + 12(y + 2)² = 216
216ல் வகுக்க கிடைப்பது,

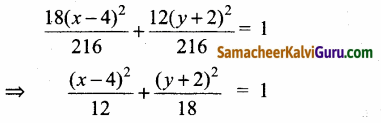
நெட்டச்சு y- அச்சுக்கு இணையான நீள்வட்டத்தின் சமன்பாடு.

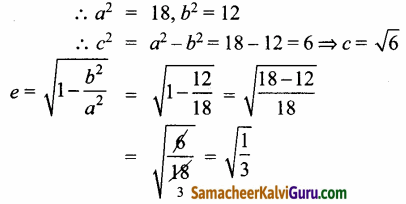
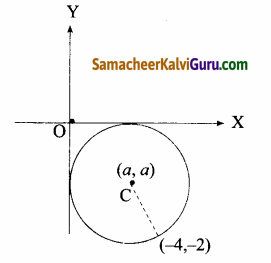
(a) மையம் (4,-2)
⇒ h = 4, k = -2
(b) முனைகள் (h, k – a), (h, k + a)
⇒ (4, -2 – 3\(\sqrt{2}\)), (4, -2 + 3\(\sqrt{2}\))
[∵ a² = 18 ⇒ a = \(\sqrt{18}\) = 3\(\sqrt{2}\))
(c) குவியங்கள் (h, k – c), (h, k + c)
⇒ (4, -2\(\sqrt{6}\)), (4, -2 + \(\sqrt{6}\))
(d) இயக்குவரைகளின் சமன்பாடுகள்

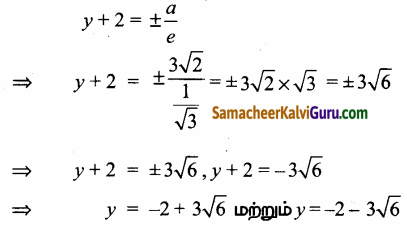
(vi) 9x² – y² – 36x – 6y + 18 = 0 கொடுக்கப்பட்ட சமன்பாடு
9x-y-36x -6y +18=0
9x² – y² – 36x – 6y + 18 = 0
⇒ 9x² – 36x – (y² + 6y) = -18
⇒ 9(x² – 4x) – (y² + 6y) = -18
⇒ 9(x² – 4x + 4 – 4) – (y² + 6y + 9 – 9)= -18
⇒ 9(x – 2)² – 36 – (y + 3)² + 9 = -18
⇒ 9(x – 2)² – (y + 3)² = -18 + 36 – 9
⇒ 9(x – 2)² – (y + 3)² = 9
9 ஆல் வகுக்க கிடைப்பது, \(\frac{(x-2)^{2}}{1}\) – \(\frac{(y+3)^{2}}{9}\) = 1
துணை அச்சு x- அச்சுக்கு இணையான அதிபர வளையத்தின் சமன்பாடு.

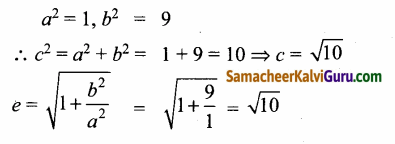
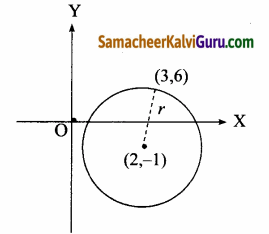
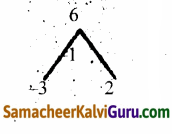
(a) மையம் (2,-3)
⇒ h = 2, k = -3
(b) குவியங்க ள் (h + c, k), (h – c, k)
= (2 + \(\sqrt{10}\),-3), (2 – \(\sqrt{10}\), -3)
(c) முனைகள் (h + a, k) (h – a, k)
= (2 + 1, -3), (2 – 1, -3)
= (3, -3) (1, -3)
(d) இயக்குவரையின் சமன்பாடுகள் x – 2 = ± \(\frac{a}{e}\)

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 5 இரு பரிமாண பகுமுறை வடிவியல் – II Ex 5.1 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 5 இரு பரிமாண பகுமுறை வடிவியல் – II Ex 5.1

கேள்வி 1.
ஆரம் 5 செ.மீ. அலகுகள் உடையதும், x-அச்சை ஆதிப்புள்ளியில் தொட்டுச் செல்வதுமான வட்டத்தின் சமன்பாட்டைத் தருவிக்க.
தீர்வு:
கொடுக்கப்பட்ட r = 5 செ.மீ

வட்டம் x அச்சை தொட்டுச் செல்வதால் அதனுடைய மையம் (0, ±5)
வட்டத்தின் சமன்பாடு (x – h)² + (y – k)² = r²
⇒ (x – 0)² + (y ± 5)² = 5²

⇒ x² + y² + 10y = 0

கேள்வி 2.
(2, -1) என்ற புள்ளியை மையமாகவும், (3, 6) என்ற புள்ளி வழிச் செல்வதுமான வட்டத்தின் சமன்பாடு காண்க.
தீர்வு:

கொடுக்கப்பட்ட (2, -1) மையம் மற்றும் (3, 6) புள்ளி வழிச் செல்கிறது.
∴ r = இடைப்பட்ட தூரம் (2, -1) மற்றும் (3, 6)க்கு
= \(\sqrt{(2-3)^{2}+(-1-6)^{2}}\)
= \(\sqrt{(-1)^{2}+(-7)^{2}}\)
= \(\sqrt{1+49}\) = \(\sqrt{50}\)
∴ வட்டத்தின் சமன்பாடு
(x – h)² + (y – k)² = r²
(x – 2)² + (y + 1)² = \((\sqrt{50})\)²
⇒ (x – 2)² + (y + 1)² = 50

கேள்வி 3.
இரு அச்சுக்களையும் தொட்டுச் செல்வதும், (4, -2) என்ற புள்ளி வழிச் செல்வதுமான வட்டத்தின் சமன்பாடு காண்க.
தீர்வு:
வட்டமானது இரு அச்சுகளையும் தொட்டு செல்வதால் அதனுடைய சமன்பாடு
(x – a)² + (y – a)² = a² … (1)
இது (-4, -2) வழிச் செல்கிறது
∴ (-4 – a)² + (-2 – a)² = a²

⇒ a² + 12a + 20 = 0
⇒ (a + 10)(a + 2) = 0
a = -10 அல்ல து – 2

நிலை (i)
a = -10 எனில், (1) ஆனது
(x + 10)² + (y + 10)² = 10²

⇒ x² + y² + 20x + 20y + 100 = 0
நிலை (ii)
a = -2 எனில், (1) ஆனது
(x + 2)² + (y + 2)² = 2²

⇒ x² + y² + 4x + 4y + 4 = 0
ஆகையால் வட்டங்களின் சமன்பாடுகள்
x² + 4² + 4x + 4y + 4 = 0
அல்லது x² + y² + 20x + 20y + 100 = 0

கேள்வி 4.
மையம் (2, 3) உடையதும் 3x – 2y – 1 = 0 மற்றும் 4x + y – 27 = 0 என்ற கோடுகள் வெட்டும் புள்ளி வழிச் செல்வதுமான வட்டத்தின் சமன்பாடு காண்க.
தீர்வு:
கொடுக்கப்பட்ட மையம் (2, 3)
தீர்க்க 3x – 2y = 1 ….. (1)
மற்றும் 4x + y = 27 ….. (2)

வட்டமானது (5, 7) வழிச் செல்கிறது.
[∵ (5, 7) மற்றும் (2, 3) க்கு இடைப்பட்ட தூரம்]
r = \(\sqrt{(5-2)^{2}+(7-3)^{2}}\)
= \(\sqrt{3^{2}+4^{2}}\)
= \(\sqrt{9+16}\) = \(\sqrt{25}\) = 5
வட்டத்தின் சமன்பாடு
(x – h)² + (y – k)² = r²
⇒ (x – 2)² + (y – 3)² = 5²
⇒ x² – 4x + 4 + y² – 6y + 9 = 25
⇒ x² + y² – 4x – 6y + 13 – 25 = 0
⇒ x² + y² – 4x – 6y – 12 = 0

கேள்வி 5.
(3, 4) மற்றும் (2, -7) என்ற புள்ளிகளை விட்டத்தின் முனைப்புள்ளிகளாகக் கொண்ட வட்டத்தின் சமன்பாட்டைப் பெறுக.
தீர்வு:
கொடுக்கப்பட்ட விட்டத்தின் முனைகள் (3,4)2,-7)
∴ வட்டத்தின் சமன்பாடு
(x – x₁) (x – x₂) = (y – y₁) (y – y₂) = 0
⇒ (x – 3)(x – 2) + (y – 4)(y + 7) = 0
⇒ x² – 2x – 3x + 6 + y² + 7y – 4y – 28 = 0
⇒ x² + y² – 5x + 3y – 22 = 0

கேள்வி 6.
(1, 0), (-1, 0) மற்றும் (0, 1) என்ற புள்ளிகள் வழிச்செல்லும் வட்டத்தின் சமன்பாடு காண்க.
தீர்வு:
வட்டத்தின் சமன்பாடானது
x² + y² + 2gx + 2fy + c = 0 ….. (1)
(1, 0) வழி (1) செல்கிறது
⇒ 1 + 0 + 2g(1) + 2f(0) + c = 0
⇒ 2g + c = -1 … (2)
(-1, 0) வழி (1) செல்கிறது
⇒ (-1)² + 0 + 2g(-1) + 2f(0) + c = 0
⇒ -2g + c = -1 …(3)
மேலும் (0, 1) வழி (1) செல்கிறது
⇒ 0 + 1² + 2g(0) + 2f (1) + c = 0
⇒ 2f + c = -1 …(4)
(2) + (3) ⇒ 2c = -2
⇒ c = -1
c = -1 என (2) ல் பிரதியிட கிடைப்பது
2g – 1 = -1
⇒ 2g = 0
⇒ g = 0
c = -1 என (4) ல் பிரதியிட கிடைப்பது
2f – 1 = -1
⇒ 2f = 0
⇒ f = 0
∴ (1) லிருந்து
x² + y² + 0 + 0 – 1 = 0
⇒ x² + y² = 1

கேள்வி 7.
9π சதுர அலகுகள் பரப்பு கொண்ட வட்டத்தின் விட்டங்கள், x + y = 5 மற்றும் x – y = 1 என்ற நேர்கோடுகள் மீது அமைந்துள்ளன எனில் அந்த வட்டத்தின் சமன்பாடு காண்க.
தீர்வு:
வட்டத்தின் பரப்பு = 9π சதுர அலகுகள்
πr² = 9π ⇒ r² = 9 ⇒ r = 3
விட்டங்கள் x + y = 5 (1) மற்றும் x – y = 1 (2)
விட்டங்கள் வெட்டிக் கொள்ளும் புள்ளி மையம் என அறிவோம்.
∴ மையத்தை காண (1) மற்றும் (2) ஐ தீர்க்க.

⇒ x = 3
∴ (1) ⇒ 3 + y = 5
⇒ y = 5 – 3 = 2
∴ மையம் (3, 2)
ஆகையால் வட்டத்தின் சமன்பாடு
(x – h)² + (y – k)² = r²
(x – 3)² + (y – 2)² = 3²

⇒ x² + y² – 6x – 4y + 4 = 0

கேள்வி 8.
y = 2\(\sqrt{2}\)x+ c என்ற கோடு x² + y² = 16, என்ற வட்டத்தின் தொடுகோடு எனில், -ன் மதிப்பு காண்க.
தீர்வு:
கொடுக்கப்பட்ட வட்டத்தின் சமன்பாடு
x² + y² = 16
⇒ a² = 16
மற்றும் தொடுகோட்டின் சமன்பாடு
y = 2\(\sqrt{2}\)x + c
⇒ m = 2\(\sqrt{2}\) மற்றும் c = c
[தொடுகோடானது y = mx + c]
y = mx + c என்ற கோடு x² + y² = a² என்ற வட்டத்திற்கு தொடுகோடாக இருப்பதற்கான நிபந்தனை
c² = a² (1 + m²)
⇒ c² = 16(1 + (2\(\sqrt{2}\))²)
⇒ c² = 16(1 + 8)
⇒ c² = 16(9)
⇒ c = +4(3)
⇒ c = +12

கேள்வி 9.
x² + y² – 6x + 6y – 8 = 0 என்ற வட்டத்தின் தொடுகோடு மற்றும் செங்கோட்டுச் சமன்பாடுகளை (2, 2) என்ற புள்ளியில் காண்க.
தீர்வு:
வட்டத்தின் சமன்பாடு x² + y² – 6x + 6y – 8 = 0.
∴ (x₁, y₁) தொடுகோட்டின் சமன்பாடு
xx₁ + yy₁ – \(\frac{6}{2}\) (x + x₁) + \(\frac{6}{2}\) (y + y₁) – 8 = 0
கொடுக்கப்பட்ட (x₁, y₁), (2, 2)
(2, 2) -ல் தொடுகோட்டின் சமன்பாடு
x(2) +y(2) – 3(x + 2) + 3(y+ 2) – 8 = 0

⇒ -x + 5y – 8 = 0
⇒ x – 5y + 8 = 0
செங்கோட்டின் சமன்பாடு
yx₁ – xy₁ + g(y – y₁) – f(x – x₁) = 0
⇒ y(2) – x(2) – 3(y – 2) -3(x – 2) = 0
[∵ 2g = -6 ⇒ g = -3; 2f = 6 ⇒ f = 3]
⇒ 2y – 2x – 3y + 6 – 3x + 6 = 0
⇒ -5x – y + 12 =0
⇒ 5x + y – 12 = 0

கேள்வி 10.
(-2, 1), (0, 0) மற்றும் ( 4, -3) என்ற புள்ளிகள் x² + y² – 5x + 2y – 5 = 0 என்ற வட்டத்திற்கு வெளியே, வட்டத்தின் மீது அல்லது உள்ளே இவற்றில் எங்கே உள்ளன எனத் தீர்மானிக்கவும்.
தீர்வு:
கொடுக்கப்பட்ட வட்டத்தின் சமன்பாடு
x² + y² – 5x + 2y – 5 = 0
(-2, 1) ல், (1) ஆனது
(-2)² + 1² – 5(-2) + 2(1) – 5
= 4 + 1 + 10 + 2 – 5
= 17 – 5 = 12 > 0.
∴ (-2, 1) வட்டத்திற்கு வெளியே உள்ளது
(0, 0)-ல், (1) ஆனது -5 < 0
∴ (0, 0) வட்டத்தின் உள் அமைந்துள்ளது.
(4,-3) ல், (1) லிருந்து
(-4)² + (-3)² – 5(4) + 2(-3) – 5
= 16 + 9 + 20 – 6 – 5
= 45 – 11 = 34 > 0
(4,-3) வட்டத்தின் வெளியே அமைந்துள்ளது.

கேள்வி 11.
பின்வரும் வட்டங்களுக்கு மையத்தையும் ஆரத்தையும் காண்க.
(i) x² + (y + 2)² = 0
(ii) x² + y² + 6x – 4y + 4 = 0
(iii) x² + y² – x + 2y – 3 = 0
(iv) 2x² + 2y² – 6x + 4y + 2 = 0
தீர்வு:
(i) வட்டத்தின் சமன்பாடு x² + (y + 2)² = 0
மையம் (0, -2) மற்றும் ஆரம் 0.
(ii) வட்டத்தின் சமன்பாடு
x² + y² + 6x – 4y + 4 = 0.
இங்கு 2g = 6 = g=3
2f = – 4
⇒ f = -2 மற்றும் c = 4
மற்றும் (-g, -f) = (-3, 2)
r = \(\sqrt{g^{2}+f^{2}-c}\) = \(\sqrt{3^{2}+(-2)^{2}-4}\)
= \(\sqrt{9+4-4}\)
= \(\sqrt{9}\)
= 3 அலகுகள்

(iii) வட்டத்தின் சமன்பாடு x² + y² – x + 2y – 3 = 0
இங்கு 2g = -1 ⇒ g = \(\frac{-1}{2}\)
2f = 2
⇒ f = 1 மற்றும் c = -3

r = \(\sqrt{\frac{17}{2}}\) அலகுகள்.

(iv) வட்டத்தின் சமன்பாடு
2x² + 2y² – 6x + 4y + 2 = 0
2 ஆல் வகுக்க, கிடைப்பது
x² + y² – 3x + 2y + 1 = 0

கேள்வி 12.
3x² + (3 – p) xy + qy² – 2px = 8pq என்ற சமன்பாடு வட்டத்தைக் குறிக்கும் எனில் p மற்றும் புன் மதிப்பு காண்க. மேலும் அந்த வட்டத்தின் மையம் மற்றும் ஆரம் காண்க.
தீர்வு:
கொடுக்கப்பட்ட வட்டத்தின் சமன்பாடு
3x² + (3 – p)xy + qy² – 2px = 8pg
வட்டத்திற்கு xy-ன் கெழு = 0
⇒ 3 – p = 0 ⇒ p = 3
மேலும் , x² – ன் கெழு = y²-ன் கெழு
⇒ 3 = q
∴ வட்டத்தின் சமன்பாடு
3x² + 3y² – 6x = 8(3)(3)
3x² + 3y² – 6x – 72 = 0
3 ஆல் வகுக்க, கிடைப்பது
x² + y² – 2x – 24 = 0
இங்கு 2g = -2 ⇒ g = -1
f = 0 மற்றும் c = -24
மையம் (-g, -f) = (1, 0)
மற்றும் r = \(\sqrt{g^{2}+f^{2}-c}\)
= \(\sqrt{(-1)^{2}+0+24}\)
= \(\sqrt{25}\) = 5 அலகுகள்

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 7 வகை நுண்கணிதத்தின் பயன்பாடுகள் Ex 7.9 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 7 வகை நுண்கணிதத்தின் பயன்பாடுகள் Ex 7.9

கேள்வி 1.
கீழ்க்காணும் வளைவரைகளுக்கு தொலைத் தொடுகோடுகளைக் காண்க :

தீர்வு:
(i) f(x) = \(\frac{x^{2}}{x^{2}-1}\)
கொடுக்கப்பட்ட f (x) = \(\frac{x^{2}}{x^{2}-1}\)

∴ x = -1 மற்றும் x = 1 நிலைகுத்து தொலைத் தொடுகோடுகள்.
மேலம் \(\lim _{x \rightarrow \infty} \frac{x^{2}}{x^{2}-1}=\lim _{\frac{1}{x} \rightarrow 0} \frac{1}{1-\frac{1}{x^{2}}}=1\)
[தொகுதி மற்றும் பகுதியை ல் வகுக்க]
∴ y= 1 என்பது கிடைமட்டத் தொலைத் தொடுகோடு

(ii) f (x) = \(\frac{x^{2}}{x+1}\)
கொடுக்கப்பட்ட f (x) = \(\frac{x^{2}}{x+1}\)

∴ x = 1 என்பது நிலைகுத்து தொலைத் தொடுகோடு ஆகும்.
நிலைகுத்து தொலைத் தொடுகோடு தொகுதியின் படி பகுதியின் படியைவிட அதிகமாதலால் x + 1 ஆல் x² வகுக்க

∴ y = x – 1 என்பது சாய்ந்த தொலைத் தொடுகோடு ஆகும்.

(iii) f(x) = \(\frac{3 x}{\sqrt{x^{2}+2}}\)
\(\lim _{x \rightarrow \infty} \frac{3 x}{\sqrt{x^{2}+2}}=\lim _{\frac{1}{x} \rightarrow 0} \frac{3}{\sqrt{1+\frac{2}{x^{2}}}}\)
= \(\frac{3}{\sqrt{1+0}}=3\)
∴ y = 3 என்பது கிடைமட்டத் தொலை தொடுகோடு
மேலும் \(\lim _{x \rightarrow \infty} \frac{3 x}{\sqrt{x^{2}+2}}=\lim _{\frac{1}{x} \rightarrow 0} \frac{3}{\sqrt{1+\frac{2}{x^{2}}}}\) = -3
∴ y = -3 என்பது கிடைமட்டத் தொலை தொடுகோடு ஆகும்.

(iv) f(x) = \(\frac{x^{2}-6 x-1}{x+3}\)
கொடுக்கப்பட்ட f (x) = \(\frac{x^{2}-6 x-1}{x+3}\)
\(\lim _{x \rightarrow-3^{+}} \frac{x^{2}-6 x-1}{x+3}=\lim _{h \rightarrow 0^{+}} \frac{(-3+h)^{2}-6(-3+h)-1}{-3+h+3}\)

∴ x = -3 என்பது கிடைமட்டத் தொலைத் தொடுகோடு மேலும்

∴ y = x – 9 என்பது சாய்ந்த தொலைத் தொடு கோடாகும்.

(v) f (x) = \(\frac{x^{2}+6 x-4}{3 x-6}\)
கொடுக்கப்பட்ட f (x) = \(\frac{x^{2}+6 x-4}{3 x-6}\)

∴ x = 2 என்பது நிலைகுத்து தொலைத் தொடு கோடாகும்.
மேலும்

∴ y = \(\frac{1}{3} x+\frac{8}{3}\), என்பது சாய்ந்த தொலைத் தொடுகோடாகும்.

கேள்வி 2.
கீழ்க்காணும் சார்புகளை வரைக :

தீர்வு:
(i) y = \(-\frac{1}{3}\left(x^{3}-3 x+2\right)\)
கொடுக்கப்பட்ட y = \(-\frac{1}{3}\left(x^{3}-3 x+2\right)\)
சார்பை காரணிபடுத்த கிடைப்பது

1. சார்பு f(x) -ன் சார்பகம் மற்றும் வீச்சகம் முழு மெய் எண் கோடாகும்.
2. y = 0 என பிரதியிட கிடைப்பது x = 1. மற்ற ! இரண்டு மூலங்களும் கற்பனை
∴ X வெட்டுத்துண்டு (1,0) ஆகும்
x = 0 என பிரதியிட கிடைப்பது y = \(-\frac{2}{3}\)
∴ Y வெட்டுத்துண்டு \(\left(0,-\frac{2}{3}\right)\) ஆகும்.

3. f'(x) = \(-\frac{1}{3}\) (3x² – 3) = -x² + 1
f'(x) = 0
⇒ – x² = -1
⇒ x = ±1
∴ நிலை புள்ளிகளாவன x = 1, x = -1.

4. f” (x) = \(\frac{-1}{3}\) (6x) =-2:
f” (1) = -2,f” (-1) = 2.
∴ x = 1-ல் f (x)-க்கு இடஞ்சார்ந்த சிறுமம் ஆகும்
f(1) = \(\frac{-1}{3}\) (1 – 3 + 2)
⇒ f(1) = \(\frac{-1}{3}\) (0) = 0
x = -1-ல் f (x)க்கு இடஞ்சார்ந்த சிறுமம் ஆகும்
⇒ f(-1) = \(\frac{-1}{3}\) (-1 + 3 + 2) = \(\frac{-4}{3}\)
∴ நிலை புள்ளிகளாவன x = 1, x = -1 ஆகும்.

5. f” (x) = -2x < 0 ∀ x > 0 ஆதலால் சார்பு மிகை மெய் கோட்டில் கீழ் நோக்கிய குழிவுடையது மற்றும் f” (x) = -2x > 0 ∀ x < 0,சார்பு குறை மெய் கோட்டில் மேல் நோக்கிய குழிவுடையது.

6. x = 0 -ல் மற்றும் f “(x) தனது குறியை மாற்றுவதால், வளைவு மாற்றப் புள்ளி (0, f (0)) = \(\left(0, \frac{-2}{3}\right)\), ஆகும்.

7. வளைவரைக்கு தொலைத் தொடுகோடுகள் இல்லை .

(ii) y = \(x \sqrt{4-x}\)
⇒ y² = x² (4 – x)
1. f(x) is {x ∈ ℝ / – ∞ < x ≤ 4} -ன் சார்பகம்
⇒ x ∈ (-∞, 4].

2. y = 0 என பிரதியிட கிடைப்பது, 0 = \(x \sqrt{4-x}\)
⇒ x = 0, 4
∴ (4,0) வெட்டுத்துண்டு X மற்றும் வளைவரை ஆதி வழி செய்கிறது

3. x = 0 என பிரதியிட கிடைப்பது, y = 0
∴ (0, 0) வெட்டுத்துண்டு Y ஆகும்.

⇒ -3x + 8 = 0
⇒ -3x = -8
⇒ x = \(\frac{8}{3}\)
∴ சாத்தியமான இடைவெளிகள் \(\left(-\infty, \frac{8}{3}\right)\left(\frac{8}{3}, 4\right)\)

5. x = \(\frac{8}{3}\) ;-ல் f’ (x) மிகையிலிருந்து குறையாக மாறுவதால் இடஞ்சார்ந்த சிறும மதிப்பை கொண்டுள்ளது.

6. வளைவரைக்கு தொலைத் தொடுகோடுகள் i இல்லை .
∴ சார்பின் தோராய வரைபடம்

(iii) y = \(\frac{x^{2}+1}{x^{2}-4}\)
1. f(x) is R ∈/ {-2, 2} -ன் சார்பகம்
2. f (x, y) = f (-x, y) என்பதால் வளைவரை
Y – அச்சை பொறுத்து சமச்சீரானது.

3. y = 0 என பிரதியிட கிடைப்பது,
x² = -1 ⇒ x = \(\pm \sqrt{-1}\) சாத்தியமில்லை
∴ X – வெட்டுத்துண்டு இல்லை

4. x = 0 என பிரதியிட கிடைப்பது, y = \(\frac{-1}{4}\)
∴ Y-வெட்டுத்துண்டு \(\left(0, \frac{-1}{4}\right)\)

5. f'(x) = \(\frac{\left(x^{2}-4\right)(2 x)-\left(x^{2}+1\right)(2 x)}{\left(x^{2}-4\right)^{2}}\)
= \(\frac{2 x^{3}-8 x-2 x^{3}-2 x}{\left(x^{2}-4\right)^{2}}=\frac{-10 x}{\left(x^{2}-4\right)^{2}}\)
f'(x) = 0 ⇒ x = 0 மற்றும் x = -2, 2-ல் வளைவரை வரையறுக்கப்படவில்லை.
∴ நிலை எண்கள் 0, -2, 2.
∴ ஒரியல்பு இடைவெளிகள் (-∞, -2) (-2, 0) (0, 2) (2, ∞).

∴ f (x) -ல் (-∞, -2) (-2, 0) ஏறும் மற்றும் (0, 2) (2, ∞) -ல் இறங்கும்.

6. f”(x) குறி மிகையிலிருந்து குறையாக x = 0-ல் மாறுவதால், அது x = 0-ல் இடஞ்சார்ந்த சிறுமத்தை கொண்டிருக்கும்.

7. f”(x) = \(-10\left[\frac{\left(x^{2}-4\right)^{2}(1)-x(2)\left(x^{2}-4\right)(2 x)}{\left(x^{2}-4\right)^{4}}\right]\)
= \(-10\left[\frac{\left(x^{2}-4\right)^{2}-4 x^{2}\left(x^{2}-4\right)}{\left(x^{2}-4\right)^{4}}\right]\)
= \(-10\left(x^{2}-4\right)\left[\frac{x^{2}-4-4 x^{2}}{\left(x^{2}-4\right)^{4}}\right]\)
= \(-10\left(\frac{-3 x^{2}-4}{\left(x^{2}-4\right)^{3}}\right)=\frac{10\left(3 x^{2}+4\right)}{\left(x^{2}-4\right)^{3}}\)
∴ f”(x) = 0 ⇒ 3x² + 4 = 0 ⇒ x² = \(\frac{-4}{3}\)
f”(x) = 0 சாத்தியமில்லை மற்றும் x = 2, -2-ல் வரையறுக்கப்படவில்லை .
குழிவுத் தன்மைக்கான இடைவெளிகள் பின்வருமாறு பட்டியலிடப்பட்டுள்ளன.

8. வளைவரை வரையறுக்கப்படாததால் x = 2, x = – 2 நேர்குத்து தொலைத் தொடு கோடுகள் மற்றும் y = 1 கிடைமட்டத் தொலைத் தொடுகோடு

(iv) y = \(\frac{1}{1+e^{-x}}\)
f(x) = y = \(\frac{1}{1+e^{-x}}\) என்க
1. y-ன் சார்பகம் ℝ
2. சமச்சீரற்றது
3. y = 0 எனபிரதியிட கிடைப்பது,x -க்கு மதிப்பில்லை
∴ X வெட்டுத்துண்டு இல்லை

4. x = 0 என பிரதியிட கிடைப்பது,
y = \(\frac{1}{1+e^{0}}=\frac{1}{1+1}=\frac{1}{2}\)
∴ Y-வெட்டுத்துண்டு \(\left(0, \frac{1}{2}\right)\)

5. f'(x) = \(\frac{d}{d x}\) (1 + e^-x)^-1 = -1(1 + e^-x)^-2 (-e^-x)
= \(\frac{e^{-x}}{\left(1+e^{-x}\right)^{2}}\) = e^-x (1 + e^-x)^-2
f'(x) = 0 ⇒ e^-x = 0 ⇒ -x = log 0 ⇒ x = ∞
மேலும் f (x) > 0 ∀ x ∈ ℝ
∴ (- ∞, ∞) -ல் f (x) ஆனது ஏறும்.

6. f'(x)க்கு குறி மாற்றம் இல்லாததால் அதற்கு இடஞ்சார்ந்த சிறும, பெரு மதிப்புகள் இல்லை.

7. f”(x) = e^-x (-2)(1 + e^-x)^-3 (-e^-x) + (1 + e^-x)^-2 (-e^-x)
= 2e^-2x (1 + e^-x)^-3 – e^-x(1 + e^-x)^-2
= e^-2x (1 + e^-x)^-3 [2 – e^-x(1 + e^-x)]
= e^-2x (1 + e^-x)^-3 [2 – e^x – 1]
= \(\frac{e^{-2 x}\left(1-e^{x}\right)}{\left(1+e^{x}\right)^{3}}\)
f”(x) = 0 ⇒ x = (0)
குழிவுத் தன்மைக்கான இடைவெளிகள் பின்வருமாறு அட்டவணைப்படுத்தப்பட்டு உள்ளன.

8. \(\lim _{x \rightarrow \infty} \frac{1}{1+e^{-x}}=1\)
⇒ y = 1
ஆனது கிடைமட்டத் தொலைத் தொடுகோடு மற்றும்
\(\lim _{x \rightarrow-\infty} \frac{1}{1+e^{-x}}=0\)
⇒ y = 0 என்பது கிடைமட்டத் தொலைத் தொடுகோடு
∴ தோராய வரைபடம்

(v) y = \(\frac{x^{3}}{24}\) – log x
f (x) = y = \(\frac{x^{3}}{24}\) – log x என்க
1. (0, ∞)-ன் சார்பகம் f (x) என்க.
2. வளைவரை சமச்சீரற்றது

3. x = 0 என பிரதியிட கிடைப்பது, y = -∞
X – வெட்டுத்துண்டு இல்லை

4. y = 0 என பிரதியிட கிடைப்பது 0 = \(\frac{x^{3}}{24}\) – log x
⇒ log x = \(\frac{x^{3}}{24}\) ⇒ x = e^{\(\frac{x^{3}}{24}\)}
∴ Y – வெட்டுத்துண்டு இல்லை

5. f'(x) = \(\frac{3 x^{2}}{24}-\frac{1}{x}=\frac{x^{2}}{8}-\frac{1}{x}\)
f'(x) = 0 ⇒ \(\frac{x^{2}}{8}=\frac{1}{x}\) ⇒ x³ = 8 ⇒ x = 2
∴ சாத்தியப்படும் இடைவெளிகள் (0, 2) (2, ∞)

∴ f (x) ஆனது (0, 2)-ல் ஏறும் மற்றும் (2, ∞) -ல் , இறங்கும்.

6. f'(x)-ல்.x = 2 ஆனது குறையிலிருந்து மிகையாக மாறுவதால் இடஞ்சார்ந்த சிறுமம் ஆகும்.

∴ குழிவுத் தன்மைக்கான இடைவெளிகள் (-∞, 0) (0, ∞) ஆகும்.

8. y = 0 -ல் வரையறுக்கப்படாததால் அதற்கு கிடை மட்டத் தொலைத் தொடுகோடு y = 0 உண்டு.

9. f”(x) ஆனது குறியை குறையிலிருந்து மிகையாக மாற்றுவதால், அதனுடைய வளைவு மாற்று புள்ளி — ve to + ve, (0, f (0)) = (0, ∞) ஆகும்.

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 7 வகை நுண்கணிதத்தின் பயன்பாடுகள் Ex 7.8 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 7 வகை நுண்கணிதத்தின் பயன்பாடுகள் Ex 7.8

கேள்வி 1.
இரண்டு மிகை எண்களின் கூட்டுத் தொகை 12, மேலும் அதன் பெருக்குத் தொகை பெருமம் எனில் அந்த எண்களைக் காண்க.
தீர்வு:
x மற்றும் y இரண்டு மிகை எண்கள் என்க.
கொடுக்கப்பட்ட x + y = 12
⇒ y = 12 – x ……………. (1)
f (x) = xy என்க
= x (12 – x) = 12x – x²
f'(x) = 12 – 2x
f'(x) = 0
⇒ 12 – 2x = 0
⇒ 12 = 2x
⇒ x = 6
∴ நிலை எண் 6.
f”(x) = -2x
f”(6) = -2(6) = -12 < 0
∴ f(x)-ல் x = 6-ன் பெருமம்
⇒ x = 6 எனில் அதன் பெருக்குத் தொகையின் பெருமம் ஆகும்.
x = 6 எனில் y = 12 – 6 = 6 [(1) லிருந்து]
எனவே தேவையான எண்கள் 6, 6 ஆகும்.

கேள்வி 2.
இரண்டு மிகை எண்களின் பெருக்குத்தொகை 20, மேலும் அதன் கூடுதல் சிறுமம் எனில் அந்த எண்களைக் காண்க.
தீர்வு:
அந்த இரண்டு மிகை எண்கள் x மற்றும் y என்க.
கொடுக்கப்பட்ட x y = 20
⇒ y = \(\frac{20}{x}\)
f (x) = x + y என்க
f(x) = x + \(\frac{20}{x}\)
f'(x) = \(1-\frac{20}{x^{2}}\)
f'(x) = 0
⇒ \(1-\frac{20}{x^{2}}\) = 0
⇒ 1 = \(\frac{20}{x^{2}}\)
⇒ x² = 20
⇒ x = ±\(\sqrt{20}\)
⇒ x = ±2\(\sqrt{5}\)
∴ நிலை எண்கள் 2\(\sqrt{5}\) , -2\(\sqrt{5}\) .
f”(x) = \(\frac{40}{x^{2}}\)
x = 2\(\sqrt{5}\) எனில்,
f”(x) = \(\frac{40}{(2 \sqrt{5})^{3}}\) > 0
∴ f(x) எனில் x = 2\(\sqrt{5}\) -ன் சிறுமம் ஆகும்
x = 2\(\sqrt{5}\), y = \(\frac{20}{2 \sqrt{5}}\) எனில்,
= \(\frac{10}{\sqrt{5}} \times \frac{\sqrt{5}}{\sqrt{5}}=\frac{10 \sqrt{5}}{5}=2 \sqrt{5}\)
எனவே தேவையான மிகை எண்கள் 2\(\sqrt{5}\), 2\(\sqrt{5}\).

கேள்வி 3.
x² + y² -ன் குறைந்த மதிப்பினை x + y = 10 எனக் கொண்டு காண்க.
தீர்வு:
கொடுக்கப்பட்ட x + y = 10
⇒ y = 10 – x …………… (1)
f(x) = x² + y² என்க
= x² + (10 – x)²
= x² + 100 + x² – 20x
f(x) = 2x² – 20x + 100
f'(x) = 4x – 20
f'(x) = 0
4x- 20 = 0
4x = 20
⇒ x = 5
∴ நிலை எண் 5 ஆகும்.
f”(x) = 4
∴ f”(5) = 4 > 0
∴ f(x) எனில் x = 5 சிறுமம் ஆகும்.
x = 5, y = 10 – 5 = 5 எனில் [(1) லிருந்து]
∴ x² + y² -ன் குறைந்த மதிப்பு
= 5² + 5² = 25 + 25 = 50

கேள்வி 4.
ஒருதோட்டம் செவ்வகவடிவில் அமைக்கப்பட்டு கம்பி வேலி மூலம் பாதுகாக்கப்பட வேண்டும். 40 மீட்டர் வேலிக் கம்பி மூலம் பாதுகாக்கப்படும் தோட்டத்தின் பெரும பரப்பினைக் காண்க.
தீர்வு:
X என்பது தோட்டத்தின் நீளம் மற்றும் y என்பது அகலம் ஆகும்.
கொடுக்கப்பட்ட 2 (x + y) = 40

[∵ கம்பியின் நீளம் = 40 சுற்றளவு = 40 மீ]
⇒ x + y = 20
⇒ y = 20 – x …………… (1)
f(x) = xy என்க
= x(20 – x) = 20x – x²
f'(x) = 20 – 2x
f'(x) = 0
⇒ 20 – 2x = 0
⇒ 20 = 2x
x = 10
∴ நிலை எண் 10 ஆகும்
f”(x) = -2
இங்கு f”(10) = -2 < 0
∴ f (x) -ல் x = 10 -ன் சிறுமம்
x = 10 எனில்,
y = 20 – 10 = 10
∴ பரப்பு = f (x) =xy
= 10(10) = 100மீ.²
∴ தோட்டத்தின் பெரும பரப்பு = 100 மீ’²

கேள்வி 5.
ஒரு செவ்வக வடிவிலான பக்கத்தில் 24 செ.மீ அளவிற்கு அச்சிடப்பட்டுள்ளது. மேற்புற மற்றும் கீழ்ப்புற ஓரங்கள் 1.5 செ.மீ அளவிலும் மற்ற பக்கங்களின் ஓரங்கள் 1 செ.மீ அளவிலும் இடைவெளி விடப்பட்டுள்ளது. காகித பக்கத்தின் குறைந்த பரப்பளவிற்கு அதன் நீள, அகலங்கள் என்னவாக இருக்க வேண்டும்?.
தீர்வு:
X மற்றும் y அச்சிடப்பட்ட பக்கத்தின் நீளம் மற்றும் அகலம் என்க.

கொடுக்கப்பட்ட xy = 24
⇒ y = \(\frac{24}{x}\) …………. (1)
ஓரங்களுடன் சேர்த்து பக்கத்தின் நீளம்
= x + 1 + 1 = x + 2
ஒரங்களுடன் சேர்த்து பக்கத்தின் அகலம்
= y + 1.5 + 1.5 = y + 3
பக்கத்தின் பரப்பு = (x + 2) (y+ 3)
f (x) = (x + 2) (y + 3) என்க
= (x + 2) \(\left(\frac{24}{x}+3\right)\)
= 24 + 3.x + \(\frac{48}{x}\) +6
= 3x + \(\frac{48}{x}\) + 30
f'(x) = 3 – \(\frac{48}{x^{2}}\)
f'(x) = 0
⇒ 3 – \(\frac{48}{x^{2}}\) = 0 ⇒ 3 = \(\frac{48}{x^{2}}\)
⇒ x² = 16 ⇒ x = ±4
∴ நிலை எண்கள் 4, 4 ஆகும்
f”(x) = \(-48\left(\frac{-2}{x^{3}}\right)=\frac{96}{x^{3}}\)
f”(4) = \(\frac{96}{64}\) > 0
∴ f(x)-ல் x = 4-ன் சிறுமம் ஆகும்
x = 4 எனில், y = \(\frac{24}{4}\) = 6 [(1) லிருந்து] ,
∴ பக்கத்தின் நீளம் = x + 2 = 4 + 2 = 6 செ.மீ
பக்கத்தின் அகலம் = y + 3 = 6 + 3 = 9 செ.மீ

கேள்வி 6.
ஒரு விவசாயி ஒரு நதியை ஒட்டிய செவ்வக மேய்ச்சல் நிலத்திற்கு வேலி அமைக்க திட்டமிட்டுள்ளார். மந்தைகளுக்கு போதுமான புல் வழங்க மேய்ச்ச ல் நிலம் 1,80,000 சதுர மீட்டர் பரப்பளவு இருக்க வேண்டும். ஆற்றின் குறுக்கே வேலி அமைக்கத் தேவையில்லை. தேவையான குறைந்தபட்ச வேலிக் கம்பியின் நீளம் என்ன?
தீர்வு:
மேய்ச்சல் நிலத்தின் நீளம் x மற்றும் அகலம் y
என்க. கொடுக்கப்பட்ட xy = 1,80,000
⇒ y = \(\frac{1,80,000}{x}\) ………….. (1)
ஆற்றின் குறுக்கே வேலி அமைக்கத் தேவையில்லை
சுற்றளவு = 2x + y
f(x) = 2x + y என்க
= 2x + \(\frac{1,80,000}{x}\) [(1)-ஐ பயன்படுத்தி]
f'(x) = 2 – \(\frac{1,80,000}{x^{2}}\)
f'(x) = 0

⇒ 2 = \(\frac{1,80,000}{x^{2}}\)
⇒ x² = 90,000
⇒ x = ± 300
∴ நிலை எண்கள் 300,-300 ஆகும்
f”(x) = \(-1,80,000\left(\frac{-2}{x^{3}}\right)=\frac{360000}{x^{3}}\)
f”(300) = \(\frac{360000}{(300)^{3}}\) > 0
∴ x = 300 எனில் f (x) ன் சிறுமம் ஆகும்.
(1) லிருந்து x = 300 எனில், y = \(\frac{1,80,000}{x}\) = 600
∴ தேவையான குறைந்தபட்ச வேலிக் கம்பியின் நீளம் = 2x + y
= 2(300) + 600 = 600 + 600 = 1200மீ

கேள்வி 7.
10 செ.மீ ஆரமுள்ள வட்டத்தினுள் அமைக்கப்படும் செவ்வகங்களுள் மீப்பெரு பரப்புடைய செவ்வகத்தின் பரிமாணங்களைக் காண்க.
தீர்வு:
வட்டத்தின் மீதுள்ள புள்ளி என்பது

x = r cos θ,
y = r sin θ
⇒ x = 10 cos θ,
y = 10 sin θ
∴ செவ்வகத்தின் நீளம் = 2x மற்றும் செவ்வகத்தின் அகலம் = 2y என்க.
∴ 2x = 20 cos θ, 2y = 20 sin θ
∴ பரப்பு = f (θ) = 2x (2y)
= 400 cos θ sine θ
f(θ) = 200 sin 2θ
f'(θ) = 200 (2) cos 2θ = 400 cos 2θ
f'(θ) = 0
⇒ 400 cos 2θ = 0
⇒ cos 2θ = 0 = cos \(\frac{\pi}{2}\)
⇒ 2θ = \(\frac{\pi}{2}\)
⇒ θ = \(\frac{\pi}{4}\)
∴ நிலை எண் θ = \(\frac{\pi}{4}\)
f”(θ) = 400 (2) (-sin 2θ)
= – 800 sin 2θ
f”(7) = -800 sin 2 × \(\frac{\pi}{4}\)
= – 800 sin \(\frac{\pi}{2}\) = – 800 < 0
= \(\frac{\pi}{4}\) -இல் () -ன் பெருமம் ஆகும். செவ்வகத்தின் நீளம் = 2x
θ = 20 cos 0 = 20 cos
∴ செவ்வகத்தின் அகலம் = 2x
= 20 cos θ = 20 cos \(\frac{\pi}{4}\) = \(\frac{20}{\sqrt{2}}\)
∴ செவ்வகத்தின் அகலம் = 2y
= 20 sin θ = 20 sin \(\frac{\pi}{4}\) = \(\frac{20}{\sqrt{2}}\)

கேள்வி 8.
கொடுக்கப்பட்ட சுற்றளவுள்ள செவ்வகங்களுள், சதுரம் மட்டுமே பெரும் பரப்பைக் கொண்டிருக்கும் என நிறுவுக.
தீர்வு:
செவ்வகத்தின் நீளம் X மற்றும் அகலம் y என்க.
∴ சுற்றளவு P = 2x + 2y
⇒ 2y = P – 2x ⇒ y = \(\frac{\mathrm{P}-2 x}{2}\)
f(x) = பரப்பு
= xy = \(\left(\frac{\mathrm{P}-2 x}{2}\right)\) என்க
f(x) = \(\frac{\mathrm{P} x-2 x^{2}}{2}\)
f'(x) = \(\frac{1}{2}\) [P – 4x]
f'(x) = 0
⇒ \(\frac{1}{2}\) [P – 4x] = 0
⇒ P = 4x
⇒ x = \(\frac{\mathrm{P}}{4}\)
∴ நிலை எண் \(\frac{\mathrm{P}}{4}\)
f”(x) = \(\frac{1}{2}\) [-4] = -2
இங்கு f”(\(\frac{\mathrm{P}}{4}\)) = -2 < 0
∴ x = \(\frac{\mathrm{P}}{4}\) எனில் f (x) -ன் பெருமம் ஆகும்
x = \(\frac{\mathrm{P}}{4}\) எனில்
⇒ \(\frac{P-2\left(\frac{P}{4}\right)}{2}=\frac{P-\frac{P}{2}}{2}=\frac{P}{4}\)
∴ x = y = \(\frac{\mathrm{P}}{4}\)
∴ கொடுக்கப்பட்ட சுற்றளவுள்ள செவ்வகங்களுள், ! சதுரம் மட்டுமே பெரும பரப்பைக் கொண்டிருக்கும்.

கேள்வி 9.
r செ.மீ ஆரமுள்ள அறை வட்டத்தினுள் அமைக்கப்படும் செவ்வகங்களுள் மீப்பெரு செவ்வகத்தின் பரிமாணங்களைக் காண்க?
தீர்வு:
அறை வட்டத்தின் மையம் (0,0) மற்றும் ஆரம் r என்க . .

x = r cos θ,
y = r sin θ
∴ செவ்வகத்தின் நீளம் = 2x = 2r cos θ
செவ்வகத்தின் அகலம் = y = r sin θ
∴ பரப்பு = 2xy = 2r² cos θ sin θ
= r² sin 2θ
f'(θ) என்க = r² 2 cos 2θ
f'(θ) = 0
⇒ 2 r² cos 2θ = 0
⇒ cos 2θ = 0 = cos \(\frac{\pi}{2}\)
⇒ 2θ = \(\frac{\pi}{2}\)
⇒ θ = \(\frac{\pi}{4}\)
f”(θ) = 2r² (2) (-sin 2θ)
= 4r² sin 2θ
∴ \(f^{\prime \prime}\left(\frac{\pi}{4}\right)\) = 4r² sin 2\(\left(\frac{\pi}{4}\right)\)
= -4r² sin \(\frac{\pi}{4}\) = – 4r² < 0
∴ θ = \(\frac{\pi}{4}\) எனில் f(θ) -ன் சிறுமம் ஆகும்.
∴ செவ்வகத்தின் நீளம் (x) = 2r cos \(\frac{\pi}{4}\)
= \(2 r \times \frac{1}{\sqrt{2}}=\sqrt{2} r\)
∴ செவ்வகத்தின் அகலம் = y = r sin θ
= \(r \sin \frac{\pi}{4}=\frac{r}{\sqrt{2}}\)

கேள்வி 10.
ஒரு உற்பத்தியாளர் ஒரு சதுர அடித்தளத்தையும் . 108 சதுர செ.மீ வெளிப்புறப்பரப்பையும் கொண்ட திறந்த பெட்டியை வடிவமைக்க விரும்புகிறார். அதிகபட்ச கன அளவிற்கான பெட்டியின் பரிமாணங்களைக் காண்க. –
தீர்வு:
திறந்த பெட்டி சதுர பரப்பை கொண்டிருப்பதால் பெட்டியின் அகலம், நீளம் மற்றும் உயரம் முறையே l, l மற்றும் b என்க.
∴ மேற்பரப்பு = l² + 41b = 108
l(l + 4b) = 108

f(l) = பெட்டியின் கன அளவு என்க
= l × l × b = l² b

∴ நிலை எண் 6
f”(l) = \(-\frac{6 l}{4}=-\frac{3 l}{2}\)
∴ f”(6) = \(-\frac{3(6)}{2}\) < 0
∴ l = 6 எனில் f”(l) -ன் பெருமம் ஆகும்.
l = 6 எனில் b = \(\frac{27}{6}-\frac{6}{4}\)
= \(\frac{9}{2}-\frac{3}{2}=\frac{6}{2}\) = 3 செ.மீ
எனவே தேவையான பெட்டியின் அளவுகள் முறையே 6 செ.மீ, 6 செ.மீ மற்றும் 3 செ.மீ.

கேள்வி 11.
ஒரு உருளையின் கன அளவு V = πr² h மேலும் r + h = 6 எனில் கன அளவின் மீப்பெரு மற்றும் மீச்சிறு மதிப்புகளைக் காண்க.
தீர்வு:
கொடுக்கப்பட்ட r + h = 6
⇒ h = 6 – r …………. (1)
f(r) என்க = V = πr² h
= πr² (6 – r) = π (6r² – 1³)
f'(r) = π (12r – 3r²)
∴ f'(r) = 0
⇒ π (12r – 3r²) = 0
⇒ 12r – 3r² = 0
⇒ 3r (4 – r) = 0
⇒ r = 0 (அ) r = 4
∴ நிலை எண்கள் 0, 4
f”(r) = π (12 – 6r)
r = 4 எனில், f”(r) = π (12 – 24) < 0
∴ r = 4 எனில் f (r)-ன் பெருமம் ஆகும்
r = 4 எனில், h = 6 – 4 = 2
r = 0 எனில்,h = 6 – 0 = 6
∴ உருளையின் கன அளவு V = πr² h = π (4)² (2)
= 32 π கன அலகுகள்
அல்லது உருளையின் கன அளவு V = π (0²) (6) = 0 கன அலகுகள்

கேள்வி 12.
ஆரம் a செ.மீ. மற்றும் உயரம் 5 செ.மீ கொண்ட ஒரு வெற்றுக் கூம்பு ஒரு மேசையின் மீது வைக்கப்படுகிறது. இதன் அடியில் மறைத்து வைக்கக் கூடிய மிகப்பெரிய உருளையின் கன அளவு கூம்பின் கன அளவைப் போல் \(\frac{4}{9}\) மடங்கு என்பதைக் காட்டுக.
தீர்வு:
கொடுக்கப்பட்ட AC = b மற்றும் CD = a
உயரம் h மற்றும் ஆரம் r என்க
∴ AB = AC – BC = b – h
படத்தில்,

∆ABE ~ ∆ACD
∴ \(\frac{\mathrm{AB}}{\mathrm{BE}}=\frac{\mathrm{AC}}{\mathrm{CD}}\)
⇒ \(\frac{b-h}{r}=\frac{b}{a}\)
⇒ r = \(\frac{a(b-h)}{b}\) …………. (1)
உருளையின் கன அளவு = πr² h

‘h’ ஐ பொறுத்து வகையிட கிடைப்பது

∴ h = \(\frac{b}{3}\) -ல் V-ன் பெருமம் ஆகும்.
∴ உருளையின் பெரும கன அளவு

= \(\frac{4}{9}\) (கூம்பின் கன அளவு)
எனவே மறைத்து வைக்கக் கூடிய மிகப்பெரிய உருளையின் கன அளவு கூம்பின் கன அளவைப் போல் \(\frac{4}{9}\) மடங்காகும்.

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 4 நேர்மாறு முக்கோணவியல் சார்புகள் Ex 4.2 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 4 நேர்மாறு முக்கோணவியல் சார்புகள் Ex 4.2

கேள்வி 1.
அனைத்து x -ன் மதிப்புகளையும் காண்க.
(i) -6π ≤ x ≤ 6π மற்றும் cos x = 0
(ii) – 5π ≤ x ≤ 5π மற்றும் cos x = -1.
தீர்வு:
(i) cosx = 0 = x = (2n + 1)\(\frac{\pi}{2}\), n ∈ ℤ
– π ≤ x ≤ 6π
∴n ஆனது – 5 லிருந்து 5 வரை மதிப்புகளை எடுத்துக் கொள்ளும்.
x = (2n + 1)\(\frac{\pi}{2}\), n = 0, ±1, ±2, … ±5

(ii) – 5π ≤ x ≤ 5π மற்றும் cos x = -1.
cos x = -1
cos x = cos π
x = 2nπ + π, n ∈ ℤ [∵ cos θ = cos α
⇒ (2n + 1)π, n ∈ ℤ ⇒ θ = 2πr + α, n ∈ ℤ]
⇒ ஆனால் -5π ≤ x ≤ 5π
n = 0, ±1, ±2, மற்றும் -3 என பிரதியிட கிடைப்பது
⇒ x = -5π, -3π, -π, π, 3π, 5π
⇒ x = (2n + 1)π, n = 0, ±1, ±2, மற்றும் -3.

கேள்வி 2.

தீர்வு:
cos^-1\(\left[\cos \left(\frac{-\pi}{6}\right)\right] \neq \frac{-\pi}{6}\)
\(\frac{-\pi}{6}\) ≠ [0, π] இது கொசைன் சார்பின் முதன்மை சார்பகம்.

கேள்வி 3.
cos^-1(-x) = π – cos^-1(x) என்பது மெய்யாகுமா? விடைக்கு தக்க காரணம் கூறுக.
தீர்வு:
cos^-1(-x) = θ என்க … (1)
⇒ -x = cos θ
⇒ x = -cos θ = cos (π – θ)
⇒ π – θ = cos^-1(x)
⇒ θ = π – cos^-1x …. (2)
(1) மற்றும் (2) லிருந்து cos^-1(-x) = π – cos^-1(x)
∴ cos^-1(-x) = π – cos^-1(x) சரி

கேள்வி 4.

தீர்வு:

கேள்வி 5.

தீர்வு :
(i) 2cos^-1\(\left(\frac{1}{2}\right)\) + sin^-1\(\left(\frac{1}{2}\right)\)

[∵ முதன்மை சார்பகம் சைன்க்கு \(\left[\frac{-\pi}{2}, \frac{\pi}{2}\right]\) மற்றும் கொசைனுக்கு முதன்மை சார்பகம் [0, π]]
sin y = \(\frac{1}{2}\)
sin y = sin \(\frac{\pi}{6}\) [∵\(\frac{\pi}{6}\) ∈-\(\frac{\pi}{2}\), \(\frac{\pi}{6}\)]
⇒ x = \(\frac{\pi}{3}\) மற்றும் y = \(\frac{\pi}{6}\)
∴ 2 cos^-1\(\left(\frac{1}{2}\right)\) + sin^-1\(\left(\frac{1}{2}\right)\)
= 2\(\left(\frac{\pi}{3}\right)\) + \(\frac{\pi}{6}\) = \(\frac{2 \pi}{3}\) + \(\frac{\pi}{6}\) = \(\frac{4 \pi+\pi}{6}\) = \(\frac{5 \pi}{6}\)

(ii) cos^-1\(\left(\frac{1}{2}\right)\) + sin^-1

(iii)

கேள்வி 6.
சார்பகம் காண்க .
(i) f(x) = sin^-1\(\left(\frac{|x|-2}{3}\right)\) + cos^-1\(\left(\frac{1-|x|}{4}\right)\)
(ii) g(x) = sin^-1x + cos^-1x
தீர்வு:
(i) கொடுக்கப்பட்ட

sin^-1 x இன் வரையறையிலிருந்து
-1 ≤ \(\frac{|x|-2}{3}\) ≤ 1
⇒ -3 ≤ |x| – 2 ≤ 3
⇒ -3 + 2 ≤ |x| ≤ 3 + 2
⇒ -1 ≤ |x| ≤ 5
என்பதை சுருக்கி 0 ≤ |x| ≤ 5
⇒ 0 ≤ |x| மற்றும் |x| ≤ 5
⇒ |x| ≥ 0 மற்றும் -5 ≤ x ≤ 5 … (1)
cos^-1x என் வரையறைப்படி \(-1 \leq \frac{1-|x|}{4} \leq 1\)
⇒ -4 ≤ 1 – |x| ≤ 4 ⇒ -4 – 1 ≤ -|x| ≤ 4 – 1
⇒ -5 ≤ -|x| ≤ 3 ⇒ -3 ≤ |x| ≤ 5
என்ப தை சுருக்கி 0 ≤ |x| ≤ 5 – 5 ≤ x ≤ 5 …. (2)
(1) மற்றும் (2)லிருந்து,
சார்பகமானது [-5,5]

(ii) கொடுக்கப்பட்ட g(x) = sin^-1x + cos^-1x
sin^-1x ன் வரையறையிலிருந்து -1 ≤ x ≤ 1 …. (1)
மேலும் cos’ ன் வரையறைப்படி-1 ≤ x ≤ 1… (2)
∴ (1) மற்றும் (2) லிருந்து
g(x)ன் சார்பகம் = [-1, 1] ∪ [-1, 1] = [-1, 1] எனவே g(x) ன் சார்பகம் [-1, 1].

கேள்வி 7.
x-ன் எந்த மதிப்பிற்கு சமநிலை \(\frac{\pi}{2}\) < cos^-1(3x – 1) < π மெய்யாகும்?
தீர்வு:
கொடுக்கப்பட்ட \(\frac{\pi}{2}\) < cos^-1(3x – 1) < π
cos \(\frac{\pi}{2}\) < 3x – 1 < cos π ⇒ 0 < 3x – 1 < -1
0 + 1 < 3x < -1 + 1 ⇒ 1 < 3x < 0
\(\frac{1}{3}\) < x < 0
0 < x < \(\frac{1}{3}\) மட்டும் இந்த அசமன்பாடு சரி.

கேள்வி 8.
மதிப்பு காண்க.

தீர்வு:

(ii)

[∵கொசைன் சார்பின் காலம் 2π]

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 8 வகையீடுகள் மற்றும் பகுதி வகைக்கெழுக்கள் Ex 8.3 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 8 வகையீடுகள் மற்றும் பகுதி வகைக்கெழுக்கள் Ex 8.3

கேள்வி 1.
சார்பு g(x, y) = \(\frac{3 x^{2}-x y}{x^{2}+y^{2}+3}\) க்கு எல்லை மதிப்பு இருக்குமானால், \(\lim _{(x, y) \rightarrow(1,2)}\) g (x,y) -ஐ மதிப்பிடுக.
தீர்வு:
கொடுக்கப்பட்ட

கேள்வி 2.
எல்லை மதிப்பு இருக்குமானால் \(\lim _{(x, y) \rightarrow(0,0)}\) cos \(\left(\frac{\dot{x}^{3}+y^{3}}{x+y+2}\right)\) -ஐ மதிப்பிடுக.
தீர்வு:
\(\lim _{(x, y) \rightarrow(0,0)}\) cos \(\left(\frac{\dot{x}^{3}+y^{3}}{x+y+2}\right)\)
= cos \(\left(\frac{0+0}{0+0+2}\right)\) = cos 0 = 1

கேள்வி 3.
(x, y) + (0, 0)- க்கு f(x, y) = \(\frac{y^{2}-x y}{\sqrt{x}-\sqrt{y}}\) எனில், \(\lim _{(x, y) \rightarrow(0,0)}\) f(x, y) = 0 என நிறுவுக.
தீர்வு:

கேள்வி 4.
எல்லை மதிப்பு இருக்குமானால்,
\(\lim _{(x, y) \rightarrow(0,0)} \cos \left(\frac{e^{x} \sin y}{y}\right)\) -ஐ மதிப்பிடுக.
தீர்வு:

கேள்வி 5.
(x, y) ≠ (0,0)-க்கு g (x, y) = \(\frac{x^{2} y}{x^{4}+y^{2}}\), மற்றும் g(0, 0) = 0 என்க .
(i) ஒவ்வொரு y = mx, m ∈ ℝ நேர்கோட்டுப் பாதையிலும் \(\lim _{(x, y) \rightarrow(0,0)}\) g(x, y) = 0 என நிறுவுக.
(ii) ஒவ்வொரு y = kx², k ∈ ℝ\{0} பரவளையப் பாதையிலும் \(\lim _{(x, y) \rightarrow(0,0)}\) g (x, y) = \(\frac{k}{1+k^{2}}\) என நிறுவுக.”
தீர்வு:
(i) கொடுக்கப்பட்ட

இங்கு , \(\lim _{(x, y) \rightarrow(0,0)}\) g(x, y) = \(\frac{m(0)}{0^{2}+m^{2}}=\frac{0}{m^{2}}\) = 0, m இன் எல்லா மதிப்புகளுக்கும்
∴ ஒவ்வொரு y = mx, m ∈ ℝ. நேர்க்கோட்டுப்
பாதையிலும் \(\lim _{(x, y) \rightarrow(0,0)}\) (x, y) = 0

கேள்வி 6.
சார்பு f(x, y)= \(\frac{x^{2}-y^{2}}{y^{2}+1}\), ஒவ்வொரு (x, y) ∈ ℝ² -க்கும் தொடர்ச்சியானது என நிறுவுக.
தீர்வு:
(a, b) ∈ ℝ² என்பது ஒரு தன்னிச்சையான புள்ளி என்க . f இன் தொடர்ச்சி தன்மையை (a, b)-இல் ஆராய்வோம்.

அதாவது f இல் (a, b) தொடர்ச்சிக்கான மூன்று நிபந்தனைகளும் நிறைவு செய்யப்படுகிறதா சோதிப்போம்.

எனவே f எல்லா மூன்று நிபந்தனைகளும் (a, b) என்ற R² இன் தன்னிச்சையான புள்ளியில் பூர்த்தி செய்வதால் ஆனது R² இன் எல்லா புள்ளிகளிலும் தொடர்ச்சியுடையது.

கேள்வி 7.
சார்பு g(x, y) = \(\frac{e^{y} \sin x}{x}\), x ≠ 0 மற்றும் g(0, 0) = 1 என்க. புள்ளி (0,0) இல் தொடர்ச்சியானது என நிறுவுக.
தீர்வு:
கொடுக்கப்பட்ட g (x, y) = \(\frac{e^{y} \sin x}{x}\) இங்கு x ≠ 0 மற்றும் g(0, 0) = 1
எல்லா (x, y) ∈ ℝ² க்கும் g சார்பு ஆனது வரையறுக்கப்பட்டுள்ளது.
g-இல் (0, 0) க்கான ட எல்லை மற்றும் L = g(0, 0) = 1 என சோதிக்க.

(0,0 ) வில் தொடர்ச்சியுடையது என நிரூபிக்கிறது.
∴ புள்ளி (0, 0) g(x, y) தொடர்ச்சியுடையது.

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 4 நேர்மாறு முக்கோணவியல் சார்புகள் Ex 4.6 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 4 நேர்மாறு முக்கோணவியல் சார்புகள் Ex 4.6

கொடுக்கப்பட்ட நான்கு மாற்று விடைகளிலிருந்து சரியான அல்லது மிகவும் ஏற்புடைய விடையினைத் தேர்ந்தெடுக்கவும்.

கேள்வி 1.
sin^-1 (cos x), 0 ≤ x ≤ π -ன் மதிப்பு
(1) π – x
(2) x – \(\frac{\pi}{2}\)
(3) \(\frac{\pi}{2}\) – x
(4) x – π
விடை:
(3) \(\frac{\pi}{2}\) – x

கேள்வி 2.
sin^-1x + sin^-1y = \(\frac{2 \pi}{3}\); எனில் cos^-1 x + cos^-1 y என்பதன் மதிப்பு
(1) \(\frac{2 \pi}{3}\)
(2) \(\frac{\pi}{3}\)
(3) \(\frac{\pi}{6}\)
(4) π
விடை:
(2) \(\frac{\pi}{3}\)
குறிப்பு:
நமக்கு தெரியும்,
sin^-1x + cos^-1x = \(\frac{\pi}{2}\); அல்லது
cos^-1x = \(\frac{\pi}{2}\) – sin^-1x
∴ cos^-1 x + cos^-1 y = \(\frac{\pi}{2}\) – sin^-1x + \(\frac{\pi}{2}\) – sin^-1y

கேள்வி 3.
sin^-1 \(\frac{3}{5}\) – cos^-1 \(\frac{12}{13}\) + sec^-1 \(\frac{5}{3}\) – cosec^-1 \(\frac{13}{12}\) என்பதன் மதிப்பு
(1) 2π
(2) π
(3) 0
(4) tan^-1\(\frac{12}{65}\)
விடை:
(3) 0

கேள்வி 4.
sin^-1 x = 2 sin^-1 α -க்கு ஒரு தீர்வு இருந்தால், பின்னர்
(1) |α| ≤ \(\frac{1}{\sqrt{2}}\)
(2) |α| ≥ \(\frac{1}{\sqrt{2}}\)
(3) |α| < \(\frac{1}{\sqrt{2}}\) (4) |α| > \(\frac{1}{\sqrt{2}}\)
விடை:
(1) |α| ≤ \(\frac{1}{\sqrt{2}}\)
குறிப்பு:
sin^-1x = 2sin^-1α

கேள்வி 5.
பின்வருவனவற்றில் எம்மதிப்புகளுக்கு sin^-1 (cos x) = \(\frac{\pi}{2}\) – x க்கு மெய்யாகும்
(1) -π ≤ x ≤ 0
(2) 0 ≤ x ≤ π
(3) –\(\frac{\pi}{2}\) ≤ x ≤ \(\frac{\pi}{2}\)
(4) –\(\frac{\pi}{4}\) ≤ x ≤ \(\frac{3 \pi}{4}\)
விடை:
(2) 0 ≤ x ≤ π

கேள்வி 6.
sin^-1 x + sin^-1 y + sin^-1 z = \(\frac{3 \pi}{2}\) எனில் x²⁰¹⁷ + y²⁰¹⁸ + z²⁰¹⁹ – \(\frac{9}{x^{101}+y^{101}+z^{101}}\) – ன் மதிப்பு
(1) 0
(2) 1
(3) 2
(4) 3
விடை:
(1) 0

கேள்வி 7.
சில x ∈ R-க்கு cot^-1x = \(\frac{2 \pi}{5}\) எனில் tan^-1x-ன் மதிப்பு
(1) – \(\frac{\pi}{10}\)
(2) \(\frac{\pi}{5}\)
(3) \(\frac{\pi}{10}\)
(4) –\(\frac{\pi}{5}\)
விடை:
(3) \(\frac{\pi}{10}\)

கேள்வி 8.
f (x) = sin^-1\(\sqrt{x-1}\) என வரையறுக்கப்படும் சார்பின் சார்பகம்
(1) [1, 2]
(2) [-1, 1]
(3) [0, 1]
(4) [-1, 0]
விடை:
(1) [1, 2]
குறிப்பு:
-1 ≤ x – 1 ≤ 1 மற்றும் x – 1 ≥ 0
⇒ 0 ≤ x – 1 ≤ 1 ⇒ 1 ≤ x ≤ 2

கேள்வி 9.
x = \(\frac{1}{5}\) எனில் , cos(cos^-1 x + 2sin^-1 x)-ன் மதிப்பு
(1) –\(\sqrt{\frac{24}{25}}\)
(2) \(\sqrt{\frac{24}{25}}\)
(3) \(\frac{1}{5}\)
(4) –\(\frac{1}{5}\)
விடை:
(4) –\(\frac{1}{5}\)
குறிப்பு:
cos (cos^-1x + sin^-1x + sin^-1x)
⇒ cos (\(\frac{\pi}{2}\) + sin^-1x) = – sin (sin^-1x) = -x = –\(\frac{1}{5}\)
[∵ cos^-1x + sin^-1x = \(\frac{\pi}{2}\)]

கேள்வி 10.
tan^-1 \(\left(\frac{1}{4}\right)\) + tan^-1 \(\left(\frac{2}{9}\right)\) என்பதின் சமம்
(1) \(\frac{1}{2}\)cos^-1\(\left(\frac{3}{5}\right)\)
(2) \(\frac{1}{2}\)sin^-1\(\left(\frac{3}{5}\right)\)
(3) \(\frac{1}{2}\)tan^-1\(\left(\frac{3}{5}\right)\)
(4) \(\frac{1}{2}\)tan^-1\(\left(\frac{1}{2}\right)\)
விடை:
(4) \(\frac{1}{2}\)tan^-1\(\left(\frac{1}{2}\right)\)
குறிப்பு:

கேள்வி 11.
சார்பு f(x) = sin^-1 x (x² – 3) x இருக்கும் இடைவெளி
(1) [–1, 1]
(2) [\(\sqrt{2}\), 2]
(3) [-2, –\(\sqrt{2}\)] ∪ [ \(\sqrt{2}\), 2]
(4) [-2, –\(\sqrt{2}\)]
விடை:
(3) [-2, –\(\sqrt{2}\)] ∪ [ \(\sqrt{2}\), 2]
குறிப்பு:
-1 ≤ x² – 3 ≤ 1
⇒ 2 ≤ x² ≤ 4
∴ 2 ≤ x² மற்றும் x² ≤ 4

கேள்வி 12.
cot^-1 2 மற்றும் cot^-1 3 ஆகியன ஒரு முக்கோணத்தின் இரு கோணங்கள் எனில், மூன்றாவது கோணமானது
(1) \(\frac{\pi}{4}\)
(2) \(\frac{3 \pi}{4}\)
(3) \(\frac{\pi}{6}\)
(4) \(\frac{\pi}{3}\)
விடை:
(2) \(\frac{3 \pi}{4}\)

கேள்வி 13.

(1) x² – x – 6 = 0
(2) x² – x – 12 = 0
(3) x² + x – 12 = 0
(4) x² + x – 6 = 0
விடை:
(2) x² – x – 12 = 0

கேள்வி 14.
sin^-1 (2 cos²x – 1) + cos^-1 (1 – 2sin² x) =
(1) \(\frac{\pi}{2}\)
(2) \(\frac{\pi}{3}\)
(3) \(\frac{\pi}{4}\)
(4) \(\frac{\pi}{6}\)
விடை:
(1) \(\frac{\pi}{2}\)

கேள்வி 15.
cot^-1 \((\sqrt{\sin \alpha})\) + tan^-1 \((\sqrt{\sin \alpha})\) = u எனில்,
cos 2u பன் மதிப்பு
(1) tan²α
(2) 0
(3) -1
(4) tan 2α
விடை:
(3) -1

கேள்வி 16.
|x| ≤ 1, எனில், 2tan^-1 x – sin^-1 \(\frac{2 x}{1+x^{2}}\) என்பதற்கு சமம்
(1) tan^-1x
(2) sin^-1x
(3) 0
(4) π
விடை:
(3) 0

கேள்வி 17.
tan^-1x – cot^-1x = tan^-1\(\left(\frac{1}{\sqrt{3}}\right)\) என்ற
சமன்பாட்டிற்கு
(1) தீர்வு இல்லை
(2) ஒரேயொரு தீர்வு
(3) இரு தீர்வுகள்
(4) எண்ண ற்றத் தீர்வுகள்
விடை:
(2) ஒரேயொரு தீர்வு .

கேள்வி 18.
sin^-1x+ cos^-1 \(\) = \(\) எனில் x-ன் மதிப்பு
(1) \(\frac{1}{2}\)
(2) \(\frac{1}{\sqrt{5}}\)
(3) \(\frac{2}{\sqrt{5}}\)
(4) \(\frac{\sqrt{3}}{2}\)
விடை:
(2) \(\frac{1}{\sqrt{5}}\)

கேள்வி 19.
sin^-1 \(\frac{x}{5}\) + cos^-1 \(\frac{5}{4}\) = \(\frac{\pi}{2}\) எனில், x-ன் மதிப்பு
(1) 4
(2) 5
(3) 2
(4) 3
விடை:
(4) 3

கேள்வி 20.
|x| < 1 எனில், sin(tan-1 x) -ன் மதிப்பு

விடை:
(4) \(\frac{x}{\sqrt{1+x^{2}}}\)

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 3 சமன்பாட்டியல் Ex 3.4 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 3 சமன்பாட்டியல் Ex 3.4

கேள்வி 1.
தீர்க்க:
(i) (x – 5)(x – 7)(x + 6)(x + 4) = 504
தீர்வு:
உறுப்புகளை பின்வருமாறு மறுவரிசைப்படுத்த
(x – 5) (x + 4) (x – 7) (x + 6) = 504
⇒(x² – x – 20) (x² – x – 42) = 504

பிரதியிடு x² – x = y
⇒ (y – 20) (y – 42) = 504
⇒ y² – 62y + 840 – 504 = 0
⇒ y² – 62y + 336 = 0
⇒ (y – 56) (y – 6) = 0
⇒ y = 56, 6
நிலை (i) y = 56 எனில், x² – x = 56

⇒ x² – x – 56 = 0
⇒ (x – 8) (x + 7) = 0
⇒ x = 8, -7
நிலை (ii)
y = 6 எனில்,
x² – x = 6

⇒ (x – 3) (x + 2) = 0
⇒ x = 3, – 2
எனவே மூலங்கள் -2, 3, 8, -7.

(ii) (x – 4)(x – 7)(x – 2)(x + 1) = 16
தீர்வு:
கொடுக்கப்பட்ட (x – 4) (x – 7) (x – 2) (x + 1) = 16
உறுப்புகளை பின்வருமாறு மறு வரிசைப்படுத்த
(x – 4) (x – 2) (x – 7) (x + 1) = 16
⇒ (x² – 6x + 8) (x² – 6x – 7) = 16
பிரதியிடு x² – 6x = y
⇒ (y + 8) (y – 7) = 16
⇒ y² + y – 56 – 16 = 0
⇒ y² + y – 72 = 0

⇒ (y + 9) (y – 8) = 0
⇒ y = -9, 8
நிலை (i)
y = -9 எனில்,
x² – 6x = -9
⇒ x² – 6x + 9 = 0
⇒ (x – 3)² = 0
⇒ x = 3, 3
நிலை (ii)
y = 8 எனில்,

⇒ x² – 6x = 8
⇒ x² – 6x – 8 = 0

∴ மூலங்கள் 3.3.3 + \(\sqrt{17}\) மற்றும் 3 – \(\sqrt{17}\)

கேள்வி 2.
தீர்க்க : (2.3 – 1)(x + 3)(x – 2)(2x + 3) + 20 = 0
நீர்வு:
உறுப்புகளை பின்வருமாறு மறு வரிசைப்படுத்த
(2x – 1) (2x + 3) (x + 3) (x – 2) + 20 = 0
⇒ (4x² + 6² – 2x – 3) (x² – 2x + 3x – 6) + 20 =0
⇒ (4x² + 4x – 3) (x² + x – 6) + 20 = 0
பிரதியிட x² + x = y
⇒ (4y – 3) (y – 6) + 20 = 0
⇒ 4y² – 24y – 3y + 18 + 20 = 0
⇒ 4y² – 27y + 38 = 0
⇒ (y – 2) (4y – 19) = 0
y = 2, \(\frac{19}{4}\)

நிலை (i)
y = 2 எனில்,
x² + x = 2
⇒ x² + x – 2 = 0
⇒ (x + 2) (x – 1) = 0
⇒ x = -2, 1

நிலை (ii)

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 7 வகை நுண்கணிதத்தின் பயன்பாடுகள் Ex 7.7 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 7 வகை நுண்கணிதத்தின் பயன்பாடுகள் Ex 7.7

கேள்வி 1.
கீழ்க்காணும் சார்புகளுக்கு குழிவு இடைவெளிகள் மற்றும் வளைவு மாற்றுப் புள்ளிகளைக் காண்க:
(i) f (x) = x(x – 4)³
(ii) f(x) = sin x + cos x, 0 < x < 2π
(iii) f (x) = \(\frac{1}{2}\) (e^x – e^-x)
தீர்வு:
(i) f (x) = x(x – 4)³
கொடுக்கப்பட்ட f (x) = x (x – 4)³
f'(x) = x .3(x – 4)² + (x – 4)³ (1)
= 3x (x – 4)² + (x – 4)³
= (x – 4)² (3x + x – 4)
= (x – 4)² (4x – 4)
= 4 (x – 1) (x – 4)²
f”(x) = 4 [(x – 1)² (x – 4) + (x – 4)² (1)]
= 4 [2(x – 4)(x – 1) + (x – 4)²]
= 4(x – 4) [2x – 2 + x – 4)]
= 4(x – 4) (3x – 6)
= 12 (x – 4) (x – 2)
f”(x) = 0
⇒ 12 (x – 4) (x – 2) = 0
⇒ x = 2, 4
(-∞, 2) (2, 4) மற்றும் (4, ∞) தேவையான இடைவெளிகள் ஆகும்.

∴ (-∞, 2) (4, ∞) ல் வளைவரை மேல்நோக்கி குழிவுடையது மற்றும் (2, 4) கீழ் நோக்கி குழிவுடையது. f”(x) -ன் குறி x = 2 மற்றும் x = 4 ஐ கடக்கும் போது!
மாறுவதால் வளைவு மாற்றப் புள்ளிகள் (2, f (2)) மற்றும் (4, f (4)) வளைவு மாற்றப் புள்ளிகளாகும்.
f(2) = 2(2 – 4)³
= 2 (-2)³ = 2 (-8) = -16
f(4) = 4 (4 – 4)³ = 0
∴ வளைவு மாற்றப்புள்ளிகள் (2,- 16) மற்றும் (4, 0) ஆகும்.

(ii) f (x) = sin x + cos x, 0 < x < 2π
கொடுக்கப்பட்ட f (x) = sin x + cos x, 0 < x < 2π
f'(x) = cos x – sin x
f”(x) = sin x – cos x
∴ f”(x) = 0
⇒ – sin x – cos x = 0
⇒ – sin x = cos x
⇒ sin (-x) = cos x
⇒ x = \(\frac{3 \pi}{4}, \frac{7 \pi}{4}, 2 \pi\)
∴ சாத்தியமாக இடைவெளிகள் \(\left(0, \frac{3 \pi}{4}\right)\left(\frac{3 \pi}{4}, \frac{7 \pi}{4}\right)\) மற்றும் \(\left(\frac{7 \pi}{4}, 2 \pi\right)\)

∴ f(x) -ல் \(\left(\frac{3 \pi}{4}, \frac{7 \pi}{4}\right)\) ஆனது மேல் நோக்கி குழிவடையது மற்றும் \(\left(0, \frac{3 \pi}{4}\right)\left(\frac{7 \pi}{4}, 2 \pi\right)\) கீழ்நோக்கி குழிவுடையது. f”(x) -ன் குறியானது \(\frac{3 \pi}{4}\) -ஐ கடக்கும் போது குறையிலிருந்து மிகையாகவும் மற்றும் \(\frac{7 \pi}{4}\) -ஐ கடக்கும் போது மிகையிலிருந்து குறையாக மாறுவதால், f (x) ஆனது வளைவு மாற்றப் புள்ளிகளாக \(\left(\frac{3 \pi}{4}, f\left(\frac{3 \pi}{4}\right)\right)\) மற்றும் \(\left(\frac{7 \pi}{4}, f\left(\frac{7 \pi}{4}\right)\right)\) -ஐ கொண்டிருக்கும்.

∴ வளைவு மாற்றப்புள்ளிகள் \(\left(\frac{3 \pi}{4}, 0\right)\) மற்றும் \(\left(\frac{7 \pi}{4}, 0\right)\) ஆனம்

(iii) f (x) = \(\frac{1}{2}\) (e^x – e^-x)
f(x) ஆனது x ∈ (-∞, ∞)-ல்வரையறுக்கப்படுகிறது மற்றும் f (x).
f'(x) = \(\frac{1}{2}\) (e^x – e^-x)
f”(r) = \(\frac{1}{2}\) (e^x – e^-x)
f”(x) = 0
⇒ \(\frac{1}{2}\) (e^x – e^-x) = 0 ⇒ e^x – e^-x = 0
⇒ e^x = e^-x ⇒ e^x = \(\frac{1}{e^{x}}\)
⇒ e^2x = 1 ⇒ e^2x = e⁰
⇒ 2x = 0 ⇒ x = 0
சாத்தியமான இடைவெளிகள் (-∞, 0) மற்றும் (0, ∞)

∴ f(x) -ல் (0, ∞) ஆனது மேல் நோக்கி குழிவு மற்றும் (-∞, 0)-ல் கீழ்நோக்கி குழிவு.
f”(x) -ன் குறியானது x = 0 வை கடக்கும் போது குறையிலிருந்து மிகையாக மாறுவதால் வளைவு மாற்றுப்புள்ளி (0, f (0)) ஆகும்.
f(0) = \(\frac{1}{2}\) (e⁰ – e⁰) = – (1 – 1) = 0
∴ வளைவு மாற்றப்புள்ளி (0, 0) ஆகும்.

கேள்வி 2.
இரண்டாம் வகைக்கெழு சோதனையை பயன்படுத்தி இடஞ்சார்ந்த அறுதி மதிப்புகளைக் காண்க.
(i) f(x) = -3x⁵ + 5x³
(ii) f(x) = x log x
(iii) f(x) = x² e^-2x
தீர்வு:
(i) f (x) = -3x⁵ + 5x³
f(x) = -3x⁵ + 5x³
f'(x) = -15x⁴ + 15x⁰
f'(x) = 0
⇒ – 15x⁴ + 15x² = 0
⇒ 15x² (1 – x²) = 0
⇒ x² = 0, 1 – x² = 0
⇒ x = 0, x = 1, x = -1
∴ தேக்கநிலை எண்கள் 0, 1,-1 ஆகும்.
f”(x) = – 60x³ + 30x
f”(0) = 0
f”(1) = – 60(1)³ + 30 (1)
= – 60 + 30 = -30
f”(-1) = – 60(-1)³ + 30 (-1)
= 60 – 30 = 30
f”(1) < 0 ஆகையால் அது இடஞ்சார்ந்த பெருமத்தை x = 1-ல் கொண்டிருக்கும்.
∴ f(1) = -3(-1)⁵ + 5(-1)³
= – 3 + 5 = 2
f”(-1) > 0 ஆகையால் இடஞ்சார்ந்த பெருமத்தை x= -1-ல் கொண்டிருக்கும்.
∴ f(-1) = -3(1)⁵ + 5(1)³
= 3 – 5 = -2
∴ 2 -ல் இடஞ்சார்ந்த பெரு மதிப்பு x = 1 மற்றும் -2-ல் இடஞ்சார்ந்த சிறும மதிப்பு.x = -1 ஆகும்.

(ii) f(x) = x log x
f(x) = x log x
f'(x) = x . \(\frac{1}{x}\) + log x (1)
= 1 + log x
f'(x) = 0
⇒ 1 + log x = 0
⇒ log x = -1 |
⇒ x = e^-1 = \(\frac{1}{e}\)
∴ நிலை எண்கள் \(\frac{1}{e}\)
f”(x) = \(\frac{1}{x}\)
\(f^{\prime \prime}\left(\frac{1}{e}\right)=\frac{1}{\frac{1}{e}}\) = e > 0
f”\(\left(\frac{1}{e}\right)\) > 0 ஆதலால் x = \(\frac{1}{e}\) ‘-ல் இடஞ்சார்ந்த சிறுமம் அமைந்துள்ளது.
∴ \(f\left(\frac{1}{e}\right)=\frac{1}{e} \log \frac{1}{e}\)
= \(\frac{1}{e} \log e^{-1}\)
= \(\frac{-1}{e} \log _{e} e=\frac{-1}{e}(1)=\frac{-1}{e}\)
∴ –\(\frac{1}{e}\) –ல் இடஞ்சார்ந்த சிறும் மதிப்பு x = \(\frac{1}{e}\) அமைந்துள்ளது.

(iii) f(x) = x² e^-2x
f(x) = x² e^-2x
f'(x) = x² (-2) e^-2x + e^-2x (2x)
f'(x) = 2xe^-2x (1 – x)
f'(x) = 0
⇒ 2x e^-2x (1 – x) = 0
⇒ x = 0, 1
∴ நிலை எண்கள் x = 0, 1 ஆகும்.
f”(x) = [x e^-2x (-1) + x (-2)e^-2x – (1 – x) + 1 e^-2x (1 – x)]
= 2e^-2x (-x – 2x + 2x² + 1 – x)
= 2e^-2x (2x² – 4x + 1)
f”(0) = 2(1) (1)= 2 > 0
f”(1) = 2e^-2 (2 – 4 + 1)
= 2e^-2 (-1)
= -2e^-2 = \(\frac{-2}{e^{2}}\) < 0 f”(0) > 0 ஆதலால் இடஞ்சார்ந்த சிறுமம் x = 0 -ல் ‘ உள்ளது.
∴ f (0) = 0² e⁰ = 0
f”(1) < 0 ஆதலால் இடஞ்சார்ந்த சிறுமம் x = 1-ல் அமைந்துள்ளது.
∴ f(1) = 1² e^-2(1) = e^-2 = \(\frac{1}{e^{2}}\)

கேள்வி 3.
f(x) = 4x³ + 3x² – 6x + 1 என்ற சார்பிற்கு ஓரியல்பு இடைவெளிகள், இடஞ்சார்ந்த அறுதி மதிப்புகள், குழிவு இடைவெளிகள் மற்றும் வளைவு மாற்றுப் புள்ளிகளைக் காண்க.
தீர்வு:
கொடுக்கப்பட்ட f (x)= 4x³ + 3x² – 6x + 1
f'(x) = 12x² + 6x – 6
f”(x) = 24x + 6
f'(x) = 0

⇒ 12 x² + 6x – 6 = 0
⇒ 2x² + x – 1 = 0
⇒ (x+ 1)(2x- 1) = (0
⇒ x= -1, \(\frac{1}{2}\)
நிலை எண்கள் -1, \(\frac{1}{2}\) ஆகும். தேவையான ஒரியல்பு இடைவெளிகள் (-∞, -1) \(\left(-1, \frac{1}{2}\right)\left(\frac{1}{2}, \infty\right)\) ஆகும்.

∴ f(x) -ல் (-∞, -1) \(\left(\frac{1}{2}, \infty\right)\) ஆனது திட்டமாக ஏறும் \(\left(-1, \frac{1}{2}\right)\) -ல் திட்டமாக இறங்கும்.
f”(x) = 0
⇒ 24x + 6 = 0 ⇒ 24x = -6
x = \(\frac{-6}{24}=\frac{-1}{4}\)
குழிவுத் தன்மைக்கு சாத்தியமான இடைவெளிகள் \(\left(-\infty, \frac{-1}{4}\right)\left(\frac{-1}{4}, \infty\right)\) ஆகும்.

∴ f(x)-ல் \(\left(-\infty, \frac{-1}{4}\right)\), ஆனது கீழ்நோக்கிய குழிவுடையது மற்றும் \(\left(\frac{-1}{4}, \infty\right)\) -ல் மேல் நோக்கிய குழிவுடையது.

f”(x) ஆனது x = \(\frac{-1}{4}\) வழி செல்லும் போது குறி மாற்றமடைகிறது, வளைவு மாற்றுப் புள்ளிகள் \(\left(-\frac{1}{4}, f\left(-\frac{1}{4}\right)\right)\) ஆகும்.

∴ வளைவு மாற்றப்புள்ளி \(\left(\frac{-1}{4}, \frac{21}{8}\right)\) ஆகும்.
f'(x) -ல் x = -1ஆனது மிகையிலிருந்து குறையாக மாறுவதால், அது இடஞ்சார்ந்த சிறுமத்தை x=-1-ல் கொண்டுள்ளது
∴ f(-1) = 4 (-1)³ + 3 (-1)² – 6(-1) + 1
= -4 + 3 + 6 + 1 = 6
f'(x) ஆனது குறையிலிருந்து மிகையாக x = \(\frac{1}{2}\) குறி மாற்றமடைவதால், அது இடஞ்சார்ந்த மதிப்பை x = \(\frac{1}{2}\) கொண்டிருக்கும்.

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 8 வகையீடுகள் மற்றும் பகுதி வகைக்கெழுக்கள் Ex 8.7 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 8 வகையீடுகள் மற்றும் பகுதி வகைக்கெழுக்கள் Ex 8.7

கேள்வி 1.
பின்வரும் ஒவ்வொரு சார்பும் சமபடித்தானதா இல்லையா எனக்கண்டு சமபடித்தானது எனில் அதன் படியையும் காண்க.
(i) f(x, y) = x² y + 6x³ + 7
(ii) h (x,y) = \(\frac{6 x^{2} y^{3}-\pi y^{5}+9 x^{4} y}{2020 x^{2}+2019 y^{2}}\)
(iii) g (x, y, z) = \(\frac{\sqrt{3 x^{2}+5 y^{2}+z^{2}}}{4 x+7 y}\)
(iv) U (x, y, z) = xy + sin\(\left(\frac{y^{2}-2 x^{2}}{x y}\right)\)
தீர்வு:
f(x, y) = x² y + 6x³ + 7
கொடுக்கப்பட்ட f (x, y) = x² y + 6x³ + 7
f(λx, λy) = λ²x²λy + 6λ³x² +7
= λ³x²y + 6λ³x³ + 7
≠ λf(x, y)
∴ ஆனது சமப்படித்தான் சார்பு அல்ல

(ii) h (x,y) = \(\frac{6 x^{2} y^{3}-\pi y^{5}+9 x^{4} y}{2020 x^{2}+2019 y^{2}}\)
கொடுக்கப்பட்ட ர்

∴ h (x, y) ஆனது படி 3 உடைய சமப்படித்தான் சார்பு

(iii) g (x, y, z) = \(\frac{\sqrt{3 x^{2}+5 y^{2}+z^{2}}}{4 x+7 y}\)
கொடுக்கப்பட்ட ர

∴ g(x, y, z) ஒரு படி ) உடைய சமப்படித்தான சார்பு.

(iv) U (x, y, z) = xy + sin\(\left(\frac{y^{2}-2 x^{2}}{x y}\right)\)
கொடுக்கப்பட்ட

∴ u (x, y, z) ஒரு சமப்படித்தான சார்பல்ல.

கேள்வி 2.
f(x, y) = x³ – 2x² y + 3xy² + y³ என் சார்பு சமபடித்தானது என நிறுவுக. f-ன் படியைக் கணக்கிட்டு f-க்கு ஆய்லரின் தேற்றத்தைச் சரிபார்க்க .
தீர்வு:
கொடுக்கப்பட்ட f (x, y) = x³ – 2x² y + 3xy² + y³ ………….. (1)
f (tx, ty)) = (tx)³ – 2(tx)² (ty) + 3 (tx) (ty)² + (ty)³
= t³x³ – 2t² x² ty + 3txt² y² + t³y³
= t³ (x³ – 2x²y + 3xy² + y³) f(tx, ty) = t³(x, y)
∴ ஆனது படி 3 உடைய சமப்படித்தான் சார்பு. சமன்பாடு ‘x’ மற்றும் ‘y’ பொறுத்து (1) ஐ பகுதி வகையிட கிடைப்பது
\(\frac{\partial f}{\partial x}\)= 3x² – 4xy + 3y²
⇒ \(x \frac{\partial f}{\partial x}\)= 3x² – 4xy + 3xy² …………… (2)
\(\frac{\partial f}{\partial x}\) = -2x² + 6xy + 3y²
⇒ \(y \frac{\partial f}{\partial y}\) = y = -2x² + 6xy² + 3y² ……….. (3)
(2) மற்றும் (3) ஐ கூட்ட கிடைப்பது,
[latexx \frac{\partial f}{\partial x}+y \frac{\partial f}{\partial y}][/latex] = 3x² – 4x²y + 3xy² – 2x²y + 6xy² +3y³
= 3x² – 6x²y + 9xy² + 3y³
= 3(x³ – 2x²y – 3xy² + y³)
= 3f    [(1) ஐ பயன்படுத்தி]
∴ \(x \frac{\partial f}{\partial x}+y \frac{\partial f}{\partial y}\) = 3f = nf இங்கு f (x, y ) இன் படி 3 ஆகும்.
ஆகையால், ஆய்லரின் தேற்றம் சரிபார்க்கப்பட்டது.

கேள்வி 3.
g (x, y) = x log \(\left(\frac{y}{x}\right)\) என்ற சார்பு சமபடித்தானது என நிறுவுக. g-ன் படியைக் கணக்கிட்டு , g-க்கு ஆய்லரின் தேற்றத்தைச் சரிபார்க்க.
தீர்வு :
கொடுக்கப்பட்ட g (x, y) = x log\(\left(\frac{y}{x}\right)\)
g (λx, λy) = λx log\(\left(\frac{\lambda y}{\lambda x}\right)\)
= λx log\(\left(\frac{y}{x}\right)\)
= λ’ g (x, y)
∴ g (x,y) படி 1 உடைய ஒரு சம்படித்தான சார்பு.
\(x \frac{\partial g}{\partial x}+y \frac{\partial g}{\partial y}\) = 1 g என பரிசோதிக்க
[ஆய்லரின் தேற்றம்]

எனவே தேற்றம் சரிபார்க்கப்பட்டது.

கேள்வி 4.
u(x, y) = \(\frac{x^{2}+y^{2}}{\sqrt{x+y}}\) எனில், \(x \frac{\partial u}{\partial x}+y \frac{\partial u}{\partial y}=\frac{3}{2} u\) அது என நிறுவுக.
தீர்வு:
கொடுக்கப்பட்ட u (x, y) = \(\frac{x^{2}+y^{2}}{\sqrt{x+y}}\)
u (λx, λy) = \(\frac{\lambda^{2} x^{2}+\lambda^{2} y^{2}}{\sqrt{\lambda x+\lambda y}}=\frac{\lambda^{2}\left(x^{2}+y^{2}\right)}{\sqrt{\lambda}(\sqrt{x+y})}\)
= λ^{\(2-\frac{1}{2}\)} u (x, y) = λ^{\(\frac{3}{2}\)} u (x,y)
∴ u (x,y) படி , உடைய சமப்படித்தான சார்பு.
∴ ஆய்லரின் தேற்றப்படி,
\(x \frac{\partial u}{\partial x}+y \frac{\partial u}{\partial y}=n . u \Rightarrow x \frac{\partial u}{\partial x}+y \frac{\partial u}{\partial y}=\frac{3}{2} u\)
எனவே நிரூபிக்கப்பட்டது.

கேள்வி 5.
v(x, y) = log\(\left(\frac{x^{2}+y^{2}}{x+y}\right)\), எனில் \(x \frac{\partial v}{\partial x}+y \frac{\partial v}{\partial y}=1\) என நிறுவுக.
தீர்வு:
கொடுக்கப்பட்ட v (x, y) = log \(\left(\frac{x^{2}+y^{2}}{x+y}\right)\)
log \(\left(\frac{x^{2}+y^{2}}{x+y}\right)\) சமப்படுத்தானது அல்ல
f(x, y) = \(\frac{x^{2}+y^{2}}{x+y}\) என்க.
⇒ v = log f
⇒ e^v = f ………………. (1)
இங்கு , f (tx, ty) = \(\frac{t^{2} x^{2}+t^{2} y^{2}}{t x+t y}=\frac{t^{2}\left(x^{2}+y^{2}\right)}{t(x+y)}\)
= t’ f (x, y)
∴ f படி 1 உடைய சமப்படித்தான சார்பாகும்.
∴ ஆய்லரின் தேற்றப்படி,
⇒ \(x \frac{\partial f}{\partial x}+y \frac{\partial f}{\partial y}\) = 1 . f
(1) லிருந்து, \(\)     [(1)-ஐ பயன்படுத்தி]
⇒ \(x \cdot e^{v} \cdot \frac{\partial v}{\partial x}+y \cdot e^{v} \cdot \frac{\partial v}{\partial y}=\cdot e^{v}\)
⇒ \(x \frac{\partial v}{\partial x}+y \frac{\partial v}{\partial y}=1\)    [e^v ஆல் வகுக்கர்]

கேள்வி 6.
w(x, y, z) = log \(\left(\frac{5 x^{3} y^{4}+7 y^{2} x z^{4}-75 y^{3} z^{4}}{x^{2}+y^{2}}\right)\) எனில் \(x \frac{\partial w}{\partial x}+y \frac{\partial w}{\partial y}+z \frac{\partial w}{\partial z}\) -ஐக் காண்க.
தீர்வு:
கொடுக்கப்பட்ட

∴ f(x, y, z) ஒரு படி 5 உடைய சமப்படித்தான சார்பாகும்.
∴ ஆய்லரின் தேற்றப்படி,