Samacheer Kalvi 12th Maths Guide Chapter 8 வகையீடுகள் மற்றும் பகுதி வகைக்கெழுக்கள் Ex 8.3

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 8 வகையீடுகள் மற்றும் பகுதி வகைக்கெழுக்கள் Ex 8.3 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 8 வகையீடுகள் மற்றும் பகுதி வகைக்கெழுக்கள் Ex 8.3

கேள்வி 1.
சார்பு g(x, y) = \(\frac{3 x^{2}-x y}{x^{2}+y^{2}+3}\) க்கு எல்லை மதிப்பு இருக்குமானால், \(\lim _{(x, y) \rightarrow(1,2)}\) g (x,y) -ஐ மதிப்பிடுக.
தீர்வு:
கொடுக்கப்பட்ட

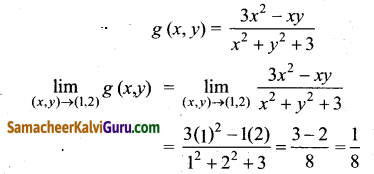
கேள்வி 2.
எல்லை மதிப்பு இருக்குமானால் \(\lim _{(x, y) \rightarrow(0,0)}\) cos \(\left(\frac{\dot{x}^{3}+y^{3}}{x+y+2}\right)\) -ஐ மதிப்பிடுக.
தீர்வு:
\(\lim _{(x, y) \rightarrow(0,0)}\) cos \(\left(\frac{\dot{x}^{3}+y^{3}}{x+y+2}\right)\)
= cos \(\left(\frac{0+0}{0+0+2}\right)\) = cos 0 = 1

கேள்வி 3.
(x, y) + (0, 0)- க்கு f(x, y) = \(\frac{y^{2}-x y}{\sqrt{x}-\sqrt{y}}\) எனில், \(\lim _{(x, y) \rightarrow(0,0)}\) f(x, y) = 0 என நிறுவுக.
தீர்வு:

கேள்வி 4.
எல்லை மதிப்பு இருக்குமானால்,
\(\lim _{(x, y) \rightarrow(0,0)} \cos \left(\frac{e^{x} \sin y}{y}\right)\) -ஐ மதிப்பிடுக.
தீர்வு:

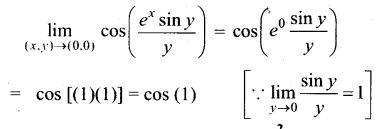
கேள்வி 5.
(x, y) ≠ (0,0)-க்கு g (x, y) = \(\frac{x^{2} y}{x^{4}+y^{2}}\), மற்றும் g(0, 0) = 0 என்க .
(i) ஒவ்வொரு y = mx, m ∈ ℝ நேர்கோட்டுப் பாதையிலும் \(\lim _{(x, y) \rightarrow(0,0)}\) g(x, y) = 0 என நிறுவுக.
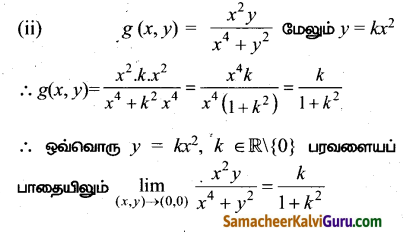
(ii) ஒவ்வொரு y = kx², k ∈ ℝ\{0} பரவளையப் பாதையிலும் \(\lim _{(x, y) \rightarrow(0,0)}\) g (x, y) = \(\frac{k}{1+k^{2}}\) என நிறுவுக.”
தீர்வு:
(i) கொடுக்கப்பட்ட

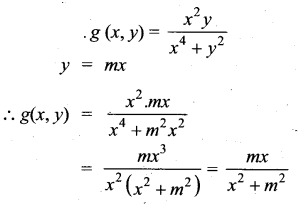
இங்கு , \(\lim _{(x, y) \rightarrow(0,0)}\) g(x, y) = \(\frac{m(0)}{0^{2}+m^{2}}=\frac{0}{m^{2}}\) = 0, m இன் எல்லா மதிப்புகளுக்கும்
∴ ஒவ்வொரு y = mx, m ∈ ℝ. நேர்க்கோட்டுப்
பாதையிலும் \(\lim _{(x, y) \rightarrow(0,0)}\) (x, y) = 0

கேள்வி 6.
சார்பு f(x, y)= \(\frac{x^{2}-y^{2}}{y^{2}+1}\), ஒவ்வொரு (x, y) ∈ ℝ² -க்கும் தொடர்ச்சியானது என நிறுவுக.
தீர்வு:
(a, b) ∈ ℝ² என்பது ஒரு தன்னிச்சையான புள்ளி என்க . f இன் தொடர்ச்சி தன்மையை (a, b)-இல் ஆராய்வோம்.

அதாவது f இல் (a, b) தொடர்ச்சிக்கான மூன்று நிபந்தனைகளும் நிறைவு செய்யப்படுகிறதா சோதிப்போம்.

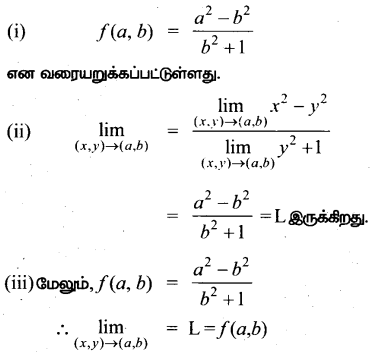
எனவே f எல்லா மூன்று நிபந்தனைகளும் (a, b) என்ற R² இன் தன்னிச்சையான புள்ளியில் பூர்த்தி செய்வதால் ஆனது R² இன் எல்லா புள்ளிகளிலும் தொடர்ச்சியுடையது.

கேள்வி 7.
சார்பு g(x, y) = \(\frac{e^{y} \sin x}{x}\), x ≠ 0 மற்றும் g(0, 0) = 1 என்க. புள்ளி (0,0) இல் தொடர்ச்சியானது என நிறுவுக.
தீர்வு:
கொடுக்கப்பட்ட g (x, y) = \(\frac{e^{y} \sin x}{x}\) இங்கு x ≠ 0 மற்றும் g(0, 0) = 1
எல்லா (x, y) ∈ ℝ² க்கும் g சார்பு ஆனது வரையறுக்கப்பட்டுள்ளது.
g-இல் (0, 0) க்கான ட எல்லை மற்றும் L = g(0, 0) = 1 என சோதிக்க.

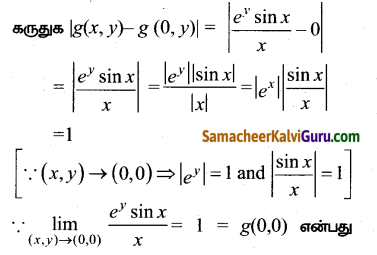
(0,0 ) வில் தொடர்ச்சியுடையது என நிரூபிக்கிறது.
∴ புள்ளி (0, 0) g(x, y) தொடர்ச்சியுடையது.