Samacheer Kalvi 12th Maths Guide Chapter 5 இரு பரிமாண பகுமுறை வடிவியல் – II Ex 5.1

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 5 இரு பரிமாண பகுமுறை வடிவியல் – II Ex 5.1 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 5 இரு பரிமாண பகுமுறை வடிவியல் – II Ex 5.1

கேள்வி 1.
ஆரம் 5 செ.மீ. அலகுகள் உடையதும், x-அச்சை ஆதிப்புள்ளியில் தொட்டுச் செல்வதுமான வட்டத்தின் சமன்பாட்டைத் தருவிக்க.
தீர்வு:
கொடுக்கப்பட்ட r = 5 செ.மீ

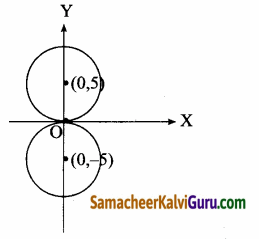
வட்டம் x அச்சை தொட்டுச் செல்வதால் அதனுடைய மையம் (0, ±5)
வட்டத்தின் சமன்பாடு (x – h)² + (y – k)² = r²
⇒ (x – 0)² + (y ± 5)² = 5²

⇒ x² + y² + 10y = 0

கேள்வி 2.
(2, -1) என்ற புள்ளியை மையமாகவும், (3, 6) என்ற புள்ளி வழிச் செல்வதுமான வட்டத்தின் சமன்பாடு காண்க.
தீர்வு:

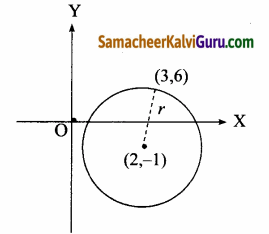
கொடுக்கப்பட்ட (2, -1) மையம் மற்றும் (3, 6) புள்ளி வழிச் செல்கிறது.
∴ r = இடைப்பட்ட தூரம் (2, -1) மற்றும் (3, 6)க்கு
= \(\sqrt{(2-3)^{2}+(-1-6)^{2}}\)
= \(\sqrt{(-1)^{2}+(-7)^{2}}\)
= \(\sqrt{1+49}\) = \(\sqrt{50}\)
∴ வட்டத்தின் சமன்பாடு
(x – h)² + (y – k)² = r²
(x – 2)² + (y + 1)² = \((\sqrt{50})\)²
⇒ (x – 2)² + (y + 1)² = 50

கேள்வி 3.
இரு அச்சுக்களையும் தொட்டுச் செல்வதும், (4, -2) என்ற புள்ளி வழிச் செல்வதுமான வட்டத்தின் சமன்பாடு காண்க.
தீர்வு:
வட்டமானது இரு அச்சுகளையும் தொட்டு செல்வதால் அதனுடைய சமன்பாடு
(x – a)² + (y – a)² = a² … (1)
இது (-4, -2) வழிச் செல்கிறது
∴ (-4 – a)² + (-2 – a)² = a²

⇒ a² + 12a + 20 = 0
⇒ (a + 10)(a + 2) = 0
a = -10 அல்ல து – 2

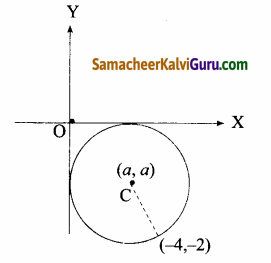
நிலை (i)
a = -10 எனில், (1) ஆனது
(x + 10)² + (y + 10)² = 10²

⇒ x² + y² + 20x + 20y + 100 = 0
நிலை (ii)
a = -2 எனில், (1) ஆனது
(x + 2)² + (y + 2)² = 2²

⇒ x² + y² + 4x + 4y + 4 = 0
ஆகையால் வட்டங்களின் சமன்பாடுகள்
x² + 4² + 4x + 4y + 4 = 0
அல்லது x² + y² + 20x + 20y + 100 = 0

கேள்வி 4.
மையம் (2, 3) உடையதும் 3x – 2y – 1 = 0 மற்றும் 4x + y – 27 = 0 என்ற கோடுகள் வெட்டும் புள்ளி வழிச் செல்வதுமான வட்டத்தின் சமன்பாடு காண்க.
தீர்வு:
கொடுக்கப்பட்ட மையம் (2, 3)
தீர்க்க 3x – 2y = 1 ….. (1)
மற்றும் 4x + y = 27 ….. (2)

வட்டமானது (5, 7) வழிச் செல்கிறது.
[∵ (5, 7) மற்றும் (2, 3) க்கு இடைப்பட்ட தூரம்]
r = \(\sqrt{(5-2)^{2}+(7-3)^{2}}\)
= \(\sqrt{3^{2}+4^{2}}\)
= \(\sqrt{9+16}\) = \(\sqrt{25}\) = 5
வட்டத்தின் சமன்பாடு
(x – h)² + (y – k)² = r²
⇒ (x – 2)² + (y – 3)² = 5²
⇒ x² – 4x + 4 + y² – 6y + 9 = 25
⇒ x² + y² – 4x – 6y + 13 – 25 = 0
⇒ x² + y² – 4x – 6y – 12 = 0

கேள்வி 5.
(3, 4) மற்றும் (2, -7) என்ற புள்ளிகளை விட்டத்தின் முனைப்புள்ளிகளாகக் கொண்ட வட்டத்தின் சமன்பாட்டைப் பெறுக.
தீர்வு:
கொடுக்கப்பட்ட விட்டத்தின் முனைகள் (3,4)2,-7)
∴ வட்டத்தின் சமன்பாடு
(x – x₁) (x – x₂) = (y – y₁) (y – y₂) = 0
⇒ (x – 3)(x – 2) + (y – 4)(y + 7) = 0
⇒ x² – 2x – 3x + 6 + y² + 7y – 4y – 28 = 0
⇒ x² + y² – 5x + 3y – 22 = 0

கேள்வி 6.
(1, 0), (-1, 0) மற்றும் (0, 1) என்ற புள்ளிகள் வழிச்செல்லும் வட்டத்தின் சமன்பாடு காண்க.
தீர்வு:
வட்டத்தின் சமன்பாடானது
x² + y² + 2gx + 2fy + c = 0 ….. (1)
(1, 0) வழி (1) செல்கிறது
⇒ 1 + 0 + 2g(1) + 2f(0) + c = 0
⇒ 2g + c = -1 … (2)
(-1, 0) வழி (1) செல்கிறது
⇒ (-1)² + 0 + 2g(-1) + 2f(0) + c = 0
⇒ -2g + c = -1 …(3)
மேலும் (0, 1) வழி (1) செல்கிறது
⇒ 0 + 1² + 2g(0) + 2f (1) + c = 0
⇒ 2f + c = -1 …(4)
(2) + (3) ⇒ 2c = -2
⇒ c = -1
c = -1 என (2) ல் பிரதியிட கிடைப்பது
2g – 1 = -1
⇒ 2g = 0
⇒ g = 0
c = -1 என (4) ல் பிரதியிட கிடைப்பது
2f – 1 = -1
⇒ 2f = 0
⇒ f = 0
∴ (1) லிருந்து
x² + y² + 0 + 0 – 1 = 0
⇒ x² + y² = 1

கேள்வி 7.
9π சதுர அலகுகள் பரப்பு கொண்ட வட்டத்தின் விட்டங்கள், x + y = 5 மற்றும் x – y = 1 என்ற நேர்கோடுகள் மீது அமைந்துள்ளன எனில் அந்த வட்டத்தின் சமன்பாடு காண்க.
தீர்வு:
வட்டத்தின் பரப்பு = 9π சதுர அலகுகள்
πr² = 9π ⇒ r² = 9 ⇒ r = 3
விட்டங்கள் x + y = 5 (1) மற்றும் x – y = 1 (2)
விட்டங்கள் வெட்டிக் கொள்ளும் புள்ளி மையம் என அறிவோம்.
∴ மையத்தை காண (1) மற்றும் (2) ஐ தீர்க்க.

⇒ x = 3
∴ (1) ⇒ 3 + y = 5
⇒ y = 5 – 3 = 2
∴ மையம் (3, 2)
ஆகையால் வட்டத்தின் சமன்பாடு
(x – h)² + (y – k)² = r²
(x – 3)² + (y – 2)² = 3²

⇒ x² + y² – 6x – 4y + 4 = 0

கேள்வி 8.
y = 2\(\sqrt{2}\)x+ c என்ற கோடு x² + y² = 16, என்ற வட்டத்தின் தொடுகோடு எனில், -ன் மதிப்பு காண்க.
தீர்வு:
கொடுக்கப்பட்ட வட்டத்தின் சமன்பாடு
x² + y² = 16
⇒ a² = 16
மற்றும் தொடுகோட்டின் சமன்பாடு
y = 2\(\sqrt{2}\)x + c
⇒ m = 2\(\sqrt{2}\) மற்றும் c = c
[தொடுகோடானது y = mx + c]
y = mx + c என்ற கோடு x² + y² = a² என்ற வட்டத்திற்கு தொடுகோடாக இருப்பதற்கான நிபந்தனை
c² = a² (1 + m²)
⇒ c² = 16(1 + (2\(\sqrt{2}\))²)
⇒ c² = 16(1 + 8)
⇒ c² = 16(9)
⇒ c = +4(3)
⇒ c = +12

கேள்வி 9.
x² + y² – 6x + 6y – 8 = 0 என்ற வட்டத்தின் தொடுகோடு மற்றும் செங்கோட்டுச் சமன்பாடுகளை (2, 2) என்ற புள்ளியில் காண்க.
தீர்வு:
வட்டத்தின் சமன்பாடு x² + y² – 6x + 6y – 8 = 0.
∴ (x₁, y₁) தொடுகோட்டின் சமன்பாடு
xx₁ + yy₁ – \(\frac{6}{2}\) (x + x₁) + \(\frac{6}{2}\) (y + y₁) – 8 = 0
கொடுக்கப்பட்ட (x₁, y₁), (2, 2)
(2, 2) -ல் தொடுகோட்டின் சமன்பாடு
x(2) +y(2) – 3(x + 2) + 3(y+ 2) – 8 = 0

⇒ -x + 5y – 8 = 0
⇒ x – 5y + 8 = 0
செங்கோட்டின் சமன்பாடு
yx₁ – xy₁ + g(y – y₁) – f(x – x₁) = 0
⇒ y(2) – x(2) – 3(y – 2) -3(x – 2) = 0
[∵ 2g = -6 ⇒ g = -3; 2f = 6 ⇒ f = 3]
⇒ 2y – 2x – 3y + 6 – 3x + 6 = 0
⇒ -5x – y + 12 =0
⇒ 5x + y – 12 = 0

கேள்வி 10.
(-2, 1), (0, 0) மற்றும் ( 4, -3) என்ற புள்ளிகள் x² + y² – 5x + 2y – 5 = 0 என்ற வட்டத்திற்கு வெளியே, வட்டத்தின் மீது அல்லது உள்ளே இவற்றில் எங்கே உள்ளன எனத் தீர்மானிக்கவும்.
தீர்வு:
கொடுக்கப்பட்ட வட்டத்தின் சமன்பாடு
x² + y² – 5x + 2y – 5 = 0
(-2, 1) ல், (1) ஆனது
(-2)² + 1² – 5(-2) + 2(1) – 5
= 4 + 1 + 10 + 2 – 5
= 17 – 5 = 12 > 0.
∴ (-2, 1) வட்டத்திற்கு வெளியே உள்ளது
(0, 0)-ல், (1) ஆனது -5 < 0
∴ (0, 0) வட்டத்தின் உள் அமைந்துள்ளது.
(4,-3) ல், (1) லிருந்து
(-4)² + (-3)² – 5(4) + 2(-3) – 5
= 16 + 9 + 20 – 6 – 5
= 45 – 11 = 34 > 0
(4,-3) வட்டத்தின் வெளியே அமைந்துள்ளது.

கேள்வி 11.
பின்வரும் வட்டங்களுக்கு மையத்தையும் ஆரத்தையும் காண்க.
(i) x² + (y + 2)² = 0
(ii) x² + y² + 6x – 4y + 4 = 0
(iii) x² + y² – x + 2y – 3 = 0
(iv) 2x² + 2y² – 6x + 4y + 2 = 0
தீர்வு:
(i) வட்டத்தின் சமன்பாடு x² + (y + 2)² = 0
மையம் (0, -2) மற்றும் ஆரம் 0.
(ii) வட்டத்தின் சமன்பாடு
x² + y² + 6x – 4y + 4 = 0.
இங்கு 2g = 6 = g=3
2f = – 4
⇒ f = -2 மற்றும் c = 4
மற்றும் (-g, -f) = (-3, 2)
r = \(\sqrt{g^{2}+f^{2}-c}\) = \(\sqrt{3^{2}+(-2)^{2}-4}\)
= \(\sqrt{9+4-4}\)
= \(\sqrt{9}\)
= 3 அலகுகள்

(iii) வட்டத்தின் சமன்பாடு x² + y² – x + 2y – 3 = 0
இங்கு 2g = -1 ⇒ g = \(\frac{-1}{2}\)
2f = 2
⇒ f = 1 மற்றும் c = -3

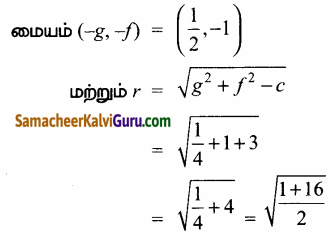
r = \(\sqrt{\frac{17}{2}}\) அலகுகள்.

(iv) வட்டத்தின் சமன்பாடு
2x² + 2y² – 6x + 4y + 2 = 0
2 ஆல் வகுக்க, கிடைப்பது
x² + y² – 3x + 2y + 1 = 0

கேள்வி 12.
3x² + (3 – p) xy + qy² – 2px = 8pq என்ற சமன்பாடு வட்டத்தைக் குறிக்கும் எனில் p மற்றும் புன் மதிப்பு காண்க. மேலும் அந்த வட்டத்தின் மையம் மற்றும் ஆரம் காண்க.
தீர்வு:
கொடுக்கப்பட்ட வட்டத்தின் சமன்பாடு
3x² + (3 – p)xy + qy² – 2px = 8pg
வட்டத்திற்கு xy-ன் கெழு = 0
⇒ 3 – p = 0 ⇒ p = 3
மேலும் , x² – ன் கெழு = y²-ன் கெழு
⇒ 3 = q
∴ வட்டத்தின் சமன்பாடு
3x² + 3y² – 6x = 8(3)(3)
3x² + 3y² – 6x – 72 = 0
3 ஆல் வகுக்க, கிடைப்பது
x² + y² – 2x – 24 = 0
இங்கு 2g = -2 ⇒ g = -1
f = 0 மற்றும் c = -24
மையம் (-g, -f) = (1, 0)
மற்றும் r = \(\sqrt{g^{2}+f^{2}-c}\)
= \(\sqrt{(-1)^{2}+0+24}\)
= \(\sqrt{25}\) = 5 அலகுகள்