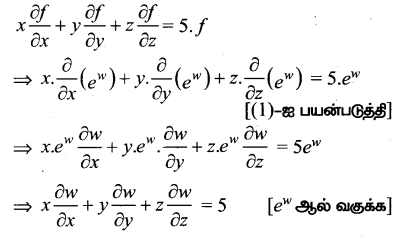Samacheer Kalvi 12th Maths Guide Chapter 8 வகையீடுகள் மற்றும் பகுதி வகைக்கெழுக்கள் Ex 8.7

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 8 வகையீடுகள் மற்றும் பகுதி வகைக்கெழுக்கள் Ex 8.7 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 8 வகையீடுகள் மற்றும் பகுதி வகைக்கெழுக்கள் Ex 8.7

கேள்வி 1.
பின்வரும் ஒவ்வொரு சார்பும் சமபடித்தானதா இல்லையா எனக்கண்டு சமபடித்தானது எனில் அதன் படியையும் காண்க.
(i) f(x, y) = x² y + 6x³ + 7
(ii) h (x,y) = \(\frac{6 x^{2} y^{3}-\pi y^{5}+9 x^{4} y}{2020 x^{2}+2019 y^{2}}\)
(iii) g (x, y, z) = \(\frac{\sqrt{3 x^{2}+5 y^{2}+z^{2}}}{4 x+7 y}\)
(iv) U (x, y, z) = xy + sin\(\left(\frac{y^{2}-2 x^{2}}{x y}\right)\)
தீர்வு:
f(x, y) = x² y + 6x³ + 7
கொடுக்கப்பட்ட f (x, y) = x² y + 6x³ + 7
f(λx, λy) = λ²x²λy + 6λ³x² +7
= λ³x²y + 6λ³x³ + 7
≠ λf(x, y)
∴ ஆனது சமப்படித்தான் சார்பு அல்ல

(ii) h (x,y) = \(\frac{6 x^{2} y^{3}-\pi y^{5}+9 x^{4} y}{2020 x^{2}+2019 y^{2}}\)
கொடுக்கப்பட்ட ர்

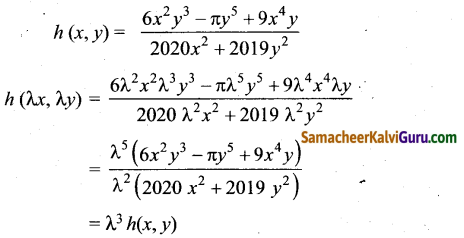
∴ h (x, y) ஆனது படி 3 உடைய சமப்படித்தான் சார்பு

(iii) g (x, y, z) = \(\frac{\sqrt{3 x^{2}+5 y^{2}+z^{2}}}{4 x+7 y}\)
கொடுக்கப்பட்ட ர

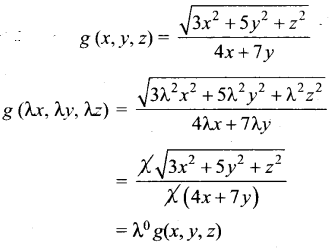
∴ g(x, y, z) ஒரு படி ) உடைய சமப்படித்தான சார்பு.

(iv) U (x, y, z) = xy + sin\(\left(\frac{y^{2}-2 x^{2}}{x y}\right)\)
கொடுக்கப்பட்ட

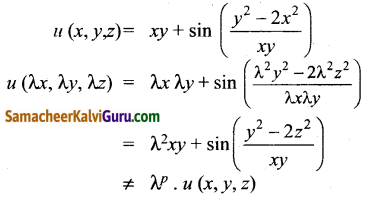
∴ u (x, y, z) ஒரு சமப்படித்தான சார்பல்ல.

கேள்வி 2.
f(x, y) = x³ – 2x² y + 3xy² + y³ என் சார்பு சமபடித்தானது என நிறுவுக. f-ன் படியைக் கணக்கிட்டு f-க்கு ஆய்லரின் தேற்றத்தைச் சரிபார்க்க .
தீர்வு:
கொடுக்கப்பட்ட f (x, y) = x³ – 2x² y + 3xy² + y³ ………….. (1)
f (tx, ty)) = (tx)³ – 2(tx)² (ty) + 3 (tx) (ty)² + (ty)³
= t³x³ – 2t² x² ty + 3txt² y² + t³y³
= t³ (x³ – 2x²y + 3xy² + y³) f(tx, ty) = t³(x, y)
∴ ஆனது படி 3 உடைய சமப்படித்தான் சார்பு. சமன்பாடு ‘x’ மற்றும் ‘y’ பொறுத்து (1) ஐ பகுதி வகையிட கிடைப்பது
\(\frac{\partial f}{\partial x}\)= 3x² – 4xy + 3y²
⇒ \(x \frac{\partial f}{\partial x}\)= 3x² – 4xy + 3xy² …………… (2)
\(\frac{\partial f}{\partial x}\) = -2x² + 6xy + 3y²
⇒ \(y \frac{\partial f}{\partial y}\) = y = -2x² + 6xy² + 3y² ……….. (3)
(2) மற்றும் (3) ஐ கூட்ட கிடைப்பது,
[latexx \frac{\partial f}{\partial x}+y \frac{\partial f}{\partial y}][/latex] = 3x² – 4x²y + 3xy² – 2x²y + 6xy² +3y³
= 3x² – 6x²y + 9xy² + 3y³
= 3(x³ – 2x²y – 3xy² + y³)
= 3f    [(1) ஐ பயன்படுத்தி]
∴ \(x \frac{\partial f}{\partial x}+y \frac{\partial f}{\partial y}\) = 3f = nf இங்கு f (x, y ) இன் படி 3 ஆகும்.
ஆகையால், ஆய்லரின் தேற்றம் சரிபார்க்கப்பட்டது.

கேள்வி 3.
g (x, y) = x log \(\left(\frac{y}{x}\right)\) என்ற சார்பு சமபடித்தானது என நிறுவுக. g-ன் படியைக் கணக்கிட்டு , g-க்கு ஆய்லரின் தேற்றத்தைச் சரிபார்க்க.
தீர்வு :
கொடுக்கப்பட்ட g (x, y) = x log\(\left(\frac{y}{x}\right)\)
g (λx, λy) = λx log\(\left(\frac{\lambda y}{\lambda x}\right)\)
= λx log\(\left(\frac{y}{x}\right)\)
= λ’ g (x, y)
∴ g (x,y) படி 1 உடைய ஒரு சம்படித்தான சார்பு.
\(x \frac{\partial g}{\partial x}+y \frac{\partial g}{\partial y}\) = 1 g என பரிசோதிக்க
[ஆய்லரின் தேற்றம்]

எனவே தேற்றம் சரிபார்க்கப்பட்டது.

கேள்வி 4.
u(x, y) = \(\frac{x^{2}+y^{2}}{\sqrt{x+y}}\) எனில், \(x \frac{\partial u}{\partial x}+y \frac{\partial u}{\partial y}=\frac{3}{2} u\) அது என நிறுவுக.
தீர்வு:
கொடுக்கப்பட்ட u (x, y) = \(\frac{x^{2}+y^{2}}{\sqrt{x+y}}\)
u (λx, λy) = \(\frac{\lambda^{2} x^{2}+\lambda^{2} y^{2}}{\sqrt{\lambda x+\lambda y}}=\frac{\lambda^{2}\left(x^{2}+y^{2}\right)}{\sqrt{\lambda}(\sqrt{x+y})}\)
= λ^{\(2-\frac{1}{2}\)} u (x, y) = λ^{\(\frac{3}{2}\)} u (x,y)
∴ u (x,y) படி , உடைய சமப்படித்தான சார்பு.
∴ ஆய்லரின் தேற்றப்படி,
\(x \frac{\partial u}{\partial x}+y \frac{\partial u}{\partial y}=n . u \Rightarrow x \frac{\partial u}{\partial x}+y \frac{\partial u}{\partial y}=\frac{3}{2} u\)
எனவே நிரூபிக்கப்பட்டது.

கேள்வி 5.
v(x, y) = log\(\left(\frac{x^{2}+y^{2}}{x+y}\right)\), எனில் \(x \frac{\partial v}{\partial x}+y \frac{\partial v}{\partial y}=1\) என நிறுவுக.
தீர்வு:
கொடுக்கப்பட்ட v (x, y) = log \(\left(\frac{x^{2}+y^{2}}{x+y}\right)\)
log \(\left(\frac{x^{2}+y^{2}}{x+y}\right)\) சமப்படுத்தானது அல்ல
f(x, y) = \(\frac{x^{2}+y^{2}}{x+y}\) என்க.
⇒ v = log f
⇒ e^v = f ………………. (1)
இங்கு , f (tx, ty) = \(\frac{t^{2} x^{2}+t^{2} y^{2}}{t x+t y}=\frac{t^{2}\left(x^{2}+y^{2}\right)}{t(x+y)}\)
= t’ f (x, y)
∴ f படி 1 உடைய சமப்படித்தான சார்பாகும்.
∴ ஆய்லரின் தேற்றப்படி,
⇒ \(x \frac{\partial f}{\partial x}+y \frac{\partial f}{\partial y}\) = 1 . f
(1) லிருந்து, \(\)     [(1)-ஐ பயன்படுத்தி]
⇒ \(x \cdot e^{v} \cdot \frac{\partial v}{\partial x}+y \cdot e^{v} \cdot \frac{\partial v}{\partial y}=\cdot e^{v}\)
⇒ \(x \frac{\partial v}{\partial x}+y \frac{\partial v}{\partial y}=1\)    [e^v ஆல் வகுக்கர்]

கேள்வி 6.
w(x, y, z) = log \(\left(\frac{5 x^{3} y^{4}+7 y^{2} x z^{4}-75 y^{3} z^{4}}{x^{2}+y^{2}}\right)\) எனில் \(x \frac{\partial w}{\partial x}+y \frac{\partial w}{\partial y}+z \frac{\partial w}{\partial z}\) -ஐக் காண்க.
தீர்வு:
கொடுக்கப்பட்ட

∴ f(x, y, z) ஒரு படி 5 உடைய சமப்படித்தான சார்பாகும்.
∴ ஆய்லரின் தேற்றப்படி,