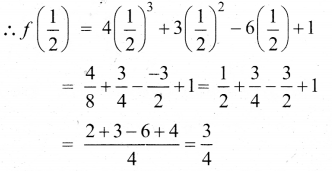Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 7 வகை நுண்கணிதத்தின் பயன்பாடுகள் Ex 7.7 Textbook Questions and Answers, Notes.
TN Board 12th Maths Solutions Chapter 7 வகை நுண்கணிதத்தின் பயன்பாடுகள் Ex 7.7
கேள்வி 1.
கீழ்க்காணும் சார்புகளுக்கு குழிவு இடைவெளிகள் மற்றும் வளைவு மாற்றுப் புள்ளிகளைக் காண்க:
(i) f (x) = x(x – 4)3
(ii) f(x) = sin x + cos x, 0 < x < 2π
(iii) f (x) = \(\frac{1}{2}\) (ex – e-x)
தீர்வு:
(i) f (x) = x(x – 4)3
கொடுக்கப்பட்ட f (x) = x (x – 4)3
f'(x) = x .3(x – 4)2 + (x – 4)3 (1)
= 3x (x – 4)2 + (x – 4)3
= (x – 4)2 (3x + x – 4)
= (x – 4)2 (4x – 4)
= 4 (x – 1) (x – 4)2
f”(x) = 4 [(x – 1)2 (x – 4) + (x – 4)2 (1)]
= 4 [2(x – 4)(x – 1) + (x – 4)2]
= 4(x – 4) [2x – 2 + x – 4)]
= 4(x – 4) (3x – 6)
= 12 (x – 4) (x – 2)
f”(x) = 0
⇒ 12 (x – 4) (x – 2) = 0
⇒ x = 2, 4
(-∞, 2) (2, 4) மற்றும் (4, ∞) தேவையான இடைவெளிகள் ஆகும்.

∴ (-∞, 2) (4, ∞) ல் வளைவரை மேல்நோக்கி குழிவுடையது மற்றும் (2, 4) கீழ் நோக்கி குழிவுடையது. f”(x) -ன் குறி x = 2 மற்றும் x = 4 ஐ கடக்கும் போது!
மாறுவதால் வளைவு மாற்றப் புள்ளிகள் (2, f (2)) மற்றும் (4, f (4)) வளைவு மாற்றப் புள்ளிகளாகும்.
f(2) = 2(2 – 4)3
= 2 (-2)3 = 2 (-8) = -16
f(4) = 4 (4 – 4)3 = 0
∴ வளைவு மாற்றப்புள்ளிகள் (2,- 16) மற்றும் (4, 0) ஆகும்.
![]()
(ii) f (x) = sin x + cos x, 0 < x < 2π
கொடுக்கப்பட்ட f (x) = sin x + cos x, 0 < x < 2π
f'(x) = cos x – sin x
f”(x) = sin x – cos x
∴ f”(x) = 0
⇒ – sin x – cos x = 0
⇒ – sin x = cos x
⇒ sin (-x) = cos x
⇒ x = \(\frac{3 \pi}{4}, \frac{7 \pi}{4}, 2 \pi\)
∴ சாத்தியமாக இடைவெளிகள் \(\left(0, \frac{3 \pi}{4}\right)\left(\frac{3 \pi}{4}, \frac{7 \pi}{4}\right)\) மற்றும் \(\left(\frac{7 \pi}{4}, 2 \pi\right)\)

∴ f(x) -ல் \(\left(\frac{3 \pi}{4}, \frac{7 \pi}{4}\right)\) ஆனது மேல் நோக்கி குழிவடையது மற்றும் \(\left(0, \frac{3 \pi}{4}\right)\left(\frac{7 \pi}{4}, 2 \pi\right)\) கீழ்நோக்கி குழிவுடையது. f”(x) -ன் குறியானது \(\frac{3 \pi}{4}\) -ஐ கடக்கும் போது குறையிலிருந்து மிகையாகவும் மற்றும் \(\frac{7 \pi}{4}\) -ஐ கடக்கும் போது மிகையிலிருந்து குறையாக மாறுவதால், f (x) ஆனது வளைவு மாற்றப் புள்ளிகளாக \(\left(\frac{3 \pi}{4}, f\left(\frac{3 \pi}{4}\right)\right)\) மற்றும் \(\left(\frac{7 \pi}{4}, f\left(\frac{7 \pi}{4}\right)\right)\) -ஐ கொண்டிருக்கும்.
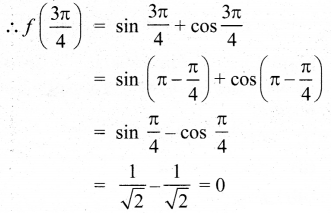
∴ வளைவு மாற்றப்புள்ளிகள் \(\left(\frac{3 \pi}{4}, 0\right)\) மற்றும் \(\left(\frac{7 \pi}{4}, 0\right)\) ஆனம்
(iii) f (x) = \(\frac{1}{2}\) (ex – e-x)
f(x) ஆனது x ∈ (-∞, ∞)-ல்வரையறுக்கப்படுகிறது மற்றும் f (x).
f'(x) = \(\frac{1}{2}\) (ex – e-x)
f”(r) = \(\frac{1}{2}\) (ex – e-x)
f”(x) = 0
⇒ \(\frac{1}{2}\) (ex – e-x) = 0 ⇒ ex – e-x = 0
⇒ ex = e-x ⇒ ex = \(\frac{1}{e^{x}}\)
⇒ e2x = 1 ⇒ e2x = e0
⇒ 2x = 0 ⇒ x = 0
சாத்தியமான இடைவெளிகள் (-∞, 0) மற்றும் (0, ∞)
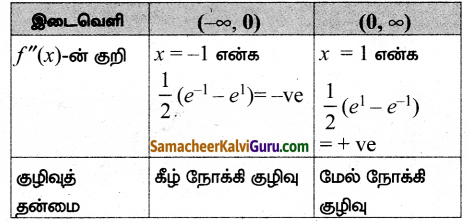
∴ f(x) -ல் (0, ∞) ஆனது மேல் நோக்கி குழிவு மற்றும் (-∞, 0)-ல் கீழ்நோக்கி குழிவு.
f”(x) -ன் குறியானது x = 0 வை கடக்கும் போது குறையிலிருந்து மிகையாக மாறுவதால் வளைவு மாற்றுப்புள்ளி (0, f (0)) ஆகும்.
f(0) = \(\frac{1}{2}\) (e0 – e0) = – (1 – 1) = 0
∴ வளைவு மாற்றப்புள்ளி (0, 0) ஆகும்.
![]()
கேள்வி 2.
இரண்டாம் வகைக்கெழு சோதனையை பயன்படுத்தி இடஞ்சார்ந்த அறுதி மதிப்புகளைக் காண்க.
(i) f(x) = -3x5 + 5x3
(ii) f(x) = x log x
(iii) f(x) = x2 e-2x
தீர்வு:
(i) f (x) = -3x5 + 5x3
f(x) = -3x5 + 5x3
f'(x) = -15x4 + 15x0
f'(x) = 0
⇒ – 15x4 + 15x2 = 0
⇒ 15x2 (1 – x2) = 0
⇒ x2 = 0, 1 – x2 = 0
⇒ x = 0, x = 1, x = -1
∴ தேக்கநிலை எண்கள் 0, 1,-1 ஆகும்.
f”(x) = – 60x3 + 30x
f”(0) = 0
f”(1) = – 60(1)3 + 30 (1)
= – 60 + 30 = -30
f”(-1) = – 60(-1)3 + 30 (-1)
= 60 – 30 = 30
f”(1) < 0 ஆகையால் அது இடஞ்சார்ந்த பெருமத்தை x = 1-ல் கொண்டிருக்கும்.
∴ f(1) = -3(-1)5 + 5(-1)3
= – 3 + 5 = 2
f”(-1) > 0 ஆகையால் இடஞ்சார்ந்த பெருமத்தை x= -1-ல் கொண்டிருக்கும்.
∴ f(-1) = -3(1)5 + 5(1)3
= 3 – 5 = -2
∴ 2 -ல் இடஞ்சார்ந்த பெரு மதிப்பு x = 1 மற்றும் -2-ல் இடஞ்சார்ந்த சிறும மதிப்பு.x = -1 ஆகும்.
(ii) f(x) = x log x
f(x) = x log x
f'(x) = x . \(\frac{1}{x}\) + log x (1)
= 1 + log x
f'(x) = 0
⇒ 1 + log x = 0
⇒ log x = -1 |
⇒ x = e-1 = \(\frac{1}{e}\)
∴ நிலை எண்கள் \(\frac{1}{e}\)
f”(x) = \(\frac{1}{x}\)
\(f^{\prime \prime}\left(\frac{1}{e}\right)=\frac{1}{\frac{1}{e}}\) = e > 0
f”\(\left(\frac{1}{e}\right)\) > 0 ஆதலால் x = \(\frac{1}{e}\) ‘-ல் இடஞ்சார்ந்த சிறுமம் அமைந்துள்ளது.
∴ \(f\left(\frac{1}{e}\right)=\frac{1}{e} \log \frac{1}{e}\)
= \(\frac{1}{e} \log e^{-1}\)
= \(\frac{-1}{e} \log _{e} e=\frac{-1}{e}(1)=\frac{-1}{e}\)
∴ –\(\frac{1}{e}\) –ல் இடஞ்சார்ந்த சிறும் மதிப்பு x = \(\frac{1}{e}\) அமைந்துள்ளது.
![]()
(iii) f(x) = x2 e-2x
f(x) = x2 e-2x
f'(x) = x2 (-2) e-2x + e-2x (2x)
f'(x) = 2xe-2x (1 – x)
f'(x) = 0
⇒ 2x e-2x (1 – x) = 0
⇒ x = 0, 1
∴ நிலை எண்கள் x = 0, 1 ஆகும்.
f”(x) = [x e-2x (-1) + x (-2)e-2x – (1 – x) + 1 e-2x (1 – x)]
= 2e-2x (-x – 2x + 2x2 + 1 – x)
= 2e-2x (2x2 – 4x + 1)
f”(0) = 2(1) (1)= 2 > 0
f”(1) = 2e-2 (2 – 4 + 1)
= 2e-2 (-1)
= -2e-2 = \(\frac{-2}{e^{2}}\) < 0 f”(0) > 0 ஆதலால் இடஞ்சார்ந்த சிறுமம் x = 0 -ல் ‘ உள்ளது.
∴ f (0) = 02 e0 = 0
f”(1) < 0 ஆதலால் இடஞ்சார்ந்த சிறுமம் x = 1-ல் அமைந்துள்ளது.
∴ f(1) = 12 e-2(1) = e-2 = \(\frac{1}{e^{2}}\)
கேள்வி 3.
f(x) = 4x3 + 3x2 – 6x + 1 என்ற சார்பிற்கு ஓரியல்பு இடைவெளிகள், இடஞ்சார்ந்த அறுதி மதிப்புகள், குழிவு இடைவெளிகள் மற்றும் வளைவு மாற்றுப் புள்ளிகளைக் காண்க.
தீர்வு:
கொடுக்கப்பட்ட f (x)= 4x3 + 3x2 – 6x + 1
f'(x) = 12x2 + 6x – 6
f”(x) = 24x + 6
f'(x) = 0
⇒ 12 x2 + 6x – 6 = 0
⇒ 2x2 + x – 1 = 0
⇒ (x+ 1)(2x- 1) = (0
⇒ x= -1, \(\frac{1}{2}\)
நிலை எண்கள் -1, \(\frac{1}{2}\) ஆகும். தேவையான ஒரியல்பு இடைவெளிகள் (-∞, -1) \(\left(-1, \frac{1}{2}\right)\left(\frac{1}{2}, \infty\right)\) ஆகும்.
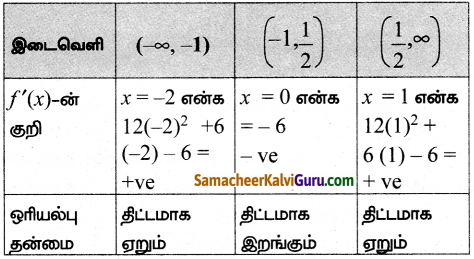
∴ f(x) -ல் (-∞, -1) \(\left(\frac{1}{2}, \infty\right)\) ஆனது திட்டமாக ஏறும் \(\left(-1, \frac{1}{2}\right)\) -ல் திட்டமாக இறங்கும்.
f”(x) = 0
⇒ 24x + 6 = 0 ⇒ 24x = -6
x = \(\frac{-6}{24}=\frac{-1}{4}\)
குழிவுத் தன்மைக்கு சாத்தியமான இடைவெளிகள் \(\left(-\infty, \frac{-1}{4}\right)\left(\frac{-1}{4}, \infty\right)\) ஆகும்.

∴ f(x)-ல் \(\left(-\infty, \frac{-1}{4}\right)\), ஆனது கீழ்நோக்கிய குழிவுடையது மற்றும் \(\left(\frac{-1}{4}, \infty\right)\) -ல் மேல் நோக்கிய குழிவுடையது.
![]()
f”(x) ஆனது x = \(\frac{-1}{4}\) வழி செல்லும் போது குறி மாற்றமடைகிறது, வளைவு மாற்றுப் புள்ளிகள் \(\left(-\frac{1}{4}, f\left(-\frac{1}{4}\right)\right)\) ஆகும்.
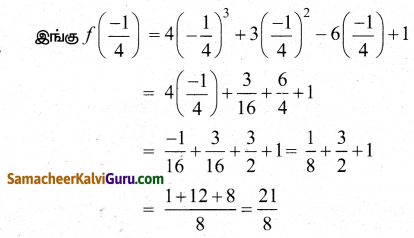
∴ வளைவு மாற்றப்புள்ளி \(\left(\frac{-1}{4}, \frac{21}{8}\right)\) ஆகும்.
f'(x) -ல் x = -1ஆனது மிகையிலிருந்து குறையாக மாறுவதால், அது இடஞ்சார்ந்த சிறுமத்தை x=-1-ல் கொண்டுள்ளது
∴ f(-1) = 4 (-1)3 + 3 (-1)2 – 6(-1) + 1
= -4 + 3 + 6 + 1 = 6
f'(x) ஆனது குறையிலிருந்து மிகையாக x = \(\frac{1}{2}\) குறி மாற்றமடைவதால், அது இடஞ்சார்ந்த மதிப்பை x = \(\frac{1}{2}\) கொண்டிருக்கும்.