Laxmi

Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 7 தகவல் செயலாக்கம் Ex 7.1 Textbook Questions and Answers, Notes.

TN Board 8th Maths Solutions Chapter 7 தகவல் செயலாக்கம் Ex 7.1

கேள்வி 1.
நீங்கள் பனிக்கூழ் (ice cream) அல்லது இனிப்பு ரொட்டி (cake) வாங்க கடைக்குச் செல்கிறீர்கள். கடை யில் பனிக்கூழில் (ice cream), சாக்லேட், ஸ்டாபெர்ரி மற்றும் வெண்ணிலா என 3 வகைகளும், இனிப்பு ரொட்டியில் ( c a k e ) ஆரஞ்சு மற்றும் வெல்வெட் என 2 வகைகளும் விற்கப்படுகிறது. எனில் நீங்கள் 1 பனிக்கூழோ(ice cream) அல்லது 1 இனிப்புரொட்டியோ (cake) வாங்குவதற்கு எத்தனை விதமான வாய்ப்புகள் உள்ளது?
தீர்வு:

A என்பது பனிக்கூழ் என்க
Bஎன்பது இனிப்புரொட்டி என்க
A = 3 வகைகள், B = 2 வகைகள்.
மொத்த வாய்ப்புகள் = பனிக்கூழ் + இனிப்புரொட்டி = 3 + 2 = 5.

கேள்வி 2.
சாந்தியிடம் 5 சுடிதார்களும் 4 கவுன்களும் உள்ளன எனில், எத்தனை விதமான வழிகளில் சாந்தி ஒரு சுடிதாரையோ அல்லது ஒரு கவுனையோ அணிவதற்கு வாய்ப்புகள் உள்ளது?
தீர்வு:
சுடிதாருக்காக = 5
கவுன்களுக்காக = 4.
அணிவதற்கான வாய்ப்புகள்
= 5 + 4
= 9.

கேள்வி 3.
ஒரு மேல்நிலைப் பள்ளியில் பதினோறாம் வகுப்பில் கீழ்வரும் 3 பிரிவுகள் உள்ளன.
I. அறிவியல் பிரிவு:
(i) இயற்பியல், வேதியியல், உயிரியல் மற்றும் கணிதம்
(ii) இயற்பியல், வேதியியல், கணிதம் மற்றும் கணிணி அறிவியல்
(iii) இயற்பியல், வேதியியல், உயிரியல் மற்றும் மனையியல்

II. கலைப்பிரிவு:
(i) கணக்கு பதிவியல், வணிகவியல், பொருளாதாரம் மற்றும் வணிக கணிதம்
(ii) கணக்குபதிவியல், வணிகவியல், பொருளாதாரம் மற்றும் கணிணி அறிவியல்
(iii) வரலாறு, புவியியல், பொருளாதாரம் மற்றும் வணிகவியல்

II. தொழில்கல்வி பிரிவு:
(i) உயிரியல், செவிலியம் கருத்தியல், செவிலியம் செய்முறை I மற்றும் செவிலியம் செய்முறை II
(ii) மனையியல், ஆடை அலங்காரம், கருத்தியல், ஆடை அலங்காரம் செய்முறை I மற்றும் ஆடை அலங்காரம் செய்முறை ! உள்ளது எனில், ஒரு மாணவர் தனக்கு வேண்டியப் பாடப் பிரிவைத் தேர்ந்தெடுப்பதற்கு எத்தனை விதமான வாய்ப்புகள் உள்ளது?
தீர்வு:
1. அறிவியல் பிரிவு = 3
2. கலைப்பிரிவு = 3
3. தொழில்கல்வி பிரிவு = 2
தேர்ந்தெடுப்பதற்கான வாய்ப்புகள்
= 3 + 3 + 2. = 8.

கேள்வி 4.
உங்களிடத்தில் பள்ளிக்கு கொண்டு செல்வதற்காக 2 வகையான கைப்பைகளும் 3 வெவ்வேறு வண்ண நீர்குவளைகளும் (water bottles) உள்ளது எனில், நீங்கள் பள்ளிக்குச் செல்லும்போது 1 கைப்பை மற்றும் 1 வண்ண BNGQUGOGTTGOW (water bottles) கொண்டுச் செல்வதற்கு எத்தனை விதமான வாய்ப்புகள் உள்ளது?
தீர்வு:

(B) கைப்பைகள் = 2 வகை
(W) நீர் குவளைகள் = 3 வகை
கொண்டு செல்வதற்கான வாய்ப்புகள்
= 2 × 3
= 6 வழிகள்

கேள்வி 5.
பள்ளி மாணவர்களுக்கான நான்கு இலக்க வரிசை எண்ணில், முதல் இலக்கம் A,B,C,D மற்றும் E என்ற ஐந்து எழுத்துக்களில் ஏதாவது ஒரு ஆங்கில எழுத்தினைக் கொண்டும், அதனைத் தொடர்ந்து வரும் மூன்று இலக்கங்கள் ஒவ்வொன்றும் 0 முதல் 9 வரையிலான 10 எண்களைக் கொண்டும் அமைந் துள்ளது எனில் வரிசை எண் அமைப்பதற்கு எத்தனை விதமான வழிகள் உள்ளது? (A000, B000, C000, D000 மற்றும் E000 தவிர
தீர்வு:

ஆங்கில எழுத்துக்கள் = 5
3 இலக்கங்கள் = 10 × 10 × 10 அமைப்பதற்கான வழிகள்
= 5 × 1000
= 5000

கேள்வி 6.
ஒரு நகைக் கடையில் உள்ள
பாதுகாப்பு பெட்டகத்திற்கான திறவு கோல் எண் 4 இலக்கங்களைக் கொண்ட தனித்துவமான எண்ணாக அமைப்பதற்கு, ஒவ்வொரு இடமதிப்பிலும் 0 முதல் 9 வரையிலான 10 எண்களை கொண்டு உருவாக்க வேண்டுமெனில் ஒரு தனித்துவமானத் திறவுகோல் எண் அமைப்பதற்கு எத்தனை விதமான வழிகள் உள்ளது?

தீர்வு:

இலக்கங்களின் எண்ணிக்கை = 4
தனித்துவமான எண் அமைக்க
= 10 × 10 × 10 × 10
எண் அமைப்பதற்கான வழிகள்
=10 × 10 × 10 × 10
= 10000.

கேள்வி 7.
ஒரு தேர்வில் வழங்கப்பட்ட வினாத்தாளில் ஒவ்வொரு பிரிவிலும் 5 வினாக்கள் வீதம் 3 பிரிவுகள் உள்ளது. மாணவர்கள் ஒவ்வொரு பிரிவிலும் உள்ள அனைத்து வினாக்களுக்கும் பதிலளிக்க வேண்டுமெனில், அவர்களுக்கு எத்தனை விதமான வழிகள் உள்ளது?
தீர்வு:
பிரிவுகள் = 3.
வினாக்கள் = 5.
வழிகள் = 3 × 5
= 15.

கேள்வி 8.
கொடுக்கப்பட்டுள்ள சுழல் சக்கரத்தினை இருமுறை சுழற்றும் போது கிடைக்கும் எண்களைக் கொண்டு இரண்டிலக்க எண்களை அமைத்தால் எத்தனை விதமான இரண்டிலக்க எண்களை அமைக்க முடியும்?
(இலக்கங்களை மறுமுறையும் பயன்படுத்த இயலாது)

தீர்வு:

சுழலும் நேரம் = 2
இரண்டிலக்க எண்ணிக்கை = 2
மொத்த எண் = 5
இரண்டிலக்க எண்களை அமைக்கும் வழிகள்
= 2 × 2 × 5 = 20.

கேள்வி 9.
ரம்யா தனது வீட்டின் முகப்பறை சுவற்றில் உள்ள அமைப்பில் மிகக் குறைந்த செலவில் வண்ணமிட விரும்புகிறாள். அவள் இரண்டு வண்ணங்களை மட்டுமே பயன் படுத்தி அடுத்தடுத்த இரண்டு பகுதிகள் ஒரே வண்ண த்தில் அமையாதவாறு அந்த அமைப்பை வண்ண மிட உதவுங்கள்.
தீர்வு:

கேள்வி 10.
கொடுக்கப்பட்டுள்ள நில வரைபடத்தில் மிகக் குறைந்த அளவு எண்ணிக்கையிலான வண்ணங்களைக் கொண்டு அடுத்தடுத்த இரண்டு பகுதிகள் ஒரே வண்ணத்தில் அமையாதவாறு வண்ண மிடுக.
தீர்வு:

கொள்குறி வகை வினாக்கள்

கேள்வி 11.
பள்ளிகளுக்கிடையிலான வினாடிவினா போட்டிக்கு, பள்ளியின் சார்பாக ஒருவரைத் தேர்ந்தெடுக்க, 26 மாணவர்கள் மற்றும் 15 மாணவிகளுக்கு ஆசிரியர் பயிற்சியளிக்கிறார். எனில், இவர்களிலிருந்து ஒருவரை ஆசிரியர் தேர்ந்தெடுக்க எத்தனை விதமான வாய்ப்புகள் உள்ளது.?
(அ) 41
(ஆ) 26
(இ) 15
(ஈ) 390
விடை:
(அ) 4

கேள்வி 12.
மூன்று நாணயங்களை ஒரே சமயத்தில் சுண்டும்போது எத்தனை விதமான விளைவுகள் கிடைக்கும்?
(அ) 6
(ஆ) 8
(இ) 3
(ஈ) 2
விடை:
(ஆ) 8

(ஆ) 8

கேள்வி 13.
மூன்று பலவுள் தெரிவு (multiple choice questions) வினாக்களில் A, B, C மற்றும் D தெரிவுகளிலிருந்து சரியான விடையைத் தேர்ந்தெடுக்க எத்தனை விதமான வழிகள் உள்ளன?
(அ) 4
(ஆ) 3
(இ) 12
(ஈ) 64
விடை:
(ஈ) 64

கேள்வி 14.
7 ஐ ஓர் இலக்கமாகக் கொண்ட ஈரிலக்க எண்கள் எத்தனை உள்ளன?
(அ) 10
(ஆ) 18
(இ) 19
(ஈ) 20
விடை:
(இ) 19

Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 6 புள்ளியியல் Ex 6.3 Textbook Questions and Answers, Notes.

TN Board 8th Maths Solutions Chapter 6 புள்ளியியல் Ex 6.3

பல்வகைத் திறனறிப் பயிற்சிக் கணக்குகள்

கேள்வி 1.
கொடுக்கப்பட்ட அட்டவணைக்கு வட்ட விளக்கப்படம் வரைக.

தீர்வு :

கேள்வி 2.
பள்ளிக்கு வருவதற்கு மாணவர்களால் பயன்படுத்தப்படும் வாகனங்களின் விவரங்கள் கீழே கொடுக்கப்பட்டுள்ளன. அந்த விவரங்களுக்கு வட்ட விளக்கப்படம் வரைக.

தீர்வு :

கேள்வி 3.
கீழே கொடுக்கப்பட்டுள்ள விவரங்களுக்கு நிகழ்வுச் செவ்வகம் வரைக.

தீர்வு :

கேள்வி 4.
கீழ்க்காணும் விவரத்திற்கு ஒரே படத்தில் நிகழ்வுச் செவ்வகம் மற்றும் நிகழ்வுப் பலகோணம் வரைக.

தீர்வு :

கேள்வி 5.
ஆண்கள் மற்றும் பெண்களின் தினசரி வருமானம் கொடுக்கப்பட்டுள்ளது. எனில், ஆண்களுக்கும் பெண்களுக்கும் தனிதனி நிகழ்வுச் செவ்வகம் வரைக.

தீர்வு :

மேற்சிந்தனைக் கணக்குகள்

கேள்வி 6.
கீழ்க்காணும் விவரத்திற்குத் தொடர்ச்சியான நிகழ்வெண் பரவல் அட்டவணையைத் தயார் செய்க. மேலும் நிகழ்வு செவ்வகம் வரைக.

தீர்வு :

கேள்வி 7.
துணி உற்பத்திச் செய்யும் தொழிற்சாலையின் 1 ரூபாய்க்கான செலவு கீழே கொடுக்கப்பட்டுள்ளது.

தீர்வு :

கேள்வி 8.
கீழ்க்காணும் விவரங்களுக்கு நிகழ்வுச் செவ்வகம் வரைக.

தீர்வு :

Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 6 புள்ளியியல் Ex 6.2 Textbook Questions and Answers, Notes.

TN Board 8th Maths Solutions Chapter 6 புள்ளியியல் Ex 6.2

கேள்வி 1.
கீழ்க்காணும் எந்தத் தரவுகளை நிகழ்வுச் செவ்வகத்தில் குறித்துக் காட்ட முடியும்?

i) 20 முதல் 60 வயதுப் பிரிவிலுள்ள மலை ஏறுபவர்களின் எண்ணிக்கை
விடை :
ஆம்

ii) வெவ்வேறு ஆண்டுகளில் தயாரிக்கப்பட்ட மிதிவண்டிகளின் எண்ணிக்கை.
விடை :
இல்லை

iii) ஒரு பள்ளியிலுள்ள ஒவ்வொரு பிரிவு மாணவர்களின் எண்ணிக்கை.
விடை :
இல்லை

iv) ஒரு பொதுத் தேர்தலில் காலை 7 மணி முதல் மாலை 6 மணி வரை பதிவான வாக்குகளின் எண்ணிக்கை
விடை :
ஆம்

v) ஒரு நாள் கிரிக்கெட் போட்டியில் முதல் ஓவரிலிருந்து 50 வது ஓவர் வரை வெளியேறிய வீரர்களின் எண்ணிக்கை.
விடை :
ஆம்

கேள்வி 2.
கோடிட்ட இடத்தை நிரப்புக.

i) நிகழ்வுச் செவ்வகத்தின் மொத்தப் பரப்பளவானது கொடுக்கப்பட்ட மொத்த நிகழ்வெண்களின் கூடுதலுக்கு ……………………………. இருக்கும்.
விடை :
விகிதச் சமத்தில்

ii) …………………………….  என்பது ஒரு வரைபடம். அது ஒரு குறிப்பிட்ட கால இடைவெளியில் தொடர்ச்சியாக மாறிக்கொண்டே இருக்கும் மதிப்புகளின் இடப்பெயர்ச்சி ஆகும்.
விடை :
நிகழ்வுச் செவ்வகம்

iii) நிகழ்வுச் செவ்வகம் என்பது …………………………….  விவரங்களின் வரைபட விளக்க முறை ஆகும்
விடை :
தொகுக்கப்பட்ட

கேள்வி 3.
ஒரு கிராமத்தில் 570 பேர் அலைபேசி வைத்துள்ளார்கள் ஒரு தன்னார்வத் தொண்டு நிறுவனம் அவர்களின் அலைபேசிப் பயன்பாட்டை ஆய்வு செய்தது அந்த ஆய்வின்படி ஒரு நிகழ்வுச் செவ்வகம் வரைந்துள்ளனர் அதைக்கொண்டு கீழ்க்காணும் வினாக்களுக்கு விடையளிக்க.
i) 3 மணிநேரத்திற்குக் குறைவாக அலைபேசிப் பயன்படுத்துபவர்கள் எத்தனை பேர்?
ii) 5 மணிநேரத்திற்கு அதிகமாக அலைபேசிப் பயன்படுத்துபவர்கள் எத்தனை பேர்?
iii) 1 மணிநேரத்திற்கும் குறைவாக அலைபேசியைப் பயன்படுத்துபவர்கள் இருக்கிறார்களா?

தீர்வு :
i) 3 மணி நேரத்திற்குக் குறைவாக அலைபேசிப் பயன்படுத்துபவர்கள் 330 பேர்
ii) 5 மணி நேரத்திற்கு அதிகமாக அலைபேசிப் பயன்படுத்துபவர்கள் 150 பேர்
iii) இல்லை 1 மணி நேரத்திற்கும் குறைவாக யாரும் பயன்படுத்தவில்லை.

கேள்வி 4.
கீழ்க்காணும் விவரங்களுக்கு நிகழ்வுச் செவ்வகம் வரைக.

தீர்வு :

கேள்வி 5.
ஒரு வகுப்பிலுள்ள 40 மாவணர்களின் மொத்த மதிப்பெண் பரவல் கீழேக் கொடுக்கப்பட்டுள்ளது. அதற்கு நிகழ்வுச் செவ்வகம் வரைக.

தீர்வு :

கேள்வி 6.
100 பேரின் உயரங்களின் பரவல் கீழேக் கொடுக்கப்பட்டுள்ளது. எனில் நிகழ்வுச் செவ்வகத்தின் மீதுள்ளவாறு நிகழ்வுப் பலகோணம் வரைக

தீர்வு :

கேள்வி 7.
பல் பிரச்சனைகளுக்கான ஆய்வில் கீழ்க்கண்ட விவரங்கள் பெறப்பட்டன.

மேற்காணும் விவரங்களுக்கு நிகழ்வுப் பலகோணம் வரைக.
தீர்வு :

கேள்வி 8.
50 மாணவர்களின் கணித மதிப்பெண்கள் கீழேக் கொடுக்கப்பட்டுள்ளது.
(i) பிரிவு அளவு 10 மதிப்பெண்கள் என எடுத்துக்கொண்டு நிகழ்வெண் பரவல் அட்டவணையைத் தயார் செய்க.
(ii) நிகழ்வுச் செவ்வகம் மற்றும் நிகழ்வுப் பல கோணம் வரைக.


தீர்வு :

கொள்குறி வகை வினாக்கள்

கேள்வி 9.
தரவு என்பது ………………………….. இன் தொகுப்பு
அ) எண்கள்
ஆ) எழுத்துகள்
இ) அளவுகள்
ஈ) இவை அனைத்தும்
விடை :
ஈ) இவை அனைத்தும்

கேள்வி 10.
கொடுக்கப்பட்டத் தரவுகளில் ஒரு மதிப்பு எத்தனை முறை வருகிறது எனக் கூறுவது அம்மதிப்பின் …………………………..
அ) நேர்க் கோட்டுக் குறிகள்
ஆ) தரவு
இ) நிகழ்வெண்
ஈ) எதுவுமில்லை
விடை :
இ) நிகழ்வெண்

கேள்வி 11.
கொடுக்கப்பட்ட விவரங்களில் மிகப்பெரிய மற்றும் மிகச்சிறிய அளவுகளின் வித்தியாசம் …………………………..
அ) வீச்சு
ஆ) நிகழ்வெண்
இ) மாறி
ஈ) ஏதுமில்லை
விடை :
அ) வீச்சு

கேள்வி 12.
கொடுக்கப்பட்டத் தரவுகளை ஒரு குறிப்பிட்ட இடைவெளியில் எடுத்துக்கொள்வது …………………………..
அ) தொகுக்கப்படாத
ஆ) தொகுக்கப்பட்டது
இ) நிகழ்வெண்
ஈ) ஏதுமில்லை
விடை :
ஆ) தொகுக்கப்பட்டது

கேள்வி 13.
உள்ளடக்கியத் தொடர் ஒரு ………………………….  தொடர்
அ) தொடர்ச்சியான
ஆ) தொடர்ச்சியற்ற
இ) இரண்டும்
ஈ) ஏதுமில்லை
விடை :
ஆ) தொடர்ச்சியற்ற

கேள்வி 14.
பிரிவு இடைவெளிகளில், ஒரு பிரிவு இடைவெளியின் மேல் எல்லையானது
அடுத்தப் பிரிவு இடைவெளியின் கீழ் எல்லையாக இருந்தால் அது ………………………….  தொடர்.
அ) உள்ளடக்கிய
ஆ) விலக்கிய
இ) தொகுக்கப்படாத
ஈ) ஏதுமில்லை
விடை :
ஆ) விலக்கிய

கேள்வி 15.
தொகுக்கப்படாத விவரங்களின் வரைபட விளக்கமுறை ………………………….
அ) நிகழ்வுச் செவ்வகம்
ஆ) கிகழ்வுப் பலகோணம்
இ) வட்ட விளக்கப்படம்
ஈ) இவை அனைத்தும்
விடை :
இ) வட்ட விளக்கப்படம்

கேள்வி 16.
நிகழ்வுச் செவ்வகம் என்பது ஒரு ………………………….  நிகழ்வெண் பரவல்.
அ) தொடர்ச்சியான
ஆ) தொடர்ச்சியற்ற
இ) தனித்த
ஈ) ஏதுமில்லை
விடை :
அ) தொடர்ச்சியான

கேள்வி 17.
………………………….  என்பது வரைபட முறையில் தொடர்ச்சியான நிகழ்வெண் பரவலுக்கான நேர்கோட்டு வரைபடம் ஆகும்.
அ) நிகழ்வுப் பலகோணம்
ஆ) நிகழ்வுச் செவ்வகம்
இ) வட்ட விளக்கப்படம்
ஈ) பட்டை விளக்கப்படம்
விடை :
அ) நிகழ்வுப் பலகோணம்

கேள்வி 18.
தொகுக்கப்பட்ட விவரங்களுக்கான வரைபட விளக்கப்படம் ………………………….
அ) பட்டை விளக்கப்படம்
ஆ) பட விளக்க முறை
இ) வட்ட விளக்கப் படம்
ஈ) நிகழ்வுச் செவ்வகம்
விடை :
ஈ) நிகழ்வுச் செவ்வகம்

Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 6 புள்ளியியல் Ex 6.1 Textbook Questions and Answers, Notes.

TN Board 8th Maths Solutions Chapter 6 புள்ளியியல் Ex 6.1

கேள்வி 1.
கோடிட்ட இடங்களை நிரப்புக.

i) வேறாருவரால் முன்பே சேகரித்து வைத்திருக்கும் தரவுகள்
தரவுகள் .
விடை :
இரண்டாம் நிலை

ii) (25 – 35) பிரிவு இடைவெளியின் மேல் எல்லை
விடை :
35

iii) 200, 15, 20, 103, 3, 197 இன் வீச்சு
விடை :
197

iv) பிரிவு அளவு 10 மற்றும் வீச்சு 80 எனில், பிரிவுகளின் எண்ணிக்கை
விடை :
8

v) வட்ட விளக்கப்படம் என்பது வரைபடம்.
விடை :
வட்டவடிவியலான

கேள்வி 2.
சரியா தவறா எனக் கூறுக.

i) உள்ளடக்கியத் தொடர் ஒரு தொடர்ச்சியானத் தொடர்
விடை :
தவறு

ii) வட்ட விளக்கப்படம் மூலம் மொத்த பகுதிகளின் கூறுகளை ஒப்பிட்டு பார்க்க முடியும்
விடை :
சரி

iii) ஊடக மற்றும் தொழிற்துறையினர் வட்ட விளக்கப்படத்தைப் பயன்படுத்துகின்றனர்.
விடை :
சரி

iv) வட்ட விளக்கப்படம் என்பது வட்டத்தைப் பல்வேறு வட்டக்கோணபகுதிக் கூறுகளாகப் பிரிப்பது.
விடை :
சரி

கேள்வி 3.
25 குடும்பங்களிலுள்ள குழந்தைகளின் எண்ணிக்கைக்கு கீழே கொடுக்கப்பட்டுள்ளது.
இதனைத் தொகுக்கப்படாத நிகழ்வெண் பரவல் அட்டவணையில் குறிக்க.
1, 3, 0, 2, 5, 2, 3, 4, 1, 0, 5, 4, 3, 1, 3, 2, 5, 2, 1, 1, 2, 6, 2, 1, 4.
விடை :

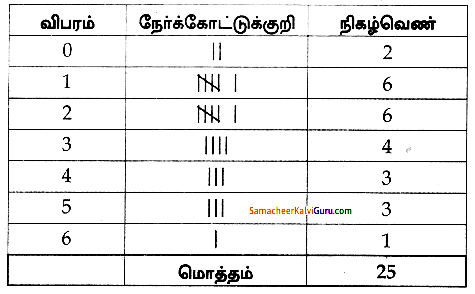
கேள்வி 4.
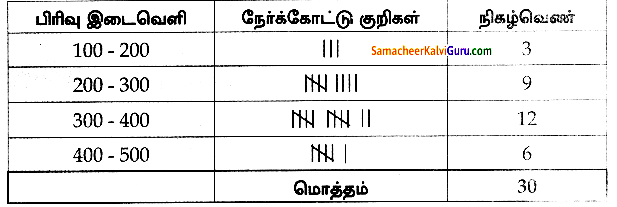
பத்தாம் வகுப்பு பொதுத் தேர்வில் 30 மாணவர்கள் எடுத்த மதிப்பெண்களுக்குத் தொகுக்கப்பட்ட நிகழ்வெண் பரவல் அட்டவணையைத் தயார் செய்க. 328. 470, 405, 375,298, 326, 276,362, 410, 255,391,370, 455, 229, 300, 183, 283, 366, 400, 495, 215, 157, 374, 306, 280, 409, 321, 269, 398, 200.
விடை :

கேள்வி 5.
ஒரு வண்ண உற்பத்தித் தொழிற்சாலை நிர்வாகத்தினர் ஒரு பகுதி மாணவர்களிடம் தங்களுக்கு விருப்பமான வண்ணம் பற்றி கேட்டு, அத்தரவுகளுக்கு வட்ட விளக்கப்படம் வரைந்துள்ளார்கள். அத்தகவல்களைப் பயன்படுத்திக் கீழ்க்காணும் வினாக்களுக்கு விடையளிக்க.
i) எத்தனைச் சதவீத மாணவர்கள் சிவப்பு
வண்ணத்தை விரும்புகின்றனர்?
ii) எத்தனை மாணவர்கள் பச்சை வண்ணத்தை
விரும்புகின்றனர்?
iii) நீலவண்ணத்தை விரும்பும் மாணவர்களின் பின்னம் என்ன?
iv) எத்தனை மாணவர்கள் சிவப்பு வண்ணத்தை விரும்பவில்லை ?
v) எத்தனை மாணவர்கள் இளஞ்சிவப்பு அல்லது நீல வண்ணத்தை விரும்புகின்றனர்?
vi) எத்தனை மாணவர்களிடம் தங்களுக்குப் பிடித்தமான வண்ணம் பற்றிக் கேட்கப்பட்டது? 10% என்பது 50 மாணவர்கள்

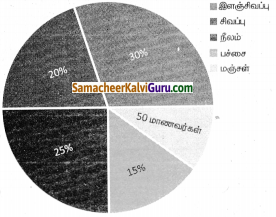
தீர்வு :
i) 20% மாணவர்கள் சிவப்பு வண்ணத்தை விரும்புகின்றனர்.
ii) 75 மாணவர்கள் பச்சை வண்ணத்தை விரும்புகின்றனர்.
iii) \(\frac{125}{500}=\frac{1}{4}\) மாணவர்கள் நீல வண்ணத்தை விரும்புகின்றனர்.
iv) 400 மாணவர்கள் சிவப்பு வண்ணத்தை விரும்பவில்லை.
v) 275 மாணவர்கள் இளஞ்சிவப்பு அல்லது நீல வண்ணத்தை விரும்புகின்றனர்.
vi) 500 மாணவர்களிடம் தங்களுக்கு பிடித்தமான வண்ணம் பற்றிக் கேட்கப்பட்டது.

கேள்வி 6.
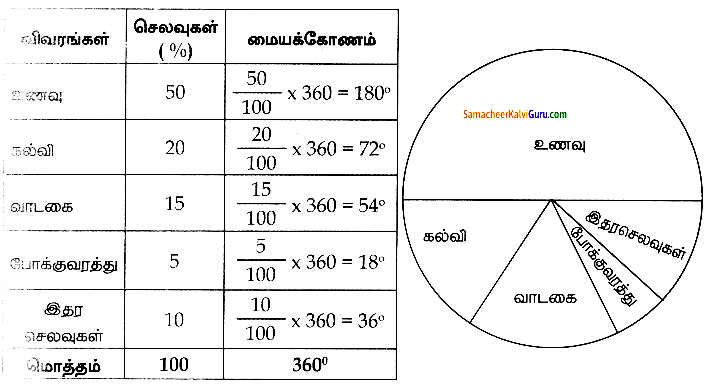
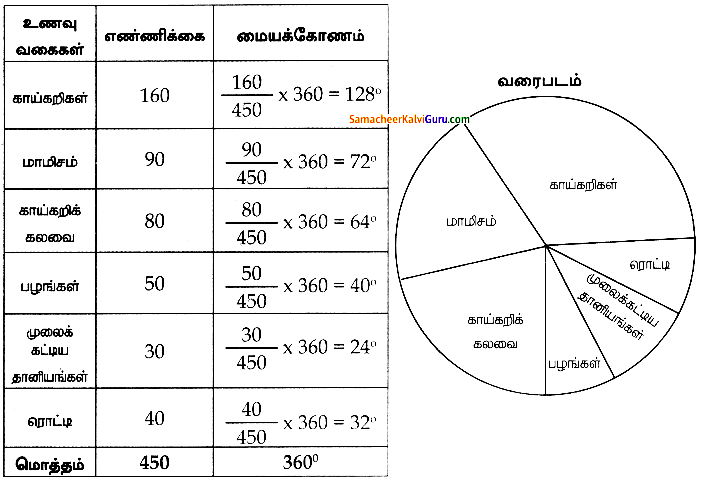
ஒரு கருத்துக் கேட்பில், அப்பகுதி மக்களால் விரும்பப்படும் உணவு வகைகள் பற்றிய விவரங்கள் கீழேக் கொடுக்கப்பட்டுள்ளது. அவ்விவரங்களுக்கு வட்ட விளக்கப்படம் வரைக.

தீர்வு :

கேள்வி 7.
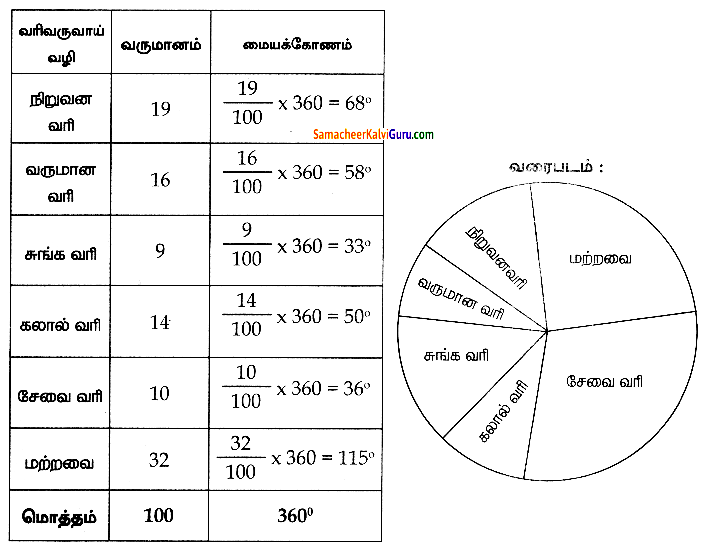
இந்திய அரசாங்கத்திற்குப் பல்வேறு வரிவருவாய் வழிகளில் இருந்துவரும் ஒரு ரூபாயிற்கான வருமானம் கொடுக்கப்பட்டுள்ளது. அதற்கு வட்ட விளக்கப்படம் வரைக.

தீர்வு :

கேள்வி 8.
குமரனின் மாத குடும்பச் செலவு கீழேக் கொடுக்கப்பட்டுள்ளது. அதற்குப் பொருத்தமான வட்ட விளக்கப்படம் வரைக.
1. குமரன் வாடகைக்காக ₹6000 ஐ செலவுச் செய்தால் அவர் கல்விக்குச் செய்யும் செலவைக் காண்க.
2. குமரனின் மொத்த மாத வருமானம் எவ்வளவு?
3. கல்வியை விட உணவுக்கு எவ்வளவு அதிகமாகச் செலவு செய்கிறார்?
15% வாடகைக்காக செலவு செய்கிறார் = ₹6000
மாத வருமானம் 10% = ₹4000
i. கல்விக்காக செலவிடப்படும் பணம் = 4000ல் 20% = \(\frac{20}{100}\) x 40000 = ₹8000
ii. மொத்த வருமானம் = 100% =₹ 4000
iii. கல்வியை விட உணவுக்கு 30% அதிகமாக செலவு செய்கிறார்

தீர்வு :

Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 5 வடிவியல் Ex 5.5 Textbook Questions and Answers, Notes.

TN Board 8th Maths Solutions Chapter 5 வடிவியல் Ex 5.5

I. கொடுக்கப்பட்டுள்ள அளவுகளைக் கொண்டு பின்வரும் இணைகரங்களை வரைந்து, அவற்றின் பரப்பளவுகளைக் காண்க.

(i) ARTS, AR = 6 செ.மீ, RT = 5 செ.மீ மற்றும் ∠ART = 70°
விடை :
வரைமுறை:
படி 1 : AR = 6 செ.மீ அளவுள்ள கோட்டுத்துண்டு வரைக
படி 2 : \(\overline{\mathrm{AR}}\) ன் மீது Rல் ∠ART =70° ஐ அமைக்க
படி 3 : Rஐ மையமாகக் கொண்டு, 5 செ.மீ ஆரமுள்ள வட்ட வில்லானது RX ஐ Tல் வெட்டுமாறு வரைக
படி 4 : A மற்றும் T ஐ மையங்களாகக் கொண்டு, முறையே 5செ.மீ மற்றும் 6 செ.மீ ஆரமுள்ள வட்ட விற்கள் வரைக அவை Sல் வெட்டட்டும்.
படி 5 : AS மற்றும் TS ஐ இணைக்க
படி 5 : ARTS என்பது
தேவையான இணைகரம் ஆகும்

பரப்பளவு கணக்கிடுதல் :
ARTS என்பது இணைகரத்தின் பரப்பளவு = bh சதுர அலகுகள்
= 6 × 4.7
= 28.2 ச.செ.மீ

ii. CAMP, CA = 6 செ.மீ, AP = 8 செ.மீ மற்றும் CP = 5.5 செ.மீ.
விடை :
வரைமுறை:
படி 1 : CA = 6 செ.மீ அளவுள்ள கோட்டுத்துண்டு வரைக.
படி 2 : C மற்றும்A ஐ மையங்களாகக் கொண்டு 5.5 செ.மீ மற்றும் 8 செ.மீ ஆரமுள்ள வட்டவிற்கள் வரைக. அவை P ல் வெட்டட்டும்.
படி 3 : CP மற்றும் APஐ இணைக்க.
படி 4 : A மற்றும் P ஐ மையங்களாகக் கொண்டு முறையே 5.5 செ.மீ மற்றும் 6 செ.மீ ஆரமுள்ள வட்ட விற்கள் வரைக. அவை Mல் வெட்டட்டும்
படி 5 : AM மற்றும் PM ஐ இணைக்க
படி 6 : CAMP என்பது தேவையான இணைகரம் ஆகும்.
பரப்பளவு கணக்கிடுதல்:
CAMP என்ற இணைகரத்தின் பரப்பளவு = bh சதுர அலகுககள்
= 6 × 5.6
= 33.6 ச.செ.மீ

iii. EARN, ER = 10 செ.மீ , AN = 7 செ.மீ மற்றும் ∠EOA = 110°, \(\overline{\text { ER }}\) மற்றும் \(\overline{\text { AN }}\) ஆகியவை O இல் வெட்டுகின்றன
விடை :
வரைமுறை:
படி 1 : ER = 10 செ.மீ அளவுள்ள கோட்டுத்துண்டு வரைக
படி 2 : \(\overline{\text { ER }}\) . ன் மையப்புள்ளி O ஐக் குறிக்க
படி 3 : O வழியாக ∠EOY = 110° என இருக்குமாறு \(\overline{\text { XY }}\) என்ற கோடு வரைக.
படி 4: O ஐ மையமாகக் கொண்டு \(\overline{\text { ER }}\) ன் இரு புறங்களிலும், \(\overline{\text { XY }}\) ன் மீது 3.5 செ.மீ ஆரமுள்ள இரண்டு வட்ட விற்களை வரைக. \(\overline{\text { OX }}\) ஐ N லும், \(\overline{\text { OY }}\) ஐ A லும் வெட்டட்டும்.
படி 5: \(\overline{\mathrm{EN}}, \overline{\mathrm{RN}}, \overline{\mathrm{EA}}\) மற்றும் \(\overline{\mathrm{RA}}\). ஐ இணைக்க
படி 6 : EARN என்பது தேவையான இணைகரமாகும்.

பரப்பளவு கணக்கிடுதல் :
EARN என்ற இணைகரத்தின் பரப்பளவு
= bh சதுர அலகுகள்
= 7.3 × 5.3
= 38.69 ச. அலகுகள்

iv. GAIN, GA = 7.5 செ.மீ, GI = 9 செ.மீ மற்றும் ∠GAI = 100°
விடை :
செய்முறை:
படி 1: GA = 7.5 செ.மீ அளவுள்ள கோட்டுத்துண்டு வரைக
படி 2: \(\overline{\mathrm{GA}}\) ன் மீது Aல் ∠GAI = 100° ஐ அமைக்க
படி 3 : G ஐ மையமாகக் கொண்டு, 9 செ.மீ ஆரமுள்ள வட்ட வில்லானது AX ஐ Iல் வெட்டுமாறு வரைந்து GI ஐ இணைக்க.
படி 4 : Gஐ மையமாகக் கொண்டு, \(\overline{\mathrm{AI}}\) ன் நீளத்திற்குச் சமமான ஆரமுள்ள ஒரு வட்டவில் வரைக.
படி 5: I ஐ மையமாகக் கொண்டு 7.5 செ.மீ ஆரமுள்ள ஒரு வட்ட வில் வரைக. அவை N ல் வெட்டடும்
படி 6 : IN மற்றும் GN ஐ இணைக்க
படி 7: GAIN என்பது தேவையான இணைகரம் ஆகும்

பரப்பளவு கணக்கிடுதல்:
GAIN என்ற இணைகரத்தின் பரப்பளவு = bh சதுர அலகுகள்
= 7.5 × 4
= 30 ச.செ.மீ

II. கொடுக்கப்பட்டுள்ள அளவுகளைக் கொண்டு, பின்வரும் சாய்சதுரங்கள் வரைந்து அவற்றின் பரப்பளவுகளைக் காண்க.

i) FACE, FA= 6 செ.மீ மற்றும் FC = 8 செ.மீ
ii) CAKE, CA=5 செ.மீ மற்றும் ∠A = 65°
iii) LUCK, LC =7.8 செ.மீ மற்றும் UK = 6 செ.மீ
iv) PARK, PR = 9 செ.மீ மற்றும் ∠P =70°
தீர்வு :

i) FACE, FA= 6 செ.மீ மற்றும் FC = 8 செ.மீ

வரைமுறை :
i) FA = 6 செ.மீ அளவுள்ள கோட்டுத்துண்டு வரைக.
ii) F மற்றும் A ஐ மையங்களாகக் கொண்டு, முறையே 8 செ.மீ மற்றும் 6 செ.மீ ஆரமுள்ள வட்டவிற்கள் வரைக. அவை C ல் வெட்டும்.
iii) FC மற்றும் AC ஐ இணைக்க.
iv) F மற்றும் C ஐ மையங்களாகக் கொண்டு, ஒவ்வொன்றும் 5 செ.மீ ஆரமுள்ள இரு வட்டவிற்கள் வரைக. அவை E ல் வெட்டட்டும்.
v) FE மற்றும் CE ஐ இணைக்க
vi) FACE என்பது தேவையான சாய்சதுரம் ஆகும்.

பரப்பளவைக் கணக்கிடுதல் :
FACE என்ற சாய்சதுரத்தின் பரப்பளவு = \(\frac { 1 }{ 2 }\) × d₁ × d₂ ச.அலகு
= \(\frac { 1 }{ 2 }\) × 8 × 9
= 36 ச.செ.மீ

ii) CAKE, CA = 5 செ.மீ மற்றும் ∠A = 65
தீர்வு :


வரைமுறை :
i) CA = 5 செ.மீ அளவுள்ள கோட்டுத்துண்டு வரைக.
ii) ∠A கோட்டுத்துண்டின் மீது A ல் ∠A = 65° ஐ வரைக.
iii) A ஐ மையமாகக் கொண்டு 5 செ.மீ ஆரமுள்ள வட்டவில் வரைக. அது AX ஐ K ல் வெட்டும்
iv) C மற்றும் K ஐ மையங்களாகக் கொண்டு, ஒவ்வொன்றும் 5 செ.மீ ஆரமுள்ள வட்டவிற்கள் வரைக. அவை A ல் வெட்டும்.
v) CE மற்றும் KE ஐ இணைக்க
vi)CAKE என்பது தேவையான சாய்சதுரம் ஆகும்.

பரப்பளவைக் கணக்கிடுதல் :
CAKE என்ற சாய்சதுரத்தின் பரப்பளவு = \(\frac { 1 }{ 2 }\) × d₁ × d₂ ச.அலகு
= \(\frac { 1 }{ 2 }\) × 8.5 × 5.2
= 8.5 × 2.6 = 22.1 ச, செ.மீ

iii) LUCK, LC = 7.8 செ.மீ மற்றும் UK = 6 செ.மீ
தீர்வு :


வரைமுறை :
i) LC=7.8 செ.மீ அளவுள்ள கோட்டுத்துண்டு வரைக.
ii) LC க்கு மையக்குத்துக்கோடு XYஐ வரைக அது LC ஐ O ல் வெட்டட்டும்.
iii) O ஐ மையமாகக் கொண்டு, 0 ன் இரு புறமும் 3 செ.மீ ஆரமுள்ள வட்டவிற்கள் OX ஐ K யிலும் மற்றும் OY ஐ பலும் வெட்டுமாறு வரைக.
iv) LK, LU, CK மற்றும் CU ஐ இணைக்க.
v) LUCK என்பது தேவையான சாய் சதுரம் ஆகும்.

பரப்பளவைக் கணக்கிடுதல் :
LUCK என்ற சாய் சதுரத்தின் பரப்பளவு = \(\frac { 1 }{ 2 }\) × d₁ × d₂ ச.அலகு
= \(\frac { 1 }{ 2 }\) × 7.8 × 6
= 7.8 × 3
= 23.4 ச.செமீ

iv) PARK, PR = 9 செ.மீ மற்றும் ∠P =70°
தீர்வு :


வரைமுறை :
i) PR = 9 செமீ அளவுள்ள கோட்டுத்துண்டு வரைக.
ii) P ல் PR ன் இருபுறமும் ∠RPX = ∠RPY = 350 ஐ வரைக.
iii) R & PR ன் இருபுறமும் ∠URP= ∠VRP = 35° ஐ வரைக.
iv) PX மற்றும் RU ஆனது K இலும் RV மற்றும் PY ஆனது M இலும் வெட்டட்டும்.
v) PARK என்பது தேவையான சாய்சதுரம் ஆகும்.

பரப்பளவைக் கணக்கிடுதல் :
PARK என்ற சாய்சதுரத்தின் பரப்பளவு = \(\frac { 1 }{ 2 }\) × d₁ × d₂ ச.அலகு
\(\frac { 1 }{ 2 }\) × 9 × 6.3
= 4.5 × 6.3
= 28.35 ச.செமீ

III. கொடுக்கப்பட்டுள்ள அளவுகளைக் கொண்டு, பின்வரும் செவ்வகங்களை வரைந்து அவற்றின் பரப்பளவுகளைக் காண்க.

i) HAND, HA = 7 செ.மீ மற்றும் AN = 4 செ.மீ
ii) LAND, LA = 8 செ.மீ மற்றும் AD = 10 செ.மீ
தீர்வு :
i) HAND, HA = 7 செ.மீ மற்றும்
AN = 4 செ.மீ

வரைமுறை :
i) HA = 7 செ.மீ அளவுள்ள கோட்டுத்துண்டு வரைக.
ii) E ல் HX ⊥ HA ஐ வரைக.
iii) H ஐ மையமாகக் கொண்டு 4 செ.மீ ஆரமுள்ள வட்டவில் வரைக அது H X ஐ Dல் வெட்டட்டும்.
iv) A மற்றும் D ஐ மையங்களாகக் கொண்டு முறையே 4 செ.மீ மற்றும் 7 செ.மீ ஆரமுள்ள வட்டவிற்கள் வரைக. அவை N ல் வெட்டட்டும்.
v) DN மற்றும் AN ஐ இணைக்க
vi) HAND என்பது தேவையான செவ்வகம் ஆகும்.

பரப்பளவைக் கணக்கிடுதல் :
HAND என்ற செவ்வகத்தின் பரப்பளவு = l × b ச.அ
=7 × 4 = 28 ச.செமீ

ii) LAND, LA = 8 செ.மீ மற்றும்
AD = 10 செ.மீ

வரைமுறை :
i) LA = 8 செ.மீ அளவுள்ள கோட்டுத்துண்டு வரைக.
ii) L ல் LX ⊥ LA ஐ வரைக.
iii) A ஐ மையமாகக் கொண்டு 10செ.மீ ஆரமுள்ள வட்டவில் வரைக. அது LX ஐ Dல் வெட்டட்டும்.
iv) I மற்றும் Dஐமையங்களாகவும் முறையே LD மற்றும் LAன் நீளங்களை ஆரங்களாகவும்
கொண்டு வட்டவிற்கள் வரைக. அவை N ல் வெட்டட்டும்.
v) DN மற்றும் AN ஐ இணைக்க
vi) LAND என்பது தேவையான செவ்வகம் ஆகும்.

பரப்பளவைக் கணக்கிடுதல் :
LAND என்ற செவ்வகத்தின் பரப்பளவு = l × b ச.அலகு
= 8 × 6
= 48 ச.செமீ

IV. கொடுக்கப்பட்டுள்ள அளவுகளைக் கொண்டு, பின்வரும் சதுரங்கள் வரைந்து அவற்றின் பரப்பளவுகளைக் காண்க.

i) EAST, EA = 6.5 செ.மீ
ii) WEST, WS = 7.5 செ.மீ
தீர்வு :
i) EAST, EA = 6.5 செ.மீ


வரைமுறை :
i) EA = 6.5 செமீ அளவுள்ள கோட்டுத்துண்டு வரைக.
ii) Eல், EX I EA ஐ வரைக.
iii) E ஐ மையமாகக் கொண்டு 6.5 செமீ ஆரமுள்ள வட்டவில் வரைக. அது EX ஐ Tல் வெட்டட்டும்.
iv) A மற்றும் T ஐ மையங்களாகவும், ஒவ்வொன்றும் 6.5 செமீ ஆரமுள்ள இரு வட்டவிற்கள்
வரைக. அவை S ல் வெட்டட்டும்.
v) AS மற்றும் TS ஐ இணைக்க EAST என்பது தேவையான சதுரம் ஆகும்.

பரப்பளவைக் கணக்கிடுதல் :
EAST என்ற சதுரத்தின் பரப்பளவு = a² ச.அலகு
= 6.5 × 6.5 = 42.25 ச.செமீ

ii) WEST, WS = 7.5 செ.மீ


வரைமுறை :
i) WS = 7.5 செ.மீ அளவுள்ள கோட்டுத்துண்டு வரைக.
ii) WS க்கு மையக்குத்துக்கோடு XY ஐ வரைக. அது WS R Oல் இருசமக்கூறிடும்.
iii) O ஐ மையமாகக் கொண்டு, 0 ல் இருபுறமும் 3.7 செமீ ஆரமுள்ள வட்ட விற்கள் OX ஐ
T இலும் மற்றும் OY ஐE லும் வெட்டுமாறு வரைக.
iv) WT, ST, WE மற்றும் SE ஐ இணைக்க
v) WEST என்பது தேவையான சதுரம் ஆகும்.

பரப்பளவைக் கணக்கிடுதல் :
WEST என்ற சதுரத்தின் பரப்பளவு = a² ச.அ
= 5.2²
= 27.04 ச.செமீ

Tamilnadu State Board New Syllabus Samacheer Kalvi 9th Maths Guide Pdf Chapter 5 ஆயத்தொலை வடிவியல் Ex 5.6 Textbook Questions and Answers, Notes.

TN Board 9th Maths Solutions Chapter 5 ஆயத்தொலை வடிவியல் Ex 5.6

பலவுள் தெரிவு வினாக்கள்

கேள்வி 1.
ஒரு புள்ளியின் x அச்சுத் தொலைவு பூச்சியம் எனில் அது எப்பொழுதும் ……………… அமையும்
(1) முதல் காற்பகுதியில்
(2) இரண்டாம் காற்பகுதியில்
(3) x – அச்சின் மீது
(4) x – அச்சின் மீது
விடை:
(3) x – அச்சின் மீது

கேள்வி 2.
(-5, 2) மற்றும் (2, -5) என்ற புள்ளியில் ………………. அமையும்
(1) ஒரே காற்பகுதியில்
(2) முறையே II, III காற்பகுதியில்
(3) முறையே II, IV காற்பகுதியில்
(4) முறையே IV, II காற்பகுதியில்
விடை:
(3) முறையே II, IV காற்பகுதியில்

கேள்வி 3.
புள்ளிகள் O(0, 0), A(3, -4), B(3, 4) மற்றும் C(0, 4) ஐக் குறித்து அவற்றை OA, AB, BC, மற்றும் CO என இணைத்தால் கிடைக்கும் உருவம் ……………… முறையே
(1) சதுரம்
(2) செவ்வகம்
(3) சரிவகம்
(4) சாய்சதுரம்
விடை:
(2) செவ்வகம்

கேள்வி 4.
புள்ளிகள் P(-1, 1), Q(3, -4), R(1, -1), S(-2, -3) மற்றும் T(-4, 4) என்பன ஒரு வரைபடத் தாளில் குறிக்கப்பட்டால் நான்காவது காற்பகுதியில் அமையும் புள்ளிகள் ………………….
(1) P மற்றும் T
(2) Q மற்றும் R
(3) மற்றும் S
(4) P மற்றும் Q
விடை:
(2) Q மற்றும் R

கேள்வி 5.
ஒரு புள்ளியின் y அச்சுத் தொலைவு 4 மற்றும் அப்புள்ளி y அச்சில் அமைந்தால் அப்புள்ளி …………… ஆகும்.
(1) (4, 0)
(2) (0, 4)
(3) (1, 4)
(4) (4, 2)
விடை:
(2) (0, 4)

கேள்வி 6.
(2, 3) மற்றும் (1, 4) என்ற புள்ளிகளுக்கு இடையே உள்ள தொலைவு …………………
(1) 2
(2) \(\sqrt{56}\)
(3) \(\sqrt{10}\)
(4) √2
விடை:
(4) √2

கேள்வி 7.
புள்ளிகள் A(2, 0), B(-6, 0), C(3, a-3) ஆனது x அச்சின் மீது அமைந்தால் a இன் மதிப்பு …………………….
(1) 0
(2) 2
(3) 3
(4) -6
விடை:
(3) 3

கேள்வி 8.
(x + 2,4) = (5, y – 2) எனில் (x, y) இன் மதிப்பு …………………….
(1) (7, 12)
(2) (6, 3)
(3) (3, 6)
(4) (2, 1)
விடை:
(3) (3,-6)

கேள்வி 9.
Q₁, Q₂, Q₃, Q₄, என்பன கார்ட்டீசியன் தளத்தின் நான்கு காற்பகுதிகள் எனில், Q₂ ∪ Q₃, என்பது ……………………
(1)Q₂ ∪ Q₁
(2) Q₂ ∪ Q₃
(3) வெற்றுக்கணம்
(4) x அச்சின் குறைப்பகுதி
விடை:
(3) வெற்றுக்கணம் R

கேள்வி 10.
(5, -1) என்ற புள்ளிக்கு ஆதிப் புள்ளிக்கும் இடையே உள்ள தொலைவு …………………..
(1) \(\sqrt{24}\)
(2) \(\sqrt{37}\)
(3) \(\sqrt{26}\)
(4) \(\sqrt{17}\)
விடை:
(3) \(\sqrt{26}\)

கேள்வி 11.
P(2,4) மற்றும் Q(5, 7) ஆகிய புள்ளிகளை இணைக்கும் கோட்டுத் துண்டை 2 : 1 என்ற விகிதத்தில் உட்புறமாகப் பிரிக்கும் புள்ளி C இன் ஆயத்தொலைவுகள்
(1) \(\left(\frac{7}{2}, \frac{11}{2}\right)\)
(2) (3, 5)
(3) (4, 4)
(4) (4, 6)
விடை:
(4) (4, 6)

கேள்வி 12.
A(-4,3) மற்றும் B(-2,4) ஆகிய புள்ளிகளை இணைக்கும் கோட்டுத்துண்டின் நடுப்புள்ளி P \(\left(\frac{a}{3}, \frac{b}{2}\right)\) எனில் (a,b) ஆனது
(1) (-9, 7)
(2) \(\left(-3, \frac{7}{2}\right)\)
(3) (9,-7)
(4) \(\left(3,-\frac{7}{2}\right)\)
விடை:
(1) (-9, 7)

கேள்வி 13.
P(2,7) மற்றும் R(-2,3) ஆகிய புள்ளிகளை இணைக்கும் கோட்டுத்துண்டை Q(1, 6) என்ற புள்ளியானது என்ன விகிதத்தில் பிரிக்கும்?
(1) 1 : 2
(2) 2 : 1
(3) 1 : 3
(4) 3 : 1
விடை:
(3) 1 : 3

கேள்வி 14.
(-3, 2) என்ற புள்ளியை மையமாகக் கொண்ட வட்டத்தில் (3, 4) ஐ ஒரு முனையாகக் கொண்ட விட்டத்தின் மற்றொரு முனையைக் காண்க.
(1) (0,-3)
(2) (0, 9)
(3) (3, 0)
(4) (-9, 0)
விடை:
(4) (-9, 0)

கேள்வி 15.
A(a1, b1) மற்றும் B(a2, b2) ஆகிய புள்ளிகளை இணைக்கும் கோட்டுத் துண்டை X – அச்சு எந்த விகிதத்தில் பிரிக்கும்?
(1) b1 : b2
(2) – b1 : b2
(3) a1 : a2
(4) – a1 : a2
விடை:
(2) -b1 : b2

கேள்வி 16.
(6, 4) மற்றும் (1, -7) ஆகிய புள்ளிகளை இணைக்கும் கோட்டுத் துண்டை X – அச்சு எந்த விகிதத்தில் பிரிக்கும்?
(1) 2 : 3
(2) 3 : 4
(3) 4 : 7
(4) 4 : 3
விடை :
(3) 4 : 7

கேள்வி 17.
ஒரு முக்கோணத்தின் பக்கங்கள் AB, BC மற்றும் CA ஆகியவற்றின் நடுப்புள்ளிகளின் ஆயத் தொலைவுகள் முறையே (3,4), (1,1) மற்றும் (2,-3) எனில் A மற்றும் B இன் ஆயத்தொலைவுகள் யாவை?
(1) (3, 2), (2, 4)
(2) (4, 0), (2, 8)
(3) (3, 4) (2, 0)
(4) (4, 3) (2,4)
விடை:
(2) (4, 0), (2, 8)

கேள்வி 18.
(-a, 2b) மற்றும் (-3a, -4b) ஆகிய புள்ளிகளை இணைக்கும் கோட்டுத்துண்டின் நடுப்புள்ளியானது
(1) (2a, 3b)
(2) (-2a, -b)
(3) (2a, b)
(4) (-2a, -3b)
விடை:
(2) (-2a, -b)

கேள்வி 19.
(-5, 1) மற்றும் (2, 3) ஆகிய புள்ளிகளை இணைக்கும் கோட்டை Y – அச்சு உட்புறமாக என்ன விகிதத்தில் பிரிக்கும்?
(1) 1 : 3
(2) 2 : 5
(3) 3 : 1
(4) 5 : 2
விடை:
(4) 5 : 2

கேள்வி 20.
(1, -2) (3, 6), (x, 10) மற்றும் (3,2) ஆகியன ஓர் இணைகரத்தின் வரிசையாக எடுக்கப்பட்ட முனைப்புள்ளிகள் எனில் X இன் மதிப்பானது
(1) 6
(2) 5
(3) 4
(4) 3
விடை:
(2) 5

Tamilnadu State Board New Syllabus Samacheer Kalvi 9th Maths Guide Pdf Chapter 5 ஆயத்தொலை வடிவியல் Ex 5.5 Textbook Questions and Answers, Notes.

TN Board 9th Maths Solutions Chapter 5 ஆயத்தொலை வடிவியல் Ex 5.5

கேள்வி 1.
பின்வரும் புள்ளிகளை முனைப் புள்ளிகளாகக் கொண்ட முக்கோணத்தின் நடுக்கோட்டு மையம் காண்க.
(i) (2, -4), (-3, -7) மற்றும் (7,2)
(ii) (-5, -5) (1, -4) மற்றும் (-4,-2).
விடை:
(i) A = (2, -4) B (-3,-7) மற்றும் C(7,2) ஆகிய புள்ளிகளைக் கொண்ட முக்கோணத்தின் நடுக்கோட்டு மையம். G (x,y)
(x₁,y₁) = (2,-4)
(x₂, y₂) = (-3,-7)
(x₃, y₃) = (7, 2)
நடுக்கோட்டு மையம் G (x,y)
= G \(\left(\frac{2-3+7}{3}, \frac{-4-7+2}{3}\right)\)
= G \(\left(\frac{6}{3}, \frac{-9}{3}\right)\)
= G (2,-3)

(ii) A (-5, -5) B (1,-4) மற்றும் C(-4,-2) ஆகிய புள்ளிகளைக் கொண்ட முக்கோணத்தின் நடுக் கோட்டு மையம்.
G = \(\left(\frac{x_{1}+x_{2}+x_{3}}{3}, \frac{y_{1}+y_{2}+y_{3}}{3}\right)\)
(x₁, y₁) = (-5, -5)
(x₂, y₂) = (1, -4)
(x₃,y₃) = (-4, -2)
நடுக்கோட்டு மையம் G (x,y)
G = \(\left(\frac{-5+1-4}{3}, \frac{-5-4-2}{3}\right)\)
G = \(\left(\frac{-8}{3}, \frac{-11}{3}\right)\)

கேள்வி 2.
ஒரு முக்கோணத்தின் நடுகோட்டு மையம் [4,-2] மற்றும் அதன் இரு முனைப்புள்ளிகள் [3, -2] மற்றும் [5, 2] எனில் மூன்றாவது முனைப் புள்ளியைக் காண்க.
விடை:
(i) (3, -2) மற்றும் (5, 2) ஆகியன முனைப்புள்ளிகள்.
(4, -2) என்பது நடுக்கோட்டு மையம் என்க.

\(\frac{x_{1}+x_{2}+x_{3}}{3}\) = 4
\(\frac{3+5+x_{3}}{3}\) = 4
x₃ = 12 + 8
x₃ = 12 – 8
x₃ = 4

\(\frac{\mathrm{y}_{1}+\mathrm{y}_{2}+\mathrm{y}_{3}}{3}\) = -2
\(\frac{-2+2+y_{3}}{3}\) = -2
y₃ = -6
மூன்றாவது முனைப்புள்ளி (4, -6)

கேள்வி 3.
A (-1,3) B (1, -1) மற்றும் C (5,1) ஆகியன ஒரு முக்கோணத்தின் முனைப்புள்ளிகள் எனில் A வழியே செல்லக்கூடிய நடுக்கோட்டின் நீளத்தைக் காண்க.
விடை:

D, E, F என்பன BC, AC மற்றும் AB என்ற பக்கங்களின் நடுப்புள்ளிகள் என்க.
AD, BE மற்றும் CF ஆகியன நடுக்கோடுகள் என்க.

BC இன் நடுப்புள்ளி = C\(\left(\frac{1+5}{2}, \frac{-1+1}{2}\right)\)
\(=\quad C\left(\frac{6}{2}, \frac{0}{2}\right)\)
= C(3, 0)
AC இன் நடுப்புள்ளி = E\(\left(\frac{-1+5}{2}, \frac{3+1}{2}\right)\)
= E\(\left(\frac{4}{2}, \frac{4}{2}\right)\) =E(2, 2)
AB இன் நடுப்புள்ளி
= F\(\left(\frac{-1+1}{2}, \frac{3-1}{2}\right)\) = F\(\left(\frac{0}{2}, \frac{2}{2}\right)\)
= F(0, 1)

நடுக்கோடு AD இன் நீளம் (-1, 3) (3, 0)
AD = \(\sqrt{(3+1)^{2}+(0+3)^{2}}\) (4) (3)
(-1, 3) (3, 0) = \(\sqrt{(4)^{2}+(3)^{2}}\)
= \(\sqrt{16+9}\)
= 5

நடுக்கோடு BE இன் நீளம் (1, -1) (2, 2)
BE = \(\sqrt{(2-1)^{2}+(2+1)^{2}}\)
(1, -1) (2, 2)
\(=\sqrt{1+(3)^{2}}\)
\(=\sqrt{1+9}\)
\(=\sqrt{10}\)

நடுக்கோடு CF இன் நீளம் (5, 1) (0, 1)
\(=\sqrt{(0-5)^{2}+(1-1)^{2}}=\sqrt{(-5) 2+(0)}\)
\(=\sqrt{25}\)
= 5

கேள்வி 4.
(1, 2) (h, – 3) மற்றும் (-4, k) ஆகியன ஒரு முக்கோணத்தின் முனைப்புள்ளிகள். மேலும் புள்ளி (5,-1) ஆனது அந்த முக்கோணத்தின் இருக்கோட்டு மையம் எனில்,\(\sqrt{(h+k)^{2}+(h+3 k)^{2}}\) இன் மதிப்பைக் காண்க.
வடை:
(i) (1, 2) (h, – 3) மற்றும் (-4, k)) ஆகியன ஒரு முக்கோணத்தின் முனைப்புள்ளிகள் (5, -1) அந்த முக்கோணத்தின் நடுக்கோட்டு மையம் G(x, y) = G\(\left(\frac{\mathbf{x}_{1}+\mathbf{x}_{2}+\mathbf{x}_{3}}{3}, \frac{\mathbf{y}_{1}+\mathbf{y}_{2}+\mathbf{y}_{3}}{3}\right)\)
(x1, y1) = (1, 2)
(x2, y2) = (h, -3)
(x3, y3) = (-4, k)

கேள்வி 5.
A(-3, 5) மற்றும் B(3, 3) ஆகியன முறையே ஒரு முக்கோணத்தின் செங்கோட்டு மையம் மற்றும் நடுக்கோட்டு மையம் ஆகும். C ஆனது இந்த முக்கோணத்தின் சுற்று வட்ட மையம் எனில், கோட்டுத்துண்டு AC ஐ விட்டமாகக் கொண்ட வட்டத்தின் ஆரம் காண்க.

விடை : [-3, 5]
நடுக்கோட்டு மையம் செங்கோட்டு மையத் தையும் உள்வட்ட மையத்தையும் 2:1 என்ற விகிதத்தில் பிரிக்கிறது. உள்வட்ட மையம் (x, y) என்க. பிரிவு சூத்திரத்தின் படி,
\(\left(\frac{2(x)-3}{3}, \frac{2 y+5}{3}\right)\) = (3,3)
2x – 3 = 9
2x = 9 + 3
2x = 12
x = \(\frac{12}{2}\)
x = 6

2y + 5 = 9
2y = 9 – 5
2y = 4
y = \(\frac{4}{2}\)
y = 2
உள்வட்ட மையம் = (6,2)
வட்டத்தின் ஆரம்
\(=\sqrt{(6+3)^{2}+(5-2)^{2}}\)
\(=\sqrt{(9)^{2}+(3)^{2}}=\sqrt{81+9}\)
\(=\sqrt{90}\)
= 3\(\sqrt{10}\) அலகுகள்.

கேள்வி 6.
A (3, 4) B (-2, -1) மற்றும் C (5, 3) என்ப ன முக்கோணம் ABC இன் முனைப் புள்ளிகள். G ஆனது அதன் நடுக்கோட்டு மையம் மற்றும் BDCG ஆனது ஒர் இணைகரம் எனில் முனைப்புள்ளி D இன் ஆயத்தொலைவுகளைக் காண்க.
விடை:
(i) A (3, 4) B (-2, -1) மற்றும் C (5, 3)) என்பன ΔABC இன் முனைப்புள்ளிகள் என்க.
G ஆனது அதன் நடுக்கோட்டு மையம்
(x₁,y₁) = (3, 4)
(x₂, y₂) = (-2, -1)
(x₃,y₃) = (5, 3)
நடுக்கோட்டு மையம் (x,y)

G (x,y) = G(2, 2)

கேள்வி 7.
முக்கோணத்தின் பக்கங்களின் நடுப்புள்ளிகள் \(\left(\frac{3}{2}, 5\right),\left(7, \frac{-9}{2}\right)\) மற்றும் \(\left(\frac{13}{2}, \frac{-13}{2}\right)\)
எனில் அந்த முக்கோணத்தின் நடுக்கோட்டு மையம் காண்க.
விடை:
A (x₁, y₁) B (x₂, y₂) C (x₃, y₃) என்பன முனைப்புள்ளிகள் மற்றும் \(\left(\frac{3}{2}, 5\right),\left(7, \frac{-9}{2}\right)\) மற்றும் \(\left(\frac{13}{2}, \frac{-13}{2}\right)\) ஆகியன பக்கங்களின் நடுப்புள்ளிகள் என்க.
G ஆனது அதன் நடுக்கோட்டு மையம்
\(\frac{\mathrm{X}_{1}+\mathrm{x}_{2}}{2}=\frac{3}{2}\) ⇒ x₁ + x₂ = 3 ……………(1)
\(\frac{x_{2}+x_{3}}{2}\) = 7 ⇒ x₂ + x₃ = 14 …………… (2)
\(\frac{\mathrm{X}_{3}+\mathrm{X}_{1}}{2}=\frac{13}{2}\) ⇒ x₃ + x₁ = 13 ………………. (3)
(1) + (2) + (3) r 2x₁ + 2x₂ + 2x₃ = 30
2(x₁ + x₂ + x₃) = 30
x₁ + x₂ + x₃ = 15 …………… (4)
\(\frac{\mathrm{y}_{1}+\mathrm{y}_{2}}{2}\) = 5 ⇒ y₁ + y₂ = 10 …………….. (5)
\(\frac{\mathrm{y}_{2}+\mathrm{y}_{3}}{2}=\frac{-9}{2}\) ⇒ y₂ + y₃ = -9 ……………….(6)
\(\frac{\mathrm{y}_{3}+\mathrm{y}_{1}}{2}=\frac{-13}{2}\) ⇒ y₃ + y₁ = -13 ……………..(7)
(5) + (6) + (7) r 2y₁ + 2y₂ + 2y₃ = -12
2(y₁ + y₂ + y₃)= -12
y₁ + y₂ + y₃ = -6 …………. (8)
(4) – (2) rx₁ = 15 – 14 = 1
(4) – (3) rx₂ = 15 – 13 = 2
(4) – (1) rx₃ = 15 – 3 = 12
(8) – (6) ry₁ = -6 + 9 = 3
(8) – (7) ry₂ = -6 + 13 = 7
(8) – (5) ry₃ = -6- 10 = -16 முனைப்புள்ளிகள் = A (1, 3) B (2,7) C (12, -16) நடுக்கோட்டு மையம்

G (x,y) = G(5, -2)

Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 5 வடிவியல் Ex 5.4 Textbook Questions and Answers, Notes.

TN Board 8th Maths Solutions Chapter 5 வடிவியல் Ex 5.4

கேள்வி 1.
கொடுக்கப்பட்டுள்ள அளவுகளைக் கொண்ட நாற்கரங்கள் வரைந்து, அவற்றின் பரப்பளவைக் காண்க.

1. நாற்கரம் ABCD, AB = 5 செ.மீ, BC = 4.5 செ.மீ, CD = 3.8 செ.மீ, DA = 4.4 செ.மீ
மற்றும் AC = 6.2 செ.மீ.
தீர்வு :
AB = 5 செ.மீ, BC = 4.5 செ.மீ
CD = 3.8 செ.மீ, DA = 4.4 செ.மீ, AC = 6. செ.மீ

படிகள்:

1. AB= 5 செ.மீ அளவுள்ள ஒரு கோட்டுத்துண்டு வரைக.
2. A மற்றும் B ஐ மையங்களாகக் கொண்டு, முறையே 6.2 செ.மீ மற்றும் 4.5 செ.மீ ஆரமுள்ள இரண்டு வட்டங்கள் வரைக. அவை Cல் வெட்டட்டும்.
3. AC மற்றும் BC ஐ இணைக்க.
4. A மற்றும் C ஐ மையங்களாகக் கொண்டு, முறையே 4.4 செ.மீ மற்றும் 3.8 செ.மீ ஆரமுள்ள இரண்டு விற்கள் வரைக. அவை D ல் வெட்டட்டும்.
5. AD மற்றும் CD ஐ இணைக்க.
6. ABCD என்பது தேவையான நாற்கரமாகும்.

பரப்பளவு கணக்கிடுதல் :
ABCD என்ற நாற்கரத்தின் பரப்பளவு = \(\frac { 1 }{ 2 }\) x d x (h₁ + h₂) ச.அ
= \(\frac { 1 }{ 2 }\) x 6.2 x (2.7 + 3.7)
= \(\frac { 1 }{ 2 }\) x 6.2 x 6.4
= 19.84 ச.செ.மீ

2. நாற்கரம் PLAY, PL = 7 செ.மீ, LA = 6 செ.மீ, AY = 6 செ.மீ, PA = 8 செ.மீ மற்றும்
LY = 7 செ.மீ.
தீர்வு :
PL = 7 செ.மீ AY = 6 செ.மீ
LA = 6 செ.மீ PA = 8 செ.மீ LY = 7செ.மீ

படிகள் :

1. PL = 7 செ.மீ அளவுள்ள கோட்டுத்துண்டு வரைக.
2. P மற்றும் 1 ஐ மையங்களாகக் கொண்டு, முறையே 8 செ.மீ மற்றும் 6 செ.மீ ஆரமுள்ள இரண்டு விற்கள் வரைக. அவை A ல் வெட்டட்டும்.
3. PA மற்றும் LA ஐ இணைக்க
4. A மற்றும் L ஜ மையங்களாகக் கொண்டு, முறையே 6 செ.மீ மற்றும் 8 ஆரமுள்ள இரண்டு விற்கள் வரைக. அவை Y ல் வெட்டட்டும்.
5. AY, LY மற்றும் PYஜ இணைக்க.
6. PLAY என்பது தேவையான நாற்கரமாகும்.

பரப்பளவு கணக்கிடுதல் :
PLAY என்ற நாற்கரத்தின் பரப்பு = \(\frac { 1 }{ 2 }\) x d x (h₁ + h₂) ச. அ
= \(\frac { 1 }{ 2 }\) x 8 (1.6 + 5.6)
= 4 x 7.2
= 28.8 ச. செ.மீ

கேள்வி 3.
நாற்கரம் PQRS, PQ = QR = 3.5 செ.மீ, RS = 5.2 செ.மீ, SP = 5.3 செ.மீ மற்றும் ∠Q= 120
தீர்வு :
PQ = QR = 3.5 செ.மீ
RS = 5.2 செ.மீ SP= 5.3 செ.மீ ∠Q = 120°

படிகள் :

1. PQ = 3.5 செ.மீ அளவுள்ள கோட்டுத்துண்டு வரைக.
2.  ∠Q= 120° ஐ வரைக.
3. Q ஐ மையமாகக் கொண்டு 3.5 செ.மீ ஆரமுள்ள வில் வரைக அது கதிர் QX ஐ Rல் வெட்டட்டும்
4. P மற்றும் R ஜ மையங்களாகக் கொண்டு, முறையே 5.3 செ.மீ மற்றும் 5.2 செ.மீ ஆரமுள்ள இரண்டு விற்கள் வரைக. அவை S ல் வெட்டட்டும்
5. PS மற்றும் RS ஐ இணைக்க.
6. PQRS என்பது தேவையான நாற்கரமாகும்.

பரப்பளவைக் கணக்கிடுதல்
PQRS என்ற நாற்கரத்தின் பரப்பளவு = \(\frac { 1 }{ 2 }\) x d x (h₁ + h₂) ச. அ
= \(\frac { 1 }{ 2 }\) x 6.1(4.3 + 2.3)
= \(\frac { 1 }{ 2 }\) x 6.1 x 6.6
= 20.13 ச.செ.மீ

கேள்வி 4.
நாற்கரம் MIND, MI = 3.6செ.மீ, ND = 4 செ.மீ, MD = 4 செ.மீ, ∠ M = 50 மற்றும்
∠D= 100°
தீர்வு :
MI = 3.6 செ.மீ MD = 4 செ.மீ
ND = 4 செ.மீ ∠M = 50°
∠D= 100°

படிகள் :

1. MD = 3.6 செ.மீ அளவுள்ள கோட்டுத்துண்டு வரைக.
2. MI ன் மேல் Mல் ; ∠IMY = 50° மற்றும் Dல் ∠D = 100°
3. M மற்றும் N ஐ மையங்களாகக் கொண்டு 4 செ.மீ ஆரமுள்ள விற்கள் வரைக அவை N ஐ வெட்டட்டும்
4. DN மற்றும் IN ஜ இணைக்க.
5. MIND என்பது தேவையான நாற்கரம் ஆகும்.

பரப்பளவு கணக்கிடுதல் :
MIND என்ற நாற்கரத்தின் பரப்பளவு = \(\frac { 1 }{ 2 }\) x d x (h₁ + h₂) ச. அ
= \(\frac { 1 }{ 2 }\) x 8(1.2 + 2.2)
= 4 x 3.4
= 13.6 ச.செ.மீ

கேள்வி 5.
நாற்கரம் AGRI, AG = 4.5 செ.மீ, GR = 3.8 செ.மீ, ∠ A = 90°, ∠ G = 110° மற்றும் ∠R= 90°
தீர்வு :
AG = 4.5 செ.மீ ∠A = 90°
GR = 3.8 செ.மீ ∠G = 110° ∠R = 90°

படிகள் :

1. AG = 4.5 செ.மீ அளவுள்ள கோட்டுத்துண்டு வரைக.
2. AGன் மேல் ∠AGX = 110 ஜ உருவாக்கு.
3. G ஐ மையமாகக் கொண்டு 3.8செ.மீ ஆரமுள்ள வில் வரைக. அது G X ஐ R ல் வெட்டட்டும்.
4. AG,ன் மேல் Aல் ∠GAI = 90° ஐயும் மற்றும் AR ன் மேல் Rல் ∠ARI = 90°
   ஐயும் உருவாக்கு. அவை 1 ல் வெட்டட்டும்.
5. AGRI என்பது தேவையான நாற்கரமாகும்.

பரப்பளவு கணக்கிடுதல்.
AGRI என்ற நாற்கரத்தின் பரப்பளவு = \(\frac { 1 }{ 2 }\) x d x (h₁ + h₂) ச. அ
= \(\frac { 1 }{ 2 }\) x 6.8(10.2 + 2.4)
= 3.4 x 12.6
= 42.84 ச.செ.மீ

II. கொடுக்கப்பட்டுள்ள அளவுகளைக் கொண்டு, பின்வரும் சரிவகங்கள் வரைந்து அவற்றின் பரப்பளவுகளை காண்க.

கேள்வி 1.
AIMS \(\overline{\mathrm{AI}} \| \overline{\mathrm{SM}}\) , AI = 6 செ.மீ, IM = 5 செ.மீ, AM = 9 செ.மீ மற்றும் MS = 6.5 செ.மீ.
தீர்வு :

வரைமுறை:

1. படி 1: AI = 6 செ.மீ அளவுள்ள கோட்டுத்துண்டு வரைக
2. படி 2: A மற்றும் 1 ஐ மையங்களாகக் கொண்டு, முறையே 9செ.மீ மற்றும் 5செ.மீ
   ஆரமுள்ள வட்டவிற்கள் வரைக. அவை Mல் வெட்டட்டும்.
3. படி 3 : AM மற்றும் IM ஐ இணைக்க.
4. படி 4 : AI க்கு இணையாக MX ஐ வரைக.
5. படி 5: Mஐ மையமாகக் கொண்டு, 6.5 செ.மீ ஆரமுள்ள வட்டவில்லானது MX ஐ S ல் வெட்டுமாறு வரைக.
6. படி 6 : AS ஐ இணைக்க AIMS என்பது தேவையான சரிவகம் ஆகும்.

பரப்பளவு கணக்கிடுதல் :
AIMS என்ற சரிவகத்தின் பரப்பளவு = \(\frac { 1 }{ 2 }\) h(a+b) சதுர அலகுகள்
= \(\frac { 1 }{ 2 }\) x 4.8(6 + 6.5)
= 2.4 (12.5)
= 30 ச.செ.மீ

கேள்வி 2.
CUTE, \(\overline{\mathrm{CU}} \| \overline{\mathrm{ET}}\), CU = 7 செ.மீ, ∠UCE = 80°, CE = 6 செ.மீ மற்றும் TE = 5 செ.மீ
தீர்வு :

1. படி 1: CU = 7 செ.மீ அளவுள்ள கோட்டுத்துண்டு வரைக.
2. படி 2 : C ல் ∠UCE = 80° ஐ அமைக்க.
3. படி 3 : C ஐ மையமாகக் கொண்டு
   6 செ.மீ ஆரமுள்ள வட்டவில்லானது CX ஐ E ல் வெட்டுமாறு வரைக.
4. படி 4 : CU க்கு இணையாக ET வரைக. :
5. படி 5: E ஐ மையமாகக் கொண்டு, 5 செ.மீ ஆரமுள்ள வட்ட வில்லானது EY ஐ T ல் வெட்டுமாறு வரைக.
6. படி 6 : TU. ஐ இணைக்க.CUTE என்பது தேவையான சரிவகம் ஆகும்.

பரப்பளவு கணக்கிடுதல் :
CUTE என்ற சரிவகத்தின் பரப்பளவு
= \(\frac { 1 }{ 2 }\) x h x (a + b) சதுர அலகுகள்
= \(\frac { 1 }{ 2 }\) x 6(7 + 5)
= 3 x 12 = 36 செ.மீ

கேள்வி 3.
ARMY AR ||YM, AR = 7 செ.மீ, RM = 6.5 செ.மீ ∠RAY = 100° மற்றும் ∠ARM = 60°
தீர்வு :

1. படி1 : AR = 7 செ.மீ அளவுள்ள IY 4.5 செ.மீ கோட்டுத்துண்டு வரைக.
2. படி2 : RA ZARM = 60° ஐ வரைக.
3. படி3 : R மையமாகக் கொண்டு 6.5 செ.மீ ஆரமுள்ள வட்ட வில்லானது RX ஐ Mல் வெட்டுமாறு வரைக.
4. படி4 : AR க்கு இணையாக MZ வரைக
5. படி5 : AW ஐ Y ல் வெட்டுமாறு Aல் ∠RAY = 100° ஐ அமைக்க
6. படி6 :ARMY என்பது தேவையான சரிவகம் ஆகும்

பரப்பளவு கணக்கிடுதல் :
ARMY என்ற சரிவகத்தின் பரப்பளவு = \(\frac { 1 }{ 2 }\) x h x (a + b) சதுர அலகுகள்
= \(\frac { 1 }{ 2 }\) x 5.6 (7+4.5)
= 2.8 (11.5)
= 32.2 ச.செ.மீ

கேள்வி 4.
CITY \(\overline{\mathrm{CI}} \| \overline{\mathrm{YT}}\), CI = 7 செ.மீ, IT = 5.5 செ.மீ, TY = 4 செ.மீ மற்றும் YC = 6 செ.மீ.
தீர்வு :

1. படி1 : CI = 7 செ,மீ அளவுள்ள கோட்டுத்துண்டு வரைக.
2. படி2 : CA = 4 செ.மீ இருக்குமாறு CIன் மேல் A என்ற புள்ளியைக் குறிக்க
3. படி3 : A மற்றும் I ஐ மையமாகக் கொண்டு, முறையே 6 செ.மீ மற்றும் 5.5 செ.மீ ஆரமுள்ள வட்ட விற்கள் வரைக. அவை T ல் வெட்டட்டும் AT மற்றும் IT ஐ இணைக்க.
4. படி4 : C மற்றும் T ஐ மையமாகக் கொண்டு முறையே 6செ,மீ மற்றும் 4செ.மீ ஆரமுள்ள வட்ட விற்கள் வரைக. அவை Yல் வெட்டட்டும். CY மற்றும் TY ஐ இணைக்க
5. படி5 : CITY என்பது தேவையான சரிவகம் ஆகும்

பரப்பளவு கணக்கிடுதல் :
CITY என்ற சரிவகத்தின் பரப்பளவு = \(\frac { 1 }{ 2 }\) x h x (a + b) சதுர அலகுகள்
= \(\frac { 1 }{ 2 }\) x 5.6 (7 + 4)
= 2.8 (11.)
= 30.8 ச.செ.மீ

Tamilnadu State Board New Syllabus Samacheer Kalvi 9th Maths Guide Pdf Chapter 5 ஆயத்தொலை வடிவியல் Ex 5.4 Textbook Questions and Answers, Notes.

TN Board 9th Maths Solutions Chapter 5 ஆயத்தொலை வடிவியல் Ex 5.4

கேள்வி 1.
A (4,-3) மற்றும் B (9,7) ஆகிய புள்ளிகளை இணைக்கும் கோட்டுத்துண்டை 3:2 என்ற விகிதத்தில்
உட்புறமாகப் பிரிக்கும் புள்ளியின் ஆயத் தொலைவுகளைக் காண்க.
விடை:
கொடுக்கப்பட்ட புள்ளிகள் A (4, -3) மற்றும் B(9,7). P(x,y) ஆனது AB ஐ உட்புறமாக 3:2 என்ற விகிதத்தில் பிரிக்கின்றது
பிரிவு சூத்திரத்தின் படி

= P(7,3)

கேள்வி 2.
A (-3,5) மற்றும் B (-4,9) ஆகிய புள்ளிகளை இணைக்கும் கோட்டுத்துண்டைப் புள்ளி P (2,-5) என்ன விகிதத்தில் பிரிக்கும்?
விடை:
A (-3,5) மற்றும் B (4,9). P(2,-5) ஆனது AB ஐ m:n என்ற விகிதத்தில் பிரிக்கின்றது
பிரிவு சூத்திரத்தின் படி

4m – 3 n = 2m + 2n
2m = 5n
\(\frac{m}{n}=\frac{5}{2}\)
m : n = 5 : 2

கேள்வி 3.
A (1,2) மற்றும் B (6,7) ஆகிய புள்ளிகளை இணைக்கும் கோட்டுத்துண்டில் AP = \(\frac{2}{5}\) AB என்றவாறு அமையும் புள்ளி P இன் ஆயத்தொலைவுகளைக் காண்க.
விடை:
A (1,2) மற்றும் B (6,7). P ஆனது AB ஐ m:n என்ற விகிதத்தில் பிரிக்கின்றது
பிரிவு சூத்திரத்தின் படி

\(=\sqrt{50}\)
= 5√2
∴ P இன் ஆயத்தொலைவுகள் = (3, 4)

கேள்வி 4.
A (-5,6) மற்றும் B (4, -3) ஆகிய புள்ளிகளை இணைக்கும் கோட்டுத்துண்டை மூன்று சமப் பாகங்களாகப் பிரிக்கும் புள்ளிகளின் ஆயத்தொலைவுகளைக் காண்க.
விடை:
தீர்வு:

பரிவு சூத்திரம்:

= (1,0)

கேள்வி 5.
A(6,3) மற்றும் B(-1, -4) ஆகிய புள்ளிகளை இணைக்கும் கோட்டுத்துண்டானது, ABஇன் நீளத்தில் பாதி அளவினை இருமுனைகளிலும் இணைத்து இருமடங்காக ஆக்கப்படுகின்றது எனில் புதிய முனைகளின் ஆயத்தொலைவுகளைக் காண்க.
தீர்வு:

பிரிவு சூத்திரம்:

A ஆனது CD ஐ 1:2 என பிரிக்கிறது. இங்கு A(6,3) B(-1, -4) C(x₁, y₁ ) CA : AD = 1 : 2
\(\left(\frac{2 x 1-1}{2+1}, \frac{2 y 1-4}{2+1}\right)\) = (6,3)
\(\frac{2 x 1-1}{3}\) = 6
2×1 – 1 = 18
2×1 = 19
x1 = \(\frac{19}{2}\)

\(\frac{2 y 1-4}{3}\) = 3
2y1 – 4 = 9
2y1 = 9 + 4
2y1 = 13
y1 = \(\frac{13}{2}\)
B ஆனது CD ஐ 2 : 1 என பிரிக்கிறது.
\(\left(\frac{2 x 2+6}{3}, \frac{2 y 2+3}{3}\right)\) = (-1,-4)

\(\frac{2 x 2+6}{3}\) = -1
2×2 + 6 = -3
2×2 = -3 -6
2×2 = -9
x2 = \(\frac{-9}{2}\)

\(\frac{2 y 2+3}{3}\) = -4
2y2+3 = -12
2y2 = -12-3
2y2 = -15
y2 = \(\frac{-15}{2}\)
C \(\left(\frac{19}{2}, \frac{13}{2}\right)\) மற்றும் D \(\left(\frac{-19}{2}, \frac{-15}{2}\right)\)என்பன
புதிய முனைகளின் ஆயத்தொலைவுகளாகும்.

கேள்வி 6.
பிரிவுச் சூத்திரத்தைப் பயன்படுத்தி A(7,-5) B(9,-3) மற்றும் C (13,1) ஆகியன ஒரே கோட்டில் அமையும் என நிரூபிக்க.
தீர்வு:

(புள்ளி (9,-3) ஆனது A(7,-5), C(13, 1) என்ற கோட்டை r : 1 என்ற விகிதத்தில் பிரிக்கிறது என்க.
பிரிவு சூத்திரம்:

\(\frac{13 r+7}{r+1}\) = 9
13r + 7 = 9(r + 1)
13r + 7= 9r + 9
13r – 9r = 9 – 7
4r = 2
r = \(\frac{2}{4}\)

\(\frac{r-5}{r+1}\) = -3
r – 5 = -3(r + 1)
r – 5 = -3r – 3
r + 3r = 5 – 3
4r = 2
r = \(\frac{2}{4}\)

கேள்வி 7.
கோட்டுத்துண்டு AB ஆனது முனை B இலிருந்து C இக்கு அதன் நீளம் 25% அதிகரிக்குமாறு நீட்டப்படுகின்றது. புள்ளிகள் A மற்றும் B இன் ஆயத் தொலைவுகள் முறையே (-2, -3) மற்றும் (2, 1) எனில் C இன் ஆயத்தொலைவுகளைக் காண்க.

m : n என AB யை வெளிப்புறமாக பிரிக்கிறது.
ie, m: n = 5 : 11
பிரிவு சூத்திரம் – வெளிப்புறமாக பிரித்தல்

Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 5 வடிவியல் Ex 5.3 Textbook Questions and Answers, Notes.

TN Board 8th Maths Solutions Chapter 5 வடிவியல் Ex 5.3

பல்வகைத் திறனறிப் பயிற்சிக் கணக்குகள்

கேள்வி 1.
படத்தில் , ∠1 ≡ ∠2 மற்றும் ∠3 ≡ ∠4 ஆகும் எனில், ΔMUG ≡ ΔTUB என நிரூபி.

தீர்வு :
∠1 = ∠2 மற்றும் ∠3 = ∠4
GB || MT. MG = BT
ΔBUG ~ ΔMUT
∴ ΔMUG ≡ ΔTUB

கேள்வி 2.
படத்திலிருந்து, Δ SUN – Δ RAY என நிரூபி.

தீர்வு :

⇒ \(\frac{10}{5}=\frac{12}{6}=\frac{14}{7}\) = 2
~ ∆ SUN ~ ∆ RAY

கேள்வி 3.
ஒரு கோபுரத்தின் உச்சியானது தரையில் R என்ற இடத்தில் உள்ள ஒரு கண்ணாடியின் மூலம் பிரதிபலித்து பார்க்கப்படுகிறது ∆PQR ~ ∆STR எனில், கோபுரத்தின் உயரத்தைக் காண்க.

தீர்வு :
∠ P= ∠ S, ∠ Q = Z ∠T = 90°
∠R = ∠R. (பொதுவான கோணம்)
∴ Δ PQR ~ Δ STR
∴ \(\frac{\mathrm{PQ}}{\mathrm{ST}}=\frac{\mathrm{QR}}{\mathrm{RT}}\)
\(\frac{\mathrm{PQ}}{8}=\frac{60}{10}\)
PQ = \(\frac{60 \times 8}{10}\)
PQ = 48 அடி
∴ கோபுரத்தின் உயரம் 48 அடி.

கேள்வி 4.
படத்தில், ஒரு கம்பத்தினைத் தரையுடன் நிலைநிறுத்தத் தேவையான கம்பியின் நீளம் என்ன ?

தீர்வு :

AC² = AB² + BC² (பித்தாகரஸ் தேற்றத்தின் படி)
AC² = AB² + BC²
x² = 400 + 225
x² = 625
x² = 25²
x = 25 அடி

கேள்வி 5.
ரித்திகா என்பவர் 25 அங்குலம் திரை (screen) கொண்ட ஓர் எல்.இ.டி. (LED)
தொலைக்காட்சியை வாங்குகிறார். அதன் உயரம் 7 அங்குலம் எனில், திரையின் அகலம் என்ன? மேலும், அவளது தொலைக்காட்சிப் பெட்டகம் 20 அங்குலம் அகலம் கொண்டது எனில், தொலைக்காட்சியை அந்த பெட்டகத்தினுள் வைக்க இயலுமா? காரணம் கூறுக?
தீர்வு:
பித்தாகரஸ் தேற்றத்தின் படி,
BC² = AC² – AB²
= 25² – 7²
= 625 – 49 = 576
BC² = 24²

⇒ BC = 24 அங்குலம் இல்லை.
திரையின் அகலத்தைவிட தொலைக்காட்சி அறையின் அகலம் குறைவாக இருப்பதால் வைக்க இயலாது.

மேற்சிந்தனைக் கணக்குகள்

கேள்வி 6.
படத்தில், ∠TMA ≡ ∠IAM மற்றும் ∠TAM ≡ ∠IMA. P ஆனது MI இன் மையப்புள்ளி மற்றும் N ஆனது AI இன் மையப்புள்ளி எனில், ΔPIN ~ ΔATM . என நிரூபி.

தீர்வு :
∠TMA ≡ ∠IAM
∠TAM ≡ ∠IMA
MI ன் மையப்புள்ளி P.
AIன் மையப்புள்ளி N
IM ≡ TM, IA ≡ TA
தேல்ஸ் தேற்றப்படி
\(\frac{\mathrm{PI}}{\mathrm{IM}}=\frac{\mathrm{IN}}{\mathrm{IA}}\)
⇒ \(\frac{\mathrm{PI}}{\mathrm{TM}}=\frac{\mathrm{IN}}{\mathrm{TA}}\)
∴ ΔPIN ~ ΔATM

கேள்வி 7.
படத்தில் ∠FEG = ∠1 DG² = DE.DF என நிரூபி.
im 12
தீர்வு :
∠FEG = ∠1
கோண இருசமவெட்டி தேற்றப்படி,
\(\frac{D G}{D E}=\frac{D F}{D G}\)
DG² = DE x DF. நிரூபிக்கப்பட்டது.

கேள்வி 8.
ஒரு சாய்சதுரத்தின் மூலை விட்டங்கள் 12செ.மீ மற்றும் 16 செ.மீ எனில், அதன் சுற்றளவைக் காண்க. (குறிப்பு : சாய்சதுரத்தின் மூலைவிட்டங்கள் ஒன்றுக்கொன்று செங்குத்தாக இருசமக் கூறிடும்).
தீர்வு :
AE = EC, BE = DE

AC = 2AE
16 = 2AE ⇒ AE = 8 செ.மீ
EC = 8 செ.மீ
BD = 2BE
12 = 2BE ⇒ BE = 6 செ.மீ
DE = 6 செ.மீ
Δ ΑΒΕ AB² = BE² + EA²
= 6² + 8²
= 36 + 64 = 100 = 10²
AB² = 10² ⇒ AB = 10 செ.மீ
BC = 10 செ.மீ
CD = 10 செ.மீ
AD = 10 செ.மீ
சுற்றளவு = AB+ BC+CD+DA அலகுகள்
= 10 + 10 + 10 + 10 செ.மீ
= 40 செ.மீ

கேள்வி 9.
படத்தில், AR ஐக் காண்க.

தீர்வு :
Δ AFI
AI² = AF² + FI²
AF² = AI² – FI²
= 25² – 15² = 625 – 225 = 400
AF² = 400 = 20² ⇒ AF = 20
Δ FIR
IR² = FI² + FR²
FR² = IR² – FI²
= 17² – 15²
= 289 – 225 = 64
FR² = 64 = 8² ⇒ FR = 8
AR = AF + FR = 20 + 8 = 28அடி

கேள்வி 10.
ΔDEF இல் DN, EO, FM ஆகியவை நடுக்கோடுகள் மற்றும் புள்ளி P ஆனது நடுக்கோட்டுமையம் ஆகும். எனில் பின்வருவனவற்றைக் காண்க.
i) DE = 44, எனில் DM = ?
ii) PD = 12, எனில் PN = ?
iii) DO = 8, எனில் FD = ?
iv) OE = 36 எனில் EP = ?

தீர்வு:
i) DE = 44 எனில் DM = \(\frac{\mathrm{DE}}{2}\)
[Mன் நடுப்புள்ளி]
DM = \(\frac{44}{2}\) = 22
∵ DM = ME, 2DM = DE
DM = 22

ii) PD = 12 எனில் PN = ?
PD : PN = 2:1
12 : PN = 2:1
\(\frac{12}{\mathrm{PN}}=\frac{2}{1}\)
2PN = 12 ⇒ PN = 6

iii) DO = 8, எனில் [
[0 ன் நடுப்புள்ளி :OD = OF/2DO = FD]
OD = \(\frac{\mathrm{FD}}{2}\) ⇒ FD = 2OD = 2 x 8 = 16
FD = 16

iv) OE = 36,
EP = X என்க
x : 36 – X = 2:1
\(\frac{x}{36-x}=\frac{2}{1}\)
x = 72 – 2x
x + 2x = 72
3x = 72
x = \(\frac{72}{3}\)
x = 24
EP = 24