Tamilnadu State Board New Syllabus Samacheer Kalvi 9th Maths Guide Pdf Chapter 5 ஆயத்தொலை வடிவியல் Ex 5.5 Textbook Questions and Answers, Notes.
TN Board 9th Maths Solutions Chapter 5 ஆயத்தொலை வடிவியல் Ex 5.5
கேள்வி 1.
பின்வரும் புள்ளிகளை முனைப் புள்ளிகளாகக் கொண்ட முக்கோணத்தின் நடுக்கோட்டு மையம் காண்க.
(i) (2, -4), (-3, -7) மற்றும் (7,2)
(ii) (-5, -5) (1, -4) மற்றும் (-4,-2).
விடை:
(i) A = (2, -4) B (-3,-7) மற்றும் C(7,2) ஆகிய புள்ளிகளைக் கொண்ட முக்கோணத்தின் நடுக்கோட்டு மையம். G (x,y)
(x1,y1) = (2,-4)
(x2, y2) = (-3,-7)
(x3, y3) = (7, 2)
நடுக்கோட்டு மையம் G (x,y)
= G \(\left(\frac{2-3+7}{3}, \frac{-4-7+2}{3}\right)\)
= G \(\left(\frac{6}{3}, \frac{-9}{3}\right)\)
= G (2,-3)
(ii) A (-5, -5) B (1,-4) மற்றும் C(-4,-2) ஆகிய புள்ளிகளைக் கொண்ட முக்கோணத்தின் நடுக் கோட்டு மையம்.
G = \(\left(\frac{x_{1}+x_{2}+x_{3}}{3}, \frac{y_{1}+y_{2}+y_{3}}{3}\right)\)
(x1, y1) = (-5, -5)
(x2, y2) = (1, -4)
(x3,y3) = (-4, -2)
நடுக்கோட்டு மையம் G (x,y)
G = \(\left(\frac{-5+1-4}{3}, \frac{-5-4-2}{3}\right)\)
G = \(\left(\frac{-8}{3}, \frac{-11}{3}\right)\)
![]()
கேள்வி 2.
ஒரு முக்கோணத்தின் நடுகோட்டு மையம் [4,-2] மற்றும் அதன் இரு முனைப்புள்ளிகள் [3, -2] மற்றும் [5, 2] எனில் மூன்றாவது முனைப் புள்ளியைக் காண்க.
விடை:
(i) (3, -2) மற்றும் (5, 2) ஆகியன முனைப்புள்ளிகள்.
(4, -2) என்பது நடுக்கோட்டு மையம் என்க.
\(\frac{x_{1}+x_{2}+x_{3}}{3}\) = 4
\(\frac{3+5+x_{3}}{3}\) = 4
x3 = 12 + 8
x3 = 12 – 8
x3 = 4
\(\frac{\mathrm{y}_{1}+\mathrm{y}_{2}+\mathrm{y}_{3}}{3}\) = -2
\(\frac{-2+2+y_{3}}{3}\) = -2
y3 = -6
மூன்றாவது முனைப்புள்ளி (4, -6)
கேள்வி 3.
A (-1,3) B (1, -1) மற்றும் C (5,1) ஆகியன ஒரு முக்கோணத்தின் முனைப்புள்ளிகள் எனில் A வழியே செல்லக்கூடிய நடுக்கோட்டின் நீளத்தைக் காண்க.
விடை:
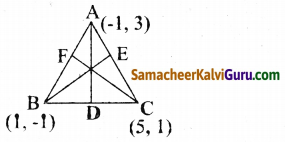
D, E, F என்பன BC, AC மற்றும் AB என்ற பக்கங்களின் நடுப்புள்ளிகள் என்க.
AD, BE மற்றும் CF ஆகியன நடுக்கோடுகள் என்க.
BC இன் நடுப்புள்ளி = C\(\left(\frac{1+5}{2}, \frac{-1+1}{2}\right)\)
\(=\quad C\left(\frac{6}{2}, \frac{0}{2}\right)\)
= C(3, 0)
AC இன் நடுப்புள்ளி = E\(\left(\frac{-1+5}{2}, \frac{3+1}{2}\right)\)
= E\(\left(\frac{4}{2}, \frac{4}{2}\right)\) =E(2, 2)
AB இன் நடுப்புள்ளி
= F\(\left(\frac{-1+1}{2}, \frac{3-1}{2}\right)\) = F\(\left(\frac{0}{2}, \frac{2}{2}\right)\)
= F(0, 1)
நடுக்கோடு AD இன் நீளம் (-1, 3) (3, 0)
AD = \(\sqrt{(3+1)^{2}+(0+3)^{2}}\) (4) (3)
(-1, 3) (3, 0) = \(\sqrt{(4)^{2}+(3)^{2}}\)
= \(\sqrt{16+9}\)
= 5
நடுக்கோடு BE இன் நீளம் (1, -1) (2, 2)
BE = \(\sqrt{(2-1)^{2}+(2+1)^{2}}\)
(1, -1) (2, 2)
\(=\sqrt{1+(3)^{2}}\)
\(=\sqrt{1+9}\)
\(=\sqrt{10}\)
நடுக்கோடு CF இன் நீளம் (5, 1) (0, 1)
\(=\sqrt{(0-5)^{2}+(1-1)^{2}}=\sqrt{(-5) 2+(0)}\)
\(=\sqrt{25}\)
= 5
![]()
கேள்வி 4.
(1, 2) (h, – 3) மற்றும் (-4, k) ஆகியன ஒரு முக்கோணத்தின் முனைப்புள்ளிகள். மேலும் புள்ளி (5,-1) ஆனது அந்த முக்கோணத்தின் இருக்கோட்டு மையம் எனில்,\(\sqrt{(h+k)^{2}+(h+3 k)^{2}}\) இன் மதிப்பைக் காண்க.
வடை:
(i) (1, 2) (h, – 3) மற்றும் (-4, k)) ஆகியன ஒரு முக்கோணத்தின் முனைப்புள்ளிகள் (5, -1) அந்த முக்கோணத்தின் நடுக்கோட்டு மையம் G(x, y) = G\(\left(\frac{\mathbf{x}_{1}+\mathbf{x}_{2}+\mathbf{x}_{3}}{3}, \frac{\mathbf{y}_{1}+\mathbf{y}_{2}+\mathbf{y}_{3}}{3}\right)\)
(x1, y1) = (1, 2)
(x2, y2) = (h, -3)
(x3, y3) = (-4, k)
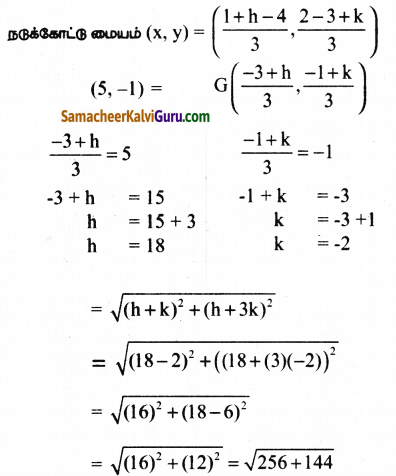
கேள்வி 5.
A(-3, 5) மற்றும் B(3, 3) ஆகியன முறையே ஒரு முக்கோணத்தின் செங்கோட்டு மையம் மற்றும் நடுக்கோட்டு மையம் ஆகும். C ஆனது இந்த முக்கோணத்தின் சுற்று வட்ட மையம் எனில், கோட்டுத்துண்டு AC ஐ விட்டமாகக் கொண்ட வட்டத்தின் ஆரம் காண்க.
விடை : [-3, 5]
நடுக்கோட்டு மையம் செங்கோட்டு மையத் தையும் உள்வட்ட மையத்தையும் 2:1 என்ற விகிதத்தில் பிரிக்கிறது. உள்வட்ட மையம் (x, y) என்க. பிரிவு சூத்திரத்தின் படி,
\(\left(\frac{2(x)-3}{3}, \frac{2 y+5}{3}\right)\) = (3,3)
2x – 3 = 9
2x = 9 + 3
2x = 12
x = \(\frac{12}{2}\)
x = 6
2y + 5 = 9
2y = 9 – 5
2y = 4
y = \(\frac{4}{2}\)
y = 2
உள்வட்ட மையம் = (6,2)
வட்டத்தின் ஆரம்
\(=\sqrt{(6+3)^{2}+(5-2)^{2}}\)
\(=\sqrt{(9)^{2}+(3)^{2}}=\sqrt{81+9}\)
\(=\sqrt{90}\)
= 3\(\sqrt{10}\) அலகுகள்.
![]()
கேள்வி 6.
A (3, 4) B (-2, -1) மற்றும் C (5, 3) என்ப ன முக்கோணம் ABC இன் முனைப் புள்ளிகள். G ஆனது அதன் நடுக்கோட்டு மையம் மற்றும் BDCG ஆனது ஒர் இணைகரம் எனில் முனைப்புள்ளி D இன் ஆயத்தொலைவுகளைக் காண்க.
விடை:
(i) A (3, 4) B (-2, -1) மற்றும் C (5, 3)) என்பன ΔABC இன் முனைப்புள்ளிகள் என்க.
G ஆனது அதன் நடுக்கோட்டு மையம்
(x1,y1) = (3, 4)
(x2, y2) = (-2, -1)
(x3,y3) = (5, 3)
நடுக்கோட்டு மையம் (x,y)
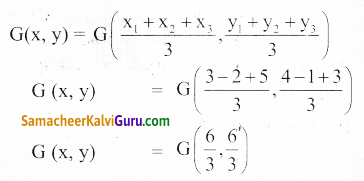
G (x,y) = G(2, 2)
கேள்வி 7.
முக்கோணத்தின் பக்கங்களின் நடுப்புள்ளிகள் \(\left(\frac{3}{2}, 5\right),\left(7, \frac{-9}{2}\right)\) மற்றும் \(\left(\frac{13}{2}, \frac{-13}{2}\right)\)
எனில் அந்த முக்கோணத்தின் நடுக்கோட்டு மையம் காண்க.
விடை:
A (x1, y1) B (x2, y2) C (x3, y3) என்பன முனைப்புள்ளிகள் மற்றும் \(\left(\frac{3}{2}, 5\right),\left(7, \frac{-9}{2}\right)\) மற்றும் \(\left(\frac{13}{2}, \frac{-13}{2}\right)\) ஆகியன பக்கங்களின் நடுப்புள்ளிகள் என்க.
G ஆனது அதன் நடுக்கோட்டு மையம்
\(\frac{\mathrm{X}_{1}+\mathrm{x}_{2}}{2}=\frac{3}{2}\) ⇒ x1 + x2 = 3 ……………(1)
\(\frac{x_{2}+x_{3}}{2}\) = 7 ⇒ x2 + x3 = 14 …………… (2)
\(\frac{\mathrm{X}_{3}+\mathrm{X}_{1}}{2}=\frac{13}{2}\) ⇒ x3 + x1 = 13 ………………. (3)
(1) + (2) + (3) r 2x1 + 2x2 + 2x3 = 30
2(x1 + x2 + x3) = 30
x1 + x2 + x3 = 15 …………… (4)
\(\frac{\mathrm{y}_{1}+\mathrm{y}_{2}}{2}\) = 5 ⇒ y1 + y2 = 10 …………….. (5)
\(\frac{\mathrm{y}_{2}+\mathrm{y}_{3}}{2}=\frac{-9}{2}\) ⇒ y2 + y3 = -9 ……………….(6)
\(\frac{\mathrm{y}_{3}+\mathrm{y}_{1}}{2}=\frac{-13}{2}\) ⇒ y3 + y1 = -13 ……………..(7)
(5) + (6) + (7) r 2y1 + 2y2 + 2y3 = -12
2(y1 + y2 + y3)= -12
y1 + y2 + y3 = -6 …………. (8)
(4) – (2) rx1 = 15 – 14 = 1
(4) – (3) rx2 = 15 – 13 = 2
(4) – (1) rx3 = 15 – 3 = 12
(8) – (6) ry1 = -6 + 9 = 3
(8) – (7) ry2 = -6 + 13 = 7
(8) – (5) ry3 = -6- 10 = -16 முனைப்புள்ளிகள் = A (1, 3) B (2,7) C (12, -16) நடுக்கோட்டு மையம்
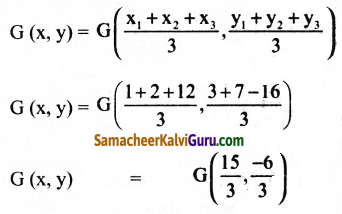
G (x,y) = G(5, -2)