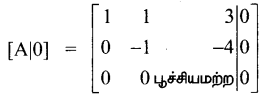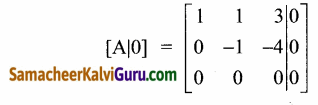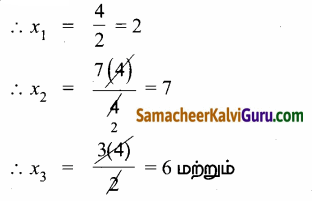Prasanna

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 2 கலப்பு எண்கள் Ex 2.2 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 2 கலப்பு எண்கள் Ex 2.2

கேள்வி 1.
z = 5-21 மற்றும் w = –1 + 3i எனக்கொண்டு கீழ்க்காண்பவைகளின் மதிப்புகளைக் காண்க.
(i) z + w
(ii) z – iw
(iii) 2z + 3w
(iv) zw
(v) z² + 2zw + w²
(vi) (z +w)²
தீர்வு :
(i) z +w
= (5 – 2i) + (-1 + 3i)
= (5 – 1) + i (-2 + 3)
= 4 + i (1) = 4 + i

(ii) z – iw
= (5 – 2i) -i (-1 + 3i)
= (5 – 2i) + (+i – 3i²)
= 5 – 2i + i – 3 (-1) = 5 – i + 3 = 8 – i

(iii) 2z + 3w
= 2 (5 – 2i) + 3 (-1 + 3i)
= 10 – 4i – 3 + 9i
= (10 – 3) + i(4 + 9) = 7 + 5i

(iv) zw
= (5 – 2i) (-1 + 3i)
= -5 + 15i + 2i – 6i²
=-5 + 17i – 6(-1)
= -5 + 17i + 6 = 1 + 17i

(v) z² + 2zw + w²
= (5 – 2i)² + 2(5 – 2i) (-1 + 3i) + (-1 + 3i)²
=25 + 4i² -20i + 2[-5 + 15i + 2i – 6i²] +1 +9i² – 6i
= 25 – 4 – 20i + 2 (-5 + 17i + 6) + 1 – 9 – 6i
[∴ i² =-1]
= 21 – 20i + 2 (1 + 17i) – 8 – 6i
= 21 – 20i + 2 + 34i – 8 – 6i = 15 + 8i

(vi) (z+w)²
= [[5-2i) + (-1 + 3i)]² = (4 + i)²
= 16 + i² + 8i = 16 -1 + 8i = 15 + 8i

கேள்வி 2.
z = 2 + 3i எனக்கொண்டு கீழ்க்காணும் கலப்பெண்களை ஆர்கண்ட் தளத்தில் குறிக்க.
(i) z, iz, மற்றும் z + iz
(ii) z, -iz, மற்றும் z -iz.
தீர்வு:
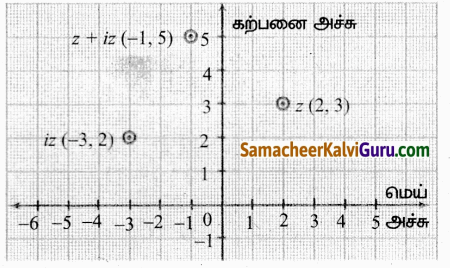
(i) z, iz மற்றும் z + iz ஐ ஆர்கண்ட் தளத்தில் குறிக்க
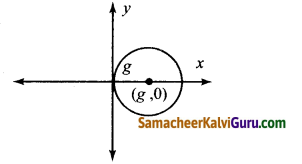
z = 2 + 3i, (2, 3) எனக் குறிக்கலாம்.
iz = i (2 + 3i) = 2i + 3i² = 2i – 3 = -3 + 2i
(-3, 2) எனக் குறிக்கலாம்.
z+iz = 2 + 3i – 3 + 2i = -1 + 5i, (-1, 5) என
ஆர்கண்ட் தளத்தில் குறிக்கலாம்.

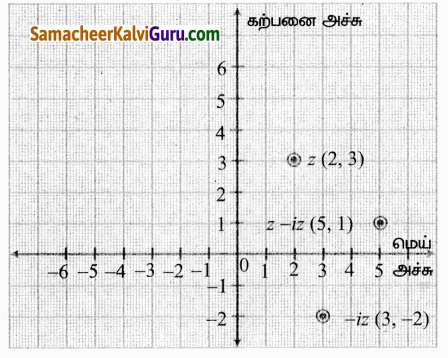
(ii) z = 2 + 3i , (2, 3) எனக் குறிக்கலாம்.
-iz =-i (2 + 3i) =-2i – 3i² = -2i – 3(-1)= 3 – 2i
Z – iz = 2 + 3i + 3 – 2i = 5 + i(5, 1) என ஆர்க ண்ட் தளத்தில் குறிக்கலாம்.

கேள்வி 3.
(3 – i)x – (2 – i)y + 2i + 5 மற்றும் 2x + (-1 + 2i)y + 3 + 2i ஆகிய கலப்பெண்கள் சமம் எனில் x மற்றும் y-ன் மதிப்புகளைக் காண்க. தீர்வு:
கொடுக்கப்பட்ட (3 -i) x – (2 – i) y + 2i +5
= 2x + (-1 + 2i) y + 3 + 2i
⇒ 3x – ix – 2y + iy + 2i + 5 = 2x – y + 2iy + 3 +2i
மெய் மற்றும் கற்பனை பகுதிகளை தேர்ந்தெடுக்க
(3x – 2y + 5) + i(-x + y + 2) = 2x – y + 3 + i(2y + 2)
இருபுறமும் மெய் மற்றும் கற்பனை பகுதிகளை ஒப்பிட கிடைப்பது
3x – 2y + 5 = 2x – y + 3
⇒ 3x – 2y + 5 – 2x + y – 3 = 0
⇒ x – y + 2 = 0 …. (1)
⇒ -x + y + 2 = 2y + 2
⇒ -x + y + 2 – 2y – 2 = 0
⇒ – x – y = 0 ⇒ x + y = 0 ….. (2)
(1) – (2) கிடைப்பது,

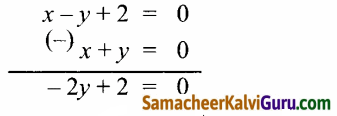
⇒ – 2y = -2 ⇒ y = 1
y= 1 என (2) ல் பிரதியிட கிடைப்பது,
x + 1 = 0 ⇒ x = -1
∴ x = – 1 மற்றும் y = 1

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 10 சாதாரண வகைக்கெழுச் சமன்பாடுகள் Ex 10.5 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 10 சாதாரண வகைக்கெழுச் சமன்பாடுகள் Ex 10.5

கேள்வி 1.
நிறை M உடைய ஒரு தானியங்கி இயந்திரத்தின் இயக்கியால் உருவாக்கப்படும் மாறாத விசை F எனில், அதனுடைய திசைவேகம் V என்பது M\(\frac{dV}{d t}\) = F – AV எனும் சமன்பாட்டால் குறிக்கப்படுகிறது. . என்பது மாறிலியாகும். t = 0 எனில் V = 0 எனக் கொடுக்கப்படும்போது V ஐ-ன் சார்பாக எழுதுக.
தீர்வு:
மாறிகளைப் பிரிக்க கொடுக்கப்பட்ட சமன்பாடு
m \(\frac{d v}{d t}\) = F — kv இலிருந்து கிடைப்பது,

⇒ \(\frac{\mathrm{F}-k v}{c}=\frac{1}{e^{\frac{k t}{m}}}\)
⇒ c = \((\mathrm{F}-k v) e^{\frac{k t}{m}}\) ……. (1)
t = 0 ⇒ v = 0 எனில் c = (F -0)e⁰ ⇒ c = F
∴ (1) லிருந்து, F = \((\mathrm{F}-k v) e^{\frac{k t}{m}}\)

கேள்வி 2.
செங்குத்தாக விழும் வான்குடை மிதவை (Parachute)ன் திசைவேகம் v ஆனது \(v \frac{d v}{d x}=g\left(1-\frac{v^{2}}{k^{2}}\right)\) எனும் சமன்பாட்டை நிறைவு செய்கிறது. இங்கு g மற்றும் k என்பன மாறிலிகள் ஆகும். ஆரம்ப நிலையில் மற்றும் x ஆகிய இரண்டும் பூச்சியமானால், -ஐ X-இன் சார்பாகக் காண்க.
தீர்வு:
கொடுக்கப்பட்டது
\(v \frac{d v}{d x}=g\left(1-\frac{v^{2}}{k^{2}}\right)=g\left(\frac{k^{2}-v^{2}}{k^{2}}\right)\)
மாறிகளைப் பிரிக்க கிடைப்பது,
\(\frac{v d v}{k^{2}-v^{2}}=\frac{g}{k^{2}} \cdot d x\)
இருபுறமும் -2 ஆல் பெருக்கக் கிடைப்பது,
\(\frac{-2 v d v}{k^{2}-v^{2}}=\frac{-2 g}{k^{2}} d x\)
தொகையிட,

கேள்வி 3.
ஒரு வளைவரையின் சாய்வு, \(\frac{y-1}{x^{2}+x}\) ஆகும். வளைவரை (1, 0) எனும் புள்ளி வழிச் செல்லுமெனில், அதன் சமன்பாட்டைக் காண்க.
தீர்வு:
கொடுக்கப்பட்ட சாய்வு = \(\frac{y-1}{x^{2}+x}\)

⇒ y – 1 = \(\frac{c x}{x+1}\)
வளைவரை (1, 0) என்ற புள்ளி வழியாகச் செல்வதால் கிடைப்பது,

கேள்வி 4.
பின்வரும் வகைக்கெழுச் சமன்பாடுகளின் தீர்வுகளைக் காண்க.
(i) \(\frac{d y}{d x}=\sqrt{\frac{1-y^{2}}{1-x^{2}}}\)
(ii) ydx + (1 + x²) tan^-1 xdy = 0
(iii) sin\(\frac{d y}{d x}\) = a, y (0) = 1
(iv) \(\frac{d y}{d x}\) = e^x+y + x³ e^y
(v) (e^y + 1) cos x dx + e^y sin x dy = 0
(vi) (vdx = xdy) \(\cot \left(\frac{x}{y}\right)\) = ny² dx
(vii) \(\frac{d y}{d x}-x \sqrt{25-x^{2}}=0\)
(viii) x cos y dy = e^x (x log x+ 1]dx
(ix) tan y \(\frac{d y}{d x}\) = cos (x + y) + cos (x – y)
(x) \(\frac{d y}{d x}\) = tan² (x + y)
தீர்வு:
(i) \(\frac{d y}{d x}=\sqrt{\frac{1-y^{2}}{1-x^{2}}}\)
மாறிகளைப் பிரிக்க கிடைப்பது,
\(\frac{d y}{\sqrt{1-y^{2}}}=\frac{d x}{\sqrt{1-x^{2}}}\)
sin^-1y = sin^-1x + c

(ii) ydx + (1 + x²) tan^-1 xdy = 0
y dx = (1 + x²) tan^-1x dy
⇒ dt = \(\frac{1}{1+x^{2}} d x\) இல்
t = tan^-1x என பிரதியிடுக
⇒ \(\frac{d x}{\left(1+x^{2}\right) \tan ^{-1} x}=\frac{-d y}{y}\)
⇒ \(\int \frac{d x}{\left(1+x^{2}\right) \tan ^{-1} x}=\int \frac{-d y}{y}\)
∴ \(\int \frac{d t}{t}\) = -log y = log c
⇒ log (tan^-1 x) = -log y + log c
⇒ log (tan^-1‘ x) + log y = log c
⇒ logy (tan^-1 x) = log c
⇒ y tan^-1 x = c

(iii) sin\(\frac{d y}{d x}\) = a, y (0) = 1
sin\(\frac{d y}{d x}\) = a,

(iv) \(\frac{d y}{d x}\) = e^x+y + x³ e^y
\(\frac{d y}{d x}\) = e^x e^y + x³ e^y = e^y(e^x + x³)
⇒ \(\frac{d y}{e^{y}}\) = (e^x + x³)dx
⇒ e^-y dy = (e^x + x³)dx
∴ \(\int e^{-y} d y=\int\left(e^{x}+x^{3}\right) d x\)
⇒ -e^-y = e^x + \(\frac{x^{4}}{4}\) + c
⇒ e^x + e^-y + \(\frac{x^{4}}{4}\) = -c = c
[இதுவும் ஒரு மாறாத எண் ஆகும்]

(v) (e^y + 1) cos x dx + e^y sin x dy = 0
⇒ (e^y + 1) cos x dx = -e^y sin x dy
⇒ \(\frac{\cos x}{\sin x} d x=\frac{-e^{y}}{e^{y}+1} d y\)
t = e^y+ 1
dt = e^y dy
\(-\int \frac{d t}{t}\) = -log t = log(e) + 1)
⇒ \(\int \cot x d x=-\int \frac{e^{y}}{e^{y}+1} d y\)
⇒ log (sin x) + log (e^y + 1) = log c.
⇒ log sin x (e^y + 1) = log c
⇒ (e^y + 1) sin x = c

(vi) (ydx = xdy) \(\cot \left(\frac{x}{y}\right)\) = ny² dx

மாறிகளைப் பிரிக்க கிடைப்பது,
cot (t) dt = n dx
⇒ \(\int \cot (t) d t=n \int d x\)
⇒ log(sin t) = nx + c
⇒ log(sin t) = nx + c
⇒ sin t = e^nx+c
⇒ \(\sin \left(\frac{x}{y}\right)\) = e^nx+c [∵ t = \(\frac{x}{y}\)]

(vii) \(\frac{d y}{d x}-x \sqrt{25-x^{2}}=0\)

⇒ 3y = -t^{\(\frac{3}{2}\)} + 3c
⇒ 3y = -(25 – x²)^{\(\frac{3}{2}\)} + 3c [∵t = 25 – x²]

(viii) x cos y dy = e^x (x log x + 1)dx
x cos y dy = e^x (x log x + 1) dx

(ix) tan y \(\frac{d y}{d x}\) = cos (x + y) + cos (x – y)
⇒ tan y \(\frac{d y}{d x}\) = cosx cosy – sinx siny + cosx cosy + sinx siny
= 2 cos x sin y
[∵ cos (A + B) = cos A cos B – sin A sin B cos (A-B) = cos A cos B + sin A sin B]
⇒ \(\frac{\tan y}{\cos y}\) dy = 2 cos x dx
⇒ \(\int\) tan y sec y dy = 2\(\int\) cos x dx
⇒ sec y = 2 sin x + c

(x) \(\frac{d y}{d x}\) = tan²(x + y)
\(\frac{d y}{d x}\) = tan²(x + y) …………. (1)

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 2 கலப்பு எண்கள் Ex 2.1 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 2 கலப்பு எண்கள் Ex 2.1

பின்வருவனவற்றை சுருக்குக :

(i) i¹⁹⁴⁷ + i¹⁹⁵⁰
(ii) i¹⁹⁴⁸ – i^-1869
(iii) \(\sum_{n-1}^{12} i^{n}\)
(iv) i⁵⁹ + \(\frac{1}{i^{59}}\)
(v) i i² i³ …….. i²⁰⁰⁰
(vi) \(\sum_{n-1}^{10} i^{n+50}\)
தீர்வு:
(i) i¹⁹⁴⁷ + i¹⁹⁵⁰
i¹⁹⁴⁷ + i¹⁹⁵⁰ = i¹⁹⁴⁴ . i³ + i¹⁹⁴⁸ .i²
[ ∵1944 என்பது 4 -ன் பெருக்கல், 1948 என்பது மேலும் 4 – ன் பெருக்கல்]
= (i⁴)⁴⁸⁶ . i² . i¹ + (i⁴)⁴⁸⁷ .i² [i⁴ = 1]
= (1⁴⁸⁶)(-1)(i) + (1)⁴⁸⁷ (-1) [i² = -1]
= i – 1 = -1 – i

(ii) i¹⁹⁴⁸ – i^-1869
= (i⁴)⁴⁸⁷ – [i^-1868 .i^-1]
= 1⁴⁸⁷ – [(i⁴)^-467.\(\frac{1}{i}\)] [i⁴ = 1]
= 1-[1.(-i)) [∵ i^-1 = \(\frac{1}{i}\) = -i]
[1 – ன் எந்த அடுக்கும் 1 ஆகும்]
= 1 + i

(iii) \(\sum_{n-1}^{12} i^{n}\)
\(\sum_{n=1}^{12} i^{n}\) = (i¹ + i² + i³ + i⁴) + (i⁵ + i⁶ + i⁷ + ii⁸) + (i⁹ + i¹⁰ + i¹¹ + i¹²)
= (i – 1 – i + 1) + (i⁴⁺¹ + i⁴⁺² + i⁴⁺³ + (i⁴)²) + (i⁸⁺¹ + i⁸⁺² + i⁸⁺³ + (i⁴)³)
= 0 + (i + i² + i³ + i⁴) + (i¹ + i² + i³ + i⁴)
[∵ i² = -1, i³ = -i, i⁴ = 1]
0 + (i – 1 – i + 1) + (i – 1 – i + 1 )
= 0 + 0 + 0 = 0

(iv) i⁵⁹ + \(\frac{1}{i^{59}}\)
i^{4×14 + 3} + i^-(4×14+3)
= (i⁴)¹⁴. i³ + (i⁴)^-14. i^-3
= 1. i³ + 1.i^-3 [∵ i⁴ = 1]
= -i + i= 0 [∵ i³= -i மற்றும் i^-3 = i]

(v) i i²….. i²⁰⁰⁰
= i. i² 3…..i²⁰⁰⁰

= i^1000×2001 = i^2001000 = 1
[∵ 2001000 என்பது 4 ஆல் வகுபடும் அதன் கடைசி இரண்டு எண்களும் 4 ஆல் வகுபடும்]

(vi) \(\sum_{n-1}^{10} i^{n+50}\)
i¹⁺⁵⁰ + i²⁺⁵⁰ + ……+ i¹⁰⁺⁵⁰
= i⁵¹ + i⁵² + ……+ i⁶⁰
i⁵⁰ ஐ பொதுவாக எடுக்க கிடைப்பது,
i⁵⁰ [(i + 1² + i³ + i⁴) + (i⁵ + i⁶ + i⁷ + i⁸) + i⁹ + i¹⁰]
= i⁵⁰ [0 + (i⁴⁺¹ + i⁴⁺² + i⁴⁺³ + i⁴⁺⁴) + (i⁸⁺¹ + i⁸⁺²)]
= i⁵⁰ [0 + 0 + i + i²] [∵ i + i² + i + i⁴ = 0]
= i⁵⁰ [i-1] = i⁴⁸⁺² (i -1)
= i² (i-1) [∵ i⁴⁸ = 1]
= -1 (i-1) = -i + 1 = 1 – i

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 10 சாதாரண வகைக்கெழுச் சமன்பாடுகள் Ex 10.4 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 10 சாதாரண வகைக்கெழுச் சமன்பாடுகள் Ex 10.4

கேள்வி 1.
பின்வரும் சமன்பாடுகள் ஒவ்வொன்றும் அவற்றிற்கெதிரே கொடுக்கப்பட்டுள்ள வகைக் கெழுச் சமன்பாட்டின் தீர்வாகும் எனக்காட்டுக.
(i) y = 2x²; xy’ = 2y
(ii) y = a^ex + be^-x; y – y =0
தீர்வு:
(i) y = 2x²; xy’ = 2y
y = ax² எனக் கருதுவோம்
‘x’ஐ பொறுத்து வகையிட கிடைப்பது,
y’ = a(2x)
⇒ \(\frac{y^{\prime}}{2 x}\) = a ………… (2)
(2) ஐ (1) ல் பிரதியிட கிடைப்பது,
y = \(\frac{y^{\prime}}{2 x}\) ∙ x²
⇒ y = \(\frac{y^{\prime} x}{2}\)
2y = xy’
∴ கொடுக்கப்பட்ட வகைக்கெழு சமன்பாட்டின்
தீர்வு y = ax²

(ii) y = ax^ex + be^-x; y – y = 0
கருதுக y = ae^x + be^-x ………… (1)
‘x’ஐ பொறுத்து வகையிட கிடைப்பது,
y’ = ae^x – be^-x
‘x’ ஐ பொறுத்து மீண்டும் வகையிட கிடைப்பது,
y” = ae^x + be^-x = y [(1)ஐ பயன்படுத்தி]
⇒ y” – y = 0
∴ y” – y = 0 ன் ஒரு தீர்வு y = ae^x + be^-x

கேள்வி 2.
y = e^mx எனும் சார்பு கொடுக்கப்பட்ட வகைக் கெழுச் சமன்பாட்டிற்கு தீர்வாக அமையுமாறு m-ன் மதிப்புகளைக் காண்க.
(i) y’ + 2y = 0
(ii) y”- 5y’ + 6y = 0
தீர்வு:
(i) y’ + 2y =0
y’ + 2y = 0 இன் தீர்வு y = e^mx …. (1)
என கொடுக்கப்பட்டுள்ளது.
y = e^mx
⇒ y’ = m.e^mx
⇒ y’ = my ………… (2)
(2) ஐ (1) ல் பிரதியிட கிடைப்பது,
my + 2y = 0 = y(m + 2) = 0
⇒ m+ 2 = 10 [∵y ≠ 0]
⇒ m = -2

(ii) y”- 5y’ + 6y=0
y” – 5y’ + 6y = 0 இன் தீர்வு y = e^mx …… (1)
எனக் கொடுக்கப்பட்டுள்ளது.
y = e^mx
⇒ y’ = me^mx
⇒ y’ = my ………….. (2)
‘X’ஐ பொறுத்து மீண்டும் வகையிட கிடைப்பது,
y” = my’
⇒ y” = m(my) = m²y ……. (3)
(2) மற்றும் (3)-ஐ (1)ல் பிரதியிட கிடைப்பது
m²y – 5my + 6y = 0
⇒ y(m² – 5m + 6) = 0
⇒ m² – 5m + 6 = 0 [∵ y ≠ 0]
⇒ (m – 3)(m – 2) = 0
m = 3, 2

கேள்வி 3.
ஏதேனும் ஒரு புள்ளியில் ஒரு வளைவரையின் தொடுகோட்டின் சாய்வு, அப்புள்ளியின் y அச்சுத் தொலைவின் 4 மடங்கின் தலை கீழியாகும். மேலும் வளைவரை (2,5 ) எனும் புள்ளி ! வழியாகச் செல்கிறது எனில், வளைவரையின் சமன்பாட்டைக் காண்க.
தீர்வு:
கொடுக்கப்பட்டது சாய்வு எந்த ஒரு புள்ளியிலும்
சாய்வு =
⇒ \(\frac{d y}{d x}=\frac{1}{4 y}\)
⇒ 4y dy = dx
இருபுறமும் தொகையிட கிடைப்பது,
\(4 \int y d y=\int d x\)
⇒ \(4 \cdot \frac{y^{2}}{2}\) = x + c
⇒ 2y = x + c ………….. (1)
வளைவரை (2, 5) எனும் புள்ளி வழிச் செல்வதால் கிடைப்பது,
2(5)² = 2 + c
⇒ 50 – 2 = c
⇒ c = 48.
∴ (1) லிருந்து, 2y = x + 48 என்பது தேவையான வளைவரையின் சமன்பாடாகும்.

கேள்வி 4.
y = e^-x + mx + n என்பது \(e^{x}\left(\frac{d^{2} y}{d x^{2}}\right)\) = 0 எனும் வகைக்கெழுச் சமன்பாட்டின் தீர்வாகும் எனக் காட்டுக.
தீர்வு:
கருதுக y = e^-x + mx + n
‘X’ ஐ பொறுத்து வகையிட கிடைப்பது,
\(\frac{d y}{d x}\) = -e^-x + m
‘x’ஐ பொறுத்து மீண்டும் வகையிட கிடைப்பது,

y = e^-x + mx + n ஆகும்.

கேள்வி 5.
y = ax + \(\frac{b}{x}\), x ≠ 0 என்பது x²y” + xy – y = 0 எனும் வகைக்கெழுச் சமன்பாட்டின் தீர்வாகும் எனக் காட்டுக.
தீர்வு:
கருதுக y = ax + \(\frac{b}{x}\), x ≠ 0
இருபுறமும் X ஆல் பெருக்க கிடைப்பது, xy = ax² + b
‘x’ ஐ பொறுத்து இருபுறமும் வகையிட கிடைப்பது,
xy’ + y(1) = 2a(x)
⇒ xy’+ y = 2ax
X ஆல் வகுக்க கிடைப்பது,
y’ + \(\frac{y}{x}\) = 2a
‘x’ஐ பொறுத்து மீண்டும் வகையிட கிடைப்பது,
y” + \(\frac{x y^{\prime}-y}{x^{2}}\) = 0
x² ஆல் பெருக்க கிடைப்பது, x²y” +xy’ – y=0
∴ x²y” + xy’ – y = 0 இன் ஒரு தீர்வு y = ax + \(\frac{b}{x}\) ஆகும்.

கேள்வி 6.
y = ae^-3x + b என்பது \(\frac{d^{2} y}{d x^{2}}+3 \frac{d y}{d x}=0\) எனும் வகைக்கெழுச் சமன்பாட்டின் தீர்வாகும் எனக் காட்டுக. இங்கு a, b ஏதேனும் இரு எதேச்சை மாறிலிகள்.
தீர்வு:
கருதுக y= ae^-3x + b
‘x’ஐ பொறுத்து வகையிட கிடைப்பது,
\(\frac{d y}{d x}\)= -3ae^-3x.
⇒ \(\frac{y^{\prime}}{e^{-3 x}}\) = -3a
‘x’ஐ பொறுத்து மீண்டும் வகையிட கிடைப்பது,
\(\frac{e^{-3 x}\left(y^{\prime \prime}\right)-y^{\prime}(-3) e^{-3 x}}{e^{-6 x}}\) = 0
⇒ y” e^-3x + 3y’ e^-3x = 0
⇒ e^-3x ( y” + 3y”) = 0
⇒ y” + 3y’ = 0 [∵ e^-3x ≠ 0]
∴ y” + 3y” = 0 -இன் தீர்வு y = ae^-3x + b ஆகும்.

கேள்வி 7.
y² = \(2 a\left(x+a^{\frac{2}{3}}\right)\) எனும் வளைவரைத் தொகுதியைக் குறிக்கும் வகைக்கெழுச் சமன்பாடு \(\left(y^{2}-2 x y \frac{d y}{d x}\right)^{3}=8\left(y \frac{d y}{d x}\right)^{5}\) எனக் காட்டுக. இங்கு 1 என்பது மிகை மதிப்புடைய துணையலகாகும்.
தீர்வு:
கருதுக y² = \(2 a\left(x+a^{\frac{2}{3}}\right)\)
⇒ y²2 == 2ax + 2^{\(\frac{2}{3}\)} ………… (1)
‘X’ஐ பொறுத்து வகையிட கிடைப்பது,
2yy’ = 2a(1) ⇒ a = yy’ ………. (2)
(2) ஐ (1)ல் பிரதியிட கிடைப்பது,
y² = 2xyy’ + 2(yy’)^{\(\frac{5}{3}\)}
⇒ y² – 2xvy’ = 2 (yy’)^{\(\frac{5}{3}\)}
இருபுறமும் 3-ன் அடுக்கை எடுக்க கிடைப்பது,
(y² – 2xyy’)³ = 2³ (yy’)^{\(\frac{5}{3} \times 3\)}
⇒ (y² – 2xyy’)³ = 8(yy’)⁵
\(\left(y^{2}-2 x y \frac{d y}{d x}\right)^{3}=8\left(y \frac{d y}{d x}\right)^{5}\) என் தீர்வு
y² = 2a(x + a^{\(\frac{2}{3}\)}) ஆகும்.

கேள்வி 8.
y = a cos hx என்பது \(\frac{d^{2} y}{d x^{2}}+b^{2} y=0\) எனும் வகைக்கெழுச் சமன்பாட்டின் தீர்வாகும் எனக் காட்டுக.
தீர்வு:
கருதுக y = a cos bx …….(1)
‘x’ஐ பொறுத்து வகையிட கிடைப்பது,
y’ = -a sin bx(b) = -ab sin(bx)
‘X’ ஐ பொறுத்து மீண்டும் வகையிட கிடைப்பது,
y” = -ab cos (bx)(6)
= -ab² cos(bx)
⇒ y” = -b²[acos bx]
⇒ y” = -b²y [(1) ஐ பயன்ப டுத்தி]
⇒ y” + b²y = 0
∴ \(\frac{d^{2} y}{d x^{2}}+b^{2} y=0\) இன் ஒரு தீர்வு
y = a cos bx ஆகும்.

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 1 அணிகள் மற்றும் அணிக்கோவைகளின் பயன்பாடுகள் Ex 1.8 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 1 அணிகள் மற்றும் அணிக்கோவைகளின் பயன்பாடுகள் Ex 1.8

கொடுக்கப்பட்ட நான்கு விடைகளிலிருந்து சரியான அல்லது மிகப் பொருத்தமான விடையைத் தேர்ந்தெடுக்க.

கேள்வி 1.
|adj (adjA) |=|A|⁹, எனில், சதுர அணி A -யின் வரிசையானது
(1) 3
(2) 4
(3) 2
(4) 5
விடை:
(2) 4
குறிப்பு:
adj (adj)AI = |A|^(n-1)2
∴ (n-1)² = 9
⇒ (n-1)² = 3² ⇒ n-1 = 3
⇒ n = 4

கேள்வி 2.
A என்ற 3 x 3 பூச்சியமற்றக் கோவை அணிக்கு AA^T = A^T A மற்றும் B = A^-1A^T, என்றவாறு இருப்பின் BB^T=
(1) A
(2) B
(3) I₃
(4) B^T
விடை:
(3) I₃
குறிப்பு:
BB^T = (A^-1A^T)(A^-1A^T)^T
= (A^-1A^T) (A^T)^T – (A^-1)^T
= (A^-1A^T) (AA^-1)^T
= A^-1(A.A^T)(A^-1)^T
= (A^-1A). A^T (A^T)^-1
[∵ (A^-1)^T = (A^T)^-1]
[∵ A^T-(A^T)^-1 = I]
= I.I = I

கேள்வி 3.
A = \(\left[\begin{array}{ll}
3 & 5 \\
1 & 2
\end{array}\right]\), B = adj A மற்றும் C = 3A எனில், \(\frac{|\mathbf{a d j} \mathbf{B}|}{|\mathbf{C}|}\) =
(1) \(\frac{1}{3}\)
(2) \(\frac{1}{9}\)
(3) \(\frac{1}{4}\)
(4) 1
விடை:
(2) \(\frac{1}{9}\)
குறிப்பு:

கேள்வி 4.


விடை:
(3) \(\left[\begin{array}{rr}
4 & 2 \\
-1 & 1
\end{array}\right]\)
குறிப்பு:

கேள்வி 5.

(1) A^-1
(2) \(\frac{\mathrm{A}^{-1}}{2}\)
(3) 3A^-1
(4) 2A^-1
விடை:
(4) 2A^-1
குறிப்பு:
9I-A = \(\left[\begin{array}{ll}
9 & 0 \\
0 & 9
\end{array}\right]\)–\(\left[\begin{array}{ll}
7 & 3 \\
4 & 2
\end{array}\right]\)
\(\left[\begin{array}{ll}
9-7 & 0-3 \\
0-4 & 9-2
\end{array}\right]\) = \(\left[\begin{array}{rr}
2 & -3 \\
-4 & 7
\end{array}\right]\) = adj A
ஆனால் A^-1 = \(\frac{1}{|\mathrm{~A}|}\) adj A = \(\frac{1}{2}\) ⇒ adj A = 2A^-1

கேள்வி 6.
A = \(\left[\begin{array}{ll}
2 & 0 \\
1 & 5
\end{array}\right]\) மற்றும் B = \(\left[\begin{array}{ll}
1 & 4 \\
2 & 0
\end{array}\right]\) கொலை, |adj (AB)| =
(1) -40
(2) -80
(3) -60
(4) -20
விடை:
(2) -80
குறிப்பு:

|adj (AB)| = 8 – 88 = -80

கேள்வி 7.
P = \(\left|\begin{array}{rrr}
1 & x & 0 \\
1 & 3 & 0 \\
2 & 4 & -2
\end{array}\right|\) என்பது 3 × 3 வரிசையுடைய அணி A -ன் சேர்ப்பு அணி மற்றும் |A| = 4, எனில், x ஆனது
(1) 15
(2) 12
(3) 14
(4) 11
விடை:
(4) 11
குறிப்பு :
|adj A| = |A|^n-1

⇒ -6-x (-2) = 4² ⇒ -6 + 2x = 16
⇒ 2x = 22 ⇒ x = 11

கேள்வி 8.
A= \(\left[\begin{array}{rrr}
3 & 1 & -1 \\
2 & -2 & 0 \\
1 & 2 & -1
\end{array}\right]\) மற்றும் A^-1= \(\left[\begin{array}{lll}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{array}\right]\) எனில், a₂₃ – ன் மதிப்பானது
(1) 0
(2) -2
(3) -3
(4) -1
விடை:
(4) -1
குறிப்பு:

கேள்வி 9.
A, B மற்றும் C என்பன நேர்மாறு காணத்தக்கவாறு ஏதேனுமொரு வரிசையில் இருப்பின் பின்வருவனவற்றில் எது ! உண்மையல்ல?
(1) adj A= |A|A^-1
(2) adj (AB) = (adj A) (adj B)
(3) det A^-1 = (det A)^-1
(4) (ABC)^-1 = C^-1 B^-1 A^-1
விடை:
(2) adj (AB) = (adj A) (adj B)

கேள்வி 10.
(AB)^-1 = \(\left[\begin{array}{rr}
12 & -17 \\
-19 & 27
\end{array}\right]\) மற்றும் \(\left[\begin{array}{rr}
1 & -1 \\
-2 & 3
\end{array}\right]\) எனில், B^-1=

விடை:
(1) \(\left[\begin{array}{rr}
2 & -5 \\
-3 & 8
\end{array}\right]\)
குறிப்பு:
(AB)^-1 = B^-1A^-1 ஆதலால் கிடைப்பது
\(\left[\begin{array}{rr}
12 & -17 \\
-19 & 27
\end{array}\right]\) = B^-1\(\left[\begin{array}{rr}
1 & -1 \\
-2 & 3
\end{array}\right]\)
X = B^-1Y என்க.

கேள்வி 11.
A^TA^-1, ஆனது சமச்சீர் எனில், A² =
(1) A^-1
(2) (A^T)^-1
(3) A^T
(4) (A^-1)²
விடை:
(2) (A^T)²
குறிப்பு:
⇒ A^TA^-1 = (A^TA^-1)^T
⇒ (A^-1)^T (A^T)^T = (A^-1)^TA
⇒ A = A^T ⇒ A சமச்சீர் அணி
∴ A² = (A^T)²

கேள்வி 12.
A என்பது பூச்சியமற்றக் கோவை அணி மற்றும்
A^-1 = \(\left[\begin{array}{rr}
5 & 3 \\
-2 & -1
\end{array}\right]\) எனில், (A^T)^-1 =
(1) \(\left[\begin{array}{rr}
-5 & 3 \\
2 & 1
\end{array}\right]\)
(2) \(\left[\begin{array}{rr}
5 & 3 \\
-2 & -1
\end{array}\right]\)
(3) \(\left[\begin{array}{rr}
-1 & -3 \\
2 & 5
\end{array}\right]\)
(4) \(\left[\begin{array}{ll}
5 & -2 \\
3 & -1
\end{array}\right]\)
விடை:
(4) \(\left[\begin{array}{ll}
5 & -2 \\
3 & -1
\end{array}\right]\)
குறிப்பு:
(A^T)^-1 = (A^-1)^T= \(\left[\begin{array}{ll}
5 & -2 \\
3 & -1
\end{array}\right]\)

கேள்வி 13.
A = \(\left[\begin{array}{ll}
\frac{3}{5} & \frac{4}{5} \\
x & \frac{3}{5}
\end{array}\right]\) மற்றும் A^T = A^-1 எனில், x -ன் மதிப்பு
(1) \(\frac{-4}{5}\)
(2) \(\frac{-3}{5}\)
(3) \(\frac{3}{5}\)
(4) \(\frac{4}{5}\)
விடை:
(1) \(\frac{-4}{5}\)
குறிப்பு:
A^T = A^-1, AA^T = A^T A = 1
[∵ அவைகள் செங்குத்து]

[இருபுறமும் a, ஐ ஒப்பிட கிடைப்பது]
⇒ \(\frac{3x}{5}\) = \(\frac{-12}{25}\) × \(\frac{5}{3}\) = –\(\frac{4}{5}\)

கேள்வி 14.
A = \(\left[\begin{array}{rr}
1 & \tan \frac{\theta}{2} \\
-\tan \frac{\theta}{2} & 1
\end{array}\right]\) மற்றும் AB=I₂ எனில், B =

விடை:
(2) \(\left(\cos ^{2} \frac{\theta}{2}\right)\)A^T
குறிப்பு:

கேள்வி 15.
A= \(\left[\begin{array}{rr}
\cos \theta & \sin \theta \\
-\sin \theta & \cos \theta
\end{array}\right]\) மற்றும் A(adj A) = \(\left[\begin{array}{ll}
\boldsymbol{k} & \mathbf{0} \\
\mathbf{0} & \boldsymbol{k}
\end{array}\right]\) எனில், k =
(1) 0
(2) sin θ
(3) cos θ
(4) 1
விடை:
(4) 1
குறிப்பு:
A (adj A) = (adj A)A = |A| I என அறிவோம்
⇒ |A|=K
∴ K= \(\left|\begin{array}{rr}
\cos \theta & \sin \theta \\
-\sin \theta & \cos \theta
\end{array}\right|\) = cos²θ + sin²θ = 1

கேள்வி 16.
A = \(\left[\begin{array}{rr}
2 & 3 \\
5 & -2
\end{array}\right]\) மற்றும் λA^-1 = A எனில், λ – ன் மதிப்பு
(1) 17
(2) 14
(3) 19
(4) 21
விடை:
(3) 19
குறிப்பு :

கேள்வி 17.

(1) \(\left[\begin{array}{rr}
-7 & -1 \\
7 & -9
\end{array}\right]\)
(2) \(\left[\begin{array}{rr}
-6 & 5 \\
-2 & -10
\end{array}\right]\)
(3) \(\left[\begin{array}{rr}
-7 & 7 \\
-1 & -9
\end{array}\right]\)
(4) \(\left[\begin{array}{rr}
-6 & -2 \\
5 & -10
\end{array}\right]\)
விடை:
(2) \(\left[\begin{array}{rr}
-6 & 5 \\
-2 & -10
\end{array}\right]\)
குறிப்பு:
adj (AB) = (adj B) (adj A)

கேள்வி 18.
\(\left[\begin{array}{rrrr}
1 & 2 & 3 & 4 \\
2 & 4 & 6 & 8 \\
-1 & -2 & -3 & -4
\end{array}\right]\) ன் அணித்தரம்
(1) 1
(2) 2
(3) 4
(4) 3
விடை:
(1) 1
குறிப்பு:

∴ தரமானது 1 [∵ ஒரே ஒரு அபூச்சிய நிரை]

கேள்வி 19.
x^a y^b = e^m, △₁ = \(\left[\begin{array}{cc}
m & b \\
n & d
\end{array}\right]\), △₂ = \(\left[\begin{array}{ll}
a & m \\
c & n
\end{array}\right]\), △₃ = \(\left|\begin{array}{ll}
a & b \\
c & d
\end{array}\right|\) எனில், x மற்றும் y -ன் மதிப்புகள் முறையே.

விடை:
(4)
குறிப்பு :

கேள்வி 20.
பின்வருபனவற்றுள் எவை/எவைகள் உண்மை யானவை?
(i) ஒரு சமச்சீர் அணியின் சேர்ப்பு அணி சமச்சீராக இருக்கும்.
(ii) ஒரு மூலைவிட்ட அணியின் சேர்ப்பு அணி மூலை விட்ட அணியாக இருக்கும்.
(iii) A என்பது n வரிசையுடைய ஒரு சதுர அணி மற்றும் λ என்பது ஒரு திசையிலி எனில் adj (λA) = λ” adj (A).
(iv) A(adjA) = (adj A) A = |A|I
(1) (i) மட்டும்
(2) (ii) மற்றும் (iii)
(3) (iii) மற்றும் (iv)
(4) (i), (ii) மற்றும் (iv)
விடை:
(4) (i) (ii) மற்றும் (iv)

கேள்வி 21.
ρ(A) = ρ([A|B|) எனில், AX = B என்ற நேரியச் சமன்பாடுகளின் தொகுப்பானது
(1) ஒருங்கமைவுடையது மற்றும் ஒரே ஒரு தீர்வு பெற்றிருக்கும்
(2) ஒருங்கமைவுடையது
(3) ஒருங்கமைவுடையது மற்றும் எண்ணற்ற தீர்வுகள் பெற்றிருக்கும்
(4) ஒருங்கமைவற்றது
விடை:
(2) ஒருங்கமைவுடையது

கேள்வி 22.
0 < θ ≤ π மற்றும் x + (sin θ)y – (cos θ)z = 0, (cos θ)x – y + z = 0, (sin θ)x + y – z = 0 மற்றும் தொகுப்பானது வெளிப்படையற்றத் தீர்வு பெற்றிருப்பின், θ-ன் மதிப்பு
(1) \(\frac{2 \pi}{3}\)
(2) \(\frac{3 \pi}{4}\)
(3) \(\frac{5 \pi}{6}\)
(4) \(\frac{\pi}{4}\)
விடை:
(4) \(\frac{\pi}{4}\)
குறிப்பு:

கேள்வி 23.
ஒரு நேரியச் சமன்பாட்டுத் தொகுப்பின் விரிவுப்படுத்தப்பட்டஅணியானது \(\left[\begin{array}{rrrr}
1 & 2 & 7 & 3 \\
0 & 1 & 4 & 6 \\
0 & 0 & \lambda-7 & \mu+5
\end{array}\right]\) மற்றும் தொகுப்பானது எண்ணற்ற தீர்வுகள் பெற்றிருக்கும் எனில்,
(1) λ =7, μ ≠ -5
(2) λ = -7, μ = 5
(3) λ ≠ 7, μ ≠ -5
(4) λ =7, μ = -5
விடை:
(4) λ =7, μ = -5
குறிப்பு:
λ = 7 மற்றும் μ ≠ -5 எனில்,
[A|B] = \(\left[\begin{array}{llll}
1 & 2 & 7 & 3 \\
0 & 1 & 4 & 6 \\
0 & 0 & 0 & 0
\end{array}\right]\)
ρ(A) = ρ([A|B]) = 2 <3, மதிப்பிட வேண்டிய மாறிகளின் எண்ணிக்கை
∴ தொகுப்பு ஒருங்கமைவு உடையது மற்றும் எண்ணிக்கையற்ற தீர்வுகளை கொண்டிருக்கும்.

கேள்வி 24.
A= \(\left[\begin{array}{rrr}
2 & -1 & 1 \\
-1 & 2 & -1 \\
1 & -1 & 2
\end{array}\right]\) மற்றும் 4B = \(\left[\begin{array}{rrr}
3 & 1 & -1 \\
1 & 3 & x \\
-1 & 1 & 3
\end{array}\right]\) என்க. A-ன் நேர்மாறு B எனில், x -ன் மதிப்பு
(1) 2
(2) 4
(3) 3
(4) 1
விடை:
(4) 1
குறிப்பு:
A =B^-1 ⇒ A . B = B^-1.B ⇒ AB =I

கேள்வி 25.

(1) \(\left[\begin{array}{rrr}
3 & -3 & 4 \\
2 & -3 & 4 \\
0 & -1 & 1
\end{array}\right]\)
(2) \(\left[\begin{array}{lll}
6 & -6 & 8 \\
4 & -6 & 8 \\
0 & -2 & 2
\end{array}\right]\)
(3) \(\left[\begin{array}{rrr}
-3 & 3 & -4 \\
-2 & 3 & -4 \\
0 & 1 & -1
\end{array}\right]\)
(4) \(\left[\begin{array}{rrr}
3 & -3 & 4 \\
0 & -1 & 1 \\
2 & -3 & 4
\end{array}\right]\)
விடை:
(1) \(\left[\begin{array}{ccc}
3 & -3 & 4 \\
2 & -3 & 4 \\
0 & -1 & 1
\end{array}\right]\)
குறிப்பு:

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 10 சாதாரண வகைக்கெழுச் சமன்பாடுகள் Ex 10.3 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 10 சாதாரண வகைக்கெழுச் சமன்பாடுகள் Ex 10.3

கேள்வி 1.
ஒரு தளத்தில்
(i) நேர்க்குத்து அல்லாத நேர்க்கோடுகள்
(ii) கிடைமட்டம் அல்லாத நேர்க்கோடுகள் ஆகிய தொகுப்புகளின் வகைக்கெழுச் சமன்பாடுகளைக் காண்க.
தீர்வு:
(i) ஒருதளத்தில் நேர்க்குத்து அல்லாத நேர்க்கோடுகள் குடும்பத்தின் சமன்பாடு ax + by = 1, b ≠ 0, a ∈ ℝ.
‘X’-ஐப் பொறுத்து வகையிட கிடைப்பது,
a + b\(\frac{d y}{d x}\) = 0
‘X’-ஐப் பொறுத்து மீண்டும் வகையிட கிடைப்பது,
\(b \frac{d^{2} y}{d x^{2}}\) = 0 ⇒ \(\frac{d^{2} y}{d x^{2}}\) = 0 [∵ b ≠ 0]

(ii) ஒரு தளத்தில் கிடைமட்டம் அல்லாத நேர்க்கோடுகள் குடும்பத்தின் சமன்பாடு ax + by = 1, a # 0, மற்றும் b ∈ ℝ.
‘y’-ஐப் பொறுத்து வகையிட கிடைப்பது,
a\(\frac{d x}{d y}\) + b = 0
மீண்டும் ‘y’-ஐப் பொறுத்து வகையிட கிடைப்பது,
a\(\frac{d^{2} x}{d y^{2}}\) = 0 ⇒ \(\frac{d^{2} x}{d y^{2}}\) = 0 [∵ a ≠ 0]

கேள்வி 2.
x² + y² = r² எனும் வட்டத்தைத் தொடும் எல்லா நேர்க்கோடுகளின் வகைக்கெழுச் சமன்பாட்டைக் காண்க.
தீர்வு:
x² + y² = r² வட்டத்தை தொடுகின்ற கோடுகளின் குடும்பத்தின் சமன்பாடு y = mx + c என்க…………(1)
x² y² = r² என்ற வட்டத்திற்கு y = mx + c என்ற தொடுகோடாக இருக்க நிபந்தனை c² = r² (1 + m²)
c = \(r \sqrt{1+m^{2}}\) …… (2)
சமன்பாடு (2) ஐ (1)ல் பிரதியிட கிடைப்பது,
y = mx + \(r \sqrt{1+m^{2}}\)
⇒ y – mx = \(r \sqrt{1+m^{2}}\) …….. (3)
(2) லிருந்து, \(\frac{d y}{d x}\) = m …….. (4)
(4) ஐ (3) ல் பிரதியிட கிடைப்பது,
\(y-x\left(\frac{d y}{d x}\right)=r \sqrt{1+\left(\frac{d y}{d x}\right)^{2}}\)
இருபுறமும் வர்க்கப்படுத்த கிடைப்பது,
\(\Rightarrow\left[y-x\left(\frac{d y}{d x}\right)\right]^{2}=r^{2}\left[1+\left(\frac{d y}{d x}\right)^{2}\right]\)

கேள்வி 3.
ஆதிப்புள்ளி வழியாகச் செல்லும், மையத்தினை x-அச்சின் மீது கொண்ட எல்லா வட்டங்களின் வகைக்கெழுச் சமன்பாட்டைக் காண்க.
தீர்வு:
மையத்தினை x- அச்சின் மீது கொண்டுள்ளதால்,
(g, 0) மற்றும் ஆரம் g என்க.

வட்டத்தின் சமன்பாடு
(x – y)² + (y – 0)² = g²
⇒ x² – 2xg + g² + y² = g²
⇒ x² – 2xg + y² = 0 ……………. (1)
x’ஐ பொறுத்து வகையிட கிடைப்பது, =
⇒ 2x – 2g(1) + \(2 y \frac{d y}{d x}\) = 0
⇒ 2x + \(2 y \frac{d y}{d x}\) = 2g
⇒ x + \(y \frac{d y}{d x}\) = g ………….. (2)
சமன்பாடு (2) ஐ (1) ல் பிரதியிட கிடைப்பது,
x² – 2x\(\left(x+y \frac{d y}{d x}\right)\) + y² = 0
⇒ x² – 2x² – 2xy\(\frac{d y}{d x}\) + y² = 0
⇒ -x² – 2xy\(\frac{d y}{d x}\) + y² = 0
⇒ x² + 2xy\(\frac{d y}{d x}\) – y² என்பது தேவையான
வகைக்கெழு சமன்பாடு ஆகும்.

கேள்வி 4.
செவ்வகலம் 4a மற்றும் x-அச்சுக்கு இணையான அச்சுகளைக் கொண்டபரவளையத்தொகுப்பின் வகைக்கெழுச் சமன்பாட்டைக் காண்க.
தீர்வு:
செவ்வகலம் 4a மற்றும் X-அச்சுக்கு இணையான அச்சுகளைக் கொண்ட பரவளையத் தொகுப்பின் சமன்பாடு
(y – k)² = 4d(x – h)
[(h, k) பரவளையத்தின் முனை]
‘x’ஐப் பொறுத்து வகையிட கிடைப்பது,
2(y – k)y’ = 4a(1)
⇒ (y – k)y’ = 2a
⇒ yy’ – ky’ = 2a
⇒ \(\frac{y y^{\prime}-2 a}{y^{\prime}}\) = k
⇒ y – \(\frac{2 a}{y^{\prime}}\) = k ……..(1)
‘x’ஐப் பொறுத்து மீண்டும் வகையிட கிடைப்பது,
yy” + y¹² – ky” = 0
k = y – \(\frac{2 a}{y^{\prime}}\); எனப் பிரதியிட கிடைப்பது,
yy” + y’² – y” ( y – \(\frac{2 a}{y^{\prime}}\))
= y y” + y’² – y y” + \(\frac{2 a y^{\prime \prime}}{y^{\prime \prime}}\)
y’ ஆல் பெருக்க கிடைப்பது,
y’³ + 2ay” = 0 என்பது தேவையான வகைக்கெழு சமன்பாடு,

கேள்வி 5.
முனை (0, 1) மற்றும் y- அச்சை அச்சாகவும் கொண்ட பரவளையக் குடும்பத்தின் வகைக்கெழுச் சமன்பாட்டைக் காண்க.
தீர்வு:
முனை (0, -1) மற்றும் Y-அச்சை அச்சாகவும் கொண்ட பரவளையக் குடும்பத்தின் சமன்பாடு
(x – 0)² = 4a(y + 1)
⇒ x² = 4a(y + 1) …………. (1)
‘x’ஐப் பொறுத்து வகையிட கிடைப்பது,
2x = 4a \(\left(\frac{d y}{d x}\right)\)
⇒ 4a = \(\frac{2 x}{\frac{d y}{d x}}\) …………. (2)
சமன்பாடு (2) ஐ (1) ல் பிரதியிட கிடைப்பது,
x² = \(\frac{2 x}{y^{\prime}}(y+1)\)
⇒ x = \(\frac{2 x}{y^{\prime}}(y+1)\)
xy’ = 2(y+ 1)
xy’ = 2y+2
⇒ xy’ – 2y – 2 = 0.

கேள்வி 6.
ஆதிப்புள்ளியை மையமாகவும் செல்லும், y- அச்சின் மீது குவியங்களையும் கொண்ட நீள்வட்டத் தொகுதியின் வகைக்கெழுச் சமன்பாட்டைக் காண்க.
தீர்வு:
ஆதிப்புள்ளியை மையமாகவும் y-அச்சின் மீது குவியங்களை கொண்ட நீள்வட்டத் தொகுதியின் சமன்பாடு

÷ yy’ கிடைப்பது, x² – \(\frac{x y^{2}}{y y^{\prime}}\) = b²
‘x’ ஐப் பொறுத்து மீண்டும் வகையிட கிடைப்பது,
2x – \(\left[\frac{y^{\prime}\left(x y^{\prime}+y\right)-x y y^{\prime \prime}}{y^{\prime 2}}\right]\) = 0
⇒ 2xy’² – y'(xy’ + y) + xyy” = 0 [y’² ஆல் வகுக்க)]
⇒ 2xy’² – xy’² – yy’ + xyy” = 0s.
⇒ xy’² – yy’ + xyy” = 0

கேள்வி 7.
y = Ae^8x + Be^-8x எனும் சமன்பாட்டைக் கொண்ட வளைவரைக் குடும்பத்தின் வகைக்கெழுச் சமன்பாட்டைக் காண்க. இங்கு A, B என்பன ஏதேனும் இரு மாறிலிகள்.
தீர்வு:
கொடுக்கப்பட்ட வளைவரைகளின் சமன்பாடு
y = Ae^8x + Be^-8x ……. (1)
‘X’ஐ பொறுத்து வகையிட கிடைப்பது,
\(\frac{d y}{d x}\) = 8Ae^8x – 8Be^-8x
‘x’ஐ பொறுத்து மீண்டும் வகையிட கிடைப்பது,
\(\frac{d^{2} y}{d x^{2}}\) = 64Ae^8x + 64Be^-8x
= 64(Ae^8x + Be^-8x)
\(\frac{d^{2} y}{d x^{2}}\) = 64y [(1)ஐ பயன்படுத்தி) என்பது
தேவையான வகைக்கெழு சமன்பாடு.

கேள்வி 8.
xy = ae^x + be^-x + x² எனும் சமன்பாட்டால் குறிப்பிடப்படும் வளை வரையின் வகைக்கெழுச் சமன்பாட்டைக் காண்க.
தீர்வு:
கொடுக்கப்பட்ட வளைவரைகளின் சமன்பாடு
xy = ae^x + be^-x +x² …….(1)
‘x’ஐ பொறுத்து வகையிட கிடைப்பது.
xy + y = ae^x – be^-x + 2x
‘x’ஐ பொறுத்து மீண்டும் வகையிட கிடைப்பது,
xy” + y’ + y = ae^x + be^-x + 2
⇒ xy” + 2y – 2 = ae^x + be^-x
⇒ xy” + 2y – 2 = xy – x^x [(1) → xy – x^x = ae^x + be^-x]
⇒ xy” + 2y’ + x^x – xy – 2 = 0 என்பது தேவையான வகைக்கெழு சமன்பாடாகும்.

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 1 அணிகள் மற்றும் அணிக்கோவைகளின் பயன்பாடுகள் Ex 1.6 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 1 அணிகள் மற்றும் அணிக்கோவைகளின் பயன்பாடுகள் Ex 1.6

கேள்வி 1.
பின்வரும் சமன்பாடுகளின் தொகுப்பு ஒருங்கமைவு உடையதா என்பதை ஆராய்க. ஒருங்கமைவு உடையதாயின் அவற்றைத் தீர்க்க. (i) x-y+2z = 2, 2x+y+4z=7, 4x-y+z= 4
(ii) 3x+y+z=2, x-3y+2z = 1, 7x-y+4z = 5
(iii) 2x+2y+z= 5, x-y+z= 1, 3x+y+2z = 4
(iv) 2x-y+z=2,6x-Zy+3z=6,4x-2y+2z=4.
தீர்வு:
(i) x – y + 27= 2, 2x + y + 4x = 7, 4x – y + 7 = 4
சமன்பாட்டு தொகுப்பின் அணி வடிவம் AX =B
இங்கு A = \(\left[\begin{array}{rrr}
1 & -1 & 2 \\
2 & 1 & 4 \\
4 & -1 & 1
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\) மற்றும் B = \(\left[\begin{array}{l}
2 \\
7 \\
4
\end{array}\right]\)
விரிவுபடுத்தப்பட்ட அணியை ஏறுபடி வடிவத்திற்கு உருமாற்றங்கள் செய்யக் கிடைப்பது [A|B],

இங்கு ρ(A) = 3 மற்றும் ρ[A|B] = 3
∴ ρ(A) = ρ[A|B] = 3 = மதிப்பிட வேண்டிய மாறிகளின் எண்ணிக்கை எனவே தொகுப்பு ஒருங்கமைவுடன் ஒரே ஒரு தீர்வை கொண்டிருக்கும்.
ஏறுபடிவடிவத்திலுள்ள அணியிலிருந்து கிடைக்கும் சமான சமன்பாடுகளின் தொகுப்பானது.
x – y + 2z = 2
3y = 3 ⇒ y = 1 ….(2)
-7z = -7 ⇒ z = \(\frac{-7}{-7}\)=1 ….(3)
y = 1 மற்றும் z =1 என (1) ல் பிரதியிட,
x-1 + 2(1) = 2
⇒ x – 1 + 2 = 2
⇒ x + 1 = 2
⇒ x = 2 – 1 = 1
⇒ x= 1, y =1, z = 1
ஆகையால், தீர்வு கணம் {1, 1, 1}.

(ii) 3x+y+z=2, x-3y +2z =1,7x – y +4z = 5.
தொகுப்பின் அணி வடிவம் AX = B
இங்கு A = \(\left[\begin{array}{rrr}
3 & 1 & 1 \\
1 & -3 & 2 \\
7 & -1 & 4
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\), B = \(\left[\begin{array}{l}
2 \\
1 \\
5
\end{array}\right]\)
(7 -1 4) (z)
விரிவுப்படுத்தப்பட்ட அணி [A|B] யை ஏறுபடி வடிவத்திற்கு உருமாற்றங்கள் செய்யக் கிடைப்பது,

இங்கு ρ(A) = 2, மற்றும் p[A|B] =2 [∵ 2 அபூச்சிய நிரைகள் உள்ள ன). ஆகையால், p(A) = p[A|B] =2 < 3, கொடுக்கப்பட்ட தொகுப்பு ஒருங்கமைவுடன் தீர்வுகள் ஒரு சாராமாறிக் குடும்பமாக இருக்கும். ஆகையால் z = 1, x ∈ ℝ. ஏறுபடி வடிவத்திலுள்ள அணியிலிருந்து கிடைக்கும் சமான சமன்பாடு களின் தொகுப்பு,
x-3y + 2z = 1 …. (1)
10y – 5z = -1…. (2)
z = t ….(3)
(2) லிருந்து 10y- 5t =-1
⇒ 10y = 5t-1
⇒ y = \(\frac{1}{10}\)[5t – 1]
மேலும், (1) லிருந்து, x – \(\frac{3}{10}\)[5t – 1] + 2t = 1
⇒ x = \(\frac{3}{10}\)[5t – 1] – 2t + 1 = \(\frac{15 t-3-20 t+10}{10}\)
⇒ x = \(\frac{1}{10}\)[-5t + 7]
எனவே தீர்வு கணம் என்பது
{ \(\frac{1}{10}\)(7 – 5t), \(\frac{1}{10}\)(5t – 1, t)} இங்கு t ∈ℝ.

(iii) 2x+2y+7= 5, x-y+7 = 1, 3x+y+2z = 4
ஆகையால் தொகுப்பின் அணி AX = B இங்கு
A = \(\left[\begin{array}{ccc}
2 & 2 & 1 \\
1 & -1 & 1 \\
3 & 1 & 2
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\), B = \(\left[\begin{array}{l}
5 \\
1 \\
4
\end{array}\right]\)
விரிவுபடுத்தப்பட்ட அணி [A|B] யை ஏறுபடி வடிவத்திற்கு உருமாற்றங்கள் செய்யக் கிடைப்பது,

இங்கு ρ(A)=2 [∵ 2 அபூச்சிய நிரைகள் உள்ளன]
மற்றும் p[A|B] =3 [∵ 3 அபூச்சிய நிரைகள் உள்ளன]
இங்கு (A) ≠ p[A|B]
ஆகையால், கொடுக்கப்பட்ட தொகுப்பு ஒருங்கமைவு அற்றது மற்றும் தீர்வுகள் இல்லை.

(iv) 2x – y +7 = 2, 6x – 3y +3z = 6,
4x-2y+2z = 4.
தொகுப்பின் அணி வடிவம் AX = B இங்கு
A = \(\left[\begin{array}{rrr}
2 & -1 & 1 \\
6 & -3 & 3 \\
4 & -2 & 2
\end{array}\right]\),
X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\), B = \(\left[\begin{array}{l}
2 \\
6 \\
4
\end{array}\right]\)
[A|B] என்ற விரிவுபடுத்தப்பட்ட அணியில் தொடக்கநிலை நிரைச் செயலிகள் பயன்படுத்தக் கிடைப்பது,

இங்கு p(A) = 1[∵ ஒரே ஒரு அபூச்சிய நிரை]
மற்றும் p[A|B] =1[∵ ஒரே ஒரு அபூச்சிய நிரை]
∴ ρ(A) = ρ[A|B] = 1 < 3, கொடுக்கப்பட்ட தொகுப்பு ஒருங்கமைவுடன் இரு சாராமாறிக் குடும்பமாக தீர்வுகள் இருக்கும்.
ஆகையால், z = t மற்றும் y=s இங்கு s, t ∈R. ஏறுபடி வடிவத்திலிருந்து கிடைக்கும் சமான சமன்பாடுகள்
2x-y+z = 2 …. (1)
y = s …. (2)
z = t …. (3)
(2) மற்றும் (3) ஐ (1)ல் பிரதியிட கிடைப்பது,
2x – s + 1 = 2
⇒ 2x = s – t + 2
x= \(\frac { 1 }{ 2 }\)[s-t+2]
∴ தீர்வு கணம் {\(\frac { 1 }{ 2 }\)(s-t+2), s, t} இங்கு s, t ∈ ℝ

கேள்வி 2.
k-ன் எம்மதிப்புகளுக்கு பின்வரும் சமன்பாட்டுத் தொகுப்பு kx-2y+z = 1, x- 2ky+z=-2, x-2y+kz=1;
(i) யாதொரு தீர்வும் பெற்றிராது
(ii) ஒரே ஒரு தீர்வைப் பெற்றிருக்கும்
(iii) எண்ணிக்கையற்ற தீர்வுகளைப் பெற்றிருக்கும் என்பதனை ஆராய்க
தீர்வு:
kx-2y+z = 1,x-2ky + z =-2, x – 2y+k = 1
சமன்பாட்டு தொகுப்பின் அணி வடிவம் AX = B இங்கு
A = \(\left[\begin{array}{rrr}
k & -2 & 1 \\
1 & -2 k & 1 \\
1 & -2 & k
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\), B = \(\left[\begin{array}{l}
1 \\
-2 \\
1
\end{array}\right]\)
[A|B] என்ற விரிவுபடுத்தப்பட்ட அணியில் தொடக்கநிலை நிரை செயலிகள் பயன்படுத்தக் கிடைப்பது,


நிலை (i) k = 1 எனில்

இங்கு ρ(A) = 1 மற்றும் ρ[A|B] = 2
ஆகையால், ρ(A) ≠ ρ[A|B] ⇒ தொகுப்புற்கு தீர்வு இல்லை.
நிலை (ii) k≠1, k≠-2 எனில்

⇒ ρ(A) = 3 மற்றும் ρ[A|B] = 3
ஆகையால், ρ(A) = ρ[A|B] = 3 = மதிப்பிட
வேண்டிய மாறிகளின் எண்ணிக்கை
ஆகையால், தொகுப்புக்கு ஒரே ஒரு தீர்வு உண்டு.
நிலை (iii) k =-2 எனில்

இங்கு ρ(A) = 2 மற்றும் ρ[A|B] = 2
∴ ρ(A) = ρ[A|B] = 2 < 3, மதிப்பிட வேண்டிய மாறிகளின் எண்ணிக்கை. ஆகையால் தொகுப்பு ஒருங்கமைவுடன் எண்ணிக்கையற்ற தீர்வுகளை கொண்டிருக்கும்.

கேள்வி 3.
λ, μ-இன் எம்மதிப்புகளுக்கு 2x + 3y + 5z = 9, 7x + 3y – 5z = 8, 2x + 3y + λz = μ, என்ற சமன்பாடுகளின் தொகுப்பானது.
(i) யாதொரு தீர்வும் பெற்றிராது
(ii) ஒரே ஒரு தீர்வைப் பெற்றிருக்கும்
(iii) எண்ணிக்கையற்ற தீர்வுகளைப் பெற்றிருக்கும் என்பதனை ஆராய்க.
தீர்வு:
2x + 3y=9,7x + 3y – 5z = 8, 2x + 3y + λz = μ
சமன்பாட்டு தொகுப்பின் அணி வடிவம் AX = B இங்கு
A = \(\left[\begin{array}{rrr}
2 & 3 & 5 \\
7 & 3 & -5 \\
2 & 3 & \lambda
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\), B = \(\left[\begin{array}{l}
9 \\
8 \\
\mu
\end{array}\right]\)
[A|B] என்ற விரிவுபடுத்தப்பட்ட அணியில் தொடக்கநிலை நிரைச் செயலிகள் பயன்படுத்தக் கிடைப்பது,

இங்கு ρ(A) = 2 மற்றும் ρ[A|B] = 3
ஆகையால், ρ(A) ≠ ρ[A|B]
ஆகையால் தொகுப்பு ஒருங்கமைவு அற்றது மற்றும் தீர்வு இல்லை.
நிலை (ii) λ ≠ 5, μ ≠ 9 எனில்

∴ ρ(A) = ρ[A|B] = 3 = மதிப்பிட வேண்டிய மாறிகளின் எண்ணிக்கை ஆகையால் தொகுப்பு ஒருங்கமைவுடன் ஒரே ஒரு தீர்வை கொண்டிருக்கும். நிலை (iii) λ = 5 மற்றும் μ = 9 எனில்

இங்கு ρ(A) =2, ρ[A|B] = 2
∴ ρ(A) = [A|B] = 2 < மதிப்பிட வேண்டிய மாறிகளின் எண்ணிக்கை
∴ தொகுப்பு ஒருங்கமைவுடன் மற்றும் எண்ணிக்கையற்ற தீர்வுகளை கொண்டிருக்கும்.

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 11 நிகழ்தகவு பரவல்கள் Ex 11.5 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 11 நிகழ்தகவு பரவல்கள் Ex 11.5

கேள்வி 1.
கீழ்காணும் ஈருறுப்பு பரவல் B(n, p)-க்காக P(X = k) என்பதைக் கணிக்க.
(i) n = 6, p = \(\frac{1}{3}\), k = 3
(ii) n = 10, p = \(\frac{1}{5}\), k = 4
(i) n = 9, n = \(\frac{1}{2}\), k = 7
தீர்வு:
கொடுக்கப்பட்டா n = 6, p = \(\frac{1}{3}\), k = 3
ஈருறுப்பு பரவல்

கேள்வி 2.
எந்த முயற்சியிலும் ஒரு இலக்கைத் திரு. தாக்க நிகழ்தகவு \(\frac{1}{4}\) ஆகும். பத்து முறை இலக்கை அவர் தாக்க முயற்சிக்கிறார் எனக் கொள்க. இலக்கைத் தாக்க
(i) சரியாக 4 முறைகள்
(ii) குறைந்தபட்சம் ஒரு முறை தாக்குவதற்கு ஆகியவற்றிற்கான நிகழ்தகவு காண்க.
தீர்வு:
கொடுக்கப்பட்ட P(இலக்கத்தை தாக்க) = \(\frac{1}{4}\) ⇒ p = \(\frac{1}{4}\)
n = 10.
(i) P(X = 4) = \(\left(\begin{array}{l}
n \\
x
\end{array}\right)\) p^x(1 – p)^n-x, x
= 0, 1, 2, ……… n

P(x=4) = \(\left(\begin{array}{l}
10 \\
4
\end{array}\right)\) (\(\frac{1}{4}\))⁴ (1 – \(\frac{1}{4}\))^10-4
= 10C₄ (\(\frac{1}{4}\))⁴ (\(\frac{3}{4}\))⁶

(ii) P(குறைந்தபட்சம் ஒரு முறை)
= P(X ≥ 1) = 1 – P(X < 1)
= 1 – P(X = 0)
= 1 – 10C₀(\(\frac{1}{4}\))⁰ (1 – \(\frac{1}{4}\))¹⁰
= 1 – 1(1) (\(\frac{3}{4}\))¹⁰
P(X ≥ 1) = 1 – \(\frac{3^{10}}{4^{10}}\)

கேள்வி 3.
கீழ்க்காணும் சோதனைகளில் ஈருறுப்பு பரவலைப் பயன்படுத்தி சமவாய்ப்பு மாறி X -ன் சராசரி மற்றும் பரவற்படி காண்க.
(i) 100 தடவை ஒரு சீரான நாணயம் சுண்டப்படுகிறது. தலைகளின் எண்ணிக்கையை X குறிக்கிறது.
(ii) 240 தடவை ஒரு சீரான பகடை ! சுண்டப்படுகிறது. எண் நான்கு தோன்றுவதற்கான எண்ணிக்கையை X குறிக்கிறது.
தீர்வு:
(i) கொடுக்கப்பட்ட n = 100
X என்பது தலைகளின் எண்ணிக்கையை குறிப்பதால், p = \(\frac{1}{2}\);
சராசரி = np = 100 × \(\frac{1}{2}\) = 50
பரவற்படி = npq = 100 × \(\frac{1}{2}\) × \(\frac{1}{2}\) = 25.

(ii) கொடுக்கப்பட்ட n = 240 மேலும், X- என்பது எண் நான்கு தோன்றுவதற்கான எண்ணிக்கையை குறிக்கிறது.
p = \(\frac{1}{6}\) [∵ 4 ஒருமுறை மட்டும் தோன்றும்]
∴ சராசரி = 240 × \(\frac{1}{6}\) = 40
பரவற்படி = npq = 240 × \(\frac{1}{6}\) × \(\frac{5}{6}\) [∵ q = 1 – p = 1 – \(\frac{1}{6}\) = \(\frac{5}{6}\)]
பரவற்படி = \(\frac{100}{3}\)

கேள்வி 4.
ஒரு மின்சோதனையில் ஒரு குறிப்பிட்ட சாதனத்தின் தாங்கும் திறனுக்கான நிகழ்தகவு \(\frac{3}{4}\). சோதிக்கப்பட ஐந்தில் சரியாக மூன்று சாதனங்களின் தாங்கு திறனுக்கான நிகழ்தகவைக் கண்டறிக.
தீர்வு:
கொடுக்கப்பட்ட p = \(\frac{3}{4}\)
n = 5

கேள்வி 5.
ஒரு உற்பத்தியாளரிடமிருந்து ஒரு குறிப்பிட்ட மின்வகைக் கருவியை ஒரு விற்பனையாளர் கொள்முதல் செய்கிறார். உற்பத்தியாளர் கருவியின் பழுதாகும் சதவீதம் 5 எனக்கூறுகிறார். கொள்முதல் செய்யப்பட்ட சரக்கிலிருந்து 10 பொருட்களை விற்பனையாளரின் பரிசோதகர் சமவாய்ப்பு முறையில் பரிசோதிக்கிறார். அவற்றுள்
(i) குறைந்தபட்சம் ஒரு பழுதான பொருள்
(ii) சரியாக இரு பொருட்கள் பழுதாக இருக்க நிகழ்தகவு காண்க.
தீர்வு : கொடுக்கப்பட்ட n = 10
P = 5% = \(\frac{5}{100}\)

(i) P(குறைந்த பட்சம் ஒரு பழுதான பொருள்)
P(X ≥ 1) = 1 – P(X < 1)
= 1 – P(X = 0)
= 1 – 10C₀\(\left(\frac{5}{100}\right)^{0}\left(1-\frac{5}{100}\right)^{10}\)
– 1 – (1)(1)\(\)
P(X > 1) = 1 (0.95)^10</sup<

(ii) P(X = 2) = 10C₂ \(\left(\frac{5}{100}\right)^{2}\left(1-\frac{5}{100}\right)^{10-2}\)
= 10C₂(0.05)² \(\left(\frac{95}{100}\right)^{8}\)
P(X = 2) = 10C₂(0.05)² (0.95)⁸

கேள்வி 6.
ஒரு பாதரச ஆவி விளக்கின் பயன்படும் காலம் குறைந்தபட்சம் 600 மணித்துளிகளுக்கான நிகழ்தகவு 0.9. எனில் அத்தகைய 12 விளக்குகளில்
(i) சரியாக 10 விளக்குகளின் பயன்படும் காலம் குறைந்தபட்சம் 600 மணித்துளிகளுக்கான நிகழ்தகவு;
(ii) குறைந்தபட்சம் 11 விளக்குகளின் பயன்படும் காலம் குறைந்தபட்சம் 600 மணித்துளிகளுக்கான நிகழ்தகவு
(iii) குறைந்தபட்சம் 2 விளக்குகளின் பயன்படும் காலம் குறைந்தபட்சம் 600 மணித்துளிகள் கூட இல்லாததற்கான நிகழ்தகவு ஆகியவற்றைக் காண்க.
தீர்வு:
கொடுக்கப்பட்ட n = 12
P = 0.9
(i) P(X = 10) = 12C₁₀(0.9)¹⁰ (1 – 0.9)²
= 12C₁₀(0.9)¹⁰ (0.1)²

(ii) P(X ≥ 11) = P(X = 11) + P(X = 12)
= 12C₁₁(0.9)¹¹ (0.1)¹ + 12C₁₂(0.9)¹² (0.1)⁶
= 12C₁(0.9)¹¹ (0.1) + (0.9)¹²
= 12(0.9)¹¹ (0.1) + (0.9)¹²
= (0.9)¹¹ ((12)(0.1) + 0.9)
= (0.9)¹¹ (1.2 + 0.9) = (0.9)¹¹ (2.1)

(iii) P(குறைந்தபட்சம் 2 விளக்குகளில் பயன்படும்
காலம் 600 மணித்துளிகள் கூட இல்லாதது)
= 1 – P(குறைந்தபட்சம் 11 விளக்குகளில் பயன்படும் காலம் -600 மணித்துளிகளாவது உள்ளது)
= 1 – P(X ≥ 11) = 1 – 2.1 (0.9)¹¹

கேள்வி 7.
ஓர் ஈருறுப்பு சமவாய்ப்பு மாறி X -ன் சராசரி மற்றும் திட்ட விலக்கம் முறையே 6 மற்றும் 2 ஆகும்.
(i) நிகழ்தகவு நிறை சார்பு
(ii) P(X = 3)
(iii) P(X ≥ 2)ஆகியவற்றைக் காண்க.
தீர்வு:
கொடுக்கப்பட்ட சராசரி = np = 6 …. (1)
திட்ட விலக்கம் = \(\sqrt{npq}\) = 2
⇒ npq = 4 …………(2)
(2) ÷ (1) → \(\frac{n p q}{n p}=\frac{4}{6}=\frac{2}{3}\)
⇒ q = \(\frac{2}{3}\)
⇒ 1 – p = \(\frac{2}{3}\)
⇒ 1 – \(\frac{2}{3}\) = p
∴ p = \(\frac{1}{3}\)
p = \(\frac{1}{3}\) என்பதை (1)ல் பிரதியிட கிடைப்பது.
n × \(\frac{1}{3}\) = 6 ⇒ n = 18

(i) நிகழ்தகவு நிறைச் சார்பு

= 1 – \(\left(\frac{2}{3}\right)^{17}\left(\frac{20}{3}\right)\)
= 1 – \(\frac{20}{3}\left(\frac{2}{3}\right)^{17}\)

கேள்வி 8.
4P(X = 4) = P(X = 2) மற்றும் n = 6 எனும்படி உள்ள X ~ B(n, p)-ன் பரவலின், சராசரி மற்றும் திட்டவிலக்கம் ஆகியவற்றைக் காண்க.
தீர்வு:
கொடுக்கப்பட்ட 4 – P(X = 4) = P(X = 2) மற்றும்
n = 6.
4 – [6C₄p⁴ (1 – p)²] = 6C₂p⁴ (1 – p)⁴
⇒ \(\frac{6 \times 5}{2 \times 1}\) × p⁴(1 – p)² = \(\frac{6 \times 5}{2 \times 1}\) p² (1 – p)⁴
⇒ p²(1 – p)² [4 × p²] = p²(1 – p)⁴
⇒ 4p² = (1 – p)² [∵ நீக்க p² (1 – p)²]
⇒ 4p² = 1 + p² – 2p
⇒ 3p² + 2p – 1 = 0
⇒ (p+ 1) (3p – 1) = 0
p = -1, p = \(\frac{1}{3}\) [∵ p =- 1க்கு] சாத்தியமில்லை]

∴ ஈருறுப்பு பரவல்
P(X = x) = nC_xp^x (1 – p)^n-x, x = 0, 1, 2,…n
(i) P(X = x) = 6C_x \(\left(\frac{1}{3}\right)^{x}\left(\frac{2}{3}\right)^{6-x}\), x = 0, 1, 2 –

(ii) சராசரி = np= 6 × \(\frac{1}{3}\) = 2

(iii) திட்ட விலக்கம் = \(\sqrt{n p q}=\sqrt{6 \times \frac{1}{3} \times \frac{2}{3}}\)
= \(\sqrt{\frac{12}{9}}=\sqrt{\frac{4}{3}}\)

கேள்வி 9.
5 சார்பற்ற சோதனைகளை உடைய ஒரு ஈருறுப்பு பரவலின் 1 மற்றும் 2 வெற்றிக்கான நிகழ்தகவுகள் முறையே 0.4096 மற்றும் 0.2048 ஆகும். ஈருப்பு பரவலின் சராசரி மற்றும் பரவற்படி காண்க.
தீர்வு:
கொடுக்கப்பட்ட n = 5 மற்றும்
P(X = 1) = 0.4096,
P(X = 2) = 0.2048
∴ nC₁p¹q⁴ = 0.4096
⇒ 5C₁p¹q⁴ = 0.4096 ………. (1)
p(x = 2) = 0.2048
5C₂p²q³= 0.2048
⇒ p²q³ = 0.2048 ……… (2)
(2) ஐ (1) ஆல் வகுக்க கிடைப்பது
\(\frac{10 p^{2} q^{3}}{5 p q^{4}}=\frac{0.2048}{0.4096}\)
⇒ \(\frac{2 p}{q}=\frac{1}{2}\) ⇒ 4p = q
⇒ 4p = 1 – p ⇒ 5p = 1
⇒ p = \(\frac{1}{5}\)
∴ q = 1 – p = 1 – \(\frac{1}{5}\) = \(\frac{4}{5}\)
சராசரி = np = 5 × \(\frac{1}{5}\) = 1
பரவற்படி = npq = 5 ×\(\frac{1}{5}\) × \(\frac{4}{5}\) = \(\frac{4}{5}\)

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 1 அணிகள் மற்றும் அணிக்கோவைகளின் பயன்பாடுகள் Ex 1.7 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 1 அணிகள் மற்றும் அணிக்கோவைகளின் பயன்பாடுகள் Ex 1.7

கேள்வி 1.
பின்வரும் சமப்படித்தான நேரியச் சமன்பாட்டுத் தொகுப்பைத் தீர்க்கவும்.

(i) 3x+2y +73 = 0, 4x-3y-2z = 0,
5x+9y+23z=0
(ii) 2x+3y-z=0, x-y-2z = 0, 3x+y+3z = 0.
தீர்வு:
(i) 3x+2y+7z = 0, 4x-3y-2x = 0,
5x+9y+23z =0
விரிவுபடுத்தப்பட்ட அணியில் தொடக்கநிலை நிரை செயலிகள் பயன்படுத்தக் கிடைப்பது,
[A|0] =


இங்கு ρ(A) = 2 மற்றும் ρ[A|0] = 2
ஆகையால், ρ(A) = ρ([A|0]) = 2 < 3 = மதிப்பிட வேண்டிய மாறிகளின் எண்ணிக்கை
இங்கு, தொகுப்பு ஒருங்கமைவுடன் ஒரு சாராமாறிக்
குடும்பமாக தீர்வுகளை கொண்டிருக்கும்.
ஆகையால் z = t என பிரதியிடு இங்கு t ∈ ℝ.
ஏறுபடி வடிவத்திலிருந்து சமன்பாடுகளை எழுத கிடைப்பது
3x + 2y +7z = 0 …. (1)
y+2z = 0 …(2)
z = t, என பிரதியிடு (2) லிருந்து
y+ 2t = 0
⇒ y = -2t
∴ (1) லிருந்து , 3x + 2 (-2t) + 71 = 0
⇒ 3x – 4t + 7t = 0
⇒ 3x + 3t = 0
⇒ 3x = -3t
⇒ x = -t
∴ தீர்வு கணம் {-t, -2t, t} இங்கு t ∈ ℝ

(ii) 2x+3y-z=0, x-y-2z = 0, 3x+y+3z = 0.
விரிவுபடுத்தப்பட்ட அணியில் தொடக்கநிலை நிரை செயலிகள் பயன்படுத்தக் கிடைப்பது

இங்கு ρ(A) = 3 மற்றும் ρ([A|0]) = 3
ρ(A) = ρ[[A|0]) = 3 = மதிப்பிட வேண்டிய மாறிகளின் எண்ணிக்கை
ஆகையால் தொகுப்பு ஒருங்கமைவுடன் ஒரே ஒரு தீர்வை கொண்டிருக்கும்.
ஆகையால் தொகுப்பு வெளிப்படை தீர்வை மட்டும் கொண்டிருக்கும்.

கேள்வி 2.
λ -வின் எம்மதிப்பிற்கு
x + y + 3z = 0, 4x + 3y + λz = 0, 2x + y + 2z =0 என்ற தொகுப்பிற்கு
(i) வெளிப்படைத் தீர்வு
(ii) வெளிப்படையற்ற தீர்வு கிடைக்கும்
தீர்வு:
x+y+ 3z = 0, 4x+3y +λz = 0, 2x+y+2z=0
விரிவுப்படுத்தப்பட்ட அணியை ஏறுபடி வடிவத்திற்கு மாற்ற கிடைப்பது,


நிலை (i) 1 ≠ 8 எனில்

இங்கு ρ(A) = 3,ρ([A/O]) = 3
∴ ρ(A) = ρ[[A/0]) = 3 = மதிப்பிட வேண்டிய மாறிகளின் எண்ணிக்கை
∴ கொடுக்கப்பட்ட தொகுப்பு ஒருங்கமைவுடன் ஒரே ஒரு தீர்வை கொண்டிருக்கும். நிலை (ii) λ = 8 எனில்

இங்கு ρ(A) = 2, ρ([A|0]) = 2
∴ ρ(A) = ρ[[A|0]) = 2 < 3, மதிப்பிட வேண்டிய மாறிகளின் எண்ணிக்கை,
∴ தொகுப்பு ஒருங்கமைவுடன் வெளிப்படையற்ற தீர்வுகளை உடையது.

கேள்வி 3.
காஸ்ஸியன் நீக்கல் முறையைப் பயன்படுத்தி :
C₂H₆ + O₂ → H₂ O + CO₂, என்ற வேதியியல் எதிர்வினைச்சமன்பாட்டை சமநிலைப்பலைப் படுத்துக.
தீர்வு:
கொடுக்கப்பட்ட C₂ H₆ + O₂ → H₂O + CO₂
நாம் மிகை எண்கள் , x₁, x₂, x₃, மற்றும் x₄ இவ்வாறு காண வேண்டும்.
x₁, C₂, H₆, + x₂ O₂ → x₃ H₂O +x₄ CO₂ ….(1)
(1) ல் இடது பக்கத்தில் உள்ள கார்பன் அணுக் களின் எண்ணிக்கை வலது பக்கத்தில் உள்ள கார்பன் அணுக்களின் எண்ணிக்கைக்கு சமமாக இருக்க வேண்டும்.
∴ 2x₁ = 1x₄
⇒ 2x₁ – x₄ = 0 …. (2)
ஹைட்ரஜன் அணுக்களால் கிடைப்பது,
6x₁ = 2x₃
⇒ 6x₁ – 2x₃ = 0
⇒ 3x₁ – x₃ = 0 ….. (3)
மேலும், ஆக்ஸிஜன் அணுக்களால் கிடைப்பது,
2x₂ = 1x₃ +2x₄
⇒ 2x₂ – x₃ – 2x₄ = 0 …. (4)
4 மாறிகளில் அமைந்த நேரியில் சமபடித்தான தொகுப்பு சமன்பாடுகள் (2), (3) மற்றும் (4)
∴ விரிவுபடுத்தப்பட்ட அணி [A|0]
\(\left[\begin{array}{rrrr|r}
2 & 0 & 0 & -1 & 0 \\
3 & 0 & -1 & 0 & 0 \\
0 & 2 & -1 & -2 & 0
\end{array}\right]\)
காஸ்ஸியன் நீக்கல் முறை மூலம் கிடைப்பது,


இங்கு ρ(A)=ρ([A|B])=3<4, மதிப்பிட வேண்டிய மாறிகளின் எண்ணிக்கை.
∴ தொகுப்பு ஒருங்கமைவுடன் ஒரு சாராமாறிக் குடும்ப தீர்வுகளை கொண்டிருக்கும், ஆகையால் x⁴ = t என்க. ஏறுபடிவத்திலிருந்து சமன்பாடுகளை எழுத கிடைப்பது
2x₁ – x₄ = 0
⇒ 2x₁ = x₄
⇒ 2x = t
⇒ x₁ = \(\frac{t}{2}\)
4x₂ – 7x₄ = 0
⇒ 4x₂ = 7t ⇒ x₂ = \(\frac{7t}{4}\)
-2x₃ + 3x₄ = 0 ⇒ 2x₃ = 3x₄
⇒ x₃ = \(\frac{3t}{2}\)
x₁, x₂, x₃, மற்றும் x₄, மிகை முழுக்கள், ஆதலால், t = 4 என தேர்ந்தெடுக்க

x₄ = t = 4
ஆகையால் சமநிலைப்படுத்தப்பட்ட சமன்பாடு
2 C₂H₆ +7O₂ → 6H₂O + 4CO₂

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 10 சாதாரண வகைக்கெழுச் சமன்பாடுகள் Ex 10.2 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 10 சாதாரண வகைக்கெழுச் சமன்பாடுகள் Ex 10.2

கேள்வி 1.
பின்வரும் இயற்பியல் கூற்றுகள் ஒவ்வொன்றையும், வகைக்கெழுச் சமன்பாடாக எழுதுக.
(i) ரேடியம் சிதைவுறும் வீதமானது காணப்படும் அளவு Q-க்கு நேர்விகிதத்தில் இருக்கும்.

(ii) ஒரு நகரத்தின் மக்கள் தொகை P ஆனது. மக்கள் தொகை மற்றும் 5,00,000-க்கும் மக்கள் தொகைக்கும் உள்ள வேறுபாடு ஆகியவற்றை பெருக்கிக் கிடைக்கும் மதிப்புக்கு நேர்விகிதத்தில் அதிகரிக்கிறது.

(iii) ஒரு பொருளின் வெப்பநிலை Tஐப் பொருத்து ஆவி அழுத்தம் P-ன் மாறுவீதமானது, ஆவி அழுத்தத்திற்கு நேர்விகிதத்திலும் ,வெப்பநிலையின் வர்க்கத்திற்கு எதிர்விகிதத்திலும் உள்ளது.

(iv) ஒரு சேமிப்புத் தொகைக்கு ஒரு வருடத்திற்கு வழங்கப்படும் 8% வட்டித் தொகையானது தொடர்ச்சியாக அசலுடன் சேர்க்கப்படுகிறது. மேலும், மற்றொரு முதலீட்டிலிருந்து ஒவ்வொரு ஆண்டும் கிடைக்கும் வரவு ₹400 இத்தொகையுடன் தொடர்ச்சியாக சேர்க்கப்படுகிறது.
தீர்வு:
(i) Q ஆனது ரேடியத்தின் அளவைக் குறிக்கும் என்க.
கொடுக்கப்பட்டது – \(\frac{d \mathrm{Q}}{d t} \alpha \mathrm{Q}\)
\(\frac{d \mathrm{Q}}{d t}\) = kQ இங்கு k ஒரு மாறிலி

(ii) ஒரு நகரத்தின் மக்கள் தொகை P என்க.
கொடுக்கப்பட்டது – \(\frac{d \mathrm{P}}{d t}\) α P(5,00,000 – P)
∵ [P மற்றும் (50,000 – P) இன் பெருக்கல் பலன்]
⇒ \(\frac{d \mathrm{P}}{d t}\) = kP (5,00,000 – P)
இங்கு k ஒரு மாறிலி

(iii) ஆவி அழுத்தத்தை P குறிக்கிறது மற்றும் ஆவி வெப்பத்தை T குறிக்கிறது என்க.
கொடுக்கப்பட்டது –\(\frac{d \mathrm{P}}{d t} \alpha \mathrm{P} \cdot \frac{1}{\mathrm{~T}^{2}}\)
[∴ வெப்பநிலையின் வர்க்கத்திற்கு எதிர்விகிதத்தில் உள்ளது]
⇒ \(\frac{d \mathrm{P}}{d t}=\frac{k \mathrm{P}}{\mathrm{T}^{2}}\) இங்கு k ஒரு மாறிலி.

(iv) x என்பது சேமிப்புக் கணக்கிலுள்ள அசலைக் குறிக்கிறது என்க.
R = 8% மற்றும் N = 1.
∴ வட்டி = \(\frac{\text { PNR }}{100}=\frac{x \times 1 \times 8}{100}=\frac{2 x}{25}\)
கொடுக்கப்பட்டது
\(\frac{d x}{d t}\) = வட்டி +₹400.
∴ \(\frac{d x}{d t}=\frac{2 x}{25}+400\)

கேள்வி 2.
ஒரு கோள வடிவ மழைத்துளியானது அதன் வளைபரப்பின் மாறுவீதத்திற்கு நேர்விகிதத்தில் ஆவியாகிறது. மழைத்துளியின் ஆரத்தின் மாறுவீதத்தை உள்ளடக்கிய வகைக்கெழுச் சமன்பாட்டை உருவாக்குக. –
தீர்வு:
V கோள மழை துளியின் கன அளவு மற்றும் A வளைபரப்பு மற்றும் r ஆரம் என்க
∴ V = \(\frac{4}{3}\) πr² மற்றும்
A = 4πr²
கொடுக்கப்பட்டது
\(\frac{d \mathrm{~V}}{d t}\) = -kA
[∵ மழைத்துளி ஆவியாகிறது]
⇒ \(\frac{d}{d t}\left(\frac{4}{3} \pi r^{3}\right)\) = -k(4πr²)
⇒ \(\frac{4}{3} \pi \cdot \frac{d}{d t}\left(r^{3}\right)\) = -4kπr²
⇒ \(\frac{4}{3}\) ∙ π ∙ 3 ∙ r² \(\frac{d r}{d t}\) = -4 ∙ k ∙ π ∙ r²
⇒ \(\frac{d r}{d t}\) = -k
என்பது தேவையான வகைக்கெழு சமன்பாடு.