Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 1 அணிகள் மற்றும் அணிக்கோவைகளின் பயன்பாடுகள் Ex 1.6 Textbook Questions and Answers, Notes.
TN Board 12th Maths Solutions Chapter 1 அணிகள் மற்றும் அணிக்கோவைகளின் பயன்பாடுகள் Ex 1.6
கேள்வி 1.
பின்வரும் சமன்பாடுகளின் தொகுப்பு ஒருங்கமைவு உடையதா என்பதை ஆராய்க. ஒருங்கமைவு உடையதாயின் அவற்றைத் தீர்க்க. (i) x-y+2z = 2, 2x+y+4z=7, 4x-y+z= 4
(ii) 3x+y+z=2, x-3y+2z = 1, 7x-y+4z = 5
(iii) 2x+2y+z= 5, x-y+z= 1, 3x+y+2z = 4
(iv) 2x-y+z=2,6x-Zy+3z=6,4x-2y+2z=4.
தீர்வு:
(i) x – y + 27= 2, 2x + y + 4x = 7, 4x – y + 7 = 4
சமன்பாட்டு தொகுப்பின் அணி வடிவம் AX =B
இங்கு A = \(\left[\begin{array}{rrr}
1 & -1 & 2 \\
2 & 1 & 4 \\
4 & -1 & 1
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\) மற்றும் B = \(\left[\begin{array}{l}
2 \\
7 \\
4
\end{array}\right]\)
விரிவுபடுத்தப்பட்ட அணியை ஏறுபடி வடிவத்திற்கு உருமாற்றங்கள் செய்யக் கிடைப்பது [A|B],

இங்கு ρ(A) = 3 மற்றும் ρ[A|B] = 3
∴ ρ(A) = ρ[A|B] = 3 = மதிப்பிட வேண்டிய மாறிகளின் எண்ணிக்கை எனவே தொகுப்பு ஒருங்கமைவுடன் ஒரே ஒரு தீர்வை கொண்டிருக்கும்.
ஏறுபடிவடிவத்திலுள்ள அணியிலிருந்து கிடைக்கும் சமான சமன்பாடுகளின் தொகுப்பானது.
x – y + 2z = 2
3y = 3 ⇒ y = 1 ….(2)
-7z = -7 ⇒ z = \(\frac{-7}{-7}\)=1 ….(3)
y = 1 மற்றும் z =1 என (1) ல் பிரதியிட,
x-1 + 2(1) = 2
⇒ x – 1 + 2 = 2
⇒ x + 1 = 2
⇒ x = 2 – 1 = 1
⇒ x= 1, y =1, z = 1
ஆகையால், தீர்வு கணம் {1, 1, 1}.
![]()
(ii) 3x+y+z=2, x-3y +2z =1,7x – y +4z = 5.
தொகுப்பின் அணி வடிவம் AX = B
இங்கு A = \(\left[\begin{array}{rrr}
3 & 1 & 1 \\
1 & -3 & 2 \\
7 & -1 & 4
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\), B = \(\left[\begin{array}{l}
2 \\
1 \\
5
\end{array}\right]\)
(7 -1 4) (z)
விரிவுப்படுத்தப்பட்ட அணி [A|B] யை ஏறுபடி வடிவத்திற்கு உருமாற்றங்கள் செய்யக் கிடைப்பது,

இங்கு ρ(A) = 2, மற்றும் p[A|B] =2 [∵ 2 அபூச்சிய நிரைகள் உள்ள ன). ஆகையால், p(A) = p[A|B] =2 < 3, கொடுக்கப்பட்ட தொகுப்பு ஒருங்கமைவுடன் தீர்வுகள் ஒரு சாராமாறிக் குடும்பமாக இருக்கும். ஆகையால் z = 1, x ∈ ℝ. ஏறுபடி வடிவத்திலுள்ள அணியிலிருந்து கிடைக்கும் சமான சமன்பாடு களின் தொகுப்பு,
x-3y + 2z = 1 …. (1)
10y – 5z = -1…. (2)
z = t ….(3)
(2) லிருந்து 10y- 5t =-1
⇒ 10y = 5t-1
⇒ y = \(\frac{1}{10}\)[5t – 1]
மேலும், (1) லிருந்து, x – \(\frac{3}{10}\)[5t – 1] + 2t = 1
⇒ x = \(\frac{3}{10}\)[5t – 1] – 2t + 1 = \(\frac{15 t-3-20 t+10}{10}\)
⇒ x = \(\frac{1}{10}\)[-5t + 7]
எனவே தீர்வு கணம் என்பது
{ \(\frac{1}{10}\)(7 – 5t), \(\frac{1}{10}\)(5t – 1, t)} இங்கு t ∈ℝ.
![]()
(iii) 2x+2y+7= 5, x-y+7 = 1, 3x+y+2z = 4
ஆகையால் தொகுப்பின் அணி AX = B இங்கு
A = \(\left[\begin{array}{ccc}
2 & 2 & 1 \\
1 & -1 & 1 \\
3 & 1 & 2
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\), B = \(\left[\begin{array}{l}
5 \\
1 \\
4
\end{array}\right]\)
விரிவுபடுத்தப்பட்ட அணி [A|B] யை ஏறுபடி வடிவத்திற்கு உருமாற்றங்கள் செய்யக் கிடைப்பது,
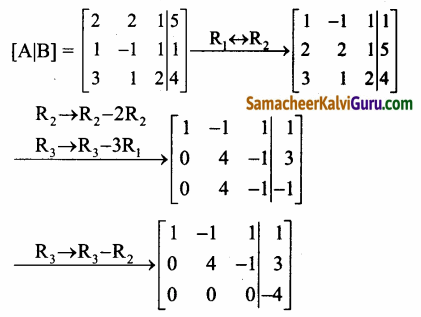
இங்கு ρ(A)=2 [∵ 2 அபூச்சிய நிரைகள் உள்ளன]
மற்றும் p[A|B] =3 [∵ 3 அபூச்சிய நிரைகள் உள்ளன]
இங்கு (A) ≠ p[A|B]
ஆகையால், கொடுக்கப்பட்ட தொகுப்பு ஒருங்கமைவு அற்றது மற்றும் தீர்வுகள் இல்லை.
(iv) 2x – y +7 = 2, 6x – 3y +3z = 6,
4x-2y+2z = 4.
தொகுப்பின் அணி வடிவம் AX = B இங்கு
A = \(\left[\begin{array}{rrr}
2 & -1 & 1 \\
6 & -3 & 3 \\
4 & -2 & 2
\end{array}\right]\),
X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\), B = \(\left[\begin{array}{l}
2 \\
6 \\
4
\end{array}\right]\)
[A|B] என்ற விரிவுபடுத்தப்பட்ட அணியில் தொடக்கநிலை நிரைச் செயலிகள் பயன்படுத்தக் கிடைப்பது,

இங்கு p(A) = 1[∵ ஒரே ஒரு அபூச்சிய நிரை]
மற்றும் p[A|B] =1[∵ ஒரே ஒரு அபூச்சிய நிரை]
∴ ρ(A) = ρ[A|B] = 1 < 3, கொடுக்கப்பட்ட தொகுப்பு ஒருங்கமைவுடன் இரு சாராமாறிக் குடும்பமாக தீர்வுகள் இருக்கும்.
ஆகையால், z = t மற்றும் y=s இங்கு s, t ∈R. ஏறுபடி வடிவத்திலிருந்து கிடைக்கும் சமான சமன்பாடுகள்
2x-y+z = 2 …. (1)
y = s …. (2)
z = t …. (3)
(2) மற்றும் (3) ஐ (1)ல் பிரதியிட கிடைப்பது,
2x – s + 1 = 2
⇒ 2x = s – t + 2
x= \(\frac { 1 }{ 2 }\)[s-t+2]
∴ தீர்வு கணம் {\(\frac { 1 }{ 2 }\)(s-t+2), s, t} இங்கு s, t ∈ ℝ
![]()
கேள்வி 2.
k-ன் எம்மதிப்புகளுக்கு பின்வரும் சமன்பாட்டுத் தொகுப்பு kx-2y+z = 1, x- 2ky+z=-2, x-2y+kz=1;
(i) யாதொரு தீர்வும் பெற்றிராது
(ii) ஒரே ஒரு தீர்வைப் பெற்றிருக்கும்
(iii) எண்ணிக்கையற்ற தீர்வுகளைப் பெற்றிருக்கும் என்பதனை ஆராய்க
தீர்வு:
kx-2y+z = 1,x-2ky + z =-2, x – 2y+k = 1
சமன்பாட்டு தொகுப்பின் அணி வடிவம் AX = B இங்கு
A = \(\left[\begin{array}{rrr}
k & -2 & 1 \\
1 & -2 k & 1 \\
1 & -2 & k
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\), B = \(\left[\begin{array}{l}
1 \\
-2 \\
1
\end{array}\right]\)
[A|B] என்ற விரிவுபடுத்தப்பட்ட அணியில் தொடக்கநிலை நிரை செயலிகள் பயன்படுத்தக் கிடைப்பது,
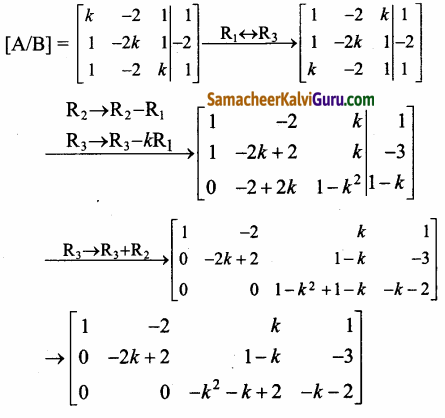
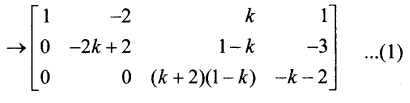
நிலை (i) k = 1 எனில்
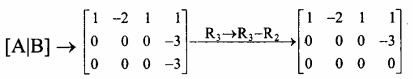
இங்கு ρ(A) = 1 மற்றும் ρ[A|B] = 2
ஆகையால், ρ(A) ≠ ρ[A|B] ⇒ தொகுப்புற்கு தீர்வு இல்லை.
நிலை (ii) k≠1, k≠-2 எனில்

⇒ ρ(A) = 3 மற்றும் ρ[A|B] = 3
ஆகையால், ρ(A) = ρ[A|B] = 3 = மதிப்பிட
வேண்டிய மாறிகளின் எண்ணிக்கை
ஆகையால், தொகுப்புக்கு ஒரே ஒரு தீர்வு உண்டு.
நிலை (iii) k =-2 எனில்

இங்கு ρ(A) = 2 மற்றும் ρ[A|B] = 2
∴ ρ(A) = ρ[A|B] = 2 < 3, மதிப்பிட வேண்டிய மாறிகளின் எண்ணிக்கை. ஆகையால் தொகுப்பு ஒருங்கமைவுடன் எண்ணிக்கையற்ற தீர்வுகளை கொண்டிருக்கும்.
![]()
கேள்வி 3.
λ, μ-இன் எம்மதிப்புகளுக்கு 2x + 3y + 5z = 9, 7x + 3y – 5z = 8, 2x + 3y + λz = μ, என்ற சமன்பாடுகளின் தொகுப்பானது.
(i) யாதொரு தீர்வும் பெற்றிராது
(ii) ஒரே ஒரு தீர்வைப் பெற்றிருக்கும்
(iii) எண்ணிக்கையற்ற தீர்வுகளைப் பெற்றிருக்கும் என்பதனை ஆராய்க.
தீர்வு:
2x + 3y=9,7x + 3y – 5z = 8, 2x + 3y + λz = μ
சமன்பாட்டு தொகுப்பின் அணி வடிவம் AX = B இங்கு
A = \(\left[\begin{array}{rrr}
2 & 3 & 5 \\
7 & 3 & -5 \\
2 & 3 & \lambda
\end{array}\right]\), X = \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]\), B = \(\left[\begin{array}{l}
9 \\
8 \\
\mu
\end{array}\right]\)
[A|B] என்ற விரிவுபடுத்தப்பட்ட அணியில் தொடக்கநிலை நிரைச் செயலிகள் பயன்படுத்தக் கிடைப்பது,

இங்கு ρ(A) = 2 மற்றும் ρ[A|B] = 3
ஆகையால், ρ(A) ≠ ρ[A|B]
ஆகையால் தொகுப்பு ஒருங்கமைவு அற்றது மற்றும் தீர்வு இல்லை.
நிலை (ii) λ ≠ 5, μ ≠ 9 எனில்

∴ ρ(A) = ρ[A|B] = 3 = மதிப்பிட வேண்டிய மாறிகளின் எண்ணிக்கை ஆகையால் தொகுப்பு ஒருங்கமைவுடன் ஒரே ஒரு தீர்வை கொண்டிருக்கும். நிலை (iii) λ = 5 மற்றும் μ = 9 எனில்
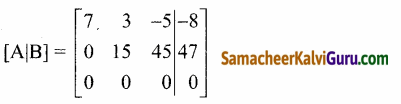
இங்கு ρ(A) =2, ρ[A|B] = 2
∴ ρ(A) = [A|B] = 2 < மதிப்பிட வேண்டிய மாறிகளின் எண்ணிக்கை
∴ தொகுப்பு ஒருங்கமைவுடன் மற்றும் எண்ணிக்கையற்ற தீர்வுகளை கொண்டிருக்கும்.