Samacheer Kalvi 12th Maths Guide Chapter 1 அணிகள் மற்றும் அணிக்கோவைகளின் பயன்பாடுகள் Ex 1.7

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 1 அணிகள் மற்றும் அணிக்கோவைகளின் பயன்பாடுகள் Ex 1.7 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 1 அணிகள் மற்றும் அணிக்கோவைகளின் பயன்பாடுகள் Ex 1.7

கேள்வி 1.
பின்வரும் சமப்படித்தான நேரியச் சமன்பாட்டுத் தொகுப்பைத் தீர்க்கவும்.

(i) 3x+2y +73 = 0, 4x-3y-2z = 0,
5x+9y+23z=0
(ii) 2x+3y-z=0, x-y-2z = 0, 3x+y+3z = 0.
தீர்வு:
(i) 3x+2y+7z = 0, 4x-3y-2x = 0,
5x+9y+23z =0
விரிவுபடுத்தப்பட்ட அணியில் தொடக்கநிலை நிரை செயலிகள் பயன்படுத்தக் கிடைப்பது,
[A|0] =


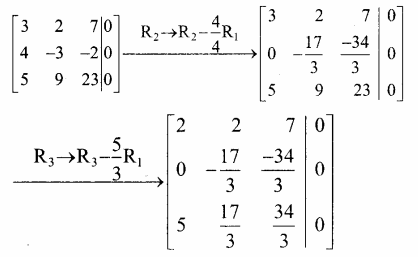
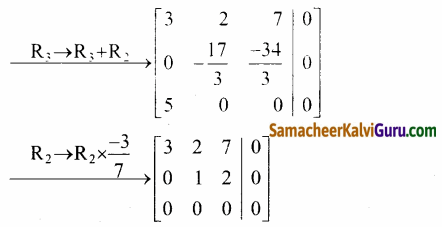
இங்கு ρ(A) = 2 மற்றும் ρ[A|0] = 2
ஆகையால், ρ(A) = ρ([A|0]) = 2 < 3 = மதிப்பிட வேண்டிய மாறிகளின் எண்ணிக்கை
இங்கு, தொகுப்பு ஒருங்கமைவுடன் ஒரு சாராமாறிக்
குடும்பமாக தீர்வுகளை கொண்டிருக்கும்.
ஆகையால் z = t என பிரதியிடு இங்கு t ∈ ℝ.
ஏறுபடி வடிவத்திலிருந்து சமன்பாடுகளை எழுத கிடைப்பது
3x + 2y +7z = 0 …. (1)
y+2z = 0 …(2)
z = t, என பிரதியிடு (2) லிருந்து
y+ 2t = 0
⇒ y = -2t
∴ (1) லிருந்து , 3x + 2 (-2t) + 71 = 0
⇒ 3x – 4t + 7t = 0
⇒ 3x + 3t = 0
⇒ 3x = -3t
⇒ x = -t
∴ தீர்வு கணம் {-t, -2t, t} இங்கு t ∈ ℝ

(ii) 2x+3y-z=0, x-y-2z = 0, 3x+y+3z = 0.
விரிவுபடுத்தப்பட்ட அணியில் தொடக்கநிலை நிரை செயலிகள் பயன்படுத்தக் கிடைப்பது

இங்கு ρ(A) = 3 மற்றும் ρ([A|0]) = 3
ρ(A) = ρ[[A|0]) = 3 = மதிப்பிட வேண்டிய மாறிகளின் எண்ணிக்கை
ஆகையால் தொகுப்பு ஒருங்கமைவுடன் ஒரே ஒரு தீர்வை கொண்டிருக்கும்.
ஆகையால் தொகுப்பு வெளிப்படை தீர்வை மட்டும் கொண்டிருக்கும்.

கேள்வி 2.
λ -வின் எம்மதிப்பிற்கு
x + y + 3z = 0, 4x + 3y + λz = 0, 2x + y + 2z =0 என்ற தொகுப்பிற்கு
(i) வெளிப்படைத் தீர்வு
(ii) வெளிப்படையற்ற தீர்வு கிடைக்கும்
தீர்வு:
x+y+ 3z = 0, 4x+3y +λz = 0, 2x+y+2z=0
விரிவுப்படுத்தப்பட்ட அணியை ஏறுபடி வடிவத்திற்கு மாற்ற கிடைப்பது,


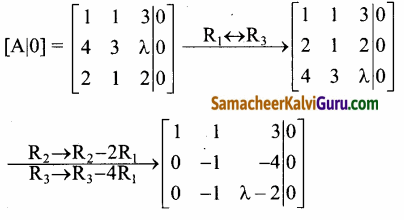
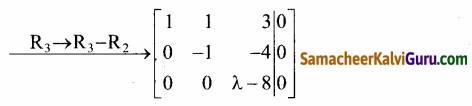
நிலை (i) 1 ≠ 8 எனில்

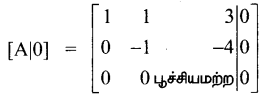
இங்கு ρ(A) = 3,ρ([A/O]) = 3
∴ ρ(A) = ρ[[A/0]) = 3 = மதிப்பிட வேண்டிய மாறிகளின் எண்ணிக்கை
∴ கொடுக்கப்பட்ட தொகுப்பு ஒருங்கமைவுடன் ஒரே ஒரு தீர்வை கொண்டிருக்கும். நிலை (ii) λ = 8 எனில்

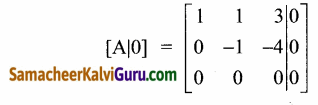
இங்கு ρ(A) = 2, ρ([A|0]) = 2
∴ ρ(A) = ρ[[A|0]) = 2 < 3, மதிப்பிட வேண்டிய மாறிகளின் எண்ணிக்கை,
∴ தொகுப்பு ஒருங்கமைவுடன் வெளிப்படையற்ற தீர்வுகளை உடையது.

கேள்வி 3.
காஸ்ஸியன் நீக்கல் முறையைப் பயன்படுத்தி :
C₂H₆ + O₂ → H₂ O + CO₂, என்ற வேதியியல் எதிர்வினைச்சமன்பாட்டை சமநிலைப்பலைப் படுத்துக.
தீர்வு:
கொடுக்கப்பட்ட C₂ H₆ + O₂ → H₂O + CO₂
நாம் மிகை எண்கள் , x₁, x₂, x₃, மற்றும் x₄ இவ்வாறு காண வேண்டும்.
x₁, C₂, H₆, + x₂ O₂ → x₃ H₂O +x₄ CO₂ ….(1)
(1) ல் இடது பக்கத்தில் உள்ள கார்பன் அணுக் களின் எண்ணிக்கை வலது பக்கத்தில் உள்ள கார்பன் அணுக்களின் எண்ணிக்கைக்கு சமமாக இருக்க வேண்டும்.
∴ 2x₁ = 1x₄
⇒ 2x₁ – x₄ = 0 …. (2)
ஹைட்ரஜன் அணுக்களால் கிடைப்பது,
6x₁ = 2x₃
⇒ 6x₁ – 2x₃ = 0
⇒ 3x₁ – x₃ = 0 ….. (3)
மேலும், ஆக்ஸிஜன் அணுக்களால் கிடைப்பது,
2x₂ = 1x₃ +2x₄
⇒ 2x₂ – x₃ – 2x₄ = 0 …. (4)
4 மாறிகளில் அமைந்த நேரியில் சமபடித்தான தொகுப்பு சமன்பாடுகள் (2), (3) மற்றும் (4)
∴ விரிவுபடுத்தப்பட்ட அணி [A|0]
\(\left[\begin{array}{rrrr|r}
2 & 0 & 0 & -1 & 0 \\
3 & 0 & -1 & 0 & 0 \\
0 & 2 & -1 & -2 & 0
\end{array}\right]\)
காஸ்ஸியன் நீக்கல் முறை மூலம் கிடைப்பது,


இங்கு ρ(A)=ρ([A|B])=3<4, மதிப்பிட வேண்டிய மாறிகளின் எண்ணிக்கை.
∴ தொகுப்பு ஒருங்கமைவுடன் ஒரு சாராமாறிக் குடும்ப தீர்வுகளை கொண்டிருக்கும், ஆகையால் x⁴ = t என்க. ஏறுபடிவத்திலிருந்து சமன்பாடுகளை எழுத கிடைப்பது
2x₁ – x₄ = 0
⇒ 2x₁ = x₄
⇒ 2x = t
⇒ x₁ = \(\frac{t}{2}\)
4x₂ – 7x₄ = 0
⇒ 4x₂ = 7t ⇒ x₂ = \(\frac{7t}{4}\)
-2x₃ + 3x₄ = 0 ⇒ 2x₃ = 3x₄
⇒ x₃ = \(\frac{3t}{2}\)
x₁, x₂, x₃, மற்றும் x₄, மிகை முழுக்கள், ஆதலால், t = 4 என தேர்ந்தெடுக்க

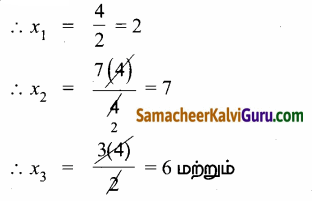
x₄ = t = 4
ஆகையால் சமநிலைப்படுத்தப்பட்ட சமன்பாடு
2 C₂H₆ +7O₂ → 6H₂O + 4CO₂