Samacheer Kalvi 12th Maths Guide Chapter 1 அணிகள் மற்றும் அணிக்கோவைகளின் பயன்பாடுகள் Ex 1.8

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 1 அணிகள் மற்றும் அணிக்கோவைகளின் பயன்பாடுகள் Ex 1.8 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 1 அணிகள் மற்றும் அணிக்கோவைகளின் பயன்பாடுகள் Ex 1.8

கொடுக்கப்பட்ட நான்கு விடைகளிலிருந்து சரியான அல்லது மிகப் பொருத்தமான விடையைத் தேர்ந்தெடுக்க.

கேள்வி 1.
|adj (adjA) |=|A|⁹, எனில், சதுர அணி A -யின் வரிசையானது
(1) 3
(2) 4
(3) 2
(4) 5
விடை:
(2) 4
குறிப்பு:
adj (adj)AI = |A|^(n-1)2
∴ (n-1)² = 9
⇒ (n-1)² = 3² ⇒ n-1 = 3
⇒ n = 4

கேள்வி 2.
A என்ற 3 x 3 பூச்சியமற்றக் கோவை அணிக்கு AA^T = A^T A மற்றும் B = A^-1A^T, என்றவாறு இருப்பின் BB^T=
(1) A
(2) B
(3) I₃
(4) B^T
விடை:
(3) I₃
குறிப்பு:
BB^T = (A^-1A^T)(A^-1A^T)^T
= (A^-1A^T) (A^T)^T – (A^-1)^T
= (A^-1A^T) (AA^-1)^T
= A^-1(A.A^T)(A^-1)^T
= (A^-1A). A^T (A^T)^-1
[∵ (A^-1)^T = (A^T)^-1]
[∵ A^T-(A^T)^-1 = I]
= I.I = I

கேள்வி 3.
A = \(\left[\begin{array}{ll}
3 & 5 \\
1 & 2
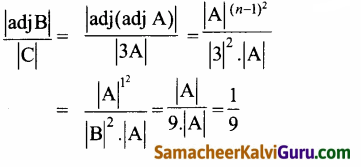
\end{array}\right]\), B = adj A மற்றும் C = 3A எனில், \(\frac{|\mathbf{a d j} \mathbf{B}|}{|\mathbf{C}|}\) =
(1) \(\frac{1}{3}\)
(2) \(\frac{1}{9}\)
(3) \(\frac{1}{4}\)
(4) 1
விடை:
(2) \(\frac{1}{9}\)
குறிப்பு:

கேள்வி 4.


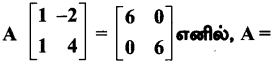
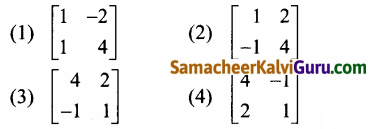
விடை:
(3) \(\left[\begin{array}{rr}
4 & 2 \\
-1 & 1
\end{array}\right]\)
குறிப்பு:

கேள்வி 5.

(1) A^-1
(2) \(\frac{\mathrm{A}^{-1}}{2}\)
(3) 3A^-1
(4) 2A^-1
விடை:
(4) 2A^-1
குறிப்பு:
9I-A = \(\left[\begin{array}{ll}
9 & 0 \\
0 & 9
\end{array}\right]\)–\(\left[\begin{array}{ll}
7 & 3 \\
4 & 2
\end{array}\right]\)
\(\left[\begin{array}{ll}
9-7 & 0-3 \\
0-4 & 9-2
\end{array}\right]\) = \(\left[\begin{array}{rr}
2 & -3 \\
-4 & 7
\end{array}\right]\) = adj A
ஆனால் A^-1 = \(\frac{1}{|\mathrm{~A}|}\) adj A = \(\frac{1}{2}\) ⇒ adj A = 2A^-1

கேள்வி 6.
A = \(\left[\begin{array}{ll}
2 & 0 \\
1 & 5
\end{array}\right]\) மற்றும் B = \(\left[\begin{array}{ll}
1 & 4 \\
2 & 0
\end{array}\right]\) கொலை, |adj (AB)| =
(1) -40
(2) -80
(3) -60
(4) -20
விடை:
(2) -80
குறிப்பு:

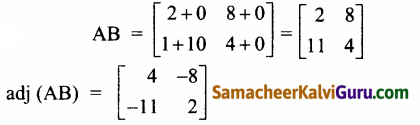
|adj (AB)| = 8 – 88 = -80

கேள்வி 7.
P = \(\left|\begin{array}{rrr}
1 & x & 0 \\
1 & 3 & 0 \\
2 & 4 & -2
\end{array}\right|\) என்பது 3 × 3 வரிசையுடைய அணி A -ன் சேர்ப்பு அணி மற்றும் |A| = 4, எனில், x ஆனது
(1) 15
(2) 12
(3) 14
(4) 11
விடை:
(4) 11
குறிப்பு :
|adj A| = |A|^n-1

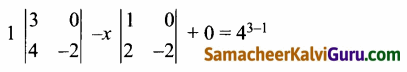
⇒ -6-x (-2) = 4² ⇒ -6 + 2x = 16
⇒ 2x = 22 ⇒ x = 11

கேள்வி 8.
A= \(\left[\begin{array}{rrr}
3 & 1 & -1 \\
2 & -2 & 0 \\
1 & 2 & -1
\end{array}\right]\) மற்றும் A^-1= \(\left[\begin{array}{lll}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{array}\right]\) எனில், a₂₃ – ன் மதிப்பானது
(1) 0
(2) -2
(3) -3
(4) -1
விடை:
(4) -1
குறிப்பு:

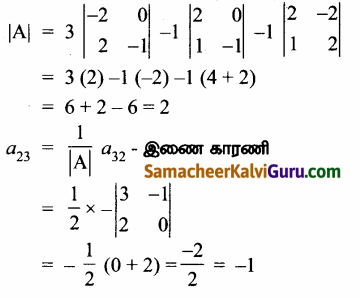
கேள்வி 9.
A, B மற்றும் C என்பன நேர்மாறு காணத்தக்கவாறு ஏதேனுமொரு வரிசையில் இருப்பின் பின்வருவனவற்றில் எது ! உண்மையல்ல?
(1) adj A= |A|A^-1
(2) adj (AB) = (adj A) (adj B)
(3) det A^-1 = (det A)^-1
(4) (ABC)^-1 = C^-1 B^-1 A^-1
விடை:
(2) adj (AB) = (adj A) (adj B)

கேள்வி 10.
(AB)^-1 = \(\left[\begin{array}{rr}
12 & -17 \\
-19 & 27
\end{array}\right]\) மற்றும் \(\left[\begin{array}{rr}
1 & -1 \\
-2 & 3
\end{array}\right]\) எனில், B^-1=

விடை:
(1) \(\left[\begin{array}{rr}
2 & -5 \\
-3 & 8
\end{array}\right]\)
குறிப்பு:
(AB)^-1 = B^-1A^-1 ஆதலால் கிடைப்பது
\(\left[\begin{array}{rr}
12 & -17 \\
-19 & 27
\end{array}\right]\) = B^-1\(\left[\begin{array}{rr}
1 & -1 \\
-2 & 3
\end{array}\right]\)
X = B^-1Y என்க.

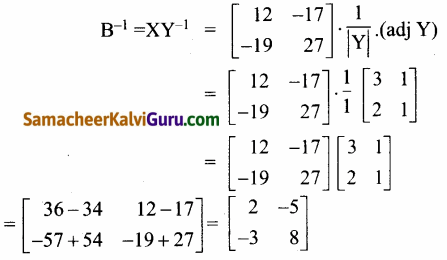
கேள்வி 11.
A^TA^-1, ஆனது சமச்சீர் எனில், A² =
(1) A^-1
(2) (A^T)^-1
(3) A^T
(4) (A^-1)²
விடை:
(2) (A^T)²
குறிப்பு:
⇒ A^TA^-1 = (A^TA^-1)^T
⇒ (A^-1)^T (A^T)^T = (A^-1)^TA
⇒ A = A^T ⇒ A சமச்சீர் அணி
∴ A² = (A^T)²

கேள்வி 12.
A என்பது பூச்சியமற்றக் கோவை அணி மற்றும்
A^-1 = \(\left[\begin{array}{rr}
5 & 3 \\
-2 & -1
\end{array}\right]\) எனில், (A^T)^-1 =
(1) \(\left[\begin{array}{rr}
-5 & 3 \\
2 & 1
\end{array}\right]\)
(2) \(\left[\begin{array}{rr}
5 & 3 \\
-2 & -1
\end{array}\right]\)
(3) \(\left[\begin{array}{rr}
-1 & -3 \\
2 & 5
\end{array}\right]\)
(4) \(\left[\begin{array}{ll}
5 & -2 \\
3 & -1
\end{array}\right]\)
விடை:
(4) \(\left[\begin{array}{ll}
5 & -2 \\
3 & -1
\end{array}\right]\)
குறிப்பு:
(A^T)^-1 = (A^-1)^T= \(\left[\begin{array}{ll}
5 & -2 \\
3 & -1
\end{array}\right]\)

கேள்வி 13.
A = \(\left[\begin{array}{ll}
\frac{3}{5} & \frac{4}{5} \\
x & \frac{3}{5}
\end{array}\right]\) மற்றும் A^T = A^-1 எனில், x -ன் மதிப்பு
(1) \(\frac{-4}{5}\)
(2) \(\frac{-3}{5}\)
(3) \(\frac{3}{5}\)
(4) \(\frac{4}{5}\)
விடை:
(1) \(\frac{-4}{5}\)
குறிப்பு:
A^T = A^-1, AA^T = A^T A = 1
[∵ அவைகள் செங்குத்து]

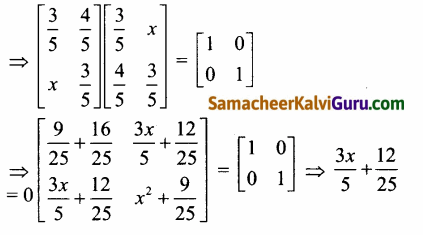
[இருபுறமும் a, ஐ ஒப்பிட கிடைப்பது]
⇒ \(\frac{3x}{5}\) = \(\frac{-12}{25}\) × \(\frac{5}{3}\) = –\(\frac{4}{5}\)

கேள்வி 14.
A = \(\left[\begin{array}{rr}
1 & \tan \frac{\theta}{2} \\
-\tan \frac{\theta}{2} & 1
\end{array}\right]\) மற்றும் AB=I₂ எனில், B =

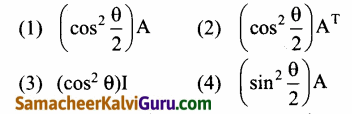
விடை:
(2) \(\left(\cos ^{2} \frac{\theta}{2}\right)\)A^T
குறிப்பு:

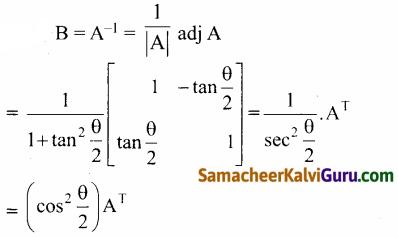
கேள்வி 15.
A= \(\left[\begin{array}{rr}
\cos \theta & \sin \theta \\
-\sin \theta & \cos \theta
\end{array}\right]\) மற்றும் A(adj A) = \(\left[\begin{array}{ll}
\boldsymbol{k} & \mathbf{0} \\
\mathbf{0} & \boldsymbol{k}
\end{array}\right]\) எனில், k =
(1) 0
(2) sin θ
(3) cos θ
(4) 1
விடை:
(4) 1
குறிப்பு:
A (adj A) = (adj A)A = |A| I என அறிவோம்
⇒ |A|=K
∴ K= \(\left|\begin{array}{rr}
\cos \theta & \sin \theta \\
-\sin \theta & \cos \theta
\end{array}\right|\) = cos²θ + sin²θ = 1

கேள்வி 16.
A = \(\left[\begin{array}{rr}
2 & 3 \\
5 & -2
\end{array}\right]\) மற்றும் λA^-1 = A எனில், λ – ன் மதிப்பு
(1) 17
(2) 14
(3) 19
(4) 21
விடை:
(3) 19
குறிப்பு :

கேள்வி 17.

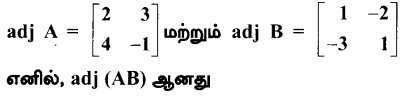
(1) \(\left[\begin{array}{rr}
-7 & -1 \\
7 & -9
\end{array}\right]\)
(2) \(\left[\begin{array}{rr}
-6 & 5 \\
-2 & -10
\end{array}\right]\)
(3) \(\left[\begin{array}{rr}
-7 & 7 \\
-1 & -9
\end{array}\right]\)
(4) \(\left[\begin{array}{rr}
-6 & -2 \\
5 & -10
\end{array}\right]\)
விடை:
(2) \(\left[\begin{array}{rr}
-6 & 5 \\
-2 & -10
\end{array}\right]\)
குறிப்பு:
adj (AB) = (adj B) (adj A)

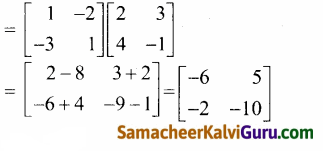
கேள்வி 18.
\(\left[\begin{array}{rrrr}
1 & 2 & 3 & 4 \\
2 & 4 & 6 & 8 \\
-1 & -2 & -3 & -4
\end{array}\right]\) ன் அணித்தரம்
(1) 1
(2) 2
(3) 4
(4) 3
விடை:
(1) 1
குறிப்பு:

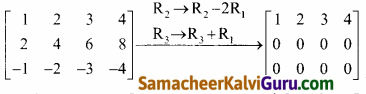
∴ தரமானது 1 [∵ ஒரே ஒரு அபூச்சிய நிரை]

கேள்வி 19.
x^a y^b = e^m, △₁ = \(\left[\begin{array}{cc}
m & b \\
n & d
\end{array}\right]\), △₂ = \(\left[\begin{array}{ll}
a & m \\
c & n
\end{array}\right]\), △₃ = \(\left|\begin{array}{ll}
a & b \\
c & d
\end{array}\right|\) எனில், x மற்றும் y -ன் மதிப்புகள் முறையே.

விடை:
(4)
குறிப்பு :

கேள்வி 20.
பின்வருபனவற்றுள் எவை/எவைகள் உண்மை யானவை?
(i) ஒரு சமச்சீர் அணியின் சேர்ப்பு அணி சமச்சீராக இருக்கும்.
(ii) ஒரு மூலைவிட்ட அணியின் சேர்ப்பு அணி மூலை விட்ட அணியாக இருக்கும்.
(iii) A என்பது n வரிசையுடைய ஒரு சதுர அணி மற்றும் λ என்பது ஒரு திசையிலி எனில் adj (λA) = λ” adj (A).
(iv) A(adjA) = (adj A) A = |A|I
(1) (i) மட்டும்
(2) (ii) மற்றும் (iii)
(3) (iii) மற்றும் (iv)
(4) (i), (ii) மற்றும் (iv)
விடை:
(4) (i) (ii) மற்றும் (iv)

கேள்வி 21.
ρ(A) = ρ([A|B|) எனில், AX = B என்ற நேரியச் சமன்பாடுகளின் தொகுப்பானது
(1) ஒருங்கமைவுடையது மற்றும் ஒரே ஒரு தீர்வு பெற்றிருக்கும்
(2) ஒருங்கமைவுடையது
(3) ஒருங்கமைவுடையது மற்றும் எண்ணற்ற தீர்வுகள் பெற்றிருக்கும்
(4) ஒருங்கமைவற்றது
விடை:
(2) ஒருங்கமைவுடையது

கேள்வி 22.
0 < θ ≤ π மற்றும் x + (sin θ)y – (cos θ)z = 0, (cos θ)x – y + z = 0, (sin θ)x + y – z = 0 மற்றும் தொகுப்பானது வெளிப்படையற்றத் தீர்வு பெற்றிருப்பின், θ-ன் மதிப்பு
(1) \(\frac{2 \pi}{3}\)
(2) \(\frac{3 \pi}{4}\)
(3) \(\frac{5 \pi}{6}\)
(4) \(\frac{\pi}{4}\)
விடை:
(4) \(\frac{\pi}{4}\)
குறிப்பு:

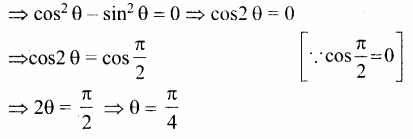
கேள்வி 23.
ஒரு நேரியச் சமன்பாட்டுத் தொகுப்பின் விரிவுப்படுத்தப்பட்டஅணியானது \(\left[\begin{array}{rrrr}
1 & 2 & 7 & 3 \\
0 & 1 & 4 & 6 \\
0 & 0 & \lambda-7 & \mu+5
\end{array}\right]\) மற்றும் தொகுப்பானது எண்ணற்ற தீர்வுகள் பெற்றிருக்கும் எனில்,
(1) λ =7, μ ≠ -5
(2) λ = -7, μ = 5
(3) λ ≠ 7, μ ≠ -5
(4) λ =7, μ = -5
விடை:
(4) λ =7, μ = -5
குறிப்பு:
λ = 7 மற்றும் μ ≠ -5 எனில்,
[A|B] = \(\left[\begin{array}{llll}
1 & 2 & 7 & 3 \\
0 & 1 & 4 & 6 \\
0 & 0 & 0 & 0
\end{array}\right]\)
ρ(A) = ρ([A|B]) = 2 <3, மதிப்பிட வேண்டிய மாறிகளின் எண்ணிக்கை
∴ தொகுப்பு ஒருங்கமைவு உடையது மற்றும் எண்ணிக்கையற்ற தீர்வுகளை கொண்டிருக்கும்.

கேள்வி 24.
A= \(\left[\begin{array}{rrr}
2 & -1 & 1 \\
-1 & 2 & -1 \\
1 & -1 & 2
\end{array}\right]\) மற்றும் 4B = \(\left[\begin{array}{rrr}
3 & 1 & -1 \\
1 & 3 & x \\
-1 & 1 & 3
\end{array}\right]\) என்க. A-ன் நேர்மாறு B எனில், x -ன் மதிப்பு
(1) 2
(2) 4
(3) 3
(4) 1
விடை:
(4) 1
குறிப்பு:
A =B^-1 ⇒ A . B = B^-1.B ⇒ AB =I

கேள்வி 25.

(1) \(\left[\begin{array}{rrr}
3 & -3 & 4 \\
2 & -3 & 4 \\
0 & -1 & 1
\end{array}\right]\)
(2) \(\left[\begin{array}{lll}
6 & -6 & 8 \\
4 & -6 & 8 \\
0 & -2 & 2
\end{array}\right]\)
(3) \(\left[\begin{array}{rrr}
-3 & 3 & -4 \\
-2 & 3 & -4 \\
0 & 1 & -1
\end{array}\right]\)
(4) \(\left[\begin{array}{rrr}
3 & -3 & 4 \\
0 & -1 & 1 \\
2 & -3 & 4
\end{array}\right]\)
விடை:
(1) \(\left[\begin{array}{ccc}
3 & -3 & 4 \\
2 & -3 & 4 \\
0 & -1 & 1
\end{array}\right]\)
குறிப்பு: