Samacheer Kalvi 12th Maths Guide Chapter 10 சாதாரண வகைக்கெழுச் சமன்பாடுகள் Ex 10.3

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 10 சாதாரண வகைக்கெழுச் சமன்பாடுகள் Ex 10.3 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 10 சாதாரண வகைக்கெழுச் சமன்பாடுகள் Ex 10.3

கேள்வி 1.
ஒரு தளத்தில்
(i) நேர்க்குத்து அல்லாத நேர்க்கோடுகள்
(ii) கிடைமட்டம் அல்லாத நேர்க்கோடுகள் ஆகிய தொகுப்புகளின் வகைக்கெழுச் சமன்பாடுகளைக் காண்க.
தீர்வு:
(i) ஒருதளத்தில் நேர்க்குத்து அல்லாத நேர்க்கோடுகள் குடும்பத்தின் சமன்பாடு ax + by = 1, b ≠ 0, a ∈ ℝ.
‘X’-ஐப் பொறுத்து வகையிட கிடைப்பது,
a + b\(\frac{d y}{d x}\) = 0
‘X’-ஐப் பொறுத்து மீண்டும் வகையிட கிடைப்பது,
\(b \frac{d^{2} y}{d x^{2}}\) = 0 ⇒ \(\frac{d^{2} y}{d x^{2}}\) = 0 [∵ b ≠ 0]

(ii) ஒரு தளத்தில் கிடைமட்டம் அல்லாத நேர்க்கோடுகள் குடும்பத்தின் சமன்பாடு ax + by = 1, a # 0, மற்றும் b ∈ ℝ.
‘y’-ஐப் பொறுத்து வகையிட கிடைப்பது,
a\(\frac{d x}{d y}\) + b = 0
மீண்டும் ‘y’-ஐப் பொறுத்து வகையிட கிடைப்பது,
a\(\frac{d^{2} x}{d y^{2}}\) = 0 ⇒ \(\frac{d^{2} x}{d y^{2}}\) = 0 [∵ a ≠ 0]

கேள்வி 2.
x² + y² = r² எனும் வட்டத்தைத் தொடும் எல்லா நேர்க்கோடுகளின் வகைக்கெழுச் சமன்பாட்டைக் காண்க.
தீர்வு:
x² + y² = r² வட்டத்தை தொடுகின்ற கோடுகளின் குடும்பத்தின் சமன்பாடு y = mx + c என்க…………(1)
x² y² = r² என்ற வட்டத்திற்கு y = mx + c என்ற தொடுகோடாக இருக்க நிபந்தனை c² = r² (1 + m²)
c = \(r \sqrt{1+m^{2}}\) …… (2)
சமன்பாடு (2) ஐ (1)ல் பிரதியிட கிடைப்பது,
y = mx + \(r \sqrt{1+m^{2}}\)
⇒ y – mx = \(r \sqrt{1+m^{2}}\) …….. (3)
(2) லிருந்து, \(\frac{d y}{d x}\) = m …….. (4)
(4) ஐ (3) ல் பிரதியிட கிடைப்பது,
\(y-x\left(\frac{d y}{d x}\right)=r \sqrt{1+\left(\frac{d y}{d x}\right)^{2}}\)
இருபுறமும் வர்க்கப்படுத்த கிடைப்பது,
\(\Rightarrow\left[y-x\left(\frac{d y}{d x}\right)\right]^{2}=r^{2}\left[1+\left(\frac{d y}{d x}\right)^{2}\right]\)

கேள்வி 3.
ஆதிப்புள்ளி வழியாகச் செல்லும், மையத்தினை x-அச்சின் மீது கொண்ட எல்லா வட்டங்களின் வகைக்கெழுச் சமன்பாட்டைக் காண்க.
தீர்வு:
மையத்தினை x- அச்சின் மீது கொண்டுள்ளதால்,
(g, 0) மற்றும் ஆரம் g என்க.

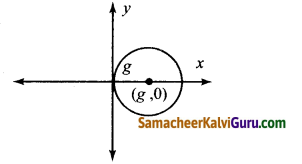
வட்டத்தின் சமன்பாடு
(x – y)² + (y – 0)² = g²
⇒ x² – 2xg + g² + y² = g²
⇒ x² – 2xg + y² = 0 ……………. (1)
x’ஐ பொறுத்து வகையிட கிடைப்பது, =
⇒ 2x – 2g(1) + \(2 y \frac{d y}{d x}\) = 0
⇒ 2x + \(2 y \frac{d y}{d x}\) = 2g
⇒ x + \(y \frac{d y}{d x}\) = g ………….. (2)
சமன்பாடு (2) ஐ (1) ல் பிரதியிட கிடைப்பது,
x² – 2x\(\left(x+y \frac{d y}{d x}\right)\) + y² = 0
⇒ x² – 2x² – 2xy\(\frac{d y}{d x}\) + y² = 0
⇒ -x² – 2xy\(\frac{d y}{d x}\) + y² = 0
⇒ x² + 2xy\(\frac{d y}{d x}\) – y² என்பது தேவையான
வகைக்கெழு சமன்பாடு ஆகும்.

கேள்வி 4.
செவ்வகலம் 4a மற்றும் x-அச்சுக்கு இணையான அச்சுகளைக் கொண்டபரவளையத்தொகுப்பின் வகைக்கெழுச் சமன்பாட்டைக் காண்க.
தீர்வு:
செவ்வகலம் 4a மற்றும் X-அச்சுக்கு இணையான அச்சுகளைக் கொண்ட பரவளையத் தொகுப்பின் சமன்பாடு
(y – k)² = 4d(x – h)
[(h, k) பரவளையத்தின் முனை]
‘x’ஐப் பொறுத்து வகையிட கிடைப்பது,
2(y – k)y’ = 4a(1)
⇒ (y – k)y’ = 2a
⇒ yy’ – ky’ = 2a
⇒ \(\frac{y y^{\prime}-2 a}{y^{\prime}}\) = k
⇒ y – \(\frac{2 a}{y^{\prime}}\) = k ……..(1)
‘x’ஐப் பொறுத்து மீண்டும் வகையிட கிடைப்பது,
yy” + y¹² – ky” = 0
k = y – \(\frac{2 a}{y^{\prime}}\); எனப் பிரதியிட கிடைப்பது,
yy” + y’² – y” ( y – \(\frac{2 a}{y^{\prime}}\))
= y y” + y’² – y y” + \(\frac{2 a y^{\prime \prime}}{y^{\prime \prime}}\)
y’ ஆல் பெருக்க கிடைப்பது,
y’³ + 2ay” = 0 என்பது தேவையான வகைக்கெழு சமன்பாடு,

கேள்வி 5.
முனை (0, 1) மற்றும் y- அச்சை அச்சாகவும் கொண்ட பரவளையக் குடும்பத்தின் வகைக்கெழுச் சமன்பாட்டைக் காண்க.
தீர்வு:
முனை (0, -1) மற்றும் Y-அச்சை அச்சாகவும் கொண்ட பரவளையக் குடும்பத்தின் சமன்பாடு
(x – 0)² = 4a(y + 1)
⇒ x² = 4a(y + 1) …………. (1)
‘x’ஐப் பொறுத்து வகையிட கிடைப்பது,
2x = 4a \(\left(\frac{d y}{d x}\right)\)
⇒ 4a = \(\frac{2 x}{\frac{d y}{d x}}\) …………. (2)
சமன்பாடு (2) ஐ (1) ல் பிரதியிட கிடைப்பது,
x² = \(\frac{2 x}{y^{\prime}}(y+1)\)
⇒ x = \(\frac{2 x}{y^{\prime}}(y+1)\)
xy’ = 2(y+ 1)
xy’ = 2y+2
⇒ xy’ – 2y – 2 = 0.

கேள்வி 6.
ஆதிப்புள்ளியை மையமாகவும் செல்லும், y- அச்சின் மீது குவியங்களையும் கொண்ட நீள்வட்டத் தொகுதியின் வகைக்கெழுச் சமன்பாட்டைக் காண்க.
தீர்வு:
ஆதிப்புள்ளியை மையமாகவும் y-அச்சின் மீது குவியங்களை கொண்ட நீள்வட்டத் தொகுதியின் சமன்பாடு

÷ yy’ கிடைப்பது, x² – \(\frac{x y^{2}}{y y^{\prime}}\) = b²
‘x’ ஐப் பொறுத்து மீண்டும் வகையிட கிடைப்பது,
2x – \(\left[\frac{y^{\prime}\left(x y^{\prime}+y\right)-x y y^{\prime \prime}}{y^{\prime 2}}\right]\) = 0
⇒ 2xy’² – y'(xy’ + y) + xyy” = 0 [y’² ஆல் வகுக்க)]
⇒ 2xy’² – xy’² – yy’ + xyy” = 0s.
⇒ xy’² – yy’ + xyy” = 0

கேள்வி 7.
y = Ae^8x + Be^-8x எனும் சமன்பாட்டைக் கொண்ட வளைவரைக் குடும்பத்தின் வகைக்கெழுச் சமன்பாட்டைக் காண்க. இங்கு A, B என்பன ஏதேனும் இரு மாறிலிகள்.
தீர்வு:
கொடுக்கப்பட்ட வளைவரைகளின் சமன்பாடு
y = Ae^8x + Be^-8x ……. (1)
‘X’ஐ பொறுத்து வகையிட கிடைப்பது,
\(\frac{d y}{d x}\) = 8Ae^8x – 8Be^-8x
‘x’ஐ பொறுத்து மீண்டும் வகையிட கிடைப்பது,
\(\frac{d^{2} y}{d x^{2}}\) = 64Ae^8x + 64Be^-8x
= 64(Ae^8x + Be^-8x)
\(\frac{d^{2} y}{d x^{2}}\) = 64y [(1)ஐ பயன்படுத்தி) என்பது
தேவையான வகைக்கெழு சமன்பாடு.

கேள்வி 8.
xy = ae^x + be^-x + x² எனும் சமன்பாட்டால் குறிப்பிடப்படும் வளை வரையின் வகைக்கெழுச் சமன்பாட்டைக் காண்க.
தீர்வு:
கொடுக்கப்பட்ட வளைவரைகளின் சமன்பாடு
xy = ae^x + be^-x +x² …….(1)
‘x’ஐ பொறுத்து வகையிட கிடைப்பது.
xy + y = ae^x – be^-x + 2x
‘x’ஐ பொறுத்து மீண்டும் வகையிட கிடைப்பது,
xy” + y’ + y = ae^x + be^-x + 2
⇒ xy” + 2y – 2 = ae^x + be^-x
⇒ xy” + 2y – 2 = xy – x^x [(1) → xy – x^x = ae^x + be^-x]
⇒ xy” + 2y’ + x^x – xy – 2 = 0 என்பது தேவையான வகைக்கெழு சமன்பாடாகும்.