Samacheer Kalvi 12th Maths Guide Chapter 11 நிகழ்தகவு பரவல்கள் Ex 11.5

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 11 நிகழ்தகவு பரவல்கள் Ex 11.5 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 11 நிகழ்தகவு பரவல்கள் Ex 11.5

கேள்வி 1.
கீழ்காணும் ஈருறுப்பு பரவல் B(n, p)-க்காக P(X = k) என்பதைக் கணிக்க.
(i) n = 6, p = \(\frac{1}{3}\), k = 3
(ii) n = 10, p = \(\frac{1}{5}\), k = 4
(i) n = 9, n = \(\frac{1}{2}\), k = 7
தீர்வு:
கொடுக்கப்பட்டா n = 6, p = \(\frac{1}{3}\), k = 3
ஈருறுப்பு பரவல்

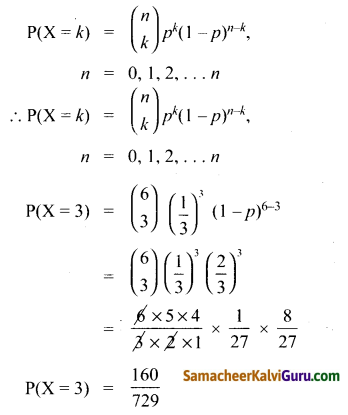
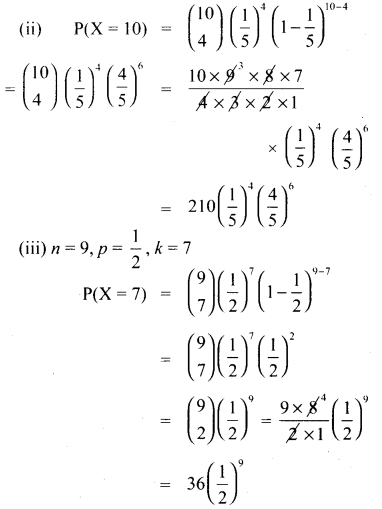
கேள்வி 2.
எந்த முயற்சியிலும் ஒரு இலக்கைத் திரு. தாக்க நிகழ்தகவு \(\frac{1}{4}\) ஆகும். பத்து முறை இலக்கை அவர் தாக்க முயற்சிக்கிறார் எனக் கொள்க. இலக்கைத் தாக்க
(i) சரியாக 4 முறைகள்
(ii) குறைந்தபட்சம் ஒரு முறை தாக்குவதற்கு ஆகியவற்றிற்கான நிகழ்தகவு காண்க.
தீர்வு:
கொடுக்கப்பட்ட P(இலக்கத்தை தாக்க) = \(\frac{1}{4}\) ⇒ p = \(\frac{1}{4}\)
n = 10.
(i) P(X = 4) = \(\left(\begin{array}{l}
n \\
x
\end{array}\right)\) p^x(1 – p)^n-x, x
= 0, 1, 2, ……… n

P(x=4) = \(\left(\begin{array}{l}
10 \\
4
\end{array}\right)\) (\(\frac{1}{4}\))⁴ (1 – \(\frac{1}{4}\))^10-4
= 10C₄ (\(\frac{1}{4}\))⁴ (\(\frac{3}{4}\))⁶

(ii) P(குறைந்தபட்சம் ஒரு முறை)
= P(X ≥ 1) = 1 – P(X < 1)
= 1 – P(X = 0)
= 1 – 10C₀(\(\frac{1}{4}\))⁰ (1 – \(\frac{1}{4}\))¹⁰
= 1 – 1(1) (\(\frac{3}{4}\))¹⁰
P(X ≥ 1) = 1 – \(\frac{3^{10}}{4^{10}}\)

கேள்வி 3.
கீழ்க்காணும் சோதனைகளில் ஈருறுப்பு பரவலைப் பயன்படுத்தி சமவாய்ப்பு மாறி X -ன் சராசரி மற்றும் பரவற்படி காண்க.
(i) 100 தடவை ஒரு சீரான நாணயம் சுண்டப்படுகிறது. தலைகளின் எண்ணிக்கையை X குறிக்கிறது.
(ii) 240 தடவை ஒரு சீரான பகடை ! சுண்டப்படுகிறது. எண் நான்கு தோன்றுவதற்கான எண்ணிக்கையை X குறிக்கிறது.
தீர்வு:
(i) கொடுக்கப்பட்ட n = 100
X என்பது தலைகளின் எண்ணிக்கையை குறிப்பதால், p = \(\frac{1}{2}\);
சராசரி = np = 100 × \(\frac{1}{2}\) = 50
பரவற்படி = npq = 100 × \(\frac{1}{2}\) × \(\frac{1}{2}\) = 25.

(ii) கொடுக்கப்பட்ட n = 240 மேலும், X- என்பது எண் நான்கு தோன்றுவதற்கான எண்ணிக்கையை குறிக்கிறது.
p = \(\frac{1}{6}\) [∵ 4 ஒருமுறை மட்டும் தோன்றும்]
∴ சராசரி = 240 × \(\frac{1}{6}\) = 40
பரவற்படி = npq = 240 × \(\frac{1}{6}\) × \(\frac{5}{6}\) [∵ q = 1 – p = 1 – \(\frac{1}{6}\) = \(\frac{5}{6}\)]
பரவற்படி = \(\frac{100}{3}\)

கேள்வி 4.
ஒரு மின்சோதனையில் ஒரு குறிப்பிட்ட சாதனத்தின் தாங்கும் திறனுக்கான நிகழ்தகவு \(\frac{3}{4}\). சோதிக்கப்பட ஐந்தில் சரியாக மூன்று சாதனங்களின் தாங்கு திறனுக்கான நிகழ்தகவைக் கண்டறிக.
தீர்வு:
கொடுக்கப்பட்ட p = \(\frac{3}{4}\)
n = 5

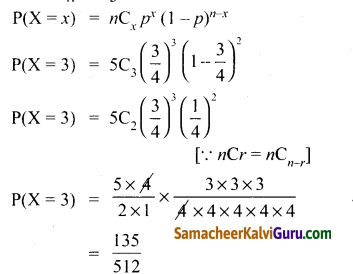
கேள்வி 5.
ஒரு உற்பத்தியாளரிடமிருந்து ஒரு குறிப்பிட்ட மின்வகைக் கருவியை ஒரு விற்பனையாளர் கொள்முதல் செய்கிறார். உற்பத்தியாளர் கருவியின் பழுதாகும் சதவீதம் 5 எனக்கூறுகிறார். கொள்முதல் செய்யப்பட்ட சரக்கிலிருந்து 10 பொருட்களை விற்பனையாளரின் பரிசோதகர் சமவாய்ப்பு முறையில் பரிசோதிக்கிறார். அவற்றுள்
(i) குறைந்தபட்சம் ஒரு பழுதான பொருள்
(ii) சரியாக இரு பொருட்கள் பழுதாக இருக்க நிகழ்தகவு காண்க.
தீர்வு : கொடுக்கப்பட்ட n = 10
P = 5% = \(\frac{5}{100}\)

(i) P(குறைந்த பட்சம் ஒரு பழுதான பொருள்)
P(X ≥ 1) = 1 – P(X < 1)
= 1 – P(X = 0)
= 1 – 10C₀\(\left(\frac{5}{100}\right)^{0}\left(1-\frac{5}{100}\right)^{10}\)
– 1 – (1)(1)\(\)
P(X > 1) = 1 (0.95)^10</sup<

(ii) P(X = 2) = 10C₂ \(\left(\frac{5}{100}\right)^{2}\left(1-\frac{5}{100}\right)^{10-2}\)
= 10C₂(0.05)² \(\left(\frac{95}{100}\right)^{8}\)
P(X = 2) = 10C₂(0.05)² (0.95)⁸

கேள்வி 6.
ஒரு பாதரச ஆவி விளக்கின் பயன்படும் காலம் குறைந்தபட்சம் 600 மணித்துளிகளுக்கான நிகழ்தகவு 0.9. எனில் அத்தகைய 12 விளக்குகளில்
(i) சரியாக 10 விளக்குகளின் பயன்படும் காலம் குறைந்தபட்சம் 600 மணித்துளிகளுக்கான நிகழ்தகவு;
(ii) குறைந்தபட்சம் 11 விளக்குகளின் பயன்படும் காலம் குறைந்தபட்சம் 600 மணித்துளிகளுக்கான நிகழ்தகவு
(iii) குறைந்தபட்சம் 2 விளக்குகளின் பயன்படும் காலம் குறைந்தபட்சம் 600 மணித்துளிகள் கூட இல்லாததற்கான நிகழ்தகவு ஆகியவற்றைக் காண்க.
தீர்வு:
கொடுக்கப்பட்ட n = 12
P = 0.9
(i) P(X = 10) = 12C₁₀(0.9)¹⁰ (1 – 0.9)²
= 12C₁₀(0.9)¹⁰ (0.1)²

(ii) P(X ≥ 11) = P(X = 11) + P(X = 12)
= 12C₁₁(0.9)¹¹ (0.1)¹ + 12C₁₂(0.9)¹² (0.1)⁶
= 12C₁(0.9)¹¹ (0.1) + (0.9)¹²
= 12(0.9)¹¹ (0.1) + (0.9)¹²
= (0.9)¹¹ ((12)(0.1) + 0.9)
= (0.9)¹¹ (1.2 + 0.9) = (0.9)¹¹ (2.1)

(iii) P(குறைந்தபட்சம் 2 விளக்குகளில் பயன்படும்
காலம் 600 மணித்துளிகள் கூட இல்லாதது)
= 1 – P(குறைந்தபட்சம் 11 விளக்குகளில் பயன்படும் காலம் -600 மணித்துளிகளாவது உள்ளது)
= 1 – P(X ≥ 11) = 1 – 2.1 (0.9)¹¹

கேள்வி 7.
ஓர் ஈருறுப்பு சமவாய்ப்பு மாறி X -ன் சராசரி மற்றும் திட்ட விலக்கம் முறையே 6 மற்றும் 2 ஆகும்.
(i) நிகழ்தகவு நிறை சார்பு
(ii) P(X = 3)
(iii) P(X ≥ 2)ஆகியவற்றைக் காண்க.
தீர்வு:
கொடுக்கப்பட்ட சராசரி = np = 6 …. (1)
திட்ட விலக்கம் = \(\sqrt{npq}\) = 2
⇒ npq = 4 …………(2)
(2) ÷ (1) → \(\frac{n p q}{n p}=\frac{4}{6}=\frac{2}{3}\)
⇒ q = \(\frac{2}{3}\)
⇒ 1 – p = \(\frac{2}{3}\)
⇒ 1 – \(\frac{2}{3}\) = p
∴ p = \(\frac{1}{3}\)
p = \(\frac{1}{3}\) என்பதை (1)ல் பிரதியிட கிடைப்பது.
n × \(\frac{1}{3}\) = 6 ⇒ n = 18

(i) நிகழ்தகவு நிறைச் சார்பு

= 1 – \(\left(\frac{2}{3}\right)^{17}\left(\frac{20}{3}\right)\)
= 1 – \(\frac{20}{3}\left(\frac{2}{3}\right)^{17}\)

கேள்வி 8.
4P(X = 4) = P(X = 2) மற்றும் n = 6 எனும்படி உள்ள X ~ B(n, p)-ன் பரவலின், சராசரி மற்றும் திட்டவிலக்கம் ஆகியவற்றைக் காண்க.
தீர்வு:
கொடுக்கப்பட்ட 4 – P(X = 4) = P(X = 2) மற்றும்
n = 6.
4 – [6C₄p⁴ (1 – p)²] = 6C₂p⁴ (1 – p)⁴
⇒ \(\frac{6 \times 5}{2 \times 1}\) × p⁴(1 – p)² = \(\frac{6 \times 5}{2 \times 1}\) p² (1 – p)⁴
⇒ p²(1 – p)² [4 × p²] = p²(1 – p)⁴
⇒ 4p² = (1 – p)² [∵ நீக்க p² (1 – p)²]
⇒ 4p² = 1 + p² – 2p
⇒ 3p² + 2p – 1 = 0
⇒ (p+ 1) (3p – 1) = 0
p = -1, p = \(\frac{1}{3}\) [∵ p =- 1க்கு] சாத்தியமில்லை]

∴ ஈருறுப்பு பரவல்
P(X = x) = nC_xp^x (1 – p)^n-x, x = 0, 1, 2,…n
(i) P(X = x) = 6C_x \(\left(\frac{1}{3}\right)^{x}\left(\frac{2}{3}\right)^{6-x}\), x = 0, 1, 2 –

(ii) சராசரி = np= 6 × \(\frac{1}{3}\) = 2

(iii) திட்ட விலக்கம் = \(\sqrt{n p q}=\sqrt{6 \times \frac{1}{3} \times \frac{2}{3}}\)
= \(\sqrt{\frac{12}{9}}=\sqrt{\frac{4}{3}}\)

கேள்வி 9.
5 சார்பற்ற சோதனைகளை உடைய ஒரு ஈருறுப்பு பரவலின் 1 மற்றும் 2 வெற்றிக்கான நிகழ்தகவுகள் முறையே 0.4096 மற்றும் 0.2048 ஆகும். ஈருப்பு பரவலின் சராசரி மற்றும் பரவற்படி காண்க.
தீர்வு:
கொடுக்கப்பட்ட n = 5 மற்றும்
P(X = 1) = 0.4096,
P(X = 2) = 0.2048
∴ nC₁p¹q⁴ = 0.4096
⇒ 5C₁p¹q⁴ = 0.4096 ………. (1)
p(x = 2) = 0.2048
5C₂p²q³= 0.2048
⇒ p²q³ = 0.2048 ……… (2)
(2) ஐ (1) ஆல் வகுக்க கிடைப்பது
\(\frac{10 p^{2} q^{3}}{5 p q^{4}}=\frac{0.2048}{0.4096}\)
⇒ \(\frac{2 p}{q}=\frac{1}{2}\) ⇒ 4p = q
⇒ 4p = 1 – p ⇒ 5p = 1
⇒ p = \(\frac{1}{5}\)
∴ q = 1 – p = 1 – \(\frac{1}{5}\) = \(\frac{4}{5}\)
சராசரி = np = 5 × \(\frac{1}{5}\) = 1
பரவற்படி = npq = 5 ×\(\frac{1}{5}\) × \(\frac{4}{5}\) = \(\frac{4}{5}\)