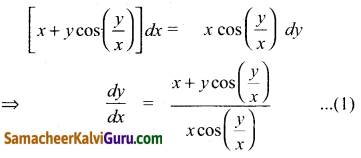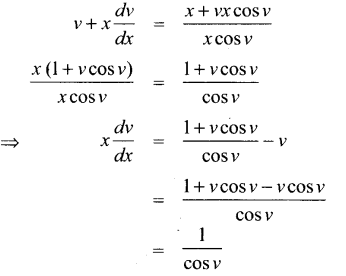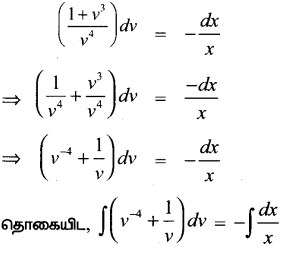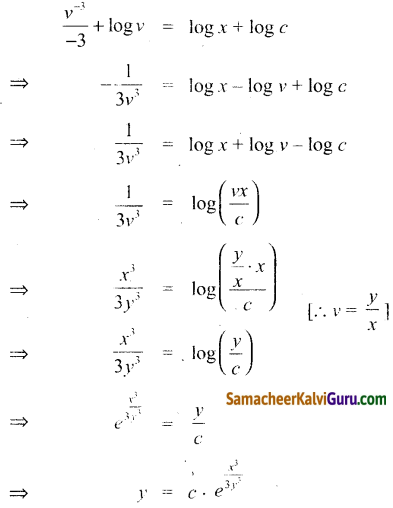Prasanna

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 9 தொகை நுண்கணிதத்தின் பயன்பாடுகள் Ex 9.7 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 9 தொகை நுண்கணிதத்தின் பயன்பாடுகள் Ex 9.7

பின்வருவனவற்றை மதிப்பிடுக:
கேள்வி 1.
(i) \(\int_{0}^{\infty} x^{5} e^{-3 x} d x\)
(ii) \(\int_{0}^{\frac{\pi}{2}} \frac{e^{-\tan x}}{\cos ^{6} x} d x\)
தீர்வு:

கேள்வி 2.
\(\int_{0}^{\infty} e^{-a x^{2}} x^{3} d x\) = 32, α > 0 எனில் 0-ன் மதிப்பைக் காண்க.
தீர்வு:

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 9 தொகை நுண்கணிதத்தின் பயன்பாடுகள் Ex 9.6 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 9 தொகை நுண்கணிதத்தின் பயன்பாடுகள் Ex 9.6

கேள்வி 1.
பின்வருவனவற்றை மதிப்பிடுக :

தீர்வு:

(ii) \(\int_{0}^{\frac{\pi}{2}} \cos ^{7} x d x\)
I_n = \(\int_{0}^{\pi / 2} \cos ^{7} x d x=\frac{n-1}{n} \mathrm{I}_{n-2}\), n ≥ 2
∴ I₇ = \(\int_{0}^{\pi / 2} \cos ^{7} x d x=\frac{6}{7} \times \frac{4}{5} \times \frac{2}{3} \times 1=\frac{16}{35}\)

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 9 தொகை நுண்கணிதத்தின் பயன்பாடுகள் Ex 9.3 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 9 தொகை நுண்கணிதத்தின் பயன்பாடுகள் Ex 9.3

கேள்வி 1.
பின்வரும் வரையறுத்த தொகையிடலின் மதிப்பு காண்க :

தீர்வு:
(i) \(\int_{3}^{4} \frac{d x}{x^{2}-4}\)
\(\int_{3}^{4} \frac{d x}{x^{2}-4}=\int_{3}^{4} \frac{d x}{x^{2}-2^{2}}\)

(ii) \(\int_{-1}^{1} \frac{d x}{x^{2}+2 x+5}\)

(iii) \(\int_{0}^{1} \sqrt{\frac{1-x}{1+x}} d x\)
= \(\int_{0}^{1} \sqrt{\frac{(1-x)(1-x)}{(1+x)(1-x)}} d x\)
(தொகுதி மற்றும் பகுதியை 1-3 ஆல் பெருக்க)
= \(\int_{0}^{1} \frac{1-x}{\sqrt{1-x^{2}}} d x\)
= \(\int_{0}^{1} \frac{1}{\sqrt{1-x^{2}}} d x-\int_{0}^{1} \frac{x}{\sqrt{1-x^{2}}} d x\)

கேள்வி 2.
பின்வரும் வரையறுத்த தொகையிடல்களை, தொகையிடலின் பண்புகளைப் பயன்படுத்தி மதிப்பு காண்க :


(xi) \(\int_{0}^{\pi}\) x[sin² (sin x) + cos² (cos x)] dx
தீர்வு:

= -f(x)

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 2 கலப்பு எண்கள் Ex 2.7 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 2 கலப்பு எண்கள் Ex 2.7

கேள்வி 1.
கீழ்காணும் கலப்பெண்களின் வடிவினைக் காண்க.

(i) 2+i2\(\sqrt{3}\)
(ii) 3-i\(\sqrt{3}\)
(iii) -2-i2
(iv) \(\frac{i-1}{\cos \frac{\pi}{3}+i \sin \frac{\pi}{3}}\)
தீர்வு:
(i) 2 +i2\(\sqrt{3}\)
2+i 2\(\sqrt{3}\) = x + iy = r (cos θ + i sin θ) என்க
r = எண் மதிப்பு = \(\sqrt{x^{2}+y^{2}}\)
= \(\sqrt{2^{2}+(2 \sqrt{3})^{2}}\)
= \(\sqrt{4+12}\) = \(\sqrt{16}\) = 4

2 + i2\(\sqrt{3}\) என்ற கலப்பெண் முதலாம் கால் பகுதியில் அமைவதால் [x, y இரண்டும் மிகை) அதன் முதன்மை வீச்சு
θ = α = \(\frac{\pi}{3}\)
அதன் துருவ வடிவம் 2 +i2\(\sqrt{3}\)

(ii) 3 – i\(\sqrt{3}\)
x + iy = 3 – i\(\sqrt{3}\) என்க.
= r (cos θ + i sin θ)

3 – i\(\sqrt{3}\) என்ற கலப்பெண் நான்காம் கால்பகுதியில் அமைவதால்,
[∵ x → + ve, y → – ve]
அதன் முதன்மை வீச்சு θ = -α
⇒ θ = \(\frac{\pi}{6}\)
∴ துருவ வடிவம்
3-i\(\sqrt{3}\) = 2\(\sqrt{3}\)

(iii) – 2 – i2
x + iy = -2- 2i = r (cos θ + i sin θ) என்க

-2 – 2i என்ற கலப்பெண் மூன்றாம் கால்பகுதியின் அமைவதால்
[x குறை y குறை]
அதன் முதன்மை வீச்சு θ = α – π
⇒ θ = \(\frac{\pi}{4}\)-π=\(\frac{\pi-4 \pi}{4}\)=\(-\frac{3 \pi}{4}\)
அதன் துருவ வடிவம்

(iv)

(-1 + i) என்ற கலப்பெண் II-ம் கால் பகுதியில்
அமைவதால் [x → குறை y → மிகை)
அதன் முதன்மை வீச்சு θ = π – \(\frac{\pi}{4}\) = \(-\frac{3 \pi}{4}\)

எனவே துருவ வடிவம்

கேள்வி 2.
பின்வருவனவற்றை செவ்வக வடிவில் எழுதுக.
(i) (cos \(\frac{\pi}{6}\) + i sin\(\frac{\pi}{6}\))(cos \(\frac{\pi}{12}\) + isin \(\frac{\pi}{12}\))
(ii)
தீர்வு:
(i) (cos \(\frac{\pi}{6}\) + i sin\(\frac{\pi}{6}\))(cos \(\frac{\pi}{12}\) + isin \(\frac{\pi}{12}\))
[ ∵ (cos θ₁ + i sin θ₁) (cos θ₂ + i sin θ₂)
= cos (θ₁ + θ₂) +i sin (θ₁ + θ₂)

(ii)

கேள்வி 3.
(x₁ + iy₁) (x₂ + iy₂) …… (x_n + iy_n) = a + ib எனில்,

தீர்வு:

இருபுறமும் மட்டு மதிப்பு காண கிடைப்பது

இருபுறமும் வர்க்கப்படுத்த கிடைப்பது,

(ii)
(x₁ + iy₁)(x₂ + iy₁) …. (x_n + iy_n) = a + ib
arg((x₁ + iy₁)(x₂ + iy₂)…….(x_n + iy_n)) = arg(a + ib)
⇒ arg(x₁ + iy₁) + arg(x₂ + iy₂) + ….. + arg(x_n + iy_n) = arg(a + ib)
(∵ arg(z₁z₂….z_n) = arg z₁ + arg z₂ + … + arg z_n)
⇒ tan^-1\(\left(\frac{y_{1}}{x_{1}}\right)\) + tan^-1\(\left(\frac{y_{2}}{x_{2}}\right)\) + ….. + tan^-1\(\left(\frac{y_{n}}{x_{n}}\right)\)
= tan^-1\(\left(\frac{b}{a}\right)\) + 2kπ _k∈ℤ

கேள்வி 4.

தீர்வு:

அதாவது \(\frac{1+z}{1-z}\) = cos 2θ + i sin 2θ
⇒ \(\frac{1+x+i y}{1-x-i y}\) = cos 2θ + i sin 2θ …… (1)
மட்டு மதிப்பு காண கிடைப்பது,
\(\frac{1+x+i y}{1-x-i y}\) = |cos 2θ + i sin2θ| ⇒ |\(\frac{1+x+i y}{1-x-i y}\)|
= \(\sqrt{\cos ^{2} 2 \theta+\sin ^{2} 2 \theta}\) = 1

கற்பனை பகுதியை தனியாக எடுக்க கிடைப்பது

⇒ \(\frac{2 \tan \theta}{1+\tan ^{2} \theta}\) = sin 2θ
∴ y ஆனது tan 8 ற்கு சமமாக இருக்க வேண்டும்.
⇒ y = tan θ
∴ z = 0 + i tan θ = z ⇒ tan θ

கேள்வி 5.
cos α + cos β + cos γ = sin α + sin β + sin γ = 0, எனில்,
(i) cos 3α + cos 3β + cos 3γ = 3 cos (α + β + γ) மற்றும்
(ii) sin 3γ + sin 3β + sin 3γ= 3 sin (α + β + γ) என நிறுவுக.
தீர்வு:
(i) cos 3α + cos 3β + cos 3γ = 3 cos (α + β + γ)
கொடுக்கப்பட்ட cos α + cos β + cos γ = sin α +sin β + sin γ = 0
⇒ (cos α + cos β + cos γ) + i (sin α + sin β+ sin γ)=0
⇒ (cos α + i sin α) + (cos β + i sin β) + (cos γ + i sin γ) = 0
⇒ a + b + c = 0 இங்கு a = cos α + i sin α, b = cos β + i sin β, c = cos γ + i sin γ
a + b + c = 0, எனில் a³ + b³ + c³ = 3abc.
∴ (cos α + i sin α)³ + (cos β + i sin β)³ + (cos γ + i sin γ)³ = 3[(cos α + i sin α) + (cos β + i sin β) + (cos γ + i sin γ)]
டி மாய்வரின் தேற்றப்படி,
⇒ cos 3α + i sin 3α + cos 3β + i sin 3β + cos 3γ + i sin 3γ
⇒ 3 [(cos (α + β + γ) + i sin (α + β + γ)]
⇒ (cos 3α + cos 3β + cos 3γ) + i [sin 3α + sin 3β + sin 3γ)]
= 3 [(cos (α + β + γ) + i sin (α + β + γ)]
மெய் மற்றும் கற்பனை பகுதிகளை சமப்படுத்த கிடைப்பது
cos 3α + cos 3β + cos 3γ = 3 cos (α + β + γ)
மற்றும் sin 3α + sin 3β + sin 3γ = 3sin (α + β + γ) எனவே நிரூபிக்கப்பட்டது.

கேள்வி 6.
z = x + iy மற்றும் arg \(\left(\frac{z-i}{z+2}\right)\) = \(\frac{\pi}{4}\) எனில்,
x² + y² + 3x – 3y + 2 = 0 எனக்காட்டுக.
தீர்வு:
கொடுக்கப்பட்ட z =x + iy மற்றும்
arg \(\left(\frac{z-i}{z+2}\right)\) = \(\frac{\pi}{4}\)
⇒ arg (z – i) – arg(z + 2) = \(\frac{\pi}{4}\)
⇒ arg (x + iy – i) – arg(x + iy + 2) = \(\frac{\pi}{4}\)
⇒ arg (x + i(y – 1)) – arg((x + 2) + iy) = \(\frac{\pi}{4}\)


⇒ -x + 2y – 2 = x² + 2x + y² – y
⇒ x² + 2x + y² – y + x – 2y + 2 = 0
⇒ x² + y² + 3x – 3y + 2 = 0
எனவே நிரூபிக்கப்பட்டது.

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 2 கலப்பு எண்கள் Ex 2.6 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 2 கலப்பு எண்கள் Ex 2.6

கேள்வி 1.
z = x + iy என்ற ஏதேனும் ஒரு கலப்பெண் \(\left|\frac{z-4 i}{z+4 i}\right|\)
= 1 எனுமாறு அமைந்தால் z -ன் நியமப் பாதை மெய் அச்சு எனக்காட்டுக.
தீர்வு:
கொடுக்கப்பட்ட z =x+iy
கருதுக \(\left|\frac{z-4 i}{z+4 i}\right|\) =1 ⇒ \(\left|\frac{x+i y-4 i}{x+i y+4 i}\right|\) = 1
⇒ \(\left|\frac{x+i(y-4)}{x+i(y+4)}\right|\) = 1

இருபுறமும் வர்க்கப்படுத்த கிடைப்பது,
x² + (y – 4)² = x² + (y + 4)²

⇒ 8y + 8y = 0
⇒ 16y = 0
⇒ y = 0 [∵ 16 ≠ 0]
y = 0 என்பது மெய் அச்சின் சமன்பாடு
∴z-ன் நியமப்பாதை மெய் அச்சு ஆகும்.

கேள்வி 2.
z = x + iy என்ற ஏதேனும் ஒரு கலப்பெண் Im\(\left(\frac{2 z+1}{i z+1}\right)\) = 0 எனுமாறு அமைந்தால் z -ன் நியமப்பாதை 2x² + 2y² + x – 2y = 0 எனக் காட்டுக.
தீர்வு:
கொடுக்கப்பட்ட z = x+iy

பகுதியின் இணையால் தொகுதி மற்றும் பகுதியை பெருக்க கிடைப்பது

கற்பனை பகுதியை தேர்ந்தெடுக்க கிடைப்பது,

⇒ – 2x² – x + 2y – 2y² = 0
⇒ 2x² + 2y² + x – 2y = 0
எனவே z -ன் நியமப்பாதை
2x² + 2y² + x- 2y = 0

கேள்வி 3.
பின்வ ரும் சமன்பாடுகளில் z = x + iy – ன் நியமப்பாதையை கார்ட்டீசியன் வடிவில் காண்க.
(i) [Re (iz)]² = 3
(ii) Im [(1 – i) z + 1] = 0
(iii) |z + i| = |z – 1|
(iv) \(\bar{z}\) = z^-1
தீர்வு:
(i) [Re (iz)]² = 3
iz = i (x + iy) = ix +i²y = ix – y = -y + ix
⇒ Re (iz) = -y
[Re (iz)]² = 3 ⇒ (-y)² = 3
⇒ y² = 3.
எனவே கார்ட்டீசியன் சமன்பாடானது y² = 3

(ii) Im [[1- i) z + 1] = 0
(1 – i) z + 1 = (1 – i) (x + iy) + 1
= x + iy – ix – iy + 1
= x + iy – ix + y + 1
= (x + y + 1) + i(y – x)
∴I_m[(1 – i) z + 1] = y – x = 0.
⇒ x – y = 0.
எனவே கார்ட்டீசியன் சமன்பாடானது x – y = 0.

(iii) |z + i| = |z -1|
⇒ |x + iy + il = |x + iy – 1|
⇒ x + i (y + 1) = |(x – 1) + iy|
⇒ \(\sqrt{x^{2}+(y+1)^{2}}\) = \(\sqrt{(x-1)^{2}+y^{2}}\)
⇒ x² + (y+ 1)² = (x – 1)² + y²
[இருபுறமும் வர்க்கப்படுத்த கிடைப்பது]

⇒ 2y + 2x = 0 ⇒ x + y = 0
எனவே கார்ட்டீசியன் சமன்பாடானது x + y = 0.

(iv) \(\bar{z}\) = z^-1
\(\bar{z}\) = z^-1
\(\bar{z}\) = \(\frac{1}{z}\) ⇒ z\(\bar{z}\) = 1
⇒ |z|² =1
⇒ x² – y² = 1 தேவையான கார்ட்டீசியன் சமன்பாடு.

கேள்வி 4.
பின்வரும் சமன்பாடுகள் வட்டத்தை குறிக்கிறது எனக்காட்டுக. மேலும் இதன் மையம் மற்றும் ஆரத்தைக் காண்க.)
(i) |z – 2 – i| = 3
(ii) |2z + 2 – 4i| = 2
(iii) |3z – 6 + 12i| = 8
தீர்வு:
(i) |z – 2 – i| = 3.
⇒ |z – (2 +i)| = 3
இது |z – z₀| =r என்ற வடிவம் கொண்டது. ஆகவே இது வட்டத்தை குறிக்கின்றது.
இதன் மையம் ( 2 + i ) மற்றும் ஆரம் 3 ஆகும்.

(ii) |2z + 2 – 4i| = 2
2|z + 1 – 2i | = 2
⇒ |z – (-1 + 2i) = 1
இது |z – z₀| = r என்ற வடிவம் கொண்டது. ஆகவே இது வட்டத்தை குறிக்கின்றது.
இதன் மையம் (-1 + 2i) மற்றும் ஆரம் 1 ஆகும்.

(iii) |3z – 6 + 12i| = 8
⇒ 3|z – 2 + 4i| = 8
⇒ z – (2 – 4i) = \(\frac{8}{3}\)
இது |z – z₀| = r என்ற வடிவம் உள்ளது. ஆகவே இது வட்டத்தை குறிக்கின்றது.
இதன் மையம் (2 – 4i) மற்றும் ஆரம் \(\frac{8}{3}\) ஆகும்.

கேள்வி 5.
பின்வ ரும் சமன்பாடுகளில் z = x + iy -ன் நியமப்பாதையை கார்டீசியன் வடிவில் காண்க.
(i) |z – 4| = 16
(ii) |z – 4|² – |z – 1|² = 16
தீர்வு:
(i) |z – 4| = 16
கொடுக்கப்பட்ட z = x + iy
⇒ |z – 4| = 16
⇒ |x + iy – 4| = 16
⇒ |(x – 4) + iy| = 16
⇒ \(\sqrt{(x-4)^{2}+y^{2}}\) = 16
⇒ (x – 4)² + y² = 16
[இருபுறமும் வர்க்கப்படுத்த]
⇒ x² – 8x + 16 + y² = 256
⇒ x² – 8x + y² + 16 – 256 = 0
⇒ x² – 8x + y² – 240 = 0. என்பது தேவையான கார்ட்டீசியன் சமன்பாடு ஆகும்.

(ii) |z – 4|² – |z – 1|² = 16
|x + iy – 4|² – |x + iy – 1|² = 16
⇒ |(x – 4) + iy|² – |(x – 1) + iy|² = 16
⇒ [(x – 4)² + y²] – [(x – 1)² + y²] = 16
⇒ x² – 8x + 16 + y² – [x² – 2x + 1 + y²] = 16

⇒ -6x + 15 – 16 = 0
⇒ -6x – 1 = 0
⇒ 6x + 1 = 0 என்பது தேவையான கார்ட்டீசியன் சமன்பாடு ஆகும்.

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 9 தொகை நுண்கணிதத்தின் பயன்பாடுகள் Ex 9.2 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 9 தொகை நுண்கணிதத்தின் பயன்பாடுகள் Ex 9.2

கேள்வி 1.
கீழ்க்காணும் தொகையீடுகளை கூட்டலின் எல்லைகளாக கணக்கிடுக :
(i) \(\int_{0}^{1}(5 x+4) d x\)
(ii) \(\int_{1}^{2}\left(4 x^{2}-1\right) d x\)
தாவு:
(i) \(\int_{0}^{1}(5 x+4) d x\)
இங்கு a = 0, b = 1, f(x) = 5x + 4

∴ \(\int_{1}^{2}\left(4 x^{2}-1\right) d x=\frac{25}{3}\)

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 9 தொகை நுண்கணிதத்தின் பயன்பாடுகள் Ex 9.1 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 9 தொகை நுண்கணிதத்தின் பயன்பாடுகள் Ex 9.1

கேள்வி 1.
{1.1, 1.2, 1.3, 1.4, 1.5} எனும் பிரிவினையுடன் இடது – முனை விதியைப் பயன்படுத்தி
\(\begin{array}{l}
1.5 \\
\int \\
1
\end{array}\) xdx -க்கு தோராய மதிப்பு காண்க.
தீர்வு:
இங்கு a = 1,
b = 1.5, n = 5, f (x) =x
∴ h = ∆x = \(\frac{b-a}{n}=\frac{1.5-1}{5}=\frac{0.5}{5}\) = 0.1
சம அளவு A கொண்ட ரீமன் கூட்டலுக்கான இடது விதியானது
\(\begin{array}{l}
b \\
\int \\
a
\end{array}\) xdx = [f(x₀) + f(x₁)+…..+ f(x_n-1})]∆x
= [f(1) + f(1.1) + f(1.2) + f (1.3) + f (1.4)](0.1)
= (1 + 1.1 + 1.2 + 1.3 + 1.4) (0.1)
= 6(0.1)
∴ \(\begin{array}{l}
1.5 \\
\int \\
1
\end{array}\) = 0.6

கேள்வி 2.
{1.1, 1.2, 1.3, 1.4, 1.5} எனும் பிரிவினையுடன் வலது-முனை விதியைப் பயன்படுத்தி \(\begin{array}{l}
1.5 \\
\int \\
1
\end{array}\) x² dx -க்கு தோராய மதிப்பு காண்க.
தீர்வு:
இங்கு a = 1, b = 1.5,
h = ∆x = \(\frac{b-a}{n}=\frac{1.5-1}{5}=\frac{0.5}{5}\) = 0.1
சம அளவு A கொண்ட ரீமன் கூட்டலுக்கான வலது முனை விதியானது
S= [f (x₁) + f (x₂) + f (x₃) + f(x₄) + f (x₅)]∆x
=[f (1.1) + f (1.2) + f(1.3) + f (1.4) + f(1.5)](0.1)
= [(1.1)² – (1.2)² + (1.3)² – (1.4)² – (1.5)²](0.1)
= (1.21 + 1.44 + 1.69 + 1.96 + 2.25) (0.1)
= (8.55) (0.1)
∴ \(\begin{array}{l}
1.5 \\
\int \\
1
\end{array}\) x² dx = 0.855

கேள்வி 3.
{1.1, 1.2, 1.3, 1.4, 1.5} எனும் பிரிவினையுடன் நடு – முனை விதியைப் பயன்படுத்தி
\(\begin{array}{l}
1.5 \\
\int \\
1
\end{array}\) (2 – x)dx-க்கு தோராய மதிப்பு காண்க.
தீர்வு:
இங்கு a = 1, b = 1.5, n = 5 மற்றும் f(x) = 2 -x
h = ∆r = \(\frac{b-a}{n}=\frac{1.5-1}{5}=\frac{0.5}{5}\) = 0.1
சம அளவு ∆r கொண்ட ரீமன் கூட்டலுக்கான நடுமுனை விதியானது

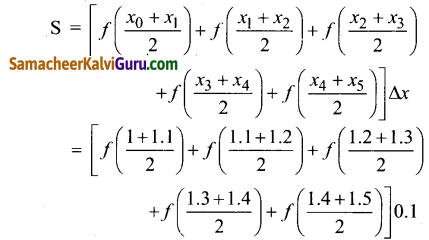
= [f (1.05) + f (1.15) + f (1.25) + f (1.35) + f (1.45)](0.1)
= [0.95 + 0.85 +0.75 + 0.65 + 0.55)](0.1)
= [(2 – 1.05) + (2 – 1.15) + (2 – 1.25) + (2 – 1.35) + (2 – 1.45)](0.1)
= (3.75) (0.1) = 0.375
∴ \(\begin{array}{l}
1.5 \\
\int \\
1
\end{array}\) (2 – x)dx = 0.375

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 9 தொகை நுண்கணிதத்தின் பயன்பாடுகள் Ex 9.5 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 9 தொகை நுண்கணிதத்தின் பயன்பாடுகள் Ex 9.5

கேள்வி 1.
பின்வருவனவற்றை மதிப்பிடுக :
(i) \(\int_{0}^{\frac{\pi}{2}} \frac{d x}{1+5 \cos ^{2} x}\)
(ii) \(\int_{0}^{\frac{\pi}{\sqrt{2}}} \frac{d x}{5+4 \sin ^{2} x}\)
தீர்வு:
(i) \(\int_{0}^{\frac{\pi}{2}} \frac{d x}{1+5 \cos ^{2} x}\)
I = \(\int_{0}^{\frac{\pi}{2}} \frac{d x}{1+5 \cos ^{2} x}\) என்க
u = tanx என பிரதியிடு ⇒ du = sec² x dr பகுதி மற்றும் தொகுதியை cos²r ஆல் வகுக்க கிடைப்பது

(ii) \(\int_{0}^{\frac{\pi}{\sqrt{2}}} \frac{d x}{5+4 \sin ^{2} x}\)
பகுதி மற்றும் தொகுதியை cos²x ஆல் வகுக்க கிடைப்பது

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 9 தொகை நுண்கணிதத்தின் பயன்பாடுகள் Ex 9.4 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 9 தொகை நுண்கணிதத்தின் பயன்பாடுகள் Ex 9.4

கேள்வி 1.
பின்வருவனவற்றை மதிப்பிடுக

தீர்வு: