Samacheer Kalvi 12th Maths Guide Chapter 10 சாதாரண வகைக்கெழுச் சமன்பாடுகள் Ex 10.7

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 10 சாதாரண வகைக்கெழுச் சமன்பாடுகள் Ex 10.7 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 10 சாதாரண வகைக்கெழுச் சமன்பாடுகள் Ex 10.7

பின்வரும் நேரியல் வகைக்கெழுச் சமன்பாடுகளின் தீர்வுகளைக் காண்க.
கேள்வி 1.
cosx \(\frac{d y}{d x}\) + y sin x = 1
தீர்வு:

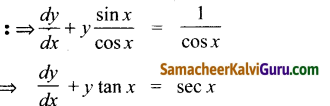
இது ஒரு நேரியல் வகைக்கெழு சமன்பாடாகும்.
∴ P= tan x; Q = sec x
\(\int\) p dx = \(\int\) tan x dx = log sec x
∴ I.F. = e^{\(\int p d x\)} =e^{log sec x} = sec x
y e^{\(\int p d x\)} = \(\int\) Qe^{\(\int p d x\)} dx + c தீர்வாகும்.
⇒ y sec x = \(\int\) sec.x ∙ sec x dx + c
⇒ y sec x = \(\int\) sec’ x dx + c
⇒ y sec x = tan x + c
⇒ \(\frac{y}{\cos x}=\frac{\sin x}{\cos x}+c\)
⇒ y = sinx + c (cos x)

கேள்வி 2.
(1 – x²)\(\frac{d y}{d x}\) – xy = 1
தீர்வு:
\(\frac{d y}{d x}+\left(\frac{-x}{1-x^{2}}\right) y=\frac{1}{1-x^{2}}\)
இது ஒரு நேரியல் வகைக்கெழு சமன்பாடாகும்.

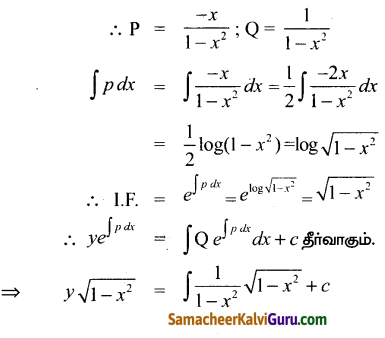
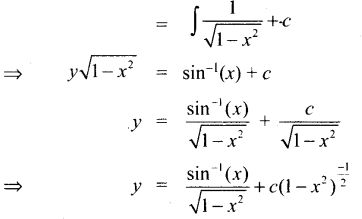
கேள்வி 3.
\(\frac{d y}{d x}+\frac{y}{x}\) = sin x
தீர்வு:
இது ஒரு நேரியல் வகைக்கெழு சமன்பாடாகும்.
∴ P = \(\frac{1}{x}\); Q = sin x
\(\int\) p dx = \(\int\) \(\frac{1}{x}\) dx = log x
I.F. = e^{\(\int p d x\)} = e^{log x} = x
∴ ye^{\(\int p d x\)} = \(\int\) Q e^{\(\int p d x\)} dx + c தீர்வாகும்
u = x; dv = sin x
du = dx; v = -cos x
∵ \(\int\) u dv = uv – \(\int\) v du
⇒ yx = \(\int\) x sinx ∙ dx + c
⇒ xy = -x cos x + \(\int\) cosx dx
⇒ xy = -x cos x + sin x + c
⇒ xy + x cos x = sin x + c
⇒ x(y + cos x) = sin x + c

கேள்வி 4.
(x² + 1) \(\frac{d y}{d x}\) + 2xy = \(\sqrt{x^{2}+4}\)
தீர்வு:
⇒ \(\frac{d y}{d x}+\left(\frac{2 x}{x^{2}+1}\right) y=\frac{\sqrt{x^{2}+4}}{x^{2}+1}\)
இது ஒரு நேரியல் வகைக்கெழு சமன்பாடாகும்.

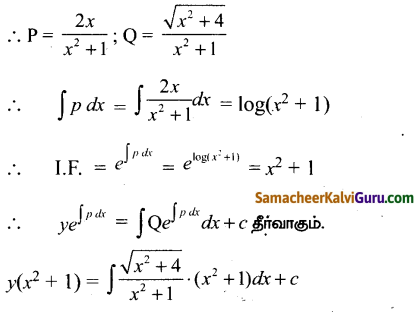
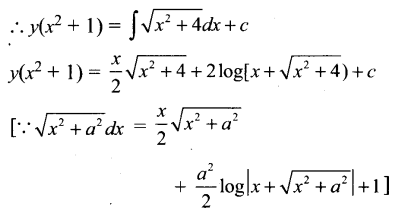
கேள்வி 5.
(2x – 10y³) dy + ydx = 0
தீர்வு:
⇒ 2x dy – 10y³ dy + y dx = 0
⇒ 2x dy + y dx = 10y³ dy

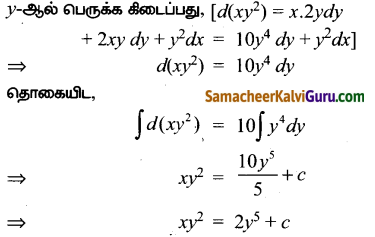
கேள்வி 6.
x sin x \(\frac{d y}{d x}\) + (x cos x + sin x)y = sin x
தீர்வு:
⇒ \(\frac{d y}{d x}+\left(\frac{x \cos x+\sin x}{x \sin x}\right)=\frac{\sin x}{x \sin x}=\frac{1}{x}\)
இது ஒரு நேரியல் வகைக்கெழு சமன்பாடு

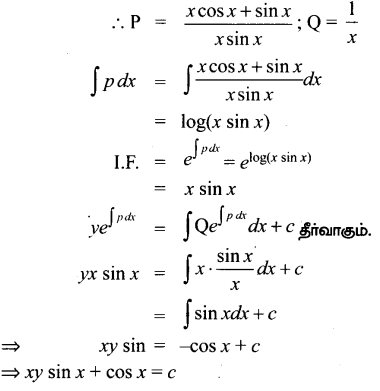
கேள்வி 7.
(y – e^sin-1x \(\frac{d x}{d y}+\sqrt{1-x^{2}}\) = 0
தீர்வு:

தொகையிட,

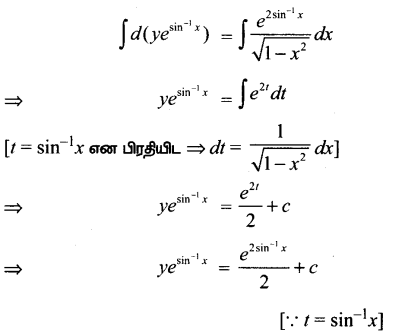
கேள்வி 8.
\(\frac{d y}{d x}+\frac{y}{(1-x) \sqrt{x}}=1-\sqrt{x}\)
தீர்வு:
இது ஒரு நேரியல் வகைக்கெழு சமன்பாடாகும்.


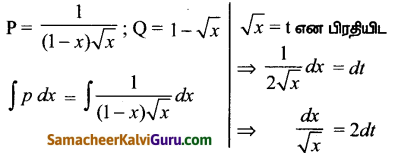
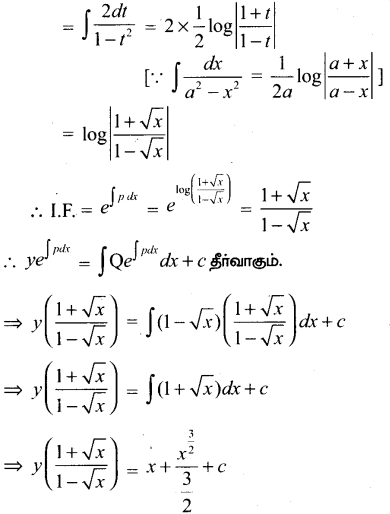
⇒ \(y\left(\frac{1+\sqrt{x}}{1-\sqrt{x}}\right)=x+\frac{2}{3} x \sqrt{x}+c\)

கேள்வி 9.
(1 + x + xy²) \(\frac{d y}{d x}\) + (y + y³) = 0
தீர்வு:

கேள்வி 10.
\(\frac{d y}{d x}+\frac{y}{x \log x}=\frac{\sin 2 x}{\log x}\)
தீர்வு:
இது ஒரு நேரியல் வகைக்கெழு சமன்பாடாகும்.

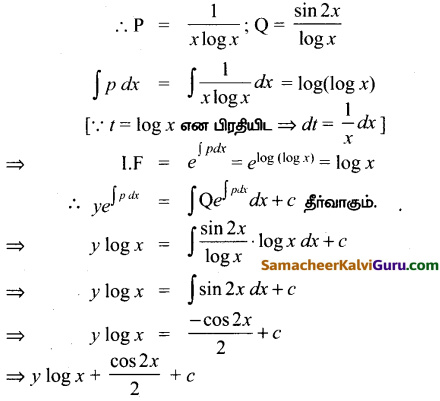
கேள்வி 11.
(x + a) \(\frac{d y}{d x}\) – 2y = (x + a)⁴
தீர்வு:

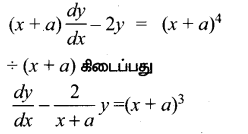
இது ஒரு நேரியல் வகைக்கெழு சமன்பாடாகும்.

2y = (x + a)⁴ + 2c (x + a)²

கேள்வி 12.
\(\frac{d y}{d x}=\frac{\sin ^{2} x}{1+x^{3}}-\frac{3 x^{2}}{1+x^{3}} y\)
தீர்வு:
\(\frac{d y}{d x}+\frac{3 x^{2} y}{1+x^{3}}=\frac{\sin ^{2} x}{1+x^{3}}\)
இது ஒரு நேரியல் வகைக்கெழு சமன்பாடாகும்.

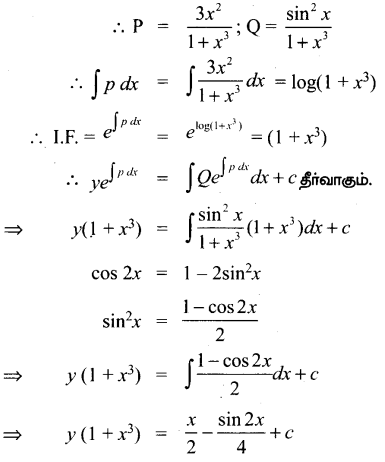
கேள்வி 13.
x\(\frac{d y}{d x}\) + y = x log x
தீர்வு:
x ஆல் வகுக்க கிடைப்பது,
\(\frac{d y}{d x}\) + \(\frac{1}{x}\) y = log x
இது ஒரு நேரியல் வகைக்கெழு சமன்பாடாகும்.

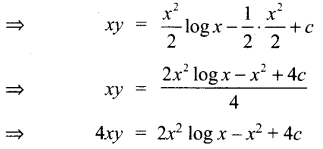
கேள்வி 14.
x \(\frac{d y}{d x}\) + 2y – x² log x = 0
தீர்வு:
x \(\frac{d y}{d x}\) + 2y = x² log x
x-ஆல் வகுக்க கிடைப்பது,
\(\frac{d y}{d x}+\frac{2}{x} y\) = x log x
இது ஒரு நேரியல் வகைக்கெழு சமன்பாடாகும்.

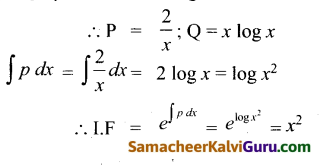
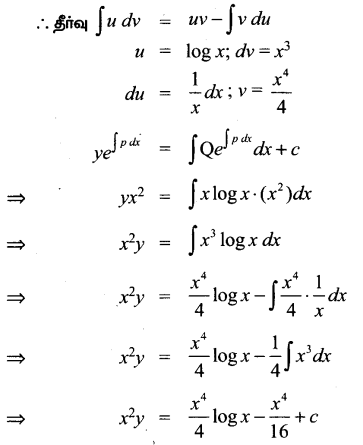
கேள்வி 15.
\(\frac{d y}{d x}+\frac{3 y}{x}=\frac{1}{x^{2}}\), கொடுக்கப்பட்டது y = 2 எனில் x = 1
தீர்வு:
\(\frac{d y}{d x}+\frac{3 y}{x}=\frac{1}{x^{2}}\)
கொடுக்கப்பட்ட y = 2 எனில் x = 1
இது ஒரு நேரியல் வகைக்கெழு சமன்பாடாகும்.

∴ (1) லிருந்து,
yx³ = \(\frac{x^{2}}{2}+\frac{3}{2}\)
2x³y = x² + 3