Samacheer Kalvi 12th Maths Guide Chapter 10 சாதாரண வகைக்கெழுச் சமன்பாடுகள் Ex 10.9

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 10 சாதாரண வகைக்கெழுச் சமன்பாடுகள் Ex 10.9 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 10 சாதாரண வகைக்கெழுச் சமன்பாடுகள் Ex 10.9

கொடுக்கப்பட்ட நான்கு மாற்று விடைகளிலிருந்து சரியான அல்லது மிகவும் ஏற்புடைய விடையினைத் தேர்ந்தெடுக்கவும்:
கேள்வி 1.
\(\frac{d^{2} y}{d x^{2}}+\left(\frac{d y}{d x}\right)^{\frac{1}{3}}+x^{\frac{1}{4}}\) எனும் வகைக்கெழுச் சமன்பாட்டின் வரிசை மற்றும் படி முறையே
(1) 2, 3
(2) 3, 3
(3) 2, 6
(4) 2, 4
விடை:
(1) 2, 3
குறிப்பு:

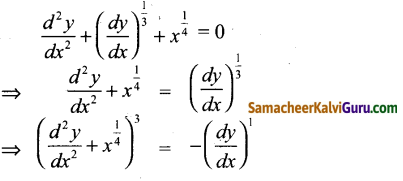
வரிசை 2, படி 3.

கேள்வி 2.
y = A cos (x+ B), இங்கு A, B என்பன எதேச்சை மாறிலிகள் எனும் சமன்பாட்டைக் கொண்ட வளைவரை குடும்பத்தின் வகைக்கெழுச் சமன்பாடு
(1) \(\frac{d^{2} y}{d x^{2}}\) – y = 0
(2) \(\frac{d^{2} y}{d x^{2}}\) + y = 0
(3) \(\frac{d^{2} y}{d x^{2}}\) = 0
(4) \(\frac{d^{2} x}{d y^{2}}\) = 0
விடை:
(2) \(\frac{d^{2} y}{d x^{2}}\) + y = 0

குறிப்பு :
\(\frac{d y}{d x}\) = -Asin (x + B)
\(\frac{d^{2} y}{d x^{2}}\) -A cos (x + B) =-y
⇒ \(\frac{d^{2} y}{d x^{2}}\) + y = 0

கேள்வி 3.
\(\sqrt{\sin x}\) (dx + dy) = \(\sqrt{\cos x}\) (dx – dy) எனும் வகைக்கெழுச் சமன்பாட்டின் வரிசை மற்றும் படி
(1) 1, 2
(2) 2, 2
(3) 1, 1
(4) 2, 1
விடை:
(3) 1, 1

குறிப்பு:

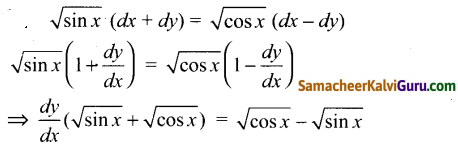
வரிசை 1, படி 1

கேள்வி 4.
மையம் (h, k) மற்றும் ஆரம் ‘a’ கொண்ட எல்லா வட்டங்களின் வகைக்கெழுச் சமன்பாட்டின் வரிசை
(1) 2
(2) 3
(3) 4
(4) 1
விடை:
(1) 2
குறிப்பு:
வட்டத்தின் சமன்பாடு (x – h)² + (y – k)² = a²
இரண்டு மாறிலிகள் உள்ளதால், வரிசை 2 ஆகும்.

கேள்வி 5.
y = Ae^x + Be^-x இங்கு A, B என்பன ஏதேனும் ஈர மாறிலிகள், எனும் வளைவரைத் தொகுதியின் வகைக்கெழுச் சமன்பாடு
(1) \(\frac{d^{2} y}{d x^{2}}\) + y = 0
(2) \(\frac{d^{2} y}{d x^{2}}\) – y = 0
(3) \(\frac{d y}{d x}\) + y = 0
(4) \(\frac{d y}{d x}\) – y = 0
விடை:
(2) \(\frac{d^{2} y}{d x^{2}}\) – y = 0
குறிப்பு :
y = Ae^x + Be^-x
\(\frac{d y}{d x}\) = Ae^x + Be^-x
\(\frac{d^{2} y}{d x^{2}}\) = Ae^x + Be^-x = -y
⇒ \(\frac{d^{2} y}{d x^{2}}\) – y = 0

கேள்வி 6.
\(\frac{d y}{d x}=\frac{y}{x}\) எனும் வகைக்கெழுச் சமன்பாட்டின் பொதுத்தீர்வு
(1) xy = k
(2) y = k log x
(3) y = kx
(4) logy = kx
விடை:
(3) y = kx

குறிப்பு :
\(\frac{d y}{d x}=\frac{y}{x}\)
⇒ \(\frac{d y}{y}=\frac{d x}{x}\)
⇒ logy = log x + log k
⇒ log y = log kx
⇒ y = kx

கேள்வி 7.
2x\(\frac{d y}{d x}\) – y = 3 எனும் வகைக்கெழுச்சமன்பாட்டின் தீர்வு குறிப்பிடுவது
(1) நேர்க்கோடுகள்
(2) வட்டங்கள்
(3) பரவளையம்
(4) நீள்வட்டம்
விடை:
(3) பரவளையம்

குறிப்பு:
2x\(\frac{d y}{d x}\) – y = 3
⇒ 2x\(\frac{d y}{d x}\) = 3 + y
⇒ \(2 \frac{d y}{3+y}=\frac{d x}{x}\)
⇒ 2 log (3 + y) = log x + log c
⇒ log(3 + y)² = log.x c.
⇒ (3 + y)² = xc
இது ஒரு பரவளையம் ஆகும்.

qm 8.
\(\frac{d y}{d x}\) + p(x)y = 0 ன் தீர்வு
(1) y = ce^{\(\int p d x\)}
(2) y = ce^{–\(\int p d x\)}
(3) x = ce^{–\(\int p d y\)}
(4) x = ce^{\(\int p d y\)}
விடை:
(2) y = ce^{–\(\int p d x\)}

குறிப்பு:

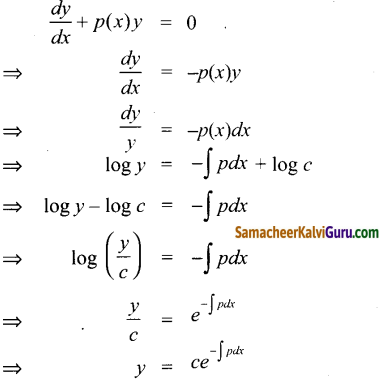
கேள்வி 9.
\(\frac{d y}{d x}+y=\frac{1+y}{\lambda}\) என்ற வகைக்கெழு சமன்பாட்டின் தொகையீட்டுக் காரணி
(1) \(\frac{x}{e^{\lambda}}\)
(2) \(\frac{e^{\lambda}}{x}\)
(3) λe^x
(4) e^x
விடை:
(2) \(\frac{e^{\lambda}}{x}\)

குறிப்பு:

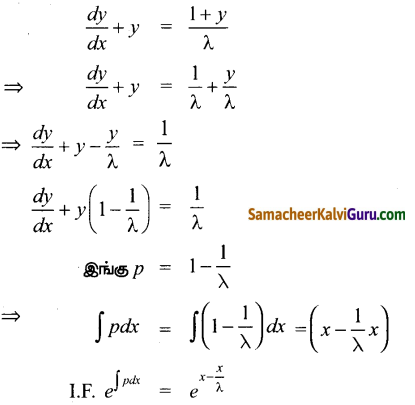
கேள்வி 10.
\(\frac{d y}{d x}\) = P(x)y = Q(x) என்ற வகைக்கெழுச் சமன்பாட்டின் தொகையீட்டுக் காரணி x எனில், P(x) என்பது
(1) 1
(2) \(\frac{x^{2}}{2}\)
(3) \(\frac{1}{x}\)
(4) \(\frac{1}{x^{2}}\)
விடை:
(3) \(\frac{1}{x}\)

குறிப்பு:
e^{\(\int p d x\)} = x
⇒ log e^{\(\int p d x\)} = log x ⇒ \(\int\) pdx = log x
d(\(\int\) pdx) = d(log x)
⇒ p = \(\frac{1}{x}\)

கேள்வி 11.
y(s) = 1 + \(\frac{d y}{d x}+\frac{1}{1.2}\left(\frac{d y}{d x}\right)^{2}+\frac{1}{1.2 .3}\left(\frac{d y}{d x}\right)^{3}+\ldots\)
எனும் வகைக்கெழுச் சமன்பாட்டின் படி
(1) 2
(2) 3
(3) 1
(4) 4
விடை:
(3) 1
குறிப்பு:
படி 1.

கேள்வி 12.
p மற்றும் பு என்பன முறையே \(y \frac{d y}{d x}+x^{3}\left(\frac{d^{2} y}{d x^{2}}\right)\) + xy = cosx எனும் வகைக்கெழுச் சமன்பாட்டின் வரிசை மற்றும் படி எனில்,
(1) p < q (2) p = q (3) p > q
(4) இவற்றில் ஏதுமில்லை .
விடை:
(3) p > q
குறிப்பு:
p = 2, q = 1 ∴ p > q

கேள்வி 13.
\(\frac{d y}{d x}+\frac{1}{\sqrt{1-x^{2}}}=0\) எனும் வகைக்கெழுச் சமன்பாட்டின் தீர்வு
(1) y + sin^-1 x = c
(2) x + sin^-1 y = 0
(3) y + 2 sin^-1 x = c
(4) x² + 2 sin^-1 y = 0
விடை:
(1) y + sin^-1 x = c

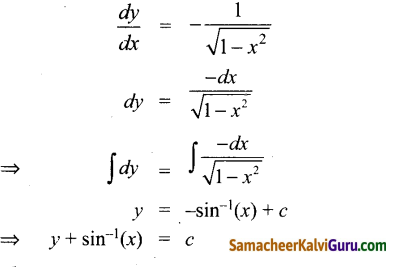
கேள்வி 14.
\(\frac{d y}{d x}\) = 2xy எனும் வகைக்கெழு சமன்பாட்டின் தீர்வு ,
(1) y = Ce^x2
(2) y = 2x² + C
(3) y = Ce^-x2 + C
(4) y = x² + C
விடை:
(1) y = Ce^x2

குறிப்பு:
\(\frac{d y}{d x}\) = 2xy
\(\frac{d y}{y}\) = 2x dx
⇒ log y = \(\) +log c
⇒ log y – log e = x² ⇒ log \(\left(\frac{y}{c}\right)\) = x²
⇒ \(\frac{y}{c}\) = e^x2 ⇒ y = ce^x2

கேள்வி 15.
log \(\left(\frac{d y}{d x}\right)\) = x + y எனும் வகைக்கெழுச் சமன்பாட்டின் தீர்வு
(1) e^x + e^y = C
(2) e^x + e^-y = C
(3) e^-x + e^y = C
(4) e^-x + e^-y = C
விடை:
(2) e^x + e^-y = C

குறிப்பு:
log \(\left(\frac{d y}{d x}\right)\) = x + y
⇒ \(\frac{d y}{d x}\) = e^x+y = e^x . e^y
⇒ \(\frac{d y}{e^{y}}\) = e^x dx
⇒ e^-y dx = e^x dx
⇒ \(\int\) e^-y dy = \(\int\) e^x dx
⇒ -e^-y = e^x + c
⇒ e^x + e = c

கேள்வி 16.
\(\frac{d y}{d x}\) = 2^y-x ன் தீர்வு
(1) 2^x + 2^y = C
(2) 2^x – 2^y = C
(3) \(\frac{1}{2^{x}}-\frac{1}{2^{y}}=C\)
(4) x + y = c
விடை:
(3) \(\frac{1}{2^{x}}-\frac{1}{2^{y}}=C\)

குறிப்பு:

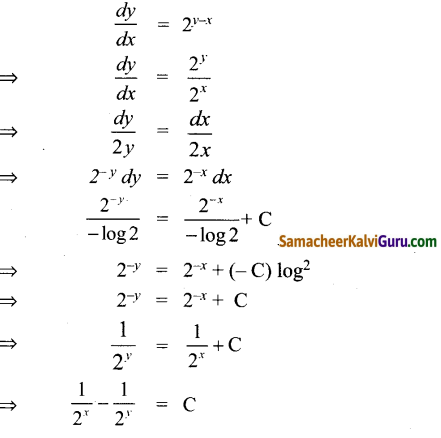
கேள்வி 17.
\(\frac{d y}{d x}=\frac{y}{x}+\frac{\phi\left(\frac{y}{x}\right)}{\phi^{\prime}\left(\frac{y}{x}\right)}\)
எனும் வகைக்கெழுச் சமன்பாட்டின் தீர்வு
(1) xΦ \(\left(\frac{y}{x}\right)\) = k
(2) Φ \(\left(\frac{y}{x}\right)\) = kx
(3) yΦ \(\left(\frac{y}{x}\right)\) = k
(4) Φ \(\left(\frac{y}{x}\right)\) = ky
விடை:
(2) Φ \(\left(\frac{y}{x}\right)\) = kx

குறிப்பு:
\(\frac{d y}{d x}=\frac{y}{x}+\frac{\phi\left(\frac{y}{x}\right)}{\phi^{\prime}\left(\frac{y}{x}\right)}\)
⇒ \(\frac{d y}{d x}\) = e^x+y = e^x . e^y

கேள்வி 18.
\(\frac{d y}{d x}\) + Py = Q , எனும் நேரியல் வகைக்கெழுச் சமன்பாட்டின் தொகையீட்டுக் காரணி sin x எனில், P என்பது
(1) log sinx
(2) cos X
(3) tan x
(4) cot x
விடை:
(4) cot x

குறிப்பு:
e^{\(\int p d x\)} = sinx
= \(\int\) pdx = log sinx
⇒ \(\frac{d}{d x}\left(\int p d x\right)\) = \(\frac{d}{d x}\) (log(sin x))
p = \(\frac{1}{\sin x}\) × cos x = cot x

கேள்வி 19.
வரிசை n மற்றும் n + 1 கொண்ட வகைக்கெழுச் சமன்பாடுகளின் பொதுத் தீர்வுகளில் உள்ள மாறத்தக்க மாறிலிகளின் எண்ணிக்கை முறையே
(1) n – 1, n
(2) n, n + 1
(3) n + 1, n + 2
(4) n + 1, n
விடை:
(2) n, n +1

கேள்வி 20.
மூன்றாம் வரிசை வகைக்கெழுச் சமன்பாட்டின் குறிப்பிட்டத் தீர்வில் உள்ள மாறத்தக்க மாறிலிகளின் எண்ணிக்கை
(1) 3
(2) 2
(3) 1
(4) 0
விடை:
(4) 0

கேள்வி 21.
\(\frac{d y}{d x}=\frac{x+y+1}{x+1}\) எனும் வகைக்கெழுச் சமன்பாட்டின் தொகையீட்டுக் காரணி
(1) \(\frac{1}{x+1}\)
(2) x +1
(3) \(\frac{1}{\sqrt{x+1}}\)
(4) \(\sqrt{x+1}\)
விடை:
(1) \(\frac{1}{x+1}\)

குறிப்பு:

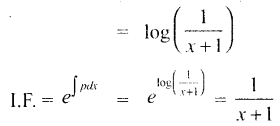
கேள்வி 22.
ஏதேனும் ஒரு வருடம் – ல் உள்ள P-ன் பெருக்க வீதமானது மக்கள் தொகைக்கு விகிதமாக அமையும் எனில், பின்னர்
(1) P = Ce^kt
(2) P = Ce^-kt
(3) P = Ckt
(4) P = C
விடை:
(1) P = Ce^kt
குறிப்பு :

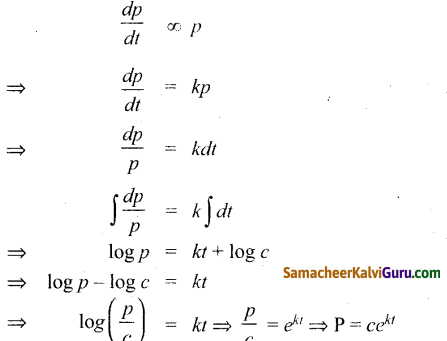
கேள்வி 23.
t எனும் நேரத்திற்குப் பிறகு மீதமுள்ள ஒரு பொருளின் அளவு P ஆகும். பொருள் ஆவியாகும் வீதமானது அந்நேரத்தில் மீதமிருக்கும் பொருளின் அளவிற்கு விகிதமாக அமைந்துள்ளது எனில், பின்னர்
(1) P = Ce^kt
(2) P = Ce^-kt
(3) P = Ckt
(4) Pt = C
விடை:
(2) P = Ce^-kt
குறிப்பு:

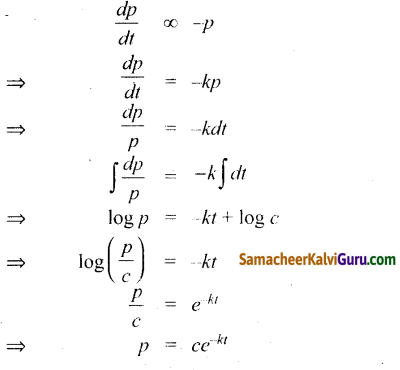
கேள்வி 24.
\(\frac{d y}{d x}=\frac{a x+3}{2 y+f}\) எனும் வகைக்கெழுச் சமன்பாட்டின் தீர்வு ஒரு வட்டத்தைக் குறிக்குமானால், a-ன் மதிப்பு
(1) 2
(2) -2
(3) 1
(4) -1
விடை:
(2) 2
குறிப்பு:

இது வட்டத்தை குறிப்பதால் x² இன் கெழு = y² இன் கெழு
\(\frac{a}{2}\) = -1 ⇒ a = -2

கேள்வி 25.
y = f(x) எனும் வளைவரையின் ஏதேனும் ஒரு புள்ளியிடத்து சாய்வு \(\frac{d y}{d x}\) = 3x² எனக் கொடுக்கப் பட்டுள்ளது. மேலும் வளைவரையானது (-1, 1) புள்ளி வழியாகச் செல்கிறது எனில், வளைவரையின் சமன்பாடு
(1) y = x³ + 2
(2) y = 3x² + 4
(3) y = 3x³ + 4
(4) y = x³ + 5
விடை:
(1) y = x³ + 2

குறிப்பு :
\(\frac{d y}{d x}\) = 3x²
⇒ dy = 3x² dx ⇒ y = \(\frac{3 x^{3}}{3}\) + c
இது (-1, 1) என்ற புள்ளி வழி செல்வதால்,
1 = (-1)³ + c ⇒ 1 = -1 + c ⇒ c = 2
∴ வளைவரையின் சமன்பாடு y = x³ + 2