Samacheer Kalvi 12th Maths Guide Chapter 10 சாதாரண வகைக்கெழுச் சமன்பாடுகள் Ex 10.8

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 10 சாதாரண வகைக்கெழுச் சமன்பாடுகள் Ex 10.8 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 10 சாதாரண வகைக்கெழுச் சமன்பாடுகள் Ex 10.8

கேள்வி 1.
நுண்ணுயிர்களின் பெருக்கத்தில், பாக்டீரியாக் களின் எண்ணிக்கையின் பெருக்க வீதமானது அதில் காணப்படும் பாக்டீரியாக்களின் எண்ணிக்கையின் விகிதமாக உள்ளது. இப் பெருக்கத்தால் பாக்டீரியாவின் எண்ணிக்கை மும்மடங்காகிறது எனில், 10 மணிநேர முடிவில் பாக்டீரியாக்களின் எண்ணிக்கை என்னவாக இருக்கும்?
தீர்வு:
எந்த நேரம் பயிலும் இருக்கும் நுண்ணுயிர்களின் எண்ணிக்கை A என்க’.
கொடுக்கப்பட்டது –\(\frac{d \mathrm{~A}}{\mathrm{~A}}\) α A

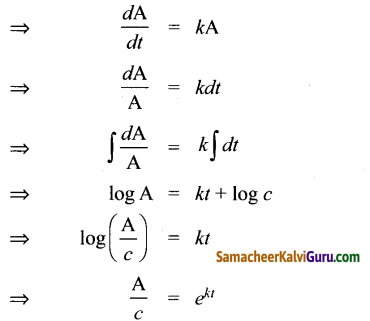
⇒ A = c.e^kt ………. (1)
தொடக்கத்தில் t = 0, எனில் A = A₀ என்க.
∴ A₀ = ce⁰ = c = A₀
∴ A = Ae^kt ………… (2)
கொடுக்கப்பட்டது t = 5 எனில், A = 3A₀
3A₀ = A₀ e^5k = 3 = e^5k
ஆகவே t = 10 எனில், (2) லிருந்து,
A = A₀ e^10k
= A₀ (e^5k)² = A₀ (3)²
⇒ A = 9A₀
எனவே 10 மணி நேர முடிவில் பாக்டீரியாக்களின் எண்ணிக்கை தொடக்கத்தில் இருந்ததை போல் 9 மடங்காகும்.

கேள்வி 2.
ஒரு நகரத்தின் மக்கள் தொகை வளர்ச்சி வீதம் நேரத்தில் உள்ள மக்கள் தொகையின் விகிதமாக அமைந்துள்ளது. மேலும் நகரத்தின் மக்கள் தொகை 40 ஆண்டுகளில் 3,00,000லிருந்து 4,00,000 ஆக அதிகரித்துள்ளது எனக் கொடுக்கப்பட்டுள்ளது எனில், 1 நேரத்தில் அந்நகரத்தின் மக்கள் தொகையைக் காண்க.
தீர்வு:
நகரத்தின் மக்கள் தொகை P என்க.
கொடுக்கப்பட்டது \(\frac{d \mathrm{P}}{d t}\) ∝ P

⇒ P = c.e^kt ………. (1)
கொடுக்கப்பட்டது t = 0 எனில் P = 3,00,000
∴ (1) → 3,00,000 = ce⁰ ⇒ c= 3,00,000
∴ P = 3,00,000 e^kt …. (2)
மீண்டும் t = 40 எனில் P = 4,00,000
∴ (2) ⇒ 4,00,000 = 3,00,000 e^40k

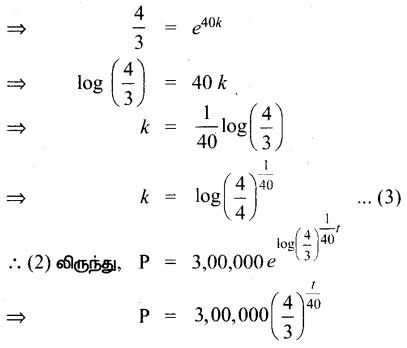
கேள்வி 3.
மின்தடை மற்றும் தன் மின்தூண்டல் கொண்ட ஒரு மின்சுற்றின் மின் இயக்குவிசையின் சமன்பாடு E = RiL \(\frac{d i}{d t}\) ஆ ஆகும். இங்கு E என்பது மின்சுற்றுக்கு கொடுக்கப்படும் மின் இயக்கு விசை , R என்பது மின்தடை மற்றும் L என்பது தன்மின் தூண்டல் எண் ஆகும். E = 0 எனும்போது நேரத்தில், மின்சாரம் ஐக் காண்க.
தீர்வு:
கொடுக்கப்பட்ட E = Ri + L \(\frac{d i}{d t}\)
\(\frac{\mathrm{E}}{\mathrm{L}}=\frac{\mathrm{R} i}{\mathrm{~L}}+\frac{d i}{d t}\)
⇒ \(\frac{\mathrm{R} i}{\mathrm{~L}}+\frac{d i}{d t}=\frac{\mathrm{E}}{\mathrm{L}}\)
இது ஒரு நேரியல் வகைக்கெழு சமன்பாடு ஆகும்.
இங்கு P = \(\frac{\mathrm{R}}{\mathrm{L}}\) மற்றும் Q = \(\frac{\mathrm{E}}{\mathrm{L}}\)

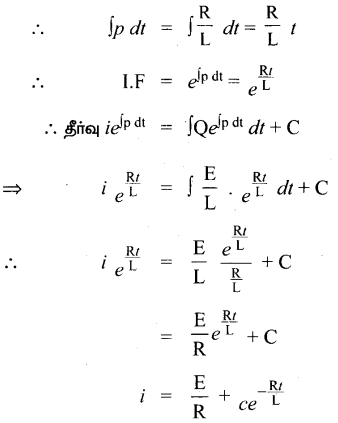
E = 0 எனில்.
i = 0 + ce^{\(-\frac{\mathrm{R} t}{\mathrm{~L}}\)}
⇒ i = ce^{\(-\frac{\mathrm{R} t}{\mathrm{~L}}\)}

கேள்வி 4.
வினாடிக்கு 10 மீட்டர் வேகத்தில் இயங்கும் ஒரு மின்விசைப் படகின் இயந்திரம் நிறுத்தப்படுகிறது. அதன் பின்னர் ஏதேனும் ஒரு நேரத்தில் (இயந்திரம் நிறுத்தப்பட்ட பிறகு ) மின் விசைப் படகின் வேகம் குறையும் வீதமானது அந்நேரத்தில் அதன் திசைவேகத்திற்கு சமமாக உள்ளது எனக் கொடுக்கப்பட்டுள்ளது. இயந்திரம் நிறுத்தப்பட்ட 2 வினாடிகளுக்குப் பிறகு விசைப்படகின் திசைவேகம் காண்க.
தீர்வு:
V என்பது திசைவேகம் மற்றும் திசை வேகம் குறையும் வீதமானது (குறை முடுக்கம்) –\(\frac{d v}{d t}\) என்க
கொடுக்கப்பட்டது \(\frac{d v}{d t}\) = -V
மாறிகளைப் பிரிக்க,
\(\frac{d v}{v}\) = -dt
⇒ \(\int \frac{d v}{v}\) = – \(\int\) dt
⇒ log v = -t + log C
⇒ log v – log C = -t
⇒ log \(\left(\frac{v}{C}\right)\) – -t
⇒ \(\frac{v}{C}\) = e^-t
⇒ v = Ce^-t …………(1)
கொடுக்கப்பட்ட t = 0 எனில், v= மீ/வினாடி
∴ (1) லிருந்து, 10 = Ce⁰ = C = 10
∴ (1) v = 10e^-t
t= 2 எனில், y = 10e^-2
⇒ v = \(\frac{10}{e^{2}}\)

கேள்வி 5.
வருடத்திற்கு 5% தொடர் கூட்டு வீதத்தில் ஒருவர் ரூபாய் 10,000-த்தை வங்கிக் கணக்கில் முதலீடு செய்கிறார். 18 மாதங்களுக்குப் பின்னர் அவர் வங்கிக் கணக்கில் எவ்வளவு தொகை இருக்கும்?
தீர்வு:
நேரம் tயில் முதலீட்டுத் தொகை P என்க.
கொடுக்கப்பட்ட விகிதம் = 5%
∴ \(\frac{d \mathrm{P}}{d t}=\mathrm{P}\left(\frac{5}{100}\right)\) = 0.05P
⇒ \(\frac{d \mathrm{P}}{\mathrm{P}}\) = 0.05dt [மாறிகளை பிரிக்க]
தொகையிட,
\(\int \frac{d P}{P}\) = 0.05 \(\int\) dt
⇒ log P = 0.051 + log C
⇒ log P – log C = 0.05 t
⇒ log\(\left(\frac{P}{C}\right)\) = 0.05t
⇒ \(\frac{\mathrm{P}}{\mathrm{C}}\) = e^0.05t
⇒ P = Ce^0.05t ……………. (1)
கொடுக்கப்பட்டது t = 0, P = ₹10,000
(1) ல் பிரதியிட கிடைப்பது,
⇒ . 10,000 = C e⁰
⇒ C = 10,000
∴ (1) லிருந்து, P = 10,000 e^0.05t
t = 18 மாதங்கள் = 1/2 வருடங்கள் = \(\frac{3}{2}\) வருடங்கள் எனில் கிடைப்பது,
P = 10,000 e^{0.05(\(\frac{3}{2}\))}
∴ P = 10,000 e^0.075

கேள்வி 6.
ஒரு மாதிரியில் காணப்படும் கதிரியக்க அணுக்கருக்கள் சிதைவுறும் வீதமானது அந்நேரத்தில் அந்த மாதிரியில் காணப்படும் அணுக்கருக்களின்
எண்ணிக்கைக்கு விகிதமாக அமைந்துள்ளது. 100 ஆண்டுகால இடைவெளியில் ஒரு மாதிரியில் ஆரம்பத்தில் காணப்படும் கதிரியக்க அணுக்கருக்களின் எண்ணிக்கையில் 10 சிதைவுறுகிறது. 1000 ஆண்டுகள் முடிவில் ஆரம்பத்தில் காணப்படும் கதிரியக்க அணுக்கருக்களின் எண்ணிக்கையில் எவ்வளவு மீதமிருக்கும்?
தீர்வு:
நேரம் -யில் மாதிரியில் காணப்படும் கதிரியக்க அணுக்கருக்கள் N என்க. N₀ தொடக்கநிலையில் உள்ள கதிரியக்க அணுக்கருக்கள் என்க. பிறகு
\(\frac{d \mathrm{~N}}{d t}\) ∞ N
⇒ \(\frac{d \mathrm{~N}}{d t}\) = -λN,
இங்கு λ > 0 ஒரு மாறிலி
⇒ \(\frac{d \mathrm{~N}}{d t}\) = -λdt
\(\int \frac{d \mathrm{~N}}{\mathrm{~N}}\) = -λ \(\int\) dt
⇒ log N = -λ t + C ………….(1)
t = 0ல், நம்மிடம் N = N₀
∴ log N₀ = 0 + C
⇒ C = log N₀
∴ (1) லிருந்து, log N = – λ t + log N₀ = logN₀
⇒ \(\log \frac{\mathrm{N}}{\mathrm{N}_{0}}\) = – λ t …………(2)
100 ஆண்டுகளில் ஒரு மாதிரியின் ஆரம்பத்தில் காணப்படும் கதிரியக்க அணுக்கருக்களின் எண்ணிக்கையில் 10% சிதைவுறுகிறது என கொடுக்கப்பட்டுள்ளது.


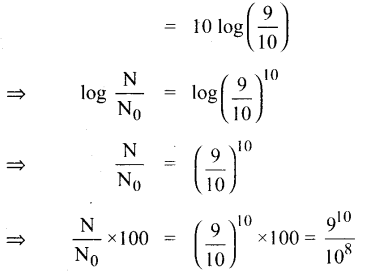
எனவே 1000 ஆண்டுகள் முடிவில் மீதமிருக்கும் அணுக்கருக்களின் எண்ணிக்கை \(\frac{9^{10}}{10^{8}}\)% ஆகும்.

கேள்வி 7.
வெப்பநிலை 25°C-ஆக உள்ள ஒரு அறையில் வைக்கப்பட்டுள்ள நீரின் வெப்பநிலை 100°C ஆகும். 10 நிமிடங்களில் நீரின் வெப்பநிலை 80°C ஆகக் குறைந்து விடுகிறது எனில், (i) 20 நிமிடங்களுக்குப் பின்னர் நீரின் வெப்பநிலை (ii) வெப்பநிலை 40°C ஆக இருக்கும் போது நேரம் காண்க. [\(\log _{e} \frac{11}{15}\) = -0.3101; log_e 5= 1.6094
தீர்வு:
நீரின் வெப்பநிலை நேரம் 1-யில் T என்க. நியூட்டனின் குளிர்ச்சி அடையும் விதிப்படி,


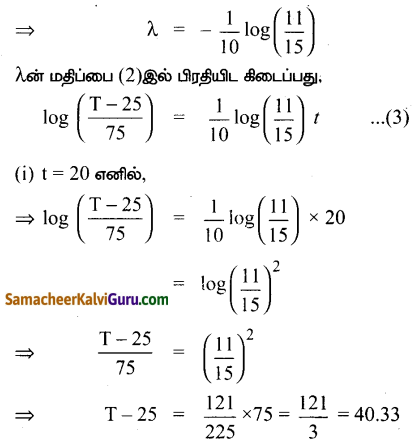
⇒ T = 40.33 + 25
= 65.33°C 20
நிமிடங்களுக்குப் பின்னர் நீரின் வெப்பநிலை 65.33°C

(ii) T = 40°C என்பதை (3) ல் பிரதியிட கிடைப்பது

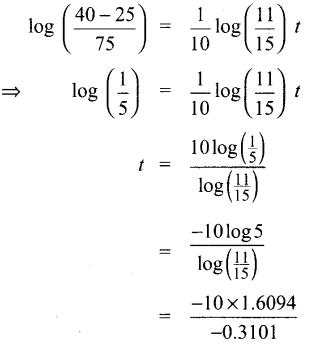
∴ t = 53.46 நிமிடங்கள்

கேள்வி 8.
காலை 10.00 மணிக்கு பெண் ஒருவர் தன்னுடைய மைக்ரோ அலை சமையல் அடுப்பிலிருந்து சூடான காபியை வெளியில் எடுத்து அது குளிர்வதற்காக அருகில் உள்ள சமையல் அறையில் வைக்கிறார். அந்நேரத்தில் காபியின் வெப்பநிலை 180°F ஆகும். மேலும், 10 நிமிடங்களுக்குப் பிறகு அதன் வெப்பநிலை 160°F ஆகும். சமையல் அறையின் நிலையான வெப்பநிலை 70°F எனில்
(i) காலை 10.15 மணிக்கு காபியின் வெப்பநிலைக் காண்க.
(ii) வெப்பநிலை 130°F- க்கும் 140°F-க்கும் இடைப்பட்டதாக இருக்கும்போது அவர் காபியை அருந்த நினைத்தால், எந்நேரத்திற்கு இடையில் அவர் காபியை அருந்த வேண்டும்?
தீர்வு:
நேரம். யில் காபியின் வெப்பநிலை T மற்றும் சமையல் அறையின் வெப்பநிலை T_m ஆகும். நியூட்டனின் குளிர்ச்சி அடையும் விதிப்படி,

⇒ T – 70 = Ce^Kt ………… (1)
t = 0 எனில் T = 180°F
∴ 180° – 70° = Ce⁰
⇒ C = 110°
∴ (1) ⇒ T – 70 – 110 e^Kt …………. (2)
t = 0 எனில் T= 160
∴ 160 – 70 == 110 e^10K
⇒ 90 = 110 e^10K
⇒ e^K = \(\left(\frac{9}{11}\right)^{\frac{1}{10}}\) …………. (3)

(i) t = 15 எனில் (2) லிருந்து,


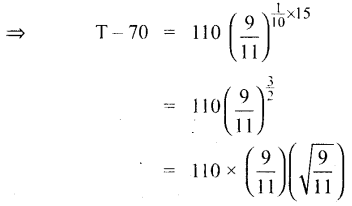
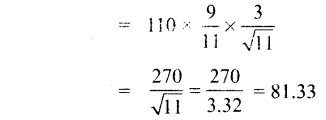
⇒ T = 81.33 + 70 = 151.3F
∴ T = 151.3F
∴ காலை 10.15 மணிக்கு காபியின் வெப்பநிலை 151.3F

(ii) T = 130F எனில் (2)லிருந்து,
T – 70 = 110 e^Kt ………… (2)
⇒ 130- 70 = 110 e^Kt
60 = 110 e^Kt

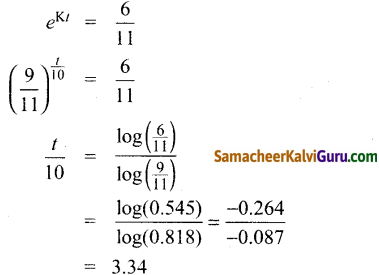
t = 30.34 நிமிடங்கள்.
T = 140F, (2) லிருந்து
140 – 70 = 110 e^Kt ……………. (2)
⇒ 70 = 110 e^Kt

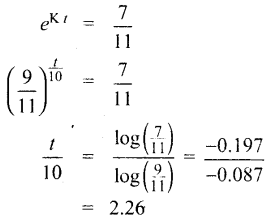
t = 22.6 நிமிடங்கள்
∴ 10.22 நிமிடத்திலிருந்து 10.30 நிமிடத்திற்குள் அவர் காபியை அருந்த வேண்டும்.

கேள்வி 9.
ஒரு பாத்திரத்தில் 100°C வெப்பநிலையில் கொதித்துக் கொண்டிருக்கும் நீரானது t= 0 எனும் நேரத்தில் அடுப்பின் மீது இருந்து இறக்கி குளிர்வதற்காக சமையலறையில் வைக்கப்படுகிறது. 5 நிமிடங்களுக்குப் பிறகு நீரின் வெப்பநிலை 80°C ஆகக் குறைகிறது. மேலும், அடுத்த 5 நிமிடங்களுக்குப் பிறகு நீரின் வெப்பநிலை 65°C-ஆக குறைகிறது எனில், சமையலறையின் வெப்பநிலையைக் காண்க.
தீர்வு:
T கொதிக்கும் நீரின் வெப்பநிலை என்க மற்றும் சமையலறையின் வெப்பநிலை T… என்க. நியூட்டனின் குளிர்ச்சி அடையும் விதிப்படி,

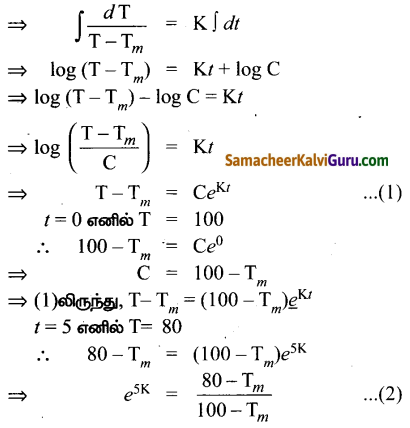
t = 10 எனில், T = 65
(2) ⇒ 65 – T_m = (100 – T_m)e^10K
= (100 – T_m)(e^5K)²
= (100 – T_m) \(\left(\frac{80-\mathrm{T}_{m}}{100-\mathrm{T}_{m}}\right)^{2}\)
[(2)-ஐ பயன்படுத்தி]
⇒ 65 – T_m = \(\frac{\left(80-\mathrm{T}_{m}\right)^{2}}{100-\mathrm{T}_{m}}\)
⇒ 6500-65 T_m – 100T_m + T_m² = 6400+ T_m²– 160T_m
⇒ 6500 – 6400 = 165T_m – 160T_m
⇒ 100 = 5T_m
T_m = \(\frac{100}{5}\) = 20°C
சமையலறையின் வெப்பநிலை 20°C.

கேள்வி 10.
ஆரம்பத்தில் ஒரு தொட்டியில் 50 லிட்டர் தூய்மையான தண்ணீர் உள்ளது. தொடக்க நேரம் 1 = 0-ல் ஒரு லிட்டர் நீரில் 2 கிராம் வீதம் கரைக்கப்பட்ட உப்புக் கரைசலானது ஒரு நிமிடத்திற்கு 3 லிட்டர் வீதம் தொட்டியில் விடப்படுகிறது. இக்கலவையானது தொடர்ந்து கலக்கப்பட்டு சீராக வைக்கப்படுகிறது. மேலும், அதே நேரத்தில் நன்கு கலக்கப்பட்ட இக்கலவையானது அதே வீதத்தில் தொட்டியிலிருந்து வெளியேறுகிறது. t = 0 எனும் ஏதேனும் ஒரு நேரத்தில் தொட்டியில் உள்ள உப்பின் அளவினைக் காண்க.
தீர்வு:
தொட்டியில் உள்ள உப்பின் அளவு நேரம் 1-யில், x(t) என்க .
அதனுடைய மாறும் வீதம்
\(\frac{d x}{d t}\) = விடப்படும் வீதம் வெளியேறும் வீதம்
இங்கு, ஒரு நிமிடத்திற்கு 2 கிராம் வீதம் 3 லிட்டர் நீரில் விடப்படும் உப்புக்கரைசலின் வீதம் = 6 கிராம் உப்பு (3 × 2 = 6)
வெளியேறும் உப்பின் அளவு \(\frac{3}{50}\) மடங்கு x = \(\frac{3x}{50}\)

t = 0 எனில், x = 0
[ொடக்க நேரத்தில் நீர் உப்பில்லாமல் தூய்மையாக இருப்பதால்]
⇒ 0 – 100 = Ce⁰
⇒ C = – 100
(1) லிருந்து x – 100 = – 100 e^{\(-\frac{3 t}{50}\)}
⇒ x = 100 – 100 e^{\(-\frac{3 t}{50}\)}
⇒ x = 100(1 – e^{\(-\frac{3 t}{50}\)})
t நேரத்தில் தொட்டி நீரில் உள்ள உப்பின் அளவு
x = 100(1 – e^{\(-\frac{3 t}{50}\)})