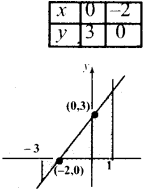
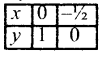
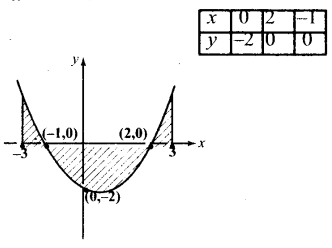
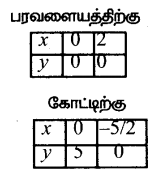
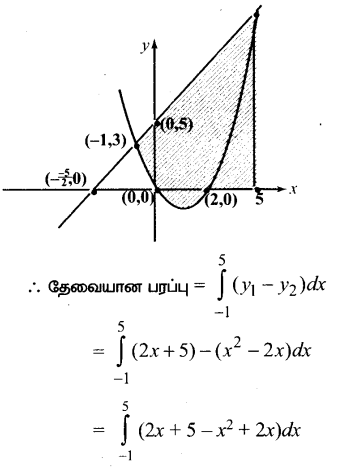
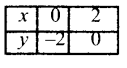
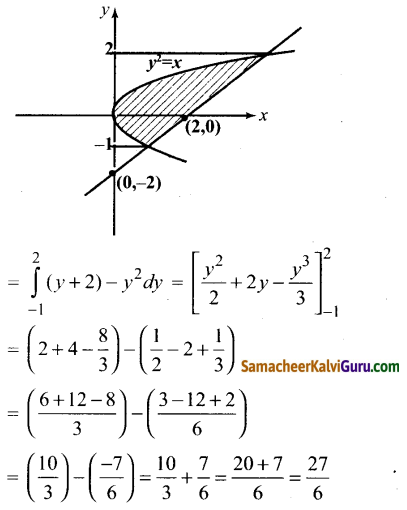
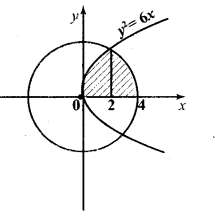
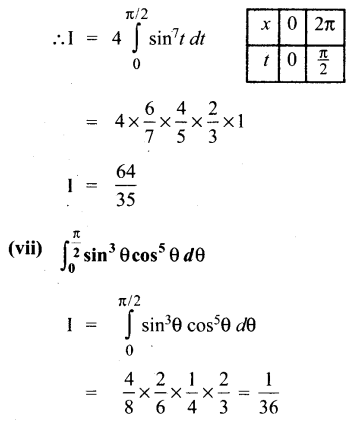
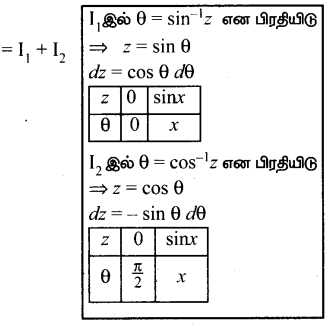
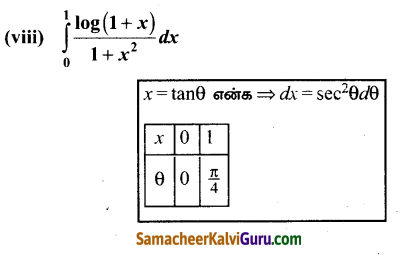
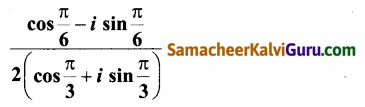
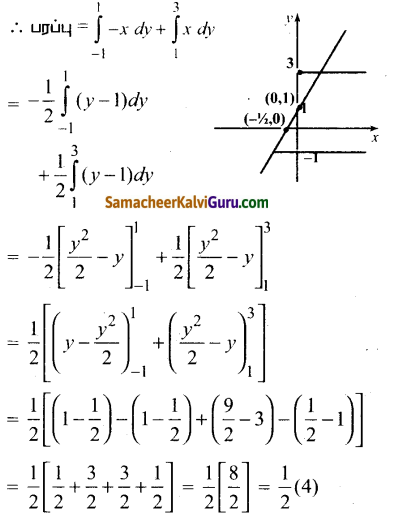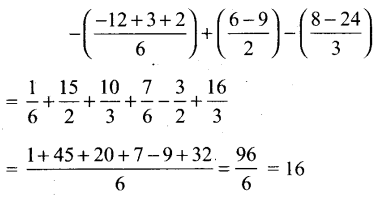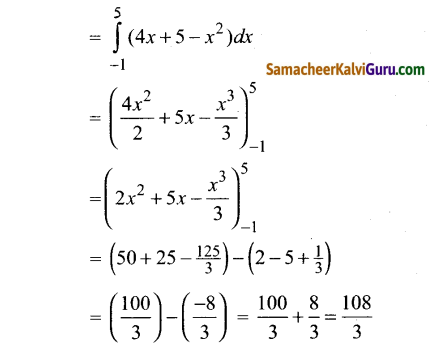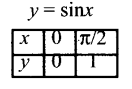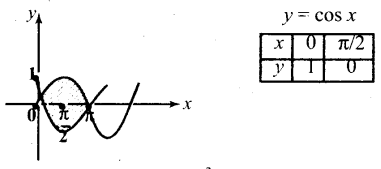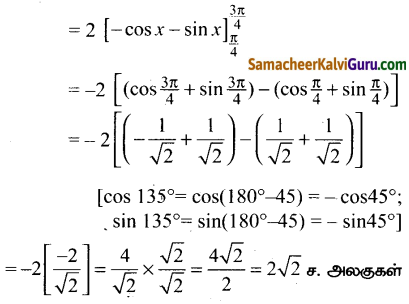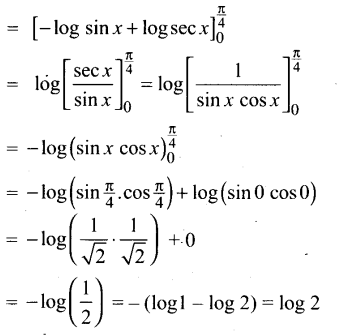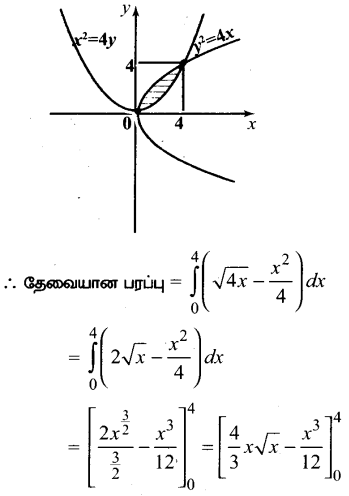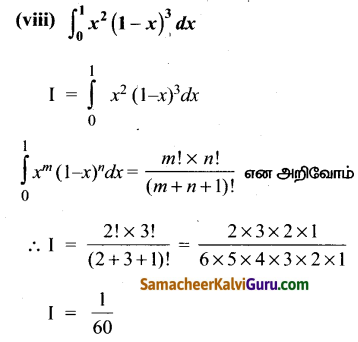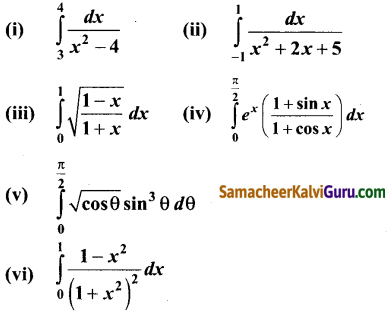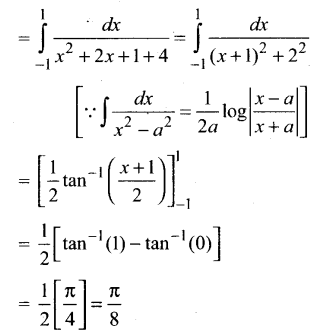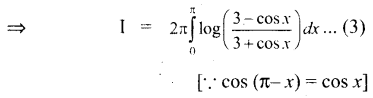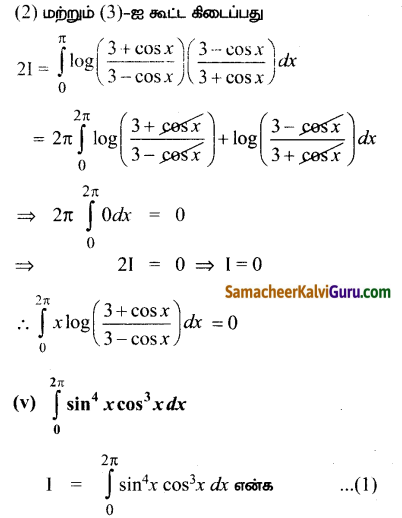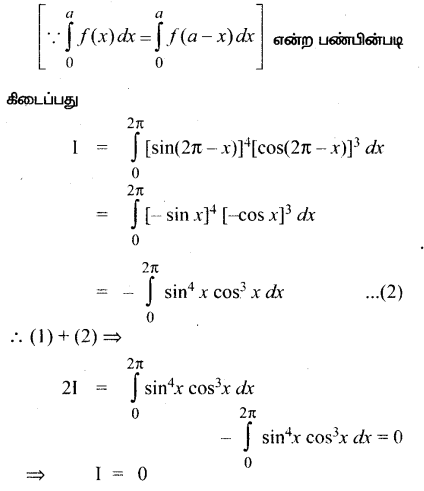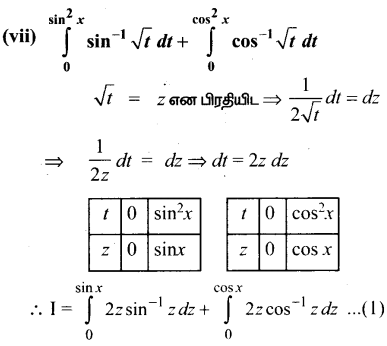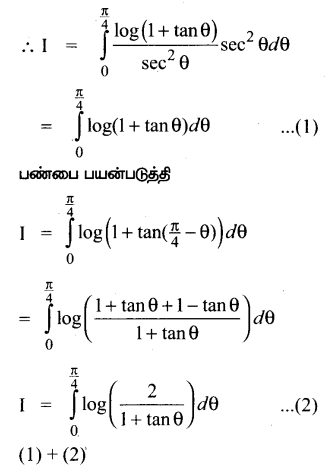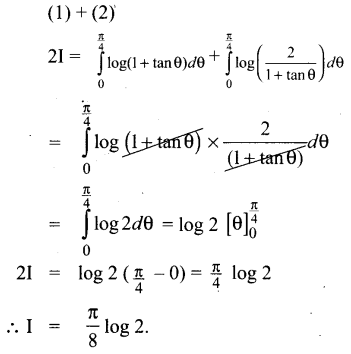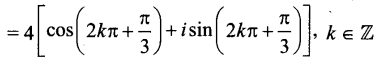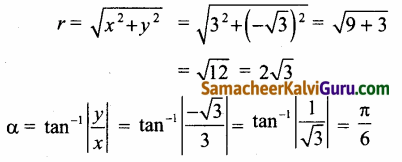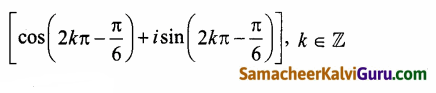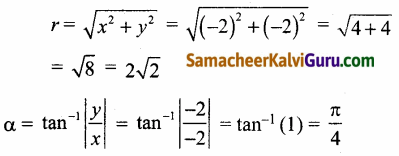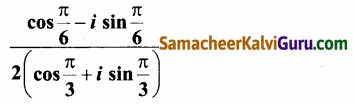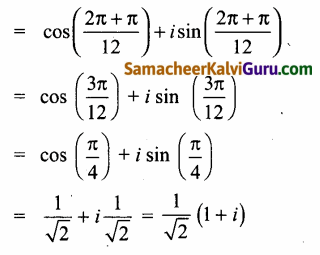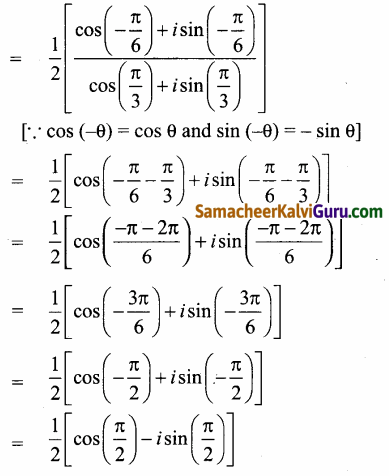Subject Matter Experts at SamacheerKalviGuru.com have created Tamil Nadu State Board Samacheer Kalvi 3rd Maths Book Answers Solutions Guide Pdf Free Download of Term 1, 2, 3 in English Medium and Tamil Medium are part of 3rd Standard Samacheer Book Solutions.
Let us look at these TN State Board New Syllabus Samacheer Kalvi 3rd Std Maths Guide Pdf of Text Book Back Questions and Answers Term 1, 2, 3, Chapter Wise Important Questions, Study Material, Question Bank, Notes, Formulas and revise our understanding of the subject.
Tamilnadu State Board Samacheer Kalvi 3rd Maths Book Back Answers Solutions Guide Term 1, 2, 3.
Samacheer Kalvi 3rd Standard Maths Book Solutions Back Answers Guide
3rd Standard Maths Guide Samacheer Kalvi Term 1
- Chapter 1 Geometry
- Chapter 2 Numbers
- Chapter 3 Patterns
- Chapter 4 Measurements
- Chapter 5 Time
- Chapter 6 Information Processing
Samacheer Kalvi 3rd Standard Maths Book Solutions Term 2
- Chapter 1 Numbers
- Chapter 2 Patterns
- Chapter 3 Measurements
- Chapter 4 Time
- Chapter 5 Information Processing
Samacheer Kalvi 3rd Standard Maths Book Answers Term 3
- Chapter 1 Geometry
- Chapter 2 Numbers
- Chapter 3 Patterns
- Chapter 4 Measurements
- Chapter 5 Money
- Chapter 6 Time
- Chapter 7 Information Processing
Samacheer Kalvi 3rd Std Maths Book Solutions in Tamil Medium
Samacheer Kalvi 3rd Maths Book Solutions Term 1
- Chapter 1 வடிவியல்
- Chapter 2 எண்கள்
- Chapter 3 அமைப்புகள்
- Chapter 4 அளவீடுகள்
- Chapter 5 நேரம்
- Chapter 6 தகவல் செயலாக்கம்
Samacheer Kalvi 3rd Maths Book Solutions Term 2
Samacheer Kalvi 3rd Maths Book Solutions Term 3
- Chapter 1 வடிவியல்
- Chapter 2 எண்கள்
- Chapter 3 அமைப்புகள்
- Chapter 4 அளவைகள்
- Chapter 5 பணம்
- Chapter 6 நேரம்
- Chapter 7 தகவல் செயலாக்கம்
We hope these Tamilnadu State Board Samacheer Kalvi Class 3rd Maths Book Solutions Answers Pdf Free Download in English Medium and Tamil Medium will help you get through your subjective questions in the exam.
Let us know if you have any concerns regarding TN State Board New Syllabus Samacheer Kalvi 3rd Standard Maths Guide Pdf of Text Book Back Questions and Answers Term 1, 2, 3, Chapter Wise Important Questions, Study Material, Question Bank, Notes, Formulas, drop a comment below and we will get back to you as soon as possible.