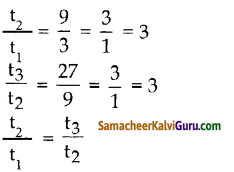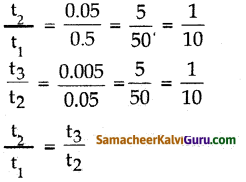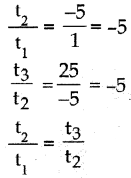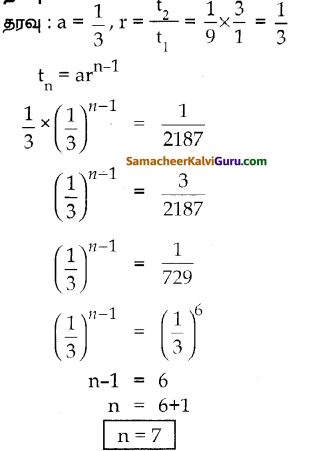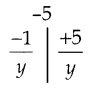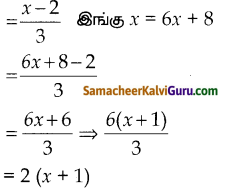Laxmi

Tamilnadu State Board New Syllabus Samacheer Kalvi 10th Maths Guide Pdf Chapter 2 எண்களும் தொடர்வரிசைகளும் Ex 2.4 Textbook Questions and Answers, Notes.

TN Board 10th Maths Solutions Chapter 2 எண்களும் தொடர்வரிசைகளும் Ex 2.4

கேள்வி 1.
பின்வரும் தொடர்வரிசைகளின் அடுத்த மூன்று உறுப்புகளைக் காண்க.
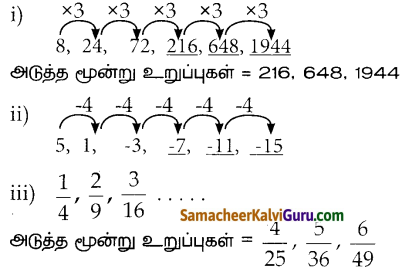
(i) 8, 24, 72, …..
(ii) 5,1,-3,…
(iii) \(\frac{1}{4}, \frac{2}{9}, \frac{3}{16}, \ldots\)
தீர்வு :

கேள்வி 2.
பின்வரும் 1-வது உறுப்புகளைக் கொண்ட தொடர்வரிசைகளின் முதல் நான்கு உறுப்புகளைக் காண்க.
(i) a_n = n³ -2
(ii) a_n = (-1)ⁿ⁺¹ n(n+1)
(iii) a_n = 2n² – 6
தீர்வு :
i) a_n = n³ – 2
a₁= 1³ – 2 = 1 – 2 = -1
a₂ = 2³ – 2 = 8 – 2 = 6
a₃ = 3³ – 2 = 27 – 2 = 25
a₄ = 4³ – 2 = 64 – 2 = 62
முதல் நான்கு உறுப்புகள் = -1, 6, 25, 62.

ii) a_n = (-1)_n+1 n(n+1)
a₁ = (-1)₁₊₁ x 1 x (1 + 1) = 1 x 1 x 2 = 2
a₂ = (-1)₂₊₁x 2 x (2 + 1) = -1 x 2 x 3 = -6
a₃ = (-1)₃₊₁ x 3 x (3 + 1) = 1 x 3 x 4 = 12
a₄ = (-1)₄₊₁ x 4 x (4 + 1) = -1 x 4 x 5 = -20
முதல் நான்கு உறுப்புகள் = 2, -6, 12, -20

iii) a_n = 2n² – 6
a₁ = 2 x 1² – 6 = 2 – 6 = -4
a₂ = 2 x 2² – 6 = 8 – 6 = 2
a₃ = 2 x 3² – 6 = 18 – 6 = 12
a₄ = 2 x 4² – 6 = 32 – 6 = 26
முதல் நான்கு உறுப்புகள் =-4, 2, 12, 26.

கேள்வி 3.
கீழே கொடுக்கப்பட்டுள்ள தொடர்வரிசைகளின் n-வது உறுப்பைக் காண்க.
(i) 2,5,10,17,….
(ii) \(0, \frac{1}{2}, \frac{2}{3}, \ldots\)
(iii) 3,8,13,18,…..
தீர்வு:
i) 2, 5, 10, 17…….
a = n² + 1 இங்கு n = 1, 2, 3, …

(ii) \(0, \frac{1}{2}, \frac{2}{3}, \ldots\)
a_n = \(\frac{\mathrm{n}-1}{\mathrm{n}}\) இங்கு n =1, 2, 3….

iii) 3, 8, 13, 18…
a_n = 5n – 2 இங்கு n = 1, 2, 3….

கேள்வி 4.
கீழ்க்கண்ட தொடர்வரிசைகள் ஒவ்வொன்றிலும் 1-வது உறுப்பு கொடுக்கப்பட்டுள்ளது. அதில் குறிப்பிடப்பட்டுள்ள உறுப்புகளைக் காண்க.
(i) a_n = n ; a₆ மற்றும் a₁₃
(ii) a_n = -(n² – 4); a₄ மற்றும் a₁₁
தீர்வு :

ii) a_n = – (n² – 4); a₄ மற்றும் a₁₁
a₄ = -(4² – 4) = -(16 – 4) = -12
a₁₁ = -(11² – 4) = -(121 – 4) = -117

கேள்வி 5.

என்பது n – வது உறுப்பு எனில், a₈ மற்றும் a₁₅ காண்க.
தீர்வு:
a₈ = ?
n ஒரு இரட்டை எண் எனில் a_n = \(\frac{n^{2}-1}{n+3}\)
a₈ = \(\frac{8^{2}-1}{8+3}=\frac{63}{11}\)
n ஒரு ஒற்றை எண் எனில் a_n = \(\frac{n^{2}}{2 n+1}\)
a₁₅ = \(\frac{15^{2}}{2(15)+1}=\frac{225}{30+1}=\frac{225}{31}\)

கேள்வி 6.
a₁ = 1, a₂ = 1 மற்றும் a_n = 2a_n-1 + a_n-2 n ≥ N எனில், தொடர்வரிசையின் முதல் ஆறு உறுப்புகளைக் காண்க.
தீர்வு :
a_n = 2a_n-1 + a_n-2
a₃ = 2a₂+ a₁ = 2+1 = 3
a₄ = 2a₃+ a₂ = 6 +1 = 7
a₅ = 2a₄ + a₃= 14 + 3 = 17
a₆ = 2a₅ + a₄ = 34 + 7 = 41
முதல் ஆறு உறுப்புகள் = 1, 1, 3, 7, 17, 41

Tamilnadu State Board New Syllabus Samacheer Kalvi 10th Maths Guide Pdf Chapter 2 எண்களும் தொடர்வரிசைகளும் Ex 2.7 Textbook Questions and Answers, Notes.

TN Board 10th Maths Solutions Chapter 2 எண்களும் தொடர்வரிசைகளும் Ex 2.7

கேள்வி 1.
பின்வரும் தொடர்வரிசைகளில் எவை பெருக்குத் தொடர்வரிசையாகும்?
(i) 3,9,27,81,…..
(ii) 4,44,444,4444…………
(iii) 0.5,0.05,0.005,…
(iv) \(\frac{1}{3}, \frac{1}{6}, \frac{1}{12}, \ldots\)
(v) 1,-5,25,-125….
(vi) 120,60,30,18,….
(vii) 16
தீர்வு :
i) 3, 9, 27, 81,…

எனவே இது ஒரு பெருக்குத் தொடர்வரிசை

ii) 4, 44, 444, 4444, .

எனவே இது பெருக்குத்தொடர் வரிசை அல்ல

iii) 0.5, 0.05, 0.005,…
தீர்வு:

எனவே இது பெருக்குத்தொடர் வரிசை ஆகும்.

எனவே இது ஒரு பெருக்குத்தொடர் வரிசை ஆகும்.

v) 1, -5, 25, -125….
தீர்வு :

எனவே இது ஒரு பெருக்குத்தொடர் வரிசை ஆகும்.

vi) 120, 60, 30, 18…
தீர்வு :

எனவே இது ஒரு பெருக்குத்தொடர் வரிசை

கேள்வி 2.
கீழே கொடுக்கப்பட்டுள்ள முதல் உறுப்பு மற்றும் பொதுவிகிதம் உடைய பெருக்குத் தொடர்வரிசையின் முதல் மூன்று உறுப்புகளை எழுதுக.
(i) a = 6, r = 3
(ii) a = √2, r = √2
(iii) a = 1000, r = \(\frac{2}{5}\)
தீர்வு :
i) a = 6, r = 3
பெருக்குத் தொடர் வரிசையில் முதல் மூன்று உறுப்புகள் a, ar, ar² = 6, 6 x 3, 6 x (3)²
= 6, 18, 54

ii) a = √2, r = √2
தீர்வு :
பெருக்குத் தொடர் வரிசையில் முதல் மூன்று உறுப்புகள்
a, ar, ar² = √2, √2 x √2, √2 x (√2)²
= √2, 2, 2√2

iii) a = 1000, r = 2/5
தீர்வு :
பெருக்குத் தொடர் வரிசையில் முதல் மூன்று உறுப்புகள் = a, ar, ar² = 1000, 1000 x \(\frac{2}{5}\) 1000 x \(\left(\frac{2}{5}\right)^{2}\)
= 1000, 400, 160

கேள்வி 3.
729, 243, 81,….. என்ற பெருக்குத் தொடர்வரிசையின் 7-வது உறுப்பைக் காண்க.
தீர்வு :

கேள்வி 4.
x + 6, x + 12 மற்றும் x+15 என்பன ஒரு பெருக்குத் தொடர்வரிசையின் தொடர்ச்சியான மூன்று உறுப்புகள் எனில் , x-யின் மதிப்பைக் காண்க. தீர்வு :
x + 6, x + 12, x + 15 என்பது ஒரு பெருக்குத்தொடர்வரிசையில் அமையும் எனில்
\(\frac{t_{2}}{t_{1}}=\frac{t_{3}}{t_{2}}\)
\(\frac{x+12}{x+6}=\frac{x+15}{x+12}\)
1 = 3
(x+12)(x+12) = (x+6)(x+15)
x² + 24x + 144 = x + 21x + 90
24x + 21x = 90 – 144
3x = -54
x = -18

கேள்வி 5.
பின்வரும் பெருக்குத் தொடர்வரிசையில் உள்ள உறுப்புகளின் எண்ணிக்கையைக் காண்க.
(i) 4, 8, 16,….., 8192
(ii) \(\frac{1}{3}, \frac{1}{9}, \frac{1}{27}, \ldots, \frac{1}{2187}\)
தீர்வு
தரவு : a = 4, r = \(\frac{t_{2}}{t_{1}}=\frac{8}{4}\) = 2

t_n = ar^n-1
4 x (2)^n-1 = 8192
(2)^n-1 = 8192/4
(2)^n-1 = 2048
(2)^n-1 = 2¹¹
n – 1 = 11
n = 11+1
n = 12

(ii) \(\frac{1}{3}, \frac{1}{9}, \frac{1}{27}, \ldots, \frac{1}{2187}\)
தீர்வு :

கேள்வி 6.
ஒரு பெருக்குத் தொடர் வரிசையின் 9-வது உறுப்பு 32805 மற்றும் 6-வது உறுப்பு 1215 எனில், 12-வது உறுப்பைக் காண்க.
தீர்வு :
தரவு : t₉ = 32805
t₆ = 1215
எனில் t₁₂ = ?
ar⁸ = 32805 ——(1)
ar⁵ = 1215 ——-(2)
(1) ÷ (2)
\(\frac{\operatorname{ar}^{8}}{\mathrm{ar}^{5}}=\frac{32805}{1215}\)
32805 ar5 1215
r³ = 27
r = 3
r = 3ஜ (2)ல் பிரதியிட
ar⁵ = 1215

t_n = ar^n-1
t₁₂ = ar^{12 – 1}
t₁₂ = 5(3)¹¹

கேள்வி 7.
ஒரு பெருக்கத்தொடர் வரிசையின் 8-வது உறுப்பு 768 மற்றும் பொது விகிதம் 2 எனில், அதன் 10-வது உறுப்பைக் காண்க.
தீர்வு :
தரவு : t₈ = 768
r = 2
t₁₀ = ?
ar⁷ = 768
a(2)⁷ = 768
a = \(\frac{768}{2^{7}}=\frac{2^{8} \times 3}{2^{7}}\)
a = 6
t_n = ar^n-1
t₁₀ = 6(2)^10-1
= 6 x (2)⁹
= 6 x 512
t₁₀ = 3072

கேள்வி 8.
a,b,c என்பன ஒரு கூட்டுத் தொடர்வரிசையில் அமையும் எனில் 3^a, 3^b 3^c ஒரு பெருக்குத் தொடர்வரிசையில் அமையும் எனக் காட்டுக.
தீர்வு :
தரவு : a, b, c என்பது ஒரு கூட்டுத்தொடர் வரிசை எனவே b – a = c – b [∵ t₂ – t₁ = t₃ – t₂]
2b = a + c
நீருபி 3^a ,3^b, 3^c ஒரு பெருக்குத்தொடர் வரிசை
நீருபி \(\frac{t_{2}}{t_{1}}=\frac{t_{3}}{t_{2}}\)
\(\frac{3^{b}}{3^{a}}=\frac{3^{c}}{3^{b}}\)
3^b-a = 3^c-b
3^b-a = 3^b-a [∵ c – b = b – a]
எனவே 3^a ,3^b, 3^c என்பது ஒரு பெருக்குத்தொடர் வரிசை

கேள்வி 9.
ஒரு பெருக்குத்தொடர்வரிசையில் அடுத்தடுத்த மூன்று உறுப்புகளின் பெருக்கற்பலன் 27 மற்றும் அவைகளில் இரண்டிரண்டு உறுப்புகளின் பெருக்கற் பலனின் கூடுதல் \(\frac { 57 }{ 2 }\) எனில், அந்த மூன்று உறுப்புகளைக் காண்க.
தீர்வு :
பெருக்குத்தொடர் வரிசையில் அடுத்தடுத்த மூன்று உறுப்புகள் = a/r, a, ar
அவற்றின் பெருக்கற்பலன் = 27
a/r x a x ar = 27
a³ = 27
a = 3
அவற்றின் இரண்டிரண்டு உறுப்புகளன் பெருக்கற்பலன்களின் கூடுதல் = \(\frac { 57 }{ 2 }\)


6 + 6r² + 6r = 19r
6r² – 13r + 6 = 0
(6r – 9) (6r – 4) = 0
r = \(\frac { 3 }{ 2 }\) (அல்லது) \(\frac { 2 }{ 3 }\),
a = 3 மற்றும் r = \(\frac { 3 }{ 2 }\) எனில்
மூன்று உறுப்புகள் = 2, 3,9/2
a = 3 மற்றும் r = \(\frac { 2 }{ 3 }\), எனில்
மூன்று உறுப்புகள் = 9/2, 3, 2

கேள்வி 10.
ஒரு நபர் ஒரு நிறுவனத்தில் துணை மேலாளராகப் பணியில் சேர்கிறார். அவருக்கு அந்நிறுவனம் முதல் மாத ஊதியமாக 160,000 வழங்குகிறது மற்றும் ஆண்டு ஊதிய உயர்வு 5% வழங்குவதாக ஒப்புக்கொள்கிறது. 5 வருட முடிவில் அவருடைய மாத ஊதியம் எவ்வளவு?
தீர்வு :
a = 60000
r = \(\frac { 105 }{ 100 }\) [5% உயர்வு)
n = 6 வருடங்கள் (5 வருடங்களுக்கு பிறகு)
t₆ = ar^n-1
= 60000\(\left(\frac{105}{100}\right)^{6-1}\)
= 60000\(\left(\frac{105}{100}\right)^{5}\)
= 60000 x 1.27628
= 76576.6
t₆ = 76577

கேள்வி 11.
சிவமணி ஒரு பணிக்கான நேர்காணலில் பங்கேற்கிறார். அந்நிறுவனம் அவருக்கு இரண்டு விதமான வாய்ப்புகளை வழங்குகிறது.
வாய்ப்பு A : முதல் மாத ஊதியம் ₹20.000 மற்றும் நிச்சயமான 6% ஆண்டு ஊதிய உயர்வு 5 ஆண்டுகளுக்கு . வாய்ப்பு B : முதல் மாத ஊதியம் ₹22.000 மற்றும் நிச்சயமான 3% ஆண்டு ஊதிய உயர்வு 5 ஆண்டுகளுக்கு.
A மற்றும் B ஆகிய இரு வாய்ப்புகளிலும் அவருடைய 4-வது வருட ஊதியம் எவ்வளவு?
தீர்வு :
வாய்ப்பு A:
106) வாய்ப்பு :a= 20000,r = \(\frac { 106 }{ 100 }\), n = 4 ஆண்டுகள்.
t₄ = ar^n-1
= 20000 \(\left(\frac{106}{100}\right)^{4-1}\)
= 20000 \(\left(\frac{106}{100}\right)^{3}\)
= 20000 x 1.191016
t₄ = 23820
வாய்ப்பு B:
தரவு: a = 22000, r = \(\frac{103}{100}\), n = 4 ஆண்டுகள்.
t₄ = ar^n-1
= 22000 \(\left(\frac{103}{100}\right)^{4-1}\)
= 22000 \(\left(\frac{103}{100}\right)^{3}\)
= 22000 x 1.092727
= 24039.9
t₄ = 24040

கேள்வி 12.
a, b, c என்பன ஒரு கூட்டுத் தொடர்வரிசையில் உள்ள மூன்று அடுத்தடுத்த உறுப்புகள் மற்றும் x, y, z என்பன ஒரு பெருக்கு தொடர்வரிசையின் மூன்று அடுத்தடுத்த உறுப்புகள் எனில் x^b-c x^c-a x z^{a – b} = 1 என நிறுவுக.
தீர்வு :
a, b, c என்பன கூட்டுத் தொடர் வரிசையில் உள்ள மூன்று அடுத்தடுத்த உறுப்புகள்.
a = a ———— (1)
b = a + d ——— (2)
c = a + 2d ——— (3)
x^b-c x^c-a x z^{a – b}
= x^a+d-a-2dy^a+2d-a. z^a-a-d
(x)^-d. y^2d. z^-d
\(\frac{y^{2 d}}{x^{d} \cdot z^{d}}\) [∴ x,y,z என்ப ன G.P]
x = x, y = xr, z = xr²
\(\frac{(x r)^{2 d}}{x^{d},\left(x r^{2}\right)^{d}}=\frac{x^{2 d} \cdot r^{2 d}}{x^{d} \cdot x^{d} \cdot x^{2 d}}\)

Tamilnadu State Board New Syllabus Samacheer Kalvi 10th Maths Guide Pdf Chapter 2 எண்களும் தொடர்வரிசைகளும் Ex 2.6 Textbook Questions and Answers, Notes.

TN Board 10th Maths Solutions Chapter 2 எண்களும் தொடர்வரிசைகளும் Ex 2.6

கேள்வி 1.
பின்வருவனவற்றின் கூடுதல் காண்க.
(i) 3, 7, 11,… 40 உறுப்புகள் வரை
(ii) 102, 97, 92,… 27 உறுப்புகள் வரை
(iii) 6+13 +20 + ……. + 97
தீர்வு:
i) 3, 7, 11, …… 40 உறுப்புகள் வரை.
a = 3, d = 7-3 = 4, n = 40
S_n = \(\frac{\mathrm{n}}{2}\) [2a+(n-1)d]
S₄₀ = \(\frac{40}{2}\)[2(3)+(40-1)(4))
= 20[6 + 39 x 4]
= 20[6 + 156)
= 20 x 162
= 3240 எனவே
S₄₀ = 3240

ii) 102, 97, 92, 27 உறுப்புகள் வரை
a = 102, d = 97-102 = -5, n = 27
S_n = \(\frac{\mathrm{n}}{2}\)[2a+(n-1)d]
S₂₇ = \(\frac{27}{2}\)[2(102)+(27-1)(-5)]
= \(\frac{27}{2}\)(204+26*(-5)] 27 x(204-130)
= \(\frac{27}{2}\) x 74
= 999
எனவே S₂₇ = 999

iii) 6+13+20+ …………….+97
a = 6, d = 13 – 6 = 7, l = 97
n = \(\frac{1-\mathrm{a}}{\mathrm{d}}\)+1
= \(\frac{97-6}{7}\) + 1
= \(\frac{91}{7}\) + 1
= 13+1
n = 14
S_n = \(\frac{n}{2}\) (a + l)
S₁₄ = \(\frac{14}{2}\) [6 + 97)
= 7 x 103
∴ S₁₄ = 721

கேள்வி 2.
5-லிருந்து தொடங்கி எத்தனை தொடர்ச்சியான ஒற்றை முழுக்களைக் கூட்டினால் கூடுதல் 480 கிடைக்கும்? தீர்வு:
5 ல் தொடங்கும் தொடர்ச்சியான ஒற்றை முழுக்க ள் = 5, 7, 9……
கணக்கின் படி S_n = 480
இங்கு a = 5, d = 7-5 = 2
\(\frac{n}{2}\)[2a + (n – 1)d] = 480
\(\frac{n}{2}\)[2(5)+(n-1)(2)] = 480
\(\frac{n}{2}\)[10 + 2n – 2] = 480
\(\frac{n}{2}\)[8+2n] = 480
\(\frac{n}{2}\) x 2(4+n) = 480
n² + 4n – 480 = 0
(n-20)(n+24) = (0)
n = 20, n = -24 என்பது பொருந்தாது எனவே கல் தொடங்கிய தொடர்ச்சியான ஒற்றை முழுக்களின் எண்ணிக்கை = 20

கேள்வி 3.
ஒரு கூட்டுத் தொடர்வரிசையின் n -ஆவது உறுப்பு 4n – 3 எனில் அதன் முதல் 28 உறுப்புகளின் கூடுதல் கான்க. தீர்வு:
தரவு : t_n = 4n – 3
t₁ = 4(1) – 3 = 4 – 3 = 1
t₂ = 4(2) – 3 = 8 – 3 = 5
எனவே t₂ – t₁ = 5 – 1 = 4
ஆகையால் a = 1, d = 4, n = 28
எனவே S_n = \(\frac{n}{2}\) [2a + (n – 1)d]
S₂₈ = \(\frac{28}{2}\) [2(1) (28 – 1)(4)
= \(\frac{28}{2}\)[2 + 27 x 4]
= 14[2 + 108]
= 14 x 110
= 1540
எனவே S₂₈= 1540

கேள்வி 4.
ஒரு குறிப்பிட்ட தொடரின் முதல் ‘n’ உறுப்புகளின் கூடுதல் 2n² – 3n எனில், அது ஒரு கூட்டுத் தொடர்வரிசை என நிரூபிக்க.
தீர்வு:
S_n = 2n² – 3n
S₁ = t₁ = 2(1)² – 3(1) = 2 x 1 – 3 = 2 – 3 = -1
∴ t₁ = a = -1|
S₂ = 2(2²) – 3(2) = 2(4) – 6 = 8 – 6 = 2
எனவே S₂ = t₁ + t₂ = 2
-1 + t₂ = 2
t₂ = 2 + 1
t₂ = 3
எனவே S₃ = t₁ + t₂ + t₃ = 2(3²) – 3(3)
= 2(9) – 3(3)
= 18 – 9
t₁ + t₂ + t₃ = 9
-1 + 3 + t₃ = 9
2 + t₃ = 9
t₃ = 9 – 2
t₃ = 2
வரிசை = -1, 3, 7, ……
இங்கே t₂ – t₁ = 3-(-1) = 4
t₃ – t₂ = 7-3 = 4
அடுத்தடுத்த உறுப்புகளின் வித்தியாசங்கள் சமம்.
எனவே -1, 3, 7 ……….. என்பது ஒரு கூட்டுத் தொடர் வரிசை ஆகும்.

கேள்வி 5.
ஒரு கூட்டுத் தொடர்வரிசையின் 104-வது உறுப்பு மற்றும் 4-வது உறுப்புகள் முறையே 125 மற்றும் 0. அத்தொடர்வரிசையின் முதல் 35 உறுப்புகளின் கூடுதல் காண்க.
தீர்வு :
t₁₀₄ = 125
t_n = a + (n – 1)d
எனவே t₁₀₄ = a + (104 – 1)d = 125
a + 103d = 125 ——-(1)
t₄ = 0
t₄ = a + (4 – 1)d = 0
a + 3d = 0 ——–(2)
(1 ) – (2)⇒

d = 5/4 ஐ சமன்பாடு (2)ல் பிரதியிட
a + 3d = 0
a + 15/4 = 0
a = -15/4
S₃₅ = ?

கேள்வி 6.
450-க்குக் குறைவாக உள்ள அனைத்து ஒற்றை மிகை முழுக்களின் கூடுதல் காண்க.
தீர்வு:
1 + 3 + 5 + …… + 449
இங்கு a = 1, d = 3 – 1 = 2, l = 449
n = \(\frac{1-a}{d}\) + 1
= \(\frac{449-1}{2}\) + 1
= \(\frac{448}{2}\)+ 1
= 224 + 1
n = 225
S_n = \(\frac{n}{2}\)(a + l)
S₂₂₅ = \(\frac{225}{2}\)(1 + 449)
= \(\frac{225}{2}\) x 450
= 225 x 225
S₂₂₅ = 50625

கேள்வி 7.
602-க்கும் 902-க்கும் இடையே 4 ஆல் வகுபடாத இயல் எண்களின் கூடுதல் காண்க.
தீர்வு:
602 க்கும் 902 க்கு இடையே உள்ள இயல் எண்க ள் = 603, 604, ……….. 901.
இங்கு d = 603, d = 1, l = 901
n = \(\frac{1-a}{d}\) + 1
= \(\frac{901-603}{1}\) + 1
= 298 + 1
n = 299
S_n = \(\frac{n}{2}\) (a + l)
A₂₉₉= \(\frac{299}{2}\) [603 + 901]
= \(\frac{299}{2}\) x 1504
= 224848

602 க்கும் 902 க்கும் இடையே உள்ள அனைத்து இயல் எண்க ளின் கூடுதல் = 224848 602 க்கும் 902 க்கும் இடையேயுள்ள 4 ஆல் வகுக்கும் அனைத்து இயல் எண்கள் = 604, 608,……… 900.
இங்கு a = 604, d = 4, 1 = 900

602 க்கும் 902 க்கும் இடையே 4 ஆல் வகுப்படும் இயல் எண்க ளின் கூடுதல் = 56400
602 க்கும் 902 க்கும் இடையே 4 ஆல் வகுபடாத அனைத்து இயல் எண்களின் கூடுதல் = 224848-56400 = 168448

கேள்வி 8.
இரகு ஒரு மடிக்கணினி வாங்க விரும்புகிறார். அவர் அதற்கான தொகையான ₹ 40,000 – ஐ உடனடியாக பணமாகவும் செலுத்தலாம் அல்லது 10 மாதத் தவணைகளில் முதல் தவணை ₹ 4800, இரண்டாம் தவணை ₹ 4750, மூன்றாம் தவணை₹1 4700 என்ற அடிப்படையிலும் செலுத்தலாம். அவர் இந்த வகையில் பணம் செலுத்துகிறார் எனில்,
(i) 10 மாதத் தவணைகளில் அவர் செலுத்திய மொத்தத் தொகை
(ii) மாதத் தவணை அடிப்படையில் பணம் செலுத்தும்போது அவர் அசலைக் காட்டிலும் கூடுதலாகச் செலுத்திய
தொகை ஆகியவற்றைக் காண்க.
தீர்வு :
i) 10 மாதத் தவணைகளில் அவர் செலுத்திய மொத்தத் தொகை = ?
a = 4800, d = 4750-4800 = -50, n = 10
S_n = \(\frac{\mathrm{n}}{2}\) [2a + (n-1)d]
S₁₀ = \(\frac{10}{2}\) [2(4800)+(10-1)(-50)]
= 5[9600 + 9x(-50)]
= 5[9600 – 450]
= 5 x 9150
= 45750
10 மாதத் தவணைகளில் அவர் செலுத்திய மொத்தத் தொகை = ₹ 45750
ii) அசலைக் காட்டிலும் அவர் கூடுதலாக செலுத்தியத் தொகை = ₹ 45750 – ₹ 40000
=₹5750

கேள்வி 9.
ஒருவர் தான் பெற்ற ₹65,000 கடனை திருப்பிச் செலுத்த முதல் மாதம் ₹400 செலுத்துகிறார். அதன் பிறகு ஒவ்வொரு மாதமும் முந்தைய மாதம் செலுத்தியதை விட ₹300 கூடுதலாகச் செலுத்துகிறார், அவர் இந்தக் கடனை அடைக்க எவ்வளவு காலம் தேவைப்படும்?
தீர்வு :
S_n இங்கு S. = 65000, a = 400, d = 300
S_n = \(\frac{\mathrm{n}}{2}\) [2a + (n – 1)d] = 65000
\(\frac{\mathrm{n}}{2}\)[2(400) +(n-1)300] = 65000
\(\frac{\mathrm{n}}{2}\)[800 + 300n – 300] = 65000
\(\frac{\mathrm{n}}{2}\) [500 + 300n] = 65000
\(\frac{\mathrm{n}}{2}\) x 100[5 + 3n] = 65000
3n² + 5n – 1300 = 0
(3n + 65)(n – 20) = 0
3n + 65 = 0, n – 20 = 0
3n = -65
n = -65/3 என்பது பொருந்தாது.
n – 20 = 0
n = 20
கடனை அடைக்கத் தேவைப்படும் காலம் = 20 மாதங்கள்

கேள்வி 10.
செங்கற்களினால் கட்டப்பட்ட ஒரு படிக்கட்டில் மொத்தம் 30 படிகட்டுகள் உள்ளன. கீழ்ப்படிக்கட்டை அமைப்பதற்கு 100 செங்கற்கள் தேவைப்படுகிறது. அடுத்தடுத்த படிக்கட்டுகள் அமைப்பதற்கு முந்தைய படிக்கட்டை விட இரண்டு செங்கற்கள் குறைவாகத் தேவைப்படுகிறது.
(i) உச்சியிலுள்ள படிக்கட்டை அமைப்பதற்கு எத்தனை செங்கற்கள் தேவை?
(ii) படிகட்டுகள் முழுவதும் அமைப்பதற்கு எத்தனை செங்கற்கள் தேவை?
தீர்வு :
100, 98, 96, 94 ……
n = 30, a = 100, d = 98-100 = -2
t_n = a+(n-1)d
t₃₀ = 100 + (30 – 1)(-2)
= 100+29x(-2)
= 100-58
t₃₀ = 42
உச்சியிலுள்ள படிக்கட்டை அமைப்பதற்கு தேவைப்படும் செங்கற்களின் எண்ணிக்கை = 42
100+98+96+94 + …..+42
a = 100, d = 98-100 = -2, n = 30
s_n = \(\frac{n}{2}\) [2a+(n-1)d]
S₃₀ = \(\frac{n}{2}\) [2(200)+(30-1)(-2)]
= 15[200 + 29 x (-2)]
= 15[200 – 58]
= 15 x 142
S₃₀ = 2130
படிக்கட்டுகள் முழுவதும் அமைப்பதற்கு தேவைப்படும் செங்கற்களின் எண்ணிக்கை = 2130.

கேள்வி 11.
S₁, S₂, S₃, ……….S_m, என்பன 1 வெவ்வேறு
கூட்டுத் தொடர்வரிசைகளின் 11 உறுப்புகளின் கூடுதலாகும். முதல் உறுப்புகள் 1, 2, 3, …n மற்றும் பொது வித்தியாசங்கள் 1, 3, 5, …, (2m -1) முறையே அமைந்தால், அந்த கூட்டுத் தொடர் வரிசையில் S₁, S₂, S₃, ……….S_m = \(\frac { 1 }{ 2 }\) mn (mn+1) என நிரூபிக்க.
தீர்வு :
a = 1, d = 1 எனில் S₁ = \(\frac{n}{2}\)[2+(n-1}1)
a = 2, d = 3 எனில் S₂ =\(\frac{n}{2}\) [4+(n-1)3)
a = 3, d = 5 எனில் S₃ = \(\frac{n}{2}\)[6+(n-1)5] –
a = m,d= 2m-1 எனில் S_m = \(\frac{n}{2}\)[2m+(n-1)(2m-1)] எனவே
S₁ + S₂ + S₃, ………. + S_m

\(\frac{n}{2}\) [m{m+1)+(n-1)m²]
= \(\frac{n}{2}\) [m²+m+nm²-m²]
= \(\frac{n}{2}\) [m{mn+1)]
= 111 [mn+1]
எனவே S₁ + S₂ + S₃ + ……………….+ S_m = \(\frac{m n}{2}\) [mn + 1]

கேள்வி 12.
\(\frac{a-b}{a+b}+\frac{3 a-2 b}{a+b}+\frac{5 a-3 b}{a+b}+\ldots 12\) உறுப்புகள் என்ற தொடரின் கூடுதல் காண்க.
தீர்வு :
a = \(\frac{a-b}{a+b}\) என்க.
d = t₂ – t₁

Tamilnadu State Board New Syllabus Samacheer Kalvi 10th Maths Guide Pdf Chapter 2 எண்களும் தொடர்வரிசைகளும் Ex 2.3 Textbook Questions and Answers, Notes.

TN Board 10th Maths Solutions Chapter 2 எண்களும் தொடர்வரிசைகளும் Ex 2.3

கேள்வி 1.
பின்வரும் சமன்பாடுகளை நிறைவு செய்யக்கூடிய குறைந்தபட்ச மிகை முழு x-ன் மதிப்பைக் காண்க.
(i) 71 = x (மட்டு 8)
(ii) 78 + x = 3 (மட்டு 5)
(iii) 89 = (x + 3) (மட்டு 4)
(iv) 96 = – (மட்டு 5)
(v) 5x = 4 (மட்டு 6)
தீர்வு :
i) 71 = x (மட்டு 8)
64 = 0 (மட்டு 8)
64 + 7 = 0 + 7 (மட்டு 8)
71 = 7 (மட்டு 8)
எனவே x = 7

ii) 78 + x = 3 (மட்டு 5)
78 + x – 3 = 5n
இங்கு n என்பது ஏதேனும் ஒரு முழு
75 + x = 5n
75+x என்பது 5ன் மடங்கு
75 ஐ விட கூடுதலான 5ன் மடங்கு 80. எனவே
x ன் குறைந்தபட்ச மதிப்பு 5 ஆகும்.

iii) 89 = (x + 3) (மட்டு 4)
89 – (x + 3) = 4n; n என்பது ஏதேனும் ஒரு
முழு
86 – x = 4n
⇒ 86 – x என்பது 4ன் மடங்கு
x ன் குறைந்தபட்ச மதிப்பு 2.
காரணம்:- 86-2 = 84 என்பது 86 ஐ விட குறைவான 4ன் மடங்கு ஆகும்.

iv) 96 = \(\frac{x}{7}\) (மட்டு 5)
96 – \(\frac{x}{7}\) = 5n (n என்பது ஏதேனும் ஒரு முழு)
96 – \(\frac{x}{7}\) என்பது 5ன் மடங்கு .
எனவே x ன் குறைந்தபட்ச மதிப்பு 7. காரணம்
96 – \(\frac{7}{7}\) = 96 – 1 = 95 என்பது
96ஐ விட குறைவான 5ன் மடங்கு ஆகும்.

v) 5x = 4 (மட்டு 6)
5x – 4 = 6n
( n என்பது ஏதேனும் ஒரு முழு) 5x-4 என்பது என் மடங்கு.
x = \(\frac{6 n+4}{5}\)
n= 1, 6, 11, 16… எனில் 6n+4 என்ப து 5 ஆல் வகுபடும்.
n = 1, எனில் x = \(\frac{6 \times 1+4}{5}\) = 2
எனவே x ன் குறைந்தபட்ச மிகை மதிப்பு = 2.

கேள்வி 2.
x ஆனது மட்டு 17-யின் கீழ் 13 உடன் ஒருங்கிசைவாக உள்ளது எனில், 7x – 3 ஆனது எந்த எண்ணுடன் ஒருங்கிசைவாக இருக்கும்?
தீர்வு:
i) x = 13 (மட்டு 17) ——(1)
7x-3 = y (மட்டு 17) —–(2)
(1), லிருந்து x-13 = 17n (n என்பது ஏதேனும் ஒரு முழு)
x – 13 என்பது 17 ஆல் வகுபடும்
x ன் குறைந்த பட்ச மிகை காரணம் 30 – 13 = 17
என்பது 17 ன் மடங்கு ஆகும்.
(2) லிருந்து
7 x 30 – 3 = y (மட்டு 17)
210 – 3 – y = 17n (n என்பது ஏதேனும் ஒரு முழு)
207 – y = 17n
207 – y எனவே 17 ன் மடங்கு
எனவே என் குறைந்த பட்ச மிகைமுழு 3.
காரணம் 207-3 = 214 என்பது 17 ன் மடங்கு.

கேள்வி 3.
தீர்க்க 5x = 4 (மட்டு 6)
தீர்வு :
5x – 4 = 6n (n என்பது ஏதேனும் ஒரு முழு)
(-4 என்பது என் மடங்கு
x = [lkatex]\frac{6 n+4}{5}[/latex]
n = 1, 6, 11, 16 …… எனில் 6n+4 என்பது ஆல் வகுபடும்.
n = 1, எனில் x = \(\frac{6 \times 1+4}{5}\) = 2
n = 6, எனில் x = \(\frac{6 \times 6+4}{5}\) = 8
5 எனவே தீர்வு = 2, 8, 14, 20…

கேள்வி 4.
தீர்க்க 3x -2 = 0 (மட்டு 11)
தீர்வு:
3x – 2 = 11n (n என்பது ஏதேனும் ஒரு முழு )
3x – 2 என்பது 11 ன் மடங்கு
x = \(\frac{11 n+2}{3}\)
n = 2, 5, 8 ……. எனில் 3
n = 2 x = \(\frac{11 \times 2+2}{3}\) = 8
n = 5, எனில் x = \(\frac{11 \times 5+2}{3}\) = 19
எனவே தீர்வு = 8, 19, 30……

கேள்வி 5.
முற்பகல் 7 மணிக்கு 100 மணி நேரத்திற்குப் பிறகு நேரம் என்ன?
தீர்வு :
7 + 100 = x (மட்டு 12)
107 – x = 12n
107 – x என்பது 12 ன் மடங்கு
x குறைந்தபட்ச மிகை மதிப்பு = 11
ஏனெனில் 107 – 11 = 96 என்பது 107க்கு குறைவான 12ன் மடங்கு ஆகும்.
முற்பகல் 7 மணிக்கு 100 மணி நேரத்திற்குப் பிறகு நேரம் = 11a.m

கேள்வி 6.
பிற்பகல் 11 மணிக்கு 15 மணி நேரத்திற்கு முன்பு நேரம் என்ன?
தீர்வு:
15 = 11-x (மட்டு 12)
15 – 11 +x = 12n: (n என்பது ஏதேனும் ஒரு முழு)
4+x = 12n
4+x என்பது 12ன் மடங்கு.
x ன் குறைந்தபட்ச மிகை மதிப்பு 8 ஆகும். ஏனெனில் 4 + 8 = 12 என்பது 12ன் மடங்கு ஆகும்.
பிற்பகல் 11 மணிக்கு 15 மணி நேரத்திற்கு முன்பு நேரம் 8p.m

கேள்வி 7.
இன்று செவ்வாய் கிழமை, என்னுடைய மாமா 45 நாட்களுக்குப் பிறகு வருவதாகக் கூறியுள்ளார். என்னுடைய மாமா எந்தக் கிழமையில் வருவார்?
தீர்வு :
இங்கு நாம் 0, 1, 2, 3, 4, 5, 6 என்பன முறையே ஞாயிறு முதல் சனி வரை உள்ள கிழமைகளைக் குறிப்பதாக எடுத்துக்கொள்வோம்.
தரவு:
“இன்று செவ்வாய் கிழமை”
செவ்வாய் கிழமைக்கான எண் = 2.
தரவு:- என்னுடைய மாமா 45 நாட்களுக்குபின் வருவதாகக் கூறியுள்ளார்.
எனவே 2 + 45 = 47 (மட்டு 7)
= 5 (மட்டு 7)
5 என்பது வெள்ளிக்கிழமைக்கான எண்.
எனவே என்னுடைய மாமா வரும் கிழமை வெள்ளிக்கிழமை ஆகும்.

கேள்வி 8.
எந்த ஒரு மிகை முழு எண் n- ற்கும் 2ⁿ + 6 x 9ⁿ ஆனது 7 ஆல் வகுபடும் என நிறுவுக.
தீர்வு:
2ⁿ + 6 x 9ⁿ = (மட்டு 7)
2ⁿ + 6 x 9ⁿ = 7n (n என்பது ஏதேனும் ஒரு முழு)
2ⁿ + 6 x 9ⁿ என்பது 7ன் மடங்கு
n = 0, எனில் 2° + 6 x 9° = 1 + 6 = 7 என்பது 7ன் மடங்கு ஆகும்.
n = 1, எனில் 2¹ + 6 x 9¹ = 2 + 54 = 56
7 என்பது 7ன் மடங்கு ஆகும்.
n = 2, எனில் 2² + 6 x 9² = 4 + 486 = 490 7ன் மடங்கு ஆகும்.
. . . . . . . . . . . . . . .
எனவே 2ⁿ + 6 x 9ⁿ என்பது 7 ஆல் வகுபடும்.

கேள்வி 9.
2⁸¹ ஐ 17 ஆல் வகுக்கும் போது கிடைக்கும் மீதி காண்க.
தீர்வு:
2⁸¹ = x (மட்டு 17)
2³ = 8 (மட்டு 17)
(2³)³ = 8³ (மட்டு 17)
2⁹ = 512 (மட்டு 17)
2⁹ = 2 (மட்டு 17)
(2⁹)⁹ = 2⁹ (மட்டு 17)
2⁸¹ = 512 (மட்டு 17)
2⁸¹ = 2 (மட்டு 17)
எனவே 2⁸¹ஐ 17 ஆல், வகுக்கும் போது கிடைக்கும் மீதி = 2.

கேள்வி 10.
பிரிட்டிஷ் ஏர்லைன்ஸ் விமானத்தில் சென்னையிலிருந்து லண்டன் செல்லப் பயணநேரம் தோராயமாக 11 மணிநேரம். விமானம் தனது பயணத்தை ஞாயிற்றுக்கிழமை 23:30 மணிக்குத் தொடங்கியது. சென்னையின் திட்ட நேரமானது லண்டனின் திட்ட நேரத்தைவிட 4.30 மணி நேரம் முன்னதாக இருக்குமெனில், விமானம் லண்டனில் தரையிறங்கும் நேரத்தைக் காண்க.
தீர்வு :
= 23.30 + 11 (மட்டு 24)
= 34.30 (மட்டு 24)
= 10.30 (மட்டு 24)
= 10.30 – 4.30 (மட்டு 24)
= 6 (மட்டு 24)
எனவே விமானம் லண்டனில் தரையிறங்கும் நேரம் = 6a.m

Tamilnadu State Board New Syllabus Samacheer Kalvi 10th Maths Guide Pdf Chapter 2 எண்களும் தொடர்வரிசைகளும் Ex 2.2 Textbook Questions and Answers, Notes.

TN Board 10th Maths Solutions Chapter 2 எண்களும் தொடர்வரிசைகளும் Ex 2.2

கேள்வி 1.
n ஓர் இயல் எண் எனில், எந்தா மதிப்புகளுக்கு 4ⁿ ஆனது 6 என்ற இலக்கத்தைக் கொண்டு முடியும்?
தீர்வு :
n = 2, எனில் 4ⁿ = 4² = 16
n = 4, எனில் 4ⁿ = 4⁴ = 256
n = 6, எனில் 4ⁿ = 4⁶ = 4096
எனவே 4ⁿ ன் மதிப்பு இறுதி இலக்கம் 6ல் முடிவு பெறும்.
ஆகையால் n என்பது ஓர் இரட்டை எண் ஆகும்.

கேள்வி 2.
m மற்றும் n இயல் எண்கள் எனில், எந்த m-யின் மதிப்புகளுக்கு 2ⁿ × 5^m என்ற எண் 5 என்ற இலக்கத்தைக் கொண்டு முடியும்?
தீர்வு :
n ∈ N, எனில் 2ⁿ என்பது இரட்டை எண்.
m ∈ N, 5^m என்பது ஒற்றை எண்
(மேலும் இறுதி இலக்கம் 5ல் முடிவுறும்)
எனவே 2ⁿ × 5^m என்பதன் மதிப்பு “0” என்ற இலக்கத்தில் முடிவுறும்.
எனவே m, n என்பவற்றிற்கு மதிப்புகள் காண இயலாது.

கேள்வி 3.
252525 மற்றும் 363636 என்ற எண்களின் மீ.பொ.வ காண்க.
தீர்வு :
252525 = 5² × 10101
363636 = 6² × 10101
252525 மற்றும் 363636 ன் மீ.பொ.வ = 10101

கேள்வி 4.
13824 = 2^a × 3^b எனில், a மற்றும் b-யின் மதிப்புக் காண்க.
தீர்வு :
13824 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3
=2⁹ × 3³
13824 = 2^a × 3^b
எனவே a = 9 மற்றும் b = 3

கேள்வி 5.
\(\mathrm{p}_{1}^{x_{1}} \times \mathrm{p}_{2}^{x_{2}} \times \mathrm{p}_{3}^{x_{3}} \times \mathrm{p}_{4}^{x_{4}}\)= 113400 இங்கு P₁, P₂, P₃ P₄, என்பன ஏறு வரிசையில் அமைந்த பகா எண்கள் மற்றும் x₁, x₂, x₃, x₄என்பன முழுக்கள் எனில், P_1, P_2, P_3, P₄ மற்றும் x₁, x₂, x₃, x₄ஆகியவற்றின் மதிப்புகளைக் காண்க.
தீர்வு :
13824 = 2 × 2 × 2 × 3 × 3 × 3 × 3 × 5 × 5 × 7
= 2³ × 3⁴ × 5² × 7¹
எனவே p₁ = 2, P₂ = 3, p₃= 5, p₄ = 7 மற்றும்
x₁ = 3, x₂ = 4, x₃ = 2, x₄ = 1

கேள்வி 6.
அடிப்படை எண்ணியல் தேற்றத்தைப் பயன்படுத்தி 408 மற்றும் 170 என்ற எண்க ளின் மீ.பொ.ம மற்றும் மீ.பொ.வ காண்க.
தீர்வு :
408 = 2³ × 3 × 17
170 = 2 × 5 × 17
408, 170 ன் மீ.பொ.ம = 2³ × 3 × 5 × 17
= 2040
408, 170 ன் மீ.பொ.வ = 2 × 17
மீ.பொ.வ = 34

கேள்வி 7.
24, 15, 36 ஆகிய எண்களால் மீதியின்றி வகுபடும் மிகப்பெரிய ஆறிலக்க எண்ணைக் காண்க.
தீர்வு :
24 = 2³ × 3
15 = 3 × 5
36 = 2³ × 3³
(24, 15 மற்றும் 36 ன் மீ.பொ.வ) = 2³ × 3² × 5
= 360
மிகப்பெரிய ஆறிலக்க எண் = 999999
24, 15, 36 ஆகிய எண்களால் மீதியின்றி வகுபடும் மிகப்பெரிய ஆறிலக்க எண்.
= 999720
குறிப்பு : (999999 + 360 = 2777.775
எனவே 360 × 2777 = 999720)

கேள்வி 8.
35, 56 மற்றும் 91 ஆல் வகுக்கும் போது மீதி 7 ஐத் தரக்கூடிய மிகச்சிறிய எண் எது?
தீர்வு :
35 = 5 × 7
56 = 2 × 2 × 2 × 7
91 = 7 × 13
35, 56 மற்றும் 91 = 2³ × 5 × 7 × 13
= 3640
35, 56 மற்றும் 91 ஆல் வகுக்கும் போது மீதி 7 ஐத் தரக்கூடிய மிகச் சிறிய எண்
= 3640 + 7
= 3647

கேள்வி 9.
முதல் 10 இயல் எண்களால் மீதியின்றி வகுப்படக்கூடிய சிறிய எண் எது?
தீர்வு :
முதல் 10 இயல் எண்கள்
= 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
= 1, 2, 3, 2², 5, 2 × 3, 7, 2³, 3², 2 × 5
முதல் 10 இயல் எண்க ளின் மீ.பொ.ம.
= 2 × 3 × 5 × 7 = 2520

Tamilnadu State Board New Syllabus Samacheer Kalvi 10th Maths Guide Pdf Chapter 2 எண்களும் தொடர்வரிசைகளும் Ex 2.1 Textbook Questions and Answers, Notes.

TN Board 10th Maths Solutions Chapter 2 எண்களும் தொடர்வரிசைகளும் Ex 2.1

கேள்வி 1.
3 ஆல் வகுக்கும் போது மீதி 2 – ஐத் தரக்கூடிய அனைத்து மிகை முழுக்களையும் காண்க.
தீர்வு :
a மற்றும் b (a>b) இரு மிகை முழுக்கள் எனில்
a = bq + r,0 ≤ r < b என்றவாறு , r எனும் தனித்த மிகை முழுக்கள் கிடைக்கும். இங்கு a = b(3)+2)
b = 0, எனில் = 0(3) + 2 = 2
b = 1, எனில் = 1(3) + 2 = 5
b = 2, எனில் = 2(3) + 2 = 8
b = 3, எனில் = 3(3) + 2 = 11.
எனவே மிகை முழுக்கள் = 2, 5, 8, 11…..

கேள்வி 2.
ஒருநபரிடம் 532 பூந்தொட்டிகள் உள்ளன. அவர் வரிசைக்கு 21 பூந்தொட்டிகள் வீதம் அடுக்க விரும்பினார். எத்தனை வரிசைகள் முழுமை பெறும் எனவும் மற்றும் எத்தனை பூந்தொட்டிகள் மீதமிருக்கும் எனவும் காண்க.
தீர்வு :
a மற்றும் b (a > b) என்பன ஏதேனும் இரு மிகை முழுக்கள் எனில் a = bq+r,0≤r<b
என்றவாறு q, r எனும் தனித்த மிகை முழுக்கள் கிடைக்கும்.
இங்கு a = 532, b = 21
532 = 25 x 21 + 7
எனவே முழுமை பெறும் வரிசைகள் = 25
மீதமிருக்கும் பூந்தொட்டிகள் எண்ணிக்கை = 7

கேள்வி 3.
தொடர்ச்சியான இரு மிகை முழுக்களின் பெருக்கற்பலன் 2 ஆல் வகுபடும் என நிறுவுக.
தீர்வு: அடுத்தடுத்த இரண்டு மிகை முழுக்கள் x, x+1 என்க.
இதன் பெருக்கல் பலன் = x(x + 1) = x² + x
தீர்வுவகை 1:
x ஒரு இரட்டை எண் எனில்,x = 2k
இப்பொழுது x + x = (2k)² +2k
= 4k² +2k
= 2(2k + 1)
= 2 ஆல் வகுபடும்.

தீர்வுவகை 2:
x ஒரு ஒற்றை எண் எனில் x = 2k +1
இப்பொழுது x² + x = (2k + 1)² + 2k + 1
= 4k² + 4k + 1 + 2k +1
= 4k² + 6k + 2
= 2(2k² + 3k + 1)
= 2 ஆல் வகுப்படும்.
எனவே தொடர்ச்சியான இருமிகை முழுக்களின் பெருக்கல்பலன் 2 ஆல் வகுப்படும்.

கேள்வி 4.
a, b மற்றும் C என்ற மிகை முழுக்களை 13 ஆல் வகுக்கும் போது கிடைக்கும் மீதிகள் முறையே 9, 7 மற்றும் 10 எனில் a+b+c ஆனது 13 ஆல் வகுபடும் என நிரூபி.
தீர்வு:
a மற்றும் b (a > b) என்பன ஏதேனும் இரு மிகை முழுக்கள் எனில் a = bq+r,0<r இங்கே a = 13q + 9
b = 13q + 7
c = 13q + 10
எனவே a + b + c = 13q + 9 + 13q + 7 + 13q + 10
= 39q + 26
= 13 (3q +2)
13 ஆல் வகுபடும்.
எனவே a+b+c ஆனது 13 ஆல் வகுபடும்.

கேள்வி 5.
எந்த மிகை முழுவின் வர்க்கத்தையும் 4 ஆல் வகுக்கும்போது மீதி 0 அல்லது 1 மட்டுமே கிடைக்கும் என நிறுவுக.
தீர்வு:
k என்பது ஏதேனும் மிகை முழு என்க
k = 4k எனில்
k² = 16k²
k² = 4 x 4k² + 0
(மீதி r = 0)
k = 4k + 1 எனில்
k² = (4k + 1)
k² = 16k² + 8k + 1
= 4(4k² + 2k) + 1
(மீதி r = 1)
எனவே எந்த மிகை முழுஎண் வர்க்கத்தையும் 4 ஆல் வகுக்கும் போது மீதி 0 அல்லது 1 மட்டுமே கிடைக்கும்.

கேள்வி 6.
யூக்ளிடின் வகுத்தல் வழிமுறையைப் பயன்படுத்திப் பின்வருவனவற்றின் மீ.பொ.வ காண்க.
(i) 340 மற்றும் 412
(ii) 867 மற்றும் 255
(iii) 10224 மற்றும் 9648
(iv) 84, 90 மற்றும் 120.
தீர்வு :
(i) 340 மற்றும் 412
a, b என்பவை ஏதேனும் இரண்டு மிகை முழுக்கள் மற்றும் (a>b) எனில்
a = bq + r,0 ≤ r < b
இங்கு 412 = 340 x 1 + 72
340 = 72 x 4 + 52
72 = 52 x 1 + 20
52 = 20 x 2 + 12
20 = 12 x 1 + 8
12 = 8 x 1 + 4
8 = 4 x 2 + 0
340 மற்றும் 412 ன் மீ.பொ.வ = 4

(ii) 867 மற்றும் 255
867 = 255 x 3 + 102
255 = 102 x 2 + 51
102 = 51 x 2 + 0
867 மற்றும் 255 ன் மீ.பொ,வ 81

(iii) 10224 மற்றும் 9648
10224 = 9648 x 1 + 576
9648 = 576 x 16 + 432
576 = 432 x 1 + 144
432 = 144 x 3 + 0
10224 மற்றும் 9648 ன் மீ. பொ. வ = 144

(iv) 84, 90 மற்றும் 120
90 = 84 x 1 +6
84 = 6 x 14 + 0
84, மற்றும் 90 மீ.பொ.வ = 6
120 = 6 x 20 + 0
84, 90 மற்றும் 120 ன் மீ. பொ. வ = 6

கேள்வி 7.
1230 மற்றும் 1926 ஆகிய எண்களை வகுக்கும்போது மீதி 12 – ஐத் தரக்கூடிய மிகப்பெரிய எண்ணைக் காண்க. தீர்வு :
1230 மற்றும் 1926 ஆகிய எண்களை வகுக்கும் போது மீதி 12 எனில் நமக்கு தேவையான எண் 1230 -12 =1218, 1926-12 =1914 ஆகியவற்றின் மீப்பெரு பொது வகுத்தியாகத்தான் இருக்கும்.
எனவே 1914 = 1218 x 1 + 696
1218 = 696 x 1 + 522
522 = 174 x 3 + 0
1218 மற்றும் 1914 ன் மீ.பொ.வ = 174

கேள்வி 8.
32 மற்றும் 60 ஆகியவற்றின் மீப்பெரு பொது வகுத்தி d என்க . d = 32x + 60y எனில் x மற்றும் y என்ற முழுக்களைக் காண்க.
தீர்வு :
‘d’ என்பது 32 மற்றும் 60ன் மீ. பொ. வ என்க.
60 = 32 x 1 + 28
32 = 28×1+4|
28 = 4×7 +0

எனவே 32 மற்றும் 60ன் மீ. பொ. வ = 4
d = 4
ஆகையால் 4 = 32x + 60y
4 = 32(2) + 60(-1)
= 64 – 60
= 4
எனவே x = 2 மற்றும் y = -1

கேள்வி 9.
ஒரு மிகை முழுவை 88 ஆல் வகுக்கும் போது 61 கிடைக்கிறது. அதே மிகை முழுவை 11 ஆல் வகுக்கும் போது கிடைக்கும் மீதியைக் காண்க.
தீர்வு :
a = 88q + 61
61 = 11 x 5 + 6 எனவே இதே மிகை முழுவை 11 ஆல் வகுக்கும்
போது கிடைக்கும் மீதி = 6.

கேள்வி 10.
எந்த இரு அடுத்தடுத்த மிகை முழுக்கள் சார்பகா எண்கள் என நிறுவுக.
தீர்வு :
15, 16 என்பவை அடுத்தடுத்த மிகை முழுக்கள் என்க.
இப்பொழுது 16 = 15 x 1 + 1
15 = 1 x 15 + 0
எனவே 15, 16 சார்பகா எண்கள் ஆகும்.
28, 29 என்பவை அடுத்தடுத்த மிகை முழுக்கள் என்க.
இப்பொழுது 29 = 28 x 1 + 1
28 = 1 x 28 + 0
எனவே 28, 29 என்பவை சார்பகா எண்கள். எனவே எந்த இரு அடுத்தடுத்த மிகை முழுவும் சார்பகா எண்கள் ஆகும்.

Tamilnadu State Board New Syllabus Samacheer Kalvi 10th Maths Guide Pdf Chapter 1 உறவுகளும் சார்புகளும் Ex 1.6 Textbook Questions and Answers, Notes.

TN Board 10th Maths Solutions Chapter 1 உறவுகளும் சார்புகளும் Ex 1.6

பலவுள் தெரிவு வினாக்கள்

கேள்வி 1.
n(A × B) = 6 மற்றும் A = {1, 3} எனில் n(B) ஆனது
அ) 1
ஆ) 2
இ) 3
ஈ) 6
விடை :
இ) 3
n(A × B) = 6
n(A) = 2
n(B) = \(\frac{n(A \times B)}{n(A)}=\frac{6}{2}\) = 3

கேள்வி 2.
A= {a, b, p}, B = {2, 3} C = {p, q, r, s} எனில், n[(A ∪ C) × B] ஆனது
அ) 8
ஆ) 20
இ) 12
ஈ) 16
விடை :
இ) 12

A∪C = {a, b, p, q, r, s} = n(A∪C) = 6
B = {2,3} ⇒ n (B) = 2
n[(A ∪ C × B)] = 6 × 2 = 12

கேள்வி 3.
A = {1, 2}, B = {1, 2, 3, 4}, C = {5, 6} மற்றும் D = {5, 6, 7, 8} எனில் கீழே
கொடுக்கப்பட்டவைகளில் எது சரியான கூற்று?
அ) (A × C) ⊂ (B × D)
ஆ) (B × D) ⊂ (A X C)
இ) (A × B) ⊂ (A × D)
ஈ) (D × A) ⊂ (B × A)
விடை :
அ) (A × C) ⊂ (B × D)
A × C = {1, 2} x {5, 6}
= {(1, 5) (1, 6) (2, 5) (2, 6)}
B × D = {1, 2, 3, 4} × {5, 6, 7, 8}
= {(1, 5) (1, 6) (1, 7) (1, 8) (2, 5) (2, 6) (2, 7) (2,8) (3, 5) (3, 6) (3, 7) (3, 8) (4, 5) (4, 6) (4, 7) (4, 8)}
∴ (A × C) ⊂ (B × D)

கேள்வி 4.
A = {1, 2, 3, 4, 5} -லிருந்து, B என்ற கணத்திற்கு 1024 உறவுகள் உள்ளது எனில் B -ல் உள்ள உறுப்புகளின் எண்ணிக்கை.
அ) 3
ஆ) 2)
இ) 4
ஈ) 8
விடை :
ஆ) 2

n(A) = 5 = p
n(B) = ? = q
2pq = 1024
2^5q = 10
5q = 10
q = 2

கேள்வி 5.
R = {(x, x² ) |X ஆனது 13 – ஐ விடக் குறைவான பகா எண்கள் } என்ற உறவின் வீச்சகமானது
அ) {2, 3, 5,7}
ஆ) {2, 3, 5, 7, 11}
இ) {4, 9, 25, 49, 121}
ஈ) {1, 4, 9, 25, 49, 121}
விடை :
இ) {4, 9, 25, 49, 121}
13 விட குறைவான பகா எண்கள் {2,3, 5, 7, 11}
தரவு f(x) = x²
f(2) = 2² = 4
f(3) = 3² =9
f(5) = 5² = 25
f(7) = 7² = 49
f(11) = 11² = 121
வீச்சகம் = {4, 9, 25, 49, 121}

கேள்வி 6.
(a + 2, 4) மற்றும் (5, 2a + b) ஆகிய வரிசைச் சோடிகள் சமம் எனில், (a, b) என்பது
அ) (2, -2)
ஆ) (5, 1)
இ) (2, 3)
ஈ) (3, -2)
விடை :
ஈ) (3, -2)
a + 2 = 5
a = 5- 2
a = 3
2a + b = 4
2(3) + b = 4
6 + b = 4
b = 4 – 6
b = -2

கேள்வி 7.
n(A) = m மற்றும் n(B) = n என்க. A -லிருந்து B-க்குவரையறுக்கப்பட்ட வெற்றுகணமில்லாத உறவுகளின் மொத்த எண்ணிக்கை
அ) mⁿ
ஆ) n^m
இ) 2^mn – 1
ஈ) 2^mn
விடை :
ஈ) 2^mn
உறவுகளின் மொத்த எண்ணிக்கை
= 2Pq = 2^mnA

கேள்வி 8.
{(a, 8), (6, b)} ஆனது ஒரு சமனிச்சார்பு எனில், a மற்றும் b மதிப்புகளாவன முறையே
அ) (8, 6)
ஆ) (8, 3)
இ) (6, 8)
ஈ) (6, 6)
விடை :
அ) (8, 6)

கேள்வி 9.
A = {1, 2, 3, 4} B = {4, 8, 9, 10} என்க. சார்பு f: A → B ஆனது f = {(1, 4), (2, 8), (3, 9), (4, 10)} எனக் கொடுக்கப்பட்டால் f – என்பது
அ) பலவற்றிலிருந்து ஒன்றுக்கான சார்பு
ஆ) சமனிச்சார்பு
இ) ஒன்றுக்கொன்றான சார்பு
ஈ) உட்சார்பு
விடை :
இ) ஒன்றுக்கொன்றான சார்பு

கேள்வி 10.
f(x) = 2x² மற்றும் g(x) = [LATEX]\(\frac { 1 }{ 3x }\)[/LATEX] எனில் fog ஆனது
அ) \(\frac{3}{2 x^{2}}\)
ஆ) \(\frac{2}{3 x^{2}}\)
இ) \(\frac{2}{9 x^{2}}\)
ஈ) \(\frac{1}{6 x^{2}}\)
விடை :
இ) \(\frac{2}{9 x^{2}}\)

கேள்வி 11.
f: A → B ஆனது இருபுறச் சார்பு மற்றும் n(B) = 7 எனில் n(A) ஆனது
அ) 7
ஆ) 49
இ) 1
ஈ) 14
விடை :
அ) 7

கேள்வி 12.
f மற்றும் g என்ற இரண்டு சார்புகளும்
f = {(0, 1), (2, 0), (3, -4), (4, 2), (5, 7)}
g = {(0, 2), (1, 0), (2, 4), (-4, 2), (7, 0)}
எனக் கொடுக்கப்பட்டால் fog-ன் வீச்சகமானது
அ) {0, 2, 3, 4, 5}
ஆ) {-4, 1, 0, 2, 7}
இ) {1, 2, 3, 4, 5}
ஈ) {0, 1, 2}
விடை :
{0, 1, 2}
g யில் உள்ள எல்லா உறுப்புகளுக்கும் f ல் தொடர்பு உள்ளது.
fog = {0, 1, 2}

கேள்வி 13.
f(x) = \(\sqrt{1+x^{2}}\)எனில்
அ) f(xy) = f(x). f(y)
ஆ) f(xy) ≥ f(x). f(y)
இ) f(xy) ≤ f(x). f(y)
ஈ) இவற்றில் ஒன்றுமில்லை
விடை :
ஆ) ஆ) f(xy) ≥ f(x). f(y)

இருபுறமும் வர்க்கம் காண
1 + x²y² = (1 + x²) (1+y²)
1 + x²y² = 1 + x² + y² + x²y²
எனவே 1+x²y² < 1 + x² + y² + x²y²

கேள்வி 14.
g = {(1, 1) (2, 3) (3, 5) (4, 7) என்ற சார்பானது
g(x) = ax + B எனக் கொடுக்கப்பட்டால் a மற்றும் -வின் மதிப்பானது
அ) (-1, 2)
ஆ) (2, -1)
இ) (-1, -2)
ஈ) (1, 2)
விடை :
(2, -1)
g(x) = ax + β

g(1) = α + β
x, y
(1,1)
g(1) = α + β ………………… (1)
g(2) = 2α + β = 3 ……………….. (2)
x, y
(2, 3)
1, 2 லிருந்து
α = 2
β = -1

கேள்வி 15.
f(x) = (x + 1)³ – (x -1)³ குறிப்பிடும் சார்பானது
அ) நேரிய சார்பு
ஆ) ஒரு கனச் சார்பு
இ) தலைகீழச் சார்பு
ஈ) இருபடிச் சார்பு
விடை :
இருபடிச் சார்பு

f(x) = (x + 1)³ – (x – 1)³
= x³ + 3x² + 3x + 1 – x³ + 3x² -3x + 1
= 6x² + 2 ஒரு இருபடிச்சார்பு

Tamilnadu State Board New Syllabus Samacheer Kalvi 10th Maths Guide Pdf Chapter 1 உறவுகளும் சார்புகளும் Ex 1.5 Textbook Questions and Answers, Notes.

TN Board 10th Maths Solutions Chapter 1 உறவுகளும் சார்புகளும் Ex 1.5

கேள்வி 1.
கீழேக் கொடுக்கப்பட்டுள்ள f மற்றும் g எனும் சார்புகளைப் பயன்படுத்தி fog மற்றும் gof – ஐக் காண்க fog = gof என்பது சரியா சோதிக்க.
i) f(x) = x – 6, g(x) = x²
ii) f(x) = \(\frac{2}{x}\) = g(x) = 2x² – 1
ii) f(x) = \(\frac{x+6}{3}\) g(x) = 3 – x
iv) f(x) = 3 + x, g(x) = x – 4
v) f(x) = 4x² – 1, g(x) = 1 + x
தீர்வு :
i) f(x) = x-6, g(x) = x² [∵ f(x) = x -6]
fog(x) = f(g(x)) = f(x²)
= x² – 6
gof(x) =g[f(x)) = g(x-6)
= (x-6)²
∴ fog ≠ gof

ii) f(x) = \(\frac{2}{x}\) g(x) = 2x² – 1
fog(x) = f(g(x)) = f(2x² – 1)
= \(\frac{2}{2 x^{2}-1}\)
gof (x) = g(f(x)) = g(\(\frac{2}{x}\))
= 2( \(\frac{2}{x}\) )² – 1
= 2 x \(\frac{4}{x^{2}}\) – 1
= \(\frac{8}{x^{2}}\) – 1
∴ fog ≠ gof

iii) f(x) = \(\frac{x+6}{3}\), g(x) = 3 – x
fog(x) = f(g(x)) = f(3-x)

iv) f(x) = 3 + x; g(x) = x – 4
fog(x) = f(g(x)) = f(x-4)
= 3 + x -4
= x -1
gof(x) = g(f(x)) = g(3 + x)
= 3 + x – 4
= x – 1
எனவே fog = gof

v) f(x) = 4x² – 1, g(x) = 1 + x
fog(x) = f(g)(x)) = f(1 + x)
= 4(1 + x)² – 1
= 4(1 + 2x + x²) – 1
= 4 + 8x + 4x² – 1
= 4x² + 8x + 3
gof(x) = g(f(x)) = g(4x² – 1)
= 1 + 4x² – 1
= 4x²
எனவே fog ≠ gof

கேள்வி 2.
fog = gof எனில் K – யின் மதிப்பைக் காண்க
i) f(x) = 3x + 2, g(x) = 6x – K
ii) f(x) = 2x – K, g(x) = 4x + 5
தீர்வு :
i) f(x) = 3x + 2
g(x) = 6x – K
fog = gof (தர்வு)
fog(x) = gof(x)
f(g(x) = g(f(x))
f(6x – k) = g(3x + 2)
3(6.x – k) + 2 = 6(3.x + 2) – k
18x-3k + 2 = 18.x + 12 – k
2k = -10
k =-5

ii) f(x) = 2x-k, g(x) = 41 + 5
தரவு fog = gof
fog(x) = gof(x)
f(g)(x) = g(f(x)
f(4x + 5) = g(2x-k)
2(4x + 5) -k = 4(2x – k) + 5
8x + 10 – k = 8x -4k + 5
3k = -5
k = -5/3

கேள்வி 3.
f(x) = 2x -1; g(x) = \(\frac{x+1}{2}\) எனில், fog = gof = x எனக் காட்டுக.
தீர்வு :
fog (x) = f(g(x)))
= f( \(\frac{x+1}{2}\) )
= \(2\left(\frac{x+1}{2}\right)-1\)
= x + 1 -1
= x gof = gof(x)
=g(f(x))
=g(2x – 1) = 2x/2
= x
எனவே fog = gof = x
எனவே நிரூபிக்கப்பட்டது.

கேள்வி 4.
f(x) = x² – 1, g(x) = x – 2 மற்றும் gof (a) = 1 எனில் , a ஐக் காண்க
தீர்வு :
i) f(x) = x² – 1;
g (x) = x – 2
தரவு gof(a) =1
g(f(a)) =1
g(a² – 1) = 1
a² – 1 – 2 = 1
a² – 3 = 1
a² = 4
a = ±2

கேள்வி 5.
A, B, C ⊆ N மற்றும் f: A → B என்ற சார்பு f(x) = 2x +1 எனவும் மற்றும்g : B → C ஆனது g(x) = x² எனவும் வரையறுக்கப்பட்டால், fog மற்றும் gof- யின் வீச்சகத்தைக் காண்க.
தீர்வு :
தரவு f(x) = 2x +1
g(x) = x²
fog = fog(x)
= f(g(x)))
= f(x²)
= 2x² + 1
gof = gof(x)|
= g(f(x))
= g(2x + 1)
= (2x +1)²
fog மற்றும் gof ன் வீச்சகம்
{y/y = 2x² + 1, x ∈ N }, {y/y = (2x + 1)², x∈N}

கேள்வி 6.
f(x) = x² – 1 எனில் i) fof ii) fofof – ஐக் காண்க
தீர்வு:
தரவு f(x) = x² – 1
a) fof(x) = f(f(x)
= f(x² – 1)
= (x² – 1)² – 1
= x⁴ – 2x² + 1 – 1
=x⁴ -2x²

b) fofof = fofof(x)
= fof(f(x))
= fof(x² – 1)
= f(f(x2-1))
= f[[x² – 1)² -1)
= f[x⁴ – 2x² + 1 – 1]
= f[x⁴ – 2x²] ⇒ (x⁴ – 2x²)² – 1

கேள்வி 7.
f: R – R மற்றும் g:R – R ஆனது முறையே,
f(x) = x⁵, g(x)= x⁴ என வரையறுக்கப்பட்டால், fg ஆகியவை ஒன்றுக்கு ஒன்றானதா மற்றும் fog ஒன்றுக்கு ஒன்றான சார்பாகுமா என்று ஆராய்க .
தீர்வு : f(x) = f(y)
x⁵ = y⁵
எனவே x = y
ஆகையால் f ஒரு ஒன்றுக்கு ஒன்றான சார்பு
g(x) = g(y) எனில்
x⁴ = y⁴
ஆகையால் x = y
எனவே g ஒரு ஒன்றுக்கு ஒன்றான சார்பு
fog = fog(x)
= f(g(x))
= f(x⁴)
= (x⁴)⁵
= x²⁰
fog(x) = fog(y) எனில்
x²⁰ = y²⁰
∴ fog ஆனது 1 – 1 சார்பு ஆகும்.

கேள்வி 8.
கொடுக்கப்பட்ட f(x), g(x), h(x) ஆகியவற்றைக் கொண்டு (fog)oh = fo(goh) எனக் காட்டுக.
i) f(x) = x-1, g(x) = 3x + 1 மற்றும் h(x) = x²
ii) f(x) = x² , g(x) = 2x மற்றும் h(x) = x + 4
iii) f(x) = x-4, g(x) = x² மற்றும் h(x) = 3.x – 5
தீர்வு :
i) f(x) = x-1 g(x) = 3x + 1 h(x) = x²
fog(x) = f(g(x)) = f(3x+1)
= (3x + 1 -1)
= 3x
(fog)oh = (fog) oh (x)
= fog(h(x))
= fog(x² )
= 3x² ……………… (1)

goh(x) = g(h(x)) = g(x² )
= 3x² + 1
fo(goh) = fo(goh(x))
= f(3x² + 1)
fo(goh)= fo(goh(x))
= f(3x² + 1)
= 3x² + 1 – 1
= 3x² ……………….. (2)
(1) , (2) லிருந்து
(fog)oh = fo(goh)

ii) f(x) = x²
g(x) = 2x
h(x) = x + 4
fog(x) = f(g(x)= f(2x)
= (2x)²
= 4x²
(fog)oh = (fog) oh(x)
= fog(h(x)
= fog(x + 4)
= 4(x+4)² =
4(x² + 8x + 16)
= 4x² + 32x + 64
goh = goh = (x) = g(h(x))
=g (x + 4)
= 2 (x + 4) = 2x + 8
fo (goh)= fo (goh)(x)
= fo (2x+8)
= (2x + 8)²
= 4x² + 32x + 64 …………………… (2)
1, 2 லிருந்து

iii) (fog)oh = fo(goh).
f(x) = x – 4
g(x) = x²
h(x) = 3x – 5
fog(x) = fo(x²)
= x² – 4
(fog)oh = (fog)oh(x)
= fog(3x – 5)
= (3x –5)² – 4
= 9x² – 30x + 25 -4
= 9x² -30x + 21 …………….. (1)

goh(x) = go(3x-5)
= (3x – 5)²
= 9x² – 30x + 25

fo(goh)x = fo(9x² -30x + 25)
= 9x² -30x + 25 -4
= 9x² -30x + 21…………………(2)
(1) மற்றும் (2) லிருந்து
(fog)oh = fo(goh)

கேள்வி 9.
f = {{-1, 3), (0, -1), (2, -9)} ஆனது I -லிருந்து Z -க்கான ஒரு நேரிய சார்பு எனில், f(x) -ஐக் காண்க.
தீர்வு :
f(x) = ax + b என்க
கணக்கின்படி f(-1) = 3
a(-1) + b = 3
-a + b = 3 ……………… (1)
மேலும் f(0) = -1
o + b = -1
b = -1
b ன் மதிப்பை (1) ல் பிரதியிட a = -4
∴ f(x) = -4x – 1

கேள்வி 10.
ஒரு மின்சுற்றுக் கோட்பாட்டின் C(t) என்ற ஒரு நேரிய சுற்று, C(at₁ +bt₂ ) = aC(t₁) +bC(t₂) ஐ பூர்த்தி செய்கிறது. மேலும் இங்கு a, b ஆகியவை மாறிலிகள் எனில், C(t) = 3t ஆனது ஒரு நேரிய சுற்று எனக் காட்டுக.
தீர்வு :
கணக்கின்படி c(t) = 3t
c(at₁) = 3at₁ ……………. (1)
c(bt₂) = 3bt₂
1 + 2
c(at₁) + c(bt₂ ) = 3at₁ + 3bt₂
c(at₁ + bt₂ ) = 3at₁ + 3bt₂
= c(at₁) + c(bt₂)
=c(at₁ + bt₂)
மின்சுற்றுக்கோட்பாட்டை பூர்த்தி செய்கிறது.
∴ c(t) = 3t என்பது ஒரு நேரிய சுற்று ஆகும்

Tamilnadu State Board New Syllabus Samacheer Kalvi 10th Maths Guide Pdf Chapter 1 உறவுகளும் சார்புகளும் Ex 1.4 Textbook Questions and Answers, Notes.

TN Board 10th Maths Solutions Chapter 1 உறவுகளும் சார்புகளும் Ex 1.4

கேள்வி 1.
கீழே கொடுக்கப்பட்ட வரைபடங்கள் சார்பைக் குறிக்கின்றனவா எனத் தீர்மானிக்கவும். விடைகளுக்கான காரணத்தையும் கொடுக்கவும்.

தீர்வு:
(i)

குத்துக்கோடானது வரைபடத்தை இரு புள்ளிகளில் வெட்டுகிறது. எனவே இது சார்பு அல்ல.

(ii)

குத்துக்கோடானது வரைபடத்தை ஒரே ஒரு புள்ளியில் வெட்டுகிறது. எனவே இது ஒரு சார்பு.

(iii)

குத்துக்கோடானது வரைபடத்தை இரு புள்ளிகளில் வெட்டுகிறது இது ஒரு சார்பு அல்ல.

(iv)

குத்துக்கோடானது வரைபடத்தை ஒரே ஒரு புள்ளியில் வெட்டுகிறது. எனவே இது ஒரு சார்பு

கேள்வி 2.
f : A → B என்ற சார்பானது f(x) = \(\frac { x }{ 2 }\) -1, என
வரையறுக்கப்படுகிறது. இங்கு A = {2, 4, 6, 10, 12} B = {0, 1, 2, 4, 5, 9} ஆக இருக்கும் போது சார்பு f-ஐ பின்வரும் முறைகளில் குறிக்க.
(i) வரிசைச் சோடிகளின் கணம்
(ii) அட்டவணை
(iii) அம்புக்குறி படம்
(iv) வரைபடம்
தீர்வு :
f(x) = \(\frac { x }{ 2 }\) – 1 எனில்
f(2) = \(\frac { 2 }{ 2 }\) – 1 = 1 – 1 = 0
f(4) = \(\frac { 4 }{ 2 }\) – 1 = 2 – 1 = 1
f(6) = \(\frac { 6 }{ 2 }\) – 1 = 3 – 1 = 2
f(10) = \(\frac { 10 }{ 2 }\) – 1 = 5 – 1 = 4
f(12) = \(\frac { 12 }{ 2 }\) – 1 = 6 – 1 = 5

i) வரிசைச் சோடிகளின் கணம்
f = {(2, 0) (4, 1) (6, 2) (10, 4) (12, 5)}
ii) அட்டவணை

iii) அம்புக்குறி படம்

iv) வரைபடம்

கேள்வி 3.
f = {(1, 2), (2, 2), (3, 2), (4, 3), (5, 4)} என்ற சார்பினை
i) அம்புக்குறி படம்
ii) அட்டவணை
iii) வரைப்படம் மூலமாகக் குறிக்கவும்.
தீர்வு :
i) அம்புக்குறி படம்

ii) அட்டவணை

iii) வரைபடம்

கேள்வி 4.
f: N → N என்ற சார்பு f(x) = 2x – 1 என வரையறுக்கப்பட்டால் அது ஒன்றுக்கு ஒன்றான ஆனால் மேல் சார்பு இல்லை எனக் காட்டுக.
தீர்வு :
f(x) = 2) – 1
f(1) = 2(1) – 1 = 2 – 1 = 1
f(2) = 2(2) – 1 = 4 – 1 = 3
f(3) = 2(3) – 1 = 6-1 = 5
f(4) = 2 x 4 – 1 = 8 – 1 = 7
துணை மதிப்பகம் = {1, 2, 3, 4, ………..} —– (1)
வீச்ச கம் = {1, 3, 5, …………….} ——– (2)
(1) ≠ (2)
∴ எனவே இது 1 – 1 சார்பு ஆனால் மேல் சார்பு இல்லை .

கேள்வி 5.
f : N → N என்ற சார்பு f(m) = m2 + m + 3 என வரையறுக்கப்பட்டால் அது ஒன்றுக்கு ஒன்றான சார்பு எனக் காட்டுக.
தீர்வு :
N = {1,2,3,……..}
f(m) = m² + m + 3
f(1) = 1² + 1 + 3 = 5
f(2) = 2² + 2 + 3 = 9
f(3) = 3² + 3 + 3 = 15
∴ f = {(1,5), (2,9), (3,15) ……}
∴ f ஆனது 1 – 1 சார்பு ஆகும்.

கேள்வி 6.
A = {1, 2, 3, 4} மற்றும் B = N என்க. மேலும் f : A → B ஆனது f(x) = x³ என வரையறுக்கப்படுகிறது எனில்.
i) f -யின் வீச்சகத்தைக் காண்க.
ii) f எவ்வகை சார்பு எனக் காண்க.
தீர்வு :
f(x) = x³ எனில்
f(1) = 1³ = 1
f(2) = 2³ = 8
f(3) = 3³ = 27
f(4) = 4³ = 64

i) வீச்சகம் = {1, 8, 27, 64}
ii) ஒன்றுக்கு ஒன்றான மற்றும் உட்சார்பு

கேள்வி 7.
கீழே கொடுக்கப்பட்ட ஒவ்வொரு சார்பும் இருபுறச் சார்பா, இல்லையா? உன் விடைக்கான காரணத்தைக் கூறுக. i) f : R → R ஆனது f(x) = 2x + 1
ii) f : R – R ஆனது f(x) = 3 – 4x²
தீர்வு :
i) f(x) = 2(x) = 1
f(0) = 2 x (0 + 1 = 1
f(1) = 2 x 1+1 = 3
f(2) = 2 x 2+ 1 = 5
f(3) = 2 x 3+ 1 = 7
வெவ்வேறான உறுப்புகள் வெவ்வேறான உருவங்களைக் கொண்டுள்ளது.
∴ இது 1 – 1 சார்பு
மேலும் n (A) = n (B) என்பதால் இது மேல் சார்பு ஆகும்.
∴ f(x) = 2x+1 ஆனது இருபுறச் சார்பு ஆகும்.
(ii) f(x) = 3 – 4x²
f(1) = 3 – 4(1²) = -1
f(2) = 3 – 4(2²) = -13
f(3) = 3 – 4(3²) = -33
f(4) = 3 – 4(4²) = -61
f(-1) = 3 – 4(-1)² = -1
இங்கு f(1) = f (-1)
ஆனால் 1 ≠ -1
∴ f(x) ஆனது இரு புறச் சார்பு அல்ல

கேள்வி 8.
A = {-1, 1} மற்றும் B = {0, 2} என்க மேலும், f : A → B ஆனது f(x) = ax + b. என் வரையறுக்கப்பட்ட மேல் சார்பு எனில் , a மற்றும் b ஐக் காண்க.
தீர்வு :
f(x) = ax + b
கணக்கின் படி f(-1) = 0
⇒ a(-1) + b = 0
-a + b = 0 …………………….(1)
மேலும் f(1) = 2
⇒ a(1) + b = 2
a + b = 2 ……………………. (2)
1 + 2
– a + b + a + b = 0 + 2
⇒ 2b = 2
b = 1
b ன் மதிப்பை (உ)ல் பிரதியிட
a = 1

கேள்வி 9.
f என்ற சார்பானது
\(f(x)=\left\{\begin{aligned}
x+2 ; & x>1 \\
2 ; &-1 \leq x \leq 1 \\
x-1 ; &-3<x<-1
\end{aligned}\right.\)
என வரையறுக்கப்பட்டால்
i) f(3)
ii) f (0)
iii) f(-1.5)
iv) f(2) + f(-2)
ஆகியவற்றின் மதிப்புகளைக் காண்க.
தீர்வு :
\(f(x)=\left\{\begin{array}{cl}
x+2 & \text { if } x=\{2,3,4,5 \ldots \ldots\} \\
2 & \text { if } x=\{-1,0,1\} \\
x-1 & \text { if } x=\{-2\}
\end{array}\right.\)

(i) f(3) = x + 2
= 3 + 2 = 5
ii) f(0) = 2
iii) f(-1.5) = x – 1
= -1.5 – 1
= -2.5
iv) f(2) + f (-2)
= x + 2 + x – 1
= 2 + 2 + (- 2) – 1
= 4 – 3

கேள்வி 10.
f : [-5,9] → R என்ற சார்பானது பின்வருமாறு வரையறுக்கப்படுகிறது.
\(f(x)=\left\{\begin{array}{ll}
6 x+1 ; & -5 \leq x<2 \\
5 x^{2}-1 ; & 2 \leq x<6 \\
3 x-4 ; & 6 \leq x \leq 9
\end{array}\right.\) என வரையறுக்கப்படுகிறது எனில், பின்வருவனவற்றைக் காண்க.
(i) f(-3) + f(2)
ii) f(7) – f(1)
iii) 2f(4) + f(8)
iv) \(\frac{2 f(-2)-f(6)}{f(4)+f(-2)}\)
தீர்வு :
\(f(x)=\left\{\begin{array}{l}
6 x+1 \text { if } x=\{-5,-4,-3,-2,-1,0,1\} \\
5 x^{2}-1 \text { if } x=\{2,3,4,5\} \\
3 x-4 \text { if } x=\{6,7,8,9\}
\end{array}\right.\)
f(-3) = 6x +1
= 6 (-3) + 1 = -18 + 1 = -17
f(2) = 5x² – 1
= 5(2²) – 1 = 5 x 4 – 1 = 20 – 1 = 19
f(7) = 3x – 4)
= 3(7) – 4 = 21 – 4 = 17

f(1) = 6x + 1
= 6 (1) + 1 = 7

f(4) = 5x² -1
= 5 x 4² – 1 = 5 x 16 – 1 = 80 – 1 = 79

f(8) = 3x – 4
= 3(8) – 4 = 24 – 4 = 20

f(-2) = 6x + 1
= 6 (-2) + 1 = -12 + 1 = -11

f(6) = 3x – 4)
= 3(6) – 4 = 18 – 4 = 14

i) f(-3) + f(2) = -17 + 19 = 2
ii) f (7) – f(1) = 17 – 7 = 10
iii) 2f(4) + f(8) = 2 x 79 + 20
= 158 + 20 )
= 178

கேள்வி 11.
புவியீர்ப்பு விசையின் காரணமாக : வினாடிகளில் ஒரு பொருள் கடக்கும் தூரமானது S(t) = \(\frac { 1 }{ 2 }\) gt² + at + b எனக் கொடுக்கப்பட்டுள்ளது. இங்கு a, b ஆகியவை மாறிலிகள் (8 ஆனது புவியீர்ப்பு விசையின் காரணமாக ஏற்படும் முடுக்கம்). S(t) ஆனது ஒன்றுக்கொன்றான சார்பாகுமா என ஆராய்க.
தீர்வு :
s{t) = \(\frac { 1 }{ 2 }\) gt² + at + b என்க
t = 0 எனில் S (o) = b
t = 1 எனில் s(1) = \(\frac { 1 }{ 2 }\) g x 1² + a x 1 + b
\(\frac { 1 }{ 2 }\) = g + a + b
S(t₁) = S(t₂) எனில்
t = 2 எனில் S(2) = \(\frac { 1 }{ 2 }\) g(2²) + a x 2 + b
= \(\frac { 4g }{ 2 }\) + 2a + b
இங்கு ஒவ்வொரு மதிப்பிற்கும் S(t)ன் மதிப்பு வேறுபட்டுள்ளது.
∴ S(t) ஆனது 1 – 1 சார்பு ஆகும்.

கேள்வி 12.
t என்ற சார்பானது செல்சியஸில் (C) உள்ள வெப்பநிலையையும், பாரன்ஹீட்டில் (F) உள்ள வெப்பநிலையையும் இணைக்கும் சார்பாகும். மேலும் அது t(C) = F என வரையறுக்கப்பட்டால், (இங்கு F = \(\frac { 9C }{ 5 }\) + 32)
(i) t(0)
(ii) t(28)
(iii) t(-10)
(iv) t(C) = 212 ஆக இருக்கும் போது C – ன் மதிப்பு
(v) செல்சியஸ் மதிப்பும் பாரன்ஹீட் மதிப்பும் சமமாக இருக்கும் போது வெப்பநிலை ஆகியவற்றைக் கண்டறிக. தீர்வு :
கணக்கின் படி t(C) = F
F = \(\frac { 9C }{ 5 }\) + 32
(i) t(0) = \(\frac { 0 }{ 5 }\) + 32 = 32°F
(ii) t(28) =\(\frac{9 \times 28}{5}\) + 32
= \(\frac{252}{5}\) + 32
= 50.4 + 32 = 82.4°F

(iii) \(\frac{9(-10)}{5}\) + 32
= \(\frac{-90}{5}\) + 32
= -18 + 32 = 24

iv) t(C) = 212
c = \(\frac{9 \mathrm{C}}{5}\) + 32 = 212
= 180
9C = 180 x 5
= 900
∴C = 100°C

v) செல்சியஸ் மதிப்பும் பாரன்ஹீட் மதிப்பும்
சமமாக இருக்கும் போது வெப்பநிலை
C = \(\frac{9 \mathrm{C}}{5}\) +32
C – 32 = \(\frac{9 \mathrm{C}}{5}\)
5(C – 32) = 9C
5C – 160 = 9C
5C – 9C = 160
-4C = 160
C = -40

Tamilnadu State Board New Syllabus Samacheer Kalvi 10th Maths Guide Pdf Chapter 1 உறவுகளும் சார்புகளும் Unit Exercise 1 Textbook Questions and Answers, Notes.

TN Board 10th Maths Solutions Chapter 1 உறவுகளும் சார்புகளும் Unit Exercise 1

கேள்வி 1.
(x² – 3x, y² + 4y) மற்றும் (-2, 5) ஆகிய வரிசைச் சோடிகள் சமம் எனில் , x மற்றும் y -ஐக் காண்க.
தீர்வு :

தரவு x² -3x = -2
x² -3x + 2 = 0
(x-1) (x – 2) = 0
x = 1 மற்றும் x = 2
தரவு y² + 4y = 5
y² + 4y -5 = 0
(y-1) (y+5) = 0
y-1 மற்றும் y =-5

x ன் மதிப்பு 1 மற்றும் 2
yன் மதிப்பு 1 மற்றும் -5

கேள்வி 2.
A × A கார்டீசியன் பெருக்கல் பலனின், 9 உறுப்புகளில், உறுப்புகள் (-1, 0) மற்றும் (0, 1)-யும் இருக்கிறது எனில், A-யில் உள்ள உறுப்புகளைக் காண்க. மற்றும் A × A-ன் மீதமுள்ள உறுப்புகளைக் காண்க.
தீர்வு :
A = {-1, 0, 1}
A × A = {(-1, -1) (-1, 1) (0, -1) (0, 0) (1, -1) (1, 0) (1, 1)}

கேள்வி 3.
f(x) = \(\left\{\begin{array}{cc}
\sqrt{x-1} & x \geq 1 \\
4 & x<1
\end{array}\right.\) எனக் கொடுக்கப்பட்டால்,
i) f(0)
ii) f(3)
iii) f(a+1)
(a ≥ 0 எனக் கொடுக்கப்பட்டுள்ளது) ஆகியவற்றை காண்க.
தீர்வு :
f(x) = \(\left\{\begin{array}{ccc}
\sqrt{x-1} & \text { if } & x=\{1,2,3,4 \ldots \ldots \ldots\} \\
4 & \text { if } & x=\{0,-1,-2 \ldots \ldots \ldots\}
\end{array}\right.\)
i) f(0) = 4
ii) f(3) =\(\sqrt{x-1}=\sqrt{3-1}=\sqrt{2}\)
iii) f(a+1) = \(\sqrt{x-1}=\sqrt{a+1-1}=\sqrt{a}\)

கேள்வி 4.
A = {9, 10, 11, 12, 13, 14, 15, 16, 17} என்க. மற்றும் f : A →N ஆனது f(n) ∈ == n-ன் அதிகப்பட்சப் பகாகாரணி (n ∈ A) என வரையறுக்கப்பட்டால் f – ன் வரிசைச் சோடிகளின் கணத்தை எழுதுக மற்றும் f – ன் வீச்சகத்தைக் காண்க.
தீர்வு :
f(n) = அதிகபட்ச பகாக்காரணி
f(9) = 3 (காரணிகள் 1, 3, 9)
f(10) = 5 (காரணிகள் 1, 2, 5)
f(11) = 11 (காரணிகள் 1, 11)
f(12) = 3 (காரணிகள் 1, 2, 3, 4, 6, 12)
f(13) = 13 (காரணிகள் 1, 13)
f(14) = 7 (காரணிகள் 1, 2, 7, 14)
f(15) = 5 (காரணிகள் 1, 3, 5, 15)
f(16) = 2 (காரணிகள் 1, 2, 4, 8, 16)
f(17) = 17 (காரணிகள் 1, 17)
வரிசை ஜோடிகளின் கணம் {(9, 3) (10, 5) (11, 11) (12, 3) (13, 13) (14, 7) (15, 5) (16, 2) (17, 7)}
fன் வீச்சகம் = {(2, 3, 5, 11, 13, 17}

கேள்வி 5.
f(x) = \(\sqrt{1+\sqrt{1-\sqrt{1-x^{2}}}}\) என்ற சார்பின்
மதிப்பகத்தை காண்க:
தீர்வு :
f(x) = \(\sqrt{1+\sqrt{1-\sqrt{1-x^{2}}}}\)

இங்கு
\(\sqrt{1-x^{2}}=\sqrt{(1+x)(1-x)}\)
x = 1 (or) x = -1
= -1 ≤ x ≤ 1
∴ மதிப்ப கம் f(x) – {-1, 0, 1}

கேள்வி 6.
f(x) = x², g(x) = 3x மற்றும் h(x) = x-2 எனில், (fog)oh = fo(goh) என நிறுவுக.
தீர்வு :
fog(x) = f(g(x)) = f(3x)
= (3x)²
=9x²
(fog)oh(x) = fog(h(x)
= fog(x-2)
= 9 (x-2)²
= 9[x² – 4x + 4)
=9×2 – 36x + 36 …………… (1)
goh(x) = g(h(x) = g(x-2)
= 3(x-2)
= 3x -6

fo(goh) (x) = fo(3x – 6)
= (3x – 6)²
= 9x² – 36x + 36………………. (2)
(1) nd (2) லிருந்து
(fog)oh = fo(goh) என்பதை பெறாலாம்.

கேள்வி 7.
A = {1, 2} B = {1, 2, 3, 4} C = {5, 6} மற்றும் D = {5, 6, 7, 8} எனில் A × C ஆனது B × D உட்கணமா எனச் சரிபார்க்க.
தீர்வு :
A × C = {1, 2}x {5, 6}
= {(1, 5) (1,6) (2, 5) (2, 6)} —– (1)
B × D = {1, 2, 3, 4}x {5, 6, 7, 8}
= \(\left\{\begin{array}{l}
(1,5)(1,6)(1,7)(1,8)(2,5)(2,6) \\
(2,7)(2,8)(3,5)(3,6) \\
(3,7)(3,8)(4,5)(4,6)(4,7)(4,8)
\end{array}\right\}\) …………….. (2)
(1), (2) லிருந்து
A x C ⊂ B X D என்பதை அறியலாம்.

கேள்வி 8.
f(x) = –, x≠ -1 என்க. x ≠ 0 எனில்,
f(x))= \(\frac{-1}{x}\) எனக் காட்டுக.

தீர்வு :

கேள்வி 9.
சார்பு f மற்றும் 8 ஆகியவை f(x) = 6x + 8,
ste) = \(\frac{x-2}{3}\) எனில்,
i) gg ( \(\frac { 1 }{ 2 }\) ) (H) -யின் மதிப்பைக் காண்க.
ii) gf(x) – ஐ எளிய வடிவில் எழுதுக.
தீர்வு :
தரவு f(x) = 6x + 8

ii) g f(x) ஐ எளிய வடிவில் எழுதுக.
தரவு : f(x) = 6x + 8
g(x) = \(\frac{x-2}{3}\)
f(x) = g(6x + 8)

கேள்வி 10.
பின்வருவனவற்றின் மதிப்பகங்களை எழுதுக.
i) f(x) = \(\frac{2 x+1}{x-9}\)
ii) P(x) = \(\frac{-5}{4 x^{2}+1}\)
iii) g(x) = \(\sqrt{x-2}\)
iv) h(x) = x + 6
தீர்வு :
i) f(x) = \(\frac{2 x+1}{x-9}\)
மதிப்பகம் = R – {9}

குறிப்பு x = 9 எனில்
f (x) = \(\frac{2(9)+1}{0}\)
வரையறுக்கப்
– படவில்லை

ii) p(x) = \(\frac{-5}{4 x^{2}+1}\)
மதிப்பகம் = R

குறிப்பு
x = 0 மற்றும் x < 0
g(0) = \(\sqrt{0-2}=\sqrt{-2}\) ∉ R

iii) g(x) = \(\sqrt{x-2}\)
மதிப்பகம் = {2, 3, 4, 5………..)

iv) h(x) = x + 6
மதிப்பகம் = R