Samacheer Kalvi 10th Maths Guide Chapter 1 உறவுகளும் சார்புகளும் Ex 1.5

Tamilnadu State Board New Syllabus Samacheer Kalvi 10th Maths Guide Pdf Chapter 1 உறவுகளும் சார்புகளும் Ex 1.5 Textbook Questions and Answers, Notes.

TN Board 10th Maths Solutions Chapter 1 உறவுகளும் சார்புகளும் Ex 1.5

கேள்வி 1.
கீழேக் கொடுக்கப்பட்டுள்ள f மற்றும் g எனும் சார்புகளைப் பயன்படுத்தி fog மற்றும் gof – ஐக் காண்க fog = gof என்பது சரியா சோதிக்க.
i) f(x) = x – 6, g(x) = x²
ii) f(x) = \(\frac{2}{x}\) = g(x) = 2x² – 1
ii) f(x) = \(\frac{x+6}{3}\) g(x) = 3 – x
iv) f(x) = 3 + x, g(x) = x – 4
v) f(x) = 4x² – 1, g(x) = 1 + x
தீர்வு :
i) f(x) = x-6, g(x) = x² [∵ f(x) = x -6]
fog(x) = f(g(x)) = f(x²)
= x² – 6
gof(x) =g[f(x)) = g(x-6)
= (x-6)²
∴ fog ≠ gof

ii) f(x) = \(\frac{2}{x}\) g(x) = 2x² – 1
fog(x) = f(g(x)) = f(2x² – 1)
= \(\frac{2}{2 x^{2}-1}\)
gof (x) = g(f(x)) = g(\(\frac{2}{x}\))
= 2( \(\frac{2}{x}\) )² – 1
= 2 x \(\frac{4}{x^{2}}\) – 1
= \(\frac{8}{x^{2}}\) – 1
∴ fog ≠ gof

iii) f(x) = \(\frac{x+6}{3}\), g(x) = 3 – x
fog(x) = f(g(x)) = f(3-x)

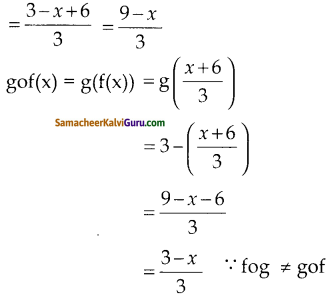
iv) f(x) = 3 + x; g(x) = x – 4
fog(x) = f(g(x)) = f(x-4)
= 3 + x -4
= x -1
gof(x) = g(f(x)) = g(3 + x)
= 3 + x – 4
= x – 1
எனவே fog = gof

v) f(x) = 4x² – 1, g(x) = 1 + x
fog(x) = f(g)(x)) = f(1 + x)
= 4(1 + x)² – 1
= 4(1 + 2x + x²) – 1
= 4 + 8x + 4x² – 1
= 4x² + 8x + 3
gof(x) = g(f(x)) = g(4x² – 1)
= 1 + 4x² – 1
= 4x²
எனவே fog ≠ gof

கேள்வி 2.
fog = gof எனில் K – யின் மதிப்பைக் காண்க
i) f(x) = 3x + 2, g(x) = 6x – K
ii) f(x) = 2x – K, g(x) = 4x + 5
தீர்வு :
i) f(x) = 3x + 2
g(x) = 6x – K
fog = gof (தர்வு)
fog(x) = gof(x)
f(g(x) = g(f(x))
f(6x – k) = g(3x + 2)
3(6.x – k) + 2 = 6(3.x + 2) – k
18x-3k + 2 = 18.x + 12 – k
2k = -10
k =-5

ii) f(x) = 2x-k, g(x) = 41 + 5
தரவு fog = gof
fog(x) = gof(x)
f(g)(x) = g(f(x)
f(4x + 5) = g(2x-k)
2(4x + 5) -k = 4(2x – k) + 5
8x + 10 – k = 8x -4k + 5
3k = -5
k = -5/3

கேள்வி 3.
f(x) = 2x -1; g(x) = \(\frac{x+1}{2}\) எனில், fog = gof = x எனக் காட்டுக.
தீர்வு :
fog (x) = f(g(x)))
= f( \(\frac{x+1}{2}\) )
= \(2\left(\frac{x+1}{2}\right)-1\)
= x + 1 -1
= x gof = gof(x)
=g(f(x))
=g(2x – 1) = 2x/2
= x
எனவே fog = gof = x
எனவே நிரூபிக்கப்பட்டது.

கேள்வி 4.
f(x) = x² – 1, g(x) = x – 2 மற்றும் gof (a) = 1 எனில் , a ஐக் காண்க
தீர்வு :
i) f(x) = x² – 1;
g (x) = x – 2
தரவு gof(a) =1
g(f(a)) =1
g(a² – 1) = 1
a² – 1 – 2 = 1
a² – 3 = 1
a² = 4
a = ±2

கேள்வி 5.
A, B, C ⊆ N மற்றும் f: A → B என்ற சார்பு f(x) = 2x +1 எனவும் மற்றும்g : B → C ஆனது g(x) = x² எனவும் வரையறுக்கப்பட்டால், fog மற்றும் gof- யின் வீச்சகத்தைக் காண்க.
தீர்வு :
தரவு f(x) = 2x +1
g(x) = x²
fog = fog(x)
= f(g(x)))
= f(x²)
= 2x² + 1
gof = gof(x)|
= g(f(x))
= g(2x + 1)
= (2x +1)²
fog மற்றும் gof ன் வீச்சகம்
{y/y = 2x² + 1, x ∈ N }, {y/y = (2x + 1)², x∈N}

கேள்வி 6.
f(x) = x² – 1 எனில் i) fof ii) fofof – ஐக் காண்க
தீர்வு:
தரவு f(x) = x² – 1
a) fof(x) = f(f(x)
= f(x² – 1)
= (x² – 1)² – 1
= x⁴ – 2x² + 1 – 1
=x⁴ -2x²

b) fofof = fofof(x)
= fof(f(x))
= fof(x² – 1)
= f(f(x2-1))
= f[[x² – 1)² -1)
= f[x⁴ – 2x² + 1 – 1]
= f[x⁴ – 2x²] ⇒ (x⁴ – 2x²)² – 1

கேள்வி 7.
f: R – R மற்றும் g:R – R ஆனது முறையே,
f(x) = x⁵, g(x)= x⁴ என வரையறுக்கப்பட்டால், fg ஆகியவை ஒன்றுக்கு ஒன்றானதா மற்றும் fog ஒன்றுக்கு ஒன்றான சார்பாகுமா என்று ஆராய்க .
தீர்வு : f(x) = f(y)
x⁵ = y⁵
எனவே x = y
ஆகையால் f ஒரு ஒன்றுக்கு ஒன்றான சார்பு
g(x) = g(y) எனில்
x⁴ = y⁴
ஆகையால் x = y
எனவே g ஒரு ஒன்றுக்கு ஒன்றான சார்பு
fog = fog(x)
= f(g(x))
= f(x⁴)
= (x⁴)⁵
= x²⁰
fog(x) = fog(y) எனில்
x²⁰ = y²⁰
∴ fog ஆனது 1 – 1 சார்பு ஆகும்.

கேள்வி 8.
கொடுக்கப்பட்ட f(x), g(x), h(x) ஆகியவற்றைக் கொண்டு (fog)oh = fo(goh) எனக் காட்டுக.
i) f(x) = x-1, g(x) = 3x + 1 மற்றும் h(x) = x²
ii) f(x) = x² , g(x) = 2x மற்றும் h(x) = x + 4
iii) f(x) = x-4, g(x) = x² மற்றும் h(x) = 3.x – 5
தீர்வு :
i) f(x) = x-1 g(x) = 3x + 1 h(x) = x²
fog(x) = f(g(x)) = f(3x+1)
= (3x + 1 -1)
= 3x
(fog)oh = (fog) oh (x)
= fog(h(x))
= fog(x² )
= 3x² ……………… (1)

goh(x) = g(h(x)) = g(x² )
= 3x² + 1
fo(goh) = fo(goh(x))
= f(3x² + 1)
fo(goh)= fo(goh(x))
= f(3x² + 1)
= 3x² + 1 – 1
= 3x² ……………….. (2)
(1) , (2) லிருந்து
(fog)oh = fo(goh)

ii) f(x) = x²
g(x) = 2x
h(x) = x + 4
fog(x) = f(g(x)= f(2x)
= (2x)²
= 4x²
(fog)oh = (fog) oh(x)
= fog(h(x)
= fog(x + 4)
= 4(x+4)² =
4(x² + 8x + 16)
= 4x² + 32x + 64
goh = goh = (x) = g(h(x))
=g (x + 4)
= 2 (x + 4) = 2x + 8
fo (goh)= fo (goh)(x)
= fo (2x+8)
= (2x + 8)²
= 4x² + 32x + 64 …………………… (2)
1, 2 லிருந்து

iii) (fog)oh = fo(goh).
f(x) = x – 4
g(x) = x²
h(x) = 3x – 5
fog(x) = fo(x²)
= x² – 4
(fog)oh = (fog)oh(x)
= fog(3x – 5)
= (3x –5)² – 4
= 9x² – 30x + 25 -4
= 9x² -30x + 21 …………….. (1)

goh(x) = go(3x-5)
= (3x – 5)²
= 9x² – 30x + 25

fo(goh)x = fo(9x² -30x + 25)
= 9x² -30x + 25 -4
= 9x² -30x + 21…………………(2)
(1) மற்றும் (2) லிருந்து
(fog)oh = fo(goh)

கேள்வி 9.
f = {{-1, 3), (0, -1), (2, -9)} ஆனது I -லிருந்து Z -க்கான ஒரு நேரிய சார்பு எனில், f(x) -ஐக் காண்க.
தீர்வு :
f(x) = ax + b என்க
கணக்கின்படி f(-1) = 3
a(-1) + b = 3
-a + b = 3 ……………… (1)
மேலும் f(0) = -1
o + b = -1
b = -1
b ன் மதிப்பை (1) ல் பிரதியிட a = -4
∴ f(x) = -4x – 1

கேள்வி 10.
ஒரு மின்சுற்றுக் கோட்பாட்டின் C(t) என்ற ஒரு நேரிய சுற்று, C(at₁ +bt₂ ) = aC(t₁) +bC(t₂) ஐ பூர்த்தி செய்கிறது. மேலும் இங்கு a, b ஆகியவை மாறிலிகள் எனில், C(t) = 3t ஆனது ஒரு நேரிய சுற்று எனக் காட்டுக.
தீர்வு :
கணக்கின்படி c(t) = 3t
c(at₁) = 3at₁ ……………. (1)
c(bt₂) = 3bt₂
1 + 2
c(at₁) + c(bt₂ ) = 3at₁ + 3bt₂
c(at₁ + bt₂ ) = 3at₁ + 3bt₂
= c(at₁) + c(bt₂)
=c(at₁ + bt₂)
மின்சுற்றுக்கோட்பாட்டை பூர்த்தி செய்கிறது.
∴ c(t) = 3t என்பது ஒரு நேரிய சுற்று ஆகும்