Samacheer Kalvi 10th Maths Guide Chapter 2 எண்களும் தொடர்வரிசைகளும் Ex 2.6

Tamilnadu State Board New Syllabus Samacheer Kalvi 10th Maths Guide Pdf Chapter 2 எண்களும் தொடர்வரிசைகளும் Ex 2.6 Textbook Questions and Answers, Notes.

TN Board 10th Maths Solutions Chapter 2 எண்களும் தொடர்வரிசைகளும் Ex 2.6

கேள்வி 1.
பின்வருவனவற்றின் கூடுதல் காண்க.
(i) 3, 7, 11,… 40 உறுப்புகள் வரை
(ii) 102, 97, 92,… 27 உறுப்புகள் வரை
(iii) 6+13 +20 + ……. + 97
தீர்வு:
i) 3, 7, 11, …… 40 உறுப்புகள் வரை.
a = 3, d = 7-3 = 4, n = 40
S_n = \(\frac{\mathrm{n}}{2}\) [2a+(n-1)d]
S₄₀ = \(\frac{40}{2}\)[2(3)+(40-1)(4))
= 20[6 + 39 x 4]
= 20[6 + 156)
= 20 x 162
= 3240 எனவே
S₄₀ = 3240

ii) 102, 97, 92, 27 உறுப்புகள் வரை
a = 102, d = 97-102 = -5, n = 27
S_n = \(\frac{\mathrm{n}}{2}\)[2a+(n-1)d]
S₂₇ = \(\frac{27}{2}\)[2(102)+(27-1)(-5)]
= \(\frac{27}{2}\)(204+26*(-5)] 27 x(204-130)
= \(\frac{27}{2}\) x 74
= 999
எனவே S₂₇ = 999

iii) 6+13+20+ …………….+97
a = 6, d = 13 – 6 = 7, l = 97
n = \(\frac{1-\mathrm{a}}{\mathrm{d}}\)+1
= \(\frac{97-6}{7}\) + 1
= \(\frac{91}{7}\) + 1
= 13+1
n = 14
S_n = \(\frac{n}{2}\) (a + l)
S₁₄ = \(\frac{14}{2}\) [6 + 97)
= 7 x 103
∴ S₁₄ = 721

கேள்வி 2.
5-லிருந்து தொடங்கி எத்தனை தொடர்ச்சியான ஒற்றை முழுக்களைக் கூட்டினால் கூடுதல் 480 கிடைக்கும்? தீர்வு:
5 ல் தொடங்கும் தொடர்ச்சியான ஒற்றை முழுக்க ள் = 5, 7, 9……
கணக்கின் படி S_n = 480
இங்கு a = 5, d = 7-5 = 2
\(\frac{n}{2}\)[2a + (n – 1)d] = 480
\(\frac{n}{2}\)[2(5)+(n-1)(2)] = 480
\(\frac{n}{2}\)[10 + 2n – 2] = 480
\(\frac{n}{2}\)[8+2n] = 480
\(\frac{n}{2}\) x 2(4+n) = 480
n² + 4n – 480 = 0
(n-20)(n+24) = (0)
n = 20, n = -24 என்பது பொருந்தாது எனவே கல் தொடங்கிய தொடர்ச்சியான ஒற்றை முழுக்களின் எண்ணிக்கை = 20

கேள்வி 3.
ஒரு கூட்டுத் தொடர்வரிசையின் n -ஆவது உறுப்பு 4n – 3 எனில் அதன் முதல் 28 உறுப்புகளின் கூடுதல் கான்க. தீர்வு:
தரவு : t_n = 4n – 3
t₁ = 4(1) – 3 = 4 – 3 = 1
t₂ = 4(2) – 3 = 8 – 3 = 5
எனவே t₂ – t₁ = 5 – 1 = 4
ஆகையால் a = 1, d = 4, n = 28
எனவே S_n = \(\frac{n}{2}\) [2a + (n – 1)d]
S₂₈ = \(\frac{28}{2}\) [2(1) (28 – 1)(4)
= \(\frac{28}{2}\)[2 + 27 x 4]
= 14[2 + 108]
= 14 x 110
= 1540
எனவே S₂₈= 1540

கேள்வி 4.
ஒரு குறிப்பிட்ட தொடரின் முதல் ‘n’ உறுப்புகளின் கூடுதல் 2n² – 3n எனில், அது ஒரு கூட்டுத் தொடர்வரிசை என நிரூபிக்க.
தீர்வு:
S_n = 2n² – 3n
S₁ = t₁ = 2(1)² – 3(1) = 2 x 1 – 3 = 2 – 3 = -1
∴ t₁ = a = -1|
S₂ = 2(2²) – 3(2) = 2(4) – 6 = 8 – 6 = 2
எனவே S₂ = t₁ + t₂ = 2
-1 + t₂ = 2
t₂ = 2 + 1
t₂ = 3
எனவே S₃ = t₁ + t₂ + t₃ = 2(3²) – 3(3)
= 2(9) – 3(3)
= 18 – 9
t₁ + t₂ + t₃ = 9
-1 + 3 + t₃ = 9
2 + t₃ = 9
t₃ = 9 – 2
t₃ = 2
வரிசை = -1, 3, 7, ……
இங்கே t₂ – t₁ = 3-(-1) = 4
t₃ – t₂ = 7-3 = 4
அடுத்தடுத்த உறுப்புகளின் வித்தியாசங்கள் சமம்.
எனவே -1, 3, 7 ……….. என்பது ஒரு கூட்டுத் தொடர் வரிசை ஆகும்.

கேள்வி 5.
ஒரு கூட்டுத் தொடர்வரிசையின் 104-வது உறுப்பு மற்றும் 4-வது உறுப்புகள் முறையே 125 மற்றும் 0. அத்தொடர்வரிசையின் முதல் 35 உறுப்புகளின் கூடுதல் காண்க.
தீர்வு :
t₁₀₄ = 125
t_n = a + (n – 1)d
எனவே t₁₀₄ = a + (104 – 1)d = 125
a + 103d = 125 ——-(1)
t₄ = 0
t₄ = a + (4 – 1)d = 0
a + 3d = 0 ——–(2)
(1 ) – (2)⇒

d = 5/4 ஐ சமன்பாடு (2)ல் பிரதியிட
a + 3d = 0
a + 15/4 = 0
a = -15/4
S₃₅ = ?

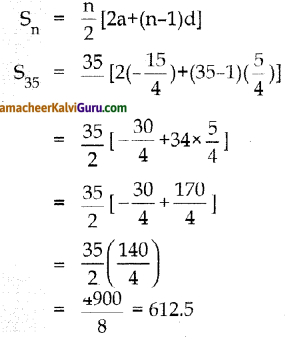
கேள்வி 6.
450-க்குக் குறைவாக உள்ள அனைத்து ஒற்றை மிகை முழுக்களின் கூடுதல் காண்க.
தீர்வு:
1 + 3 + 5 + …… + 449
இங்கு a = 1, d = 3 – 1 = 2, l = 449
n = \(\frac{1-a}{d}\) + 1
= \(\frac{449-1}{2}\) + 1
= \(\frac{448}{2}\)+ 1
= 224 + 1
n = 225
S_n = \(\frac{n}{2}\)(a + l)
S₂₂₅ = \(\frac{225}{2}\)(1 + 449)
= \(\frac{225}{2}\) x 450
= 225 x 225
S₂₂₅ = 50625

கேள்வி 7.
602-க்கும் 902-க்கும் இடையே 4 ஆல் வகுபடாத இயல் எண்களின் கூடுதல் காண்க.
தீர்வு:
602 க்கும் 902 க்கு இடையே உள்ள இயல் எண்க ள் = 603, 604, ……….. 901.
இங்கு d = 603, d = 1, l = 901
n = \(\frac{1-a}{d}\) + 1
= \(\frac{901-603}{1}\) + 1
= 298 + 1
n = 299
S_n = \(\frac{n}{2}\) (a + l)
A₂₉₉= \(\frac{299}{2}\) [603 + 901]
= \(\frac{299}{2}\) x 1504
= 224848

602 க்கும் 902 க்கும் இடையே உள்ள அனைத்து இயல் எண்க ளின் கூடுதல் = 224848 602 க்கும் 902 க்கும் இடையேயுள்ள 4 ஆல் வகுக்கும் அனைத்து இயல் எண்கள் = 604, 608,……… 900.
இங்கு a = 604, d = 4, 1 = 900

602 க்கும் 902 க்கும் இடையே 4 ஆல் வகுப்படும் இயல் எண்க ளின் கூடுதல் = 56400
602 க்கும் 902 க்கும் இடையே 4 ஆல் வகுபடாத அனைத்து இயல் எண்களின் கூடுதல் = 224848-56400 = 168448

கேள்வி 8.
இரகு ஒரு மடிக்கணினி வாங்க விரும்புகிறார். அவர் அதற்கான தொகையான ₹ 40,000 – ஐ உடனடியாக பணமாகவும் செலுத்தலாம் அல்லது 10 மாதத் தவணைகளில் முதல் தவணை ₹ 4800, இரண்டாம் தவணை ₹ 4750, மூன்றாம் தவணை₹1 4700 என்ற அடிப்படையிலும் செலுத்தலாம். அவர் இந்த வகையில் பணம் செலுத்துகிறார் எனில்,
(i) 10 மாதத் தவணைகளில் அவர் செலுத்திய மொத்தத் தொகை
(ii) மாதத் தவணை அடிப்படையில் பணம் செலுத்தும்போது அவர் அசலைக் காட்டிலும் கூடுதலாகச் செலுத்திய
தொகை ஆகியவற்றைக் காண்க.
தீர்வு :
i) 10 மாதத் தவணைகளில் அவர் செலுத்திய மொத்தத் தொகை = ?
a = 4800, d = 4750-4800 = -50, n = 10
S_n = \(\frac{\mathrm{n}}{2}\) [2a + (n-1)d]
S₁₀ = \(\frac{10}{2}\) [2(4800)+(10-1)(-50)]
= 5[9600 + 9x(-50)]
= 5[9600 – 450]
= 5 x 9150
= 45750
10 மாதத் தவணைகளில் அவர் செலுத்திய மொத்தத் தொகை = ₹ 45750
ii) அசலைக் காட்டிலும் அவர் கூடுதலாக செலுத்தியத் தொகை = ₹ 45750 – ₹ 40000
=₹5750

கேள்வி 9.
ஒருவர் தான் பெற்ற ₹65,000 கடனை திருப்பிச் செலுத்த முதல் மாதம் ₹400 செலுத்துகிறார். அதன் பிறகு ஒவ்வொரு மாதமும் முந்தைய மாதம் செலுத்தியதை விட ₹300 கூடுதலாகச் செலுத்துகிறார், அவர் இந்தக் கடனை அடைக்க எவ்வளவு காலம் தேவைப்படும்?
தீர்வு :
S_n இங்கு S. = 65000, a = 400, d = 300
S_n = \(\frac{\mathrm{n}}{2}\) [2a + (n – 1)d] = 65000
\(\frac{\mathrm{n}}{2}\)[2(400) +(n-1)300] = 65000
\(\frac{\mathrm{n}}{2}\)[800 + 300n – 300] = 65000
\(\frac{\mathrm{n}}{2}\) [500 + 300n] = 65000
\(\frac{\mathrm{n}}{2}\) x 100[5 + 3n] = 65000
3n² + 5n – 1300 = 0
(3n + 65)(n – 20) = 0
3n + 65 = 0, n – 20 = 0
3n = -65
n = -65/3 என்பது பொருந்தாது.
n – 20 = 0
n = 20
கடனை அடைக்கத் தேவைப்படும் காலம் = 20 மாதங்கள்

கேள்வி 10.
செங்கற்களினால் கட்டப்பட்ட ஒரு படிக்கட்டில் மொத்தம் 30 படிகட்டுகள் உள்ளன. கீழ்ப்படிக்கட்டை அமைப்பதற்கு 100 செங்கற்கள் தேவைப்படுகிறது. அடுத்தடுத்த படிக்கட்டுகள் அமைப்பதற்கு முந்தைய படிக்கட்டை விட இரண்டு செங்கற்கள் குறைவாகத் தேவைப்படுகிறது.
(i) உச்சியிலுள்ள படிக்கட்டை அமைப்பதற்கு எத்தனை செங்கற்கள் தேவை?
(ii) படிகட்டுகள் முழுவதும் அமைப்பதற்கு எத்தனை செங்கற்கள் தேவை?
தீர்வு :
100, 98, 96, 94 ……
n = 30, a = 100, d = 98-100 = -2
t_n = a+(n-1)d
t₃₀ = 100 + (30 – 1)(-2)
= 100+29x(-2)
= 100-58
t₃₀ = 42
உச்சியிலுள்ள படிக்கட்டை அமைப்பதற்கு தேவைப்படும் செங்கற்களின் எண்ணிக்கை = 42
100+98+96+94 + …..+42
a = 100, d = 98-100 = -2, n = 30
s_n = \(\frac{n}{2}\) [2a+(n-1)d]
S₃₀ = \(\frac{n}{2}\) [2(200)+(30-1)(-2)]
= 15[200 + 29 x (-2)]
= 15[200 – 58]
= 15 x 142
S₃₀ = 2130
படிக்கட்டுகள் முழுவதும் அமைப்பதற்கு தேவைப்படும் செங்கற்களின் எண்ணிக்கை = 2130.

கேள்வி 11.
S₁, S₂, S₃, ……….S_m, என்பன 1 வெவ்வேறு
கூட்டுத் தொடர்வரிசைகளின் 11 உறுப்புகளின் கூடுதலாகும். முதல் உறுப்புகள் 1, 2, 3, …n மற்றும் பொது வித்தியாசங்கள் 1, 3, 5, …, (2m -1) முறையே அமைந்தால், அந்த கூட்டுத் தொடர் வரிசையில் S₁, S₂, S₃, ……….S_m = \(\frac { 1 }{ 2 }\) mn (mn+1) என நிரூபிக்க.
தீர்வு :
a = 1, d = 1 எனில் S₁ = \(\frac{n}{2}\)[2+(n-1}1)
a = 2, d = 3 எனில் S₂ =\(\frac{n}{2}\) [4+(n-1)3)
a = 3, d = 5 எனில் S₃ = \(\frac{n}{2}\)[6+(n-1)5] –
a = m,d= 2m-1 எனில் S_m = \(\frac{n}{2}\)[2m+(n-1)(2m-1)] எனவே
S₁ + S₂ + S₃, ………. + S_m

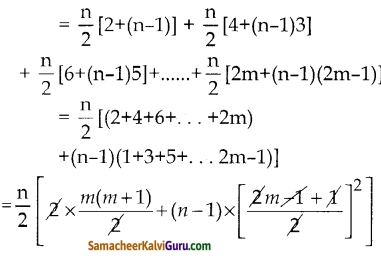
\(\frac{n}{2}\) [m{m+1)+(n-1)m²]
= \(\frac{n}{2}\) [m²+m+nm²-m²]
= \(\frac{n}{2}\) [m{mn+1)]
= 111 [mn+1]
எனவே S₁ + S₂ + S₃ + ……………….+ S_m = \(\frac{m n}{2}\) [mn + 1]

கேள்வி 12.
\(\frac{a-b}{a+b}+\frac{3 a-2 b}{a+b}+\frac{5 a-3 b}{a+b}+\ldots 12\) உறுப்புகள் என்ற தொடரின் கூடுதல் காண்க.
தீர்வு :
a = \(\frac{a-b}{a+b}\) என்க.
d = t₂ – t₁