Samacheer Kalvi 10th Maths Guide Chapter 1 உறவுகளும் சார்புகளும் Unit Exercise 1

Tamilnadu State Board New Syllabus Samacheer Kalvi 10th Maths Guide Pdf Chapter 1 உறவுகளும் சார்புகளும் Unit Exercise 1 Textbook Questions and Answers, Notes.

TN Board 10th Maths Solutions Chapter 1 உறவுகளும் சார்புகளும் Unit Exercise 1

கேள்வி 1.
(x² – 3x, y² + 4y) மற்றும் (-2, 5) ஆகிய வரிசைச் சோடிகள் சமம் எனில் , x மற்றும் y -ஐக் காண்க.
தீர்வு :

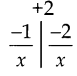
தரவு x² -3x = -2
x² -3x + 2 = 0
(x-1) (x – 2) = 0
x = 1 மற்றும் x = 2
தரவு y² + 4y = 5
y² + 4y -5 = 0
(y-1) (y+5) = 0
y-1 மற்றும் y =-5

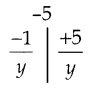
x ன் மதிப்பு 1 மற்றும் 2
yன் மதிப்பு 1 மற்றும் -5

கேள்வி 2.
A × A கார்டீசியன் பெருக்கல் பலனின், 9 உறுப்புகளில், உறுப்புகள் (-1, 0) மற்றும் (0, 1)-யும் இருக்கிறது எனில், A-யில் உள்ள உறுப்புகளைக் காண்க. மற்றும் A × A-ன் மீதமுள்ள உறுப்புகளைக் காண்க.
தீர்வு :
A = {-1, 0, 1}
A × A = {(-1, -1) (-1, 1) (0, -1) (0, 0) (1, -1) (1, 0) (1, 1)}

கேள்வி 3.
f(x) = \(\left\{\begin{array}{cc}
\sqrt{x-1} & x \geq 1 \\
4 & x<1
\end{array}\right.\) எனக் கொடுக்கப்பட்டால்,
i) f(0)
ii) f(3)
iii) f(a+1)
(a ≥ 0 எனக் கொடுக்கப்பட்டுள்ளது) ஆகியவற்றை காண்க.
தீர்வு :
f(x) = \(\left\{\begin{array}{ccc}
\sqrt{x-1} & \text { if } & x=\{1,2,3,4 \ldots \ldots \ldots\} \\
4 & \text { if } & x=\{0,-1,-2 \ldots \ldots \ldots\}
\end{array}\right.\)
i) f(0) = 4
ii) f(3) =\(\sqrt{x-1}=\sqrt{3-1}=\sqrt{2}\)
iii) f(a+1) = \(\sqrt{x-1}=\sqrt{a+1-1}=\sqrt{a}\)

கேள்வி 4.
A = {9, 10, 11, 12, 13, 14, 15, 16, 17} என்க. மற்றும் f : A →N ஆனது f(n) ∈ == n-ன் அதிகப்பட்சப் பகாகாரணி (n ∈ A) என வரையறுக்கப்பட்டால் f – ன் வரிசைச் சோடிகளின் கணத்தை எழுதுக மற்றும் f – ன் வீச்சகத்தைக் காண்க.
தீர்வு :
f(n) = அதிகபட்ச பகாக்காரணி
f(9) = 3 (காரணிகள் 1, 3, 9)
f(10) = 5 (காரணிகள் 1, 2, 5)
f(11) = 11 (காரணிகள் 1, 11)
f(12) = 3 (காரணிகள் 1, 2, 3, 4, 6, 12)
f(13) = 13 (காரணிகள் 1, 13)
f(14) = 7 (காரணிகள் 1, 2, 7, 14)
f(15) = 5 (காரணிகள் 1, 3, 5, 15)
f(16) = 2 (காரணிகள் 1, 2, 4, 8, 16)
f(17) = 17 (காரணிகள் 1, 17)
வரிசை ஜோடிகளின் கணம் {(9, 3) (10, 5) (11, 11) (12, 3) (13, 13) (14, 7) (15, 5) (16, 2) (17, 7)}
fன் வீச்சகம் = {(2, 3, 5, 11, 13, 17}

கேள்வி 5.
f(x) = \(\sqrt{1+\sqrt{1-\sqrt{1-x^{2}}}}\) என்ற சார்பின்
மதிப்பகத்தை காண்க:
தீர்வு :
f(x) = \(\sqrt{1+\sqrt{1-\sqrt{1-x^{2}}}}\)

இங்கு
\(\sqrt{1-x^{2}}=\sqrt{(1+x)(1-x)}\)
x = 1 (or) x = -1
= -1 ≤ x ≤ 1
∴ மதிப்ப கம் f(x) – {-1, 0, 1}

கேள்வி 6.
f(x) = x², g(x) = 3x மற்றும் h(x) = x-2 எனில், (fog)oh = fo(goh) என நிறுவுக.
தீர்வு :
fog(x) = f(g(x)) = f(3x)
= (3x)²
=9x²
(fog)oh(x) = fog(h(x)
= fog(x-2)
= 9 (x-2)²
= 9[x² – 4x + 4)
=9×2 – 36x + 36 …………… (1)
goh(x) = g(h(x) = g(x-2)
= 3(x-2)
= 3x -6

fo(goh) (x) = fo(3x – 6)
= (3x – 6)²
= 9x² – 36x + 36………………. (2)
(1) nd (2) லிருந்து
(fog)oh = fo(goh) என்பதை பெறாலாம்.

கேள்வி 7.
A = {1, 2} B = {1, 2, 3, 4} C = {5, 6} மற்றும் D = {5, 6, 7, 8} எனில் A × C ஆனது B × D உட்கணமா எனச் சரிபார்க்க.
தீர்வு :
A × C = {1, 2}x {5, 6}
= {(1, 5) (1,6) (2, 5) (2, 6)} —– (1)
B × D = {1, 2, 3, 4}x {5, 6, 7, 8}
= \(\left\{\begin{array}{l}
(1,5)(1,6)(1,7)(1,8)(2,5)(2,6) \\
(2,7)(2,8)(3,5)(3,6) \\
(3,7)(3,8)(4,5)(4,6)(4,7)(4,8)
\end{array}\right\}\) …………….. (2)
(1), (2) லிருந்து
A x C ⊂ B X D என்பதை அறியலாம்.

கேள்வி 8.
f(x) = –, x≠ -1 என்க. x ≠ 0 எனில்,
f(x))= \(\frac{-1}{x}\) எனக் காட்டுக.

தீர்வு :

கேள்வி 9.
சார்பு f மற்றும் 8 ஆகியவை f(x) = 6x + 8,
ste) = \(\frac{x-2}{3}\) எனில்,
i) gg ( \(\frac { 1 }{ 2 }\) ) (H) -யின் மதிப்பைக் காண்க.
ii) gf(x) – ஐ எளிய வடிவில் எழுதுக.
தீர்வு :
தரவு f(x) = 6x + 8

ii) g f(x) ஐ எளிய வடிவில் எழுதுக.
தரவு : f(x) = 6x + 8
g(x) = \(\frac{x-2}{3}\)
f(x) = g(6x + 8)

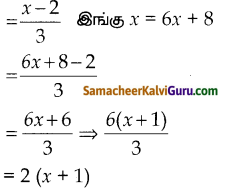
கேள்வி 10.
பின்வருவனவற்றின் மதிப்பகங்களை எழுதுக.
i) f(x) = \(\frac{2 x+1}{x-9}\)
ii) P(x) = \(\frac{-5}{4 x^{2}+1}\)
iii) g(x) = \(\sqrt{x-2}\)
iv) h(x) = x + 6
தீர்வு :
i) f(x) = \(\frac{2 x+1}{x-9}\)
மதிப்பகம் = R – {9}

குறிப்பு x = 9 எனில்
f (x) = \(\frac{2(9)+1}{0}\)
வரையறுக்கப்
– படவில்லை

ii) p(x) = \(\frac{-5}{4 x^{2}+1}\)
மதிப்பகம் = R

குறிப்பு
x = 0 மற்றும் x < 0
g(0) = \(\sqrt{0-2}=\sqrt{-2}\) ∉ R

iii) g(x) = \(\sqrt{x-2}\)
மதிப்பகம் = {2, 3, 4, 5………..)

iv) h(x) = x + 6
மதிப்பகம் = R