Tamilnadu State Board New Syllabus Samacheer Kalvi 10th Maths Guide Pdf Chapter 2 எண்களும் தொடர்வரிசைகளும் Ex 2.7 Textbook Questions and Answers, Notes.
TN Board 10th Maths Solutions Chapter 2 எண்களும் தொடர்வரிசைகளும் Ex 2.7
![]()
கேள்வி 1.
பின்வரும் தொடர்வரிசைகளில் எவை பெருக்குத் தொடர்வரிசையாகும்?
(i) 3,9,27,81,…..
(ii) 4,44,444,4444…………
(iii) 0.5,0.05,0.005,…
(iv) \(\frac{1}{3}, \frac{1}{6}, \frac{1}{12}, \ldots\)
(v) 1,-5,25,-125….
(vi) 120,60,30,18,….
(vii) 16
தீர்வு :
i) 3, 9, 27, 81,…
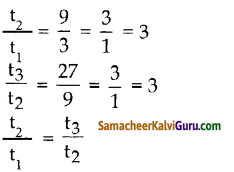
எனவே இது ஒரு பெருக்குத் தொடர்வரிசை
ii) 4, 44, 444, 4444, .

எனவே இது பெருக்குத்தொடர் வரிசை அல்ல
iii) 0.5, 0.05, 0.005,…
தீர்வு:
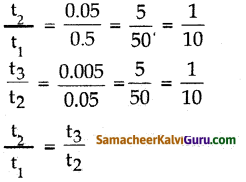
எனவே இது பெருக்குத்தொடர் வரிசை ஆகும்.

எனவே இது ஒரு பெருக்குத்தொடர் வரிசை ஆகும்.
v) 1, -5, 25, -125….
தீர்வு :
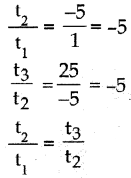
எனவே இது ஒரு பெருக்குத்தொடர் வரிசை ஆகும்.
![]()
vi) 120, 60, 30, 18…
தீர்வு :

எனவே இது ஒரு பெருக்குத்தொடர் வரிசை
கேள்வி 2.
கீழே கொடுக்கப்பட்டுள்ள முதல் உறுப்பு மற்றும் பொதுவிகிதம் உடைய பெருக்குத் தொடர்வரிசையின் முதல் மூன்று உறுப்புகளை எழுதுக.
(i) a = 6, r = 3
(ii) a = √2, r = √2
(iii) a = 1000, r = \(\frac{2}{5}\)
தீர்வு :
i) a = 6, r = 3
பெருக்குத் தொடர் வரிசையில் முதல் மூன்று உறுப்புகள் a, ar, ar2 = 6, 6 x 3, 6 x (3)2
= 6, 18, 54
ii) a = √2, r = √2
தீர்வு :
பெருக்குத் தொடர் வரிசையில் முதல் மூன்று உறுப்புகள்
a, ar, ar2 = √2, √2 x √2, √2 x (√2)2
= √2, 2, 2√2
iii) a = 1000, r = 2/5
தீர்வு :
பெருக்குத் தொடர் வரிசையில் முதல் மூன்று உறுப்புகள் = a, ar, ar2 = 1000, 1000 x \(\frac{2}{5}\) 1000 x \(\left(\frac{2}{5}\right)^{2}\)
= 1000, 400, 160
![]()
கேள்வி 3.
729, 243, 81,….. என்ற பெருக்குத் தொடர்வரிசையின் 7-வது உறுப்பைக் காண்க.
தீர்வு :

கேள்வி 4.
x + 6, x + 12 மற்றும் x+15 என்பன ஒரு பெருக்குத் தொடர்வரிசையின் தொடர்ச்சியான மூன்று உறுப்புகள் எனில் , x-யின் மதிப்பைக் காண்க. தீர்வு :
x + 6, x + 12, x + 15 என்பது ஒரு பெருக்குத்தொடர்வரிசையில் அமையும் எனில்
\(\frac{t_{2}}{t_{1}}=\frac{t_{3}}{t_{2}}\)
\(\frac{x+12}{x+6}=\frac{x+15}{x+12}\)
1 = 3
(x+12)(x+12) = (x+6)(x+15)
x2 + 24x + 144 = x + 21x + 90
24x + 21x = 90 – 144
3x = -54
x = -18
கேள்வி 5.
பின்வரும் பெருக்குத் தொடர்வரிசையில் உள்ள உறுப்புகளின் எண்ணிக்கையைக் காண்க.
(i) 4, 8, 16,….., 8192
(ii) \(\frac{1}{3}, \frac{1}{9}, \frac{1}{27}, \ldots, \frac{1}{2187}\)
தீர்வு
தரவு : a = 4, r = \(\frac{t_{2}}{t_{1}}=\frac{8}{4}\) = 2
tn = arn-1
4 x (2)n-1 = 8192
(2)n-1 = 8192/4
(2)n-1 = 2048
(2)n-1 = 211
n – 1 = 11
n = 11+1
n = 12
(ii) \(\frac{1}{3}, \frac{1}{9}, \frac{1}{27}, \ldots, \frac{1}{2187}\)
தீர்வு :
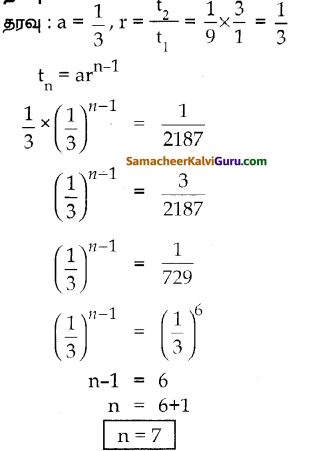
![]()
கேள்வி 6.
ஒரு பெருக்குத் தொடர் வரிசையின் 9-வது உறுப்பு 32805 மற்றும் 6-வது உறுப்பு 1215 எனில், 12-வது உறுப்பைக் காண்க.
தீர்வு :
தரவு : t9 = 32805
t6 = 1215
எனில் t12 = ?
ar8 = 32805 ——(1)
ar5 = 1215 ——-(2)
(1) ÷ (2)
\(\frac{\operatorname{ar}^{8}}{\mathrm{ar}^{5}}=\frac{32805}{1215}\)
32805 ar5 1215
r3 = 27
r = 3
r = 3ஜ (2)ல் பிரதியிட
ar5 = 1215
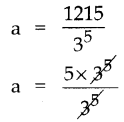
tn = arn-1
t12 = ar12 – 1
t12 = 5(3)11
கேள்வி 7.
ஒரு பெருக்கத்தொடர் வரிசையின் 8-வது உறுப்பு 768 மற்றும் பொது விகிதம் 2 எனில், அதன் 10-வது உறுப்பைக் காண்க.
தீர்வு :
தரவு : t8 = 768
r = 2
t10 = ?
ar7 = 768
a(2)7 = 768
a = \(\frac{768}{2^{7}}=\frac{2^{8} \times 3}{2^{7}}\)
a = 6
tn = arn-1
t10 = 6(2)10-1
= 6 x (2)9
= 6 x 512
t10 = 3072
![]()
கேள்வி 8.
a,b,c என்பன ஒரு கூட்டுத் தொடர்வரிசையில் அமையும் எனில் 3a, 3b 3c ஒரு பெருக்குத் தொடர்வரிசையில் அமையும் எனக் காட்டுக.
தீர்வு :
தரவு : a, b, c என்பது ஒரு கூட்டுத்தொடர் வரிசை எனவே b – a = c – b [∵ t2 – t1 = t3 – t2]
2b = a + c
நீருபி 3a ,3b, 3c ஒரு பெருக்குத்தொடர் வரிசை
நீருபி \(\frac{t_{2}}{t_{1}}=\frac{t_{3}}{t_{2}}\)
\(\frac{3^{b}}{3^{a}}=\frac{3^{c}}{3^{b}}\)
3b-a = 3c-b
3b-a = 3b-a [∵ c – b = b – a]
எனவே 3a ,3b, 3c என்பது ஒரு பெருக்குத்தொடர் வரிசை
கேள்வி 9.
ஒரு பெருக்குத்தொடர்வரிசையில் அடுத்தடுத்த மூன்று உறுப்புகளின் பெருக்கற்பலன் 27 மற்றும் அவைகளில் இரண்டிரண்டு உறுப்புகளின் பெருக்கற் பலனின் கூடுதல் \(\frac { 57 }{ 2 }\) எனில், அந்த மூன்று உறுப்புகளைக் காண்க.
தீர்வு :
பெருக்குத்தொடர் வரிசையில் அடுத்தடுத்த மூன்று உறுப்புகள் = a/r, a, ar
அவற்றின் பெருக்கற்பலன் = 27
a/r x a x ar = 27
a3 = 27
a = 3
அவற்றின் இரண்டிரண்டு உறுப்புகளன் பெருக்கற்பலன்களின் கூடுதல் = \(\frac { 57 }{ 2 }\)
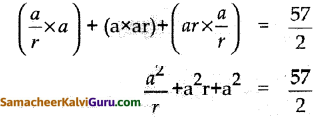

6 + 6r2 + 6r = 19r
6r2 – 13r + 6 = 0
(6r – 9) (6r – 4) = 0
r = \(\frac { 3 }{ 2 }\) (அல்லது) \(\frac { 2 }{ 3 }\),
a = 3 மற்றும் r = \(\frac { 3 }{ 2 }\) எனில்
மூன்று உறுப்புகள் = 2, 3,9/2
a = 3 மற்றும் r = \(\frac { 2 }{ 3 }\), எனில்
மூன்று உறுப்புகள் = 9/2, 3, 2
கேள்வி 10.
ஒரு நபர் ஒரு நிறுவனத்தில் துணை மேலாளராகப் பணியில் சேர்கிறார். அவருக்கு அந்நிறுவனம் முதல் மாத ஊதியமாக 160,000 வழங்குகிறது மற்றும் ஆண்டு ஊதிய உயர்வு 5% வழங்குவதாக ஒப்புக்கொள்கிறது. 5 வருட முடிவில் அவருடைய மாத ஊதியம் எவ்வளவு?
தீர்வு :
a = 60000
r = \(\frac { 105 }{ 100 }\) [5% உயர்வு)
n = 6 வருடங்கள் (5 வருடங்களுக்கு பிறகு)
t6 = arn-1
= 60000\(\left(\frac{105}{100}\right)^{6-1}\)
= 60000\(\left(\frac{105}{100}\right)^{5}\)
= 60000 x 1.27628
= 76576.6
t6 = 76577
கேள்வி 11.
சிவமணி ஒரு பணிக்கான நேர்காணலில் பங்கேற்கிறார். அந்நிறுவனம் அவருக்கு இரண்டு விதமான வாய்ப்புகளை வழங்குகிறது.
வாய்ப்பு A : முதல் மாத ஊதியம் ₹20.000 மற்றும் நிச்சயமான 6% ஆண்டு ஊதிய உயர்வு 5 ஆண்டுகளுக்கு . வாய்ப்பு B : முதல் மாத ஊதியம் ₹22.000 மற்றும் நிச்சயமான 3% ஆண்டு ஊதிய உயர்வு 5 ஆண்டுகளுக்கு.
A மற்றும் B ஆகிய இரு வாய்ப்புகளிலும் அவருடைய 4-வது வருட ஊதியம் எவ்வளவு?
தீர்வு :
வாய்ப்பு A:
106) வாய்ப்பு :a= 20000,r = \(\frac { 106 }{ 100 }\), n = 4 ஆண்டுகள்.
t4 = arn-1
= 20000 \(\left(\frac{106}{100}\right)^{4-1}\)
= 20000 \(\left(\frac{106}{100}\right)^{3}\)
= 20000 x 1.191016
t4 = 23820
வாய்ப்பு B:
தரவு: a = 22000, r = \(\frac{103}{100}\), n = 4 ஆண்டுகள்.
t4 = arn-1
= 22000 \(\left(\frac{103}{100}\right)^{4-1}\)
= 22000 \(\left(\frac{103}{100}\right)^{3}\)
= 22000 x 1.092727
= 24039.9
t4 = 24040
![]()
கேள்வி 12.
a, b, c என்பன ஒரு கூட்டுத் தொடர்வரிசையில் உள்ள மூன்று அடுத்தடுத்த உறுப்புகள் மற்றும் x, y, z என்பன ஒரு பெருக்கு தொடர்வரிசையின் மூன்று அடுத்தடுத்த உறுப்புகள் எனில் xb-c xc-a x za – b = 1 என நிறுவுக.
தீர்வு :
a, b, c என்பன கூட்டுத் தொடர் வரிசையில் உள்ள மூன்று அடுத்தடுத்த உறுப்புகள்.
a = a ———— (1)
b = a + d ——— (2)
c = a + 2d ——— (3)
xb-c xc-a x za – b
= xa+d-a-2dya+2d-a. za-a-d
(x)-d. y2d. z-d
\(\frac{y^{2 d}}{x^{d} \cdot z^{d}}\) [∴ x,y,z என்ப ன G.P]
x = x, y = xr, z = xr2
\(\frac{(x r)^{2 d}}{x^{d},\left(x r^{2}\right)^{d}}=\frac{x^{2 d} \cdot r^{2 d}}{x^{d} \cdot x^{d} \cdot x^{2 d}}\)