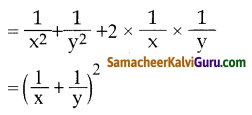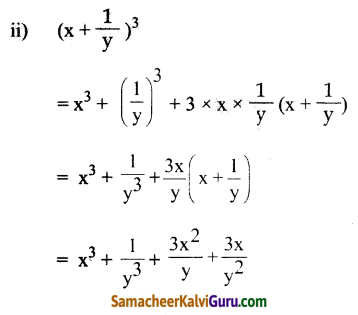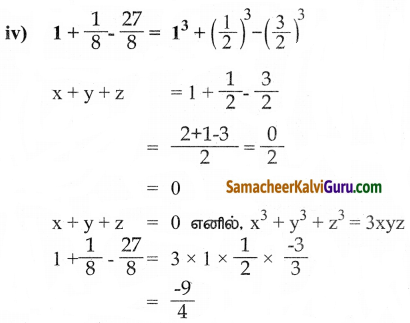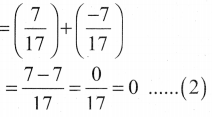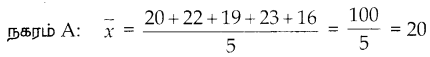Laxmi

Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 1 எண்கள் Ex 1.7 Textbook Questions and Answers, Notes.

TN Board 8th Maths Solutions Chapter 1 எண்கள் Ex 1.7

கேள்வி 1.
ஒரு பெட்டியிலுள்ள \(\frac { 3 }{ 4 }\) பங்கு ஆப்பிள்களின் எடையானது 3கிகி 225 கிராம் எனில், முழு பெட்டி ஆப்பிள்களின் எடை என்னவாக இருக்கும்?
தீர்வு :
\(\frac { 3 }{ 4 }\) பங்கு ஆப்பிள்
= 3கிகி 225 கிராம்
\(\frac { 1 }{ 4 }\) பங்கு ஆப்பிள் = கிகி 225 கிராம்/3
= 1கிகி 75 கிராம்.
ஃ முழு பெட்டியின் எடை = \(\frac { 3 }{ 4 }\) பங்கு ஆப்பிள் + \(\frac { 1 }{ 4 }\) பங்கு
ஆப்பிள் = 3 கிகி 225 கிராம்+1 கிகி 75 கி = 4கிகி 300 கிராம்

கேள்வி 2.
மங்களம் 3\(\frac { 4 }{ 5 }\) லிட்டர் கொள்ளளவு கொண்ட ஒரு தண்ணீர்க் குடுவையையும், அதைப் போன்று 2\(\frac { 2 }{ 3 }\) மடங்கு அதிகக் கொள்ளளவு கொண்ட மற்றொரு குடுவையும் வாங்குகிறாள் எனில், பெரிய குடுவை எவ்வளவு லிட்டர் தண்ணீ ரைக் கொள்ளும்?
தீர்வு :
மங்களம் வாங்கிய குடுவையின் கொள்ளளவு = 3\(\frac { 4 }{ 5 }\) லிட்டர்.
மற்றொரு பெரிய குடுவை = \(2 \frac{2}{3} \times 3 \frac{4}{5}\)
= \(\frac{8}{9} \times \frac{19}{5}\)
= \(\frac{152}{15}=10 \frac{2}{15}\) லிட்டர்.

கேள்வி 3.
இரவி \(\frac { 25 }{ 8 }\) மற்றும் \(\frac { 16 }{ 5 }\) ஆகிய எண்களைப் பெருக்கி, இந்த பெருக்கலின் வடிவமானது, \(\frac { 10 }{ 3 }\) என கூறினான். சந்துரு , எளிய வடிவில் விடையானது 3\(\frac { 1 }{ 3 }\) என கூறுகிறான். யார் கூறுவது சரி? அல்லது இருவரும் கூறுவது சரியா? விளக்குக.
தீர்வு :

இருவரும் சரியாக கூறுகிறார்கள்.

கேள்வி 4.
ஒரு அறையின் பரப்பு \(\frac { 153 }{ 10 }\) ச.மீ மற்றும் அதன் அகலம் 2\(\frac { 11 }{ 20 }\)எனில், அதன் நீளம் என்ன?
தீர்வு :
பரப்பு \(\frac { 153 }{ 10 }\)
அகலம் = 2\(\frac { 11 }{ 20 }\)மீ.
நீளம் x அகலம் = பரப்பு
நீளம் x \(\frac{51}{20}=\frac{153}{10}\)
நீளம் = \(\frac{153}{101} \times \frac{20}{1}\)
= 6மீ.

கேள்வி 5.
4489 செ.மீ 2 பரப்பளவு கொண்ட ஒரு தலைவரின் உருவப்படமானது சதுர வடிவில் உள்ளது. மேலும் படத்தைச் சுற்றிலும் 2 செ.மீ அளவு கொண்ட மரச்சட்டம் உள்ளது எனில் மரச்சட்டத்தின் பரப்பளவு என்ன?
தீர்வு :

சதுரத்தின் பரப்பு = 4489 ச.அ
பக்கம் = 67²
= 67 செ.மீ
புதிய சதுரத்தின் பக்கம் = 67 + 4
=71 செ.மீ) புதிய சதுர வடிவ படத்தின் பரப்பு = 71 x 71
= 5041 செ.மீ ²
மரச்சட்டத்தின் பரப்பு = 5041 – 4889
= 552 ச செ.மீ

கேள்வி 6.
ஒரு வாழ்த்து அட்டையின் பரப்பளவு 90 செ.மீ ‘ எந்த இரு முழு எண்களுக்கிடையே அதன் பக்க அளவின் நீளம் இருக்கும்?
தீர்வு :
அட்டையின் பரப்பளவு = 90செமீ²
= 2 x 3 x 3 x 5
= 3 x 3 x 2 x 5
= 9 x 10


அதன் பக்க அளவின் நீளங்கள் 9 செமீ மற்றும் 10 செ.மீ

கேள்வி 7.
ஒரு சதுர டெசி மீட்டர் பரப்பு கொண்ட 225 சதுர வடிவிலான நிறத்திட்டு ஓடுகள் முறையே ஒரு சதுர வடிவிலான தாழ்வாரத்தை முழுவதுமாக நிரப்புகின்றன எனில், சதுர வடிவிலான தாழ்வாரத்தின் பக்கம் ஒவ்வொன்றின் நீளமும் என்னவாக இருக்கும்?
தீர்வு :
சதுர வடிவ தாழ்வாரத்தின் பரப்பு = 225 க.டெசி மீ
a² = 225

a² = 15²
a = 15 டெசி மீட்டர்
பக்கத்தின் நீளம் 15 டெசி மீட்டர் ஆகும்.

கேள்வி 8.
\(\sqrt[3]{1906624} \times \sqrt{x}\) = 3100 எனில் x ஐக் காண்க.
தீர்வு :

இருபுறமும் வர்க்க ப்படுத்த \(\left(x^{\frac{1}{2}}\right)^{2}\) = 25²
x = 625

கேள்வி 9.
2^m-1 + 2^m+1 = 640 எனில், m ஐக் காண்க.
தீர்வு :
im 7
2^m-1 + 2^m+1 = 640
2^m x 2^-1 + 2^m x 2¹ = 640
2^m (2^-1 + 2¹) = 640
\(2^{m}\left(\frac{1}{2}+2\right)\) = 640
\(2^{m}\left(\frac{1+4}{2}\right)\)= 640
2^m \(\frac{5}{2}\) = 640
2^m = \(\frac{640 \times 2}{5}\)
2^m = 128 x 2
2^m = 27 x 21
m = 28

கேள்வி 10.
அறிவியல் குறியீட்டில் விடையை எழுதவும். ஒரு மனித இதயமானது சராசரியாக வினாடிக்கு 80 முறைத் துடிக்கிறது எனில், அது
(i) ஒரு மணி நேரத்தில்
(ii) ஒரு நாளில்
(iii) ஓர் ஆண்டில்
(iv) 100 ஆண்டுகளில் எத்தனை முறைத் துடிக்கும்?
தீர்வு :
நிமிடத்திற்கு 80 முறை துடிக்கிறது.
i) ஒரு மணி நேரத்தில் = 60 நிமிடங்கள்
= 60 x 80 முறை = 4800
= 4.8 x 10³ முறை துடிக்கிறது.

ii) ஒரு நாளில் = 24 மணி
= 24 X 60 நிமிடம்
= 24 x 60 x 80 முறை
= 115200
= 1.152 x 10⁵ முறை துடிக்கிறது.

iii) ஒரு ஆண்டில் = 365 நாட்கள்
= 365 x 115200
= 42048000 = 4.2048 x 10⁷
முறை துடிக்கிறது

iv) 100 ஆண்டுகள் = 100 x 42048000
= 4204800000
= 4.2048 x 10⁹
முறை துடிக்கிறது.

மேற்சிந்தனைக் கணக்குகள்

கேள்வி 11.
ஒரு வரைபடத்தில், ஒரு அங்குலமானது 120 கி.மீ ஐக் குறிக்கும், நகரம் A ஆனது B மற்றும் C ஆகிய நகரங்களுக்கு இடையே அமைந்துள்ளது. மேலும் நகரம் A இலிருந்து B மற்றும் C ஆகிய இரு நகரங்கள் முறையே, 4\(\frac { 1 }{ 6 }\) அங்குலம் மற்றும் 3\(\frac { 1 }{ 3 }\) அங்குலம் தொலைவுகளில் உள்ளன எனில், அவற்றுக்கிடையே உள்ள உண்மையான தொலைவினைக் காண்க.
தீர்வு :
நகரம் B = 4\(\frac { 1 }{ 6 }\) அங்குலம்
\(\frac { 25 }{ 6 }\) x 120 கி.மீ = 500 கி.மீ.
நகரம் C = 3\(\frac { 1 }{ 3 }\) அங்குலம்
= \(\frac { 10 }{ 3 }\) x 120கி.மீ = 400 கி.மீ.
தூரம் = நகரம் B +நகரம் C
= 500+ 400 =900 கி.மீ.

கேள்வி 12.
பின்வரும் கூற்றுகள் ஒவ்வொன்றையும் ஒர் எடுத்துக்காட்டுடன் சரிபார்.
(i) பூச்சியமற்ற விகிதமுறு எண்களின் தொகுப்பிற்கு, வகுத்தலானது அடைவுப் பண்பை நிறைவு செய்யும். (ii)விகிதமுறு எண்களுக்கு, கழித்த லானது பரிமாற்றுப் பண்பினை நிறைவு செய்யாது.
(iii) விகிதமுறு எண்க ளுக்கு, வகுத்த லானது சேர்ப்புப் பண்பினை நிறைவு செய்யாது
(iv) விகிதமுறு எண்க ளுக்கு, கழித் தலின் மீதான பெருக்கலின் பங்கீட்டு விதி உண்மையாகும். அதாவது
a(b – c) = ab – ac.
(v) இரு விகிதமுறு எண்களின் சராசரியானது அவற்றிற்கிடையில் அமையும் ஒரு விகிதமுறு எண்ணாகும்.
தீர்வு :

இடப்பக்கம் = வலப்பக்கம்
(iv) a = \(\frac{1}{2}\)
b = \(\frac{2}{3}\)
c = \(\frac{1}{3}\)
a (b-c) = ab- ac
இடப்பக்கம் = a(b – c)=

வலப்பக்கம் = ab – ac

இடப்பக்கம் = வலப்பக்கம் (v) \(\frac{1}{2}\) மற்றும் \(\frac{2}{3}\)

கேள்வி 13.
\(\frac { 1 }{ 4 }\) பங்கு கேழ்வரகு அடையின் எடை 120 கிராம் எனில், அதே கேழ்வரகு அடையின் \(\frac { 2 }{ 3 }\) பங்கின் எடை என்ன?
தீர்வு :
\(\frac { 1 }{ 4 }\) பங்கு கேழ்வரகு அடை = 120 கிராம்.
ஒரு பங்கு கேழ்வரகு அடை = 120 x 4 = 480 கிராம்.
\(\frac { 2 }{ 3 }\) பங்கு கேழ்வரகு அடை \(\frac { 2 }{ 3 }\) x 480
கிராம். = 320 கிராம்.

கேள்வி 14.
p + 2q =18 மற்றும் pq = 40, எனில் \(\frac{2}{p}+\frac{1}{q}\) மதிப்பைக் காண்க.
தீர்வு :

கேள்வி 15.
\(5 \frac{x}{5} \times 3 \frac{3}{4}\) = 21 எனில் x ஐக் காண்க
தீர்வு :

25 + x = 28
x = 28 – 25
x = 3

கேள்வி 16.
\(\frac{1}{(10 / 11)}\) ஆனது \(\frac{(1 / 10)}{11}\) ஐக் காட்டிலும் எவ்வளவு அதிகம்?
தீர்வு :

கேள்வி 17.
1536 படைப் பயிற்சி மாணவர்கள் சதுர வடிவில் அணிவகுப்பு செய்ய விரும்பினர். இது சாத்தியமாகுமா? சாத்தியமில்லை எனில், மேலும் எத்தனை படைப்பயிற்சி மாணவர்கள் கூடுதலாகத் தேவை?
தீர்வு :
1600 – 1536 = 64 ஃ 1600 ஒரு முழு 69 635 வர்க்கமாகும்
78 2500 64 பயிற்சி மாணவர்கள் கூடுதலாக தேவை

கேள்வி 18.
\(\sqrt{286225}\) இன் மதிப்பு காண்க அதனைப் பயன்படுத்தி \(\sqrt{2862.25}+\sqrt{28.6225}\) ஐ கணக்கிடுக.
தீர்வு :

கேள்வி 19.
சுருக்குக :  (3.769 × 10⁵) + (4.21 × 10⁵)
தீர்வு :
(3.769 × 10⁵) + (4.21 × 10⁵) = 3,76,900 + 4,21,000
= 7,97,000
= 7.979 × 10⁵

கேள்வி 20.
சிறியதிலிருந்து பெரியது என வரிசைப்படுத்துக :16²⁵, 8¹⁰⁰, 3⁵⁰⁰, 4⁴⁰⁰, 2⁶⁰⁰
தீர்வு :
16²⁵ = (2⁴)²⁵ = 2¹⁰⁰
8¹⁰⁰ = (2³)¹⁰⁰ = 2³⁰⁰
4⁴⁰⁰ = (2²)⁴⁰⁰ = 2⁸⁰⁰
2⁶⁰⁰ = 2⁶⁰⁰
2¹⁰⁰, 2³⁰⁰,2⁶⁰⁰, 2⁸⁰⁰
16²⁵, 8¹⁰⁰, 3⁵⁰⁰, 4⁴⁰⁰, 2⁶⁰⁰

Tamilnadu State Board New Syllabus Samacheer Kalvi 9th Maths Guide Pdf Chapter 3 இயற்கணிதம் Ex 3.9 Textbook Questions and Answers, Notes.

TN Board 9th Maths Solutions Chapter 3 இயற்கணிதம் Ex 3.9

கேள்வி 1.
கீழ்க்காண்பனவற்றிற்கு மீ.பொ.வ. காண்க.
(i) p⁵,p¹¹,p⁹
ii) 4x³,y³, z³
(iii) 9a²b²c³ , 15a³b²c⁴
(iv) 64x⁸, 240x⁶
(v) ab²c³, a²b³c, a³bc²
(vi) 35x⁵y³ z⁴, 49x²yz³, 14xy²z²
(vii) 25ab³c, 100a²bc, 125ab
(viii) 3abc, 5xyz, 7pqr
விடை:
i) மீ.பொ.வ. = p⁵

ii) மீ.பொ.வ. = 1

(iii) 9a²b²c³, 15a³b²c⁴
9a²b²c³ = 3 × 3 × a² × b² × c³
15a³b²c⁴ = 3 × 5 × a³ × b² × c⁴
மீ.பொ.வ. = 3a²b²c³

iv) 64x⁸, 240x⁶
64x⁸ = 2 × 2 × 2 × 2 × 2 × 2 × x⁸
240x⁶ = 2 × 2 × 2 × 2 × 3 × 5 × x⁶
மீ.பொ.வ.= 16x⁶

(v) மீ.பொ.வ.= abc

(vi) 35x⁵y³z⁴, 49x²yz³, 14xy²z²
35x⁵y³z⁴ = 5 × 7x⁵y³z⁴
49x²yz³ = 7 × 7x²yz³
14xy²z² = 7 × 2xy²z²
மீ.பொ.வ. = 7xyz²

(vii) 25ab³c, 100a²bc, 125ab
25ab³c = 5 × 5 ab³c
100a²bc = 2 × 2 × 5 × 5a²bc
125ab = 5 × 5 × 5ab
மீ.பொ .வ. = 25ab

(viii) மீ.பொ .வ. = 1

கேள்வி 2.
கீழ்க்காண்பனவற்றிற்கு மீ.பொ.வ. காண்க.
(i) (2x + 5), (5x +2)
(ii) a^m+1, a^m+2, a^m+3
(iii) 2a² + a, 4a² – 1
(iv) 3a², 5b³, 7c⁴
(v) x⁴ – 1, x² – 1
(vi) a³ – 9ax², (a – 3x)²
விடை:
(i) (2x + 5), (5x +2)
மீ.பொ.வ. = 1

(ii) a^m+1, a^m+2, a^m+3
மீ.பொ.வ. = a^m+1

(iii) 2a² + a, 4a² – 1
2a² + a = a(2a + 1)
4a² – 1 = (2a)² -1
= (2a + 1) (2a – 1)
மீ.பொ.வ. = 2a + 1

(iv) 3a², 5b³, 7c⁴
மீ.பொ.வ. =1

(v) x⁴ – 1, x² – 1
x⁴ -1 = (x²)² – 1
= (x² – 1) (x² + 1)
x⁴ – 1 = (x – 1) (x + 1) (x² + 1)
x² – 1 = (x – 1) (x + 1)
மீ.பொ.வ. = (x – 1) (x + 1)

(vi) a³ – 9ax², (a – 3x)²
a³ – 9ax² =a(a² – 9x²)
= a((a)² – (3x)²
=a(a – 3x) (a + 3x)
(a – 3x)² = (a – 3x) (a – 3x)
மீ.பொ.வ. = a – 3x

Tamilnadu State Board New Syllabus Samacheer Kalvi 9th Maths Guide Pdf Chapter 3 இயற்கணிதம் Ex 3.8 Textbook Questions and Answers, Notes.

TN Board 9th Maths Solutions Chapter 3 இயற்கணிதம் Ex 3.8

கேள்வி 1.
தொகுமுறை வகுத்தலைப் பயன்படுத்திக்காரணிப்படுத்துக.
(i) x³ – 3x² – 10x + 24
விடை :
p (x) = x³ – 3x² – 10x + 24
அனைத்து உறுப்புகளின் கெழுக்களின் கூடுதல்
= 1 – 3 – 10 + 24
= -13 + 25
= 12 ≠ 0
(x – 1) என்பது ஒரு காரணியல்ல. இரட்டைப்படை அடுக்குகள் கொண்ட உறுப்புகளின் கெழுக்கள் மற்றும் மாறிலியின் கூடுதல் = -3 + 24 = 21 இரட்டைப்படை அடுக்குகள் கொண்ட உறுப்புகளின் கெழுக்களின் கூடுதல்
= 1 – 10 = -9
(x + 1) என்பது ஒரு காரணியல்ல.
x = 2 எனில்,
P(2) = 2 – 3 x (2) – 10 x 2 + 24
= 8 – 3 x 4 – 20 + 24
= 8 – 12 – 20 + 24
= 32 – 32
= 0
(x – 2) என்பது ஒரு காரணியாகும்.

p(x) = (x – 2) (x² – x – 12)
= (x – 2) (x² – 4x + 3x – 12)
= (x – 2) (x(x – 4) + 3 (x – 4))
= (x – 2) (x + 3) (x – 4)

(ii) 2x³ – 3x³ – 3x + 2
விடை:
p(x) = 2x³ – 3x² – 3x + 2
அனைத்து உறுப்புகளின் கெழுக்களின் கூடுதல்
= 2 – 3 – 3 + 2
= 4 – 6
= -2 ≠ 0
(x – 1) என்பது காரணியல்ல.
இரட்டைப் படை அடுக்குகள் கொண்ட உறுப்புகளின் கெழுக்கள் மற்றும் மாறிலியின் கூடுதல்
= -3 + 2
= -1 ≠ 0
x = -1 எனில்
p(-1) = 2 × (-1)³ – 3(-1)² – (3) (-1) + 2
= -2 -3 + 3 + 2
= 0
(x +1) என்பது ஒரு காரணியாகும்.

p(x) = (x + 1) (2x² – 5x + 2)
= (x + 1) (2x² – 4x – x + 2)
= (x + 1) (2x(x – 2) -1(x – 2)
= (x + 1) (2x – 1) (x – 2)

(iii) -7x + 3 + 4x³
விடை:
p(x) = 4x³ – 7x + 3
x = 1 எனில், p(1) = 4 – 7 + 3 = 0
(x – 1) என்பது ஒரு காரணியாகும்.

p(x) = (x – 1) (4x² + 4x – 3)
= (x – 1) (4x² + 6x – 2x – 3)
= (x – 1) 2x(2x + 3) – 1(2x + 3)
= (x – 1) (2x – 1) (2x + 3)

(iv) x³ + x² – 14x – 24
விடை:
p(x) = x³ + x² – 14x – 24
x = 1 எனில்,
p(1) = 1 + 1 – 14 – 24
= 2 – 36
= -34 ≠ 0
(x – 1) என்பது ஒரு காரணியல்ல.
x = 4 எனில்,
p(4) = (4)³ + (4)² – 14 × 4 – 24
= 64 + 16 – 56 – 24
= 80 – 80
= 0
(x – 4) என்பது ஒரு காரணியாகும்.

p(x) = (x – 4) (x² + 5x + 6)
= (x – 4) (x² + 2x + 3x + 6)
= (x – 4) (x(x +2) + 3(x + 2)
= (x – 4) (x + 3) (x + 2)

(v) x³ – 7x + 6
விடை : p(x) = x3 – 7x + 6
x = 1 எனில், p(1) = 1 – 7 + 6 = 0
(x – 1) என்பது ஒரு காரணியாகும்.

p(x) = (x – 1) (x² + x – 6)
= (x – 1) (x² + 3x – 2x – 6)
= (x – 1) (x(x + 3) – 2(x + 3)
= (x – 1) (x – 2) (x + 3)

(vi) x³ – 10x² – x + 10)
விடை:
p(x) = x³ – 10x² – x + 10

x = 1 எனில், p(1)= 1 – 10 – 1 + 10 = 0
(x -1) என்பது ஒரு காரணியாகும்.

p(x) = (x – 1) (x² – 9x – 10)
= (x – 1) (x² – 10x + x – 10)
= (x – 1) (x(x – 10) + 1 (x – 10) = (x – 1) (x + 1) (x – 10)

Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 1 எண்கள் Ex 1.5 Textbook Questions and Answers, Notes.

TN Board 8th Maths Solutions Chapter 1 எண்கள் Ex 1.5

கேள்வி 1.
கோடிட்ட இடங்களை நிரப்புக.

i) 73 இன் கனத்திலுள்ள ஒன்றுகளின் இலக்கம் ………………….. ஆகும்.
விடை:
7

ii) ஓர் ஈரிலக்க எண்ணின் கனத்தில் அதிகபட்சமாக ………………….. இலக்கங்கள் இருக்கும்
விடை :
6

iii) 3333 உடன் மிகச்சிறிய எண்ணான ………………….. ஐ கூட்டினால், அது ஒரு முழு கன எண்ணாகும்.
விடை:
42

iv) 540 × 50 இன் கன மூலம் ………………….. ஆகும்.
விடை :
90

v) 0.000004913 இன் கனமூலம் ………………….. ஆகும்.
விடை :
0.017

கேள்வி 2.
சரியா? தவறா? எனக் கூறுக:

i) 24 இன் கனமானது 4 என்ற இலக்கத்தில் முடியும்
விடை:
சரி

ii) 1729 இலிருந்து 103 ஐ கழித்தால் 93 கிடைக்கும்
விடை :
சரி

iii) 0.0012 இன் கனமானது 0.000001728 ஆகும்.
விடை :
தவறு

iv) 79570 என்ற எண்ணானது ஒரு முழு கன எண்ணல்ல
விடை :
சரி

v) 250047 இன் கன மூலமானது 63 ஆகும்.
விடை :
சரி

கேள்வி 3.
1944 ஒரு முழு கன எண்ண ல்ல என நிருபிக்க
தீர்வு :

1944 = 2 × 2 × 2 × 3 × 3 × 3 × 3 × 3
1944 ஐ பகா காரணிகளை
மூன்றின் தொதிகளாக பிரித்தால்
3 x 3 மட்டும் மீதமாக இருக்கும்
ஆகவே அதை முழு கன எண்ணாக
ஆக்க நமக்கு மேலும் ஒரு 3 தேவை
எனவே 1944 ஆனது முழு கன
எண்ணல்ல

கேள்வி 4.
10985 ஐ எந்த மிகச் சிறிய எண்ணால் வகுக்க, ஈவு ஆனது ஒரு முழு கன எண்ணாகும் எனக் காண்க.
தீர்வு :

10985 = 13 × 13 × 13 × 5
10985 ஐ 5 ஆல் வகுத்தால் முழு கன எண் கிடைக்கும்.

கேள்வி 5.
200 உடன் எந்த மிகச் சிறிய எண்ணைப் பெருக்க, ஒரு முழு கன எண் கிடைக்கும் எனக் காண்க.
தீர்வு :

200 = 2 × 2 × 2 × 5 × 5
200 ஐ முழு கன எண்ணாக்க ஒரு 5 தேவை.
மிகச்சிறிய எண் 5 ஆகும்.

கேள்வி 6.
24 × 36 × 80 × 25 இன் கனமூலம் காண்க.
தீர்வு :

= \(\sqrt[3]{24 \times 36 \times 80 \times 25}\)
= \(\sqrt[3]{2 \times 2 \times 2 \times 3 \times 3 \times 3 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 5 \times 5 \times 5}\)
= 2 × 3 × 2 × 2 × 5
= 12 × 10
= 120

கேள்வி 7.
பகாக் காரணிப்படுத்தல் மூலம் 729 மற்றும் 6859 ஆகியவற்றின். கன மூலத்தைக் காண்க.
தீர்வு :

கேள்வி 8.
46656 இன் கனமூலத்தின் வர்க்க மூலம் என்ன ?
தீர்வு :

கேள்வி 9.
ஓர் வர்க்க எண்ணின் கனமானது 729 எனில், அந்த எண்ணின் வர்க்க மூலத்தைக் காண்க.
தீர்வு :
அந்த எண்
x என்க
(x²)³ = 729
x⁶ = 729
3 × 3 × 3 × 3 × 3 × 3
x⁶ = 3⁶
x = 3
√3 = 1.732

கேள்வி 10.
எந்த இரு மிகச் சிறிய முழு வர்க்க எண்களைப் பெருக்கினால் ஒரு முழு கன எண் கிடைக்கும் எனக் காண்க.
தீர்வு :
1=1²
4 = 2²
9 = 3²
16 = 4²
25 = 5²
2² × 4² = 4 × 16 = 64 = 4³
∴ அந்த எண்கள் 4 மற்றும் 16.

Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 1 எண்கள் Ex 1.6 Textbook Questions and Answers, Notes.

TN Board 8th Maths Solutions Chapter 1 எண்கள் Ex 1.6

கேள்வி 1.
கோடிட்ட இடங்களை நிரப்புக.

i) (- 1)இரட்டை முழு எண் என்பது …………………. ஆகும்
விடை :
1

ii) a ≠ 0 எனில் a⁰ …………………. ஆகும்
விடை :
20^-3

iii) 4^-3 x 5^-3 = …………………. ஆகும்
விடை :
\(\frac{-1}{128}\)

iv) (- 2)^-7 =…………………. ஆகும்
விடை :
– 243

கேள்வி 2.
சரியா? தவறா? எனக் கூறுக.

i) 8^x = \(\frac{1}{64}\), எனில் X இன் மதிப்பு – 2
விடை :
சரி

ii) \((256)^{\frac{-1}{4}} \times 4^{2}\) இன் சுருங்கிய வடிவம் \(\frac { 1 }{ 4 }\) ஆகும்.
விடை :
தவறு

iii) படி விதியைப் பயன்படுத்தி (3⁷)^-2 = 3⁵ ஆகும்
விடை :
தவறு

iv) 2 x 10^-4 இன் திட்ட வடிவம் 0.0002 ஆகும்
விடை :
சரி

v) 123.456 இன் அறிவியல் குறியீடு 1.23456 x 10^-2 ஆகும்
விடை :
தவறு

கேள்வி 3.
மதிப்பு காண்க.
(i) \(\left(\frac{1}{2}\right)^{3}\)
(ii) \(\left(\frac{1}{2}\right)^{-5}\)
(iii) \(\left(\frac{-5}{6}\right)^{-3}\)
iv) (2^-5 x 2⁷) ÷ 2^-2
v) (2^-1 x 3^-1) ÷ 6^-2
தீர்வு :

iv) (2^-5 x 2⁷) ] 2^-2
= (2^-5-7) x 2^-2 = 2^-12 x 2^-2)

v) (2^-1 x 3^-1 ) ÷ 6^-2
= (6^-1) + 6^-2 = 6^{-1- (-2)} = 6^-1+2
= 6¹ = 6

கேள்வி 4.
மதிப்பு காண்க
(i) \(\left(\frac{2}{5}\right)^{4} \times\left(\frac{5}{2}\right)^{-2}\)
(ii) \(\left(\frac{4}{5}\right)^{-2} \div\left(\frac{4}{5}\right)^{-3}\) ∵ a^m x aⁿ = a^m+n]
(iii) \(2^{7} \times\left(\frac{1}{2}\right)^{-3}\) [
தீர்வு :

(iii) 2⁷ x \(\left(\frac{1}{2}\right)^{-3}\)
= 2⁷ x 2³ = 2⁷⁺³ = 2¹⁰
= 1024

கேள்வி 5.
மதிப்பு காண்க (i) (5° + 6^-1) x 3²
(ii) (2^-1 x 3^-1) ÷ 6^-1
(iii) (3^-1 + 4^-2 + 5^-3)⁰
தீர்வு :
(i) (5° + 6^-1) x 3²
= \(\left(1+\frac{1}{6}\right) \times 9=\left(\frac{6+1}{6}\right) \times 9=\frac{7}{6} \times \varnothing^{3}=\frac{21}{2}\)
(ii) (2^-1 x 3^-1) ÷ 6^-1 = ((2 x 3)^-1) ÷ 6^-1 = 6^-1+1 = 6⁰
(iii) (3^-1 + 4^-2 + 5^-3)⁰ = 1

கேள்வி 6.
(i) (3²)³ x (2 x 3⁵)^-2 x (18)²
(ii) \(\frac{9^{2} \times 7^{3} \times 2^{5}}{84^{3}}\)
(iii) \(\frac{2^{8} \times 2187}{3^{5} \times 32}\)
தீர்வு :
(i) (3²)³ x (2 x 3⁵)^-2 x (18)²
= 3⁶ x (2^-2) x (3⁵)^-2 x (2 x 3²)²
= 3⁶ x 2^-2 x 3^-10 x 2² x 3⁴
= 3^{6-10 +4} x 2^{-2 + 2}
= 3⁰ x 2⁰ = 1 × 1 = 1

= 2^{-8 + 4-5} x 3^5-7
= 2^-9 x 3^-2
= \(\frac{2^{-9}}{3^{2}}\)

(iii) \(\)
\(\)
= 2^8-5 x 3^7-5 = 2³ x 3²
= 8 × 9 = 72

கேள்வி 7.
x இக்கு தீர்வு காண்க : (i) \(\frac{2^{2 x-1}}{2^{x+2}}\)
(ii) \(\frac{5^{5} \times 5^{-4} \times 5^{x}}{5^{12}}=5^{-5}\)
தீர்வு :
(i) \(\frac{2^{2 x-1}}{2^{x+2}}\) = 4
2(^{2x – 1) – (x + 2)} = 2²
2^{2x – 1 – x – 2} = 2²
2^x-3 = 2²
x – 3 = 2
x = 2 + 3
x = 5

ii) \(\frac{5^{5} \times 5^{-4} \times 5^{x}}{5^{12}}=5^{-5}\)
5^{+5-4+x- 12} = 5^-5
5^{5- 16 + x} = 5^-5
5^-11+x = 5^-5
– 11 + x = – 5
x = – 5 + 11
x = 6

கேள்வி 8.
அடுக்குகளைப் பயன்படுத்தி விரிவாக்கம் செய்க : (i) 6054.321 (ii) 897.14
தீர்வு :
(i) 6054.321
= 6 × 1000 + 0 × 100 + 5 × 10 + 4 × 1 + 3 × 10^-1 + 2 × 10^-2+ 1 x 10^-3
= 6 × 10³ + 5 × 10¹ + 4 × 10⁰ + 3 × 10^-1 + 2 × 10^-2 + 1 × 10^-3
(ii) 897.14 = 8 × 10² + 9 × 10¹ + 7 × 10° + 1 × 10^-1 + 4 × 10^-2

கேள்வி 9.
எண்ணைத் திட்ட வடிவில் காண்க.
(i) 8 × 10⁴ + 7 × 10³ + 6 × 10² + 5 × 10¹ + 2 × 1 + 4 × 10^-2 + 7 × 10^-4
(ii) 5 × 10³ + 5 × 10¹ + 5 × 10^-1 + 5 × 10^-3
தீர்வு :
(i) 8 × 10⁴ +7 × 10³ + 6 × 10² + 5 × 10¹ + 2 × 1 + 4 × 10^-2 + 7 × 10^-4
= 87652.0407
(ii) 5 × 10³ + 5 × 10¹ + 5 × 10^-1 + 5 × 10^-3
= 5050.505
(iii) ஹைட்ரஜன் அணுவின் ஆரம் 2.5 x 10^-11 மீ.
தீர்வு :
2.5 × 10^-11 = 0.000000000025
= 0.000000000025

கேள்வி 10.
பின்வரும் எண்களை அறிவியல் குறியீட்டில் எழுதவும்
(i) 467800000000
(ii) 0.000001972
(iii) 1642.398
(iv) பூமியின் கன அளவு சுமார் 1,083,000,000,000 கன கிலோ மீட்டர்கள் ஆகும்.
(v) நீ ஒரு வாளியில் தூசுத் துகள்களைக் கொண்டு நிரப்பினால், முழு பூமியின் பகுதியில் வாளியிலுள்ள தூசுத் துகள்களின் எடையானது 0.0000000000000000000000016 கி.கி ஆக இருக்கும்.
தீர்வு :
(i) 467800000000 = 4.678 × 10¹¹
(ii) 0.000001972 = 1.972 × 10^-6
(iii) 1642.398 = 1.642398 × 10³
(iv) 1,083,000,000,000 = 1.083 × 10¹² கன கி.மீ
(v) 0.0000000000000000000000016 = 1.6 × 10^-24

மேற்சிந்தனைக் கணக்குகள்

கேள்வி 11.
(-4)^-1 உடன் எந்த எண்ணைப் பெருக்கினால், பெருக்கலானது 10^-1 என ஆகும்?
அ) \(\frac{2}{3}\)
ஆ) \(\frac{-2}{5}\)
இ) \(\frac{5}{2}\)
ஈ) \(\frac{-5}{2}\)
விடை :
ஆ) \(\frac{-2}{5}\)

கேள்வி 12.
(- 2)^-3 x (- 2)^-2 என்பது ………. ஆகும்
அ) \(\frac{-1}{32}\)
ஆ) \(\frac{1}{32}\)
இ) 32
ஈ) – 32
விடை :
அ) \(\frac{-1}{32}\)

கேள்வி 13.
எது சரியல்ல?
அ) \(\left(\frac{-1}{4}\right)^{2}=4^{-2}\)
ஆ) \(\left(\frac{-1}{4}\right)^{2}=\left(\frac{1}{2}\right)^{4}\)
இ) \(\left(\frac{-1}{4}\right)^{2}=16^{-1}\)
ஈ) \(-\left(\frac{1}{4}\right)^{2}=16^{-1}\)
விடை
ஈ) \(-\left(\frac{1}{4}\right)^{2}=16^{-1}\)

கேள்வி 14.
\(\frac{10^{x}}{10^{-3}}=10^{9}\) எனில் x ஆனது ………. ஆகும்
அ) 4
ஆ) 5
இ) 6
ஈ) 7
விடை :
இ) 6

கேள்வி 15.
0.0000000002020 இன் அறிவியல் குறியீடு …….. ஆகும்
அ) 2.02 x 10⁹
ஆ) 2.02 x 10^-9
இ) 2.02 x 10^-8
ஈ) 2.02 x 10^-10
விடை :
ஈ) 2.02 x 10^-10

Tamilnadu State Board New Syllabus Samacheer Kalvi 9th Maths Guide Pdf Chapter 3 இயற்கணிதம் Ex 3.7 Textbook Questions and Answers, Notes.

TN Board 9th Maths Solutions Chapter 3 இயற்கணிதம் Ex 3.7

கேள்வி 1.
பின்வரும் பல்லுறுப்புக் கோவைகளை வகுத்து ஈவு மற்றும் மீதியைக் காண்க.
(i) (4x³ + 6x² – 23x + 18) ÷ (x + 3)
விடை:

ஈவு = 4x² – 6x – 5
மீதி = 33

(ii) (8y³ – 16y² + 16y – 15) ÷ (2y – 1)
விடை:

ஈவு = 4y² – 6y + 5
மீதி = -10

(iii) (8x³ – 1) ÷ (2x – 1)
விடை:

ஈவு = 4x² + 2x + 1
மீதி = 0

(iv) (-18z + 14z² + 24z³ + 18) ÷ (3z + 4)
விடை:
(24z³ + 14z² – 18z + 18) ÷ (3z + 4)

ஈவு = 8z² – 6z + 2
மீதி = 10

கேள்வி 2.
செவ்வகத்தின் பரப்பு x² + 7x +12. அதன் அகலம் x + 3 எனில், அதன் நீளம் காண்க.
விடை:
செவ்வகத்தின் பரப்பளவு = x² + 7x + 12
அகலம் = x + 3
பரப்பளவு = நீளம் × அகலம்

நீளம் = (x + 4) அலகுகள்,

கேள்வி 3.
இணைகரத்தின் பரப்பளவு 25x² – 16. அதன் அடிப்பக்கம் 5x + 4 எனில், அதன் உயரம் காண்க.
விடை:
இணைகரத்தின் பரப்பளவு = அடிப்பக்கம் × உயரம்
25x² – 16 = (5x + 4 ) × உயரம்

ஈவு = 5x – 4
மீதி = 0
உயரம் = (5x – 4) அலகுகள்.

கேள்வி 4.
x + 5 விவரங்களின் கூடுதல் x³ + 125 எனில், விவரங்களின் சராசரியைக் காண்க.
விடை:

சராசரி = x² – 5x + 25
மீதித்தேற்றம்: பல்லுறுப்புக் கோவை p(x) இன் படி ஒன்றோ அல்லது அதற்கு மேலாகவோ இருக்கும். மேலும் p(x) ஆனது நேரிய கோவை x-a ஆல் வகுபடும் எனில் அதன் மீதி p(a)
ஆகும். இங்கு a ஒரு மெய்யெண்.

கேள்வி 5.
தொகுமுறை வகுத்தலைப் பயன்படுத்தி ஈவு மற்றும் மீதி காண்க.
(i) (x³ + x² – 7x – 3) ÷ (x – 3)
விடை :
P(x) = x³ + x² – 7x – 3 என்க.

ஈவு = x² + 4x + 5
மீதி = 12

(ii) (x³ + 2x² – x – 4) ÷ (x + 2)
விடை:
P(x) =x³ + 2x² – x – 4 என்க.

ஈவு = x² + 0x – 1 = x² – 1
மீதி = -2

(iii) (3x³ – 2x² + 7x – 5) ÷ (x + 3)
விடை :
P(x) = 3x³ – 2x² + 7x – 5 என்க.

ஈவு = 3x² – 11x + 40
மீதி = -125

(iv) (8x⁴ – 2x² + 6x + 5) ÷ (4x + 1)
விடை :
P(x) = 8x⁴ – 2x² + 6x + 5 என்க.

கேள்வி 6.
(8x⁴ – 2x² + 6x – 7) ஐ (2x+1) ஆல் வகுக்கக்கிடைக்கும் ஈவு 4x³ + px² – qx+3 எனில், p, q மற்றும் மீதியைக் காண்க.
விடை :
P(x) = 8x⁴ – 2x² + 6x – 7 என்க.

ஈவு = 8x³ – 4x² + 0x + 6 = 4x³ – 2x³ + 3
x² இன் கெழு – 2 = p
p = -2
x இன் கெழு 0 =q
q = 0
மீதி = -10

கேள்வி 7.
(3x³ + 11x² + 34x + 106) ஐ (x – 3) ஆல் வகுக்கக் கிடைக்கும் ஈவு 3x² + ax + b எனில், a, b மற்றும் மீதியைக் காண்க.
விடை:
P(x) = 3x³ + 11x² + 34x + 106 என்க.

ஈவு = 3x² + 20x + 94
x இன் கெழு 20 = a
a = 20
மாறிலி 94 = b
b = 94
மீதி = 388

Tamilnadu State Board New Syllabus Samacheer Kalvi 9th Maths Guide Pdf Chapter 3 இயற்கணிதம் Ex 3.6 Textbook Questions and Answers, Notes.

TN Board 9th Maths Solutions Chapter 3 இயற்கணிதம் Ex 3.6

கேள்வி 1.
பின்வருவனவற்றைக் காரணிப்படுத்துக.
(i) x² + 10x + 24
விடை:
x² + 10x + 24
=x² + 4x + 6x + 24
= x (x + 4) + 6(x + 4)
= (x + 4) (x + 6)

(ii) z² + 4z – 12
விடை : z² + 4z – 12
= z² + 6z – 2z – 12
= z (z + 6) – 2(z + 6)
= (z + 6) (z – 2)

(iii) p² – 6p – 16
விடை:
p² – 6p – 16
= p² – 8p + 2p – 16
= p (p – 8) + 2(p – 8)
= (p – 8) (p + 2)

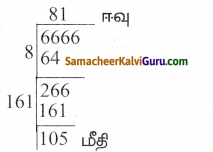
(iv) t² +72 – 17t
விடை : t² +72 – 17t
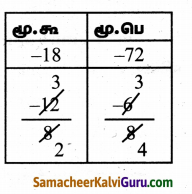
= t² – 8t – 9t + 72

கேள்வி 2.
பின்வருவனவற்றை காரணிப்படுத்துக.
i) 2a² + 9a + 10
விடை:
2a² + 9a + 10
= 2a² + 4a + 5a + 10
= 2a (a + 2) + 5(a +2)
= (a + 2) (2a +5)

(ii) 5x² – 29xy – 42y²
விடை:
5x² – 29xy – 42y²
= 5x² – 35xy + 6xy – 42y²
= 5x (x – 7y) + 6y (x – 7y)
= (5x + 6y) (x – 7y)

(iii) 8x² – 18x + 9
விடை:
8x² – 18x + 9
(2x – 3) (4x – 3)

(iv) 6x² + 16xy + 8y²
விடை:
6x² + 16xy + 8y²
= 6x² + 12xy +4xy + 8y²
= 3x (2x + 4y) + 2y (2x + 4y)
= (3x + 2y) (2x + 4y)

(v) 12x² + 36x²y + 27x²y²
விடை:
12x² + 36x²y + 27x²y²
= 3x² (4 + 12y + 9y²)
= 3x² (9y² + 12y + 4)
= 3x² (9y² + 6y + 6y + 4)
= 3x² (3y (3y + 2) + 2 (3y + 2)
= 3x² (3y + 2) (3y + 2)

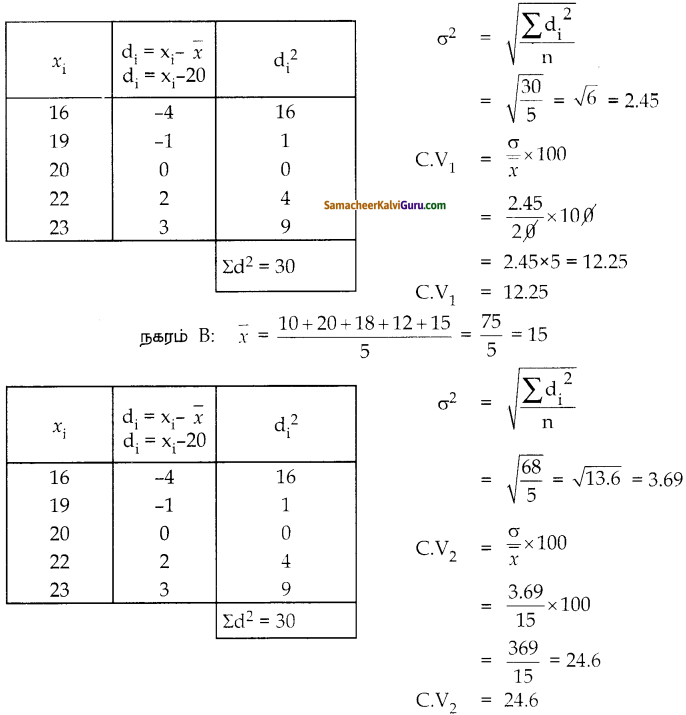
(vi) (a + b)² + 9(a + b) + 18
விடை:
(a + b)² + 9(a + b) = 18
a + b = x என்க.
x² + 9x + 18
x² + 6x + 3x + 18
x (x + 6) + 3 (x + 6)
(x + 3) (x + 6)
(a + b + 3) (a + b + 6)

கேள்வி 3.
பின்வருவனவற்றை காரணிப்படுத்துக.
(i) (p – q)² – 6(p – q) – 16
விடை:
(p – q)² – 6(p – q) – 16
p – q = y என்க.
= y² – 6y – 16
= y² – 8y + 2y – 16
= y (y – 8) + 2(y – 8)
= (y – 8) (y + 2)
= (p – q – 8) (p – q + 2)

(ii) m² + 2mn – 24n²
விடை:
m² + 2mn – 24n²
m² + 6mn – 4mn – 24n²
m (m + 6n) – 4n (m + 6n)
(m – 4n) (m + 6n)

(iii) √5 a² + 2a – 3√5
விடை:
√5a² + 2a – 3√5
= √5a² + 5a – 3a – 3√5
= a√5 (a + √5 )-3(a + √5)
= (a√5 – 3) (a + √5)

(iv) a⁴ – 3a² + 2
விடை:
a⁴ – 3a² + 2
= a⁴ – 2a² – a² + 2.
= a² (a² – 2) -1 (a² – 2)
= (a² – 1) (a² – 2)
= (a – 1) (a + 1) (a² – 2)

(v) 8m³ – 2m²n – 15mn²
விடை:
8m³ – 2m²n – 15mn²
= m (8m² – 2mn – 15n²)
= m (8m² – 12mn + 10mn – 15n²)
= m (4m (2m – 3n) + 5n (2m – 3n)
= m (4m + 5n) (2m – 3n)

(vi) \(\frac{1}{x^{2}}+\frac{1}{y^{2}}+\frac{2}{x y}\)
விடை:
\(\frac{1}{x^{2}}+\frac{1}{y^{2}}+\frac{2}{x y}\)

Tamilnadu State Board New Syllabus Samacheer Kalvi 9th Maths Guide Pdf Chapter 3 இயற்கணிதம் Ex 3.5 Textbook Questions and Answers, Notes.

TN Board 9th Maths Solutions Chapter 3 இயற்கணிதம் Ex 3.5

கேள்வி 1.
பின்வருவனவற்றைக் காரணிப்படுத்துக.
i) 2a² + 4a²b + 8a²c
விடை:
2a² + 4a²b + 8a²c
= 2a² (1 + 2b + 4c)

(ii) ab – ac – mb + mc
விடை:
ab – ac – mb + mc
= a(b – c) – m(b – c)
= (a – m) (b – c)

கேள்வி 2.
பின்வருவனவற்றைக் காரணிப்படுத்துக.
(i) x² + 4x +4
விடை:
x² + 4x + 4
= x² + 2x + 2x + 4
= x (x + 2) + 2 (x + 2)
= (x + 2) (x + 2)

(ii) 3a² – 24ab + 48b²
விடை:
3a² – 24ab + 48b²
= 3(a² – 8ab + 16b²)
= 3(a² – 4ab – 4ab + 16²)
= 3(a(a – 4b) – 4b (a – 4b))
= 3 (a – 4b) (a – 4b)
= 3 (a – 4b)²

(iii) x⁵-16x
விடை: x⁵ – 16x
= x(x⁴ – 16)
= x((x²)² – (4)²
= x(x² + 4) (x² – 4)
= x (x² + 4) (x² – 2²)
= x (x⁴ + 4) (x + 2) (x – 2)

(iv) m²+ \(\frac{1}{m^{2}}\) – 23
விடை:

(v) 6 – 216x²
விடை:
6 – 216x²
= 6 (1 – 36x²)
= 6 (1² – (6x)²)
= 6 (1 – 6x) (1 + 6x)

(vi) a² + \(\frac{1}{a^{2}}\) -18
விடை:

கேள்வி 3.
பின்வருவனவற்றைக் காரணிப்படுத்துக.
i) 4x² + 9y² + 25z² + 12xy + 30yz + 20xz
விடை:
4x² + 9y² + 25z² + 12xy + 30yz + 20xz
= (2x)² + (3y)² + (5z)² + 2 × 2x × 3y +2 × 3y × 5z + 2 × 5z × 2x
= (2x + 3y + 5z)²

(ii) 25x² + 4y² + 9z² – 20xy + 12yz – 30xz
விடை:
25x² + 4y² + 9z² – 20xy + 12yz – 30xz
விடை:
25x² + 4y² + 9z² – 20xy + 12yz – 30xz
= (-5x)² + (2y)² + (3z)² + 2 × (-5x) × 2y + (2 × 2y × 3z) + 2 × 3z × – 5x
= (-5x + 2y + 3z)²
= (5x – 2y – 3z)²

கேள்வி 4.
பின்வருவனவற்றைக் காரணிப்படுத்துக.
(i) 8x³ + 125y³
விடை:
8x³ + 125y³
a³ + b³ = (a + b)³ – 3ab (a + b)
= (2x)³ + (5y)³
= (2x + 5y)³ – 3 × 2x × 5y (2x + 5y)
= (2x + 5y)³ – 30xy (2x + 5y)
(அல்லது)

a³ + b³ = (a + b) (a² – ab + b²)
8x³ + 125y³
= (2x)³ + (5y)³
= (2x + 5y) (2x)² – 2x × 5y + (5y)²
= (2x + 5y) (4x² – 10xy + 25y²)

(ii) 27x³ – 8y³
விடை:
27x³ – 8y³
= (3x)³ – (2y)³
= (3x – 2y) (3x)² + 3x × 2y + (2y)²)
– = (3x – 2y) (9x² + 6xy + 4y)²

(iii) a⁶ – 64
விடை :
a⁶ – 64
= a⁶ – 2⁶
= (a + 2) (a – 2) (a² – 2a + 4) (a² + 2a + 4)

கேள்வி 5.
பின்வருவனற்றைக் காரணிப்படுத்துக.
(i) x³ + 8y³ + 6xy -1
விடை:
x³ + 8y³ + 6xy – 1
= x³ + (2y)³ – (1)³ + 6xy
= (x + 2y – 1) (x² +4y² + 1 – 2xy + 2y +x)

(ii) l³ – 8m³ – 27n³ – 18lmn
விடை:
l³– 8m³ – 27n³ – 18lmn
= (l³ + (-2m)³ + (-3n)³ – 3 × l × -2m × -3n
= (l – 2m – 3n) (l² + 4m² + 9n² + 2lm – 6mn + 3nl)
= t (t – 8) – 9(t – 8)
= (t – 8) (t – 9)

(v) y² – 16y – 80
விடை: y² – 16y – 80
= y² – 20y + 4y – 80
= y (y – 20) + 4(y – 20)
= (y + 4) (y – 20)

(vi) a² + 10a – 600
விடை:
a² + 10a – 600
= a² + 30a – 20a – 600
= a (a + 30) – 20(a+ 30)
= (a – 20) (a + 30)

Tamilnadu State Board New Syllabus Samacheer Kalvi 8th Maths Guide Pdf Chapter 1 எண்கள் Ex 1.4 Textbook Questions and Answers, Notes.

TN Board 8th Maths Solutions Chapter 1 எண்கள் Ex 1.4

கேள்வி 1.
கோடிட்ட இடங்களை நிரப்புக.

i) 77 இன் வர்க்கத்திலுள்ள ஒன்றுகள் இலக்கமானது ………………… ஆகும்
விடை :
9

ii) 242 மற்றும் 252 ஆகியவற்றிற்கிடையே …………… எண்ணிக்கையிலான வர்க்கமற்ற எண்கள் உள்ளன
விடை :
48

iii) 300 இக்கும் 500 இக்கும் இடையே ………………… முழு வர்க்க எண்கள் உள்ளன
விடை :
5

iv) ஓர் எண்ணில் 5 அல்லது 6 இலக்கங்கள் இருப்பின், அந்த எண்ணின் வர்க்கமூலத்தில் ……… இலக்கங்கள் இருக்கும்.
விடை :
3

v) \(\sqrt{180}\) இன் மதிப்பானது ……… மற்றும் …… என்ற முழுக்களிடையே இருக்கும்
விடை :
13,14

கேள்வி 2.
சரியா? தவறா? எனக் கூறுக :

i) ஒரு வர்க்க எண்ணானது 6 இல் முடியும் எனில், அதன் வர்க்கமூலமானது ஒன்றாம் இலக்கமாக எண் 6 ஐப் பெற்றிருக்கும்.
விடை :
சரி

ii) ஒரு வர்க்க எண்ணானது கடைசியில் ஒற்றைப்படை எண்ணிக்கையிலான பூச்சியங்களைப் பெற்றிருக்காது.
விடை :
சரி

iii) 961000 இன் வர்க்கத்தில் உள்ள பூச்சியங்களின் எண்ணிக்கை 9 ஆகும்.
விடை :
தவறு

iv) 75 இன் வர்க்கமானது 4925 ஆகும்
விடை :
தவறு

v) 225 இன் வர்க்க மூலம் 15 ஆகும்
விடை :
சரி

கேள்வி 3.
பின்வரும் எண்களின் வர்க்கம் காண்க
(i) 17 (ii) 203 (iii) 1098
தீர்வு :
(i) 17² = 289
(ii) 203² = 41209
(iii) 1098² = 1205604

கேள்வி 4.
பின்வரும் எண்களில் ஒவ்வொன்றும் முழு வர்க்கமா என ஆராய்க.
(i) 725
(ii) 190
(iii) 841
(iv) 1089
தீர்வு :
(i) 725 = 5 x 5 x 29

= 5² x 29
இரண்டாவது பகாக் காரணியான 29 க்கு சோடி இல்லை
எனவே 725 ஆனது ஒரு முழுவர்க்க எண் அல்ல

(ii) 190 = 2 x 5 x 19
பகக் காரணிகளான 2,5,29
க்கு சோடிகள் இல்லை எனவே 190 ஆனது ஒரு முழுவர்க்கம் அல்ல

(iii) 841 = 29 x 29
= 29²

841 என்பது முழுவர்க்க எண் ஆகும்.

(iv) 1089 = 3 x 3 x 11 x 11
= 3² x 11²
எனவே 1089 என்பது
முழுவர்க்க எண் ஆகும்

கேள்வி 5.
பகாக் காரணிப்படுத்துதல் முறையில் வர்க்கமூலத்தைக் காண்க.
(i) 144
(ii) 256
(iii) 784
(iv) 1156
(v) 4761
(vi) 9025
தீர்வு :
\(\sqrt{144}\)
= \(\sqrt{2 \times 2 \times 2 \times 2 \times 3 \times 3}\)
= 2 x 2 x 3 = 12

(ii) \(\sqrt{256}\)
= \(\sqrt{2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2}\)
= 2 x 2 x 2 x 2
= 16

(iii) \(\sqrt{784}\)
= \(\sqrt{2 \times 2 \times 2 \times 2 \times 7 \times 7}\)
= 2 x 2 x 7
= 28

(iv) \(\sqrt{2 \times 2 \times 2 \times 2 \times 7 \times 7}\)
= 2 x 17
= 34

(v) \(\sqrt{4761}=\sqrt{3 \times 3 \times 23 \times 23}\)
= 3 x 23 = 69

(vi) \(\sqrt{9025}=\sqrt{5 \times 5 \times 19 \times 19}\)
= 5 x 19 = 95

கேள்வி 6.
நீள் வகுத்தல் முறையில் வர்க்க மூலத்தைக் காண்க.
i) 1764
ii) 6889
iii) 11025
iv) 17956
v) 418609
தீர்வு :

கேள்வி 7.
பின்வரும் எண்களின் வர்க்க மூலங்களின் தோராய மதிப்பை, அருகிலுள்ள முழு எண்ணிற்கு மதிப்பிடவும்:
i) </440 ii) 1/800 iii) 1020
தீர்வு :
(i) \(\sqrt{440} \simeq 21\)
அருகிலுள்ள முழு எண் 21 ஆகும்

ii) \(\sqrt{800}=28\)
அருகிலுள்ள முழு எண் 28 ஆகும்

iii) \(\sqrt{1020}=32\)
அருகிலுள்ள முழு எண் 32 ஆகும்

கேள்வி 8.
பின்வரும் தசம எண்கள் மற்றும் பின்னகளின் வர்க்க மூலத்தைக் காண்க.
i) 2.89
ii) 67.24
iii) 2.0164
iv) \(\frac{144}{225}\)
v) \(7 \frac{18}{49}\)
தீர்வு :

கேள்வி 9.
6666 இலிருந்து எந்த மிகச்சிறிய எண்ணைக் கழித்தால் அது ஒரு முழு வர்க்க எண்ணாகும் எனக் காண்க. அவ்வாறு கிடைத்த முழு வர்க்க எண்ணின் வர்க்க மூலத்தையும் காண்க.
தீர்வு :

6666லிருந்து 105 ஐக் கழித்தால் அது ஒரு முழு வர்க்க எண்ணாகும்.
∴ 6666 – 105 = 6561 என்பது முழு வர்க்க எண். அவற்றின் வர்க்க மூலம் 81 ஆகும்.

கேள்வி 10.
1800 ஐ எந்த மிகச் சிறிய எண்ணால் பெருக்கினால் அது ஒரு முழு வர்க்க எண்ணாகும் எனக் காண்க. அவ்வாறு கிடைத்த முழு வர்க்க எண்ணின் வர்க்க மூலத்தையும் காண்க.
தீர்வு :
1800 = 2 x 2 x 2 x 5 x 5 x 3 x 3
= 2² x 5² x 3² x 2
பகா காரணி 2 க்கு சோடி இல்லை 1800 ஐ 2 ஆல் பெருக்கவும்
1800 x 2 = 3600
= 2² x 2² x 5² x 3²
= 6² x 10² = 602
∴ \(\sqrt{3600}\) = 60

கொள்குறிவகை வினாக்கள்

கேள்வி 11.
43இன் வர்க்க மானது …….. என்ற இலக்கத்தில் முடியும்.
(அ) 9
(ஆ) 6
(இ) 4
(ஈ) 3
விடை :
(அ) 9

கேள்வி 12.
24² உடன் …….. ஐக் கூட்டினால் 25² ஐ பெறலாம்.
(அ) 4²
(ஆ) 5²
(இ) 6²
(ஈ) 7²
விடை :
(ஈ) 7²

கேள்வி 13.
\(\sqrt{48}\) இன் தோராய மதிப்பானது ………………. இக்குச் சமம்
(அ) 5
(ஆ) 6
(இ) 7
(ஈ) 8
விடை :
(இ) 7

கேள்வி 14.
\(\sqrt{128}-\sqrt{98}+\sqrt{18}=\)
(அ) \(\sqrt{2}\)
(ஆ) \(\sqrt{8}\)
(இ) \(\sqrt{48}\)
(ஈ) \(\sqrt{32}\)
விடை :
(ஈ) \(\sqrt{32}\)

கேள்வி 15.
123454321 இன் வர்க்கமூலத்திலுள்ள இலக்கங்களின் எண்ணிக்கையானது ……………… ஆகும்.
(அ) 4
(ஆ) 5
(இ) 6
(ஈ) 7
விடை :
(ஆ) 5

Tamilnadu State Board New Syllabus Samacheer Kalvi 9th Maths Guide Pdf Chapter 3 இயற்கணிதம் Ex 3.4 Textbook Questions and Answers, Notes.

TN Board 9th Maths Solutions Chapter 3 இயற்கணிதம் Ex 3.4

கேள்வி 1.
கீழ்க்காண்பவற்றை விரிவாக்குக.
(i) (2x +3y + 4z)²
(ii) (-p + 2q + 3r)²
(iii) (2p + 3) (2p – 4) (2p – 5)
(iv) (3a + 1) (3a – 2) (3a + 4)
விடை:
(i) (2x + 3y + 4z)²
(a + b + c)² = a² + b² + c² + 2ab + 2bc + 2ca
(2x + 3y + 4z)²
= (2x)² + (3y)² + (4z)² + 2 × 2x × 3y + 2 × 3y
× 4z + 2 × 4z × 2x
= 4x² + 9y² + 16z² + 12xy + 24yz + 16zx

(ii) (-p + 2q + 3r)²
= (-p)² + (2q)² + (3r)² + 2 × -p × 2q + 2 × 2q
× 3r + 2 × 3r × -p
= p² + 4q² + 9r² – 4pq + 12qr – 6rp

(iii) (2p + 3) (2p – 4) (2p – 5)
= (2p)³ + (3 – 4 – 5) (2p)² + (3 × (-4) + -4 × -5 + -5 × 3 ) 2p + 3 × -4 × -5
= 8p³ – 24p² + (-12 + 20 – 15) 2p + 60
= 8p³ – 24p² -7 × 2p + 60
= 8p³ – 24p² – 14p + 60

(iv) (3a + 1) (3a – 2) (3a + 4)
= (3a)³ + (4 – 2 + 4) (3a)² + 1 × -2 + (-2) × 4 + 4 × (1) 3a + 1 × -2 4
= 27a³ + 54a² + (-2 – 8 + 4) 3a – 8
= 27a³ + 54a² – 18a – 8)

கேள்வி 2.
முழுவதும் விரிவாக்காமல் x² இன் கெழு , x இன் கெழு மற்றும் மாறிலி உறுப்புகளை இயற்கணித முற்றொருமையைப் பயன்படுத்திக் காண்க.
(i) (x + 5) (x + 6) (x + 7)
(ii) (2x + 3) (2x – 5) (2x – 6)
விடை :
(i) (x + 5) (x + 6) (x + 7)
x³ + 18x² + 107x + 210
x² இன் கெழு = 18
x இன் கெழு = 107
மாறிலி = 210

(ii) (2x + 3) (2x – 5) (2x – 6)
= (2x)³ + (3 – 5 – 6) (2x)² + (3 × -5 + (-5 × -6) + (-6 × 3) 2x + 3 × -5 × -6
= 8x³ – 32x² + (-15 + 30 – 18) 2x + 90
= 8x³ – 32x² – 6x + 90
x ²இன் கெழு = -32
x இன் கெழு = -6
மாறிலி = 90

கேள்வி 3.
(x + a) (x + b) (x + c) = x³ + 14x² + 59x + 70 எனில், கீழ்க்காண்பனவற்றின் மதிப்பு காண்க.
(i) a + b + c
(ii) \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\)
(iii) a² + b² + c²
(iv) \(\frac{a}{b c}+\frac{b}{a c}+\frac{c}{a b}\)
விடை :
(x + a) (x + b) (x + c)
= x³ + (a + b + c) x² + (ab + bc + ca) x + abc a + b + c = 14
= x³ + 14x² + 59x + abc
x² இன் கெழு = 14
x இன் கெழு = 59
மாறிலி = abc
(i) a + b + c = 14
(ii) \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\)
(iii) \(\frac{b a+b c+a c}{a b c}=\frac{59}{70}\)

(iii) a² + b² + c² + 2ab + 2ca + 2bc = (a + b + c)²
a² + b² + c² + 2ab + 2ca + 2bc = (a + b + c)²
a² + b² + c² = (a + b + c)² – 2ab – 2bc – 2ca (14)² – 2(ab + bc + ca) = (a² + b² + c²)
196 – 2(59) = a² + b² +c²
196 – 118 = a² + b² + c²
a² + b² + c² = 78

(iv) = a(a²cb) + b(bcab) + c(bc × ac)/(abc)²
= a³cb + b³ca + c³ab / (abc)²
= a²(abc) + b²(abc) + c²(abc) / (abc)²
\(=\frac{a b c\left(a^{2}-b^{2}+c^{2}\right)}{(a b c)(a b c)}\)
\(=\frac{78}{70}\)

கேள்வி 4.
விரிவுப்படுத்துக.
(3a – 4b)³
(a – b)3 = a³ – b³ – 3ab (a – b)
(3a – 4b)³ = (3a)³ – (4b)3 – 3 x 3a × 4b (3a – 4b)
= 27a³ – 64b³ – 36ab (3a – 4b)
27a³ – 64b³ – 108a²b + 144ab²

கேள்வி 5.
இயற்கணித முற்றொருமைகளைப்பயன்படுத்திப் பின்வருவனவற்றின் மதிப்பு காண்க.
(98)³ = (100 – 2)³
(100 – 2)³ = (100)³ – (2)³ – 3 × 100 × 2 (100 – 2)
= 1000000 – 8 – 60000 + 1200
= 1001200 – 60008
= 941192

(ii) (1001)³ = (1000 + 1)³
= (1000)³ + (1)³ + 3 × 1000 × (1000 + 1 )
= 1000000000 + 1 + 3000000 + 3000
= 1003003001

கேள்வி 6.
(x + y + z) = 9 மற்றும் (xy + yz + zx) = 26 எனில்,x² + y² + z² இன் மதிப்பைக் காண்க.
விடை:
(x + y + z)² = x² + y² + z² + 2(xy + yz + zx)
(9)² = x² + y² + z² + 2(26)
81 = x² + y² + z² + 52
81 – 52 = x² + y² + z²
x² + y² + z² = 29

கேள்வி 7.
3a + 4b = 10 மற்றும் ab = 2 எனில்,27a³ + 64b³ இன் மதிப்புக் காண்க
விடை:
27a³ + 64b³ = (3a)³ + (4b)³
(3a)³ + (4b)³ = (3a + 4b)³ – 3 × 3a × 4b(3a + 4b)
= (10)³ – 36ab × (3a + 4b)
= 1000 – 36 × 2 × 10
= 1000 – 720
= 280

கேள்வி 8.
x – y = 5 மற்றும் xy = 14 எனில், x³ – y³ இன் மதிப்புக் காண்க.
விடை:
x³ – y³ = (x – y)³ + 3 × x × y (x – y)
= (5)³ + 3xy (x – y)
= 125 + 3 × 14 × 5
= 125 + 210
= 335

கேள்வி 9.
(a + \(\frac{1}{a}\)) = G எனில், a³+ \(\frac{1}{\mathrm{a}^{3}}\) இன் மதிப்புக் காண்க.
விடை:

கேள்வி 10.
(x² + \(\frac{1}{x^{2}}\)) = 23 எனில், x + \(\frac{1}{x}\) மற்றும்
= x³ + \(\frac{1}{x^{3}}\)ஆகியவற்றின் மதிப்புகளைக் காண்க.
விடை:

கேள்வி 11.
(y – \(\frac{1}{y}\))³ = 27 எனல், y³ – \(\frac{1}{x^{3}}\) இன் மதிப்பு காண்க.
விடை:

கேள்வி 12.
சுருக்குக.
(i) (2a + 3b + 4c) (4a² + 9b² + 16c² – 6ab – 12bc-8ca)
(ii) (x – 2y + 3z) (x² + 4y² + 9z² + 2xy + 6yz – 3xz)
விடை:
(i) (2a + 3b + 4c) (4a² + 9b² +16c² – 6ab – 12bc – 8ca)
a³ + b³ + c³ – 3abc
= (2a)³ + (3b)³ + (4c)³ – 3 × 2a × 3b × 4c
= 8a³ +27b³ + 64c³ – 72abc

(ii) (x – 2y + 3z) (x² + 4y² + 9z² + 2xy + 6yz – 3xz)
a³ + b³ + c³ – 3abc
= (x)³ = (-2y)³ + (3z)³ – 3 × x × -2y × 3z
= x³ – 8y³ + 27z³ + 18xyz

கேள்வி 13.
முற்றொருமைகளைப் பயன்படுத்தி மதிப்பு காண்க.
(i) 7³ – 10³ + 3³
(ii) 729 – 216 – 27
(iii) \(\left(\frac{1}{3}\right)^{3}+\left(\frac{1}{2}\right)^{3}-\left(\frac{5}{6}\right)^{3}\)
(iv) 1 + \(\frac{1}{8}-\frac{27}{8}\)
விடை:
(i) 7³ – 10³ + 3³
x = 7
y = -10
z = 3 என்க
x + y + z = 7 – 10 + 3
= 0
x + y + z = 0 எனில்
x³ + y³ + Z³ = 3xyz
7³ – 10³ + 3 = 3 × 7 × -10 × 3
= -630

(ii) 729 – 216 – 27
= 9³ – 6³ – 3³
x = 9, y = -6, z = -3 என்க
x + y + z = 9 – 6 – 3
= 0
x + y + z = 0 எனில் x³ + y³ + z³ = 3xyz
9³ – 6³ – 3³ = 3 × 9 × -6 × -3
= 486

கேள்வி 14.
2x – 3y – 4z = 0 எனில், 8x³ – 27y³ – 64z³) ஐக்காண்க.
விடை:
8x³ – 27y³ – 64z³
=(2x)³ – (3y³ – (4z)³
2x – 3y – 4z = 0 எனில்,
8x³ – 27y³ – 64z³
= 3 × 2x × -3y × -4z
= 72xyz