Prasanna

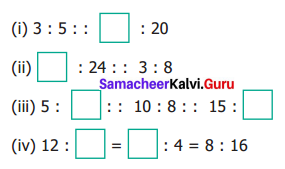
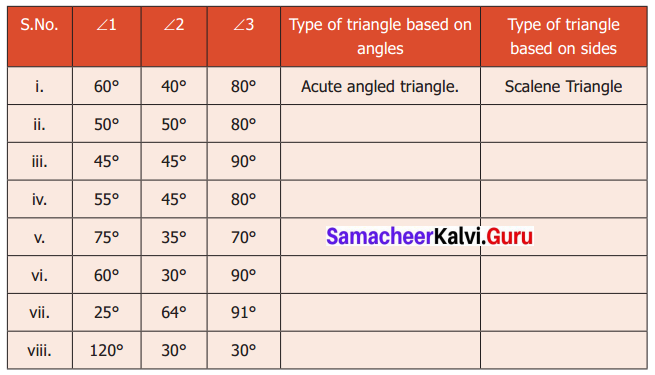
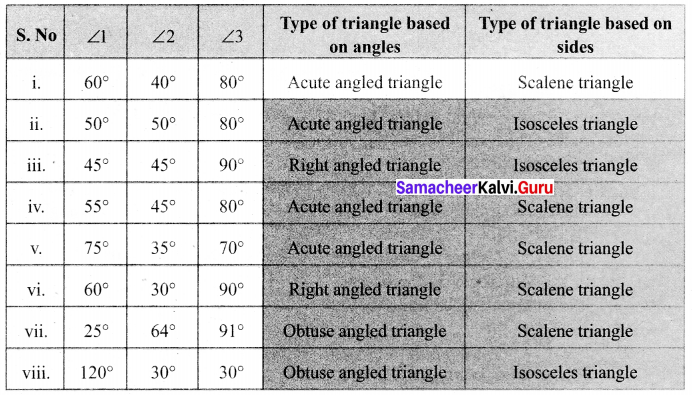
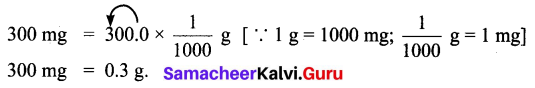You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 1 Chapter 1 Numbers Ex 1.2

Question 1.
Fill in the blanks with > or < or =

1. 48792 __ 48972
2. 1248654 __ 1246854
3. 658794 __ 658794

Solution:

1. 48792 < 48972
   [Hint: Open side can hold large number 7 < 9
2. 1248654 > 1246854
   Hint: 8 > 6
3. 658794 = 658794

Question 2.
Say True or False

1. The difference between the smallest number of seven digits and the largest number of six digits is 10.
2. The largest 4-digit number formed by the digits 8, 6, 0, 9 using each digit only once is 9086.
3. The total number of 4-digit numbers is 9000.

Solution:

1. False
2. False
3. True

Question 3.
Of the numbers 1386787215, 137698890, 86720560, which one is the largest? Which one is the smallest?
Solution:
We know that the number with more digits is greater.
The greatest number is 1386787215
The smallest number is 86720560

Question 4.
Arrange the following numbers in the descending order:
128435, 10835, 21354, 6348, 25840
Solution:
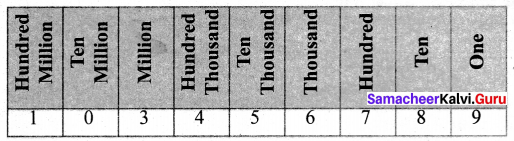
Place value chart is given by

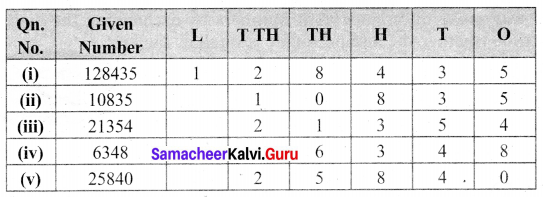
The number with more digits is the greater number
Step 1: 128435 is the larger number and 6348 is the least number
Step 2: For the remaining 5 digit numbers we can compare the left-most digits and find 25840 > 21354 > 10835.
The descending order:
128435 > 25840 > 21354 > 10835 > 6348

Question 5.
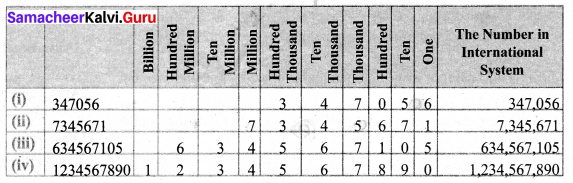
Write any eight-digit number with 6 in ten lakhs place and 9 in ten-thousandth place.
Solution:
Step (i): Preparing place value chart with 8 digits 6 in ten lakh place and 9 in Ten thousand place
Step (ii): Fill the other places with any of the numbers

The number maybe 56897432. Similarly, we can write many numbers.

Question 6.
Rajan writes a 3-digit number, using the digits 4, 7 and 9. What are the possible numbers he can write?
Solution:
The given digits are 4, 7 and 9.

Rajan can write 974, 947, 794, 749, 479, 497

Question 7.
The password to access my ATM card includes the digits 9, 4, 6 and 8. It is the smallest 4 digit even number. Find the password of my ATM card.
Solution:
4698

Question 8.
Postal Index Number consists of six digits The first three digits are 6, 3 and 1. Make the largest and the smallest Postal Index Number by using the digits 0, 3 and 6 each only once.
Solution:
Given PIN consists of six digits. First, three digits are 6, 3, and 1.
The digits 0, 3 and 6 to be used only once, in the remaining places.

Largest Postal Index Number: 631630
Smallest Postal Index Number: 631036

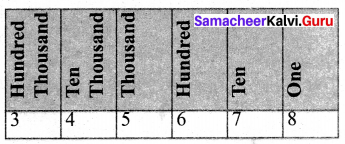
Question 9.
The height (in metres) of the mountains in Tamil Nadu as follows:

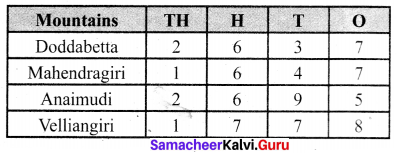
(i) Which is the highest mountain listed above?
(ii) Order the mountains from the highest to lowest.
(iii) What is the difference between the heights of the mountains Anaimudi and Mahendragiri?
Solution:
Arranging the numbers in place value chart.

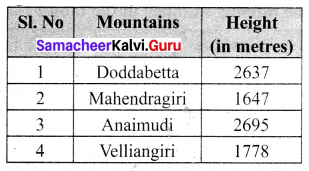
(i) The highest mountain is Anaimudi [Comparing left-most digits]
(ii) From the above chart
In thousands place, Doddabetta and Anaimudi have greater value 2.
Comparing digits of 2637 and 2695
2 = 2, 6 = 6, 3 < 9.
2637 < 2695
Again comparing the digits of 1647 and 1778
1 = 1, 6 < 7
1647 < 1778. The required order is 2695 > 2637 > 1778 > 1647.
Anaimudi > Doddabetta > Veliangiri > Mahendragiri
(iii) The height of Anaimudi mountain = 2695 m
The height of Mahendragiri mountain = 1647 m
The Difference = 1048 m

Objective Type Questions

Question 10.
Which list of numbers is in order from the smallest to the largest?
(a) 1468, 1486, 1484
(b) 2345, 2435, 2235
(c) 134205, 134208, 154203
(d) 383553,383548, 383642
Solution:
(c) 134205, 134208, 154203

Question 11.
The Arabian sea has an area of 1491000 square miles. This area lies between which numbers?
(a) 1489000 and 1492540
(b) 1489000 and 1490540
(c) 1490000 and 1490100
(c) 1480000 and 1490000
Solution:
(a) 1489000 and 1492540
Hint: 1489000 < 1491000 < 1492540

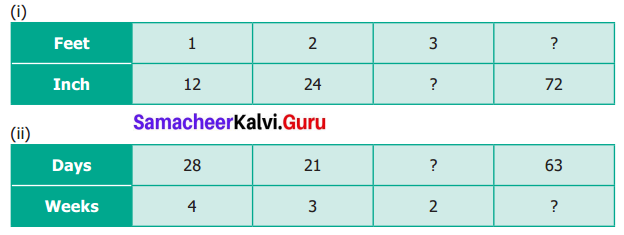
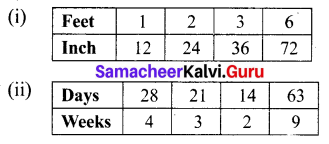
Question 12.
The chart below shows the number of newspapers sold as per the Indian Readership Survey in 2018. Which could be the missing number in the table?

(a) 8
(b) 52
(c) 77
(d) 26
Solution:
(d) 26
Hint: 50 > 26 > 10

You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 3 Chapter 4 Geometry 4.1

Question 1.
Fill in the blanks
i) The reflected image of the letter ‘q’ is ____.
Hint:

Solution:
p

ii) A rhombus has ___ lines of symmetry.
Hint:

Solution:
two

iii) The order of rotational symmetry of the letter ‘Z’ is ___
Solution:
two

iv) A figure is said to have rotational symmetry, if the order of rotation is atleast ___
Solution:
two

v) ___ symmetry occurs when an object slides to new position.
Solution:
Translation

Question 2.
Say True or False
(i) A rectangle has four lines of symmetry.
(ii) A shape has reflection symmetry if it has a line of symmetry.
(iii) The reflection of the name RANI is INAЯ.
(iv) Order of rotation of a circle is infinite.
(v) The number 191 has rotational symmetry.
Solution:
(i) False
(ii) True
(iii) False
(iv) True
(v) False

Question 3.
Match the following shapes with their number of lines of symmetry.

Solution:

Question 4.
Draw the lines of symmetry of the following.

Solution:

Question 5.
Using the given horizontal line / vertical line as a line of symmetry, complete each alphabet to discover the hidden word.

Solution:

Question 6.
Draw a line of symmetry of the given figures such that one hole coincide with the

Solution:
The lines of symmetry to coincide one hole with the other are given below.

Question 7.
Complete the other half of the following figures such that the dotted line is the line of Symmetry.

Solution:
Completing the figures about the line of symmetry we get

Question 8.
Find the order of rotation for each of the following

Solution:

Question 9.
A standard die has six faces which are shown below. Find the order of rotational symmetry of each face of a die?

Solution:
The order of rotational symmetry of all faces of die are given below

Question 10.
What pattern is translated in the given border kolams?

Solution:
The pattern that translated in each diagrams are

Objective Type Questions

Question 11.
Which of the following letter does not have a line of symmetry?
(a) A
(b) P
(c) T
(d) U
Solution:
(b) P

Question 12.
Which of the following is a symmetrical figure?

Hint:
refer eyes
Solution:

Question 13.
Which word has a vertical line of symmetry?
(a) DAD
(b) NUN
(c) MAM
(d) EVE
Solution:
(c) MAM

Question 14.
The order of rotational symmetry of 818 is
(a) 1
(b) 2
(c) 3
(d) 4
Solution:
(b) 2

Question 15.
The order of rotational symmetry of * is ……….
(a) 5
(b) 6
(c) 7
(d) 8
Solution:
(a) 5

You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 1 Chapter 3 Ratio and Proportion Ex 3.3

Question 1.
Fill in the boxes

Solution:
(i) 12
Hint:
5x = 3 × 20 ⇒ x = 12
(ii) 9
8x = 24 × 3 ⇒ x = 9
(iii) 4, 12
Hint:
10x = 8 × 5 = 40 ⇒ x = 4
10y = 8 × 15 = 120 ⇒ y = 12
(iv) 24, 2
Hint:
16y = 8 × 4 ⇒ y = 2
12 × 4 = 2x ⇒ x = 24

Question 2.
Say True or False.
(i) 2 : 7 :: 14 : 4
(ii) 7 Persons is to 49 Persons as 11 kg is to 88 kg.
(iii) 10 books is to 15 books as 3 books is to 15 books.
Solution:
(i) False
(ii) False
(iii) False

Question 3.
Using the numbers 3, 9, 4, 12 write two ratios that are in a proportion.
Solution:
(i) 3, 9, 4, 12
Here product of extremes = 3 × 12 = 36
Product of means = 9 × 4 = 36
3 : 9 :: 4 : 12
(ii) Also if we take 9, 3, 12, 4
Product of extremes = 9 × 4 = 36
Product of means = 3 × 12 = 36
9 : 3 :: 12 : 4

Question 4.
Find whether 12, 24, 18, 36 are in order that can be expressed as two ratios that are in proportion.
Solution:
Yes, they are in proportion
12 : 24 = 18 : 36
\(\frac{12}{24}\) = \(\frac{1}{2}\) Product of means = 24 × 18 = 432
\(\frac{18}{36}\) = \(\frac{1}{2}\) Product of extremes = 12 × 36 = 432
Hence a × d = b × c

Question 5.
Write the mean and extreme terms in the following ratios and check whether they are in proportion.
(i) 78 litres is to 130 litres and 12 bottles are to 20 bottles
(ii) 400 gm is to 50 gm and 25 rupees is to 625 rupees.
Solution:
(i) 78 : 130 :: 12 : 20
Extreme terms are 78 and 20.
Mean terms are 130 and 12.
Product of Extremes = 78 × 20 = 1560
Product of Means = 130 × 12 = 1560
Product of Extremes = Product of means
It is in proportion.
(ii) 400 : 50 :: 25 : 625
Product of extremes = 400 × 625 = 250,000
Product of means = 50 × 25 = 1250
Here product of extremes ≠ product of means
400 : 50 and 25 : 625 are not in proportion.

Question 6.
America’s famous Golden Gate bridge is 6480 ft long with 756 ft tall towers. A model of this bridge exhibited in a fair is 60 ft long with 7 ft tall towers. Is the model in proportion to the original bridge?

Solution:
The ratio of Golden Gate Bridge & Its model are = 6480 : 756
Product of extremes = 6480 × 7 = 45,360
Product of means = 756 x 60 = 45,360
Product of extremes = Product of means
The model is in proportion to the ordinal bridge.

Objective Type Questions

Question 7.
Which of the following ratios are in proportion?
a) 3 : 5, 6 : 11
(b) 2 : 3, 9 : 6
(c) 2 : 5, 10 : 25
(d) 3 : 1, 1 : 3
Solution:
(c) 2 : 5, 10 : 25

Question 8.
If the ratios formed using the numbers 2, 5, x, 20 in the same order are in proportion, then ‘x’ is
(a) 50
(b) 4
(c) 10
(d) 8
Solution:
(d) 8
5x = 2 × 20 ⇒ x = 8

Question 9.
If 7 : 5 is in proportion to x : 25, then ‘x’ is
(a) 27
(b) 49
(c) 35
(d) 14
Solution:
(c) 35

You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 2 Chapter 4 Geometry Ex 4.1

Question 1.
Fill in the blanks.
(a) Every triangle has at least _____ acute angles.
(b) A triangle in which none of the sides equal is called a _____.
(c) In an isosceles triangle ______ angles are equal.
(d) The sum of three angles of a triangle is ______.
(e) A right-angled triangle with two equal sides is called ______.
Solution:
(a) Two
(b) Scalene Triangle
(c) Two
(d) 180°
(e) Isosceles right-angled triangle

Question 2.
Match the following:

Solution:

Question 3.
In ∆ABC, name the

(a) Three sides: ____, _____, _____
(b) Three Angles: _____, _____, _____
(c) Three Vertices: _____, _____, _____
Solution:
(a) \(\overline{\mathrm{AB}}, \overline{\mathrm{BC}}, \overline{\mathrm{CA}}\)
(b) ∠ABC, ∠BCA, ∠CAB or ∠A, ∠B, ∠C
(c) A, B, C

Question 4.
Classify the given triangles based on its sides as scalene, isosceles or equilateral.

Solution:
(i) Equilateral Triangle
(ii) Scalene Triangle
(iii) Isosceles Triangle
(iv) Scalene Triangle

Question 5.
Classify the given triangles based on its angles as acute-angled, right-angled or obtuse-angled.

Solution:
(i) Acute angled triangle
(ii) Right angled triangle
(iii) Obtuse angled triangle
(iv) Acute angled triangle

Question 6.
Classify the following triangles based on its sides and angles.

Solution:
(i) Isosceles Acute angled triangle
(ii) Scalene Right angled triangle
(iii) Isosceles Obtuse angled triangle
(iv) Isosceles Right angled triangle
(v) Equilateral Acute angled triangle
(vi) Scalene Obtuse angled triangle

Question 7.
Can a triangle be formed with the following sides? If yes, name the type of triangle.
(i) 8 cm, 6 cm, 4 cm
(ii) 10 cm, 8 cm, 5 cm
(iii) 6.2 cm, 1.3 cm, 3.5 cm
(iv) 6 cm, 6 cm, 4 cm
(v) 3.5 cm, 3.5 cm, 3.5 cm
(vi) 9 cm, 4 cm, 5 cm
Solution:
(i) Sum of two smaller sides of the triangle
= 6 + 4 = 10 cm > 8 cm
It is greater than the third side. So, a triangle can be formed scalene triangle.

(ii) Sum of two smaller sides of the triangle
= 8 + 5 = 13 cm > 10 cm
It is greater than the third side. So, a triangle can be formed scalene triangle.

(iii) Sum of two smaller sides of the triangle
= 1.3 + 3.5 = 4.8 cm < 6.2 cm
It is not greater than the third side. So, a triangle cannot be formed.

(iv) Two sides are equal.
So, a triangle can be formed. Isosceles triangle.

(v) Three sides are equal.
So, a triangle can be formed equilateral triangle.

(vi) Sum of two smaller sides of the triangle
= 4 + 5 = 9 cm = 9 cm
It is equal to the third side. No, a triangle cannot be formed.

Question 8.
Can a triangle be formed with the following angles? if yes, name the type of triangle.
(i) 60°, 60°, 60°
(ii) 90°, 55°, 35°
(iii) 60°, 40°, 42°
(iv) 60°, 90°, 90°
(v) 70°, 60°, 50°
(vi) 100°, 50°, 30°
Solution:
(i) 60°, 60°, 60°
Sum of three angles = 60° + 60° + 60° = 180°
Yes, a triangle can be formed.
∴ It is Acute angled triangle. [∵ all the angles < 90°]

(ii) 90°, 55°, 35°.
Sum of three angles = 90° + 55° + 55° = 180°
Yes, a triangle can be formed.
∴ It is a right-angled triangle, [∵ one angle is 90°]

(iii) 60°, 40°, 42°.
Sum of three angles = 60° + 40° + 42° = 142° ≠ 180°
No, The triangle cannot be formed.

(iv) 60°, 90°, 90°.
Sum of three angles = 60° + 90° + 90° = 240° ≠ 180°
∴ No, The triangle cannot be formed. [∵ one angle is > 90°]

(v) 70°, 60°, 50°.
Sum of three angles = 70° + 60° + 50° = 180°
Yes, A triangle can be formed.
∴ It is an acute-angled triangle.

(vi) 100°, 50°, 30°.
Sum of three angles = 100° + 50° + 30° = 180°
Yes, A triangle can be formed.
∴ It is an obtuse-angled triangle.

Question 9.
Two angles of the triangles are given. Find the third angle.
(i) 80°, 60°
(ii) 52°, 68°
(iii) 75°, 35°
(iv) 50°, 90°
(v) 120°, 30°
(vi) 55°, 85°
Solution:
(i) 80°, 60°
Let the third angle be x.
Sum of the angles = 180°
80° + 60° + x = 180°
140 + x = 180°
x = 180°- 140°
x = 40°
Third angle = 40°

(ii) 52°, 68°
Let the third angle be x.
Sum of the angles = 180°
52° + 68° + x = 180°
120 + x = 180°
180° – 120°
x = 60°
Third angle = 60°

(iii) 75°, 35°
Let the third angle be x.
Sum of the angles 180°
75° + 35° + x = 180°
110 + x = 180°
x = 180° – 110°
x = 70°
Third angle = 70°

(iv) 50°, 90°
Let the third angle be x. Sum of the angles = 180°
50° + 90° + x = 180°
140 + x = 180°
x = 180° – 140°
x = 40°
Third angle = 40°

(v) 120°, 30°
Let the third angle be x.
Sum of the angles = 180°
120° + 30° + x = 180°
150 + x = 180°
x = 180° – 150°
x = 30°
Third angle = 30°

(vi) 55°, 85°
Let the third angle be x.
Sum of the angles = 180°
55° + 85° + x = 180°
140 + x = 180°
x = 180° – 140°
x = 40°
Third angle = 40°

Question 10.
I am a closed figure with each of my three angles is 60°. Who am I?
Solution:
Equilateral Triangle.

Question 11.
Using the given information, write the type of triangle in the table given below.

Solution:

Objective Type Questions

Question 12.
The given triangle is _____.

(a) a right angled triangle
(b) an equilateral triangle
(c) a scalene triangle
(d) an obtuse angled triangle
Solution:
(b) an equilateral triangle

Question 13.
If all angles of a triangle are less than a right angle, then it is called ……….
(a) an obtuse angled triangle
(b) a right angled triangle
(c) an isosceles right angled triangle
(d) an acute angled triangle
Solution:
(d) an acute angled triangle

Question 14.
If two sides of a triangle are 5 cm and 9 cm then the third side is _____.
(a) 5 cm
(b) 3 cm
(c) 4 cm
(d) 14 cm
Solution:
(a) 5 cm

Question 15.
The angles of a right angled triangle are
(a) acute, acute, obtuse
(b) acute, right, right
(c) right, obtuse, acute
(d) acute, acute, right
Solution:
(d) acute, acute, right

Question 16.
An equilateral triangle is
(a) an obtuse-angled triangle
(b) a right-angled triangle
(c) an acute-angled triangle
(d) scalene triangle
Solution:
(c) an acute-angled triangle

Read More:

HDFCAMC Pivot Point Calculator

You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 2 Chapter 4 Geometry Ex 4.3

Miscellaneous Practice Problems

Question 1.
What are the angles of an isosceles right-angled triangle?
Solution:
Since it is a right-angled triangle
One of the angles is 90°
Other two angles are equal because it is an isosceles triangle.
Other two angles must be 45° and 45°
Angles are 90°, 45°, 45°.

Question 2.
Which of the following correctly describes the given triangle.

(a) It is a right isosceles triangle.
(b) It is an acute isosceles triangle.
(c) It is an obtuse isosceles triangle.
(d) it is an obtuse scalene triangle.
Solution:
(c) It is an obtuse isosceles triangle.

Question 3.
Which of the following is not possible?
(a) An obtuse isosceles triangle
(b) An acute isosceles triangle
(c) An obtuse equilateral triangle
(d) An acute equilateral triangle
Solution:
(c) an obtuse equilateral triangle

Question 4.
If one angle of an isosceles triangle is 124°, then find the other angles.
Solution:
In an isosceles triangle, any two sides are equal. Also, two angles are equal.
Sum of three angles of a triangle = 180°
Given one angle = 124°
Sum of other two angles = 180° – 124° = 56°
Other angles are = \(\frac{56}{2}\) = 28°
28° and 28°.

Question 5.
The diagram shows a square ABCD. If the line segment joints A and C, then mention the type of triangles so formed.

Solution:
For a square all sides are equal and each angle is 90°.
∆ABC and ∆ADC are isosceles right-angled triangles.

Question 6.
Draw a line segment AB of length 6 cm. At each end of this line segment AB, draw a line perpendicular to the line AB. Are these lines parallel?
Solution:
Here CA and DB are perpendicular to AB.
Yes CA and DB are parallel.

Construction:
(i) Drawn a line segment AB of length 6 cm.
(ii) Place the set square on the line in such a way that the vertex of its right angle coincides with B first and A next and one arm of the right angle coincides with the line AB.
(iii) Drawn lines DB and CA through B and A, the other arm of the right angle of the set square.
(iv) The line CA and DB are perpendicular to AB at A and B.

Challenge Problems

Question 7.
Is a triangle possible with the angles 90°, 90° and 0°? Why?
Solution:
No, a triangle cannot have more than one right angle

Question 8.
Which of the following statements is true. Why?
(a) Every equilateral triangle is an isosceles triangle.
(b) Every isosceles triangle is an equilateral triangle.
Solution:
(a) It is true
In an equilateral triangle, all three sides are equal.
It can be an isosceles triangle also, which has two sides equal.
(b) But every isosceles triangle need not be an equilateral triangle.

Question 9.
If one angle of an isosceles triangle is 70°, then find the possibilities for the other two angles.
Solution:
70°, 40° (or) 55°, 55°

Question 10.
Which of the following can be the sides of an isosceles triangle?
(a) 6 cm, 3 cm, 3 cm
(b) 5 cm, 2 cm, 2 cm
(c) 6 cm, 6 cm, 7 cm
(d) 4 cm, 4 cm, 8 cm
Solution:
In a triangle sum of any two sides greater than the third side
(a), (b) and (d) cannot form a triangle.
(c) can be the sides of an isosceles triangle.

Question 11.
Study the given figure and identify the following triangles.

(a) equilateral triangle
(b) isosceles triangles
(c) scalene triangles
(d) acute triangles
(e) obtuse triangles
(f) right triangles
Solution:
(a) BC = 1 + 1 + 1 + 1 = 4 cm
AB = AC = 4 cm
∆ABC is an equilateral triangle.
(b) ∆ABC and ∆AEF are isosceles triangles.
Since AB = AC = 4 cm Also AE = AF.
(c) In a scalene triangle, no two sides are equal.
∆AEB, ∆AED, ∆ADF, ∆AFC, ∆ABD, ∆ADC, ∆ABF and ∆AEC are scalene triangles.
(d) In an acute-angled triangle all the three angles are less than 90°.
∆ABC, ∆AEF, ∆ABF and ∆AEC are acute-angled triangles.
(e) In an obtuse-angled triangle any one of the angles is greater than 90°.
∆AEB and ∆AFC are obtuse angled triangles.
(f) In a right triangle, one of the angles is 90°.
∆ADB, ∆ADC, ∆ADE and ∆ADF are right-angled triangles.

Question 12.
Two sides of the triangle are given in the table. Find the third side of the triangle?

Solution:

Question 13..
Complete the following table.

Solution:

(i) Always acute angles
(ii) Acute angle
(iii) Obtuse angle

You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 1 Chapter 3 Ratio and Proportion Ex 3.2

Question 1.
Fill in the blanks of the given equivalent ratios.
(i) 3 : 5 = 9 : ___
(ii) 4 : 5 = ___ : 10
(iii) 6 : ____ = 1 : 2
Solution:
(i) 15
Hint: \(\frac{3}{5}=\frac{3 \times 3}{5 \times 3}=\frac{9}{15}\)
(ii) 8
Hint: \(\frac{4}{5}=\frac{4 \times 2}{5 \times 2}=\frac{8}{10}\)
(iii) 12
Hint: \(\frac{1}{2}=\frac{1 \times 6}{2 \times 6}=\frac{6}{12}\)

Question 2.
Complete the Table:

Solution:

Question 3.
Say True or False.
(i) 5 : 7 is equivalent to 21 : 15.
(ii) If 40 is divided in the ratio 3 : 2, then the larger part is 24.
Solution:
(i) False
(ii) True

Question 4.
Give two equivalent ratios for each of the following.
(i) 3 : 2
(ii) 1 : 6
(iii) 5 : 4
Solution:

Question 5.
Which of the two ratios is larger?
(i) 4 : 5 or 8 : 15
(ii) 3 : 4 or 7 : 8
(iii) 1 : 2 or 2 : 1
Solution:

Question 6.
Divide the numbers given below in the required ratio.
(i) 20 in the ratio 3 : 2
(ii) 27 in the ratio 4 : 5
(iii) 40 in the ratio 6 : 14
Solution:
(i) Ratio = 3 : 2
Sum of the ratio = 3 + 2 = 5
5 parts = 20
1 part = \(\frac{20}{5}\)
= 4
3 parts = 3 × 4 = 12
2 parts = 2 × 4 = 8
20 can be divided in the form as 12, 8.

(ii) Ratio = 4 : 5
Sum of the ratio = 4 + 5 = 9
9 parts = 27
1 part = \(\frac{27}{9}\) = 3
4 parts = 4 × 3 = 12
5 parts = 5 × 3 =15
27 can be divided in the form as 12, 15.

(iii) 40 in the ratio 6 : 14
Ratio = 6 : 14
Sum of the ratio = 6 + 14 = 20
20 parts = 40
1 part = \(\frac{40}{20}\) = 2
6 parts = 2 × 6 = 12
14 parts = 2 × 14 = 28
40 can be divided in the form as 12, 28.

Question 7.
In a family, the amount spent in a month for buying Provisions and Vegetables are in the ratio 3 : 2. If the allotted amount is ₹ 4000, then what will be the amount spent for
(i) Provisions and
(ii) Vegetables?
Solution:
Dividing the total amount ₹ 4000 into 3 + 2 = 5 equal parts then
(i) For Provisions:
3 out of 5 parts are spent for provisions and 2 out of 5 parts for vegetables.
\(4000 \times \frac{3}{5}=2400\) for provisions
(ii) For vegetables:
\(4000 \times \frac{2}{5}=1600\) for Vegetables.
₹ 2400 spend on provisions and ₹ 1600 spend on Vegetables.

Question 8.
A line segment 63 cm long is to be divided into two parts in the ratio 3 : 4. Find the length of each part.
Solution:
Total length = 63 cm Ratio = 3 : 4
Sum of the ratio = 3 + 4 = 7
7 parts = 63 cm
1 part = \(\frac{63}{7}\) = 9 cm
3 parts = 3 × 9 cm = 27 cm
4 parts = 4 × 9 cm = 36 cm
∴ 63 cm can be divided into the parts as 27 cm and 36 cm.

Objective Type Questions

Question 9.
If 2 : 3 and 4 : ___ or equivalent ratios, then the missing term is ____
(a) 6
(b) 2
(c) 4
(d) 3
Solution:
(a) 6
Hint: \(\frac{2}{3}=\frac{2 \times 2}{3 \times 2}=\frac{4}{6}\)

Question 10.
An equivalent ratio of 4 : 7 is
(a) 1 : 3
(b) 8 : 15
(c) 14 : 8
(d) 12 : 21
Solution:
(d) 12 : 21

Question 11.
Which is not an equivalent ratio of \(\frac{16}{24}\) ?
(a) \(\frac{6}{9}\)
(b) \(\frac{12}{18}\)
(c) \(\frac{10}{15}\)
(d) \(\frac{20}{28}\)
Solution:
(d) \(\frac{20}{28}\)
Hint: \(\frac{16}{24}=\frac{8 \times 2}{8 \times 3}=\frac{2}{3}\)

Question 12.
If Rs 1600 is divided
(a) Rs 480
(b) Rs 800
(c) Rs 1000
(d) Rs 200
Solution:
(c) Rs 1000

You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 1 Chapter 4 Geometry Ex 4.3

Question 1.
Observe the diagram and fill the blanks.

(i) ‘A’, ‘O’ and ‘B’ are ______ points
(ii) ‘A’, ‘O’ and ‘C’ are ______ points
(iii) ‘A’ ‘B’ and ‘C’ are _____ points
(iv) ______ is the point of concurrency
Solution:
(i) collinear points
Hint: Points on a line.
(ii) non collinear points
Hint: Points not on a line
(iii) end points/non collinear points
(iv) O is the point of concurrency.
Hint: A points where lines meet

Question 2.
Draw any line and mark any 3 points that are collinear.
Solution:

L, M, N are collinear points

Question 3.
Draw any line and mark any 4 points that are not collinear.
Solution:

X, Y, Z and A are non-collinear points.

Question 4.
Draw any 3 lines to have a point of concurrency.
Solution:

l₁, l₂ and l₃ are the concurrent lines.
‘O’ is the point of concurrency.

Question 5.
Draw any 3 lines that are not concurrent. Find the number of points of intersection.
Solution:

l₁, l₂ and l₃ are non concurrent lines.
A, B and C are the 3 points of intersection.
There are two points of intersection X and Y

Objective Type Questions

Question 6.
A set of collinear points in the figure are ……….
(a) A. B, C
(b) A, F, C
(c) B, C, D
(d)A,C,D
Solution:
(b) A, F, C

Question 7.
A set of non-collinear points in the figure are _____
(a) A, F, C
(b) B, F, D
(c) E, F, G
(d) A, D, C
Solution:
(d) A, D, C
Hint: Non-collinear points are points which are not on a line.

Question 8.
A point of concurrency in the figure is ……..
(a) E
(b) F
(c) G
(d) H
Solution:
(b) F

You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 1 Chapter 1 Numbers Ex 1.1

Question 1.
Fill in the blanks.

1. The smallest 7 digit number is _______
2. The largest 8 digit number is _______
3. The place value of 5 in 7005380 is ________
4. The expanded form of the number 76,70,905 is _______

Solution:

1. 10,00,000
2. 9,99,99,999
3. 5 × 1000 = 5000
4. 7 × 10,00,000 + 6 × 1,00,000 + 7 × 10,000 + 0 + 9 × 100 + 0 + 5 × 1
   (or)
   70,00,000 + 6,00,000 + 70,000 + 900 + 5

Question 2.
Say True or False.

1. In the Indian System of Numeration, the number 67999037 is written as 67999037
2. The successor of a one-digit number is always a one-digit number.
3. The predecessor of a 3-digit number is always a 3 or 4-digit number.
4. 88888 = 8 × 10000 + 8 × 100 + 8 × 10 + 8 × 1

Solution:

1. True
2. False
3. False
4. False

Question 3.
Complete the given order.
Ten crore, crore, ten lakh, ____, ____, _____ , _____, _____.
Solution:
Ten crores, Crore, Ten lakh, Lakh, Ten Thousand, Thousand, Hundred, Ten, One

Question 4.
How many ten thousands are there in the smallest 6 digit number?
Solution:
Smallest six-digit number is 1,00,000
1 lakh = Ten Thousand
Another Method:
Lakh is only one place to the left of Ten thousand
1 lakh is 10 times ten thousand

1 lakh = Ten-Ten Thousand

Question 5.
Using the digits 5, 2, 0, 7, 3 forms the largest 5 digit number and the smallest 5 digit number.
Solution:
Given digits = 5, 2, 0, 7, 3
Largest 5 digit number – 75320
Smallest 5 digit number – 20357

Question 6.
Observe the commas and write down the place value of 7.

1. 56,74,56,345
2. 567,456,345

Solution:

1. 56,74,56,345
   Place value of 7 is 7 × 10,00,000 = 70,00,000 = Seventy Lakhs.
2. 567,456,345
   Place value of 7 is 7 × 1,000,000 = 7,000,000 = Seven Million.

Question 7.
Write the following numbers in the International system by using commas.
(i) 347056
(ii) 7345671
(iii) 634567105
(iv) 1234567890
Solution:

Question 8.
Write the largest six-digit number and put commas in the Indian and the International Systems.
Solution:
The largest six-digit number is 999999

Question 9.
Write the number names of the following numerals in the Indian System.
(i) 75,32,105
(ii) 9,75,63,453
Solution:
(i) 75,32,105

Seventy-Five Lakhs Thirty-Two Thousand One Hundred and Five
(ii) 9,75,63,453

Nine crores Seventy Five Lakhs Sixty Three Thousand Four Hundred and Fifty-Three.

Question 10.
Write the number names in words using the International System
(i) 345,678
(ii) 8,343,710
(iii) 103,456,789
Solution:
(i) 345,678

Three Hundred and Forty-Five Thousand Six Hundred and Seventy-Eight
(ii) 8,343,710

Eight Million Three Hundred and Forty-Three Thousand Seven Hundred and Ten.
(iii) 103,456,789

One Hundred Three Million Four Hundred Fifty-Six Thousand Seven Hundred and Eighty’ Nine.

Question 11.
Write the number name in numerals.

1. Two crores thirty lakhs fifty-one thousand nine hundred eighty.
2. Sixty-six million three hundred forty-five thousand twenty-seven.
3. Seven hundred eighty-nine million, two hundred thirteen thousand four hundred fifty six.

Solution:

1. 2,30,51,980
2. 66,345,027
3. 789,213,456

Question 12.
Tamil Nadu has about twenty-six thousand three hundred forty-five square kilometre of Forest land. Write the number mentioned in the statement in the Indian System.
Solution:
26,345 sq km.

Question 13.
The number of employees in the Indian Railways is about 10 lakhs. Write this in the International System of numeration.
Solution:
1.000,000 (one million)

Objective Type Questions

Question 14.
1 billion is equal to
(a) 100 crore
(b) 100 million
(c) 100 lakh
(d) 10000 lakh
Solution:
(a) 100 crore

Question 15.
The successor of 10 million is
(a) 1000001
(b) 10000001
(c) 9999999
(d) 100001
Solution:
(b) 10000001

Question 16.
The difference between successor and predecessor of 99999 is
(a) 90000
(b) 1
(c) 2
(d) 99001
Solution:
(c) 2

Question 17.
The expanded form of the number 6,70,905 is
(a) 6 × 10000 + 7 × 1000 + 9 × 100 + 5 × 1
(b) 6 × 10000 + 7 × 1000 + 0 × 100 + 9 × 100 + 0 × 10 + 5 × 1
(c) 6 × 1000000 + 7 × 10000 + 0 × 1000 + 9 × 100 + 0 × 10 + 5 × 1
(d) 6 × 100000 + 7 × 10000 + 0 × 1000 + 9 × 100 + 0 × 10 + 5 × 1
Solution:
(d) 6 × 100000 + 7 × 10000 + 0 × 1000 + 9 × 100 + 0 × 10 + 5 × 1

You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 2 Chapter 2 Measurements Ex 2.1

Question 1.
Fill in the blanks.
(i) 250 ml + \(\frac{1}{2}\) ml = _____ l.
(ii) 150 kg 200 g + 55 kg 750 g = ____ kg ____ g.
(iii) 20 l – 1 l 500 ml = ____ l ___ ml
(iv) 450 ml × 5 = ____ l ____ ml.
(v) 50 Kg ÷ 100 g = ______
Solution:
(i) \(\frac{3}{4}\) l
(ii) 205 kg 950 g
(iii) 18 l 500 ml
(iv) 2l 250 ml
(v) 500

Question 2.
True or False
(i) Pugazhenthi ate 100 g of nuts which is equal to 0.1 kg.
(ii) Meena bow it 250 ml of butter milk which is equal to 2.5 l.
(iii) Karkuzhali’s bag 1 kg 250 g and poong- kodi’s bag 2 kg 750 g. The total weight of their bags 4 kg.
(iv) Vanmathi bought 4 books each weighing 500 g. Total weight of 4 books is 2 kg.
(v) Gayathiri bought 1 kg of birthday cake. She shared 450 g with her friends.
The weight of cake remaining is 650 g
Solution:
(i) True
(ii) False
(iii) True
(iv) True
(v) False

Question 3.
Convert into indicated units:
(i) 10 l and 5 ml into ml
(ii) 4 km and 300 m into m
(iii) 300 mg into g
Solution:
(i) 10 l and 5 ml
= 10 × 1000 ml + 5 ml
= 10,000 ml + 5 ml [∴ 1l = 1000 ml]
= 10,005 ml.
∴ 10 l and 5 ml = 10,005 ml.
(ii) 4 km and 300 m into m.
4 km and 300 m
= 4 × 1000 m + 300 m
= 4000 m + 300 m [∴ 1 km = 1000 m]
= 4300 m
∴ 4 km and 300 m = 4300 m
(iii) 300 mg into g.

Question 4.
Convert into higher units:
(i) 13000 mm (km, m, cm)
(ii) 8257 ml (kl, l)
Solution:
(i) 13000 mm (km, m, cm)
(ii) 8257 ml (kl, l)

Question 5.
Convert into lower units:
(i) 15 km (m, cm, mm)
Solution:
15 km = 15 × 1000 m = 15000 m
15 km = 15 × 100000 cm
= 1500000 cm
15 km = 15 × 1000000 mm
= 15000000 mm

(ii) 12 kg (g, mg)
Solution:
12 kg = 12 × 1000 g
= 12000 g
12 kg = 12 × 1000000 mg
= 12000000 mg

Question 6.
Compare and put > or < or = in the following:
(i) 800 g + 150 g ____ 1 kg
(ii) 600 ml + 400 ml ____ 1 l
(iii) 6 m 25 cm ____ 600 cm + 25 cm
(iv) 88 cm ____ 8 m 8 cm
(v) 55 g ____ 550 mg
Solution:
(i) 800 g + 150g < 3kg
(ii) 600 ml + 400 ml = 1 l
(iii) 6 m 25 cm = 600 cm + 25 cm
(iv) 88 cm < 8 m 8 cm
(v) 55 g > 550 mg

Question 7.
Geetha brought 2 l and 250 ml of water in a bottle. Her friend drank 300 ml from it. How much of water is remaining in the bottle?
Solution:
Total Capacity of water = 2 l 250 ml
= (2 x 1000 + 250) l
= 2000 + 250 ml
= 2250 ml
Water Consumed = 300 ml
Water remaining in the bottle = (2250 – 300) ml
= 1950 ml
= 1 litre 950 ml

Question 8.
Thenmozhi’s height is 1.25 m now. She grows for 5 cm every year. What would be her height after 6 years?
Solution:
Thenmozhi’s present height = 1.25 m
Rate of growth per year = 5 cm
Her growth in 6 years = 5 cm × 6 = 30 cm.
After 6 years her height = 1.25 m + 30 cm
= 1.25 × 100 + 30 cm
= 125 + 30 cm
= 155 cm.
∴ After 6 years Thenmozhi’s height will be 155 cm.

Question 9.
Priya bought 22 \(\frac{1}{2}\) kg of onion/ Krishna bought 18 \(\frac{3}{4}\) kg of onion and sethu bought 9 kg 250 g of onion, what is the total weight of onion did they buy?
Solution:
Total weight of onion bought
= 22 \(\frac{1}{2}\) + 18 \(\frac{3}{4}\) + 9 \(\frac{1}{4}\) kg
= 22 kg 500 g + 18 kg 750 g + 9 kg 250 g
= 49 kg 1500 g
= 50 kg 500 g

Question 10.
Maran walks 1.5 km every day to reach the school while Mahizhan walks 1400 m. Who walks more distance and by how much?
Solution:
Distance which Maran walks = 1.5 km = 1.5 × 1000 m = 1500 m
The distance which Mahizhan walks = 1400 m.
Here 1500 > 1400
∴ Difference = 1500 – 1400 = 100 m.
∴ Maran walks more distance = 100 m.

Question 11.
In a JRC one day camp, 150 gm of rice and 15 ml oil are needed for a student. If there are 40 students to attend the camp how much of rice and oil are needed?
Solution:
Rice needed for a student = 150 gm
Rice needed for 40 students = 40 × 150 gm = 6000 gm = 6 kg
Oil needed for a student = 15 ml
Oil needed for 40 students = 40 × 15 ml = 600 ml

Question 12.
In a school, 200 litres of lemon juice is prepared. If 250 ml lemon juice is given to each student, how many students get the juice?
Solution:
Total lemon juice prepared = 200 l = 200 × 1000 ml = 2,00,000 ml.
∴ Quantity of Lemon juice given to one student = 250 ml.
∴ Number of students can get = \(\frac{2,00,000}{250}\) = 800
∴ 800 students can get the lemon juice.

Question 13.
How many glasses of the given capacity will fill a 2 litre jug?
(i) 100 ml ……….
(ii) 50 ml ……….
(iii) 500 ml ………
(iv) 1 l ………
(v) 250 ml ………
Solution:
(i) 20
(ii) 40
(iii) 4
(iv) 2
(v) 8

Objective Type Questions

Question 14.
9 m 4 cm is equal to _____
(a) 94 cm
(b) 904 cm
(c) 9.4 cm
(d) 0.94 cm
Solution:
(b) 904 cm

Question 15.
1006 g is equal to ………
(i) 1 kg 6 g
(ii) 10 kg 6 g
(iii) 100 kg 6 g
(iv) 1 kg 600 g
Solution:
(i) 1 kg 6 g

Question 16.
Every day 150 l of water is sprayed in the garden. Water sprayed in a week is ____
(a) 700 l
(b) 1000 l
(c) 950 l
(d) 1050 l
Solution:
(d) 1050 l

Question 17.
Which is the greatest? 0.007 g, 70 mg, 0.07 cg ……….
(i) 0.07 cg
(ii) 0.007 g
(iii) 70 mg
(iv) all are equal
Solution:
(iii) 70 mg

Question 18.
7 km – 4200 m is equal to
(a) 3 km 800 m
(b) 2 km 800 m
(c) 3 km 200 rn
(d) 2 km 200 m
Solution:
(b) 2 km 800 m

You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 1 Chapter 4 Geometry Ex 4.2

Question 1.
Use any number of the given dots to make different angles.

Solution:

Question 2.
Name the vertex and sides that form each angle.

Solution:

Question 3.
Pick out the Right angles from the given figures.

Solution:
(i), (iii) and (v) are Right Angles.

Question 4.
Pick out the Acute angles from the given figures.

Solution:
(i), (iii) and (iv) are the Acute Angles.

Question 5.
Pick out the Obtuse Angles from the given figures.

Solution:
(i) and (ii) are the Obtuse Angles.

Question 6.
Name the angle in each figure given below in all the possible ways.

Solution:
(i) ∠M or ∠LMN or ∠NML
(ii) ∠Q or ∠PQR or ∠RQP
(iii) ∠N or ∠MNO or ∠ONM
(iv) ∠A or ∠TAS or ∠SAT
(v) ∠Y or ∠XYZ or ∠ZYX
(vi) There are 3 angles in (vi)

• ∠ADC or ∠CDA
• ∠ CDB or ∠BDC
• ∠D or ∠ADB or ∠BDA

Question 7.
Say True or False.

1. 20° and 70° are complementary.
2. 88° and 12° are complementary.
3. 80° and 180° are supplementary.
4. 0° and 180° are supplementary.

Solution:

1. True
2. False
3. False
4. True

Question 8.
Draw and label each of the angles
(i) ∠NAS = 90°
(ii) ∠BLG = 35°
(iii) ∠SMC = 145°
Solution:

Question 9.
Identify the types of angles shown by the hands of the given clock.

Solution:
(i) Obtuse Angle.
(ii) Zero Angle.
(iii) Straight Angle.
(iv) Acute Angle.
(v) Right Angle.

Question 10.
Find the supplementary ‘l’ complementary angles in each case.

Solution:
(i) If two angles add up to 180°, they are supplementary.
We know that the straight angle ∠CBC = 180°
Given ∠CBD = 25°
∴ ∠DBA = 180° – 25° = 155°
∴ Supplementary ∠DBA = 155°

(ii) If two angles add upto 90°, they are complementary
Given ∠ABC = 25°
∠CBD = 30°
∴ ∠DBA = 90° – 30° = 60°
∴ Complementary angle ∠DBA = 60°

(iii) Given ∠CBA = 90°
∠CBD = 46°
∴ ∠DBA = 90° – 46° = 44°
We know that the sum of two angles is 90°, then they are complementary
∴ Complementary angle ∠DBA = 44°

(iv) Given ∠DBE = 180°
∠DBC = 67°
∴ ∠CBE = 180° – 67° = 113°
Here ∠DBC + ∠DBE = 180°
∴ Supplementary angle ∠CBE = 113°

Objective Type Questions

Question 11.
In this Figure, which is not the correct way of naming an angle?

(a) ∠Y
(b) ∠ZXY
(c) ∠ZYX
(d) ∠XYZ
Solution:
(b) ∠ZXY

Question 12.
In this Figure, ∠AYZ = 45°. If the point ‘A’ is shifted to point ‘B’ along the ray, then the measure of ∠BYZ is ____

(a) more than 45°
(b) 45°
(c) less than 45°
(d) 90°
Solution:
(b) 45°
Hint: ∠XYZ = ∠BYZ = ∠AYZ