You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
![]()
Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 2 Chapter 4 Geometry Ex 4.3
Miscellaneous Practice Problems
Question 1.
What are the angles of an isosceles right-angled triangle?
Solution:
Since it is a right-angled triangle
One of the angles is 90°
Other two angles are equal because it is an isosceles triangle.
Other two angles must be 45° and 45°
Angles are 90°, 45°, 45°.
Question 2.
Which of the following correctly describes the given triangle.
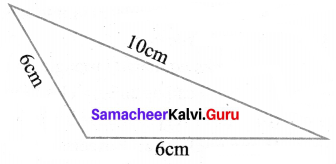
(a) It is a right isosceles triangle.
(b) It is an acute isosceles triangle.
(c) It is an obtuse isosceles triangle.
(d) it is an obtuse scalene triangle.
Solution:
(c) It is an obtuse isosceles triangle.
Question 3.
Which of the following is not possible?
(a) An obtuse isosceles triangle
(b) An acute isosceles triangle
(c) An obtuse equilateral triangle
(d) An acute equilateral triangle
Solution:
(c) an obtuse equilateral triangle
![]()
Question 4.
If one angle of an isosceles triangle is 124°, then find the other angles.
Solution:
In an isosceles triangle, any two sides are equal. Also, two angles are equal.
Sum of three angles of a triangle = 180°
Given one angle = 124°
Sum of other two angles = 180° – 124° = 56°
Other angles are = \(\frac{56}{2}\) = 28°
28° and 28°.
Question 5.
The diagram shows a square ABCD. If the line segment joints A and C, then mention the type of triangles so formed.
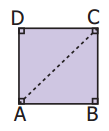
Solution:
For a square all sides are equal and each angle is 90°.
∆ABC and ∆ADC are isosceles right-angled triangles.
Question 6.
Draw a line segment AB of length 6 cm. At each end of this line segment AB, draw a line perpendicular to the line AB. Are these lines parallel?
Solution:
Here CA and DB are perpendicular to AB.
Yes CA and DB are parallel.

Construction:
(i) Drawn a line segment AB of length 6 cm.
(ii) Place the set square on the line in such a way that the vertex of its right angle coincides with B first and A next and one arm of the right angle coincides with the line AB.
(iii) Drawn lines DB and CA through B and A, the other arm of the right angle of the set square.
(iv) The line CA and DB are perpendicular to AB at A and B.
![]()
Challenge Problems
Question 7.
Is a triangle possible with the angles 90°, 90° and 0°? Why?
Solution:
No, a triangle cannot have more than one right angle
Question 8.
Which of the following statements is true. Why?
(a) Every equilateral triangle is an isosceles triangle.
(b) Every isosceles triangle is an equilateral triangle.
Solution:
(a) It is true
In an equilateral triangle, all three sides are equal.
It can be an isosceles triangle also, which has two sides equal.
(b) But every isosceles triangle need not be an equilateral triangle.
Question 9.
If one angle of an isosceles triangle is 70°, then find the possibilities for the other two angles.
Solution:
70°, 40° (or) 55°, 55°
Question 10.
Which of the following can be the sides of an isosceles triangle?
(a) 6 cm, 3 cm, 3 cm
(b) 5 cm, 2 cm, 2 cm
(c) 6 cm, 6 cm, 7 cm
(d) 4 cm, 4 cm, 8 cm
Solution:
In a triangle sum of any two sides greater than the third side
(a), (b) and (d) cannot form a triangle.
(c) can be the sides of an isosceles triangle.
Question 11.
Study the given figure and identify the following triangles.
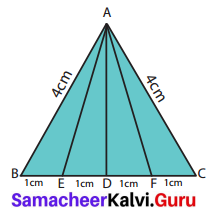
(a) equilateral triangle
(b) isosceles triangles
(c) scalene triangles
(d) acute triangles
(e) obtuse triangles
(f) right triangles
Solution:
(a) BC = 1 + 1 + 1 + 1 = 4 cm
AB = AC = 4 cm
∆ABC is an equilateral triangle.
(b) ∆ABC and ∆AEF are isosceles triangles.
Since AB = AC = 4 cm Also AE = AF.
(c) In a scalene triangle, no two sides are equal.
∆AEB, ∆AED, ∆ADF, ∆AFC, ∆ABD, ∆ADC, ∆ABF and ∆AEC are scalene triangles.
(d) In an acute-angled triangle all the three angles are less than 90°.
∆ABC, ∆AEF, ∆ABF and ∆AEC are acute-angled triangles.
(e) In an obtuse-angled triangle any one of the angles is greater than 90°.
∆AEB and ∆AFC are obtuse angled triangles.
(f) In a right triangle, one of the angles is 90°.
∆ADB, ∆ADC, ∆ADE and ∆ADF are right-angled triangles.
![]()
Question 12.
Two sides of the triangle are given in the table. Find the third side of the triangle?

Solution:

Question 13..
Complete the following table.

Solution:

(i) Always acute angles
(ii) Acute angle
(iii) Obtuse angle