You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
![]()
Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 2 Chapter 4 Geometry Ex 4.1
Question 1.
Fill in the blanks.
(a) Every triangle has at least _____ acute angles.
(b) A triangle in which none of the sides equal is called a _____.
(c) In an isosceles triangle ______ angles are equal.
(d) The sum of three angles of a triangle is ______.
(e) A right-angled triangle with two equal sides is called ______.
Solution:
(a) Two
(b) Scalene Triangle
(c) Two
(d) 180°
(e) Isosceles right-angled triangle
Question 2.
Match the following:
| (i) No sides are equal | Isosceles triangle |
| (ii) One right angle | Scalene triangle |
| (iii) One obtuse angle | Right-angled triangle |
| (iv) Two sides of equal length | Equilateral triangle |
| (v) All sides are equal | Obtuse angled triangle |
Solution:
| (i) No sides are equal | Scalene triangle |
| (ii) One right angle | Right-angled triangle |
| (iii) One obtuse angle | Obtuse angled triangle |
| (iv) Two sides of equal length | Isosceles triangle |
| (v) All sides are equal | Equilateral triangle |
Question 3.
In ∆ABC, name the
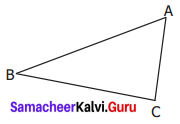
(a) Three sides: ____, _____, _____
(b) Three Angles: _____, _____, _____
(c) Three Vertices: _____, _____, _____
Solution:
(a) \(\overline{\mathrm{AB}}, \overline{\mathrm{BC}}, \overline{\mathrm{CA}}\)
(b) ∠ABC, ∠BCA, ∠CAB or ∠A, ∠B, ∠C
(c) A, B, C
![]()
Question 4.
Classify the given triangles based on its sides as scalene, isosceles or equilateral.
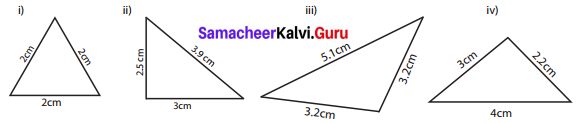
Solution:
(i) Equilateral Triangle
(ii) Scalene Triangle
(iii) Isosceles Triangle
(iv) Scalene Triangle
Question 5.
Classify the given triangles based on its angles as acute-angled, right-angled or obtuse-angled.
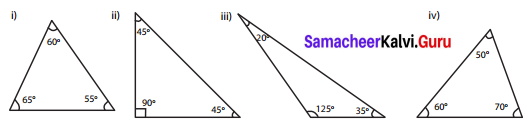
Solution:
(i) Acute angled triangle
(ii) Right angled triangle
(iii) Obtuse angled triangle
(iv) Acute angled triangle
Question 6.
Classify the following triangles based on its sides and angles.

Solution:
(i) Isosceles Acute angled triangle
(ii) Scalene Right angled triangle
(iii) Isosceles Obtuse angled triangle
(iv) Isosceles Right angled triangle
(v) Equilateral Acute angled triangle
(vi) Scalene Obtuse angled triangle
Question 7.
Can a triangle be formed with the following sides? If yes, name the type of triangle.
(i) 8 cm, 6 cm, 4 cm
(ii) 10 cm, 8 cm, 5 cm
(iii) 6.2 cm, 1.3 cm, 3.5 cm
(iv) 6 cm, 6 cm, 4 cm
(v) 3.5 cm, 3.5 cm, 3.5 cm
(vi) 9 cm, 4 cm, 5 cm
Solution:
(i) Sum of two smaller sides of the triangle
= 6 + 4 = 10 cm > 8 cm
It is greater than the third side. So, a triangle can be formed scalene triangle.
(ii) Sum of two smaller sides of the triangle
= 8 + 5 = 13 cm > 10 cm
It is greater than the third side. So, a triangle can be formed scalene triangle.
(iii) Sum of two smaller sides of the triangle
= 1.3 + 3.5 = 4.8 cm < 6.2 cm
It is not greater than the third side. So, a triangle cannot be formed.
(iv) Two sides are equal.
So, a triangle can be formed. Isosceles triangle.
(v) Three sides are equal.
So, a triangle can be formed equilateral triangle.
(vi) Sum of two smaller sides of the triangle
= 4 + 5 = 9 cm = 9 cm
It is equal to the third side. No, a triangle cannot be formed.
![]()
Question 8.
Can a triangle be formed with the following angles? if yes, name the type of triangle.
(i) 60°, 60°, 60°
(ii) 90°, 55°, 35°
(iii) 60°, 40°, 42°
(iv) 60°, 90°, 90°
(v) 70°, 60°, 50°
(vi) 100°, 50°, 30°
Solution:
(i) 60°, 60°, 60°
Sum of three angles = 60° + 60° + 60° = 180°
Yes, a triangle can be formed.
∴ It is Acute angled triangle. [∵ all the angles < 90°]
(ii) 90°, 55°, 35°.
Sum of three angles = 90° + 55° + 55° = 180°
Yes, a triangle can be formed.
∴ It is a right-angled triangle, [∵ one angle is 90°]
(iii) 60°, 40°, 42°.
Sum of three angles = 60° + 40° + 42° = 142° ≠ 180°
No, The triangle cannot be formed.
(iv) 60°, 90°, 90°.
Sum of three angles = 60° + 90° + 90° = 240° ≠ 180°
∴ No, The triangle cannot be formed. [∵ one angle is > 90°]
(v) 70°, 60°, 50°.
Sum of three angles = 70° + 60° + 50° = 180°
Yes, A triangle can be formed.
∴ It is an acute-angled triangle.
(vi) 100°, 50°, 30°.
Sum of three angles = 100° + 50° + 30° = 180°
Yes, A triangle can be formed.
∴ It is an obtuse-angled triangle.
Question 9.
Two angles of the triangles are given. Find the third angle.
(i) 80°, 60°
(ii) 52°, 68°
(iii) 75°, 35°
(iv) 50°, 90°
(v) 120°, 30°
(vi) 55°, 85°
Solution:
(i) 80°, 60°
Let the third angle be x.
Sum of the angles = 180°
80° + 60° + x = 180°
140 + x = 180°
x = 180°- 140°
x = 40°
Third angle = 40°
(ii) 52°, 68°
Let the third angle be x.
Sum of the angles = 180°
52° + 68° + x = 180°
120 + x = 180°
180° – 120°
x = 60°
Third angle = 60°
(iii) 75°, 35°
Let the third angle be x.
Sum of the angles 180°
75° + 35° + x = 180°
110 + x = 180°
x = 180° – 110°
x = 70°
Third angle = 70°
(iv) 50°, 90°
Let the third angle be x. Sum of the angles = 180°
50° + 90° + x = 180°
140 + x = 180°
x = 180° – 140°
x = 40°
Third angle = 40°
(v) 120°, 30°
Let the third angle be x.
Sum of the angles = 180°
120° + 30° + x = 180°
150 + x = 180°
x = 180° – 150°
x = 30°
Third angle = 30°
(vi) 55°, 85°
Let the third angle be x.
Sum of the angles = 180°
55° + 85° + x = 180°
140 + x = 180°
x = 180° – 140°
x = 40°
Third angle = 40°
Question 10.
I am a closed figure with each of my three angles is 60°. Who am I?
Solution:
Equilateral Triangle.
![]()
Question 11.
Using the given information, write the type of triangle in the table given below.
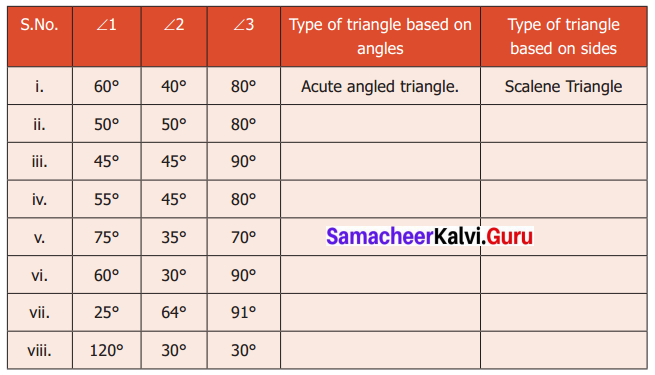
Solution:
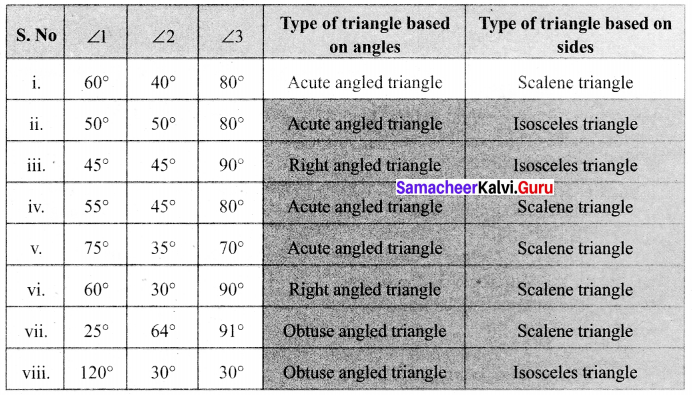
Objective Type Questions
Question 12.
The given triangle is _____.
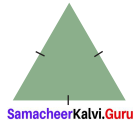
(a) a right angled triangle
(b) an equilateral triangle
(c) a scalene triangle
(d) an obtuse angled triangle
Solution:
(b) an equilateral triangle
Question 13.
If all angles of a triangle are less than a right angle, then it is called ……….
(a) an obtuse angled triangle
(b) a right angled triangle
(c) an isosceles right angled triangle
(d) an acute angled triangle
Solution:
(d) an acute angled triangle
Question 14.
If two sides of a triangle are 5 cm and 9 cm then the third side is _____.
(a) 5 cm
(b) 3 cm
(c) 4 cm
(d) 14 cm
Solution:
(a) 5 cm
Question 15.
The angles of a right angled triangle are
(a) acute, acute, obtuse
(b) acute, right, right
(c) right, obtuse, acute
(d) acute, acute, right
Solution:
(d) acute, acute, right
![]()
Question 16.
An equilateral triangle is
(a) an obtuse-angled triangle
(b) a right-angled triangle
(c) an acute-angled triangle
(d) scalene triangle
Solution:
(c) an acute-angled triangle
Read More: