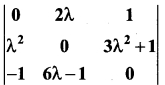Prasanna

Students can Download Tamil Nadu 11th Physics Model Question Paper 3 English Medium Pdf, Tamil Nadu 11th Physics Model Question Papers helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

TN State Board 11th Physics Model Question Paper 3 English Medium

Instructions:

1. The question paper comprises of four parts
2. You are to attempt all the parts. An internal choice of questions is provided wherever: applicable
3. All questions of Part I, II, III, and IV are to be attempted separately
4. Question numbers 1 to 15 in Part I are Multiple choice Questions of one mark each. These are to be answered by choosing the most suitable answer from the given four alternatives and writing the option code and the corresponding answer
5. Question numbers 16 to 24 in Part II are two-mark questions. These are lo be answered in about one or two sentences.
6. Question numbers 25 to 33 in Part III are three-mark questions. These are lo be answered in about three to five short sentences.
7. Question numbers 34 to 38 in Part IV are five-mark questions. These are lo be answered in detail. Draw diagrams wherever necessary.

Time: 3 Hours
Max Marks: 70

PART – I

Answer all the questions. [15 x 1 = 15]
Question 1.
A force F is applied on a square plate of side L. If percentage error in determination of L is 2% and that in F is 4%, the permissible error in pressure is ……….. .
(a) 2%
(b) 4%
(c) 6%
(d) 8%
Answer:
(d) 8%
Hint:
Pressure P = \(\frac { F }{ A }\) = \(\frac { F }{ L² }\)
\(\frac { ∆P }{ P }\) × 100 = (\(\frac { ∆F }{ F }\) × 100) + (\(\frac { ∆L }{ L }\) × 100) = 4% + 2(2%)
\(\frac { ∆P }{ P }\) × 100 = 8%

Question 2.
From the displacement – time graph shown below, particle is ……….. .

(a) continuously going in positive x – direction
(b) at rest
(c) going with increasing velocity upto a time t₀ and then becomes constant
(d) moves at a constant velocity upto a time t₀, and then stops
Answer:
(d) moves at a constant velocity upto a time t₀, and then stops

Question 3.
The potential energy of the system increases if work is done ……….. .
(a) upon the system by a non conservative force
(b) by the system against a conservative force
(c) by the system against a non conservative force
(d) upon the system by a conservative force
Answer:
(b) by the system against a conservative force

Question 4.
If x = at² + bt + c where x is displacement as a function of time. The dimension of ‘a’ and ‘b’ are respectively ……… .
(a) LT^-1 and LT^-2
(b) LT^-2 and LT^-1
(c) L and LT^-2
(d) LT^-1 and L
Answer:
(b) LT^-2 and LT^-1
Hint:
According to principle of homogeneity, the displacement, x = at² + bt + c
Dimensionally, [L] = [LT^-2] [T²] + [LT^-1] [T]
Where a = LT^-2 and b = LT^-1

Question 5.
A satellite in its orbit around earth is weightless on account of its ……….. .
(a) momentum
(b) acceleration
(c) speed
(d) none
Answer:
(b) acceleration

Question 6.
The displacement of a particle along x – axis is given by x = 7t² + 8t + 3. Its acceleration and velocity at t = 2s respectively ……….. .
(a) 36 ms^-1, 14 ms^-2
(b) 14 ms^-2, 36 ms^-1
(c) 47 ms^-2, 21 ms^-1
(d) 2 ms^-1, 47 ms^-2
Answer:
(b) 14 ms^-2, 36 ms^-1
Hint:
x = 7t² + 8t + 3 dx
V = \(\frac { dx }{ dt }\) = 14t + 8;
at t = 2s; V = 36 ms^-1
a = \(\frac { dv }{ dt }\) = 14 ms^-2

Question 7.
A sphere of radius r cm falls from rest in a viscous liquid. Heat is produced due to viscous force. The rate of production of heat when the sphere attains its terminal velocity is proportional to ……….. .
(a) r²
(b) r³
(c) r⁴
(d) r⁵
Answer:
(d) r⁵
Hint:
Rate of heat production = F.V
= 6πηrv × v = 6πηrv²
[v ∝ r²] Terminal velocity ∝ r⁵

Question 8.
A body of weight mg is hanging on a string which extends its length l. The workdone in extending the string is ……….. .
(a) mgl
(b) \(\frac { mgl }{ 2 }\)
(c) 2 mgl
(d) none of these
Answer:
(b) \(\frac { mgl }{ 2 }\)
Hint:
The extension length is
Workdone (W) = Force × distance
Workdone in extension string = Weight × Length extension
mg × \(\frac { l }{ 2 }\)
W = \(\frac { mgl }{ 2 }\)

Question 9.
If S_p and S_v denote the specific heat of nitrogen gas per unit mass at constant pressure and constant volume respectively, then ……….. .
(a) S_p– S_v = 28R
(b) S_p – S_v = \(\frac { R }{ 28 }\)
(c) S_p – S_v = \(\frac { R }{ 14 }\)
(d) S_p – S_v = R
Answer:
(b) S_p – S_v = \(\frac { R }{ 28 }\)
Hint:
According to Mayer’s relation, S_p – S_v = \(\frac { R }{ m }\)
For Nitrogen, m = 28
S_p – S_v = \(\frac { R }{ 28 }\)

Question 10.
A particle is moving eastwards with velocity of 5 m/s. In 10 sec the velocity changes to 5 m/s northwards. The average acceleration in this time is ……….. .
(a) zero
(b) \(\frac { 1 }{ √2 }\) m/s² towards north – west
(c) \(\frac { 1 }{ √2 }\) m/s² towards north – east
(d) \(\frac { 1 }{ 2 }\) m/s² towards north – west
Answer:
(b) \(\frac { 1 }{ √2 }\) m/s² towards north – west
Hint:

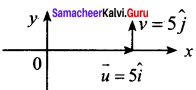
\(\vec { a } \) = \(\frac { d\vec { v } }{ dt }\)
= \(\frac { 5 }{ 2 } (\hat { j } -\hat { i) } \)
= \(\frac { 1 }{ 2 } (\hat { j } -\hat { i) } \)
a = \(\frac { 1 }{ √2 }\) m/s^-2

Question 11.
In an isochoric process, we have ……….. .
(a) W ≠ 0, U = 0, Q = 0, T = 0
(b) W ≠ 0, U ≠ 0, Q = 0, T = 0
(c) W = 0, U = 0, Q ≠ 0, T ≠ 0
(d) W = 0, U ≠ 0, Q ≠ 0, T ≠ 0
Answer:
(d) W = 0, U ≠ 0, Q ≠ 0, T ≠ 0

Question 12.
The efficiency of a carnot engine operations between boiling and freezing points of water is ……….. .
(a) 0.1
(b) 100
(c) 1
(d) 0.27
Answer:
(d) 0.27
Hint:
η = [1 – (\(\frac { { T }_{ 2 } }{ { T }_{ 1 } } \))] = [1 – \(\frac { 273 }{ 373 }\)]
η = 0.268
∴ η = 0.27

Question 13.
Bernoulli’s equation is consequences of conservation of ……….. .
(a) energy
(b) linear momentum
(c) angular momentum
(d) mass
Answer:
(a) energy

Question 14.
By what velocity a ball be projected vertically upwards so that the distance covered in 5th second is twice of that covered in 6 m second (tale g = 10 ms^-2) ……….. .
(a) 19.6 ms^-1
(b) 58.8 ms^-1
(c) 49 ms^-1
(d) 65 ms^-1
Answer:
(d) 65 ms^-1
Hint:
Distance covered int he 5^th second
S₅= u + \(\frac { 1 }{ 2 }\)(-10) × (2 × 5 – 1)
S₅ = u – 5 × 9 = u – 45
Distance covered in the 6^th second
S₆= u +\(\frac { 1 }{ 2 }\)(-10) × (2 × 6 – 1) = u – 5 × 11
S₆ = u – 55 .
Here S₅ = 6S₆ and we get solving
u = 65 ms^-1

Question 15.
Unit of Stefan’s constant is ……….. .
(a) watt m² k⁴
(b) watt m² / k⁴
(c) watt k⁴ / m²
(d) watt / m² k⁴
Answer:
(d) watt / m² k⁴

PART – II

Answer any six questions in which Q. No 23 is compulsory. [6 × 2 = 12]

Question 16.
Get an expression for stopping distance of a vehicle in terms of initial velocity v₀ and deceleration ‘a’.
Answer:
Let s be the distance travelled by a vehicle before it stops
Using v² – u² = 2as,
We can get 0² – \(v_{0}^{2}\) = -2as
∴ s = \(\frac{v_{0}^{2}}{2a}\)
The stopping distance is directly proportional to \(v_{0}^{2}\). i.e. By doubling initial velocity it increase stopping distance by 4 times. Provided deceleration is kept as constant.

Question 17.
A carnot engine has the same efficiency, when operated
(i) between 100 K and 500 K
(ii) between TK and 900 K. Find the value of T.
Answer:
(i) Here T₁ = 500 K; T₂ = 100 K
η = 1 – \(\frac{T_2}{T_1}\) =1 – \(\frac{100}{500}\) = 1 – 0.2 = 0.8

(ii) Now, T₁= 900 K; T₂ = T and n = 0.8
Again, η = 1 – \(\frac{T_2}{T_1}\)
0.8 = 1 – \(\frac{T}{900}\) = 1 – 0.8 = 0.2
∴ T = 180K

Question 18.
A block at rest explodes into 3 parts are -2p\(\vec{j}\) and p\(\vec{j}\). Calculate the magnitude of the momentum of the third part.
Answer:
Let \(\vec{P}\) be the momentum of third particle after the explosion of bomb. According to law of conservation of momentum
-2p\(\vec{i}\) + p\(\vec{j}\) + \(\vec{P}\) = 0 (or) \(\vec{P}\) = 2p\(\vec{i}\) – p\(\vec{j}\)
P = \(\sqrt{(2p)^2+(-p)^2}\) = p√5

Question 19.
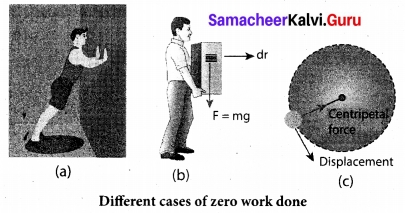
Discuss the possibilities of work done to be zero.
Answer:
Work done is zero in the following cases.
(i) When the force is zero (F = 0). For example, a body moving on a horizontal smooth frictionless surface will continue to do so as no force (not even friction) is acting along the plane. (This is an ideal situation.)

(ii) When the displacement is zero (dr = 0). For example, when force is applied on a rigid wall it does not produce any displacement. Hence, the work done is zero as shown in figure.

(iii) When the force and displacement are perpendicular (θ = 90°) to each other, when a body moves on a horizontal direction, the gravitational force (mg) does not work on the body, since it acts at right angles to the displacement as shown in Figure (b). In circular motion the centripetal force does not do work on the object moving on a circle as it is always perpendicular to the displacement as shown in Figure (c).

Question 20.
Define (a) unit of length (b) unit of electric current in SI system.
Answer:
Given v = at² + \(\frac{b}{c+t}\)
The physical quantities which are having same dimensional formula only can be added.
Dimensional formula for v = LT^-1
Dimensional formula for c = T
Dimensional formula for at² = LT^-1
a = \(\frac{LT_{-1}}{T^2}\) = LT^-3
Dimensional formula for \(\frac{b}{c+t}\) = LT^-1
∴ b = L [∵ c + t = T]

Question 21.
A solid cylinder of mass 20 kg rotates about it axis with angular speed 100 s^-1 the radius of the cylinder is 0.25 m. Calculate moment of inertia of the solid cylinder.
Answer:
Given Data : R = 0.25 m, M = 20 kg, ω = 100 s^-1
We know that
moment of inertia of the solid cylinder = \(\frac{MR^2}{2}\)
\(\frac{20×(0.25)^2}{2}\) = 0.625 kgm²
K.E of rotation = \(\frac{1}{2}\) Iω²
\(\frac{1}{2}\) × 0.625 × (100)² = 3125 J
∴ Angular momentum L = Iω = 0.625 × 100
L = 62.5 Js

Question 22.
Why moon has no atmosphere?
Answer:
The acceleration due to gravity of moon ‘g’ is small. Therefore the escape velocity on the surface of moon is also small. The molecules of in its atmosphere have greater thermal velocities than escape speed. The molecules can easily escaped from the atmosphere of moon. Hence the moon has no atmosphere.

Question 23.
A refrigerator has cop of 3. How much work must be supplied to the refrigerator in order to remove 200 J of heat from its interion?
Answer:
COP = β = \(\frac{Q_L}{W}\)
W = \(\frac{Q_c}{COP}\) = \(\frac{200}{3}\) = 66.67 J

Question 24.
What is the effect of gravitational force of attraction acting on the person be inside the satellite and stand on moon?
Answer:
The gravitational force of attraction of the Earth on the person inside the satellite provides the centripetal force necessary to move in an orbit. A person standing on the moon possesses weight due to the additional gravitational pull of the moon on the person.

PART – III

Answer any six questions in which Q.No. 29 is compulsory. [6 × 3 = 18]

Question 25.
State and prove Archimedes principle.
Answer:
Archimedes Principle: It states that when a body is partially or wholly immersed in a fluid, it experiences an upward thrust equal to the weight of the fluid displaced by it and its upthrust acts through the centre of gravity of the liquid displaced.

Proof: Consider a body of height ‘h’ lying inside a liquid of density p, at a depth x below the free surface of the liquid. Area of cross section of the body is V. The forces on the sides of the body cancel out.

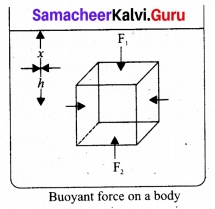
Pressure at the upper face of the body, P_1′ = xpg.
Pressure at the lower face of the body, P_2′ = (x + h) pg
Thrust acting on the upper face of the body is F₁ = P₁ a = xρga acting vertically downwards,
Thrust acting on the lower face of the body is F₂ = P₂a = (x + h) ρga acting vertically upwards.
The resultant force (F₂ – F₁) is acting on the body in the upward direction and is called upthrust (U).
U = F₂ – F₁ = (x + h) ρga – xρga = ahρg
But ah = V, Volume of the body = Volume of liquid
U = Vρg = Mg
i. e., Upthrust or buoyant force = Weight of liquid displaced.
This proves the Archimedes principle.

Question 26.
State kepler’s three laws.
Answer:

1. Law of Orbits: Each planet moves around the Sun in an elliptical orbit with the Sun at one of the foci.
2. Law of area: The radial vector (line joining the Sun to a planet) sweeps equal areas in equal intervals of time.
3. Law of period: The square of the time period of revolution of a planet around the Sun in its elliptical orbit is directly proportional to the cube of the semi-major axis of the ellipse.
   T² ∝ a³
   \(\frac{T²}{a³}\) = Constant

Question 27.
Write the properties of vector product of two vectors.
Answer:
Properties of vector product of two vectors are:
(i) The vector product of any two vectors is always another vector whose direction is perpendicular to the plane containing these two vectors, i.e., orthogonal to both the vectors \(\vec{A}\) and \(\vec{B}\), even though the vectors \(\vec{A}\) and \(\vec{B}\) may or may not be mutually orthogonal.

(ii) The vector product of two vectors is not commutative, i.e., \(\vec{A}\) × \(\vec{B}\) ≠ \(\vec{B}\) × \(\vec{A}\). But, \(\vec{A}\) × \(\vec{B}\) = –\(\vec{B}\) × \(\vec{A}\).

Here it is worthwhile to note that |\(\vec{A}\) × \(\vec{B}\)| = |\(\vec{B}\) x \(\vec{A}\)| = AB sin θ i.e., in the case of the product vectors \(\vec{A}\) × \(\vec{A}\) and \(\vec{B}\) × \(\vec{A}\), the magnitudes are equal but directions are opposite to each other.

(iii) The vector product of two vectors will have maximum magnitude when sin θ = 1, i.e., θ = 90° i.e., when the vectors \(\vec{A}\) and \(\vec{B}\) are orthogonal to each other.
(\(\vec{A}\) × \(\vec{B}\))_max = AB\(\hat{n}\)

(iv) The vector product of two non-zero vectors will be minimum when sin θ = 0, i.e., θ = 0° or 180°
(\(\vec{A}\) × \(\vec{B}\))_min = 0
i.e., the vector product of two non-zero vectors vanishes, if the vectors are either parallel or antiparallel.

(v) The self-cross product, i.e., product of a vector with itself is the null vector
\(\vec{A}\) × \(\vec{A}\) = AA sin 0° \(\hat{n}\) = \(\vec{0}\)
In physics the null vector \(\vec{0}\) is simply denoted as zero.

(vi) The self-vector products of unit vectors are thus zero.
\(\vec{i}\) × \(\vec{i}\) = \(\vec{j}\) × \(\vec{j}\) = \(\vec{k}\) × \(\vec{k}\) = 0

Question 28.
Let the two springs A and B such that K_A > K_B on which spring will more work has to be done if they are stretched by the same force.
Answer:
F = K.x so x = \(\frac{F}{K}\)
For same F

Question 29.
Differentiate slipping and sliding.
Answer:

Question 30.
Jupiter is at a distance of 824.7 million km from the earth. Its angular diameter is measured to be 35.72” calculate the diameter of Jupiter.
Answer:
Distance of Jupiter = 824.7 × 10⁶ km = 8.247 × 10¹¹ m
Angular diameter = 35.72 × 4.85 × 10^-6 rad = 173.242 × 10^-6 rad
= 1.73 × 10^-4 rad
Diameter of Jupiter D = θ × d= 1.73 × 10^-4 rad × 8.247 × 10¹¹ m
= 14.267 × 10⁷m = 1.427 × 10⁸m (or) 1.427 × 10⁵ km

Question 31.
A wire 10 m long has a cross-sectional area 1.25 × 10^-4 m². It is subjected to a load of 5 kg. If young’s modulus of the material is 4 × 10¹⁰ Nm^-2. calculate the elongation produced in the wire, [take g = 10 ms^-2]
Answer:
We know that

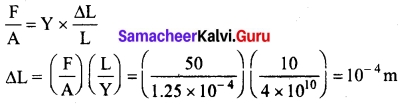
Question 32.
State and explain the law of equipartition of energy.
Answer:
According to kinetic theory, the average kinetic energy of system of molecules in thermal equilibrium at temperature T is uniformly distributed to all degrees of freedom (x or y or z directions of motion) so that each degree of freedom will get \(\frac{1}{2}\) kT of energy. This is called law of equipartition of energy.
Average kinetic energy of a monatomic molecule (with f = 3) = 3 × \(\frac{1}{2}\) KT = \(\frac{3}{2}\) KT
Average kinetic energy of diatomic molecule at low temperature (with f = 5) = 5 × \(\frac{1}{2}\) KT = \(\frac{5}{2}\) KT
Average kinetic energy of a diatomic molecule at high temperature (with f = 7) = 7 × \(\frac{1}{2}\) KT = \(\frac{7}{2}\) KT
Average kinetic energy of linear triatomic molecule (with f = 7) = 7 × \(\frac{1}{2}\) KT = \(\frac{7}{2}\) KT
Average kinetic energy of non linear triatomic molecule (with f = 6) = 6 × \(\frac{1}{2}\) KT = 3 KT

Question 33.
A cylindrical tank of height 0.4 m is open at the top and has a diameter 0.16 m. Water is filled in it up to height of 0.16 m. Find the time taken to empty the tank through a hole of radius 5 × 10^-3 m in its bottom.
Answer:
The velocity of efflux through the hole v = \(\sqrt{2gh}\)
Let R, r be the radius of cylindrical tank and hole and ‘dh’ is the decrease in height of water in time ‘dt’ sec use principle of continuity at the top and hole

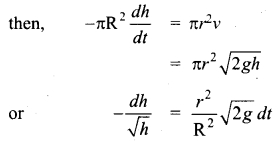
integrating it within the condition of problem,

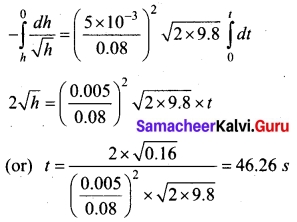
PART – IV

Answer all the questions. [5 × 5 = 25]

Question 34 (a).
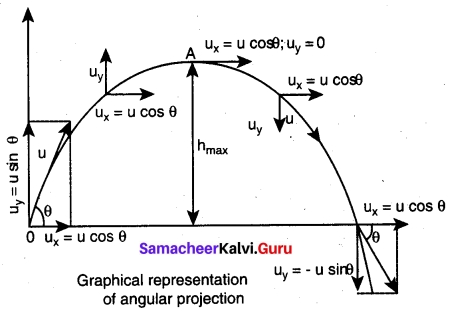
Show that the path of oblique projection is parabola.
Answer:
This projectile motion takes place when the initial velocity is not horizontal, but at some angle with the vertical, as shown in Figure.(Oblique projectile)
Examples:

1. Water ejected out of a hose pipe held obliquely.
2. Cannon fired in a battle ground.

Consider an object thrown with initial velocity at an angle θ with the horizontal.
Then,
u = u\(\vec{i}\) + u\(\vec{j}\)
where u = u cos θ is the horizontal component and u = u sin θ, the vertical component of velocity.

Since the acceleration due to gravity is in the direction opposite to the direction of vertical component u_y, this component will gradually reduce to zero at the maximum height of the projectile. At this maximum height, the same gravitational force will push the projectile to move downward and fall to the ground. There is no acceleration along the x direction throughout the motion. So, the horizontal component of the velocity (u_x = u cos θ) remains the same till the object reaches the ground.

Hence after the time t, the velocity along horizontal motion v_x = u_x + a_xt = u_x = u cos θ
The horizontal distance travelled by projectile in time t is s_x = u_xt + \(\frac{1}{2}\) a_xt²
Here, s_x = x, u_x = u cos θ, a_x = 0

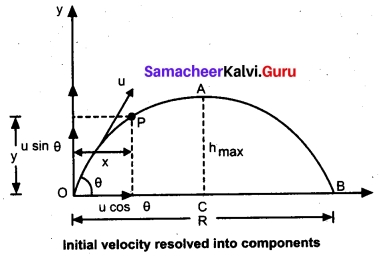
Thus, x = u cos θ.t or t = \(\frac{x}{u cos θ }\) ………..(1)
Next, for the vertical motion v_y = u_y + a_yt
Here u_y = u sin θ, a_y = -g (acceleration due to gravity acts opposite to the motion).
Thus, v_y = u sin θ – gt
The vertical distance travelled by the projectile in the same time t is
Here, s_y = y, u_y = u sin θ, a_x = -g
Then y = u sin θ t – \(\frac{1}{2}\) gt² ……..(2)
Substitute the value of t from equation (1) in equation (2), we have

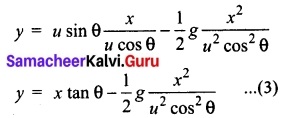
Thus the path followed by the projectile is an inverted parabola.

[OR]

(b) Explain the motion of block connected by a string in vertical motion.
Answer:

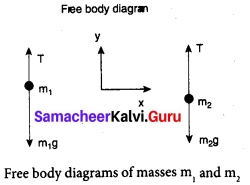
Case 1: Vertical motion: Consider two blocks of masses m₁ and m₂ (m₁ > m₂) connected by a light and inextensible string that passes over a pulley as shown in figure.

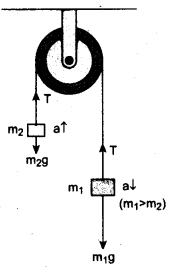
Let the tension in the string be T and acceleration a. When the system is released, both the blocks start moving, m₂ vertically upward and m₁ downward with same acceleration a. The gravitational force m₁g on mass m₁ is used in lifting the mass m₂.
The upward direction is chosen as y direction. The free body diagrams of both masses are shown in figure.
Applying Newton’s second law for mass m₂
T\(\hat{j}\) – m₂g\(\hat{j}\) = m₂a\(\hat{j}\)
The left hand side of the above equation is the total force that acts on m₂ and the right hand side is the product of mass and acceleration of m₂ in y direction.
By comparing the components on both sides, we get
T – m₂g = m₂a …..(1)
Similarly, applying Newton’s second law for mass m₁
T\(\hat{j}\) – m₁g\(\hat{j}\) = -m₁a\(\hat{j}\)
As mass m₁ moves downward (-\(\hat{j}\)), its acceleration is along (-\(\hat{j}\))
By comparing the components on both sides, we get
T – m₁g = -m₁a
m₁g – T = m₁a ……(2)
Adding equations (1) and (2), we get
m₁g – m₂g = m₁a – m₂a
(m₁ – m₂)g = (m₁ + m₁)a ……(3)
From equation (3), the acceleration of both the masses is
a = (\(\frac{m_1-m_2}{m_1+m_2}\))g …….(4)
If both the masses are equal (m₁ = m₂), from equation (4)
a = 0
This shows that if the masses are equal, there is no acceleration and the system as a whole will be at rest.
To find the tension acting on the string, substitute the acceleration from the equation (4) into the equation (1).

Equation (4) gives only magnitude of acceleration.
For mass m₁, the acceleration vector is given by \(\vec{a}\) = –\(\frac{m_1-m_2}{m_1+m_2}\)g\(\hat{j}\)
For mass m₂, the acceleration vector is given by \(\vec{a}\) = \(\frac{m_1-m_2}{m_1+m_2}\)g\(\hat{j}\)

Question 35 (a).
Derive the expression for Carnot engine efficiency.
Answer:
Efficiency of a Carnot engine: Efficiency is defined as the ratio of work done by the working substance in one cycle to the amount of heat extracted from the source.
η = \(\frac{Workdone}{Heat extracted}\) = \(\frac{W}{Q_H}\) ……..(1)
From the first law of thermodynamics, W = Q_H – Q_L
η = \(\frac{Q_H – Q_L}{Q_H}\) = 1 – \(\frac{Q_L}{Q_H}\) ……..(2)
Applying isothermal conditions, we get,
Q_H = μRT_Hln \(\frac{V_2}{V_1}\)
Q_L = μRT_Lln \(\frac{V_3}{V_4}\) ………(3)
Here we omit the negative sign. Since we are interested in only the amount of heat (Q_L) ejected into the sink, we have
\(\frac{T_L}{T_H}\) = \(\frac{Q _L ln (\frac{V_3}{V_4})}{Q _H ln (\frac{V_2}{V_1})}\) …….(4)
By applying adiabatic conditions, we get,
\(\mathrm{T}_{\mathrm{H}} \mathrm{V}_{2}^{\gamma-1}=\mathrm{T}_{\mathrm{L}} \mathrm{V}_{3}^{\gamma-1}\)
\(\mathrm{T}_{\mathrm{H}} \mathrm{V}_{1}^{\gamma-1}=\mathrm{T}_{\mathrm{L}} \mathrm{V}_{4}^{\gamma-1}\)
By dividing the above two equations, we get
\(\left(\frac{v_{2}}{V_{1}}\right)^{\gamma-1}=\left(\frac{V_{3}}{V_{4}}\right)^{\gamma-1}\)
Which implies that \(\frac{V_2}{V_1}\) = \(\frac{V_3}{V_4}\) ……(5)
Substituting equation (5) in (4), we get
\(\frac{Q_L}{Q_H}\) = \(\frac{T_L}{T_H}\) ……..(6)
∴ The efficiency η = 1 – \(\frac{T_L}{T_H}\) ………….(7)
Note : T_L and T_H should be expressed in Kelvin scale.

Important results:

1. n is always less than 1 because T_L is less than T_H. This implies the efficiency cannot be 100%.
2. The efficiency of the Carnot’s engine is independent of the working substance. It depends only on the temperatures of the source and the sink. The greater the difference between the two temperatures, higher the efficiency.
3. When T_H = T_L the efficiency n = 0. No engine can work having source and sink at the same temperature.

[OR]

(b). Explain the concepts of fundamental frequency, harmonics and overtones in detail.
Answer:
Fundamental frequency and overtones: Let us now keep the rigid boundaries at x = 0 and x = L and produce a standing waves by wiggling the string (as in plucking strings in a guitar). Standing waves with a specific wavelength are produced. Since, the amplitude must vanish at the boundaries, therefore, the displacement at the boundary must satisfy the following conditions y(x = 0, t) = 0 and y(x = L, t) = 0………….(1)
Since, the nodes formed are at a distance \(\frac{ λ_n}{2}\) apart, we have n \(\frac{ λ_n}{2}\) = L where n is an integer, L is the length between the two boundaries and λ _n is the specific wavelength that satisfy the specified boundary conditions. Hence,
λ _n = \(\frac{2L}{n}\)…………(2)
Therefore, not all wavelengths are allowed. The (allowed) wavelengths should fit with the specified boundary conditions, i.e., for n = 1, the first mode of vibration has specific wavelength λ _n= 2L. Similarly for n = 2, the second mode of vibration has specific wavelength
λ ₂ = \(\frac{2L}{2}\) = L
For n = 3, the third mode of vibration has specific wavelength
λ ₃ = \(\frac{2L}{3}\)
and so on.
The frequency of each mode of vibration (called natural frequency) can be calculated.
We have, f_n = \(\frac{v}{λ_n}\) = n \(\frac{v}{2L}\) ………..(3)
The lowest natural frequency is called the fundamental frequency.
f₁ = \(\frac{v}{λ_1}\) = \(\frac{v}{2L}\) …………(4)
The second natural frequency is called the first over tone.
f₂ = 2\(\frac{v}{2L}\) = \(\frac{1}{L} \sqrt{\frac{T}{\mu}}\)
The third natural frequency is called the second over tone.
f₃ = 3\(\frac{v}{λ_2}\) = \(3\left(\frac{1}{2L} \sqrt{\frac{T}{\mu}}\right)\)
and so on.
Therefore, the nth natural frequency can be computed as integral (or integer) multiple of fundamental frequency, i.e.,
f_n = nf₁, where n is an integer …….(5)
If natural frequencies are written as integral multiple of fundamental frequencies, then the frequencies are called harmonics. Thus, the first harmonic is f₁ = f₁(the fundamental frequency is called first harmonic), the second harmonic is f₂ = 2f₁, the third harmonic is f₃ = 3f₁ etc.

Question 36 (a).
Compare any two salient features of static and kinetic friction.
Answer:
Static Friction: Static friction is the force which opposes the initiation of motion of an object on the surface. The magnitude of static frictional force f_s lies between 0 ≤ f_s ≤ μ_sN_s
where,
_μs – coefficient of static friction
N – Normal force
Kinetic friction: The frictional force exerted by the surface when an object slides is called as kinetic friction. Also called as sliding friction or dynamic friction,
f_k = μ_kN
where:
μ_k– the coefficient of kinetic friction
N – Normal force exerted by the surface on the object

(ii) To move an object-push or pull? Which is easier? Explain.
Answer:
When a body is pushed at an arbitrary angle θ (0 to \(\frac{π}{2}\)), the applied force F can be
resolved into two components as F sin θ parallel to the surface and F cos θ perpendicular to the surface as shown in figure. The total downward force acting on the body is mg + F cos θ. It implies that the normal force acting on the body increases. Since there is no acceleration along the vertical direction the normal force N is equal to
N_Push = mg + F cos θ ….(1)
As a result the maximal static friction also increases and is equal to
\(f_{x}^{\max }\) = μ_rN_Push = μ_s(mg + F cos θ ) ……(2)
Equation (2) shows that a greater force needs to be applied to push the object into motion.

When an object is pulled at an angle θ, the applied force is resolved into two components as shown in figure. The total downward force acting on the object is
N_Pull = mg – F cos θ ……..(3)

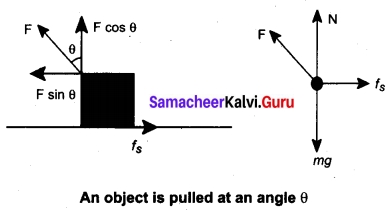
Equation (3)shows that the normal force is less than N_Pull. From equations (1) and (3), it is easier to pull an object than to push to make it move.

[OR]

(b). Describe the vertical oscillations of a spring.
Answer:
Vertical oscillations of a spring: Let us consider a massless spring with stiff ness constant or force constant k attached to a ceiling as shown in figure. Let the length of the spring before loading mass m be L. If the block of mass m is attached to the other end of spring, then the spring elongates by a length l. Let F₁, be the restoring force due to stretching of spring. Due to mass m, the gravitational force acts vertically downward. We can draw free-body diagram for this system as shown in figure. When the system is under equilibrium,
F₁+ mg = 0 ……(1)
But the spring elongates by small displacement 1, therefore,
F₁ ∝ l ⇒ F₁ = -kl …(2)
Substituting equation (2) in equation (1), we get – kl + mg = 0
-kl + mg = 0
mg = l or \(\frac{m}{k}\) = \(\frac{l}{g}\) …….(3)

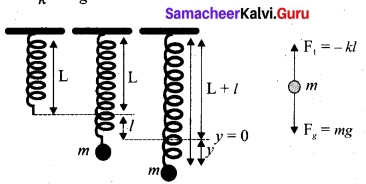
Suppose we apply a very small external force on the mass such that the mass further displaces downward by a displacement y, then it will oscillate up and down. Now, the restoring force due to this stretching of spring (total extension of spring is( y + 1) is
F2 ∝ (y + l)
F2 = -k(y + l) = -ky – kl …..(4)
Since, the mass moves up and down with acceleration \(\frac{d^2y}{dt^2}\) diagram for this case, we get
-ky – kl + mg = m\(\frac{d^2y}{dt^2}\) …….(5)
The net force acting on the mass due to this stretching is
F = F₂ + mg
F = – ky – kl + mg ……..(6)
The gravitational force opposes the restoring force. Substituting equation (3) in equation (6), we get
F = – ky – kl + kl = -ky
Applying Newton’s law, we get
m\(\frac{d^2y}{dt^2}\) = -ky
m\(\frac{d^2y}{dt^2}\) = –\(\frac{k}{m}\)y ……(7)
The above equation is in the form of simple harmonic differential equation. Therefore, we get the time period as
T = 2π, \(\sqrt{\frac{m}{k}}\) second …….(8)
The time period can be rewritten using equation (3)
T = 2π, \(\sqrt{\frac{m}{k}}\) = 2πl\(\frac{l}{g}\) second ……(9)
The acceleration due to gravity g can be computed from the formula
g = 4π²(\(\frac{1}{T^2}\)) ms^-2

Question 37 (a).
State and prove Bernoulli’s theorem
Answer:
Bernoulli’s theorem: According to Bernoulli’s theorem, the sum of pressure energy, kinetic energy, and potential energy per unit mass of an incompressible, non-viscous fluid in a streamlined flow remains a constant. Mathematically,
\(\frac{p}{roe}\) + \(\frac{1}{2}\)v² + gh = Constant
This is known as Bernoulli’s equation.
Proof : Let us consider a flow of liquid through a pipe AB. Let V be the volume of the liquid when it enters A in a time t which is equal to the volume of the liquid leaving B in the same time. Let a_A, v_A and P_A be the area of cross section of the tube, velocity of the liquid and pressure exerted by the liquid at A respectively.
Let the force exerted by the liquid at A is
F_A = P_A a_A
Distance travelled by the liquid in time t is d = v_At
Therefore, the work done is W = F_Ad = P_Aa_Av_At
But a_Av_At = a_Ad = V, volume of the liquid entering at A.
Thus, the work done is the pressure energy (at A), W = F_Ad = P_AV
Pressure energy per unit volume at
A = \(\frac{pressure energy}{volume}\) = \(\frac{P_AV}{V}\) = P_A
Pressure energy per unit mass at
A = \(\frac{pressure energy}{volume}\) = \(\frac{P_AV}{m}\) = \(\frac{P_A}{\frac{m}{v}}\) = \(\frac{P_A}{ρ}\)
Since m is the mass of the liquid entering at A in a given time, therefore, pressure energy of the liquid at A is
EP_A – P_AV = P_AV × (\(\frac{m}{m}\)) = m\(\frac{P_A}{ρ}\)
Potential energy of the liquid at A,
PE_A = mgh_A
Due to the flow of liquid, the kinetic energy of the liquid at A,
KE_A = \(\frac{π}{2}\)m \(v_{A}^{2}\)
Therefore, the total energy due to the flow of liquid at A,
E_A = EP_A + KE_A + PE_A
E_A = m\(\frac{P_A}{ρ}\) + \(\frac{1}{2}\) mv\(v_{A}^{2}\) + mg h_A
Similarly, let a_B, v_B and P_B be the area of cross section of the tube, velocity of the liquid and pressure exerted by the liquid at B. Calculating the total energy at F_B, we get
E_B = m\(\frac{P_B}{ρ}\) + \(\frac{1}{2}\) mv\(v_{B}^{2}\) + mg h_B
From the law of conservation of energy,
E_A = E_B

Thus, the above equation can be written as
\(\frac{P}{ρg}\) + \(\frac{1}{2}\) \(\frac{V_2}{g}\) + h = Constant

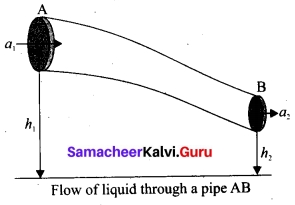
The above equation is the consequence of the conservation of energy which is true until there is no loss of energy due to friction. But iri practice, some energy is lost due to friction. This arises due to the fact that in a fluid flow, the layers flowing with different velocities exert frictional forces on each other. This loss of energy is generally converted into heat energy. Therefore, Bernoulli’s relation is strictly valid for fluids with zero viscosity or non-viscous liquids. Notice that when the liquid flows through a horizontal pipe, then
h = 0 ⇒ \(\frac{P}{ρg}\) +\(\frac{1}{2}\) \(\frac{V_2}{g}\) = Constant

[OR]

(b) Write down the postulates of kinetic theory of gases.
Answer:

1. All the molecules of a gas are identical, elastic spheres.
2. The molecules of different gases are different.
3. The number of molecules in a gas is very large and the average separation between them is larger than size of the gas molecules.
4. The molecules of a gas are in a state of continuous random motion.
5. The molecules collide with one another and also with the walls of the container.
6. These collisions are perfectly elastic so that there is no loss of kinetic energy during collisions.
7. Between two successive collisions, a molecule moves with uniform velocity.
8. The molecules do not exert any force of attraction or repulsion on each other except during collision. The molecules do not possess any potential energy and the energy is wholly kinetic.
9. The collisions are instantaneous. The time spent by a molecule in each collision is very small compared to the time elapsed between two consecutive collisions.
10. These molecules obey Newton’s laws of motion even though they move randomly.

Question 38 (a).
Discuss in detail the energy in simple harmonic motion.
Energy in simple harmonic motion:
Answer:
(a) Expression for Potential Energy
For the simple harmonic motion, the force and the displacement are related by Hooke’s law
\(\vec{F}\) = -k\(\vec{r}\)
Since force is a vector quantity, in three dimensions it has three components. Further, the force in the above equation is a conservative force field; such a force can be derived from a scalar function which has only one component. In one dimensional case
F = -kx ……(1)
We know that the work done by the conservative force field is independent of path. The potential energy U can be calculated from the following expression.
F = –\(\frac{dU}{dx}\)
Comparing (1) and (2), we get
–\(\frac{dU}{dx}\) = -kx
dU = kx dx
This work done by the force F during a small displacement dx stores as potential energy

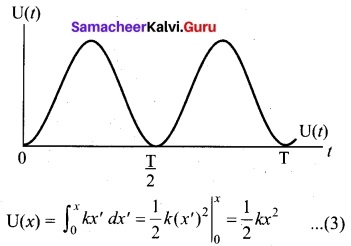
From equation to ω = \(\sqrt{\frac{k}{m}}\), we can substitute the value of force constant k = mω² in equation (3),
U(x) = \(\frac{1}{2}\)mω²x² …..(4)
where ω is the natural frequency of the oscillating system. For the particle executing simple harmonic motion from equation y = A sin ωt, we get
x = A sin ωt
U(t) = \(\frac{1}{2}\)mω²A² sin² ωt ……(5)
This variation of U is shown in figure.

(b) Expression for Kinetic Energy
Kinetic energy
KE = \(\frac{1}{2}\)m\(v_{x}^{2}\) = \(\frac{1}{2}\)m(\(\frac{dx}{dt}\))² …..(6)
Since the particle is executing simple harmonic motion, from equation
y = A sin ωt
x = A sin ωt

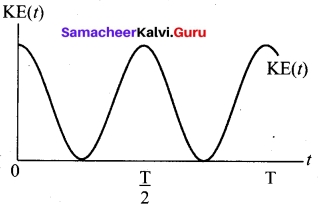
Therefore, velocity is
v_x = \(\frac{dx}{dt}\) = Aω cos ωt ….(7)

This variation with time is shown in figure.

(c) Expression for Total Energy
Total energy is the sum of kinetic energy and potential energy
E = KE + U ….(11)
E = \(\frac{1}{2}\) mω² (A² – x²) + \(\frac{1}{2}\) mω²x²
Hence, cancelling x² term,
E = \(\frac{1}{2}\) mω²A² = constant ……(12)
Alternatively, from equation (5) and equation (10), we get the total energy as
E = \(\frac{1}{2}\) mω²A² sin² ωt + \(\frac{1}{2}\) mω²A² cos² ωt
= \(\frac{1}{2}\) mω²A² (sin² ωt + cos² ωt)

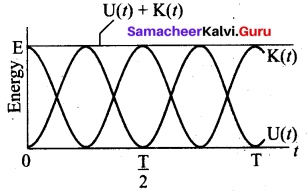
From trigonometry identity, (sin² ωt + cos² ωt) = 1
E = \(\frac{1}{2}\) mω²A² = constant
which gives the law of conservation of total energy.
Thus the amplitude of simple harmonic oscillator, can be expressed in terms of total energy.
A = \(\sqrt{\frac{2E}{mω^2}}\) =\(\sqrt{\frac{2E}{k}}\)

[OR]

(b) Explain the formation of stationary waves.
Answer:
Consider two harmonic progressive waves (formed by strings) that have the same amplitude and same velocity but move in opposite directions. Then the displacement of the first wave (incident wave) is
y₁ = A sin (kx – ωt) (waves move toward right) ……(1)
and the displacement of the second wave (reflected wave) is
y₂ = A sin (kx + ωt) (waves move toward left) …….(2)
both will interfere with each other by the principle of superposition, the net displacement is
y = y₁ + y₂ ……(3)
Substituting equation (1) and equation (2) in equation (3), we get
y = A sin (kx – ωt)+A sin (kx + ωt) …….(4)
Using trigonometric identity, we rewrite equation (4) as
y(x, t) = 2A cos (ωt) sin (kx) ……(5)
This represents a stationary wave or standing wave, which means that this wave does not move either forward or backward, whereas progressive or travelling waves will move forward or backward. Further, the displacement of the particle in equation (5) can be written in more compact form,
y(x, t) = A’ cos (ωt)
where, A’ = 2A sin (kx), implying that the particular element of the string executes simple harmonic motion with amplitude equals to A’. The maximum of this amplitude occurs at positions for which
sin (kx) = 1 ⇒ kx = \(\frac{π}{2}\), \(\frac{3π}{2}\), \(\frac{5π}{2}\), …… = mπ
where m takes half integer or half integral values. The position of maximum amplitude is known as antinode. Expressing wave number in terms of wavelength, we can represent the anti-nodal positions as
x_m = (\(\frac{2m+1}{2}\)) \(\frac{λ}{2}\) where> m = 0, 1, 2…. ……(6)
For m = 0we have maximum at x₀ = \(\frac{λ}{2}\)
For m = 1 we have maximum at x₁ = \(\frac{3λ}{4}\)
For m = 2 we have maximum at x₂ = \(\frac{5λ}{4}\) and so on.
The distance between two successive antinodes can be computed by

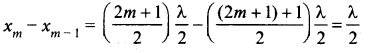
Similarly, the minimum of the amplitude A’ also occurs at some points in the space, and these points can be determined by setting
sin (kx) = 0 ⇒ kx = 0, π, 2π, 3π,…. = nπ
where n takes integer or integral values. Note that the elements at these points do not vibrate (not move), and the points are called nodes. The nth nodal positions is given by,
x_n = n\(\frac{λ}{2}\) where, n = 0,1,2,… …..(7)
For n = 0we have minimum at x₀ = 0
For n = 1 we have minimum at x₁ = \(\frac{λ}{2}\)
For n = 2 we have maximum at x₂ = λ and so on.
The distance between any two successive nodes can be calculated as
x_n – x_n-1 = n\(\frac{λ}{2}\) – (n – 1) \(\frac{λ}{2}\) = \(\frac{λ}{2}\)

Students can download 12th Business Maths Chapter 1 Applications of Matrices and Determinants Ex 1.4 Questions and Answers, Samacheer Kalvi 12th Business Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 1 Applications of Matrices and Determinants Ex 1.4

Choose the correct answer.

Question 1.
If A = (1 2 3), then the rank of AA^T is ______
(a) 0
(b) 2
(c) 3
(d) 1
Answer:
(d) 1
Hint:

Question 2.
The rank of m × n matrix whose elements are unity is _________
(a) 0
(b) 1
(c) m
(d) n
Answer:
(b) 1
Hint:
All the rows except the first row can be made zero

Question 3.
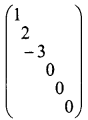
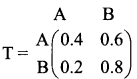If  is a transition probability matrix, then at equilibrium A is equal to
(a) \(\frac{1}{4}\)
(b) \(\frac{1}{5}\)
(c) \(\frac{1}{6}\)
(d) \(\frac{1}{8}\)
Answer:
(a) \(\frac{1}{4}\)
Hint:

Question 4.
If A = \(\left(\begin{array}{ll}
2 & 0 \\
0 & 8
\end{array}\right)\) then ρ(A) is _______
(a) 0
(b) 1
(c) 2
(d) n
Answer:
(c) 2
Hint:

Question 5.
The rank of the matrix \(\left(\begin{array}{lll}
1 & 1 & 1 \\
1 & 2 & 3 \\
1 & 4 & 9
\end{array}\right)\) is _____
(a) 0
(b) 1
(c) 2
(d) 3
Answer:
(d) 3
Hint:

Question 6.
The rank of the unit matrix of order n is _______
(a) n – 1
(b) n
(c) n + 1
(d) n²
Answer:
(b) n
Hint:
Unit matrix of order n is in echelon form with n non-zero rows

Question 7.
If ρ(A) = r then which of the following is correct?
(a) all the minors of order r which does not vanish
(b) A has at least one minor of order r which does not vanish
(c) A has at least one (r + 1) order minor which vanishes
(d) all (r + 1) and higher-order minors should not vanish
Answer:
(b) A has at least one minor of order r which does not vanish

Question 8.
If A = \(\left(\begin{array}{l}
1 \\
2 \\
3
\end{array}\right)\) then the rank of AA^T is _______
(a) 0
(b) 1
(c) 2
(d) 3
Answer:
(b) 1
Hint:

Question 9.
If the rank of the matrix \(\left(\begin{array}{ccc}
\lambda & -1 & 0 \\
0 & \lambda & -1 \\
-1 & 0 & \lambda
\end{array}\right)\) is 2. Then λ is _______
(a) 1
(b) 2
(c) 3
(d) only real number
Answer:
(a) 1
Hint:

Since rank is 2, the third order minor should vanish.
λ³ – 1 = 0
⇒ λ = 1

Question 10.
The rank of the diagonal matrix
is _______
(a) 0
(b) 2
(c) 3
(d) 5
Answer:
(c) 3
Hint:
There are only three non-zero rows as the matrix is in echelon form.

Question 11.
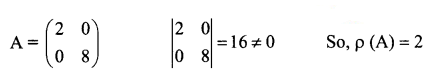
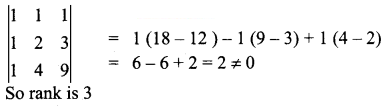
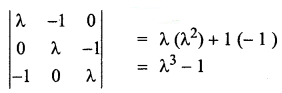
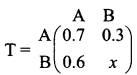If  is a transition probability matrix, then the value of x is
(a) 0.2
(b) 0.3
(c) 0.4
(d) 0.7
Answer:
(c) 0.4
Hint:
x = 1 – 0.6 = 0.4

Question 12.
Which of the following is not an elementary transformation?
(a) R_i ↔ R_j
(b) R_i → 2R_i + 2C_j
(c) R_i → 2R_i – 4R_j
(d) C_i → C_i + 5C_j
Answer:
(b) R_i → 2R_i + 2C_j
Hint:
Since rows and columns cannot be taken together.

Question 13.
If ρ(A) = ρ(A, B), then the system is _______
(a) Consistent and has infinitely many solutions
(b) Consistent and has unique solutions
(c) consistent
(d) inconsistent
Answer:
(c) consistent

Question 14.
If ρ(A) = ρ(A, B) = the number of unknowns, then the system is _______
(a) Consistent and has infinitely many solutions
(b) Consistent and has unique solutions
(c) inconsistent
(d) consistent
Answer:
(i) Consistent and has unique solutions

Question 15.
If ρ(A) ≠ ρ(A, B), then the system is ________
(a) Consistent and has infinitely many solutions
(b) Consistent and has unique solutions
(c) inconsistent
(d) consistent
Answer:
(c) inconsistent

Question 16.
In a transition probability matrix, all the entries are greater than or equal to _______
(a) 2
(b) 1
(c) 0
(d) 3
Answer:
(c) 0

Question 17.
If the number of variables in a non- homogeneous system AX = B is n, then the system possesses a unique solution only when _______
(a) ρ(A) = ρ(A, B) > n
(b) ρ(A) = ρ(A, B) = n
(c) ρ(A) = ρ(A, B) < n
(d) none of these
Answer:
(b) ρ(A) = ρ(A, B) = n

Question 18.
The system of equations 4x + 6y = 5, 6x + 9y = 7 has ________
(a) a unique solution
(b) no solution
(c) infinitely many solutions
(d) none of these
Answer:
(b) no solution

Question 19.
For the system of equations x + 2y + 3z = 1, 2x + y + 3z = 2, 5x + 5y + 9z = 4 _______
(a) there is only one solution
(b) there exists infinitely many solutions
(c) there is no solution
(d) none of these
Answer:
(a) there is only one solution
Hint:

By Cramer’s rule, there is only one solution

Question 20.
If |A| ≠ 0, then A is _______
(a) non- singular matrix
(b) singular matrix
(c) zero matrix
(d) none of these
Answer:
(a) non-singular matrix

Question 21.
The system of linear equations x + y + z = 2, 2x + y – z = 3, 3x + 2y + k = 4 has unique solution, if k is not equal to ______
(a) 4
(b) 0
(c) -4
(d) 1
Answer:
(b) 0
Hint:

Question 22.
Cramer’s rule is applicable only to get an unique solution when ______
(a) Δ_z ≠ 0
(b) Δ_x ≠ 0
(c) Δ ≠ 0
(d) Δ_y ≠ 0
Answer:
(c) Δ ≠ 0

Question 23.

Answer:

Hint:

Question 24.
|A_n×n| = 3 |adj A| = 243 then the value n is _______
(a) 4
(b) 5
(c) 6
(d) 1
Answer:
(b) 5
Hint:
|adj A| = |A|^n-1, n is order of matrix
243 = 3^n-1
3⁴ = 3^n-1
n = 5

Question 25.
Rank of a null matrix is ______
(a) 0
(b) -1
(c) ∞
(d) 1
Answer:
(a) 0

Students can download 12th Business Maths Chapter 2 Integral Calculus I Ex 2.2 Questions and Answers, Samacheer Kalvi 12th Business Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 2 Integral Calculus I Ex 2.2

Integrate the following with respect to x.

Question 1.
\(\int\left(\sqrt{2 x}-\frac{1}{\sqrt{2 x}}\right)^{2}\)
Solution:

Question 2.
\(\frac{x^{4}-x^{2}+2}{x-1}\)
Solution:

Question 3.
\(\frac{x^{3}}{x+2}\)
Solution:

Question 4.
\(\frac{x^{3}+3 x^{2}-7 x+11}{x+5}\)
Solution:
We have to find the quotient by division

Question 5.
\(\frac{3 x+2}{(x-2)(x-3)}\)
Solution:
We use partial fraction method to split the given function into two fractions and then integrate.

Question 6.
\(\frac{4 x^{2}+2 x+6}{(x+1)^{2}(x-3)}\)
Solution:
By partial fractions,

Question 7.
\(\frac{3 x^{2}-2 x+5}{(x-1)\left(x^{2}+5\right)}\)
Solution:

Question 8.
If f'(x) = \(\frac{1}{x}\) and f(1) = \(\frac{\pi}{4}\), then find f(x)
Solution:

Students can download 12th Business Maths Chapter 2 Integral Calculus I Ex 2.1 Questions and Answers, Samacheer Kalvi 12th Business Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 2 Integral Calculus I Ex 2.1

Integrate the following with respect to x.

Question 1.
\(\sqrt{3 x+5}\)
Solution:

Question 2.
\(\left(9 x^{2}-\frac{4}{x^{2}}\right)^{2}\)
Solution:

Question 3.
(3 + x)(2 – 5x)
Solution:

Question 4.
√x(x³ – 2x + 3)
Solution:

Question 5.
\(\frac{8 x+13}{\sqrt{4 x+7}}\)
Solution:

Question 6.
\(\frac{1}{\sqrt{x+1}+\sqrt{x-1}}\)
Solution:

Question 7.
If f'(x) = x + b, f(1) = 5 and f(2) = 13, then find f(x)
Solution:
f'(x) = x + b
Integrating both sides of the equations

Question 8.
If f(x) = 8x³ – 2x and f(2) = 8, then find f(x)
Solution:
f'(x) = 8x³ – 2x
Integrating both sides of the equation,

Students can download 12th Business Maths Chapter 1 Applications of Matrices and Determinants Ex 1.3 Questions and Answers, Samacheer Kalvi 12th Business Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 1 Applications of Matrices and Determinants Ex 1.3

Question 1.
The subscription department of a magazine sends out a letter to a large mailing list inviting subscriptions for the magazine. Some of the people receiving this letter already subscribe to the magazine while others do not. From this mailing list, 45% of those who already subscribe will subscribe again while 30% of those who do not now subscribe will subscribe. On the last letter, it was found that 40% of those receiving it ordered a subscription. What per cent of those receiving the current letter can be expected to order a subscription?
Solution:
Let X represent people who subscribe for the magazine and Y represent persons who do not subscribe for the magazine.
Now there are four cases,
(X, X) ⇒ those who already subscribed will subscribe again.
(X, Y) ⇒ those who already subscribed will not subscribe again.
(Y, X) ⇒ those who have not subscribed will do it now.
(Y, Y) ⇒ those who have not subscribed will not do it now also.
From the problem, we can see that
(X, X) = 45% = 0.45
(X, Y) = 100 – 45 = 55% = 0.55
(Y, X) = 30% = 0.3
(Y, Y) = (100 – 30) = 70% = 0.7
The transition probability matrix is given by

The values of X and Y are given as X = 40 % = 0.4; Y = (100 – 40 ) = 60% = 0.6
We have to predict the value of X and Y after the current letter is sent. It is done as below

That is X = 36% and Y = 64%
Thus 36% of those receiving the current letter can be expected to order a subscription.

Question 2.
A new transit system has just gone into operation in Chennai. Of those who use the transit system this year, 30% will switch over to using the metro train next year and 70% will continue to use the transit system. Of those who use metro train this year, 70% will continue to use metro train next year and 30% will switch over to the transit system. Suppose the population of Chennai city remains constant and that 60% of the commuters use the transit system and 40% of the commuters use metro train this year.
(i) What per cent of commuters will be using the transit system after one year?
(ii) What per cent of commuters will be using the transit system in the long run?
Solution:
Let T denote transit system and M denote metro train. Here again, there are four cases.
(T T) ⇒ those who use the transit system will continue to use the transit system.
(T M) ⇒ those who use the transit system will switch over to the metro train.
(M T) ⇒ those who use metro train will change to the transit system.
(M M) ⇒ those who use metro train will continue to use the metro train.
From the question,
(T T) =70% = 0.7.
(T M) = 30% = 0.3
(M T) = 30% = 0.3
(M M) = 70% = 0.7
The transition probability matrix is given by

The current position is given by T = 60% and M = 40%

We have to predict the values of T and M after one year.

i.e, T = 0.54 = 54%
M = 0.46 = 46%
So after one year, 54% of commuters will use the transit system and 46% of commuters will use the metro train.
(ii) At equilibrium which will be reached in the long run, T + M = 1
We have,

By matrix multiplications,
(0.7T + 0.3M 0.3 T + 0.7 M) = (T M)
Equating the corresponding elements,
0.7T + 0.3M = T
0.7T + 0.3 (1 – T) = T (Using T + M = 1)
0.7T + 0.3 – 0.3T = T
0.3 = 0.6T
T = 0.5
T = 50%
Thus in the long run, 50% of the commuters will be using transit system and 50% will be using metro train.

Question 3.
Two types of soaps A and B are in the market. Their present market shares are 15% for A and 85% for B. Of those who bought A the previous year, 65% continue to buy it again while 35% switch over to B. Of those who bought B the previous year, 55% buy it again and 45% switch over to A. Find their market shares after one year and when is the equilibrium reached?
Solution:
A and B are the two types of soaps. The current market shares are 15% and 85%.
This is represented as
(A B)
(0.15 0.85)
(A A) ⇒ those who bought A previous year will again buy A = 65 % = 0.65
(A B) ⇒ those who bought A previous year will buy soap B now = 35 % = 0.35
(B A) ⇒ those who bought B previous year will buy A now = 45 % = 0.45
(B B) ⇒ those who bought B previous year will buy it again = 55 % = 0.55
The transition probability matrix is

(i) Their market shares after one year is given by

So after one-year market shares of soap A will be 48% and soap B will be 52%
(ii) At equilibrium, A + B = 1
We have

By matrix multiplication,
(0.65A + 0.45B 0.35A + 0.55B) = (A B)
Equating the corresponding elements,
0.65 A + 0.45 B = A
0.65 A + 0.45 A(1 – A) = A (Using A + B = 1)
0.65 A + 0.45 – 0.45 A = A
0.45 = 0.8 A
A = 0.5625 (or) A = 56.25 %
B = 100 – 56.25 = 43.75%
The equilibrium is reached when the market share of soap A is 56.25% and the market share of soap B is 43.75%

Question 4.
Two products A and B currently share the market with shares 50% and 50% each respectively. Each week some brand switching takes place. Of those who bought A the previous week, 60% buy it again whereas 40% switch over to B. Of those who bought B the previous week, 80% buy it again whereas 20% switch over to A. Find their shares after one week and after two weeks. If the price war continues, when is the equilibrium reached?
Solution:
Given that two products A and B have shared 50 % and 50% respectively.
(A A) ⇒ those who bought A the previous week will buy it again = 60 % = 0.6
(A B) ⇒ those who bought A the previous week will buy B now = 40 % = 0.4
(B A) ⇒ those who bought B the previous week will switch to A = 20 % = 0.2
(B B) ⇒ those who bought B will again buy B = 80 % = 0.8
The transition probability matrix is given by

The current position of A and B in the market is

After one week
The shares of A and B are given by

So after one week the market share of A is \(\frac{0.4}{100}\) × 100 = 40% and that of B is \(\frac{0.6}{100}\) × 100 = 60%
After two weeks
The shares of A and B are given by

Thus after two weeks, A will have 36% of shares and B will have 64% of shares.
As time goes, equilibrium will be reached in the long run.
At this point A + B = 1
We have

By matrix multiplication,
(0.6A + 0.2B 0.4A + 0.8B) = (A B)
Equating the corresponding elements,
0.6A + 0.2B = A
0.6A + 0.2(1 – A) = A (using A + B = 1)
0.6A + 0.2 – 0.2A = A
0.2 = A – 0.4A
A = \(\frac{0.2}{0.6}\) = 0.33 = 33%
B = 1 – 0.33 = 0.67 = 67%
Thus the equilibrium is reached when the share of A is 33% and share of B is 67%.

Students can download 12th Business Maths Chapter 1 Applications of Matrices and Determinants Additional Problems Questions and Answers, Samacheer Kalvi 12th Business Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 1 Applications of Matrices and Determinants Additional Problems

I. One Mark Questions

Choose the correct statement.

Question 1.
If A is a matrix of order m × n, then ______
(a) ρ(A) = m
(b) ρ(A) = n
(c) ρ(A) = min of {m, n}
(d) ρ(A) < m
Answer:
(c) ρ(A) = min of {m, n}

Question 2.
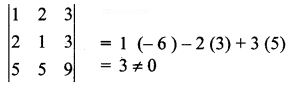
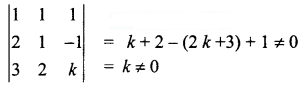
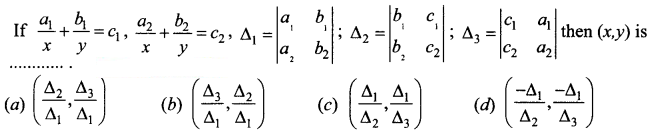
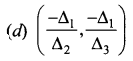
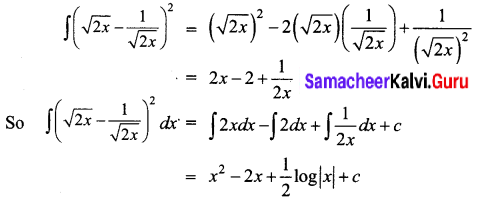
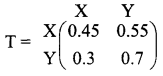
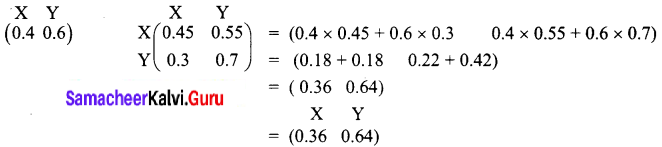
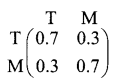
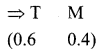
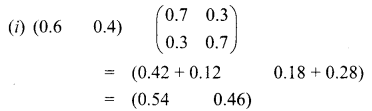
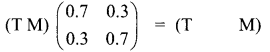
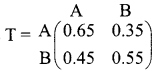
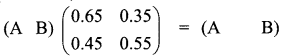
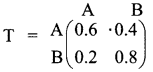
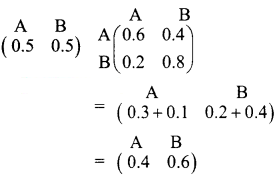
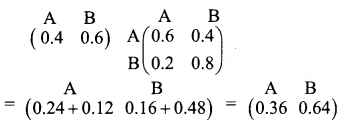
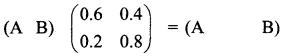
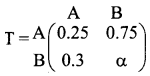If  is a transition probability matrix, then the value of a is
(a) 0.5
(b) 0.7
(c) 0
(d) 0.6
Answer:
(b) 0.7
Hint:
0.3 + α = 1
⇒ α = 1 – 0.3 = 0.7

Question 3.
Let AX = B is a system of n non-homogeneous linear equation. Then which of the following is correct.
(a) |A|= 0
(b) A = B
(c) |A| ≠ 0
(d) ρ(A) < n
Answer:
(c) |A| ≠ 0

Question 4.
Choose the incorrect pair.

Answer:
(a) (3 2 4) – Column matrix

Question 5.
If A is matrix [A, B] is the augmented matrix then which of the following is true?
(a) ρ([A, B]) = ρ(A)
(b) ρ([A, B]) ≥ ρ(A)
(c) ρ([A, B]) = ρ(A) > n
(d) ρ([A, B]) < ρ(A)
Answer:
(b) ρ([A, B]) ≥ ρ(A)

Question 6.
Choose the echelon matrix.
(a) \(\left[\begin{array}{ll}
0 & 1 \\
1 & 0 \\
0 & 0
\end{array}\right]\)
(b) \(\left[\begin{array}{ll}
1 & 2 \\
0 & 1 \\
0 & 0
\end{array}\right]\)
(c) \(\left[\begin{array}{ll}
1 & 2 \\
0 & 1 \\
0 & 1
\end{array}\right]\)
(d) \(\left[\begin{array}{ll}
1 & 0 \\
0 & 0 \\
0 & 1
\end{array}\right]\)
Answer:
(b) \(\left[\begin{array}{ll}
1 & 2 \\
0 & 1 \\
0 & 0
\end{array}\right]\)

Question 7.
Let A be a non-singular matrix of order (3 × 3). Then |adj A| is equal to _______
(a) |A|
(b) |A|²
(c) |A|³
(d) 3|A|
Answer:
(b) |A|²

Question 8.
For what value of k does the matrix. A = \(\left[\begin{array}{cc}
k & -1 \\
3 & 2
\end{array}\right]\) does not have inverse?
(a) 1
(b) \(\frac{-3}{2}\)
(c) 0
(d) -1
Answer:
(b) \(\frac{-3}{2}\)
Hint:

Question 9.
Rank of the matrix A = \(\left(\begin{array}{rrrr}
1 & -1 & 2 & 0 \\
0 & 2 & 0 & 3
\end{array}\right)\) is _______
(a) 1
(b) 0
(c) 2
(d) -1
Answer:
(c) 2
Hint:
The second order minors, \(\left|\begin{array}{cc}
1 & -1 \\
0 & 2
\end{array}\right|,\left|\begin{array}{cc}
-1 & 2 \\
2 & 0
\end{array}\right|,\left|\begin{array}{cc}
2 & 0 \\
0 & 3
\end{array}\right|\) are not zero. So rank is 2

Question 10.
Choose the correct answer.
(a) A system of the linear equation always has a unique solution.
(b) A system of the linear equation can have more than one solution.
(c) A system of the linear equation need not be consistent.
(d) All of the above
Answer:
(d) All of the above

Question 11.
For the matrix equation \(\left(\begin{array}{cc}
1 & 2 \\
3 & -1
\end{array}\right)\left(\begin{array}{l}
x \\
y
\end{array}\right)=\left(\begin{array}{l}
7 \\
3
\end{array}\right)\) the augmented matrix is _______
(a) \(\left(\begin{array}{ccc}
1 & 2 & 7 \\
3 & -1 & 3
\end{array}\right)\)
(b) \(\left(\begin{array}{ll}
1 & 7 \\
3 & 3
\end{array}\right)\)
(c) \(\left(\begin{array}{ll}
7 & 1 \\
3 & 3
\end{array}\right)\)
(d) \(\left(\begin{array}{rrr}
1 & 7 & 2 \\
3 & 3 & -1
\end{array}\right)\)
Answer:
(a) \(\left(\begin{array}{ccc}
1 & 2 & 7 \\
3 & -1 & 3
\end{array}\right)\)

Question 12.
Find the correct statement. Cramer’s rule can be used to solve, _______
(a) n equations in n unknowns
(b) When determinant of the coefficient matrix is non-zero.
(c) The number of unknowns need not be equal to a number of equations.
(d) For infinite solutions
Answer:
(a) n equations in n unknowns & (b) When determinant of the coefficient matrix is non-zero.

Question 13.
Which of the following is a transition probability matrix?
(a) \(\left(\begin{array}{cc}
0.3 & 0.6 \\
0.15 & 0.85
\end{array}\right)\)
(b) \(\left(\begin{array}{ccc}
0.9 & 0.075 & 0.025 \\
0.15 & 0.8 & 0.05 \\
0.25 & 0.25 & 0.5
\end{array}\right)\)
(c) \(\left(\begin{array}{ll}
1 & 0.2 \\
0.3 & 0.25
\end{array}\right)\)
(d) \(\left(\begin{array}{cc}
0.35 & 0.6 \\
0.2 & 0.7
\end{array}\right)\)
(i) only a
(ii) only b
(iii) both c and d
(iv) both a and b
Answer:
(iv) both a and b
Hint:
Sum of all the probabilities should be equal to one

Question 14.
Choose the correct statements.
(a) the rank of an identity matrix is zero.
(b) the rank of an adjoint matrix is more than the rank of a matrix
(c) the rank of a diagonal matrix is equal to the number of rows
(d) the rank of an echelon matrix is greater than the matrix
Answer:
(c) the rank of a diagonal matrix is equal to the number of rows

Question 15.

Answer:
1 – d, 2 – c, 3 – a, 4 – b

II. 2 Mark Questions

Question 1.
Show that the inverse of A = \(\left(\begin{array}{cc}
-6 & 9 \\
4 & -6
\end{array}\right)\) does not exist
Solution:
Show |A| = 0

Question 2.
Find the rank of A = \(\left(\begin{array}{lll}
1 & 2 & 3 \\
2 & 3 & 4 \\
3 & 5 & 7
\end{array}\right)\)
Solution:
Given A = \(\left(\begin{array}{lll}
1 & 2 & 3 \\
2 & 3 & 4 \\
3 & 5 & 7
\end{array}\right)\)
Consider \(\left(\begin{array}{lll}
1 & 2 & 3 \\
2 & 3 & 4 \\
3 & 5 & 7
\end{array}\right)\)
= 1(21 – 20) – 2(14 – 12) + 3(10 – 9)
= 1 – 4 + 3
= 0
Since third order minor equals zero, ρ(A) < 3
Consider \(\left|\begin{array}{ll}
1 & 2 \\
2 & 3
\end{array}\right|\) = 3 – 4 = -1 ≠ 0
There is a minor of order 2 which is not zero. Hence ρ(A) = 2

Question 3.
Find the rank of A = \(\left[\begin{array}{rrrr}
4 & 5 & -6 & -1 \\
7 & -3 & 0 & 8
\end{array}\right]\)
Solution:
Given A = \(\left[\begin{array}{rrrr}
4 & 5 & -6 & -1 \\
7 & -3 & 0 & 8
\end{array}\right]\)
Consider the minor \(\left|\begin{array}{cc}
5 & -6 \\
-3 & 0
\end{array}\right|=-18 \neq 0\)
Since a minor of order 2 is not zero, rank is 2

Question 4.
Solve the system by Cramer’s rule, 4x – 3y = 11; 6x + 5y = 7
Solution:
4x – 3y = 11; 6x + 5y = 7

Question 5.
Solve the system by rank method.
3x + 5y = -7; x + 4y = -14
Solution:
3x + 5y = -7; x + 4y = -14
The matrix equation of the system is

Number of non-zero rows is 2
So ρ(A) = ρ([A, B]) = 2
Now the new matrix equation is
-7y = 35 ⇒ y = -5
x + 4y = -14 ⇒ x = -14 – 4(-5) = 6
Solution is (6, -5)

Question 6.
Find the solution of the system 5x + y = -13; 3x – 2y = 0
Solution:
5x + y = -13; 3x – 2y = 0
We solve the system by Cramer’s rule

III. 3 and 5 Mark Questions

Question 1.
Find λ so that the matrix \(\left(\begin{array}{ccc}
8 & 9 & 7 \\
7 & 8 & 6 \\
9 & 10 & \lambda
\end{array}\right)\) is a singular matrix.
Solution:

Question 2.
Find k so that the matrix \(\left(\begin{array}{ccc}
1 & 2 & k \\
3 & 4 & 5 \\
7 & 10 & 12
\end{array}\right)\) is a non-singular matrix.
Solution:

Question 3.
Solve by Cramer’ rule, x – y + z = 2; 2x – y = 0; 2y – z = 1
Solution:
x – y + z = 2; 2x – y = 0; 2y – z = 1
The matrix equation corresponding to the system is

Question 4.
Solve by rank method x + 2y – 3z = -4; 2x + 3y + 2z = 2; 3x – 3y – 4z = 11
Solution:
x + 2y – 3z = -4; 2x + 3y + 2z = 2; 3x – 3y – 4z = 11
The matrix equation is

The last equivalent matrix is in echelon form.
ρ(A) = ρ([A, B]) = 3 = Number of unknowns
The new matrix equation is given by \(\left(\begin{array}{ccc}
1 & 2 & -3 \\
0 & -1 & 8 \\
0 & 0 & -67
\end{array}\right)\left(\begin{array}{l}
x \\
y \\
z
\end{array}\right)=\left(\begin{array}{c}
-4 \\
10 \\
-67
\end{array}\right)\)
x + 2y – 3z = -4 ……. (1)
-y + 8z = 10 …….. (2)
-67z = -67 ……… (3)
(3) ⇒ z = 1
(2) ⇒ -y + 8 = 10 ⇒ -y = 2 ⇒ y = -2
(1) ⇒ x = -4 -2(-2) + 3(1) ⇒ x = 3
Hence the solution is (x, y, z) = (3, -2, 1)

Question 5.
The sum of three numbers is 20. If we multiply the first by 2 and add the second number and subtract the third we get 23. If we multiply the first by 3 and add second and third to it, we get 46. By using rank method find the numbers.
Solution:
Let the three number be x, y and z respectively.
According to the problem,
x + y + z = 20
2x + y – z = 23
3x + y + z = 46
The matrix equation is given by

x + y + z = 20 …….. (1)
-y – 3z = -17 …….. (2)
4z = 20 …….. (3)
(3) ⇒ z = 5
(2) ⇒ -y = -17 + 3(5) = -2 ⇒ y = 2
(1) ⇒ x = 20 – 2 – 5 = 13
Hence the three numbers are (13, 2, 5)

Question 6.
Weekly expenditure in an office for three weeks is given as follows. Calculate the salary for each type of staff using Cramer’s rule.

Solution:
Let the salary for the three types of staff A, B and C be ₹ x, ₹ y and ₹ z respectively.
According to the problem we have,
4x + 2y + 3z = 4900
3x + 3y + 2z = 4500
4x + 3y + 4z = 5800

Question 7.
Show that the equations x – 3y – 8z = -10; 3x + y – 4z = 0; 2x + 5y + 6z = 13 are consistent and have infinite sets of solution.
Solution:

The last equivalent matrix is in echelon form. It has two non-zero rows.
ρ(A) = ρ([A, B]) = 2 < number of unknowns
The system is consistent and has infinitely many solutions
The changed matrix equation is given by \(\left(\begin{array}{ccc}
1 & -3 & -8 \\
0 & 1 & 2 \\
0 & 0 & 0
\end{array}\right)\left(\begin{array}{c}
x \\
y \\
z
\end{array}\right)=\left(\begin{array}{c}
-10 \\
3 \\
0
\end{array}\right)\)
x – 3y – 8z = -10 ……. (1)
y + 2z = 3 ……. (2)
(2) ⇒ y = 3 – 2z
(1) ⇒ x = -10 + 3y + 8z
⇒ x = -10 + 3(3 – 2z) + 8z
⇒ x = -10 + 9 – 6z + 8z
⇒ x = 2z – 1
Let us take z = k, k ∈ R. We get y = 3 – 2k and x = 2k – 1.
By giving diffemet values for k, we get different solutions.

Question 8.
Find the rank of the matrix by reducing to echelon form A = \(\left(\begin{array}{cccc}
1 & 1 & 1 & 1 \\
1 & 3 & -2 & 1 \\
2 & 0 & -3 & 2
\end{array}\right)\)
Solution:

Question 9.
Show that the equations x – 3y + 4z = 3; 2x – 5y + 7z = 6; 3x – 8y + 11z = 1 are inconsistent.
Solution:
x – 3y + 4z = 3; 2x – 5y + 7z = 6; 3x – 8y + 11z = 1

The last equivalent matrix is in the echelon form. [A, B] has 3 non-zero rows and [A] has 2 non-zero rows.
ρ([A, B]) = 3; ρ(A) = 2
ρ(A) ≠ ρ([A, B])
The system is inconsistent and has no solution.

Question 10.
Find k if the equations 2x + 3y – z = 5; 3x – y + 4z = 2; x + 7y – 6z = k are consistent.
Solution:
Given that the system 2x + 3y – z = 5; 3x – y + 4z = 2, x + 7y – 6z = k is consistent.

ρ(A) = 2 ρ([A, B]) = 2 or 3
For the equations to be consistent, ρ([A, B]) = ρ(A) = 2
-8 + k = 0 ⇒ k = 8

Question 11.
Find k if the equations x + y + z = 3; x + 3y + 2z = 6; x + 5y + 3z = k are inconsistent.
Solution:
Given that the system is inconsistent


For the equations to be inconsistent, ρ[(A, B)] ≠ ρ(A)
Here ρ(A) = 2 So ρ([A, B]) ≠ 2
That is the last row of the echelon matrix should not be zero
⇒ k ≠ 9

Question 12.
Two newspapers A and B are published in a city. Their present market shares are 15% for A and 85% for B. Of those who bought A the previous year, 65% continue to buy it again while 35% switch over to B. Of those who bought B the previous year, 55% buy it again and 45% switch over to A. Find their market shares after two years.
Solution:
Let the present shares of A and B be denoted by (0.15 0.85)
The transition probability matrix is given by

Hence their market shares after 2 years will be 0.546 × 100 = 54.6 % and 0.454 × 100 = 45.4%

Question 13.
The pattern of sunny and rainy days on a planet has two states. Every sunny day is followed by another sunny day with probability 0.8. Every rainy day is followed by another rainy day with probability 0.6. Today is sunny on the planet. What is the chance of rain the day after tomorrow?
Solution:
Let S and R denote sunny and rainy days on the planet
The transition probability matrix is given by

We have to find the probability of rain after two days. We have to find T²

Hence if today is sunny on the planet, the chance of rain the day after tomorrow is 0.28.

Students can download 12th Business Maths Chapter 1 Applications of Matrices and Determinants Ex 1.2 Questions and Answers, Samacheer Kalvi 12th Business Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 1 Applications of Matrices and Determinants Ex 1.2

Question 1.
Solve the following equations by using Cramer’s rule
(i) 2x + 3y = 7; 3x + 5y = 9
(ii) 5x + 3y = 17; 3x + 7y = 31
(iii) 2x + y – z = 3, x + y + z = 1, x – 2y – 3z = 4
(iv) x + y + z = 6, 2x + 3y – z = 5, 6x – 2y – 3z = -7
(v) x + 4y + 3z = 2, 2x – 6y + 6z = -3, 5x – 2y + 3z = -5
Solution:
(i) 2x + 3y = 7; 3x + 5y = 9

Question 2.
A commodity was produced by using 3 units of labour and 2 units of capital, the total cost is ₹ 62. If the commodity had been produced by using 4 units of labour and one unit of capital, the cost is ₹ 56. What is the cost per unit of labour and capital? (Use determinant method).
Solution:
Let the cost per unit of labour be ₹ x and cost per unit of capital be ₹ y.

Question 3.
A total of ₹ 8,600 was invested in two accounts. One account earned 4\(\frac{3}{4}\)% annual interest and the other earned 6\(\frac{1}{2}\)% annual interest. If the total interest for one year was ₹431.25, how much was invested in each account? (Use determinant method).
Solution:
Let ₹ x and ₹ y be the amounts invested in the two accounts.

Question 4.
At marina two types of games viz., Horse riding and Quad Bikes riding are available on hourly rent. Keren and Benita spent ₹ 780 and ₹ 560 during the month of May.

Find the hourly charges for the two games (rides). (Use determinant method).
Solution:
Let hourly charges for horse riding be ₹ x and hourly charges for Quad bike riding be ₹ y.
According to the problem, for Keren, we have 3x + 4y as total amount and for Benita, we have 2x + 3y as the total amount.
That is 3x + 4y = 780
2x + 3y = 560

Hence hourly charges for horse riding and bike riding are ₹ 100 and ₹ 120 respectively.

Question 5.
In a market survey three commodities A, B and C were considered. In finding out the index number some fixed weights were assigned to the three varieties in each of the commodities. The table below provides information regarding the consumption of three commodities according to the three varieties and also the total weight received by the commodity.

Find the weights assigned to the three varieties by using Cramer’s Rule.
Solution:
Let the weights assigned to the three varieties be x, y and z respectively.
According to the problem,
For variety A, x + 2y + 3z = 11
For variety B, 2x + 4y + 5z = 21
For variety C, 3x + 5y + 6z = 27

Hence the weights assigned to the three varieties are 2, 3 and 1 units respectively.

Question 6.
A total of ₹ 8,500 was invested in three interest-earning accounts. The interest rates were 2%, 3% and 6% if the total simple interest for one year was ₹ 380 and the amount invested at 6% was equal to the sum of the amounts in the other two accounts, then how much was invested in each account? (use Cramer’s rule).

Solution:
Let the amounts invested in the three accounts be Rs. x, Rs. y and Rs. z
Interest for the three accounts are \(\frac{2}{100}\)x, \(\frac{3}{100}\)y and \(\frac{6}{100}\)z
According to the problem, x + y + z = 8500 ……. (1)
\(\frac{2}{100} x+\frac{3}{100} y+\frac{6}{100} z=380\)
(or) multiplying by 100,
2x + 3y + 6z = 38000 ……… (2)
z = x + y or x + y – z = 0 ………. (3)

Students can download 12th Business Maths Chapter 1 Applications of Matrices and Determinants Ex 1.1 Questions and Answers, Samacheer Kalvi 12th Business Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Business Maths Solutions Chapter 1 Applications of Matrices and Determinants Ex 1.1

Question 1.
Find the rank of each of the following matrices.
Solution:
(i) Let A = \(\left(\begin{array}{ll}
5 & 6 \\
7 & 8
\end{array}\right)\)
Order of A is 2 × 2.
ρ(A) ≤ 2
Consider the second order minor
\(\left|\begin{array}{ll}
5 & 6 \\
7 & 8
\end{array}\right|\) = 40 – 42 = -2 ≠ 0
There is a minor of order 2, which is not zero.
ρ(A) = 2
(ii) Let A = \(\left(\begin{array}{ll}
1 & -1 \\
3 & -6
\end{array}\right)\)
Order of A is 2 × 2
ρ(A) ≤ 2
Consider the second order minor
\(\left|\begin{array}{ll}
1 & -1 \\
3 & -6
\end{array}\right|\) = -6 + 3 = -3 ≠ 0
ρ(A) = 2
(iii) Let A = \(\left(\begin{array}{ll}
1 & 4 \\
2 & 8
\end{array}\right)\)
Since A is of order 2 × 2, ρ(A) ≤ 2
Now \(\left|\begin{array}{ll}
1 & 4 \\
2 & 8
\end{array}\right|\) = 8 – 8 = 0
Since second order minor vanishes ρ(A) ≠ 2
But first order minors, |1|, |4|, |2|, |8| are non zero.
ρ(A) = 1
(iv) Let A = \(\left(\begin{array}{ccc}
2 & -1 & 1 \\
3 & 1 & -5 \\
1 & 1 & 1
\end{array}\right)\)
Order of A is 3 × 3
ρ(A) ≤ 3
Consider the third order minor
\(\left|\begin{array}{ccc}
2 & -1 & 1 \\
3 & 1 & -5 \\
1 & 1 & 1
\end{array}\right|\)
= 2(1 + 5) + 1 (3 + 5) + 1(3 – 1)
= 2(6) + 8 + 2
= 22 ≠ 0
There is a minor of order 3, which is non zero.
ρ(A) = 3
(v) Let A = \(\left(\begin{array}{ccc}
-1 & 2 & -2 \\
4 & -3 & 4 \\
-2 & 4 & -4
\end{array}\right)\)
Since order of A is 3 × 3, ρ(A) ≤ 3
Now,
\(\left|\begin{array}{ccc}
-1 & 2 & -2 \\
4 & -3 & 4 \\
-2 & 4 & -4
\end{array}\right|\)
= -1(12 – 16) -2(-16 + 8) – 2(16 – 6)
= 4 + 16 – 20
= 0
Since the third order minor vanishes, ρ(A) ≠ 3
Consider \(\left|\begin{array}{cc}
-1 & 2 \\
4 & -3
\end{array}\right|\) = 3 – 8 = -5 ≠ 0
There is a minor order 2, which is not zero
ρ(A) = 2
(vi) Let A = \(\left(\begin{array}{cccc}
1 & 2 & -1 & 3 \\
2 & 4 & 1 & -2 \\
3 & 6 & 3 & -7
\end{array}\right)\)
Let us transform the matrix A to an echelon form by using elementary transformations.

Question 2.
If A = \(\left(\begin{array}{ccc}
1 & 1 & -1 \\
2 & -3 & 4 \\
3 & -2 & 3
\end{array}\right)\) and B = \(\left(\begin{array}{ccc}
1 & -2 & 3 \\
-2 & 4 & -6 \\
5 & 1 & -1
\end{array}\right)\), then find the rank of AB and the rank of BA.
Solution:
Given A = \(\left(\begin{array}{ccc}
1 & 1 & -1 \\
2 & -3 & 4 \\
3 & -2 & 3
\end{array}\right)\) and B = \(\left(\begin{array}{ccc}
1 & -2 & 3 \\
-2 & 4 & -6 \\
5 & 1 & -1
\end{array}\right)\)

Question 3.
Solve the following system of equations by rank method.
x + y + z = 9, 2x + 5y + 7z = 52, 2x + y – z = 0
Solution:
The given equations are x + y + z = 9, 2x + 5y + 7z = 52, 2x + y – z = 0
The matrix equation corresponding to the given system is

Question 4.
Show that the equations 5x + 3y + 7z = 4, 3x + 26y + 2z = 9, 7x + 2y + 10z = 5 are consistent and solve them by rank method.
Solution:
The given equations are,
5x + 3y + 7 = 4
3x + 26y + 2z = 9
7x + 2y + 10z = 5
The matrix equation corresponding to the given system is

Question 5.
Show that the following system of equations have unique solution:
x + y + z = 3, x + 2y + 3z = 4, x + 4y + 9z = 6 by rank method.
Solution:
The given system of equations can be written in matrix equation,

The last matrix is in echelon form. It has 3 non – zero rows,
ρ(A) = ρ([A, B]) = 3 = number of unknowns.
The given system is consistent and has a unique solution.
To find the solution, we write the echelon form into matrix form.
\(\left(\begin{array}{lll}
1 & 1 & 1 \\
0 & 1 & 2 \\
0 & 0 & 2
\end{array}\right)\left(\begin{array}{l}
x \\
y \\
z
\end{array}\right)=\left(\begin{array}{l}
3 \\
1 \\
0
\end{array}\right)\)
x + y + z = 3 …… (1)
y + 2z = 1 …… (2)
2z = 0 …… (3)
(3) ⇒ z = 0
(2) ⇒ y = 1
(1) ⇒ x = 2
So the unique solution is x = 2, y = 1, z = 0

Question 6.
For what values of the parameter X, will the following equations fail to have unique solution: 3x – y + λz = 1, 2x + y + z = 2, x + 2y – λz = -1 by rank method.
Solution:
The given system can be written in matrix equation form as given below:


λ = \(\frac{-7}{2}\)
So when λ = \(\frac{-7}{2}\), the equations fail to have unique solution.
Note: The system cannot have an infinite number of solutions, since ρ([A, B]) = 3 = a number of unknowns.

Question 7.
The price of three commodities, X,Y and Z are and z respectively Mr. Anand purchases 6 units of Z and sells 2 units of X and 3 units of Y. Mr.Amar purchases a unit of Y and sells 3 units of X and 2 units of Z. Mr. Amit purchases a unit of X and sells 3 units of Y and a unit of Z. In the process they earn ₹ 5,000/-, ₹2,000/- and ₹ 5,500/- respectively. Find the prices per unit of three commodities by rank method.
Solution:

The price of three commodities X, Y, Z are given as x, y, z.
We form the following system of equations from the given conditions.
Anand → 2x + 3y – 6z = 5000
Amar → 3x – y + 2z = 2000
Amit → -x + 3y + z = 5500
The matrix equation is given by



The prices per unit of the three commodities are Rs.1000, Rs.2000 and Rs.500

Question 8.
An amount of ₹ 5,000/- is to be deposited in three different bonds bearing 6%, 7% and 8% per year respectively. Total annual income is ₹ 358/-. If the income from the first two investments is ₹ 70/- more than the income from the third, then find the amount of investment in each bond by the rank method.
Solution:
Let the amount of investment in the three different bonds be Rs. x, Rs. y and Rs. z respectively.
We get the following equations according to the given conditions,
x + y + z = 5000


The above equivalent matrix is in echelon form with 3 non-zero rows.
So ρ(A) = ρ([A, B]) = 3 = number of unknowns.
the system has a unique solution.
The matrix equation is given by
\(\left(\begin{array}{ccc}
1 & 1 & 1 \\
0 & 1 & 2 \\
0 & 0 & -16
\end{array}\right)\left(\begin{array}{l}
x \\
y \\
z
\end{array}\right)=\left(\begin{array}{c}
5000 \\
5800 \\
-28800
\end{array}\right)\)
x + y + z = 5000 …(1)
y + 2z = 5800 …(2)
-16z = -28800 …(3)
(3) ⇒ z = 1800
(2) ⇒ y = 5800 – 2(1800) = 2200
(1) ⇒ x = 5000 – 2200 – 1800 = 1000
The amount invested in the three bonds are ₹ 1000, ₹ 2200 and ₹ 1800.

Students can Download Tamil Nadu 11th Maths Model Question Paper 4 English Medium Pdf, Tamil Nadu 11th Maths Model Question Papers helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

TN State Board 11th Maths Model Question Paper 4 English Medium

General Instructions:

1. The question paper comprises of four parts.
2. You are to attempt all the parts. An internal choice of questions is provided wherever applicable.
3. All questions of Part I, II, III and IV are to be attempted separately.
4. Question numbers 1 to 20 in Part I are Multiple Choice Questions of one mark each.
   These are to be answered by choosing the most suitable answer from the given four alternatives and writing the option code and the corresponding answer
5. Question numbers 21 to 30 in Part II are two-mark questions. These are to be answered in about one or two sentences.
6. Question numbers 31 to 40 in Part III are three-mark questions. These are to be answered in above three to five short sentences.
7. Question numbers 41 to 47 in Part IV are five-mark questions. These are to be answered in detail Draw diagrams wherever necessary.

Time: 2.30 Hours
Maximum Marks: 90

PART – I

I. Choose the correct answer. Answer all the questions. [20 × 1 = 20]

Question 1.
The number of relations on a set containing 3 elements is………..
(a) 9
(b) 81
(c) 512
(d) 1024
Solution:
(c) 512

Question 2.
If n[(A × B) ∩ (A × C)] = 12 and n(B ∩ C) = 2 then n(A) is……….
(a) 2
(b) 3
(c) 4
(d) 6
Solution:
(d) 6

Question 3.
If |x – 3| ≤ 5 then x belongs to………
(a) [-2, 8]
(b) (-2, 8)
(c) [-2, ∞]
(d) (-∞, 8)
Solution:
(a) [-2, 8]

Question 4.
The number of solutions of x² + |x – 1| = 1 is
(a) 1
(b) 0
(c) 2
(d) 3
Solution:
(c) 2

Question 5.
If a, 8, b are in A.P. a, 4, b are in G.P. and a, x, b are in H.P then x = ………..
(a) 2
(b) 1
(c) 4
(d) 16
Solution:
(a) 2

Question 6.
If 10 lines are drawn in a plane such that no two of them are parallel and no three are concurrent, then the total number of points of intersection are………..
(a) 45
(b) 40
(c) 10!
(d) 210
Solution:
(a) 45

Question 7.
The value of e^2logx………..
(a) 2x
(b) x²
(c) √2
(d) \(\frac{x}{2}\)
Solution:
(b) x²

Question 8.
The nth term of the sequence 1, 2, 4, 7, 11 …. is ………..
(a) n³ + 3n² + 2n
(b) n³ – 3n² + 3n
(c) \(\frac{n(n+1)(n+2)}{3}\)
(d) \(\frac{n²-n+2}{2}\)
Solution:
(d) \(\frac{n²-n+2}{2}\)

Question 9.
The last term in the expansion (2 + √3)⁸ is
(a) 81
(b) 27
(c) 9
(d) 3
Solution:
(a) 81

Question 10.
A line perpendicular to the line 5x – y = 0 forms a triangle with the coordinate axes. If the area of the triangle is 5 sq.units, then its equation is………….
(a) x + 5y ± 5√2 = 0
(b) x – 5y ± 5√2 = 0
(c) 5x + y ± 5√2 = 0
(d) 5x – y ± 5√2 = 0
Solution:
(a) x + 5y ± 5√2 = 0

Question 11.
A factor of the determinant  is ……….
(a) x + 3
(b) 2x – 1
(c) x – 2
(d) x – 3
Solution:
(a) x + 3

Question 12.
If λ\(\vec {i}\) + 2λ\(\vec {j}\) + 2λ\(\vec {k}\) is a unit vector then the value of λ is…………
(a) \(\frac{1}{3}\)
(b) \(\frac{1}{4}\)
(c) \(\frac{1}{9}\)
(d) \(\frac{1}{2}\)
Solution:
(a) \(\frac{1}{3}\)

Question 13.
One of the diagonals of parallelogram ABCD with \(\vec {a}\) and \(\vec {b}\) are adjacent sides is The other diagonal BD is…………
(a) \(\vec {a}\) + \(\vec {b}\).
(b) \(\vec {a}\) – \(\vec {b}\)
(c) \(\vec {b}\) – \(\vec {a}\)
(d) \(\frac{\vec a+\vec b}{2}\)
Solution:
(b) \(\vec {a}\) – \(\vec {b}\)

Question 14.
If (1, 2, 4) and (2, -3λ, -3) are the initial and terminal points of the vector \(\vec {i}\) + 5\(\vec {j}\) – 7\(\vec {k}\) then the value of λ ………….
(a) \(\frac{7}{3}\)
(b) –\(\frac{7}{3}\)
(c) \(\frac{5}{3}\)
(d) \(\frac{-5}{b}\)
Solution:
(b) –\(\frac{7}{3}\)

Question 15.
If y = mx + c and f(0) = f'(0) = 1 then f(2) =…………
(a) 1
(b) 2
(c) 3
(d) 4
Solution:
(c) 3

Question 16.
The derivative of (x + \(\frac{1}{x}\))² w.r.to. x is…………
(a) 2x – \(\frac{2}{x³}\)
(b) 2x + \(\frac{2}{x³}\)
(c) 2(x + \(\frac{1}{x}\))
(d) 0
Solution:
(a) 2x – \(\frac{2}{x³}\)

Question 17.
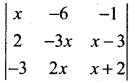If f(x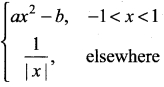) =  is differentiable at x = 1, then………
(a) a = \(\frac{1}{2}\), b = \(\frac{-3}{2}\)
(b) a = \(\frac{-1}{2}\), b = \(\frac{3}{2}\)
(c) a = –\(\frac{1}{2}\), b = –\(\frac{3}{2}\)
(d) a = \(\frac{1}{2}\), b = \(\frac{3}{2}\)
Solution:
(c) a = –\(\frac{1}{2}\), b = –\(\frac{3}{2}\)

Question 18.
∫sin 7x cos 5x dx =…………
(a) \(\frac{1}{2}\) [\(\frac{cos 12x}{2}\)+\(\frac{cos 2x}{2}\)] + c
(b) –\(\frac{1}{2}\) [\(\frac{cos 12x}{2}\)+\(\frac{cos 2x}{2}\)] + c
(c) –\(\frac{1}{2}\) [\(\frac{cos 6x}{6}\) + cos x] + c
(d) –\(\frac{1}{2}\) [\(\frac{sin 12x}{2}\)+\(\frac{sin 2x}{2}\)] + c
Solution:
(b) –\(\frac{1}{2}\) [\(\frac{cos 12x}{2}\)+\(\frac{cos 2x}{2}\)] + c

Question 19.
∫ \(\frac{1}{e^x}\) dx = ………..
(a) log e^x + c
(b) x + c
(c) \(\frac{1}{e^x}\) + c
(d) \(\frac{-1}{e^x}\)
Solution:
(d) \(\frac{-1}{e^x}\)

Question 20.
Two items are chosen from a lot containing twelve items of which four are defective. Then the probability that atleast one of the item is defective is…………
(a) \(\frac{19}{33}\)
(b) \(\frac{17}{33}\)
(c) \(\frac{23}{33}\)
(d) \(\frac{13}{34}\)
Solution:
(a) \(\frac{19}{33}\)

PART – II

II. Answer any seven questions. Question No. 30 is compulsory. [7 × 2 = 14]

Question 21.
Prove that \(\frac{tanθ+secθ-1}{tanθ-secθ+1}\) \(\frac{1+sinθ}{cosθ}\)
Solution:

Question 22.
Prove that the relation ‘friendship’ is not an equivalence relation on the set-of all people in chennai.
Solution:
S = aRa (i.e. ) a person can be a friend to himself or herself.
So it is reflextive.
aRb ⇒ bRa so it is symmetric
aRb, bRc does not ⇒ aRc
so it is not transitive
⇒ it is not an equivalence relation.

Question 23.
How many triangles can be formed by joining 15 points on the plane, in which no line joining any three points?
Solution:
No. of non-collinear points = 15
To draw a Triangle we need 3 points
∴Selecting 3 from 15 points can be done in ¹⁵C³ ways.
∴ No. of Triangle formed = ¹⁵C³
= \(\frac{15×14×13}{3×2×1}\) = 455

Question 24.
Expand (2x + 3)⁵
Solution:
By taking a = 2x, b = 3 and n = 5 in the binomial expansion of (a + b)ⁿ
we get (2x + 3)⁵ = (2x)⁵ + 5(2x)⁴3 + 10(2x)³3² + 10(2x)²3³ + 5(2x)3⁴ + 3⁵
= 32x⁵ + 240x⁴ + 720x³ + 1980x² + 810x + 243.

Question 25.
If λ = -2, determine the value of
Solution:
Given λ = -2
2λ = -4; λ² = (-2)² = 4; 3λ² + 1 = 3(4) + 1 = 13
6λ – 1 = 6(-2) – 1 = -13

expanding along R,
0(0) + 4 (0 + 13) +1 (-52 + 0) = 52 – 52 = 0
Aliter: The determinant value of a skew symmetric matrix is zero.

Question 26.
Compute \(\lim _{x \rightarrow 1} \frac{\sqrt{x}-1}{x-1}\)
Solution:
Here \(\lim _{x \rightarrow 1}\)(x – 1) = 0. In such cases, rationalise the numerator.

Question 27.
Differentiate the following \(\frac{x²}{a²}\)+ \(\frac{y²}{b²}\) = 1
Solution:
Given \(\frac{x²}{a²}\)+ \(\frac{y²}{b²}\) = 1
Differentiating w.r.to x

Question 28.
Evaluate \(\frac{1}{(x+1)²-25}\)
Solution:

Question 29.
Given that P(A) = 0.52, P(B) = 0.43, and P(A ∩ B) = 0.24, find p(A ∩ \(\bar { B }\))
Solution:
P(A ∩ \(\bar { B }\)) = P(A) – P(A ∩ B)
= 0.52 – 0.24 = 0.28
P(A ∩ \(\bar { B }\)) = 0.28

Question 30.
Show that 4x² + 4xy + y² – 6x – 3y – 4 = 0 represents a pair of parallel lines
Solution:
4x² + 4xy + y² – 6x – 3y – 4 = 0
a = 4, b = 1, h = 4/2 = 2
h² – ab = 2² – (4) (1) = 4 – 4 = 0
⇒ The given equation represents a pair of parallel lines.

PART-III

III. Answer any seven questions. Question No. 40 is compulsory. [7 × 3 = 21]

Question 31.
If A and B are two sets so that n(B – A) = 2n(A – B) = 4n(A ∩ B) and if n(A ∪ B) = 14 then find n(PA)
Solution:
To find n(P(A)), we need n(A).
Let n( A ∩ B) = t. Then n( A – B) = 2k and n(B – A) = 4k.
Now n(A ∪ B) = n(A – B) + n(B – A) + n(A ∩ B) = 7k.
It is given that n(A ∪ B) = 14. Thus 7k = 14 and hence k = 2.
So n(A – B) = 4 and n(B – A) = 8. As n(A) = n(A – B) + n(A ∩ B), we get n(A) = 6 and hence n(P(A)) = 2⁶ = 64.

Question 32.
Resolve \(\frac{1}{x²-a²}\) into partial fraction.
Solution:
Factorizing the denominator
Dr = x² – a² = (x – a) (x + a)

Equating the numerator we get
x – a = 0
⇒ x = a
x + a = 0
⇒ x = -a
1 = A (x + a) + B (x – a)
This equation is true for any value of x

Question 33.
Count the number of positive integers greater than 7000 and less than 8000 which are divisible by 5 provided that no digits are repeated.
Solution:
It should be a 4-digit number greater than 7000 and less than 8000. Then the thousand’s place will be the digit 7. Further, as the number must be divisible by 5 the unit place should be either 0 or 5.

As repetition is not permitted, the 100th place can be filled in 8 ways using remaining numbers and 10th place can be filled in 7 ways. Hence, the required number of numbers is 1 × 8 × 7 × 2 = 112.

Question 34.
Find the \(\sqrt[3]{126}\) approximately to two decimal places.
Solution:

Question 35.
Find the equation of the line through the intersection of the lines
3x + 2y + 5 = 0 and 3x – 4y + 6 = 0 and the point (1, 1)
Solution:
The family of equations of straight lines through the point of intersection of the lines is of the form (a₁x + b₁y + c₁) + (a₂x + b₂y + c₂) = 0
That is, (3x + 2y + 5) + λ (3x – 4y + 6) = 0
Since the required equation passes through the point (1, 1), the point satisfies the above equation Therefore {3 + 2(1) + 5} + λ(3 (1) – 4(1) + 6} = 0 ⇒ λ = -2
Substituting λ = -2 in the above equation we get the required equation as 3x – 10y + 7 = 0 (verify the above problem by using two points form)

Question 36.
Show that
Solution:

Question 37.
Complete the following table using calculator and use the result to estimate \(\lim _{x \rightarrow 2}\) \(\frac{x-2}{x²-x-2}\)

Solution:

Limit is 0.333…. = 0.\(\bar{3}\)

Question 38.
Differentiate \(\frac{e^{3x}}{1+e^x}\) with respect to x
Solution:

Question 39.
Evaluate: e^x (tan x + log sec x)
Solution:
Let I = ∫e^x (tan x + log sec x) dx
Take f(x) = log sec x
f(x) = \(\frac{1}{sec x}\) × sec x tan x = tan x
This is of the form ∫e^x[f(x) + f'(x)] dx = e^x f(x) + c
∴ ∫e^x(log sec x + tan x) dx = e^x log |sec x| + c

Question 40.
The position vectors of the vertices of a triangle are \(\vec{i}\) + 2\(\vec{j}\) + 3\(\vec{k}\), 3\(\vec{i}\) – 4\(\vec{j}\) + 5\(\vec{k}\) and -2\(\vec{i}\) + 3\(\vec{j}\) – 7\(\vec{k}\) Find the perimeter of a triangle.
Solution:
Let A, B, C be the vertices of triangle ABC,

PART – IV

IV. Answer all the questions. [7 × 5 = 35]

Question 41 (a).
If f : R → R is defined by f(x) = 3x – 5, prove that f is a bijection and find its inverse.
Solution:
p(x) = 3x – 5
Let g(y) = 3x – 5 ⇒ 3x = y + 5
x = \(\frac{y+5}{3}\)
Let g(y) = \(\frac{y+5}{3}\)
Now g o f(y) = g[(f(x))] = g(3x-5)

Thus g o f = I_x and f o g = I_y
f and g are bi-jections and inverse to each other. Hence f is a bi-jection and f^-1(y) = \(\frac{y+5}{3}\)
Replacing y by x we get f^-1(x) = \(\frac{x+5}{3}\)

[OR]

(b) Prove that tan^-1(\(\frac{m}{n}\)) – tan^-1(\(\frac{m-n}{m+n}\)) = \(\frac{π}{4}\)
Solution:

Question 42 (a).
Find the values of k so that the equation x² = 2x (1 + 3k) + 7(3 + 2k) = 0 has real and equal roots.
Solution:
The equation is x² – x(2) (1 + 3k) – 7 (3 + 2k) = 0
The roots are real and equal
⇒ Δ = 0 (i.e.,) b² – 4ac = 0
Here a = 1, b = -2 (1 + 3k), c = 7(3 + 2k)
So b² – 4ac = 0 ⇒ [-2 (1 + 3k)]² – 4(1) (7) (3 + 2k) = 0
(i.e.,) 4(1+ 3k)² – 28 (3 + 2k) = 0
(÷ by 4) (1 + 3k)² – 7(3 + 2k) = 0
1 + 9k² + 6k – 21 – 14k = 0
9k² – 8k – 20 = 0
(k – 2) (9k + 10) = 0
⇒ k – 2 > 0 or 9k + 10 = 0
⇒ k = 2 or k = \(\frac{-10}{9}\)
To solve the quadratic inequalities ax² + bx + c < 0 (or) ax² + bx + c > 0

[OR]

(b) If the roots of the equation (q – r) x² + (r – p)x + (p – q) = 0 are equal then show that p, q and r are in A.P.
Solution:
The roots are equal ⇒ Δ = 0
(i.e.) b² – 4ac = 0
Hence, a = q – r; b = r – p; c = p – q
b² – 4ac = 0
⇒ (r – p)² – 4(q – r)(p – q) = 0
r² + p² – 2pr – 4[qr – q² – pr + pq] = 0
r² + p² – 2pr – 4qr +4q² + 4pr – 4pq = 0
(i.e.) p² + 4q² + r² – 4pq – 4qr + 2pr = 0
(i.e.) (p – 2q + r)² = 0
⇒ p – 2q + r = 0
⇒ p + r = 2q
⇒ p, q, r are in A.P.

Question 43 (a).
Find the sum of all 4 digit-numbers that can be formed using the digits 1, 2, 3, 4 and 5 repetition not allowed?
Solution:
The given digits are 1, 2, 3, 4, 5
The no. of 4 digit numbers

= 5 × 4 × 3 × 2 = 120
(i.e) ⁵P₄ = 120
Now we have 120 numbers
So each digit occurs \(\frac{120}{5}\) = 24 times
Sum of the digits =1+2 + 3 + 4 + 5 = 15
Sum of number’s in each place = 24 × 15 = 360
Sum of numbers = 360 × 1 = 360
360 × 10 = 3600
360 × 100 = 36000
360 × 1000 = 360000
Total = 399960

[OR]

(b) Three vectors \(\vec{a}\), \(\vec{b}\) and \(\vec{c}\) are such that |\(\vec{a}\)| = 2,|\(\vec{b}\)| = 3, |\(\vec{c}\)| = 4 and \(\vec{a}\) + \(\vec{b}\) + \(\vec{c}\) = 0. Find 4\(\vec{a}\).\(\vec{b}\) + 3\(\vec{b}\).\(\vec{c}\) + 3\(\vec{c}\).\(\vec{a}\).
Solution:
Given \(\vec{a}\) + \(\vec{b}\) + \(\vec{c}\) = 0
⇒ \(\vec{a}\) + \(\vec{a}\) = –\(\vec{a}\)
so (\(\vec{a}\) + \(\vec{a}\))² = \(\vec{c}\)²
(i.e.) a² + b²+ 2\(\vec{a}\).\(\vec{b}\) = \(\vec{c}\)²
⇒ 4 + 9 + 2\(\vec{a}\).\(\vec{b}\) = 16
⇒ 2\(\vec{a}\).\(\vec{b}\) = 16 – 4 – 9 = 3
\(\vec{a}\) \(\vec{b}\) = 3/2
Again \(\vec{a}\) + \(\vec{b}\) + \(\vec{c}\) = 0
⇒ \(\vec{a}\) + \(\vec{c}\) = –\(\vec{b}\)
(\(\vec{a}\) + \(\vec{c}\))² = \(\vec{b}\)²
\(\vec{a}\)² + \(\vec{c}\)² + 2\(\vec{a}\).\(\vec{c}\) = \(\vec{b}\)²
4 + 16 + 2\(\vec{a}\) – \(\vec{a}\) = 9
2\(\vec{a}\) – \(\vec{c}\) = 9 – 4 – 16 = -11
\(\vec{a}\).\(\vec{c}\) = \(\frac{-11}{2}\) (i.e.,) \(\vec{c}\) – \(\vec{a}\) = \(\frac{-11}{2}\) (∵\(\vec{a}\).\(\vec{c}\) = \(\vec{c}\).\(\vec{a}\))
Also \(\vec{a}\) + \(\vec{b}\) + \(\vec{c}\) = 0
\(\vec{b}\) + \(\vec{c}\) = –\(\vec{a}\)
(\(\vec{b}\) + \(\vec{c}\))² = \(\vec{a}\)²
9 + 16 + 2\(\vec{b}\) – \(\vec{c}\) = 4
2\(\vec{b}\) – \(\vec{c}\) = 4 – 9 – 16 = -21
\(\vec{b}\) – \(\vec{c}\) = \(\frac{21}{2}\)
Here \(\vec{a}\).\(\vec{b}\) = 3/2 \(\vec{b}\).\(\vec{c}\) = \(\frac{-21}{2}\) and \(\vec{c}\).\(\vec{a}\) = \(\frac{-11}{2}\)

Question 44 (a).
If a, b, c are respectively the p^th, q^th and r^th terms of a G.P. show that (q – r) log a+ (r – p) log b + (p – q) log c = 0.
Solution:
Let the G.P. be l, lk, lk²,…
We are given t_p = a, t_q = b, t_r = c
⇒ a = lk^p-1; b = l k^q-1; c = l k^r-1
a = lk^p-1 ⇒ log a = log l + log k^p-1 = log l + (p – 1) log k
b = lk^q-1 ⇒ log b = log l + log k^q-1 = log l + (q – 1) log k
c = lk^r-1 ⇒ log r = log l + log k^r-1 = log l + ( r – 1) log k
LHS = (q – r) log a + (r – p) log b + (p – q) log c
= (q – r) [log l + (p – 1) log k ] + (r – p) [log l + (q – 1) log k]
(p – q) [log l + (r – 1) log k]
= log l[p – q + q – r + r – p] + log k[(q – r)(p – 1) + (r – p) (q – 1) + (p – q)(r – 1)]
= log l (0) + log k[p (q – r) + q (r – p) + r(p – q) – (q – r + r – p + p – q)]
= 0 = RHS.

[OR]

(b) If A = \(\left[\begin{array}{ll} \frac{1}{2} & \alpha \\ 0 & \frac{1}{2} \end{array}\right]\), Prove that \(\sum_{k=1}^{n}\) det(A_k) = \(\frac{1}{3}\) (1 – \(\frac{1}{4^n}\))
Solution:

Which is a G.P with a = \(\frac{1}{4}\) and r = \(\frac{1}{4}\)

Question 45 (a).
Find the equation of the straight line passing through intersection of the straight lines 5x – 6y = 1 and 3x + 2y + 5 = 0 and perpendicular to the straight line 3x – 5y + 11 = 0.
Solution:
Equation of line through the intersection of straight lines 5x – 6y = 1 and 3x + 2y + 5 = 0 is 5x – 6y – 1 + k (3x + 2y + 5) = 0 x(5 + 3k) + y(-6 + 2k) + (-1 + 5k) = 0
This is perpendicular to 3x – 5y + 11 = 0
That is, the product of their slopes is -1
–\(\frac{5+3k}{-6+2k}\) (-\(\frac{3}{-5}\)) = -1
⇒ \(\frac{15+9k}{-30+10k}\) = 1
⇒ 15 + 9k = -30 + 10k
45 = k
Required equation is 5x – 6y – 1 + 45 (3x + 2y + 5) = 0
140x + 84y + 224 = 0
20x + 12y + 32 = 0
5x + 3y + 8 = 0

[OR]

(b) Integrate the following \(\frac{√x}{1+√x}\) dx
Solution:

Question 46 (a).
If u = tan^-1(\(\frac{\sqrt{1+x^{2}}-1}{x}\)) and v = tan^-1x, find \(\frac{dx}{dy}\)
Solution:

[OR]

(b)
If y = Ae^6x + Be^-x prove that \(\frac{d²y}{dx²}\) – 5\(\frac{dx}{dy}\) – 6y = 0
Solution:
y = Ae^6x + Be^-x …. (1)
y₁ = \(\frac{dx}{dy}\) = Ae^6x(6) + Be^-x (-1)
= 6Ae^6x – Be^-x…. (2)
y₂ = \(\frac{dx}{dy}\) = 6Ae^6x (6) – Be^-x (-1)
= 36Ae^6x + Be^-x ……(3)
eliminating A and B from (1), (2) and (3) we get

y (6 + 36) – y₁ (1 – 36) + y₂ (-1 – 6) = 0
42y + 35y₁ – 7y₂ = 0
(÷ by -7) y₂ – 5y₁ – 6y = 0
(i.e.,) \(\frac{d²y}{dx²}\) – 5\(\frac{dx}{dy}\) – 6y = 0

Question 47 (a).
Evaluate \(\lim _{x \rightarrow 0} \frac{\sqrt{x^{2}+1}-1}{\sqrt{x^{2}+16}-4}\)
Solution:

[OR]
(b) Urn-I contains 8 red and 4 blue balls and urn-II contains 5 red and 10 blue balls. One urn is chosen at random and two balls are drawn from it. Find the probability that both balls are red.
Solution:
Let A₁ be the event of selecting um-I and A₂ be the event of selecting um-II.
Let B be the event of selecting 2 red balls.

We have to find the total probability of event B. That is, P(B).
Clearly A₁ and A₂A₁ are mutually exclusive and exhaustive events.
We have

You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 2 Chapter 3 Bill, Profit and Loss Ex 3.1

Question 1.
A School purchases some furniture and gets the following bill.

(i) What is the name of the store?
(ii) What is the serial number of the bill?
(iii) What is the cost of a blackboard?
(iv) How many sets of benches and desks does the school buy?
(v) Verify whether the total bill amount is correct.
Solution:
(i) Mullai Furniture Mart, Thanjavur
(ii) Serial No. 728
(iii) Cost of a blackboard is ₹ 3000
(iv) 50 sets
(v) Yes, the total bill amount is correct.

Question 2.
Prepare a bill for the following books of biographies purchased from Maruthu Book Store, Chidambaram on 12.04.2018 bearing the bill number 507.
10 copies of Subramanya Bharathiar @ ₹ 55 each, 15 copies of Thiruvalluvar @ ₹ 75 every 12 copies of Veeramamunivar @ ₹ 60 each and 12 copies of Thiru. Vi.Ka @ ₹ 70 each.
Solution:

Question 3.
Fillup the appropriate boxes in the following table.

Solution:
(i) Here Cost price < Selling price
Profit = S.P – C.P = 120 – 100 = ₹ 20
Here S.P > C.P
Profit = S.P – C.P = 120 – 110 = ₹ 10
(iii) Profit = ₹ 20
Profit = S.P. – C.P
⇒ 20 = S.P. – 120
⇒ 20 + 120 = S.P
⇒ S.P = ₹ 140
(iv) C.P = ₹ 100
S.P = ₹ 90
Here S.P < C.P
Loss = 100 – 90 = ₹ 10
(v) Profit = S.P – C.P
⇒ 25 = S.P – 120
⇒ 25 + 120 = S.P
⇒ S.P = ₹ 145

Question 4.
Fill up the appropriate boxes in the following table.

Solution:
(i) S.P. = M.P – Discount
S.P = ₹ 130
Here S.P > C.P
Profit = S.P – C.P = 130 – 110 = ₹ 20
(ii) S.P = M.P – Discount = 130 – 10 = ₹ 120
Here S.P > C.P
Profit = S.P – C.P = ₹ 120 – ₹ 110 = ₹ 10
(iii) S.P = M.P – Discount = 130 – 30 = ₹ 100
Here S.P < C.P
Loss = 110 – 100 = ₹ 10
(iv) C.P = ₹ 110
M.P = ₹ 120
Loss = ₹ 10
Loss = C.P – S.P
⇒ 10 = 110 – SP
⇒ SP = 110 – 10 = ₹ 100
Discount = M.P – S.P = 120 – 100 = ₹ 20
(v) M.P = ₹ 120
Discount = ₹ 10
Discount = M.P – S.P
⇒ 10 = 120 – S.P
⇒ S.P = 120 – 10 = ₹ 110
Profit = ₹ 20
Profit = S.P – C.P
⇒ 20 = 110 – C.P
⇒ C.P = 110 – 20 = 90

Question 5.
Rani bought a set of bangles for Rs 310. Her neighbour liked it most. So, Rani sold it to her for Rs 325. Find the profit or loss to Rani.
Solution:
CP = Rs 310
SP = Rs 325
Profit = SP – CP = Rs 325 – Rs 310 = Rs 15

Question 6.
Sugan bought a Jeans pant for ₹ 750. It did not fit him. He sold it to his friend for ₹ 710. Find the profit or loss to sugan.
Solution:
C.P of the Jeans pant = ₹ 750
S.P of the Jeans pant = ₹ 710
Here S.P < C.P
Loss = C.P – S.P = 750 – 710 = ₹ 40
Loss = ₹ 40

Question 7.
Somu bought a second hand bike for Rs 28,000 and spent Rs 2,000 on its repair. He sold it for Rs 30,000. Find his profit or loss.
Solution:
CP = Rs 28,000 + Rs 2,000
CP = Rs 30,000
SP = Rs 30,000
CP = SP
No profit / Loss

Question 8.
Muthu has a car worth ₹ 8,50,000 and he wants to sell it at a profit of ₹ 25,000. What should be the selling price of the car? Solution:
Cost price of the car = ₹ 8,50,000
Expected profit = ₹ 25,000
We know that profit = S.P – C.P
25000 = S.P – 8,50,000
⇒ 25,000 + 8,50,000 = S.P
⇒ S.P = 8,75,000
Selling Price of the car should be ₹ 8,75,000

Question 9.
Valarmathi sold her pearl set for Rs 30,000 at profit of Rs 5,000. Find the cost price of the pearl set.
Solution:
SP = Rs 30,000
Profit = Rs 5,000
CP = SP – Profit
= Rs 30,000 – Rs 5,000
= Rs 25,000

Question 10.
If Guna marks his product to be sold for ₹ 325 and gives a discount of ₹ 30, then find the S.P.
Solution:
Marked Price of the Product = ₹ 325
Discount = ₹ 30
Selling Price = M.P – Discount = 325 – 30 = ₹ 295
S.P. = ₹ 295

Question 11.
A man buys a chair for 1,500. He wants to sell it at a profit of Rs 250 after making a discount of Rs 100. What is the M.P. of the chair?
Solution:
CP = Rs 1,500
Profit = Rs 250
SP = CP + Profit
= Rs 1,500 + Rs 250
= Rs 1,750
Discount = Rs 100
SP = MP – Discount
MP = SP + Discount
= Rs 1,750 + Rs 100
= Rs 1,850

Question 12.
Amutha marked her home product of pickle as ₹ 300 per pack. But she sold it for only ₹ 275 per pack. What was the discount offered by her per pack?
Solution:
M.P of the pickle = ₹ 300
S.P = ₹ 275
S.P = M.P – Discount
⇒ 275 = 300 – Discount
⇒ Discount = 300 – 275 = ₹ 25
Discount per pack = ₹ 25

Question 13.
Valavan bought 24 eggs for Rs 96. Four of them were broken and also he had a loss of Rs 36 on selling them. What is the selling price of one egg?
Solution:
Cost of 24 eggs = Rs 96
Since 4 of the eggs were broken, the number of remaining eggs = 24 – 4 = 20
Since the loss is Rs 36
Selling price of 20 eggs
SP = CP – Loss
= Rs 96 – Rs 36
= Rs 60
∴ Cost of 1 egg = Rs 60 / 20 = Rs 3

Question 14.
Mangai bought a cell phone for ₹ 12,585. It fell down. She spent ₹ 500 on it repair. She sold it for ₹ 7,500. Find her profit or loss.
Solution:
Cost of the cell phone = ₹ 12,585
Spent on repairs = ₹ 500
Cost price = Cost of cell phone + repair charge = 12,585 + 500 = ₹ 13,085
S.P. = 7,500
Here C.P > S.P
∴ It is loss
Loss = C.P – S.P = 13,085 – 7500 = ₹ 5,585
Loss = ₹ 5,585

Objective Type Questions

Question 15.
Discount is subtracted from ……… to get S.P.
(a) M.P
(b) C.P
(c) Loss
(d) Profit
Solution:
(a) M.P

Question 16.
‘Overhead expenses’ is always included in _____.
(a) S.P
(b) C.P.
(c) Profit
(d) Loss
Solution:
(b) C.P.

Question 17.
There is no profit or loss when
(a) C.P = S.P
(b) C.P > S.P
(c) C.P < S.P
(d) M.P = Discount
Solution:
(a) C.P = S.P

Question 18.
Discount = M.P _____
(a) Profit
(b) S.P
(c) Loss
(d) C.P
Solution:
(b) S.P