Prasanna

Tamilnadu State Board New Syllabus Samacheer Kalvi 9th Maths Guide Pdf Chapter 1 கண மொழி Ex 1.2 Textbook Questions and Answers, Notes.

TN Board 9th Maths Solutions Chapter 1 கண மொழி Ex 1.2

கேள்வி 1.
பின்வரும் கணங்களின் ஆதி எண்ணைக் காண்க.
(i) M = {p, q, r, s, t, u}
விடை:
n(M) = 6

(ii) P = {x : x = 3n + 2, n ∈ W மற்றும் x < 15}
விடை:
n(P) = 5

(iii) Q = {y : y = [lat∈x]\frac{4}{3 n}[/lat∈x], n ∈ N மற்றும் 2 < n ≤ 5}
விடை:
n(Q) = 3

(iv) R = {x : x ஆனது முழுக்கள், x ∈ Z மற்றும் -5 ≤ x < 5}
விடை:
n(R) = 10

(v) S = 1882 முதல் 1906 வரை உள்ள அனைத்து நெட்டாண்டுகளின் (Leap year) கணம்.
விடை:
n(S) = 5

கேள்வி 2.
பின்வரும் கணங்களில் எவை முடிவுறு கணம்,எவை முடிவுறாக் கணம் எனக் கூறுக
(i) X = தமிழகத்தில் உள்ள மாவட்டங்களின் கணம்.
விடை:
முடிவுறு

(ii) Y = ஓரு புள்ளி வழிச் செல்லும் நேர்க்கோடுகளின் கணம்.
விடை:
முடிவுறா

(iii) A = {x : x ∈ Z மற்றும் x < 5}
விடை:
முடிவுறா

(iv) B = {x : x² – 5x + 6 = 0, x ∈ N}
விடை:
முடிவுறு பின்வருவனவற்றில் எவை சமான கணங்கள் அல்லது சமமற்ற கணங்கள் அல்லது சமகணங்கள் எனக் கூறுக.
(i) A=ஆங்கில உயிரெழுத்துகளின் கணம். B = ‘VOWEL என்ற சொல்லில் உள்ள எழுத்துகளின் கணம்.
விடை:
சமான கணங்கள்.

(ii) C = {2, 3, 4, 5}
D= x : x ∈ W, 1 < x < 5}
விடை:
சமமற்ற கணங்கள்

(iii) X = x : x என்பது “LIFE” என்ற சொல்லில் உள்ள எழுத்துகளின் கணம். Y = {F, I, L, E}
விடை:
சம கணங்கள்

(iv) G = {x : x ஒரு பகா எண் 3 < x < 23}
H = {x : x என்பது 18 இன் வகு எண்க ள்
விடை:
சமான கணங்கள்

கேள்வி 4.
பின்வருவனவற்றில் எவை வெற்றுக்கணம்; எவை ஒருறுப்புக்கணம் எனக் காண்க.
(i) A = {x : x ∈ N, 1 < x < 2}
விடை:
வெற்றுக்கணம்.

(ii) B = 2 ஆல் வகுபடாத அனைத்து இரட்டைப்படை இயல் எண்களின் கணம். விடை:
வெற்றுக்கணம்.

(iii) C = {0}
விடை:
ஒருறுப்புக்கணம்.

(iv) D = நான்கு பக்கங்களை உடைய முக்கோணங்களின் கணம்.
விடை:
வெற்றுக் கணம்.

கேள்வி 5.
கொடுக்கப்பட்ட கணச் சோடிகள் வெட்டும் கணங்களா? இல்லை வெட்டாக் கணங்களா?

(i) A = {f, i, a, s} மற்றும் B = {a, n, f, h, s}
விடை:
A = { f, i, a, s}
B = {a, n, f , h, s}
A ∩B = { f, a, s}
A மற்றும் B வெட்டும் கணங்கள்

(ii) C = {x : x ஒரு பகா எண், x > 2} மற்றும் D = {x : x ஓர் இரட்டைப்படை பகாஎண் }
விடை:
C = {3}
D = {2}
C ∩ D = {φ}
C மற்றும் D வெட்டாக் கணங்கள்

(iii) E = {x : x என்பது 24 இன் காரணி} மற்றும் F = {x : x ஆனது 3இன் மடங்கு, x < 30}
விடை:
E = {2, 4, 6, 8, 12, 24}
F = {3, 6, 9, 12, 15, 18, 21, 24, 27}
E ∩ F = {6, 12, 24}
E மற்றும் F வெட்டும் கணங்கள்.

கேள்வி 6.
S = {சதுரம், செவ்வகம், வட்டம், சாய்சதுரம், முக்கோணம்} எனில் பின்வரும், S இன் உட்கணங்களின் உறுப்புகளைப் பட்டியலிடுக
(i) நான்கு சமபக்கங்களை உடைய வடிவங்களின் கணம்.
விடை:
{சதுரம், சாய்சதுரம்)

(ii) ஆரங்களை உடைய வடிவங்களின் கணம்.
விடை:
{வட்டம்}.

(iii) உட்கோணங்களின் கூடுதல் 180° ஆக உடைய வடிவங்களின் கணம்.
விடை:
{முக்கோணம்}.

(iv) 5 பக்கங்களை உடைய தள வடிவங்களின் கணம்.
விடை:
{}

கேள்வி 7.
A = {a,{a,b}} எனில், A – இன் எல்லா உட்கணங்களையும் எழுதுக.
விடை:
A இன் உட்கணங்கள் f,{a}, {a,b}, {a,{a,b}}

கேள்வி 8.
பின்வருவனவற்றின் அடுக்குக்கணத்தைக் காண்க.
(i) A = {a, b}
விடை:
P(A) = {φ, {a}, {b}, {a, b}}

(ii) B= {1, 2, 3}
விடை:
P(B) = { { }, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1,2,3}}

(iii) D = {p, q, r, s}
விடை:
P(D) = {{ }, {p}, {q}, {r}, {s}, {p, q}, {p, r}, {p,s}, {q, r}, {q, s}, {r, s}, {p, q, r}, {p, q, s}, {p, r, s}, {q, r, s}, {p, q, r, s}}

(iv) E = φ
விடை:
P(E) = { {} }

கேள்வி 9.
பின்வரும் கணங்களின் உட்கணங்கள் மற்றும் தகு உட்கணங்களின் எண்ணிக்கையைக் காண்க.
(i) W = {சிவப்பு, நீலம், மஞ்சள்}
விடை:
இங்கு m = 3
உட்கணங்களின் எண்ணிக்கை 2^m = 2³ = 8
தகு உட்கணங்களின் எண்ணிக்கை = 2^m – 1
= 2³ – 1
= 8 – 1 = 7

(ii) X = {x² : x ∈ N, x² ≤ 100}
விடை:
X = {1, 4, 9, 16, 25, 36, 49, 64, 81} இங்கு m =9 n(X) = 9
உட்கணங்களின் எண்ணிக்கை
2^m = 2⁹ = 1024
தகு உட்கணங்களின் எண்ணிக்கை = 2^m -1
= 1024 – 1
= 1023

Question 10.
(i) n(A) = 4, எனில் n[P(A)] ஐக் காண்க
விடை:
(i) n(A) = 4 n[P(A)] = 2^m, m = 4
n[P(A)]=2^m = 2⁴
n[P(A)] = 2 x 2 x 2 x 2 = 16

(ii) If n(A)=0 எனில், n[P(A)] ஐக் காண்க
விடை:
n(A) = 0 n[P(A)]= 2^m

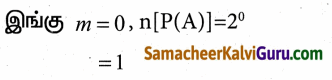
(iii) If [P(A)] = 256 எனில், n(A) ஐக் காண்க
விடை:
n[P(4)]= 256
2^m = 256
2m = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2
m = 8
2^m = 2⁸
n(A) = m
n(A) = 8

Tamilnadu State Board New Syllabus Samacheer Kalvi 9th Maths Guide Pdf Chapter 1 கண மொழி Ex 1.1 Textbook Questions and Answers, Notes.

TN Board 9th Maths Solutions Chapter 1 கண மொழி Ex 1.1

கேள்வி 1.
பின்வருவனவற்றில் எவை கணங்களாகும்?
(i) ஒன்று முதல் 100 வரையுள்ள பகாஎண்களின் தொகுப்பு.
விடை:
கணம்.

(ii) இந்தியாவில் உள்ள செல்வந்தர்களின் தொகுப்பு.
விடை:
கணமல்ல

(iii) இந்தியாவில் உள்ள ஆறுகளின் தொகுப்பு.
விடை:
கணம்

(iv) வளைகோல் பந்தாட்டத்தை நன்றாக விளையாடும் வீரர்களின் தொகுப்பு.
விடை:
கணமல்ல

கேள்வி 2.
பின்வரும் ஆங்கிலச் சொற்களிலுள்ள எழுத்துகளைப் பட்டியல் முறையில் எழுதுக.
(i) INDIA
விடை:
A = {I, N, D, A}

(ii) PARALLELOGRAM
விடை:
B = {P, A, R, L, E, G, O, M}

(iii) MISSISSIPPI
விடை:
C = {M, I, S, P}

(iv) CZECHOSLOVAKIA
விடை:
D = {C, Z, E, H, O, S, L, V, A, K, I}

கேள்வி 3.
A = {0,3,5,8}, B = {2,4,6,10} மற்றும் C = {12, 14, 18, 20} என்ற கணங்களைக் கொண்டு.
(அ) சரியா, தவறா எனக் கூறுக.
(i) 18 ∈ C
விடை:
சரி

(ii) 6 ∉ A
விடை:
சரி

(iii) 14 ∉ C
விடை:
தவறு

(iv) 10 ∈ B
விடை:
சரி

(v) 5 ∈ B
விடை:
தவறு

(vi) O ∈ B
விடை:
தவறு

(ஆ) கோடிட்ட இடங்களை நிரப்புக :

(i) 3∈___
விடை:
A

(ii) 14∈ __
விடை:
C

(iii) 1 8__ B
விடை:
4

(iv) 4 __ B
விடை:
4

கேள்வி 4.
பின்வரும் கணங்களைப் பட்டியல் முறையில் எழுதுக.
(i) A = 20 – க்கும் குறைவான இரட்டைப்படை இயல் எண்களின் கணம்.
விடை:
A = {2, 4, 6, 8, 10, 12, 14, 16, 18}

(ii) B = {y: y = \(\frac{1}{2 n}\), n ∈ N, n < 5}
1 1 1 1 11
விடை:
B = {\(\frac{1}{2}\), \(\frac{1}{4}\), \(\frac{1}{6}\), \(\frac{1}{8}\), \(\frac{1}{10}\)}

(iii) C = {x : x என்பது ஒரு முழுக்கன எண் மற்றும் 27 < x < 216}
விடை:
C = {64, 125}

(iv) D = {x : x ∈ Z – 5 < x ≤ 2}
விடை:
D = {-4, -3, -2, -1, 0, 1, 2}

கேள்வி 5.
பின்வரும் கணங்களைக் கணக் கட்டமைப்பு முறையில் எழுதுக.
(i) B = ஒரு நாள் ஆட்டங்களில் இரட்டைச் சதமடித்த இந்திய மட்டைப் பந்து வீரர்களின் தொகுப்பு.
விடை:
B = {x: x என்பது ஒரு நாள் சர்வதேச போட்டிகளில் இரட்டைச் சதமடித்த இந்திய வீரர்}

(ii) c = {\(\frac{1}{2}\), \(\frac{2}{3}\), \(\frac{3}{4}\)}
விடை:
C={x : x =\(\frac{n}{n+1}\); n ∈N)}

(iii) D ஓர் ஆண்டில் உள்ள தமிழ் மாதங்களின் தொகுப்பு.
விடை:
D = {x : x என்பது ஓர் ஆண்டிலுள்ள தமிழ் மாதம்}

(iv) E = 9 – க்கும் குறைவான ஒற்றை முழு எண்களின் கணம்.
விடை:
E = {x : x என்பது 9ஐ விடக் குறைவான ஒற்றை முழு எண்

கேள்வி 6.
பின்வரும் கணங்களை விவரித்தல் முறையில் எழுதுக.
(i) P = {சனவரி, சூன், சூலை}
விடை:
P = ‘J’ என்ற எழுத்தில் தொடங்கும் ஆங்கில மாதங்களின் கணம்.

(ii) Q = {7, 11, 13, 17, 19, 23, 29}
விடை:
Q = 5 மற்றும் 31 இக்கு இடைப்பட்ட பகா எண்களின் கணம்.

(iii) R = {x : x ∈ N, x < 5}
விடை:
R = 5 ஐ விடக் குறைவான இயல் எண்களின் கணம்.

(iv) S = {x : x ஓர் ஆங்கில மெய்யெழுத்து}
விடை:
S =ஆங்கில மெய்யெழுத்துக்களின் கணம்.

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 5 இரு பரிமாண பகுமுறை வடிவியல் – II Ex 5.3 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 5 இரு பரிமாண பகுமுறை வடிவியல் – II Ex 5.3

பின்வரும் சமன்பாடுகளிலிருந்து அவற்றின் கூம்பு வளைவு வகையை கண்டறிக.

கேள்வி 1.
2x² – y² = 7
தீர்வு:
2x² – y² = 7
இங்கு A = 1, C = -1, F = -7
இங்கு A ≠ C மற்றும் A மற்றும் C ஒன்றுக் கொன்று எதிர்குறிகளை கொண்டுள்ளன. ஆகையால் கொடுக்கப்பட்ட சமன்பாடு அதிபர வளையத்தை குறிக்கிறது.

கேள்வி 2.
3x² + 3y² – 4x + 3y + 10 = 0
தீர்வு:
3x² + 3y² – 4x + 3y + 10 = 0
இங்கு A = 3, C = 3, D = -4, E = 3 மற்றும் F = 10
இங்கு A = C மற்றும் xy உறுப்பு இல்லை.
ஆகையால் கொடுக்கப்பட்ட சமன்பாடு வட்டத்தை குறிக்கிறது.

கேள்வி 3.
3x² + 2y² = 14
தீர்வு:
3x² + 2y² = 14
இங்கு A = 3, C = 2 மற்றும் F = -14
A ≠ C மற்றும் A மற்றும் C ஒரே குறியை கொண்டுள்ளன. ஆகையால் கொடுக்கப்பட்ட சமன்பாடு நீள்வட்டத்தை குறிக்கிறது.

கேள்வி 4.
x² + y² + x – y = 0
தீர்வு:
x² + y² + x – y = 0
இங்கு A = 1, C = 1, D = 1, E = -1
இங்கு A = C மற்றும் .xy உறுப்பு இல்லை.
ஆகையால் சமன்பாடு வட்டத்தை குறிக்கிறது.

கேள்வி 5.
11x² – 25y² – 44x + 50y – 256 = 0
தீர்வு:
11x² – 25y² – 44x + 50y – 256 = 0
A = 11, C = -25, D = -44, E = 50, மற்றும் F = -256
இங்கு A ≠ C மற்றும் A மற்றும் C ஒன்றுக் கொன்று எதிரான குறிகளை கொண்டுள்ளன. ஆகையால் கொடுக்கப்பட்ட சமன்பாடு அதிபர
வளையத்தை குறிக்கிறது.

கேள்வி 6.
y² + 4x + 3y + 4 = 0
தீர்வு:
y² + 4x + 3y + 4 = 0
இங்கு A = 0, C = 1, D = 4, E = 3, F = 4 B = 0 மற்றும் A அல்லது C ஆனது 0 ஆகும். ஆகையால் கொடுக்கப்பட்ட சமன்பாடு பரவளையத்தை குறிக்கிறது.

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 4 நேர்மாறு முக்கோணவியல் சார்புகள் Ex 4.5 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 4 நேர்மாறு முக்கோணவியல் சார்புகள் Ex 4.5

கேள்வி 1.
மதிப்பு உள்ளது எனில் பின்வருவனவற்றிக்கு மதிப்பு காண்க. மதிப்பு இல்லையெனில் அதற்கான காரணம் தருக.
(i) sin^-1 (cos π)
(i) tan^-1 \(\left(\sin \left(\frac{-5 \pi}{2}\right)\right)\)
(iii) sin^-1(sin 5)
தீர்வு:
(i) sin^-1(cos π)
⇒ sin^-1(cos π) = x என்க
⇒ sin^-1(-1) = x
[∵ cos π = -1]
⇒ -1 = sin x ⇒ sin x = -sin \(\frac{\pi}{2}\)
⇒ sin x = sin \(\left(\frac{-\pi}{2}\right)\) [∵\(\frac{-\pi}{2}\) ∈ \(\left[\frac{-\pi}{2}, \frac{\pi}{2}\right]\)] ∵ sin^-1cos π = \(\frac{-\pi}{2}\)
⇒ x = \(\frac{-\pi}{2}\)

(ii)

(iii) sin^-1(sin 5)
sin^-1(sin 5) = θ; θ ∈ \(\left[\frac{-\pi}{2}, \frac{\pi}{2}\right]\) என அறிவோம்
தோராயமாக கருதுக \(\frac{\pi}{2}\) = \(\frac{11}{7}\)

sin^-1(sin 5) = sin^-1(sin(5 – π))
= 5 – 2π [∵ 5 – 2π ∈ –\(\frac{\pi}{2}\), \(\frac{\pi}{2}\)]

கேள்வி 2.
முக்கோணத்தினை மேற்கோளாகக் கொண்டு x-ன் மதிப்பு காண்க.
(i) sin(cos^-1(1 – x))
(ii) cos(tan^-1(3x – 1))
(iii) tan \(\left(\sin ^{-1}\left(x+\frac{1}{2}\right)\right)\)
தீர்வு:
(i) sin(cos^-1(1 – x))
நமக்கு தெரியும்
0 ≤ x ≤ 1 எனில், cos^-1 x = sin^-1\(\left(\sqrt{1-x^{2}}\right)\)
∴ cos^-1(1 – x) = sin^-1\(\sqrt{1-(1-x)^{2}}\) [∵ 0 ≤ 1 – x ≤ 1]
= sin^-1\(\left(\sqrt{1-\left(1+x^{2}-2 x\right)}\right)\)
= sin^-1\(\left(\sqrt{\left.1-1-x^{2}+2 x\right)}\right)\) = sin^-1\(\left(\sqrt{2 x-x^{2}}\right)\)
∴ sin^-1(cos^-1(1 – x)) = sin(sin^-1\(\left(\sqrt{2 x-x^{2}}\right)\))
= \(\sqrt{2 x-x^{2}}\)

(ii) cos(tan^-1(3x – 1))
நமக்கு தெரியும்

(iii)

கேள்வி 3.

தீர்வு:
(i)

(ii)

(iii)

கேள்வி 4.
நிரூபிக்க :
(i) tan^-1\(\) + tan^-1\(\) – tan^-1\(\)
(ii) sin^-1\(\) – cos^-1\(\) = sin^-1\(\)
தீர்வு:
(i)

எனவே நிரூபிக்கப்பட்டது.

(ii)
sin^-1\(\left(\frac{3}{5}\right)\) – cos^-1\(\left(\frac{12}{13}\right)\) = sin^-1\(\left(\frac{16}{65}\right)\)
sin^-1 \(\left(\frac{3}{5}\right)\) = x ⇒ sin x = \(\left(\frac{3}{5}\right)\)

மற்றும் cos x = \(\frac{\mathrm{adj}}{\text { hyp }}\) = \(\frac{4}{5}\)

எனவே நிரூபிக்கப்பட்டது.

கேள்வி 5.
நிரூபிக்க: tan^-1x + tan^-1y + tan^-1z = tan^-1\(\left(\frac{x+y+z-x y}{1-x y-y z-z}\right)\)
தீர்வு:
நமக்கு தெரியும்

[(1) ஐ பயன்படுத்த]

எனவே நிரூபிக்கப்பட்டது.

கேள்வி 6.
tan^-1x + tan^-1y + tan^-1z = π எனில், x + y + z = xyz எனக் காட்டுக.
தீர்வு:
கேள்வி எண் 5 லிருந்து
tan^-1x + tan^-1y+tan^-1z = tan^-1 \(\left(\frac{x+y+z-x y z}{1-x y-y z-z x}\right)\)

⇒ x + y + z – xyz = 0
⇒ x + y + z = xyz

கேள்வி 7.
|x| < \(\frac{1}{\sqrt{3}}\) எனில் tan¹ x+ tan¹\(\frac{2 x}{1-x^{2}}\) =
tan^-1\(\left(\frac{3 x-x^{3}}{1-3 x^{2}}\right)\) என நிறுவுக.
தீர்வு:
LHS = tan^-1x + tan^-1\(\frac{2 x}{1-x^{2}}\)

கேள்வி 8.

தீர்வு:

கேள்வி 9.
(i) sin^-1\(\left(\frac{\mathbf{5}}{\boldsymbol{x}}\right)\) + sin^-1\(\left(\frac{\mathbf{12}}{\boldsymbol{x}}\right)\) = \(\frac{\pi}{2}\)
(ii) 2tan^-1x = cos^-1 \(\frac{1-a^{2}}{1+a^{2}}\) – cos^-1 \(\frac{1-b^{2}}{1+b^{2}}\), a > 0, b > 0
(iii) 2tan^-1 – cos^-1(x + 2) = tan^-1(2 cosec x)
(iv) cot^-1x – cot^-1(x + 2) = \(\frac{\pi}{2}\), x > 0
தீர்வு:
(i) கொடுக்கப்பட்ட sin^-1\(\left(\frac{5}{x}\right)\) + sin^-1\(\left(\frac{12}{x}\right)\) = \(\frac{\pi}{2}\)
நமக்கு தெரியும்
sin^-1x + sin^-1y = sin^-1\(\left(x \sqrt{1-y^{2}}+y \sqrt{1-x^{2}}\right)\)
இங்கு x² + y² ≤ 1 அல்லது xy < 0

x² + y² ≤ 1 அல்லது xy < 0 எனில் மட்டுமே இது சரி
y = \(\frac{5}{x}\) மற்றும் y = \(\frac{12}{x}\) என்க

சாத்தியமில்லை
∴ x² ≥ 13 தீர்வாகும்.
கொடுக்கப்பட்ட sin^-1\(\left(\frac{5}{x}\right)\) + sin^-1\(\left(\frac{12}{x}\right)\) = \(\frac{\pi}{2}\)

x = 13 எனில் மட்டுமே இது சரி
∴ x = 13 தீர்வாகும்.

(ii) 2tan^-1x = cos^-1\(\frac{1-a^{2}}{1+a^{2}}\) – cos^-1\(\frac{1-b^{2}}{1+b^{2}}\), a > 0, b > 0

⇒ tan^-1x = θ – φ

(iii) 2tan^-1(cos x) = tan^-1(2 cosec x)



⇒ 2 sin x cos x – 2 sin²x = 0
⇒ 2 sin x(cos x – sin x) = 0

எனவே தீர்வுகள் x = nπ அல்லது
x = nπ + \(\frac{\pi}{4}\), n ∈ ℤ

(iv) cot^-1(x) – cot^-1(x + 2) = \(\frac{\pi}{12}\), x > 0



இருபுறமும் வர்க்க மூலம் எடுக்க கிடைப்பது

x = என்பது தீர்வாகும்

கேள்வி 10.
சமன்பாட்டின் தீர்வுகளின் எண்ணிக்கையைக் காண்க. tan^-1(x – 1) + tan^-1(x + 1) = tan^-1(3x)
தீர்வு:
கருதுக tan^-1(x – 1) + tan^-1(x + 1)

குறுக்கு பெருக்கல் மூலம் நமக்கு கிடைப்பது முப்படி சமன்பாடாகும்.
ஆகையால் கொடுக்கப்பட்ட சமன்பாட்டிற்கு மூன்று தீர்வுகள் இருக்கும்.

Tamilnadu State Board New Syllabus Samacheer Kalvi 9th Maths Guide Pdf Chapter 9 நிகழ்தகவு Ex 9.3 Textbook Questions and Answers, Notes.

TN Board 9th Maths Solutions Chapter 9 நிகழ்தகவு Ex 9.3

பலவுள் தெரிவு வினாக்கள்

கேள்வி 1.
0 மற்றும் 1-க்கும் இடைப்பட்ட ஓர் எண்ணைக் கொண்டு உறுதியற்றவற்றை அளவிடுவது எவ்வாறு அழைக்கப்படுகிறது.
(1) சமவாய்ப்பு மாறி
(2) முயற்சி
(3) எளிய நிகழ்ச்சி
(4) நிகழ்தகவு
விடை:
(4) நிகழ்தகவு

கேள்வி 2.
நிகழ்தகவு மதிப்பின் இடைவெளி
(1) -1 மற்றும் +1
(2) 0 மற்றும் 1
(3) 0 மற்றும் n
(4) 0 மற்றும் ∞
விடை:
(2) 0 மற்றும் 1

கேள்வி 3.
ஒப்பீட்டு நிகழ்வெண் கருத்தை அடிப்படையாகக் கொண்ட நிகழ்தகவு எவ்வாறு அழைக்கப்படுகிறது.
(1) பட்டறி நிகழ்தகவு
(2) தொன்மை நிகழ்தகவு
(3) (அ) மற்றும் (ஆ) இரண்டும்
(4) (1) வும் அல்ல (2) வும் அல்ல
விடை:
(1) பட்டறிவு நிகழ்தகவு

கேள்வி 4.
ஒரு நிகழ்ச்சியின் நிகழ்தகவு எவ்வாறு இருக்க முடியாது?
(1) பூச்சியத்திற்குச் சமம்
(2) பூச்சியத்தை விடப் பெரியது
(3) 1 இக்குச் சமம்
(4) பூச்சியத்தை விடச் சிறியது.
விடை:
(4) பூச்சியத்தை விடச் சிறியது

கேள்வி 5.
ஒரு சம வாய்ப்புச் சோதனையில் வாய்ப்புள்ள அனைத்து விளைவுகளின் நிகழ்தகவு எப்பொழுதும் இதற்குச் சமம்.
(1) ஒன்று
(2) பூச்சியம்
(3) முடிவிலி
(4) மேற்கண்ட அனைத்தும்
விடை:
(1) ஒன்று

கேள்வி 6.
A என்பது S இன் ஏதேனும் ஒரு நிகழ்ச்சி மற்றும் A’ என்பது A-ன் நிரப்பு நிகழ்ச்சி எனில் P(A^|) இன் மதிப்பு
(1) 1
(2) 0
(3) 1 – A
(4) 1 – P(A)
விடை:
(4) 1 – P(A)

கேள்வி 7.
பின்வருவனவற்றுள் எது ஒரு நிகழ்ச்சியின் நிகழ்தகவாக இருக்க முடியாது.
(1) 0
(2) 0.5
(3) 1
(4) -1
விடை:
(4) -1

கேள்வி 8.
ஒரு சோதனையின் குறிப்பிட்ட முடிவு எவ்வாறு அழைக்கப்படுகிறது?
(1) முயற்சி
(2) எளிய நிகழ்ச்சி
(3) கூட்டு நிகழ்ச்சி
(4) விளைவு
விடை:
(4) விளைவு

கேள்வி 9.
ஒரு சோதனையின் ஒன்று அல்லது அதற்கு மேற்பட்ட விளைவுகளின் தொகுப்பு ………… என அழைக்கப்படுகிறது.
(1) நிகழ்ச்சி
(2) விளைவு
(3) கூறுபுள்ளி
(4) மேற்கண்ட எதுவுமில்லை
விடை:
(1) நிகழ்ச்சி

கேள்வி 10.
ஒரு பகடையானது ………. இருக்கும்போது, அதன் ஆறு முகங்களும் சமவாய்ப்புடையவை என அழைக்கப்படுகிறது.
(1) சிறியதாக
(2) சீரானதாக
(3) ஆறு முகம் கொண்டதாக
(4) வட்டமாக
விடை:
(2) சீரானதாக

Tamilnadu State Board New Syllabus Samacheer Kalvi 9th Maths Guide Pdf Chapter 9 நிகழ்தகவு Ex 9.2 Textbook Questions and Answers, Notes.

TN Board 9th Maths Solutions Chapter 9 நிகழ்தகவு Ex 9.2

கேள்வி 1.
ஒரு நிறுவனம் ஆறு மாதத்தில் 10000 மடிக்கணினிகளை உற்பத்தி செய்தது. அவற்றில் 25 மடிக்கணினிகள் குறைபாடு உடையனவாகக் கண்டறியப்பட்டன. சம வாய்ப்பு முறையில் ஒரு மடிக்கணினியைத் தேர்ந்தெடுக்கும் போது அது குறைபாடில்லாத தாக இருக்க நிகழ்தகவு யாது?
விடை:
n(S) = 10000
குறைபாடு உடையவை = 25
E என்பது அது குறைபாடு இல்லாததாக இருக்கும் நிகழ்ச்சி என்க.
P(E) = \(\frac{\mathrm{n}(\mathrm{E})}{\mathrm{n}(\mathrm{S})}=\frac{9975}{10000}\)
= 0.9775

கேள்வி 2.
16 – 20 வயதுக்குட்பட்ட 400 இளைஞர் களிடம் நடத்தப்பட்ட ஓர் ஆய்வில், 191 பேர் வாக்காளர் அடையாள அட்டை வைத்திருப்பதாகக் கண்டறியப்பட்டது. சமவாய்ப்பு முறையில் அவர்களில் ஒருவரைத் தேர்ந்தெடுக்கும் போது அவர் வாக்காளர் அடையாள அட்டை வைத்திருக்கும் நபராக இல்லாமல் இருக்க நிகழ்தகவு என்ன?
விடை:
n(S) = 400
E என்பது வாக்காளர் அடையாள அட்டை வைத்திருக்கும் நபராக இருப்பதற்கான நிகழ்ச்சி என்க.
P(E) = \(\frac{191}{400}\)
E^| என்பது வாக்காளர் அடையாள அட்டை வைத்திருக்கும் நபராக இல்லாமல் இருப்பதற்கான நிகழ்ச்சி என்க.
P(E^|) = 1 – P(E)
= 1 – \(\frac{191}{400}=\frac{400-191}{400}\)
= \(\frac{209}{400}\)

கேள்வி 3.
ஒரு வினாவிற்கான சரியான விடையை ஊகிப்பதற்கான நிகழ்தகவு \(\frac{x}{3}\) என்க. சரியான விடையை ஊகிக்காமல் இருப்பதற்கான நிகழ்தகவு \(\frac{x}{5}\) எனில் x இன் மதிப்பு காண்க.
விடை:
A என்பது சரியான விடையை ஊகிப்பதற்கான நிகழ்ச்சி என்க.
B என்பது தவறான விடையை ஊகிப்பதற்கான நிகழ்ச்சி என்க.
P(A) = \(\frac{x}{3}\)
P(B) = \(\frac{x}{5}\)
P(S) = 1
P(A) + P(B) = \(\frac{x}{3}\) + \(\frac{x}{5}\)
1 = \(\frac{x}{3}\) + \(\frac{x}{5}\)
1 = \(\frac{5x+3x}{15}\)
1 = \(\frac{8x}{15}\)
8x = 15
x = \(\frac{15}{8}\)

கேள்வி 4.
ஒரு வரிப்பந்து (Tennis) விளையாட்டு வீரர் ஒரு குறிப்பிட்ட ஆட்டத்தில் வெற்றி பெறுவதற்கான நிகழ்தகவு 0.72 எனில் அவர் அந்த விளையாட்டில் தோல்வியடைவதற்கான நிகழ்தகவு என்ன?
விடை:
A என்பது ஒரு விளையாட்டு வீரர் ஒரு குறிப்பிட்ட ஆட்டத்தில் வெற்றி பெறுவதற்கான நிகழ்ச்சி என்க.
P(A) = 0.72
A^| என்பது அவர் அந்த விளையாட்டில் தோல்வி அடைவதற்கான நிகழ்ச்சி என்க.
P(A^|) = 1 – P(A)
= 1 – 0.72
= 0.28

கேள்வி 5.
1500 குடும்பங்களில் அவர்கள் வீட்டிலுள்ள பணிப்பெண்கள் (maids) பற்றிய தரவுகள் திரட்டப்பட்டுப் பின்வருமாறு பதிவு செய்யப்ப்பட்டுள்ளது.

சமவாய்ப்பு முறையில் ஒரு குடும்பம் தேர்ந்தெடுக்கப்படும்போது, அக்குடும்பம்
(i) இரு வகைப் பணிப்பெண்களும் வைத்திருக்க
(ii) பகுதி நேரப் பணிப்பெண் வைத்திருக்க
(iii) பணிப்பெண் வைத்திருக்காமல் இருக்க நிகழ்தகவு காண்க.
விடை:
n(S) = 1500
A என்பது ஒரு குடும்பம் இரு வகைப் பணிப்பெண்களும் வைத்திருக்கும் நிகழ்ச்சி என்க.
P(A) = \(\frac{250}{1500}=\frac{1}{6}\)

B என்பது அக்குடும்பம் பகுதி நேரப் பணிப்பெண்களை வைத்திருக்கும் நிகழ்ச்சி என்க.
P(B) = \(\frac{860}{1500}=\frac{86}{150}\)
= \(\frac{43}{75}\)

C என்பது எந்த பணிப்பெண்களும் வைத்திருக்காமல் இருக்கும் நிகழ்ச்சி என்க.
P(C) = \(\frac{20}{1500}=\frac{2}{150}\)
= \(\frac{1}{75}\)

n(C) = 1500 – (860 + 370 + 250)
= 1500 – 1480
= 20

Tamilnadu State Board New Syllabus Samacheer Kalvi 9th Maths Guide Pdf Chapter 8 புள்ளியியல் Ex 8.4 Textbook Questions and Answers, Notes.

TN Board 9th Maths Solutions Chapter 8 புள்ளியியல் Ex 8.4

பலவுள் தெரிவு வினாக்கள்

கேள்வி 1.
மையப்புள்ளி m, தொடர் நிகழ்வெண் பரவலின் ஒரு பிரிவின் மேல் எல்லை ‘b’ எனில், அதன் கீழ் எல்லை .
(1) 2m – b
(2) 2m + b
(3) m – b
(4) m – 2b
விடை:
(2) 2m – b

கேள்வி 2.
ஏழு மதிப்புகளின் சராசரி 81. அவற்றில் ஒரு மதிப்பு நீக்கப்படும் போது மற்ற மதிப்புகளின் சராசரி 78 ஆக அமைகிறது எனில், நீக்கப்பட்ட மதிப்பு எவ்வளவு?
(1) 101
(2) 100
(3) 99
(4) 98
விடை:
(3) 99

கேள்வி 3.
ஒரு தரவில் அதிகமுறை இடம் பெற்றுள்ள உறுப்பின் மதிப்பு.
(1) நிகழ்வெண்
(2) வீச்சு
(3) முகடு
(4) இடைநிலை அளவு
விடை:
(3) முகடு

கேள்வி 4.
பின்வரும் எண் தொகுதிகளில் சராசரி, இடைநிலை மற்றும் முகடு ஒரே மதிப்பாக அமையும் தொகுதி எது?
(1) 2,2,2,4
(2) 1,3,3,3,5
(3) 1,1,2,5,6
(4) 1,1,2,1,5
விடை:
(2) 1,3,3,3,5

கேள்வி 5.
சராசரியிலிருந்து, அனைத்து n உறுப்புகளின் விலக்கங்களின் கூட்டுத்தொகை
(1) 0
(2) n – 1
(3) n
(4) n + 1
விடை:
(1) 0

கேள்வி 6.
a, b, c, d மற்றும் e இன் சராசரி 28. a, C மற்றும் e இன் சராசரி 24, எனில் 5 மற்றும் d இன் சராசரி
(1) 24
(2) 35
(3)26
(4) 34
விடை:
(4) 34

கேள்வி 7.
x, x+2, x+4, x+6; x+8 என்ற தரவின் சராசரி 11 எனில் முதல் மூன்று தரவுகளின் கூட்டுச்சராசரி
(1) 9
(2) 11
(3) 13
(4) 15
விடை:
(1) 9

கேள்வி 8.
5, 9, x, 17 மற்றும் 21 இன் சராசரியானது 13 எனில், x இன் மதிப்பு
(1) 9
(2) 13
(3) 17
(4) 21
விடை:
(2) 13

கேள்வி 9.
முதல் 11 இயல் எண்களின் வர்க்கங்களின் சராசரி
(1) 26
(2) 46
(3) 48
(4) 52
விடை:
(2) 46

கேள்வி 10.
ஓர் எண் தொகுப்பின் சராசரி \(\overline{\mathrm{X}}\) . எண் தொகுப்பின் ஒவ்வொரு மதிப்பும் Z, என்ற எண்ணால் பெருக்கப்படும் போது அதன் சராசரி
(1) \(\overline{\mathrm{X}}\) + z
(2) \(\overline{\mathrm{X}}\) – z
(3) z \(\overline{\mathrm{X}}\)
(4) \(\overline{\mathrm{X}}\)
விடை:
(3) z \(\overline{\mathrm{X}}\)

Tamilnadu State Board New Syllabus Samacheer Kalvi 9th Maths Guide Pdf Chapter 8 புள்ளியியல் Ex 8.3 Textbook Questions and Answers, Notes.

TN Board 9th Maths Solutions Chapter 8 புள்ளியியல் Ex 8.3

கேள்வி 1.
10 தொழிலாளர்களின் மாத வருமானங்கள் முறையே : 5000, 7000, 5000, 7000, 8000, 7000, 7000, 8000, 7000, 5000. எனில் சராசரி, இடைநிலை அளவு, முகடு காண்க.
விடை:
5,000, 7,000, 5,000, 7,000, 8,000, 7,000, 7,000, 8,000, 7,000, 5,000
X என்பது தொழிலாளர்களின் மாத வருமானம் மற்றும் n என்பது தொழிலாளர்களின் எண்ணிக்கை என்க. இங்கு
n = 10
\(\overline{\mathrm{X}}=\frac{\sum \mathrm{x}}{\mathrm{n}}\)
5,000+7,000+5,000+7,000+8,000+7,000+7,000+8,000+7,000+5,000
= \(\frac{5,000+7,000+5,000+7,000+8,000+7,000+7,000+8,000+7,000+5,000}{10}\)
= \(\frac{66000}{10}\)
சராசரி = 6600
இடைநிலை அளவு : கொடுக்கப்பட்ட மதிப்புகளை ஏறுவரிசையில் எழுதுவோம்.
5000, 5000, 5000, 7000, 7000, 7000, 7000, 7000, 8000, 8000.
இங்கு n = 10 (இரட்டைப்படை எண்)
இடைநிலை அளவு = \(\left(\frac{\mathrm{n}}{2}\right)\) வது உறுப்பு மற்றும் \(\left(\frac{\mathrm{n}}{2}+1\right)\) வது உறுப்புகளின் சராசரி

= \(\frac{7000+7000}{2}=\frac{14000}{2}\)
இடைநிலை அளவு = 7000
முகடு : 7000, 5 முறை இடம் பெற்றுள்ளது
∴ முகடு = 7000

கேள்வி 2.
கொடுக்கப்பட்டுள்ள தரவுகளுக்கு முகடு காண்க. 3.1, 3.2, 3.3, 2.1, 1.3, 3.3, 3.1,
விடை:
இத்தரவுகளில் 3.1, 3.3 இரண்டு முறை இடம் பெற்றுள்ளது
முகடு = 3.1, 3.3 (இரட்டை முகடு)

கேள்வி 3.
11, 15, 17, x+1, 19, x-2, 3 என்ற தரவுகளின் சராசரி 14 எனில், x இன் மதிப்பைக் காண்க. மேலும் X இன் மதிப்பைக் கொண்டு தரவுகளின் முகடு காண்க.
விடை:
11, 15, 17, x + 1, x – 2, 3, 19
சராசரி \(\overline{\mathrm{X}}=\frac{\sum_{\mathrm{i}=1} \mathrm{xi}}{\mathrm{n}}\)
14 = \(\frac{11+15+17+x+1+19+x-2+3}{7}\)
14 × 7 = 64 + 2x
98 = 64 + 2x
2x = 98 – 64 = 34
x = \(\frac{34}{2}\)
x = 17
தரவுகள் 11, 15, 17, 18, 19, 15, 3.
15 இரண்டு முறை இடம் பெற்றுள்ளது.
∴ முகடு = 15

கேள்வி 4.
விளையாட்டுக் கால்சட்டைகளுக்கான தேவைப்பட்டியல் கீழே கொடுக்கப்பட்டுள்ளது.

எந்த அளவு கால்சட்டைக்கு அதிகத் தேவை உள்ளது?
விடை:
கொடுக்கப்பட்ட தரவில், மிகப்பெரிய நிகழ்வெண் 37ஐ பெற்றிருக்கும் அளவு 40. எனவே, முகடு = 40 ஆகும்.

கேள்வி 5.
தரவுகளின் முகடு காண்க.

விடை:

முகட்டுப் பிரிவு = 20 – 30 (மிகப்பெரிய நிகழ்வெண்)
முகட்டுப்பிரிவின் கீழ் எல்லை l = 20
முகட்டுப்பிரிவின் நிகழ்வெண் f = 46
முகட்டுப்பிரிவின் நிகழ்வெண்ணுக்கு முந்தைய நிகழ்வெண் 10-20
f₁ = 38
முகட்டுப்பிரிவின் நிகழ்வெண்ணுக்கு பிந்தைய நிகழ்வெண் 30-40
f₂ = 34
பிரிவு நீளம் c = 10
முகடு = l + \(\left(\frac{\mathrm{f}-\mathrm{f}_{1}}{2 \mathrm{f}-\mathrm{f}_{1}-\mathrm{f}_{2}}\right)\) × C
= 20 + \(\left(\frac{46-38}{2 \times 46-38-34}\right)\) × 10
= 20 + \(\left(\frac{8}{92-72}\right)\) × 10
= 20 + \(\left(\frac{8}{20}\right)\) × 10
= 20 + \(\left(\frac{80}{20}\right)\)
= 20 + 4
= 24

கேள்வி 6.
தரவுகளின் சராசரி, இடைநிலை அளவு, முகடு காண்க.

விடை:
சராசரி

சராசரி \(\bar{x}=\frac{\sum f_{X}}{\sum f}\)
= \(\frac{2795}{50}=\frac{559}{10}\)
சராசரி = 55.9

இடைநிலை அளவு = \(\frac{\mathrm{N}}{2}\) வது மதிப்பு
= \(\frac{50}{2}\) வது மதிப்பு
= 25 வது மதிப்பு
இடைநிலைப் பிரிவு = 55 – 64
\(\frac{\mathrm{N}}{2}\) = 25
l = 55
m = 22
C = 9
f = 14
இடைநிலை அளவு
= 55 + \(\left(\frac{\frac{\mathrm{N}}{2}-\mathrm{m}}{\mathrm{f}}\right)\) × C
= 55 + \(\left(\frac{25-22}{14}\right)\) × 9
= 55 + \(\frac{3}{14}\) × 9 = 55 + \(\frac{27}{14}\)
= 56.64

முகடு:

முகட்டுப் பிரிவு = 55 – 64 (மிகப்பெரிய நிகழ்வெண்)
முகட்டுப் பிரிவின் கீழ் எல்லை l = 55
முகட்டுப் பிரிவின் நிகழ்வெண் f = 14
முகட்டுப் பிரிவின் நிகழ்வெண்ணுக்கு முந்தைய நிகழ்வெண் f₁ = 10
முகட்டுப் பிரிவின் நிகழ்வெண்ணுக்குப் பிந்தைய நிகழ்வெண் f₂ = 8
பிரிவின் நீளம் C = 9
முகடு = l + \(\left(\frac{\mathrm{f}-\mathrm{f}_{1}}{2 \mathrm{f}-\mathrm{f}_{1}-\mathrm{f}_{2}}\right)\) × C
= 55 + \(\left(\frac{14-10}{2 \times 14-10-8}\right)\) × 9
= 55 + \(\left(\frac{4}{28-18}\right)\) 9 = 55 + \(\left(\frac{4}{10}\right)\) × 9
= 55 + \(\frac{36}{10}\)
= 55 + 3.6
= 58.6

Tamilnadu State Board New Syllabus Samacheer Kalvi 9th Maths Guide Pdf Chapter 8 புள்ளியியல் Ex 8.2 Textbook Questions and Answers, Notes.

TN Board 9th Maths Solutions Chapter 8 புள்ளியியல் Ex 8.2

கேள்வி 1.
கீழக்காணும் தரவுகளுக்கு இடைநிலை அளவு காண்க. 47, 53, 62, 71, 83, 21, 43, 47, 41
விடை:
கொடுக்கப்பட்ட மதிப்புகளை ஏறுவரிசையில் எழுதுவோம்.
21, 41, 43, 47, 47, 53, 62, 71, 83
இங்கு n = 9 (ஒற்றை எண்)
இடைநிலை அளவு = \(\left(\frac{\mathrm{n}+1}{2}\right)\) வது உறுப்பு
= \(\left(\frac{9+1}{2}\right)\) வது உறுப்பு
= \(\left(\frac{10}{2}\right)\) வது உறுப்பு
= 5 வது உறுப்பு
இடைநிலை அளவு = 47

கேள்வி 2.
கீழ்க்காணும் தரவுகளுக்கு இடைநிலை அளவு காண்க. 36, 44, 86, 31, 37, 44, 86, 35, 60, 51
விடை:
கொடுக்கப்பட்ட மதிப்புகளை ஏறுவரிசையில் எழுதுவோம்.
31, 35, 36, 37, 44, 44, 51, 60, 86, 86
n = 10 (இரட்டை எண்)
இடைநிலை அளவு = \(\left(\frac{\mathrm{n}}{2}\right)\) வது உறுப்பு மற்றும் \(\left(\frac{\mathrm{n}}{2}+1\right)\) வது உறுப்புகளின் சராசரி
= \(\left(\frac{10}{2}\right)\) வது உறுப்பு மற்றும்
= \(\left(\frac{10}{2}+1\right)\) வது உறுப்புகளின் சராசரி

இடைநிலை அளவு = 44

கேள்வி 3.
ஏறு வரிசையில் அமைக்கப்பட்ட 11, 12, 14, 18, x+2, x+4, 30, 32, 35, 41 என்ற தரவுகளின் இடைநிலை அளவு 24 எனில் X இன் மதிப்பைக் காண்க.
விடை:
11, 12, 14, 18, x+2, x+4, 30, 32, 35, 41
இங்கு n = 10 (இரட்டை எண்)
இடைநிலை அளவு = \(\left(\frac{\mathrm{n}}{2}\right)\) வது உறுப்பு மற்றும் \(\left(\frac{\mathrm{n}}{2}+1\right)\) வது உறுப்புகளின் சராசரி
24 = \(\left(\frac{10}{2}\right)\) வது உறுப்பு மற்றும் \(\left(\frac{10}{2}+1\right)\) வது உறுப்புகளின் சராசரி

24 = \(\frac{x+2+x+4}{2}\)
24 = \(\frac{2x+6}{2}\)
48 = 2x + 6
48 – 6 = 2x
42 = 2x
2x = 42
x = \(\frac{42}{2}\)
x = 21

கேள்வி 4.
ஓர் ஆராய்ச்சியாளர் 13 எலிகளின் உணவு தேடும் பழக்கத்தை மைதா மாவைக் கொண்டு ஆராய்ச்சி செய்து அவை உணவு தேட எடுத்துக் கொள்ளும் நேரத்தை 31, 33, 63, 33, 28, 29, 33, 27, 27, 34, 35, 28, 32 எனப் பட்டியலிட்டுள்ளார். எலிகள் உணவு தேட எடுத்துக்கொள்ளும் நேரத்தின்
இடைநிலை அளவு காண்க.
விடை:
எடுத்துக் கொள்ளும் நேரத்தை ஏறுவரிசையில் எழுதுவோம்.

எலிகளின் எண்ணிக்கை 13 எனில், நடுவில் உள்ள நேரம் அதன் இடைநிலை அளவு ஆகும்.
இடைநிலை அளவு =\(\left(\frac{\mathrm{n}+1}{2}\right)\) வது உறுப்பு
= \(\left(\frac{13+1}{2}\right)\) வது உறுப்பு
= \(\left(\frac{14}{2}\right)\) வது உறுப்பு
= 7 வது உறுப்பு
இடைநிலை அளவு = 32

ஒரு பிரிவின் குவிவு நிகழ்வெண் என்பது அந்தப் பிரிவு வரை உள்ள அனைத்துப் பிரிவுகளின் நிகழ்வெண்களின் கூடுதல் ஆகும்.
வகைப்படுத்தப்பட்ட நிகழ்வெண் பரவலின் இடைநிலை அளவு = l + \(\frac{\left(\frac{N}{2}-m\right)}{f} \times c\)

கேள்வி 5.
ஒரு வகுப்பில் தொகுத்தறி மதிப்பீட்டில் மாணவர்கள் எடுத்த மதிப்பெண்களுக்கு இடைநிலை அளவு காண்க.

விடை:

இங்கு N = 50
இடைநிலை அளவு = \(\frac{\mathrm{N}}{2}\) வது உறுப்பு
= \(\frac{50}{2}\) வது உறுப்பு
= 25 வது உறுப்பு
இடைநிலைப்பிரிவு = 30 – 40
\(\frac{\mathrm{N}}{2}\) = 25, l = 30, m = 24, c = 10, f = 10
இடைநிலை அளவு = l + \(\frac{\left(\frac{N}{2}-m\right)}{f} \times c\)
= 30 + \(\left(\frac{25-24}{10}\right)\) × 10
= 30 + \(\frac{1}{10}\) × 10
= 30 + 1
= 31

கேள்வி 6.
ஐந்து மிகைமுழுக்களின் சராசரியானது அதன் இடைநிலை அளவைப்போல் இருமடங்கு அதில் நான்கு முழுக்கள் 3, 4, 6, 9 மற்றும் அதன் இடைநிலை அளவு 6 எனில் ஐந்தாவது முழுவைக் காண்க.
விடை:
ஐந்தாவது முழுவை X என்க.
ஐந்து மிகை முழுக்களின் சராசரியானது அதன் இடைநிலை அளவைப்போல் இருமடங்கு
\(\bar{X}=\frac{\sum x}{n}\)இடைநிலை அளவு = 6 (தரவு)
\(\bar{X}=\frac{3+4+6+9+x}{5}\)
12 = \(\frac{3+4+6+9+x}{5}\)
12 = \(\frac{22+x}{5}\)
22 + x = 60
x = 60 – 22
∴ ஐந்தாவது முழு = 38
வகைப்படுத்தப்பட்ட நிகழ்வெண் பரவலின் முகடு = 1 + \(\left(\frac{\mathrm{f}-\mathrm{f}_{1}}{2 \mathrm{f}-\mathrm{f}_{1}-\mathrm{f}_{2}}\right)\) × c

Tamilnadu State Board New Syllabus Samacheer Kalvi 9th Maths Guide Pdf Chapter 8 புள்ளியியல் Ex 8.1 Textbook Questions and Answers, Notes.

TN Board 9th Maths Solutions Chapter 8 புள்ளியியல் Ex 8.1

கேள்வி 1.
ஓர் இடத்தின் ஒரு வாரக் குளிர்கால வெப்பநிலை 26°C, 24° C, 28° C, 31° C, 30° C, 26′ C, 24° C,எனக் கண்டறியப்பட்டது. அந்த இடத்தின் அவ்வாரத்திற்கான சராசரி வெப்பநிலையைக் காண்க.
விடை:
x என்பது வெப்பநிலை மற்றும் n என்பது நாட்களின் எண்ணிக்கை என்க.
\(\overline{\mathrm{X}}\) = \(\frac{\sum x}{n}\), n = 7
= \(\frac{(26+24+28+31+30+26+24)^{0} C}{7}\)
= \(\frac{189^{\circ} \mathrm{C}}{7}\)
= 27°C
சராசரி வெப்பநிலை = 27°C

கேள்வி 2.
ஒரு குடும்பத்தில் உள்ள 4 நபர்களின் எடைகளின் சராசரி 60 கி.கி. அவர்களில் மூவரின் எடைகள் 56 கி.கி, 68 கி.கி மற்றும் 72 கி.கி எனில், நான்காமவரின் எடையைக் காண்க.
விடை:
நான்காமவரின் எடையை X கிகி என்க.
n = 4
சராசரி எடை = 60 கி.
\(\overline{\mathrm{X}}\) = \(\frac{\sum x}{n}\)
60 = \(\frac{(56+68+72+x) K g}{4}\)
60 = \(\frac{196+x}{4}\)
240 = 196 + x
x = 240 – 196
x = 44
நான்காமவரின் எடை = 44 கி.கி

கேள்வி 3.
ஒரு வகுப்பில் கணித அலகுத் தேர்வில், 10 மாணவர்கள் 75 மதிப்பெண், 12 மாணவர்கள் 60 மதிப்பெண், 8 மாணவர்கள் 40 மதிப்பெண் மற்றும் 3 மாணவர்கள் 30 மதிப்பெண் பெற்றனர் எனில், மொத்தத்தில் சராசரி மதிப்பெண் என்ன?
விடை:
x என்பது மாணவர்கள் பெற்ற மதிபெண்கள்.
n = மாணவர்களின் எண்ணிக்கை என்க.
இங்கு,
n = (10 + 12 + 8 + 3) = 33
\(\overline{\mathrm{X}}\) = \(\frac{\sum x}{n}\)
= \(\frac{(10 \times 75)+(12 \times 60)+(8 \times 40)+(3 \times 30)}{33}\)
= \(\frac{750+720+320+90}{33}\)
= \(\frac{1880}{33}\)
= 56.96

கேள்வி 4.
ஒர் அறிவியல் ஆய்வகத்தில் 6 புற்றுநோய் பாதிக்கப்பட்ட எலிகளுக்கு இயற்கை மருந்துகளை 10 நாட்கள் கொடுத்து ஆய்வுகளை மேற்கொண்டு அதன் பிறகு அவற்றின் புற்றுநோய்க் கட்டிகளின் அளவுகள் பட்டியலிடப்பட்டுள்ளது. புற்றுநோய்க் கட்டிகளின் சராசரி அளவைக் காண்க.

விடை:
x என்பது அளவு மற்றும்
n = எலிகளின் எண்ணிக்கை என்க.
\(\overline{\mathrm{X}}=\frac{\sum x_{i}}{6}\)
= \(\frac{145+148+142+141+139+140}{6}\)
= \(\frac{855}{6}\)
= 142.5 மி.மீ³

கேள்வி 5.
கீழ்க்காணும் பரவலின் சராசரி 20.2 எனில், P, யின் மதிப்பைக் காண்க.

விடை:
x என்பது மதிப்பெண்கள் மற்றும் n என்பது மாணவர்களின் எண்ணிக்கை என்க.
\(\overline{\mathrm{X}}\) = \(\frac{\sum x}{n}\)
20.2 = \(\frac{(10 \times 6)+(15 \times 8)+(20 \times \mathrm{p})+(25 \times 10)+(30 \times 6)}{30+\mathrm{p}}\)
(20.2) (30 + p) = 60 + 120 + 20p + 250 + 180
606 + 20.2 p = 610 + 20p
20.2p = 610 – 606 + 20p
20.2P – 20p = 4
0.2p = 4

கேள்வி 6.
வகுப்பில் உள்ள மாணவர்களின் எடை வகுப்பறை பதிவேட்டிற்காக எடுக்கப்பட்டது. அவ்வகுப்பின் சராசரி எடையை நேரடி முறையின் மூலம் காண்க.

விடை:

\(\overline{\mathrm{X}}=\frac{\sum f x}{\sum f}\)
= \(\frac{2010}{50}\)
= \(\frac{201}{5}\)
= 40.2

கேள்வி 7.
கீழ்க்காணும் பரவலின் சராசரியை ஊகச் சராசரி முறையில் காண்க.

விடை:
ஊகச்சராசரி A = 25

\(\overline{\mathrm{X}}\) = A + \(\frac{\sum f d}{\sum f}\)
\(\overline{\mathrm{X}}\) = 25 + \(\frac{270}{63}\)
= 25 + \(\frac{90}{21}\)
= 25 + \(\frac{30}{7}\)
= \(\frac{175+30}{7}\)
= \(\frac{205}{7}\)
= 29.285

கேள்வி 8.
கீழ்க்காணும் பரவலின் சராசரியைப் படி விலக்க முறையில் காண்க.

விடை:

ஊகச் சராசரி A = 32
பிரிவு நீளம் = 4
\(\overline{\mathrm{X}}\) = A + \(\frac{\sum f d}{\sum f}\) × C
= 32 + \(\frac{-310}{4 \times 105}\) × 4
= 32 + \(\frac{-310}{105}\)
= \(\frac{3360+(-310)}{105}\)
= \(\frac{3050}{105}\)
= \(\frac{610}{21}\)
= 29.047
= 29.05