Samacheer Kalvi 12th Maths Guide Chapter 4 நேர்மாறு முக்கோணவியல் சார்புகள் Ex 4.5

Tamilnadu State Board New Syllabus Samacheer Kalvi 12th Maths Guide Pdf Chapter 4 நேர்மாறு முக்கோணவியல் சார்புகள் Ex 4.5 Textbook Questions and Answers, Notes.

TN Board 12th Maths Solutions Chapter 4 நேர்மாறு முக்கோணவியல் சார்புகள் Ex 4.5

கேள்வி 1.
மதிப்பு உள்ளது எனில் பின்வருவனவற்றிக்கு மதிப்பு காண்க. மதிப்பு இல்லையெனில் அதற்கான காரணம் தருக.
(i) sin^-1 (cos π)
(i) tan^-1 \(\left(\sin \left(\frac{-5 \pi}{2}\right)\right)\)
(iii) sin^-1(sin 5)
தீர்வு:
(i) sin^-1(cos π)
⇒ sin^-1(cos π) = x என்க
⇒ sin^-1(-1) = x
[∵ cos π = -1]
⇒ -1 = sin x ⇒ sin x = -sin \(\frac{\pi}{2}\)
⇒ sin x = sin \(\left(\frac{-\pi}{2}\right)\) [∵\(\frac{-\pi}{2}\) ∈ \(\left[\frac{-\pi}{2}, \frac{\pi}{2}\right]\)] ∵ sin^-1cos π = \(\frac{-\pi}{2}\)
⇒ x = \(\frac{-\pi}{2}\)

(ii)

(iii) sin^-1(sin 5)
sin^-1(sin 5) = θ; θ ∈ \(\left[\frac{-\pi}{2}, \frac{\pi}{2}\right]\) என அறிவோம்
தோராயமாக கருதுக \(\frac{\pi}{2}\) = \(\frac{11}{7}\)

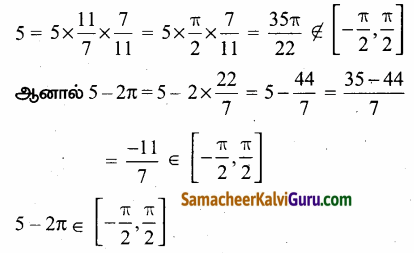
sin^-1(sin 5) = sin^-1(sin(5 – π))
= 5 – 2π [∵ 5 – 2π ∈ –\(\frac{\pi}{2}\), \(\frac{\pi}{2}\)]

கேள்வி 2.
முக்கோணத்தினை மேற்கோளாகக் கொண்டு x-ன் மதிப்பு காண்க.
(i) sin(cos^-1(1 – x))
(ii) cos(tan^-1(3x – 1))
(iii) tan \(\left(\sin ^{-1}\left(x+\frac{1}{2}\right)\right)\)
தீர்வு:
(i) sin(cos^-1(1 – x))
நமக்கு தெரியும்
0 ≤ x ≤ 1 எனில், cos^-1 x = sin^-1\(\left(\sqrt{1-x^{2}}\right)\)
∴ cos^-1(1 – x) = sin^-1\(\sqrt{1-(1-x)^{2}}\) [∵ 0 ≤ 1 – x ≤ 1]
= sin^-1\(\left(\sqrt{1-\left(1+x^{2}-2 x\right)}\right)\)
= sin^-1\(\left(\sqrt{\left.1-1-x^{2}+2 x\right)}\right)\) = sin^-1\(\left(\sqrt{2 x-x^{2}}\right)\)
∴ sin^-1(cos^-1(1 – x)) = sin(sin^-1\(\left(\sqrt{2 x-x^{2}}\right)\))
= \(\sqrt{2 x-x^{2}}\)

(ii) cos(tan^-1(3x – 1))
நமக்கு தெரியும்

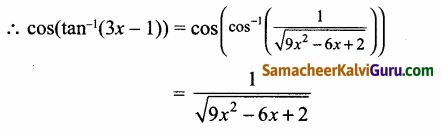
(iii)

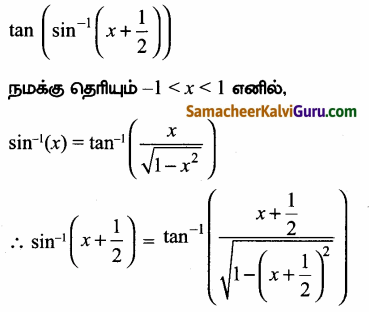
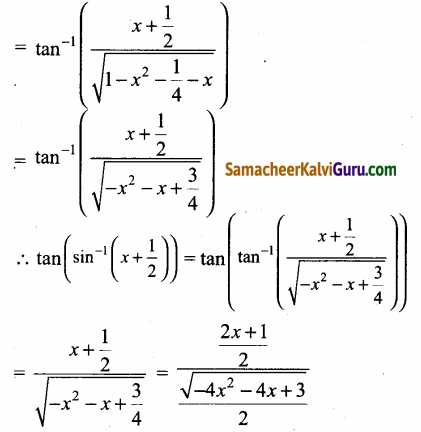
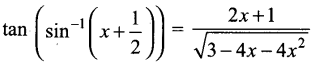
கேள்வி 3.

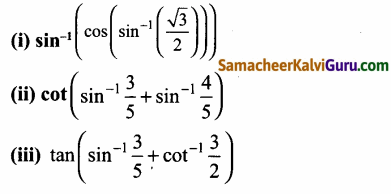
தீர்வு:
(i)

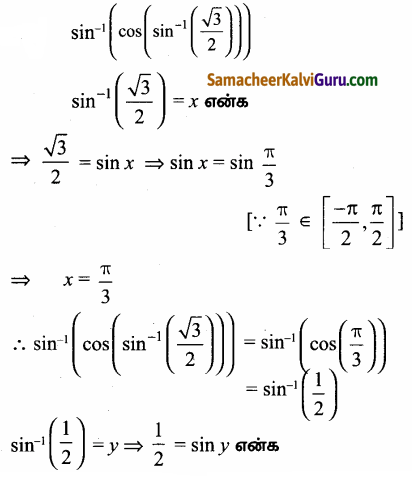
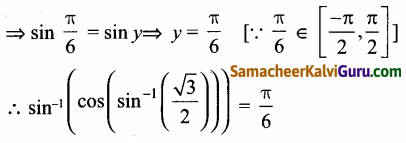
(ii)

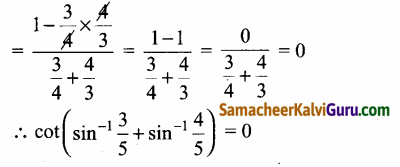
(iii)

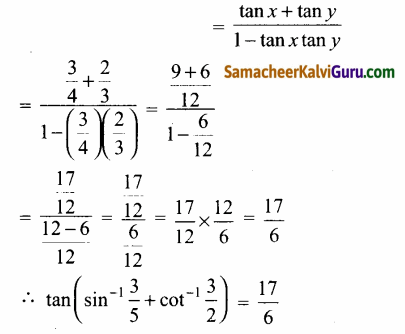
கேள்வி 4.
நிரூபிக்க :
(i) tan^-1\(\) + tan^-1\(\) – tan^-1\(\)
(ii) sin^-1\(\) – cos^-1\(\) = sin^-1\(\)
தீர்வு:
(i)

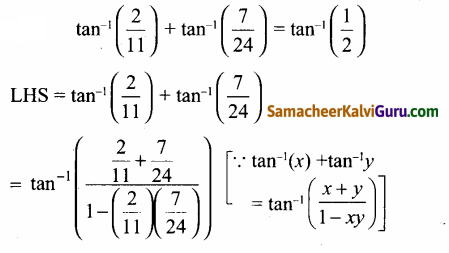
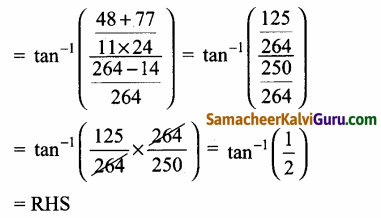
எனவே நிரூபிக்கப்பட்டது.

(ii)
sin^-1\(\left(\frac{3}{5}\right)\) – cos^-1\(\left(\frac{12}{13}\right)\) = sin^-1\(\left(\frac{16}{65}\right)\)
sin^-1 \(\left(\frac{3}{5}\right)\) = x ⇒ sin x = \(\left(\frac{3}{5}\right)\)

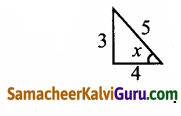
மற்றும் cos x = \(\frac{\mathrm{adj}}{\text { hyp }}\) = \(\frac{4}{5}\)

எனவே நிரூபிக்கப்பட்டது.

கேள்வி 5.
நிரூபிக்க: tan^-1x + tan^-1y + tan^-1z = tan^-1\(\left(\frac{x+y+z-x y}{1-x y-y z-z}\right)\)
தீர்வு:
நமக்கு தெரியும்

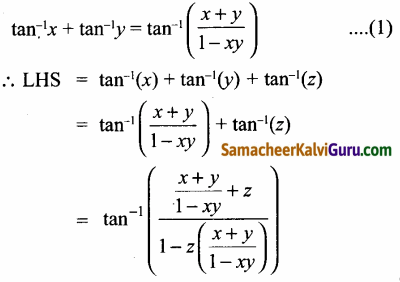
[(1) ஐ பயன்படுத்த]

எனவே நிரூபிக்கப்பட்டது.

கேள்வி 6.
tan^-1x + tan^-1y + tan^-1z = π எனில், x + y + z = xyz எனக் காட்டுக.
தீர்வு:
கேள்வி எண் 5 லிருந்து
tan^-1x + tan^-1y+tan^-1z = tan^-1 \(\left(\frac{x+y+z-x y z}{1-x y-y z-z x}\right)\)

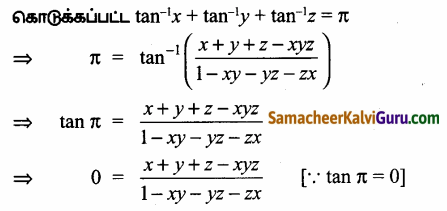
⇒ x + y + z – xyz = 0
⇒ x + y + z = xyz

கேள்வி 7.
|x| < \(\frac{1}{\sqrt{3}}\) எனில் tan¹ x+ tan¹\(\frac{2 x}{1-x^{2}}\) =
tan^-1\(\left(\frac{3 x-x^{3}}{1-3 x^{2}}\right)\) என நிறுவுக.
தீர்வு:
LHS = tan^-1x + tan^-1\(\frac{2 x}{1-x^{2}}\)

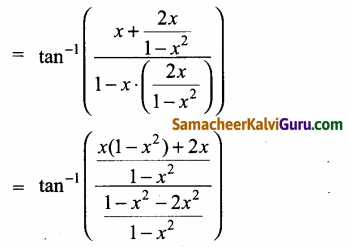
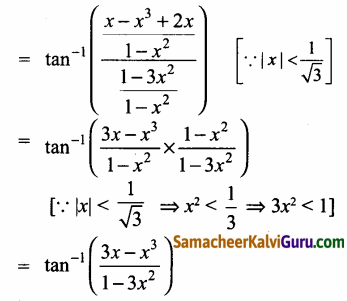
கேள்வி 8.

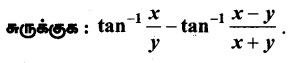
தீர்வு:

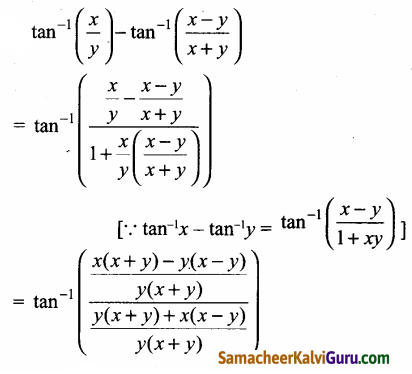
கேள்வி 9.
(i) sin^-1\(\left(\frac{\mathbf{5}}{\boldsymbol{x}}\right)\) + sin^-1\(\left(\frac{\mathbf{12}}{\boldsymbol{x}}\right)\) = \(\frac{\pi}{2}\)
(ii) 2tan^-1x = cos^-1 \(\frac{1-a^{2}}{1+a^{2}}\) – cos^-1 \(\frac{1-b^{2}}{1+b^{2}}\), a > 0, b > 0
(iii) 2tan^-1 – cos^-1(x + 2) = tan^-1(2 cosec x)
(iv) cot^-1x – cot^-1(x + 2) = \(\frac{\pi}{2}\), x > 0
தீர்வு:
(i) கொடுக்கப்பட்ட sin^-1\(\left(\frac{5}{x}\right)\) + sin^-1\(\left(\frac{12}{x}\right)\) = \(\frac{\pi}{2}\)
நமக்கு தெரியும்
sin^-1x + sin^-1y = sin^-1\(\left(x \sqrt{1-y^{2}}+y \sqrt{1-x^{2}}\right)\)
இங்கு x² + y² ≤ 1 அல்லது xy < 0

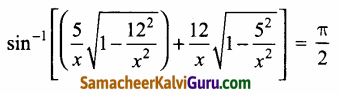
x² + y² ≤ 1 அல்லது xy < 0 எனில் மட்டுமே இது சரி
y = \(\frac{5}{x}\) மற்றும் y = \(\frac{12}{x}\) என்க

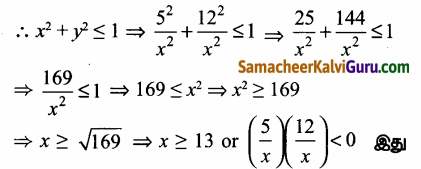
சாத்தியமில்லை
∴ x² ≥ 13 தீர்வாகும்.
கொடுக்கப்பட்ட sin^-1\(\left(\frac{5}{x}\right)\) + sin^-1\(\left(\frac{12}{x}\right)\) = \(\frac{\pi}{2}\)

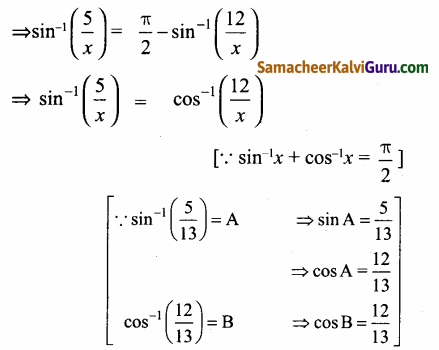
x = 13 எனில் மட்டுமே இது சரி
∴ x = 13 தீர்வாகும்.

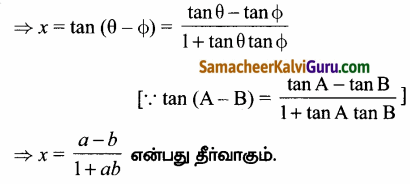
(ii) 2tan^-1x = cos^-1\(\frac{1-a^{2}}{1+a^{2}}\) – cos^-1\(\frac{1-b^{2}}{1+b^{2}}\), a > 0, b > 0

⇒ tan^-1x = θ – φ

(iii) 2tan^-1(cos x) = tan^-1(2 cosec x)



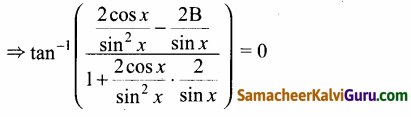
⇒ 2 sin x cos x – 2 sin²x = 0
⇒ 2 sin x(cos x – sin x) = 0

எனவே தீர்வுகள் x = nπ அல்லது
x = nπ + \(\frac{\pi}{4}\), n ∈ ℤ

(iv) cot^-1(x) – cot^-1(x + 2) = \(\frac{\pi}{12}\), x > 0



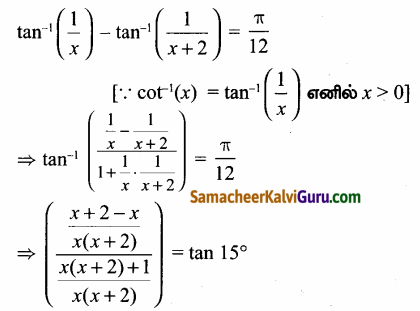
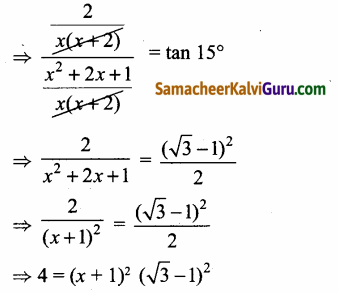
இருபுறமும் வர்க்க மூலம் எடுக்க கிடைப்பது

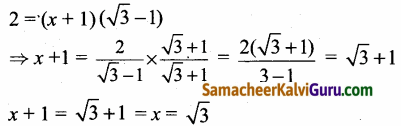
x = என்பது தீர்வாகும்

கேள்வி 10.
சமன்பாட்டின் தீர்வுகளின் எண்ணிக்கையைக் காண்க. tan^-1(x – 1) + tan^-1(x + 1) = tan^-1(3x)
தீர்வு:
கருதுக tan^-1(x – 1) + tan^-1(x + 1)

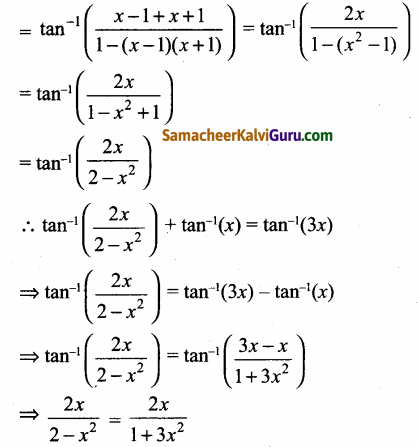
குறுக்கு பெருக்கல் மூலம் நமக்கு கிடைப்பது முப்படி சமன்பாடாகும்.
ஆகையால் கொடுக்கப்பட்ட சமன்பாட்டிற்கு மூன்று தீர்வுகள் இருக்கும்.