Tamilnadu State Board New Syllabus Samacheer Kalvi 9th Maths Guide Pdf Chapter 8 புள்ளியியல் Ex 8.2 Textbook Questions and Answers, Notes.
TN Board 9th Maths Solutions Chapter 8 புள்ளியியல் Ex 8.2
கேள்வி 1.
கீழக்காணும் தரவுகளுக்கு இடைநிலை அளவு காண்க. 47, 53, 62, 71, 83, 21, 43, 47, 41
விடை:
கொடுக்கப்பட்ட மதிப்புகளை ஏறுவரிசையில் எழுதுவோம்.
21, 41, 43, 47, 47, 53, 62, 71, 83
இங்கு n = 9 (ஒற்றை எண்)
இடைநிலை அளவு = \(\left(\frac{\mathrm{n}+1}{2}\right)\) வது உறுப்பு
= \(\left(\frac{9+1}{2}\right)\) வது உறுப்பு
= \(\left(\frac{10}{2}\right)\) வது உறுப்பு
= 5 வது உறுப்பு
இடைநிலை அளவு = 47
![]()
கேள்வி 2.
கீழ்க்காணும் தரவுகளுக்கு இடைநிலை அளவு காண்க. 36, 44, 86, 31, 37, 44, 86, 35, 60, 51
விடை:
கொடுக்கப்பட்ட மதிப்புகளை ஏறுவரிசையில் எழுதுவோம்.
31, 35, 36, 37, 44, 44, 51, 60, 86, 86
n = 10 (இரட்டை எண்)
இடைநிலை அளவு = \(\left(\frac{\mathrm{n}}{2}\right)\) வது உறுப்பு மற்றும் \(\left(\frac{\mathrm{n}}{2}+1\right)\) வது உறுப்புகளின் சராசரி
= \(\left(\frac{10}{2}\right)\) வது உறுப்பு மற்றும்
= \(\left(\frac{10}{2}+1\right)\) வது உறுப்புகளின் சராசரி

இடைநிலை அளவு = 44
கேள்வி 3.
ஏறு வரிசையில் அமைக்கப்பட்ட 11, 12, 14, 18, x+2, x+4, 30, 32, 35, 41 என்ற தரவுகளின் இடைநிலை அளவு 24 எனில் X இன் மதிப்பைக் காண்க.
விடை:
11, 12, 14, 18, x+2, x+4, 30, 32, 35, 41
இங்கு n = 10 (இரட்டை எண்)
இடைநிலை அளவு = \(\left(\frac{\mathrm{n}}{2}\right)\) வது உறுப்பு மற்றும் \(\left(\frac{\mathrm{n}}{2}+1\right)\) வது உறுப்புகளின் சராசரி
24 = \(\left(\frac{10}{2}\right)\) வது உறுப்பு மற்றும் \(\left(\frac{10}{2}+1\right)\) வது உறுப்புகளின் சராசரி

24 = \(\frac{x+2+x+4}{2}\)
24 = \(\frac{2x+6}{2}\)
48 = 2x + 6
48 – 6 = 2x
42 = 2x
2x = 42
x = \(\frac{42}{2}\)
x = 21
![]()
கேள்வி 4.
ஓர் ஆராய்ச்சியாளர் 13 எலிகளின் உணவு தேடும் பழக்கத்தை மைதா மாவைக் கொண்டு ஆராய்ச்சி செய்து அவை உணவு தேட எடுத்துக் கொள்ளும் நேரத்தை 31, 33, 63, 33, 28, 29, 33, 27, 27, 34, 35, 28, 32 எனப் பட்டியலிட்டுள்ளார். எலிகள் உணவு தேட எடுத்துக்கொள்ளும் நேரத்தின்
இடைநிலை அளவு காண்க.
விடை:
எடுத்துக் கொள்ளும் நேரத்தை ஏறுவரிசையில் எழுதுவோம்.

எலிகளின் எண்ணிக்கை 13 எனில், நடுவில் உள்ள நேரம் அதன் இடைநிலை அளவு ஆகும்.
இடைநிலை அளவு =\(\left(\frac{\mathrm{n}+1}{2}\right)\) வது உறுப்பு
= \(\left(\frac{13+1}{2}\right)\) வது உறுப்பு
= \(\left(\frac{14}{2}\right)\) வது உறுப்பு
= 7 வது உறுப்பு
இடைநிலை அளவு = 32
ஒரு பிரிவின் குவிவு நிகழ்வெண் என்பது அந்தப் பிரிவு வரை உள்ள அனைத்துப் பிரிவுகளின் நிகழ்வெண்களின் கூடுதல் ஆகும்.
வகைப்படுத்தப்பட்ட நிகழ்வெண் பரவலின் இடைநிலை அளவு = l + \(\frac{\left(\frac{N}{2}-m\right)}{f} \times c\)
கேள்வி 5.
ஒரு வகுப்பில் தொகுத்தறி மதிப்பீட்டில் மாணவர்கள் எடுத்த மதிப்பெண்களுக்கு இடைநிலை அளவு காண்க.

விடை:
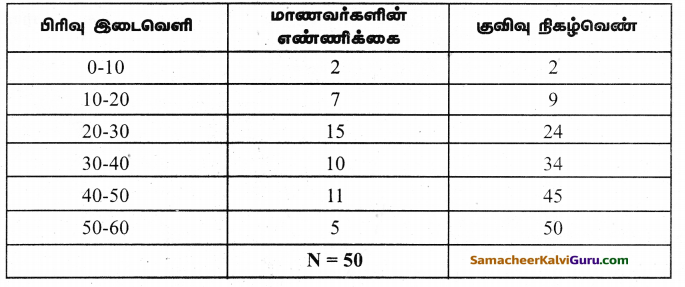
இங்கு N = 50
இடைநிலை அளவு = \(\frac{\mathrm{N}}{2}\) வது உறுப்பு
= \(\frac{50}{2}\) வது உறுப்பு
= 25 வது உறுப்பு
இடைநிலைப்பிரிவு = 30 – 40
\(\frac{\mathrm{N}}{2}\) = 25, l = 30, m = 24, c = 10, f = 10
இடைநிலை அளவு = l + \(\frac{\left(\frac{N}{2}-m\right)}{f} \times c\)
= 30 + \(\left(\frac{25-24}{10}\right)\) × 10
= 30 + \(\frac{1}{10}\) × 10
= 30 + 1
= 31
![]()
கேள்வி 6.
ஐந்து மிகைமுழுக்களின் சராசரியானது அதன் இடைநிலை அளவைப்போல் இருமடங்கு அதில் நான்கு முழுக்கள் 3, 4, 6, 9 மற்றும் அதன் இடைநிலை அளவு 6 எனில் ஐந்தாவது முழுவைக் காண்க.
விடை:
ஐந்தாவது முழுவை X என்க.
ஐந்து மிகை முழுக்களின் சராசரியானது அதன் இடைநிலை அளவைப்போல் இருமடங்கு
\(\bar{X}=\frac{\sum x}{n}\)இடைநிலை அளவு = 6 (தரவு)
\(\bar{X}=\frac{3+4+6+9+x}{5}\)
12 = \(\frac{3+4+6+9+x}{5}\)
12 = \(\frac{22+x}{5}\)
22 + x = 60
x = 60 – 22
∴ ஐந்தாவது முழு = 38
வகைப்படுத்தப்பட்ட நிகழ்வெண் பரவலின் முகடு = 1 + \(\left(\frac{\mathrm{f}-\mathrm{f}_{1}}{2 \mathrm{f}-\mathrm{f}_{1}-\mathrm{f}_{2}}\right)\) × c