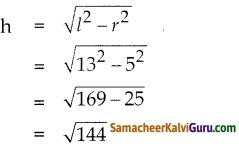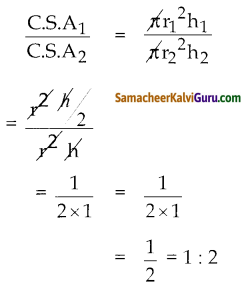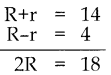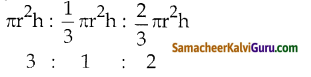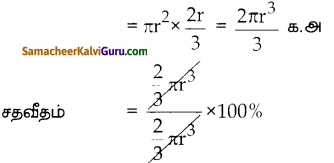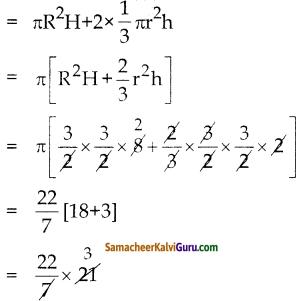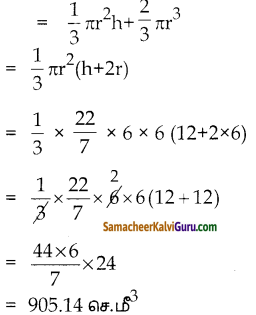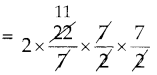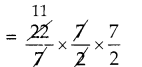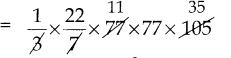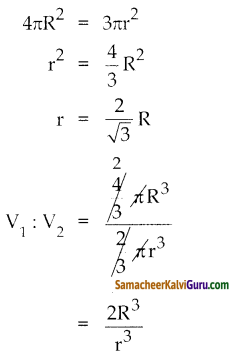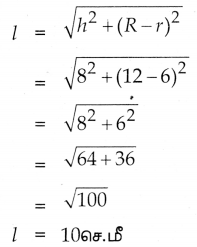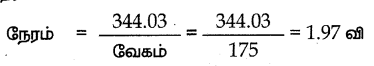Laxmi

Tamilnadu State Board New Syllabus Samacheer Kalvi 10th Maths Guide Pdf Chapter 8 புள்ளியியலும் நிகழ்தகவும் Ex 8.2 Textbook Questions and Answers, Notes.

TN Board 10th Maths Solutions Chapter 8 புள்ளியியலும் நிகழ்தகவும் Ex 8.2

கேள்வி 1.
ஒரு தரவின் திட்டவிலக்கம் மற்றும் சராசரி அகியன முறையே 6.5 மற்றும் 12.5 எனில் மாறுபாட்டுக் கெழுவைக் காண்க.
தீர்வு :
திட்டவிலக்கம் σ = 6.5 சராசரி \(\overline{\mathrm{x}}\) = 12.5
மாறுபாட்டுக்கெழு C.V = \(\frac{\sigma}{\bar{x}}\) x 100
= \(\frac{6.5}{12.5}\) x 100
விடை :
மாறுபாட்டுக்கெழு = 52 %

கேள்வி 2.
ஒரு தரவின் திட்டவிலக்கம் மற்றும் மாறுபாட்டுக்கெழு ஆகியன முறையே 1.2 மற்றும் 25.6 எனில் அதன் சராசரியைக் காண்க.
தீர்வு :
σ = 12.5
C.V = 25.6
C.V = \(\frac{1.2}{\bar{x}}\) x 100
\(\bar{x}=\frac{1.2}{25.6} \times 100\)
\(\bar{x}\) = 4.96
விடை :
\(\bar{x}\) = 4.69

கேள்வி 3.
ஒரு தரவின் சராசரி மற்றும் மாறுபாட்டுக்கெழு முறையே 15 மற்றும் 48 எனில் அதன் திட்டவிலக்கத்தைக் காண்க.
தீர்வு :
\(\bar{x}\) = 15
C.V = 48
C.V= \(\frac{s}{x}\) = x 100
σ = \(\frac{48 \times 15}{100}\) = 7.2
விடை :
திட்டவிலக்கம் = 7.2

கேள்வி 4.
n = 5, \(\bar{x}\) = 6, Σx² = 765, எனில் மாறுபாட்டுக் கெழுவைக் காண்க.
தீர்வு :
n = 5
\(\bar{x}\) = 6, Σx² = 765

= 1.8028 x 100 = 180.28%
விடை :
மாறுபாட்டுக்கெழு = 180.28%

கேள்வி 5.
24, 26, 33, 37, 29, 31 ஆகியவற்றின் மாறுபாட்டுக்கெழுவைக் காண்க
தீர்வு :
ஏறுவரிசையில் எழுத 24, 26, 29, 31, 33, 37.
\(\bar{x}=\frac{24+26+29+31+33+37}{6}=\frac{180}{6}\) = 30
\(\bar{x}\) = 30

σ = \(\frac{\Sigma \mathrm{d}_{\mathrm{i}}^{2}}{\mathrm{n}}\)
= \(=\sqrt{\frac{112}{6}}=\sqrt{18.67}\)
= 4.32
C.V = \(\frac{1.2}{\bar{x}}\) x 100
= \(\frac{4.32}{30}\) x 100 = 14.4
விடை :
மாறுபாட்டுக்கெழு = 14.4%.

கேள்வி 6.
8மாணவர்கள் ஒருநாளில் வீட்டுப்பாடத்தை முடிப்பதற்கு எடுத்துக் கொள்ளும் கால அளவுகள் (நிமிடங்களில்) பின்வருமாறு கொடுக்கப்பட்டுள்ளது. 38, 40, 47, 44, 46, 43, 49, 53 இத்தரவின் மாறுபாட்டுக் கெழுவைக் காண்க. தீர்வு :
ஏறுவரிசையில் எழுத 38,40, 43, 44,46,47,49, 53


= 0.1007 x 100 = 10.07 %
விடை :
மாறுபாட்டுக்கெழு = 10.07%

கேள்வி 7.
சத்யா மற்றும் வித்யா இருவரும் 5 பாடங்களில் பெற்ற மொத்த மதிப்பெண்கள் முறையே
460 மற்றும் 480 ஆகும். மேலும் அதன் திட்ட விலக்கங்கள் முறையே 4.6 மற்றும் 2.4 எனில், யாருடைய செயல்திறன் மிகுந்த நிலைத்தன்மை கொண்டது?
தீர்வு :
n = 5

விடை :
வித்யாவின் மாறுபாட்டுக்கெழு சத்யாவின் மாறுபாட்டுக் கெழுவைவிட குறைவாக உள்ளது.
எனவே வித்யா செயல்திறன் மிகுந்த நிலைத்தன்மை உடையது.

கேள்வி 8.
ஒரு வகுப்பில் உள்ள 40 மாணவர்கள், கணிதம், அறிவியல் மற்றும் சமூக அறிவியல் ஆகிய மூன்று பாடங்களில் பெற்ற மதிப்பெண்களின் சராசரி மற்றும் திட்டவிலக்கம் கீழே கொடுக்கப்பட்டுள்ளன.

இந்த மூன்று பாடங்களில் எது அதிக நிலைத்தன்மை கொண்டது மற்றும் எது குறைந்த நிலைத்தன்மை கொண்டது?
தீர்வு :

விடை :
அதிக நிலைத்தன்மை கொண்டது அறிவியல்
குறைந்த நிலைத்தன்மை கொண்டது சமூக அறிவியல்.

Tamilnadu State Board New Syllabus Samacheer Kalvi 9th Maths Guide Pdf Chapter 2 மெய்யெண்கள் Ex 2.9 Textbook Questions and Answers, Notes.

TN Board 9th Maths Solutions Chapter 2 மெய்யெண்கள் Ex 2.9

பலவுள் தெரிவு வினாக்கள் :
கேள்வி 1.
n என்பது ஓர் இயல் எண் எனில் √n என்பது
(1) எப்போதும் ஓர் இயல் எண்.
(2) எப்போதும் ஒரு விகிதமுறா எண்.
(3) எப்போதும் ஒரு விகிதமுறு எண்
(4) ஒரு விகிதமுறு அல்லது விகிதமுறா எண்
விடை :
(4) ஒரு விகிதமுறு அல்லது விகிதமுறா எண்

கேள்வி 2.
பின்வனவற்றுள் எது உண்மையல்ல?
(1) ஒவ்வொரு விகிதமுறு எண்ணும் மெய்யெண்.
(2) ஒவ்வொரு முழுக்களும் விகிதமுறு எண்.
(3) ஒவ்வொரு மெய்யெண்ணும் விகிதமுறா எண்.
(4) ஒவ்வோர் இயல் எண்ணும் ஒரு முழு எண்.
விடை:
(3) ஒவ்வொரு மெய்யெண்ணும் விகிதமுறா எண்.

கேள்வி 3.
இரு விகிதமுறா எண்களின் கூடுதல் பற்றிய கீழ்க்காணும் கூற்றுகளில் எது உண்மை ?
(1) எப்போதும் ஒரு விகிதமுறா எண்.
(2) ஒருவிகிதமுறு அல்லது விகிதமுறா எண்ணாக இருக்கலாம்.
(3) எப்போதும் ஒரு விகிதமுறு எண்.
(4) எப்போதும் ஒரு முழுக்களாகும்.
விடை:
(2) ஒரு விகிதமுறு அல்லது விகிதமுறா எண்ணாக இருக்கலாம்.

கேள்வி 4.
பின்வனவற்றுள் எது முடிவுறு தசமத் தீர்வு?
(1) \(\frac{5}{64}\)
(2) \(\frac{8}{9}\)
(3) \(\frac{14}{15}\)
(4) \(\frac{1}{12}\)
விடை :
(1) \(\frac{5}{64}\)

கேள்வி 5.
பின்வனவற்றுள் எது விகிதமுறா எண்?
(1) \(\sqrt{25}\)
(2) \(\sqrt{\frac{9}{4}}\)
(3) \(\frac{7}{11}\)
(4) π
விடை:
(4) π

கேள்வி 6.
2 மற்றும் 2.5 என்ற எண்களுக்கிடையே உள்ள ஒரு விகிதமுறா எண்
(1) \(\sqrt{11}\)
(2) √5
(3) \(\sqrt{2.5}\)
(4) √8
விடை:
(2) √5

கேள்வி 7.
\(\frac{1}{3}\) ஐ எந்த மிகச் சிறிய விகிதமுறு எண்ணால் பெருக்கினால் அதன் தசம விரிவு ஓர் இலக்கத்தோடு முடிவுறு தசம விரிவாக அமையும்?
(1) \(\frac{1}{10}\)
(2) \(\frac{3}{10}\)
(3) 3
(4) 30
விடை:
(2) \(\frac{3}{10}\)

கேள்வி 8.
\(\frac{1}{7}\) = \(0 . \overline{142857}\) எனில் \(\frac{5}{7}\) இன் மதிப்பு என்ன?
(1) \(0 . \overline{142857}\)
(2) \(0 . \overline{714285}\)
(3) \(0 . \overline{571428}\)
(4) 0.714285
விடை :
(2) \(0 . \overline{714285}\)

கேள்வி 9.
கீழ்க்கண்டவற்றுள் பொருந்தாததைக் காண்க.
(1) \(\sqrt{32} \times \sqrt{2}\)
(2) \(\frac{\sqrt{27}}{\sqrt{3}}\)
(3) \(\sqrt{72} \times \sqrt{8}\)
(4) \(\frac{\sqrt{54}}{\sqrt{18}}\)
விடை:
(4) \(\frac{\sqrt{54}}{\sqrt{18}}\)

கேள்வி 10.
\(0 . \overline{34}+0.3 \overline{4}\) =
(1) \(0.6 \overline{87}\)
(2) \(0 . \overline{68}\)
(3) \(0.6 \overline{8}\)
(4) \(0.68 \overline{7}\)
விடை:
(1) \(0.6 \overline{87}\)

கேள்வி 11.
கீழ்க்காணும் கூற்றுகளில் எது தவறு?
(1) 25 இன் வர்க்க மூலம் 5 அல்லது – 5
(2) \(-\sqrt{25}=-5\)
(3) \(\sqrt{25}=5\)
(4) \(\sqrt{25}=\pm 5\)
விடை :
(4) \(\sqrt{25}=\pm 5\)

கேள்வி 12.
கீழ்க்காண்பவற்றுள் எது விகிதமுறு எண் அல்ல?
(1) \(\sqrt{\frac{8}{18}}\)
(2) \(\frac{7}{3}\)
(3) \(\sqrt{0.01}\)
(4) \(\sqrt{13}\)
விடை:
(4) \(\sqrt{13}\)

கேள்வி 13.
\(\sqrt{27}+\sqrt{12}=\)
(1) \(\sqrt{39}\)
(2) 5√6
(3) 5√3
(4) 3√5
விடை:
(3) 5√3

கேள்வி 14.
\(\sqrt{80}=\mathrm{k} \sqrt{5}\) எனில் k = ?
(1) 2
(2) 4
(3) 8
(4) 16
விடை :
(2) 4

கேள்வி 15.
\(4 \sqrt{7} \times 2 \sqrt{3}=\)
(1) \(6 \sqrt{10}\)
(2) \(8 \sqrt{21}\)
(3) \(8 \sqrt{10}\)
(4) \(6 \sqrt{21}\)
விடை:
(2) \(8 \sqrt{21}\)

கேள்வி 16.
\(\frac{2 \sqrt{3}}{3 \sqrt{2}}\) இன் பகுதியை விகிதமுறு எண்ணாக மாற்றிய பின் சுருங்கிய வடிவம்
(1) \(\frac{\sqrt{2}}{3}\)
(2) \(\frac{\sqrt{3}}{2}\)
(3) \(\frac{\sqrt{6}}{3}\)
(4) \(\frac{2}{3}\)
விடை:
(3) \(\frac{\sqrt{6}}{3}\)

கேள்வி 17.
(2√5 – √2)² இன் சுருங்கிய வடிவம்
(1) 4√5 + 2√2
(2) \(22-4 \sqrt{10}\)
(3) \(8-4 \sqrt{10}\)
(4) \(2 \sqrt{10}-2\)
விடை :
(2) \(22-4 \sqrt{10}\)

கேள்வி 18.
\((0.000729)^{\frac{-3}{4}} \times(0.09)^{\frac{-3}{4}}\) = ……………………
(1) \(\frac{10^{3}}{3^{3}}\)
(2) \(\frac{10^{5}}{3^{5}}\)
(3) \(\frac{10^{2}}{3^{2}}\)
(4) \(\frac{10^{6}}{3^{6}}\)
விடை:
(4) \(\frac{10^{6}}{3^{6}}\)

கேள்வி 19.
If \(\sqrt{9^{\mathrm{X}}}=\sqrt[3]{9^{2}}\) எனில் x = ?
(1) \(\frac{2}{3}\)
(2) \(\frac{4}{3}\)
(3) \(\frac{1}{3}\)
(4) \(\frac{5}{3}\)
விடை:
(2) \(\frac{4}{3}\)

கேள்வி 20.
ஒரு செவ்வக வடிவ வீட்டு மனையின் நீளம் மற்றும் அகலங்கள் முறையே 5 × 10⁵ மற்றும் 4 x 10⁴ மீட்டர் எனில், அதன் பரப்பளவு என்ன?
(1) 9 × 10¹ மீ²
(2) 9 × 10⁹ மீ²
(3) 2 × 10¹⁰ மீ²
(4) 20 × 10²⁰ மீ²
விடை:
(3) 2 × 10¹⁰ மீ²

Tamilnadu State Board New Syllabus Samacheer Kalvi 9th Maths Guide Pdf Chapter 2 மெய்யெண்கள் Ex 2.8 Textbook Questions and Answers, Notes.

TN Board 9th Maths Solutions Chapter 2 மெய்யெண்கள் Ex 2.8

கேள்வி 1.
கீழ்க்காணும் எண்களை அறிவியல் குறியீட்டு வடிவில் எழுதுக.
(i) 569430000000
(ii) 2000.57
(iii) 0.0000006000
(iv) 0.0009000002
விடை:
(i) 5.6943 × 10¹¹
(ii)2.00057 × 10³
iii) 6.0 × 10^-7
iv) 9.000002 × 10^-4

கேள்வி 2.
கீழ்க்காணும் எண்களைத் தசம வடிவில் எழுதுக.
(i) 3.459 × 10⁶
(ii) 5.678 × 10⁴
(iii) 1.00005 × 10^-5
(iv) 2.530009 × 10^-7
விடை:
(i) 3.459 × 10⁶
= 3.459 × 1000000
= 3459000

(ii) 5.678 × 10⁴
= 5.678 × 10000
= 56780

(iii) 1.00005 ×10^-5
= 0.0000100005

(iv) 2.530009 ×10^-7
0.0000002530009

கேள்வி 3.
கீழ்க்காண்பவற்றைச் சுருக்கி அறிவியல் குறியீட்டு வடிவில் எழுதுக.
(i) (300000)² × (20000)⁴
விடை:
(300000)² × (20000)⁴
= (3 × 10⁵)² × (2 × 10⁴)⁴
= 3² × 10¹⁰ × 2⁴ × 10¹⁶
= 3² × 2⁴ × 10¹⁰ × 10¹⁶
= 9 × 16 × 10²⁶
= 144 × 10²⁶
= 1.44 × 10²⁸

(ii) (0.000001)¹¹ ÷ (0.005)³
விடை:
(0.000001)¹¹ ÷ (0.005)³
= (1 × 10^-6)¹¹ ÷ (5 × 10^-3)³
= 10^-66 ÷ (5 × 10^-3)³

= 0.008 × 10^-57
= 8 × 10^-3 × 10^-57
= 8 × 10^-60

(iii){(0.00003)⁶ × (0.00005)⁴} ÷ {(0.009)³ × (0.05)²}
விடை:
(0.00003)⁶ × (0.00005)⁴ ÷ (0.009)³ × (0.05)²
(3 × 10^-5)⁶ × (5 × 10^-5)⁴ = (9 × 10^-3)³ × (5 × 10^-2)².

25 × 10^{-50 + 13}
25 × 10^-37
2.5 × 10^-36

கேள்வி 4.
கீழ்க்காணும் தகவலை அறிவியல் குறியீட்டில் எழுதுக.
(i) உலக மக்கள் தொகை சுமார் 7000,000,000
விடை:
7 × 10⁹

(ii) ஓர் ஒளி ஆண்டு என்பது 9460528400000000 கி.மீ தூரத்தைக் குறிக்கிறது.
விடை:
9.4605284 × 10¹⁵ கி.மீ

(iii) ஓர் எலக்ட்ரானின் நிறை 0.00000000000000000000000000000091093822 கி.கி
விடை:
9.1093822 × 10^-31கி.கி

கேள்வி 5.
சுருக்குக.
(i) (2.75 × 10⁷) + (1.23 × 10⁸)
விடை :
(2.75 × 10⁷) + (1.23 × 10⁸)
= 0.275 × 10⁸ + 1.23 × 10⁸
= (0.275 + 1.23) × 10⁸
= 1.505 × 10⁸

(ii) (1.598 × 10¹⁷) – (4.58 × 10¹⁵)
விடை:
(1.598 × 10¹⁷) – (4.58 × 10¹⁵)
= 1.598 × 10¹⁷ – 0.0458 × 10¹⁷
= (1.598 – 0.0458) × 10¹⁷
= 1.5522 × 10¹⁷

(iii) (1.02 × 10¹⁰) × (1.20 × 10^-3)
விடை:
(1.02 × 10¹⁰) × (1.20 × 10^-3)
= 1.02 × 1.20 × 10¹⁰ × 10^-3
= 1.224 × 10⁷

(iv) (8.41 × 10⁴) ÷ (4.3 × 10⁵)
விடை:
(8.41 × 10⁴) ÷ (4.3 × 10⁵)
\(=\frac{8.41 \times 10^{4}}{4.3 \times 10^{5}}\)
= 1.9558 × 10^{4 – 5}
= 1.9558 × 10^-1

Tamilnadu State Board New Syllabus Samacheer Kalvi 9th Maths Guide Pdf Chapter 2 மெய்யெண்கள் Ex 2.7 Textbook Questions and Answers, Notes.

TN Board 9th Maths Solutions Chapter 2 மெய்யெண்கள் Ex 2.7

கேள்வி 1.
பகுதியை விகிதப்படுத்துக.
(i) \(\frac{1}{\sqrt{\mathbf{5 0}}}\)
விடை:
= \(\frac{1}{\sqrt{\mathbf{5 0}}}\)
\(=\frac{1}{\sqrt{50}} \times \frac{\sqrt{50}}{\sqrt{50}}=\frac{\sqrt{50}}{50}\)
\(=\frac{5 \sqrt{2}}{50}\)
\(=\frac{\sqrt{2}}{10}\)

(ii) \(\frac{5}{3 \sqrt{5}}\)
விடை:
= \(\frac{5}{3 \sqrt{5}}\)

(iii) \(\frac{\sqrt{75}}{\sqrt{18}}\)
விடை:

(iv) \(\frac{3 \sqrt{5}}{\sqrt{6}}\)
விடை :
= \(\frac{3 \sqrt{5}}{\sqrt{6}}\)
\(=\frac{3 \sqrt{5}}{\sqrt{6}} \times \frac{\sqrt{6}}{\sqrt{6}}\)
\(=\frac{3 \sqrt{30}}{6}\)
\(=\frac{\sqrt{30}}{2}\)

கேள்வி 2.
பகுதியை விகிதப்படுத்திச் சுருக்குக.
(i) \(\frac{\sqrt{48}+\sqrt{32}}{\sqrt{27}-\sqrt{18}}\)
விடை:

(ii) \(\frac{5 \sqrt{3}+\sqrt{2}}{\sqrt{3}+\sqrt{2}}\)
விடை:

(iii) \(\frac{2 \sqrt{6}-\sqrt{5}}{3 \sqrt{5}-2 \sqrt{6}}\)
விடை:

(iv) \(\frac{\sqrt{5}}{\sqrt{6}+2}-\frac{\sqrt{5}}{\sqrt{6}-2}\)
விடை:
\(\frac{\sqrt{5}}{\sqrt{6}+2}-\frac{\sqrt{5}}{\sqrt{6}-2}\)

கேள்வி 3.
\(\frac{\sqrt{7}-2}{\sqrt{7}+2}=a \sqrt{7}+b\) எனில், a மற்றும் b இன் மதிப்புகளைக் காண்க.
விடை:
\(\frac{\sqrt{7}-2}{\sqrt{7}+2}=a \sqrt{7}+b\)

கேள்வி 4.
x = √5+2 எனில்,x² + \(\frac{1}{\mathbf{x}^{2}}\) இன் மதிப்பு காண்க.
விடை:
x = √5 +2
\(\frac{1}{\mathrm{x}}\) = √5 – 2
x² + \(\frac{1}{\mathbf{x}^{2}}\) = (√5 + 2)² + (√5 – 2)²
=(5 + 4 + 4√5) + (5 + 4 – 4√5)
= 9 + 4√5 + 9 – 4√5 =18

கேள்வி 5.
√2 = 1.414 எனில், \(\frac{8-5 \sqrt{2}}{3-2 \sqrt{2}}\) இன் மதிப்பை
3 தசம இடத்திருத்தமாகக் காணவும்.
விடை :
\(\frac{8-5 \sqrt{2}}{3-2 \sqrt{2}}\)

= 5.414

Tamilnadu State Board New Syllabus Samacheer Kalvi 9th Maths Guide Pdf Chapter 2 மெய்யெண்கள் Ex 2.6 Textbook Questions and Answers, Notes.

TN Board 9th Maths Solutions Chapter 2 மெய்யெண்கள் Ex 2.6

கேள்வி 1.
முறுடுகளின் கூட்டல் மற்றும் கழித்தல் பண்புகளைப் பயன்படுத்திச் சுருக்குக.
(i) 5√3 + 18√3 – 2√3
விடை :
5√3 + 18√3 – 2√3
= (5 + 18 – 2) √3
= 21√3

ii) \(4 \sqrt[3]{5}+2 \sqrt[3]{5}-3 \sqrt[3]{5}\)
விடை :
\(4 \sqrt[3]{5}+2 \sqrt[3]{5}-3 \sqrt[3]{5}\)
= \((4+2-3) \sqrt[3]{5}\)
= \(3 \sqrt[3]{5}\)

iii) \(3 \sqrt{75}+5 \sqrt{48}-\sqrt{243}\)
விடை:

\(3 \sqrt{75}+5 \sqrt{48}-\sqrt{243}\)
\(3 \sqrt{3 \times 5 \times 5}+5 \sqrt{2 \times 2 \times 2 \times 2 \times 3}-\sqrt{3 \times 3 \times 3 \times 3 \times 3}\)
= 3 × 5√3 + 5 × 2 × 2√3 – 3 × 3√3
= 15√3 + 20√3 – 9√3
= (15 + 20- 9) √3
= 26√3

iv) \(5 \sqrt[3]{40}+2 \sqrt[3]{625}-3 \sqrt[3]{320}\)
விடை:
\(5 \sqrt[3]{40}+2 \sqrt[3]{625}-3 \sqrt[3]{320}\)


= \(10 \sqrt[3]{5}+10 \sqrt[3]{5}-12 \sqrt[3]{5}\)
= \((10+10-12) \sqrt[3]{5}\)
\(=8 \sqrt[3]{5}\)

கேள்வி 2.
முறுடுகளின் பெருக்கல் மற்றும் வகுத்தல் பண்புகளைப் பயன்படுத்திச் சுருக்குக.
(i) √3 × √5 × √2
விடை :
√3 × √5 × √2
= \(=\sqrt{3 \times 5 \times 2}\)
= \(=\sqrt{30}\)

(ii) \(\sqrt{35} \div \sqrt{7}\)
விடை:
\(\sqrt{35} \div \sqrt{7}\)
\(=\frac{\sqrt{35}}{\sqrt{7}}=\sqrt{\frac{35}{7}}\)
= √5

(iii) \(\sqrt[3]{27} \times \sqrt[3]{8} \times \sqrt[3]{125}\)
விடை:

\(\sqrt[3]{27} \times \sqrt[3]{8} \times \sqrt[3]{125}\)
= 3 × 2 × 5
= 30

iv) \((7 \sqrt{a}-5 \sqrt{b})(7 \sqrt{a}+5 \sqrt{b})\)
விடை:
\((7 \sqrt{a}-5 \sqrt{b})(7 \sqrt{a}+5 \sqrt{b})\)
\(=(7 \sqrt{a})^{2}-(5 \sqrt{b})^{2}\)
= 49a – 25b

(v) \(\left[\sqrt{\frac{225}{729}}-\sqrt{\frac{25}{144}}\right] \div \sqrt{\frac{16}{81}}\)
விடை:
\(\left[\sqrt{\frac{225}{729}}-\sqrt{\frac{25}{144}}\right] \div \sqrt{\frac{16}{81}}\)

கேள்வி 3.
√2 = 1.414, √3 = 1.732, √5 = 2.236, √10 = 3.162 எனில், கீழ்க்காண்பவற்றின் மதிப்புகளை மூன்று தசம இடத்திருத்தமாகக் காண்க.

(i) \(\sqrt{40}-\sqrt{20}\)
விடை:
\(\sqrt{40}-\sqrt{20}\)
\(=\sqrt{2 \times 2 \times 2 \times 5}-\sqrt{2 \times 2 \times 5}\)
\(=2 \sqrt{10}-2 \sqrt{5}\)
2 × 3.162 – 2 × 2.236
6.324 – 4.472
= 1.852

(ii) \(\sqrt{300}+\sqrt{90}-\sqrt{8}\)
விடை :
\(\sqrt{300}+\sqrt{90}-\sqrt{8}\)

= 10 × 1.732 + 3 × 3.162 – 2 × 1.414
= 17.320 + 9.486 – 2.828
= 26.806 – 2.828
= 23.978

கேள்வி 4.
முறுடுகளை இறங்குவரிசையில் அமைக்க.
(i) \(\sqrt[3]{5}, \sqrt[9]{4}, \sqrt[6]{3}\)
விடை :
(i) \(\sqrt[3]{5}, \sqrt[9]{4}, \sqrt[6]{3}\)
3, 6, 9ன் மீ.பொ.ம.

3, 6, 9ன் மீ.பொ.ம. = 3 × 1 × 2 × 3 = 18

ii) \(\sqrt[2]{\sqrt[3]{5}}, \sqrt[3]{\sqrt[4]{7}}, \sqrt{\sqrt{3}}\)
விடை:
\(\sqrt[2]{\sqrt[3]{5}}, \sqrt[3]{\sqrt[4]{7}}, \sqrt{\sqrt{3}}\)
\(\sqrt[6]{5}, \sqrt[12]{7}, \sqrt[4]{3}\)
4, 6, 12 ன் மீ.பொ.ம.

4, 6, 12ன் மீ.பொ.ம. = 2 × 2 × 1 × 3 × 3 = 36

கேள்வி 5.
(i) இரு முறுடுகளின் கூட்டல்
(ii) இரு முறுடுகளின் வேறுபாடு
(iii) இரு முறுடுகளின் பெருக்கல்
(iv) இரு முறுடுகளின் ஈவு
ஆகிய நிகழ்வுகளில் உம்மால் ஒரு முழுமையான முறுடைப் பெற இயலுமா? ஒவ்வொரு விடையையும் ஓர் எடுத்துக்காட்டு கொண்டு விவரிக்க.
விடை:
i) ஆம்.
\(\frac{1}{2} \sqrt{2}+\frac{1}{2} \sqrt{2}\)
\(=\left(\frac{1}{2}+\frac{1}{2}\right) \sqrt{2}\)
= √2

(ii) ஆம்.
3√5 – 2√5 = √5

(iii) ஆம்.
√2 x √3 = √6

(iv) ஆம்.
\(\sqrt[3]{4} \div \sqrt[3]{2}=\sqrt[3]{\frac{4}{2}}\)
\(=\sqrt[3]{2}\)

கேள்வி 6.
(i) இரு முறுடுகளின் கூட்டல்
(ii) இரு முறுடுகளின் வேறுபாடு
(iii) இரு முறுடுகளின் பெருக்கல்
(iv) இரு முறுடுகளின் ஈவு
ஆகிய நிகழ்வுகளில் உம்மால் ஒரு விகிதமுறு எண்ணைப் பெற இயலுமா? ஒவ்வொரு விடையையும் ஓர் எடுத்துக்காட்டுகொண்டு விவரிக்க.
விடை:
(i) ஆம்.
= \(=\frac{3+\sqrt{2}}{1}+\frac{5-\sqrt{2}}{1}\)
\(=\frac{3+\sqrt{2}+5-\sqrt{2}}{1}\)
\(=\frac{8}{1}\)

(ii) ஆம்.
= 12 + √3 -3 – √3
= (12 – 3) + √3 – √3
= 9

iii) ஆம்.
√2 x 3√2 = 6

(iv) ஆம்.
\(\sqrt[3]{27} \div \sqrt[3]{64}=\frac{\sqrt[3]{27}}{\sqrt[3]{64}}\)
\(\frac{3}{4}\)

Tamilnadu State Board New Syllabus Samacheer Kalvi 10th Maths Guide Pdf Chapter 7 அளவியல் Unit Exercise 7 Textbook Questions and Answers, Notes.

TN Board 10th Maths Solutions Chapter 7 அளவியல் Unit Exercise 7

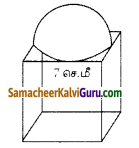
கேள்வி 1.
7 செ.மீ நீளமுள்ள ஓர் உருளை வடிவ மை குடுவையின் விட்டம் 5 மி.மீ ஆகும். மை முழுமையாகவுள்ள உருளையைக் கொண்டு சராசரியாக 330 வார்த்தைகள் எழதலாம். ஒரு லிட்டரில் ஐந்தில் ஒரு பங்கு மை ஒரு பாட்டிலில் உள்ளது எனில், அதனைப் பயன்படுத்தி எத்தனை வார்த்தைகள் எழுதலாம்?
தீர்வு :
h = 7 செ.மீ, r = \(\frac{5}{2}=\frac{5}{2 \times 10}\) செ.மீ. = \(\frac{1}{4}\)செ.மீ.
r = 0.25 செ.மீ
குடுவையின் கன அளவு = πr²h க.அ
=\(\frac{22}{7}\) x (0.25)²
= 1.375 செ.மீ³
பாட்டிலின் கன அளவு = \(\frac { 1 }{ 5 }\) லிட்டர்
\(\frac { 1 }{ 5 }\) x 1000 = 200 செ.மீ³
1.375 செ.மீ³ அளவைக் கொண்டு எழுதும் வார்த்தைகள் = 330
1செ.மீ³ அளவைக் கொண்டு எழுதும் வார்த்தைகள் \(\frac{330}{1.375}\)
200செ.மீ³ அளவைக் கொண்டு எழுதும் வார்த்தைகள்
= \(\frac{330 \times 200}{1.375}\) = 48000 வார்த்தைகள்.

கேள்வி 2.
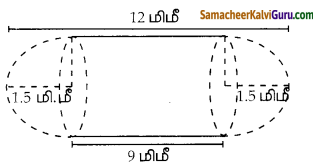
ஆரம் 1.75 மீ உள்ள ஓர் அரைக்கோள வடிவத் தொட்டி முற்றிலும் நீரால் நிரப்பப்பட்டுள்ளது. ஒரு குழாயின் மூலம் விநாடிக்கு 7 லிட்டர் வீதம் தொட்டியிலிருந்து நீர் வெளியேற்றப்படுமானால், தொட்டியை எவ்வளவு நேரத்தில் முழுவதுமாகக் காலி செய்யலாம்?
தீர்வு :
r = 1.75 மீ = 175 செ.மீ
கன அளவு = \(\frac { 2 }{ 3 }\)πr³ க.அ
= \(\frac{2}{3} \times \frac{22}{7}\) x 175 x 175 x 175
= 11229166.667 செ.மீ³
= 11229.16….1000 செ.மீ³ = 1லி
= 11229.2 லிட்டர்
நேரம் = \(\frac{\mathrm{V}}{7}\) வினாடியில்
= \(\frac{11229.2}{7} \times \frac{1}{60}\)
= \(\frac{11229.2}{420}\)
= 26.737
~ 27 நிமிடம் (தோராயமாக)

கேள்வி 3.
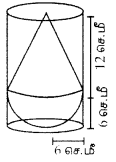
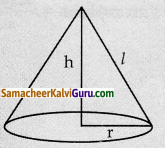
r அலகுகள் ஆரம் கொண்ட ஒரு திண்ம அரைக் கோளத்திலிருந்து வெட்டி எடுக்கப்படும் கூம்பின் மீப்பெரு கன அளவு என்ன ?
தீர்வு :
அரைக்கோளத்தின் ஆரம் = r
கூம்பின் ஆரம் = r, உயரம் = r
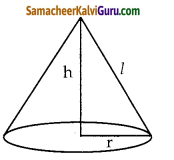
கூம்பின் கன அளவு = \(\frac { 1 }{ 3 }\)πr²h க.அ
= \(\frac { 1 }{ 3 }\)πr² = \(\frac { 1 }{ 3 }\)πr³
=\(\frac { 1 }{ 3 }\)πr³ க.அ.

கேள்வி 4.
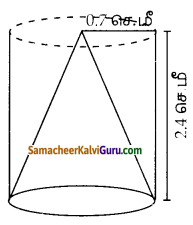
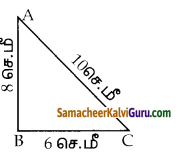
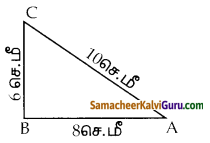
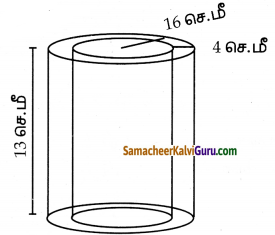
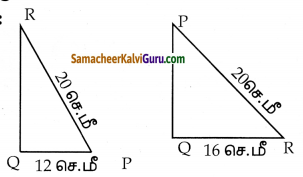
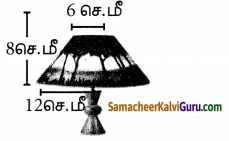
ஒரு கூம்பின் இடைக்கண்டம், 10 செ.மீ நீளமுள்ள ஓர் உருளையுடன் இணைக்கப்பட்ட எண்ணெய்ப் புனலின் மொத்த உயரம் 22 செ.மீ ஆகும். உருளையின் விட்டம் 8 செ.மீ மற்றும் புனலின் மேற்புற விட்டம் 18 செ.மீ எனில், புனலை உருவாக்கத் தேவையான தகர அட்டையின் பரப்பைக் காண்க.
தீர்வு :

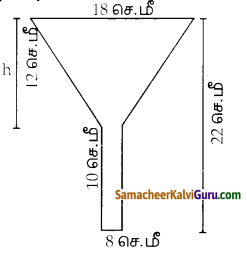
உருளை :
r =\(\frac { 8 }{ 2 }\) = 4 செ.மீ
h = 10 செ.மீ
இடைக்கண்டம் :
h = 22 – 10 = 12 செ.மீ
R = \(\frac{18}{2}\) = 9 செ.மீ
r = \(\frac{8}{2}\) = 4 செ.மீ
l = \(\sqrt{h^{2}+(R-r)^{2}}\)
l = 13 செ.மீ
புனலின் பரப்பளவு = உருளையின் புறப்பரப்பு + இடைக்கண்டத்தின் புறப்பரப்பு
= 2πrh + π[R+r)l
= 80π + 169π
= 249π
= 249 x \(\frac{22}{7}\)
= 782.57 செ.மீ²

கேள்வி 5.
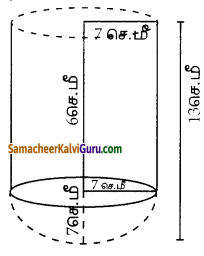
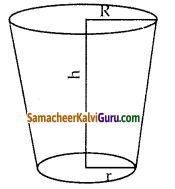
உயரம் 10 செ.மீ மற்றும் விட்டம் 4.5 செ.மீ உடைய ஒரு நேர்வட்ட உருளையை உருவாக்க 1.5 செ.மீ விட்டமும், 2 மி.மீ தடிமன் கொண்ட எத்தனை வட்ட வில்லைகள் தேவை?
தீர்வு :
வட்ட வில்லை :
D = 1.5 செ.மீ
= \(\frac { 15 }{ 10 }\) செ.மீ

R = \(\frac { 15 }{ 20 }\)
H = 2 மி.மீ
= \(\frac{2}{10}\) செ.மீ
உருளை :
d = 4.5 செ.மீ
= \(\frac{45}{10}\)
ஆரம் = \(\frac{45}{20}\) செ.மீ
உயரம் = 10 செ.மீ

வில்லைகளின் எண்ணிக்கை வில்லைகளின் கன அளவு = உருளையின் கன அளவு

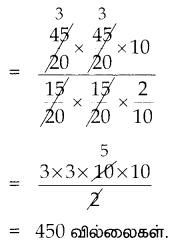
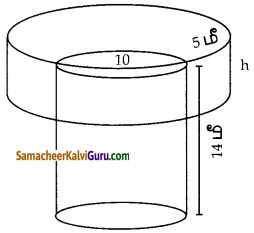
கேள்வி 6.
ஓர் உள்ளீடற்ற உலோக உருளையின் வெளிப்புற ஆரம் 4.3 செ.மீ, உட்புற ஆரம் 1.1 செ.மீ மற்றும் நீளம் 4 செ.மீ. உலோக உருளையை உருக்கி 12 செ.மீ நீளமுள்ள வேறொரு திண்ம உருளை உருவாக்கப்பட்டால் புதிய உருளையின் விட்டத்தைக் கணக்கிடுக.
தீர்வு :
உருளை:
r = ?
h = 12 செ.மீ
உள்ளீடற்ற உருளை
R = 4.3 செ.மீ
r = 1.1 செ.மீ
h = 4 செ.மீ
உருளையின் கன அளவு = உள்ளீடற்ற உருளையின் கன அளவு
πr²h = π (R² – r²)h
r² x 12 = (4.3² – 1.1²)4

r² = 5.76 = (2.4)²
r = 2.4 செ.மீ
விட்ட ம் = 2r = 2×2.4 = 4.8 செ.மீ

கேள்வி 7.
ஒர் இடைக்கண்டத்தின் இரு முனைகளின் சுற்றளவுகள் 18மீ, 16மீ மற்றும் அதன் சாயுயரம் 4 மீ ஆகும். ஒரு சதுர மீட்டருக்கு ₹100 வீதம் இடைக்கண்டத்தின் வளைபரப்பில் வர்ணம் பூச ஆகும் மொத்த செலவு என்ன?
தீர்வு :
l = 4 மீ
2πR = 18
2 x \(\frac { 22 }{ 7 }\) x R = 18
R = \(\frac{18 \times 7}{2 \times 22}\)
R = 2.86 மீ

2πr = 16
2 x \(\frac { 22 }{ 7 }\) x r = 16
r = \(\frac{16 \times 7}{2 \times 22}\)
r= 2.55 மீ
C.S.A = π(R+r)l ச. அ.
= π(2.86+2.55)4
= π(5.41)4
= 67.95மீ²
= 68 மீ²
1 ச.மீ க்கு வர்ண ம் பூச = ₹100
68ச.மீக்கு வர்ண ம் பூச =₹ 68 x 100
= ₹6800

கேள்வி 8.
ஓர் உள்ளீடற்ற அரைக்கோளக்கிண்ணத்தை உருவாக்கப் பயன்பட்ட பொருளின் கன அளவு \(\frac{436 \pi}{3}\) க .செ.மீ ஆகும். கிண்ணத்தின் வெளிவிட்டம் 14 செ.மீ எனில் அதன் தடிமனைக் கணக்கிடுக. தீர்வு :
R = 7 செ.மீ
4361 உள்ளீடற்ற உருளையின் கன அளவு = \(\frac{436 \pi}{3}\)
\(\frac { 2 }{ 3 }\)π (R³ – r³) = \(\frac{436 \pi}{3}\)
7³ – 3³ = \(\frac{436}{2}\) = 218
343-r³ = 218
r³ = 343 – 218
r³ = 218
r³ = 125
r³ = 5 செ.மீ
தடிமன் = R – r
= 7 – 5 = 2 செ.மீ

கேள்வி 9.
ஒரு கூம்பின் கன அளவு 1005\(\frac { 5 }{ 7 }\) க.செ.மீ மற்றும் கீழ் வட்டப்பரப்பு 201\(\frac { 1 }{ 7 }\)ச.செ.மீ எனில், அதன் சாயுயரம் காண்க.
தீர்வு :
வட்டப்பரப்பு= 201\(\frac { 1 }{ 7 }\) ச.செமீ
πr² = \(\frac{1408}{7}\)

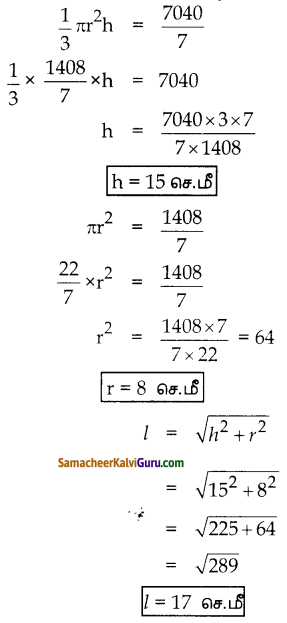
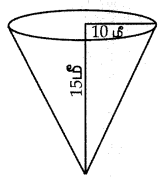
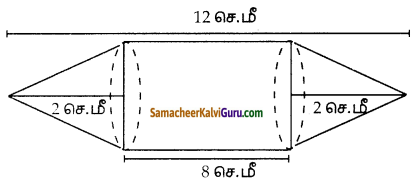
கேள்வி 10.
ஒரு வட்டக்கோண வடிவில் உள்ள உலோகத் தகட்டின் ஆரம் 21 செ.மீ மற்றும் மையக் கோணம் 216 ஆகும். வட்டக்கோணப் பகுதியின் ஆரங்களை இணைத்து உருவாக்கப்படும் கூம்பின் கன அளவைக் காண்க.
தீர்வு :
வில்லின் நீளம் = \(\frac{\theta}{360} \times 2 \pi \mathrm{r}\)
= \(\frac{216}{360} \times 2 \times \frac{22}{7} \times 21\)
2πr = 79.2 செ.மீ
2 x \(\frac { 1 }{ 7 }\) x r = 79.2
r = \(\frac{79.2 \times 7}{2 \times 22}\)
r = 12.6 செ.மீ
l = 21 செ.மீ,
r = 12.6 செ.மீ

h = 16.8 செ.மீ
கன அளவு = \(\frac { 1 }{ 3 }\)πr²
\(\frac { 1 }{ 3 }\)π1(12.6)² (16.8)
= \(\frac{8374.91}{3}\)
= 2791.64 செ.மீ

Tamilnadu State Board New Syllabus Samacheer Kalvi 10th Maths Guide Pdf Chapter 7 அளவியல் Ex 7.5 Textbook Questions and Answers, Notes.

TN Board 10th Maths Solutions Chapter 7 அளவியல் Ex 7.5

கேள்வி 1.
15 செ.மீ உயரமும் 16 செ.மீ விட்டமும் கொண்ட ஒரு நேர்வட்டக் கூம்பின் வளைபரப்பு
அ) 60 ச.செ.மீ
ஆ) 681 ச.செ.மீ
இ) 1201 ச. செ. மீ
ஈ) 136 ச. செ.மீ
விடை :
ஈ) 1361 ச.செ.மீ
தீர்வு :
1 = \(\sqrt{15^{2}+8^{2}}\)
= \(\sqrt{225+64}\)
= \(\sqrt{289}\)
l = 17செ.மீ
வளைபரப்பு = πrl ச.அ
= π × 8 × 17
= 1367π செ.மீ

கேள்வி 2.
r அலகுகள் ஆரம் உடைய இரு சம அரைக்கோளங்களின் அடிப்பகுதிகள் இணைக்கப்படும் போது உருவாகும் திண்மத்தின் புறப்பரப்பு
அ) 41 ச.அ
ஆ) 6rr ச.அ
இ) 3 ச.அ
ஈ) 8 ச.அ
விடை :
அ) 42 ச.அ
தீர்வு :
πr² + πr² = 4πr² ச.அ

கேள்வி 3.
ஆரம் 5 செ.மீ மற்றும் சாயுயரம் 13 செ.மீ உடைய நேர்வட்டக் கூம்பின் உயரம்
அ) 12 செ.மீ
ஆ) 10 செ.மீ
இ) 13 செ.மீ
ஈ) 5 செ.மீ
விடை :
அ) 12 செ.மீ
தீர்வு :

h = 12 செ.மீ

கேள்வி 4.
ஓர் உருளையின் உயரத்தை மாற்றாமல் அதன் ஆரத்தைப் பாதியாகக் கொண்டு புதிய உருளை உருவாக்கப்படுகிறது. புதிய மற்றும் முந்தைய உருளைகளின் கன அளவுகளின் விகிதம்
அ) 1:2
ஆ) 1:4
இ) 1:6
ஈ) 1:8
விடை :
அ) 1 :2
தீர்வு :

கேள்வி 5.
ஓர் உருளையின் ஆரம் அதன் உயரத்தில் மூன்றில் ஒரு பங்கு எனில், அதன் மொத்தப் புறப்பரப்பு
அ) \(\frac{9 \pi \mathrm{h}^{2}}{8}\) ச.அ
ஆ) 24πh²s ச.அ
இ) \(\frac{8 \pi h^{2}}{9}\) ச.அ
ஈ) \(\frac{56 \pi \mathrm{h}^{2}}{9}\) ச.அ
விடை :
இ) \(\frac{8 \pi h^{2}}{9}\) ச.அ
தீர்வு :
r = \(\frac { 1 }{ 3 }\)h, h = h
புறப்பரப்பு = 2πr(h+r) ச.அ
= 2π × \(\frac { h }{ 3 }\) (h+\(\frac { h }{ 3 }\))
= \(\frac{2 \mathrm{~h}}{3}\left(\frac{4 \mathrm{~h}}{3}\right)\)
= \(\frac{8 \pi \mathrm{h}^{2}}{9}\)ச.அ

கேள்வி 6.
ஓர் உள்ளீடற்ற உருளையின் வெளிப்புற மற்றும் உட்புற ஆரங்களின் கூடுதல் 14 செ.மீ மற்றும் அதன் தடிமன் 4 செ.மீ ஆகும். உருளையின் உயரம் 20 செ.மீ எனில், அதனை உருவாக்கப் பயன்பட்ட பொருளின் கன அளவு
அ) 5600 1 க.செ.மீ
ஆ) 11200 1 க .செ.மீ
இ) 561 க. செ. மீ
ஈ) 3600 க . செ.மீ
விடை :
ஆ) 11200 1 க. செ.மீ
தீர்வு :

w = R – r
R = 9 செ.மீ
r = 5 செ.மீ
V = π(R² – r²)h க. அ
= (9² – 5²)20 = (56)20
= 1120 π க.செ.மீ

கேள்வி 7.
ஒரு கூம்பின் அடிப்புற ஆரம் மும்மடங்காவும் உயரம் இரு மடங்காகவும் மாறினால் கன அளவு எத்தனை மடங்காக மாறும்
அ) 6 மடங்கு
ஆ) 18 மடங்கு
இ) 12மடங்கு
ஈ) மாற்றமில்லை
விடை :
அ) 6 மடங்கு
தீர்வு :
r = 3r, h = 2h
V = \(\frac { 1 }{ 3 }\)πr2h
= \(\frac { 1 }{ 3 }\)π(3r)²(2h)
= \(\frac { 1 }{ 3 }\)π9r² × 2h
= \(\frac { 1 }{ 3 }\)πr²h
= 6 × \(\frac { 1 }{ 3 }\) πr²h
= 6 × கூம்பின் கனஅளவு

கேள்வி 8.
ஓர் அரைக்கோளத்தின் மொத்தப்பரப்பு அதன் ஆரத்தினுடைய வர்க்கத்தின் மடங்காகும்.
அ) π
ஆ) 4π
இ) 3π
ஈ) 2π
விடை :
இ) 3π
தீர்வு :
மொத்தப்பரப்பு = 3πr²
ஆரத்தினுடைய வர்க்கத்தின் 3π மடங்கு ஆகும்.

கேள்வி 9.
x செ.மீ ஆரமுள்ள ஒரு திண்மக் கோளம் அதே ஆரமுள்ள ஒரு கூம்பாக மாற்றப்படுகிறது எனில் கூம்பின் உயரம்
அ) 3x செ.மீ
ஆ) x செ.மீ
இ) 4x செ.மீ
ஈ) 2x செ.மீ
விடை :
இ) 4x செ.மீ
தீர்வு
r = x செ.மீ
கூம்பின் கள அளவு = கோளத்தின் கன அளவு
\(\frac { 1 }{ 3 }\) = \(\frac { 4 }{ 3 }\)
h = 4x செ.மீ

கேள்வி 10.
16 செ.மீ உயரமுள்ள ஒரு நேர்வட்டக் கூம்பின் இடைக்கண்ட ஆரங்கள் 8 செ.மீ மற்றும் 20 செ.மீ எனில், அதன் கன அளவு
அ) 3328π க செ.மீ
ஆ) 3228π க செ.மீ
இ) 3240π க செ.மீ
ஈ) 3340π க செ.மீ
விடை :
அ) 33287 க.செ.மீ தீர்வு :
V = \(\frac{1}{3}\)πh (R² + r² + Rr) க.அ
= \(\frac{1}{3}\)π × 16 (20² + 8² + 20 × 8)
= \(\frac{16 \pi}{3}\) (400 + 64 + 160)
= \(\frac{16 \pi}{3}\) × 584
V = 3328π க . செ.மீ

கேள்வி 11.
கீழ்க்காணும் எந்த இரு உருவங்களை இணைத்தால் ஓர் இறகுபந்தின் வடிவம் கிடைக்கும்.
அ) உருளை மற்றும் கோளம்
ஆ) அரைக்கோளம் மற்றும் கூம்பு
இ) கோளம் மற்றும் கூம்பு
ஈ) கூம்பின் இடைக்கண்டம் மற்றும் அரைக்கோளம்
விடை :
ஈ) கூம்பின் இடைக்கண்டம் மற்றும் அரைக்கோளம்
தீர்வு

கேள்வி 12.
r₁ அலகுகள் ஆரமுள்ள ஒரு கோளப்பந்து உருக்கப்பட்டு r₂ அலகுகள் ஆரமுடைய 8 சமகோள பந்துகளாக ஆக்கப்படுகிறது எனில் r₁ : r₂
அ) 2:1
ஆ) 1:2
இ) 4:1
ஈ) 1:4
விடை :
அ) 2:1
தீர்வு :
கோளத்தின் கன அளவு = 8 × பந்தின் கன அளவு

கேள்வி 13.
1செ.மீ ஆரமும் 5 செ.மீ உயரமும் கொண்ட ஒரு மர உருளையிலிருந்து அதிகபட்சக் கன அளவு கொண்ட கோளம் வெட்டி எடுக்கப்படுகிறது எனில், அதன் கன அளவு (க. செ.மீ – ல்)
ஆ) \(\frac{4}{3}\)π
அ) \(\frac{10}{3}\)π
இ) 5π
ஈ) \(\frac{20}{3}\)π
விடை :
ஆ) \(\frac{4}{3}\)π
தீர்வு :
கன அளவு = πr²h
= π × 1 × 5
= 5π செ.மீ²
கோளத்தின் கன அளவு = \(\frac { 4 }{ 3 }\)πr³க.அ
= \(\frac { 4 }{ 3 }\)π(1)³ = \(\frac { 4 }{ 3 }\)πக.அ

கேள்வி 14.
இடைக்கண்டத்தை ஒரு பகுதியாகக் கொண்ட ஒரு கூம்பின் உயரம் மற்றும் ஆரம் முறையே h₁ அலகுகள் மற்றும் r₁ அலகுகள் ஆகும். இடைக்கண்டத்தின் உயரம் மற்றும் சிறிய பக்க ஆரம் முறையே h₂ அலகுகள் மற்றும் r₂ அலகுகள் மற்றும் h₁ : h₂ = r₁:r₂ எனில் நான் மதிப்பு
அ) 1 : 3
ஆ) 1 : 2
இ) 2 : 1
ஈ) 3 : 1
விடை :
ஆ) 1 : 2
தீர்வு :
h₁;h₂ = 1:2 = r₂ : r₁ = 1 : 2

கேள்வி 15.
சமமான விட்டம் மற்றும் உயரம் உடைய ஓர் உருளை, ஒரு கூம்பு மற்றும் ஒரு கோளத்தின் கன அளவுகளின் விகிதம்
அ) 1 : 2 : 3
ஆ) 2 : 1 : 3
இ) 1 : 3 : 2
ஈ) 3 : 1 : 2
விடை :
ஈ) 3 : 1 : 2
தீர்வு :

Tamilnadu State Board New Syllabus Samacheer Kalvi 9th Maths Guide Pdf Chapter 2 மெய்யெண்கள் Ex 2.5 Textbook Questions and Answers, Notes.

TN Board 9th Maths Solutions Chapter 2 மெய்யெண்கள் Ex 2.5

கேள்வி 1.
பின்வருவனவற்றை 5ⁿ வடிவத்தில் எழுதுக.
(i) 625
விடை:
625 = 5 × 5 × 5 × 5
= 5⁴

(ii) \(\frac{1}{5}\)
விடை:
\(\frac{1}{5}\) = 5^-1

(iii) √5
விடை:
√5 = 5^1/2

(iv) \(\sqrt{125}\)
விடை:
\(\sqrt{125}\) = \(\sqrt{5 \times 5 \times 5}\)
= \(\sqrt{5^{3}}\)
= \(5^{\frac{3}{2}}\)

கேள்வி 2.
பின்வருவனவற்றை 4ⁿ வடிவத்தில் எழுதுக.
(i) 16
விடை:
16 = 4 × 4
= 4²

(ii) 8
விடை:
8 = 4 × 2
= 4 × √4
4 × 4^1/2 = 4^{1 + 1/2}
= \(4^{\frac{3}{2}}\)

(iii) 32
விடை:
8 = 4 × 4 × 2
= 4² × √4
= 4² × (4)^1/2 = 4^{2 + 1/2}
= \(4^{\frac{5}{2}}\)

கேள்வி 3.
மதிப்புக் காண்க.
(i) (49)^1/2
விடை:
= (49)^1/2
= (7²)^1/2 = 7\(7^{\frac{2}{2}}\)
= 7

(ii) \(243^{\frac{2}{5}}\)
விடை:
\(243^{\frac{2}{5}}\)
\((3 \times 3 \times 3 \times 3 \times 3)^{\frac{2}{5}}\)
= \(\left(3^{5}\right)^{\frac{2}{5}}\) = 3²
= 9

(iii) \((9)^{\frac{-3}{2}}\)
விடை:
\((9)^{\frac{-3}{2}}\)
\(=\left(3^{2}\right)^{\frac{-3}{2}}\)
= 3^-3 = \(\frac{1}{3^{3}}\)
\(=\frac{1}{27}\)

(iv) \(\left(\frac{64}{125}\right)^{-2}\)
விடை:

கேள்வி 4.
பின்ன அடுக்கைப் பயன்படுத்தி எழுதுக.
(i) √5
விடை:
√5 = 5^1/2

(ii) √7
விடை:
√7 = 7^1/2

(iii) \((\sqrt[3]{49})^{5}\)
விடை:
\((\sqrt[3]{49})^{5}\) = \(\left(\sqrt[3]{7^{2}}\right)^{5}=\left(7^{\frac{2}{3}}\right)^{5}\)
\(=7^{\frac{10}{3}}\)

(iv) \(\left(\frac{1}{\sqrt[3]{100}}\right)^{7}\)
= \(\left(\frac{1}{\sqrt[3]{100}}\right)^{7}\)
\(=\left(\frac{1}{(100)^{\frac{1}{3}}}\right)^{7}\)
\(=\left(100^{\frac{-1}{3}}\right)^{7}\)
\(=\left(10^{2}\right)^{-7}\)
\(=10^{\frac{-14}{3}}\)

கேள்வி 5.
கீழ்க்காண்பனவற்றின் 5வது மூலத்தைக் காண்க.
(i) 32
விடை:
\(\sqrt[5]{32}\) = \(\sqrt[5]{2 \times 2 \times 2 \times 2 \times 2}=\sqrt[5]{2^{5}}\)
\(=\left(2^{5}\right)^{\frac{1}{5}}\)
= 2

(ii) 243
விடை:
\(\sqrt[5]{243}=\sqrt[5]{3 \times 3 \times 3 \times 3 \times 3}=\sqrt[5]{3^{5}}\)
= \(=\left(3^{5}\right)^{\frac{1}{5}}\)
= 3

(iii) 100000
விடை:
\(\sqrt[5]{100000}=\sqrt[5]{10 \times 10 \times 10 \times 10 \times 10}=\sqrt[5]{10^{5}}\)
\(=\left(10^{5}\right)^{\frac{1}{5}}\)
= 10

(iv) \(\frac{1024}{3125}\)
விடை:
\(=\sqrt[5]{\frac{1024}{3125}}\)
\(=\sqrt[5]{\frac{4 \times 4 \times 4 \times 4 \times 4}{5 \times 5 \times 5 \times 5 \times 5}}=\sqrt[5]{\left(\frac{4}{5}\right)^{5}}\)
\(=\left(\frac{4}{5}\right)^{\frac{5}{5}}\)
\(=\frac{4}{5}\)

Tamilnadu State Board New Syllabus Samacheer Kalvi 10th Maths Guide Pdf Chapter 7 அளவியல் Ex 7.4 Textbook Questions and Answers, Notes.

TN Board 10th Maths Solutions Chapter 7 அளவியல் Ex 7.4

கேள்வி 1.
12 செ.மீ ஆரமுள்ள ஓர் அலுமினியக் கோளம் உருக்கப்பட்டு 8 செ.மீ ஆரமுள்ள ஓர் உருளையாக – மாற்றப்படுகிறது. உருளையின் உயரம் காண்க.
தீர்வு :
உருளை :
R = 8 செ.மீ
H = ?
கோளம் :
r = 12 செ.மீ
உருளையின் கன அளவு= கோளத்தின் கன அளவு
πR²H = \(\frac { 4 }{ 3 }\)/ r³
8 x 8 x H = \(\frac { 4 }{ 3 }\) x 12 x 12 x 12
H = \(\frac{4 \times 12 \times 12 \times 12}{3 \times 8 \times 8}\)
H = 36 செ.மீ

கேள்வி 2.
14 செ.மீ விட்டமுள்ள குழாயிலிருந்து 15கி.மீ/மணி என்ற வேகத்தில் 50மீ நீளம் மற்றும் 44 மீ அகலம் கொண்ட ஒரு செவ்வக வடிவத் தொட்டியினுள் தண்ணீர் பாய்கிறது. எவ்வளவு நேரத்தில் தண்ணீ ரின் மட்டம் 21 செ.மீ – க்கு உயரும்.
தீர்வு :
உருளை : r = 7 செ.மீ
h= 1500000 செ.மீ
செவ்வக வடிவ தொட்டி :
l = 50 மீ = 5000 செ.மீ
b = 44 மீ = 4400 செ.மீ
h = 21 செ.மீ
உருளையின் கன அளவு = πr² க.அ
= \(\frac { 22 }{ 7 }\) x 7 x 7 x 1500000
= 231000000 செ.மீ³
தொட்டியின் கன அளவு
= lbh கன அ
= 5000 x 4400 x 21
= 462000000 செ.மீ

நேரம் = தொட்டியின் கன அளவு / உருளையின் கன அளவு
= \(\frac{462000000}{231000000}\)
= 2 மணிகள்.

கேள்வி 3.
முழுமையாக நீரால் நிரம்பியுள்ள ஒரு கூம்பு வடிவக் குடுவையின் ஆரம் r அலகுகள் மற்றும் உயரம் h அலகுகள் ஆகும். நீரானது xr அலகுகள் ஆரமுள்ள மற்றொரு உருளை வடிவக் குடுவைக்கு மாற்றப்பட்டால் நீரின் உயரம் காண்க.
தீர்வு :
உருளை :
உயரம் = ?
ஆரம் = xr அலகுகள்

கூம்புவடிவ குடுவை :
ஆரம் r அலகுகள்
உயரம் h அலகுகள்

உருளையின் கன அளவு = கூம்பின் கன அளவு
πR²H = \(\frac { 1 }{ 3 }\) πr²H
(xr)²H = \(\frac { 1 }{ 3 }\)r²H
x²r²H = \(\frac { 1 }{ 3 }\)r²H
H = \(\frac{r^{2} \mathrm{~h}}{3 x^{2}{r}^{2}}\)
H = \(\frac{\mathrm{h}}{3 x^{2}}\) செ.மீ³

கேள்வி 4.
விட்டம் 14 செ.மீ. உயரம் 8செ.மீ உடைய ஒரு திண்ம நேர்வட்டக் கூம்பு , ஓர் உள்ளீடற்ற கோளமாக உருமாற்றப்படுகிறது. கோளத்தின் வெளிவிட்டம் 10 செ.மீ எனில், உள்விட்டத்தைக் காண்க.
தீர்வு :
உள்ளீடற்ற கோளம் :
R = 5 செ.மீ
r = ?
கூம்பு :
r = 7 செ.மீ
h = 8 செ.மீ
அரைக்கோளத்தின் கன அளவு = கூம்பின் கன அளவு
\(\frac { 4 }{ 3 }\) π(R³-r³) = \(\frac { 1 }{ 3 }\) πr²H
4(5³ – r³) = 7 x 7 x 8
(125-r³) = \(\frac{7 \times 7 \times 8}{4}\)
125 – r³ = 98
-r³ = 98 – 125
-r³ = -27
r³ = 27 = 3³
r = 3 செ.மீ)
விட்டம் = 2r = 2 x 3 = 6 செ.மீ

கேள்வி 5.
சீனு வீட்டின் மேல்நிலை நீர்த்தொட்டி உருளை வடிவில் உள்ளது. அதன் ஆரம் 60 செ.மீ மற்றும் உயரம் 105 செ.மீ 2மீ x 1.5 மீ x 1 மீ பரிணாமங்களை உடைய ஒரு கனச்செவ்வகக் கீழ்நிலை நீர் தொட்டியிலிருந்து நீர் உந்தப்பட்டு மேலேயுள்ள உருளை வடிவத் தொட்டி முழுமையாக
நிரப்பப்படுகிறது. தொடக்கத்தில் கீழ்த் தொட்டியில் நீர் முழுமையாக இருப்பதாகக் கருதுக. மேல் தொட்டிக்கு நீர் ஏற்றிய பிறகு மீதமுள்ள நீரின் கன அளவைக் காண்க.
தீர்வு :
உருளை :
r = 60 செ.மீ
h = 105 செ.மீ

செவ்வக வடிவ தொட்டி :
l = 2 மீ = 200 செ.மீ
b = 1.5 மீ = 150 செ.மீ
h = 1 மீ = 100 செ.மீ

உருளையின் கன அளவு = πr²h க.அ.
= \(\frac { 22 }{ 7 }\) x 60 x 60 x 105
= 1188000 செ.மீ³
செவ்வக தொட்டியின் கன அளவு = lbh க.அ
= 200 x 150 x 100
= 3000000 செ.மீ³
மேல் தொட்டிக்கு நீர் ஏற்றிய பிறகு மீதமுள்ள நீரின் கன அளவு = செவ்வக தொட்டியின் க.அ – உருளையின் க.அ
= 3000000 – 1188000
= 1812000 செ.மீ³

கேள்வி 6.
ஓர் உள்ளீடற்ற அரைக்கோள ஓட்டின் உட்புற மற்றும் வெளிப்புற விட்டங்கள் முறையே 6 செ.மீ மற்றும் 10 செ.மீ ஆகும். அது உருக்கப்பட்டு 14 செ.மீ விட்டமுள்ள ஒரு திண்ம உருளையாக்கப்பட்டால், அவ்வுருளையின் உயரம் காண்க.
தீர்வு :
உருளை :
R = 7 செ.மீ
H = ?
உள்ளீடற்ற அரைக் கோளத்தின் கன அளவு r = 3 செ.மீ
R = 5 செ.மீ
உருளையின் கன அளவு = உள்ளீடற்ற அரைக்கோளத்தின் கன அளவு

கேள்வி 7.
6 செ.மீ ஆரமுள்ள ஒரு திண்மக் கோளம் உருக்கப்பட்டுச் சீரான தடிமனுள்ள ஓர் உள்ளீடற்ற உருளையாக மாற்றப்படுகிறது. உருளையின் வெளி ஆரம் 5 செ.மீ மற்றும் உயரம் 32 செ.மீ எனில், உருளையின் தடிமனைக் காண்க.
தீர்வு :
உள்ளீடற்ற உருளை:
R = 5 செ.மீ
r = ?
h = 32 செ.மீ
கோளம் :
r = 6 செ.மீ
உள்ளீடற்ற உருளையின் கனஅளவு = கோளத்தின் கனஅளவு
π(R² – r²)h = \(\frac { 4 }{ 3 }\) πr³
(5² – r²)32 = \(\frac { 4 }{ 3 }\) x 6 x 6 x 6
(25 – r²) = \(\frac{4 \times 2 \times 6 \times 6}{32}\)
25 – r² = 16
r = 4 செ.மீ
தடிமன் = R-r = 5-4 செ.மீ = 1 செ.மீ

கேள்வி 8.
ஓர் அரைக்கோள வடிவக் கிண்ணத்தின் விளிம்புவரையில் பழச்சாறுநிரம்பியுள்ளது. உயரத்தைவிட 50% அதிக ஆரம் கொண்ட உருளை வடிவப்பாத்திரத்திற்குப் பழச்சாறு மாற்றப்படுகிறது. அரைக்கோளம் மற்றும் உருளை ஆகியவற்றின் விட்டங்கள் சமமானால் கிண்ணத்திலிருந்து எவ்வளவு சதவீதப் பழச்சாறு உருளை வடிவ பாத்திரத்திற்கு மாற்றப்படும்?
தீர்வு :
அரைக்கோள கிண்ணத்தின் கன அளவு = \(\frac{2}{3}\)πr³க.அ
உயரம் = h
r = h + h x \(\frac { 50 }{ 100 }\) = h(1 + \(\frac { 1 }{ 2 }\)) = \(\frac{3 h}{2}\)
r = \(\frac{3 h}{2}\) ⇒ h = \(\frac{2 r}{3}\)
உருளை பாத்திரத்தின் கன அளவு

= 100%