Samacheer Kalvi 10th Maths Guide Chapter 6 முக்கோணவியல் Ex 6.4

Tamilnadu State Board New Syllabus Samacheer Kalvi 10th Maths Guide Pdf Chapter 6 முக்கோணவியல் Ex 6.4 Textbook Questions and Answers, Notes.

TN Board 10th Maths Solutions Chapter 6 முக்கோணவியல் Ex 6.4

கேள்வி 1.
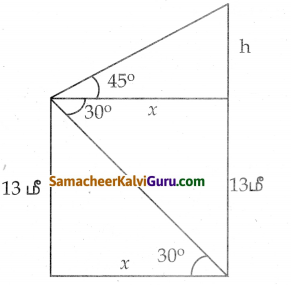
13மீ உயரமுள்ள ஒருமரத்தின் உச்சியிலிருந்து மற்றொரு மரத்தின் உச்சி மற்றும் அடியின் ஏற்றக்கோணம் மற்றும் இறக்கக்கோணம் முறையே 45° மற்றும் 30° எனில், இரண்டாவது மரத்தின் உயரத்தைக் காண்க. (√3 = 1.732)
தீர்வு :
tanθ =
tan 45° = h/x
1 = h/x
x = h ———(1)
tan 30° = 13/x
\(\frac{1}{\sqrt{3}}=\frac{13}{x}\)

x = 13√3 ——–(2)
(1) & (2) லிருந்து
h = 13√3 = 13 x 1.732
h = 22.516 மீ
இரண்டாவது மரத்தின் உயரம் = 13 + h
= 13 + 22.52
= 35.52 மீ

கேள்வி 2.
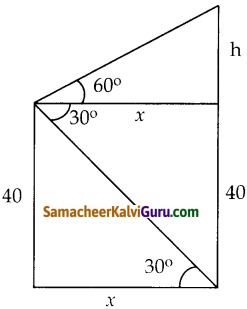
கடலின் நீர் மட்டத்திலிருந்து 40மீட்டருக்கு மேலே உள்ள ஒரு கப்பலின் மேல் பகுதியில் நின்று கொண்டிருக்கிற ஒருவர், குன்றின் உச்சியை 60° ஏற்றக்கோணத்திலும் அடிப்பகுதியை 30° இறக்கக்கோணத்திலும் காண்கிறார் எனில், கப்பலிலிருந்து குன்றுக்கு உள்ள தொலைவையும், குன்றின் உயரத்தையும் காண்க. ( √3 = 1.732)
தீர்வு :
tan θ =
tan 60° = h/x
√3 = h/x
x = h/√3 ——-(1)
tan 30° = 40/x
\(\frac{1}{\sqrt{3}}=\frac{40}{x}\)
x = 40√3 ——(2)

(1) மற்றும் (2) லிருந்து
\(40 \sqrt{3}=\frac{h}{\sqrt{3}}\)
h = 40√3 x √3 = 40 x 3 = 120
h = 120 மீ
மொத்த உயரம் = 120 + 40 மீ = 160 மீ

கேள்வி 3.
ஏரியின் நீர் மட்டத்திலிருந்து ‘he உயரத்திலுள்ள ஒரு புள்ளியிலிருந்து ஒரு மேகத்தின் ஏற்றக்கோணம், θ₁ மற்றும் ஏரி நீரில் விழும் மேகப் பிம்பத்தின் இறக்கக்கோணம் θ₂ எனில் தரையிலிருந்து மேகத்தின் உயரம் \(\frac{h\left(\tan q_{1}+\tan q_{2}\right)}{\tan q_{2}-\tan q_{1}}\) என நிரூபி.
தீர்வு :
tanθ = 
EF = DC = h , AD = b – h
AC = BC = b BD = b + h

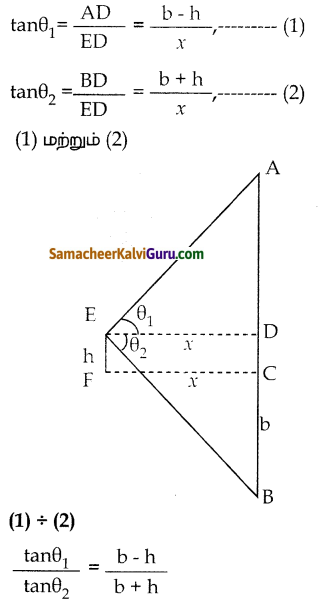
tanθ₁ (b + h) = tanθ₂ (b – h)
b tanθ₁ + h tanθ₁ = b tanθ₂ – h tanθ₂
h tanθ₁ + h tanθ₂ = b tanθ₂ – b tanθ₁
h (tanθ₁ + tanθ₂) = b (tanθ₂ – b tanθ₁)
= b(tanθ₂ – tanθ₁) = h(tanθ₁ + tanθ₂)
b = h ( \(\frac{\tan \theta_{1}+\tan \theta_{2}}{\tan \theta_{2}-\tan \theta_{1}}\) )

கேள்வி 4.
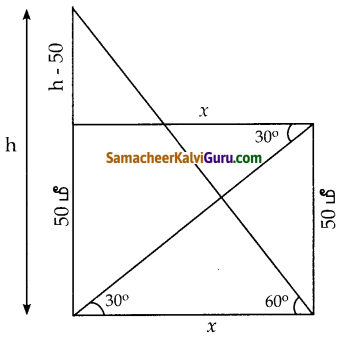
உயரமான அடுக்குமாடிக் குடியிருப்பின் அடியிலிருந்து அலைபேசி கோபுர உச்சியின் ஏற்றக்கோணம் 60° மற்றும் குடியிருப்பின் உச்சியிலிருந்து கோபுர அடியின் இறக்கக்கோணம் 30 ஆகும். அடுக்குமாடி குடியிருப்பின் உயரம் 50 மீ எனில் அலைபேசிக் கோபுரத்தின் உயரத்தைக் காண்க. கதிர்வீச்சுக்கட்டுப்பாடு விதியின்படி அலைபேசிக் கோபுரத்தின் குறைந்தபட்ச உயரம் 120மீ இருக்க வேண்டும். மேற்கண்ட அலைக்கோபுரம் இந்தக் கட்டுப்பாட்டிற்கு உட்படுகிறதா?
தீர்வு :
tanθ =
tan 30° – \(\frac{50}{x}\)
x = 50√3 ————— (1)
tan 60° = h/x
√3 = h/x
x = h/√3 ————— (2)

(1) மற்றும் (2) லிருந்து
\(\frac{\mathrm{h}}{\sqrt{3}}\) = 50√3
h = 50√3 x √3 = 50 x 3 = 150
h = 150 மீ
ஆம். மேற்கண்ட அலைக்கோபுரம் இந்தக் கட்டுப்பாட்டிற்கு உட்படுகிறது.

கேள்வி 5.
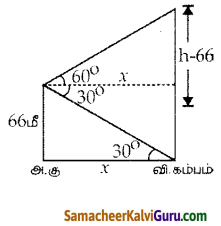
66 மீ உயரமான அடுக்குமாடிக் குடியிருப்பின் உச்சியிலிருந்து ஒரு விளக்குக் கம்பத்தின் உச்சி மற்றும் அடியின் ஏற்றக்கோணம் மற்றும் இறக்கக்கோணம் முறையே 60°, 30° எனில் பின்வருவனவற்றைக் காண்க.
i) விளக்குக் கம்பத்தின் உயரம்.
ii) விளக்குக் கம்ப உயரத்திற்கும் அடுக்குமாடியின் உயரத்திற்கும் இடையேயுள்ள வித்தியாசம்.
iii) விளக்குக் கம்பத்திற்கும் அடுக்குமாடிக்கும் இடையே உள்ள தொலைவு. ( √3 = 1.732)
தீர்வு :
tanθ =
tan 60° = \(\frac{\mathrm{h}-66}{x}\)
√3 = \(\frac{\mathrm{h}-66}{x}\)
x = \(\frac{\mathrm{h}-66}{\sqrt{3}}\) ———(1)
tan 30° = \(\frac{66}{x}\)
\(\frac{1}{\sqrt{3}}=\frac{66}{x}\)
x = 66√3 ——– (2)

(1) மற்றும் (2) லிருந்து
\(\frac{\mathrm{h}-66}{\sqrt{3}}=66 \sqrt{3}\)
h – 66 = 66√3 x 66 x 3 = 198
h = 198 + 66
i) h = 264 மீ
ii) விளக்குக் கம்ப உயரத்திற்கும் அடுக்குமாடியின் உயரத்திற்கும் இடையேயுள்ள வித்தியாசம்
= 264 – 66 = 198 மீ.
iii) விளக்குக் கம்பத்திற்கும் அடுக்குமாடிக்கும் இடையேயுள்ள தொலைவு x = 66√3 = 66 x 1.732
= 114.31மீ

கேள்வி 6.
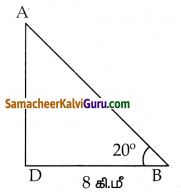
A, B மற்றும் C என்ற மூன்று கிராமவாசிகள் ஒரு பள்ளத்தாக்கில் ஒருவருக்கொருவர் பார்க்குமாறு உள்ளனர். A-க்கும், B-க்கும் இடைப்பட்ட கிடைமட்டத் தொலைவு 8கி.மீ மற்றும் B-க்கும், C-க்கும் இடைப்பட்ட கிடைமட்டத் தொலைவு 12கி.மீ A-லிருந்து B-க்கு உள்ள இறக்கக்கோணம் 20° மற்றும் B-யிலிருந்து C-க்கு உள்ள ஏற்றக்கோணம் 30 எனில் பின்வருவனவற்றைக் கணக்கிடுக.
(i) A-க்கும் B-க்கும் இடையேயுள்ள செங்குத்து உயரம்.
(ii) B-க்கும் C-க்கும் இடையேயுள்ள செங்குத்து உயரம்.
(tan 20° = 0.3640, √3 = 1.732)
தீர்வு :

tanθ =
tan 20° = \(\begin{array}{l}
\text { AD } \\
\hline B D
\end{array}\)
0.3640 = \(\frac{\mathrm{AD}}{8}\)
AD = 0.3640 x 8 = 2.91 கி.மீ
AD = 2.91கி.மீ

tan 30° = \(\frac{\mathrm{CE}}{B E}\)
\(\frac{1}{\sqrt{3}}=\frac{C E}{12}\)
\(\frac{12}{\sqrt{3}}\) = CE
CE = 4√3 = 4 x 1.732
CE = 6.39 கி.மீ