Samacheer Kalvi 10th Maths Guide Chapter 6 முக்கோணவியல் Unit Exercise 6

Tamilnadu State Board New Syllabus Samacheer Kalvi 10th Maths Guide Pdf Chapter 6 முக்கோணவியல் Unit Exercise 6 Textbook Questions and Answers, Notes.

TN Board 10th Maths Solutions Chapter 6 முக்கோணவியல் Unit Exercise 6

கேள்வி 1.
(i) நிரூபிக்கவும் \(\cot ^{2} \mathrm{~A}\left[\frac{\sec \mathrm{A}-1}{1+\sin \mathrm{A}}\right]+\operatorname{Sec}^{2} \mathrm{~A}\left[\frac{\operatorname{Sin} \mathrm{A}-1}{1+\mathrm{Sec} \mathrm{A}}\right]=0\)
தீர்வு:
இடப்பக்கம்

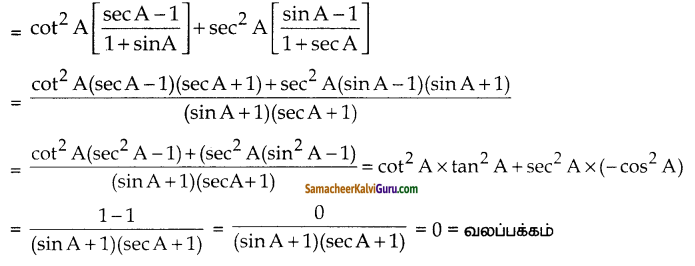
ii) \(\frac{\tan ^{2} q-1}{\tan ^{2} q+1}\) = 1 – 2cos²q
தீர்வு :
இடப்பக்கம்

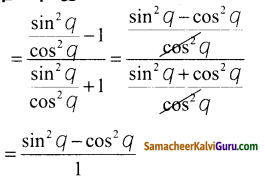
= 1 – cos²q – cos²q
1-2cos² = வலப்பக்கம்

கேள்வி 2.
\(\left[\frac{(1+\sin q)-\cos q}{(1+\sin q)+\cos q}\right]^{2}=\frac{1-\cos q}{1+\cos q}\) என்பதை நிரூபிக்கவும்.
தீர்வு:
இடப்பக்கம்

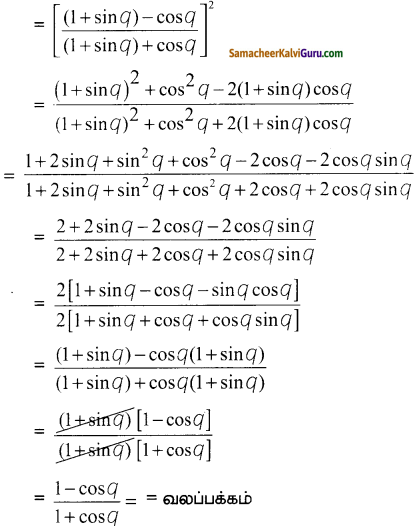
கேள்வி 3.
x sin³θ + ycos³θ = sinθ cosθ மற்றும் xsinθ = ycosθ
= y cose, எனில் x² + y² = 1 என நிரூபிக்கவும்.
தீர்வு:
⇒ x sin³θ+ y cos³θ = sin θ cosθ
⇒ x sinθ (sin²θ) + ycosθ (cos²θ) = sinθ cosθ
(∵ x sinθ= y cosθ)
⇒ x sinθ (sin²θ+ cos²θ) = sinθ cosoθ
⇒ x = cosθ
கணக்கின் படி, x sin θ = y cosθ
⇒ cosθ sin θ = y cosθ
∴ y = sinθ
இடப்பக்கம் x² + y² = cos²θ + sin²θ = 1

கேள்வி 4.
a cosθ – b sinθ = C, எனில் (a sinθ + bcosθ) = \(\sqrt{a^{2}+b^{2}-c^{2}}\) என நிரூபிக்கவும்.
தீர்வு :
வலப்பக்கம் = a² + b² – c²
= a² + b² – [a cosθ – b sinθ]2
= a² + b² -[a² cos²θ + b²sin²θ – 2ab sinθ cosθ
= a² + b² – a² cos2θ – b²sin²θ + 2ab sinθ cosθ
= a²[1-cos²θ] + b²[1-sin²θ]+ 2 ab sinθ cosθ)
= a² sin²θ + b²cos²9 + 2ab sinθ cosθ
= [asinθ + bcosθ] ²
= (a sinθ + b cosθ]² = a² + b² – c²
இருபுறமும் வர்க்க மூலம் காண.
a sinθ + b cosθ = \(\pm \sqrt{a^{2}+b^{2}-c^{2}}\) நிரூபிக்கப்பட்டது.

கேள்வி 5.
80மீ உயரமுள்ள மரத்தின் உச்சியில் ஒரு பறவை இருக்கிறது. தரையில் உள்ள ஒரு புள்ளியிலிருந்து பறவையின் ஏற்றக்கோணம் 45. பறவை ஒரே உயரத்தில் கிடைமட்டத்தில் பறந்து செல்கிறது. 2வினாடிகள் கழித்து அதே புள்ளியிலிருந்து பறவையின் ஏற்றக்கோணம் 30 எனில், பறவை பறக்கும் வேகத்தினைக் காண்க . ( √ 3 = 1.732)
தீர்வு:
tan θ =
tan 45° = \(\frac{80}{x}\)
x = 80
tan 30° = \(\frac{80}{x+y}\)
\(\frac{1}{\sqrt{3}}=\frac{80}{x+y}\)
x + y = 80√ 3
y = 80√ 3 – x = 80√ 3 – 80
y = ( √ 3 – 1)80 = (1.732-1)80 = 0.732:8 = 58.56
நேரம் x வேகம் = தொலைவு
2 x வேகம் = 58.56
வேகம் = 29.28 மீ/வி

கேள்வி 6.
விமானம் ஒன்று புவிப் பரப்பிற்கு இணையாக 600மீ உயரத்தில் 175 மீ/வி வேகத்தில் செல்கிறது. புவியின் மீது ஒரு புள்ளியிலிருந்து விமானத்திற்கு உள்ள ஏற்றக்கோணம் 37 ஆகும். அதே புள்ளியிலிருந்து ஏற்றக்கோணம் 53°-க்கு அதிகரிக்க எவ்வளவு நேரம் தேவைப்படும் ? (tan 53° = 1.3270, tan 37° = 0.7536)
தீர்வு :
tan θ =
0.7536 = \(\)
tan 37° = \(\)
(0.7536) (x + y) = 600
tan 53° = \(\)
1.3270 = \(\)
x = \(\)
x = 452.15
0.7536x + 75361 = 600
0.7536 X 452.15 + 0.7536y = 600
0.75.36y = 600 – 340.74
0.7356y = 259.26
y = \(\frac{259.26}{0.7356}\)
y = 344.03
தொலைவு = 344.03
நேரம் x வேகம் = 344.03

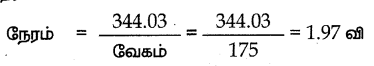
நேரம் = 1.97 வி

கேள்வி 7.
ஒரு பறவை A என்ற இடத்திலிருந்து 30 கி.மீ தொலைவில் B என்ற இடத்திற்கு 35, கோணத்தில் பறக்கிறது. B-ல் 48 கோணத்திலிருந்து விலகி 32கி.மீ தொலைவில் உள்ள C என்ற இடத்திற்குச் செல்கிறது.
i) A-ன் வடக்குப் புறமாக B-ன் தொலைவு எவ்வளவு?
ii) A-ன் மேற்குப் புறமாக B-ன் தொலைவு எவ்வளவு?
iii) B-ன் வடக்குப் புறமாக C-ன் தொலைவு எவ்வளவு?
iv) B-ன் கிழக்குப் புறமாக (-ன் தொலைவு எவ்வளவு?
sin 55° = 0.8192, cos55° = 0.5736
sin42° = 0.6691, cos 42° = 07431
தீர்வு:

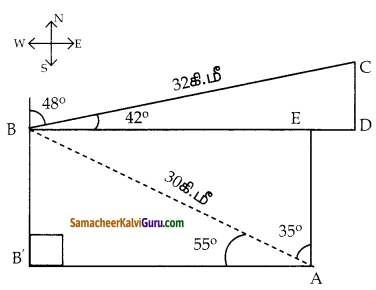
i) sin 55° = \(\frac{\mathrm{BB}^{\prime}}{\mathrm{AB}}\) ( ΔABB’ ல்)
0.8192 = \(\frac{\mathrm{BB}^{\prime}}{30}\)
BB’ = 30 x 0.8192 = 24.58கி.மீ.

ii) ΔABB’ல் cos 55° = \(\frac{\mathrm{AB}^{\prime}}{\mathrm{AB}}\)
0.5736 = \(\frac{\mathrm{AB}^{\prime}}{30}\)
AB’ = 30 x 0.5736 = 17.21கி.மீ

iii) B – ன் வடக்குப் புறமாக என் தொலைவு என்பது CD ஆகும்.
ΔBCD-ல் sin 42° = \(\frac{B D}{B C}\)
0.6691 = \(\frac{C D}{32}\)
CD = 32 x 0.6691 = 21.41 கி.மீ

iv) B ன் கிழக்குப் புறமாக என் தொலைவு என்பது BD ஆகும்.
ΔBDCல், cos 42° = \(\frac{B D}{B C}\)
0.7431 = \(\frac{B D}{32}\)
BD = 0.7431 x 32 = 23.78 கி.மீ

கேள்வி 8.
கலங்கரை விளக்கம் இருக்கும் இடத்திலிருத்து கடலில் எதிரெதிர்த் திசையில் இரு கப்பல்கள் பயணம் செய்கின்றன. கலங்கரை விளக்கத்தின் உச்சியிலிருந்து இரு கப்பல்களின் இறக்கக் கோணங்கள் முறையே 60° மற்றும் 45′ கப்பல்களுக்கு இடையே உள்ள தொலைவு
200 (\(\frac{\sqrt{3}+1}{\sqrt{3}}\)) மீ எனில், கலங்கரை விளக்கத்தின் உயரம் காண்க.
தீர்வு :

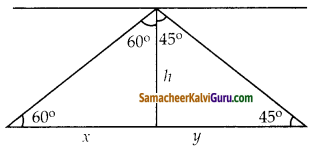
tanθ =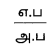
tan 45° = \(\frac { h }{ y }\)
1 = \(\frac { h }{ y }\)
y = h
tan 60° = \(\frac { h }{ y }\)

கேள்வி 9.
ஒரு தெருவில் கட்டடமும், சிலையும் எதிரெதிர்த் திசையில் 35 மீ இடைவெளியில் அமைந்துள்ளன.
கட்டடத்தின் உச்சியிலிருந்து, சிலை உச்சியின் ஏற்றக்கோணம் 24 மற்றும் சிலை அடியின் இறக்கக்கோணம் 34 எனில், சிலையின் உயரம் என்ன?
(tan24° = 0.4452, tan 34° = 0.6745)
தீர்வு :

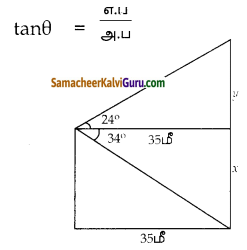
tan 24° = \(\frac{\mathrm{y}}{35}\)
h = 0.4452 x 35
y = 15.58 மீ)
tan 34° = \(\frac{\mathrm{x}}{35}\)
x = 0.6745 x 35
x = 23.61 மீ
சிலையின் உயரம் = x + y = 23.61 + 15.58மீ
= 39.19 மீ