Samacheer Kalvi 10th Maths Guide Chapter 7 அளவியல் Ex 7.1

Tamilnadu State Board New Syllabus Samacheer Kalvi 10th Maths Guide Pdf Chapter 7 அளவியல் Ex 7.1 Textbook Questions and Answers, Notes.

TN Board 10th Maths Solutions Chapter 7 அளவியல் Ex 7.1

கேள்வி 1.
ஓர் உருளையின் ஆரம் மற்றும் உயரங்களின் விகிதம் 5:7 ஆகும். அதன் வளைபரப்பு 5500 ச.செ.மீ எனில், உருளையின் ஆரம் மற்றும் உயரம் காண்க.
தீர்வு :
r: h = 5:7
\(\frac{r}{h}=\frac{5}{7}\)
r = \(\frac { 5 }{ 7 }\)h—–(1)
உருளையின் வளைபரப்பு = 5500 ச.செ.மீ
2πrh = 5500
2 x \(\frac{22}{7} \times \frac{5}{7}\) x h x h = 5500
h² = \(\frac{5500 \times 7 \times 7}{2 \times 22 \times 5}\)
h² = 5² x 7²
= (5 x 7)² = (35)²
h = 35 செ.மீ) —-(2)
(2) ஐ (1) ல் பயன்படுத்துக
r = \(\frac{5}{7}\)h
r = \(\frac{5}{7}\) x 35
r = 25
செ.மீ

கேள்வி 2.
ஒரு திண்ம இரும்பு உருளையின் மொத்தப்புறப்பரப்பு 1848 சமீ மேலும் அதன் வளைபரப்பு மொத்த புறப்பரப்பில் ஆறில் ஐந்து பங்காகும் எனில், இரும்பு உருளையின் ஆரம் மற்றும் உயரம் காணவும்.
தீர்வு :
உருளையின் புறப்பரப்பு = 1848 ச.மீ
2πr(h + r) = 1848
2πrh + 2πr² = 1848 ச.மீ —-(1)
உருளையின் வளைபரப்பு = \(\frac{5}{6}\) x புறப்பரப்பு
2πrh = \(\frac{5}{6}\) x 1848
2πrh = 1540 —–(2)
(2)ஐ (1) ல் பயன்படுத்து
2πrh + 2πr² = 1848
1540 + 2πr² = 1848
2πr² = 1848-1540
2 x \(\frac{22}{7}\) x r² = 308
r² = \(\frac{308 \times 7}{2 \times 22}\)
r² = 7²
r = 7 மீ —-(3)
(3) ஐ (2) ல் பயன்படுத்து
2πrh = 1540
2 x \(\frac{22}{7}\) x 7 x h = 1540
h = \(\frac{1540}{2 \times 22}\)
h = 35 மீ

கேள்வி 3.
ஓர் உள்ளீடற்ற மர உருளையின் வெளிப்புற ஆரம் மற்றும் நீளம் முறையே 16 செ.மீ மற்றும் 13 செ.மீ ஆகும். அதன் தடிமன் 4 செ.மீ எனில் உருளையின் மொத்தப் புறப்பரப்பு எவ்வளவு?
தீர்வு :

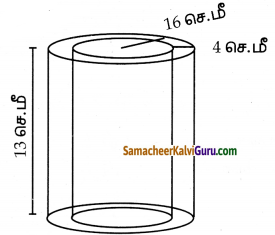
கொடுக்கப்பட்டவை
R = 16 செ.மீ
r = 12 செ.மீ
h = 13செ.மீ
R = r + w
r = R-W
= 16 – 4 = 12
உள்ளீடற்ற உருளையின் மொத்தப்பரப்பு
= 2π x (R + r)(R – r + h) ச.அ
= 2 x \(\frac{22}{7}\)(16+12) (16-12+13)
= 2 x \(\frac{22}{7}\) x 28 x 17
= 88 x 34
T.S.A = 2992 செ.மீ²

கேள்வி 4.
PQR என்ற செங்கோண முக்கோணத்தில் QR = 16 செ.மீ PR = 20 செ.மீ மற்றும் ∠Q = 90 ஆகும். QR மற்றும் PQ ஐ மைய அச்சுக்களாகக் கொண்டு சுழற்றும்போது உருவாகும் கூம்புகளின் வளைபரப்புகளை ஒப்பிடுக.
தீர்வு :

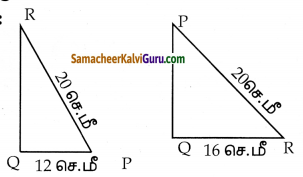
QR மைய அச்சாக கொண்டு
r = 12 செ.மீ
1 = 20 செ.மீ
உருளையின் வளைபரப்பு = πrl ச.அ
= π x 12 x 20
= 2400 செ.மீ²
PQ ஐ மைய அச்சாக கொண்டு
r = 16 செ.மீ
1 = 20 செ.மீ
உருளையின் வளைபரப்பு = πrl ச.அ
= π x 16 x 20
= 3207 செ.மீ²
PQ ஐ பொருத்து சுழற்றும் போது கூம்பின் புறப்பரப்பு அதிகமாக இருக்கும்.

கேள்வி 5.
சாயுயரம் 19மீ கொண்ட கூம்பு வடிவக் கூடாரத்தில் நால்வர் உள்ளனர். ஒருவருக்கு 22 ச.மீ பரப்பு தேவை எனில், கூடாரத்தின் உயரத்தைக் கணக்கிடவும்.
தீர்வு :

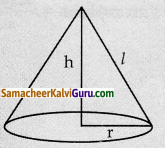
l = 19மீ
பரப்பு = πr² = 22செ.மீ²
\(\frac { 22 }{ 7 }\) x r² = 22
r² = \(\frac{22 \times 7}{22}\)
r² = 7

கேள்வி 6.
ஒரு சிறுமி தனது பிறந்த நாளைக் கொண்டாடக் கூம்பு வடிவத் தொப்பிகளை 5720 ச.செ.மீ பரப்புள்ள காகிதத்தாளை பயன்படுத்தித் தயாரிக்கிறாள். 5 செ.மீ ஆரமும், 12 செ.மீ உயரமும் கொண்ட எத்தனை தொப்பிகள் தயாரிக்க முடியும்?
தீர்வு :
r = 5செ.மீ
l = 12செ.மீ
l = \(\sqrt{h^{2}+r^{2}}\)
= \(\sqrt{12^{2}+5^{2}}\)
= \(\sqrt{144+25}\)
= \(\sqrt{169}\)
l = 13 செ.மீ
உருளையின் வளைபரப்பு = 5720 செ.மீ²

கேள்வி 7.
சம உயரங்களையுடைய இரு நேர் வட்டக் கூம்புகளின் ஆரங்கள் 1:3 என்ற விகிதத்தில் உள்ளன. கூம்புகளின் உயரம் சிறிய கூம்பின் ஆரத்தின் மூன்று மடங்கு எனில், வளைபரப்புகளின் விகிதம் காண்க.
தீர்வு :
கூம்புகளின் ஆரம் x என்க.
r₁ = x அலகு r₂ = 3x அலகு r₁ < r₂ h₁ = 3x அலகு
h₂ = 3x அலகு

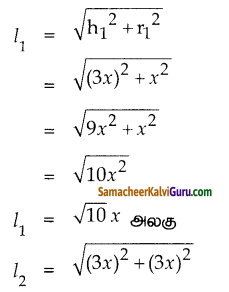
கேள்வி 8.
ஒரு கோளத்தின் ஆரம் 25% அதிகரிக்கும்போது, அதிகமாகும் புறப்பரப்பின் சதவீதம் காண்க.
தீர்வு :
கோளத்தின் ஆரம் r
கோளத்தின் மொத்தபரப்பு = 4πr2 ச.அ
அதிகரித்த கோளத்தின் ஆரம்
= \(r+\frac{25}{100} r=r+\frac{r}{4}=\frac{5 r}{4}\)அ
புதிய கோளத்தின் மொத்த பரப்பு = 5
4πr² ச.அ

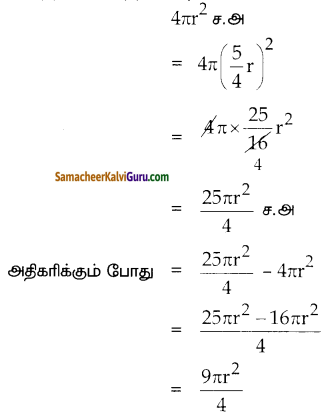
கேள்வி 9.
உள்ளீடற்ற ஓர் அரைக்கோள வடிவக் கிண்ண த்திற்கு ஒரு சதுர செ.மீ க்கு வர்ணம் பூச 0.14 வீதம் செலவாகும். அதன் உட்புற மற்றும் வெளிப்புற விட்டங்கள் முறையே 20 செ.மீ மற்றும் 28 செ.மீ எனில், அதனை முழுமையாக வர்ணம் பூச எவ்வளவு செலவாகும்?
தீர்வு :
உள் விட்டம் = 20 செ.மீ
உள் ஆரம் r = 10 செ.மீ
வெளி விட்டம் = 28 செ.மீ
வெளி ஆரம் R = 14 செ.மீ
உள்ளீடற்ற அரைக் கோளத்தின் மொத்தப்பரப்பு
= π(3R² + r² ) ச.அ
= \(\frac { 22 }{ 7 }\)[3(14)² + 10²]
= \(\frac { 22 }{ 7 }\) [3 x 196 x 100]
= \(\frac { 22 }{ 7 }\)[588 + 100]
= \(\frac{22 \times 688}{7}\)
= \(\frac{15136}{7}\)
= 2162.29 செ.மீ²
1 செ.மீ² வர்ணம் பூச =10.14
2162.29 ச.செ.மீ² வர்ண ம் பூச
= 2162.29 x 0.14
= ₹302.72

கேள்வி 10.
ஒரு மேஜை விளக்கின் வெளிப்புறத்திற்கு (மேல்பகுதியுடன்) மட்டும் வர்ணம் பூசப்படுகிறது. 1 ச.செ.மீ வர்ணம் பூச ₹2செலவாகுமெனில் விளக்கிற்கு வர்ணம் பூசுவதற்கான மொத்தச் செலவைக் கணக்கிடுக.
தீர்வு :

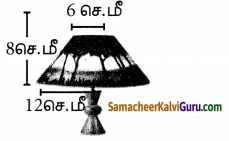
R = 12செ.மீ,
r = 6செ.மீ,
h = 8செ.மீ

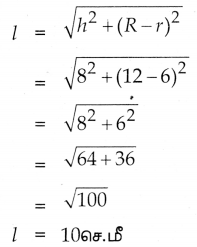
இடைக்கண்டத்தின் புறப்பரப்பு = π (R+r)l ச.அ
= \(\frac { 22 }{ 7 }\) (12 + 6)10
= \(\frac { 22 }{ 7 }\) x 18 x 10
565.71ச.செ.மீ
வர்ணம் பூசப்பட்ட பரப்பு = புறப்பரப்பு + πr² ச.அ
= 565.71+\(\frac { 22 }{ 7 }\) x 6²
= 565.71 + 113.04
= 678.75 செ.மீ²
1 ச.செ.மீ க்கு வர்ணம் பூச = ₹2
678.75 செ.மீ² ச.செ.மீ க்கு வர்ண ம் பூச
= ₹678.75 x 2
= ₹1357.5