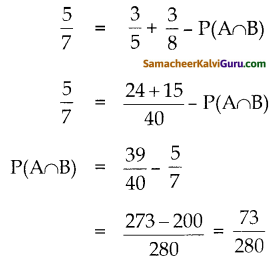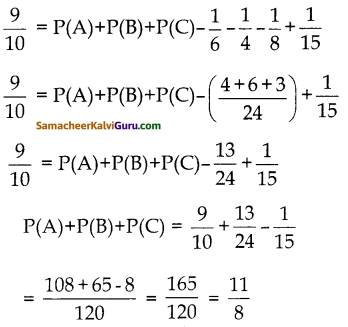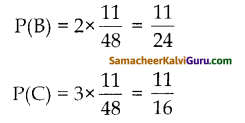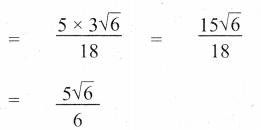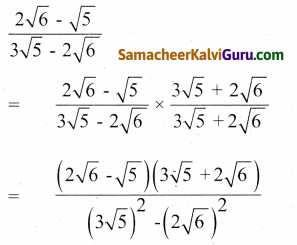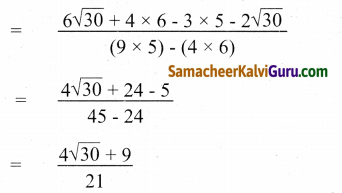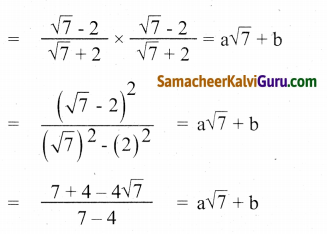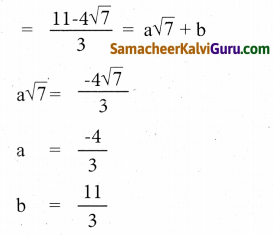Laxmi

Tamilnadu State Board New Syllabus Samacheer Kalvi 9th Maths Guide Pdf Chapter 3 இயற்கணிதம் Ex 3.1 Textbook Questions and Answers, Notes.

TN Board 9th Maths Solutions Chapter 3 இயற்கணிதம் Ex 3.1

கேள்வி 1.
பின்வரும் கோவைகளில் எவை பல்லுறுப்புக்கோவைகள் ஆகும்? பல்லுறுப்புக் கோவை இல்லை எனில், அதற்கான காரணம் கூறுக.
(i) \(\frac{1}{x^{2}}\) + 3x – 4
(ii) x²(x – 1)
(iii) \(\frac{1}{x}\)(x + 5)
(iv) \(\frac{1}{x^{-2}}+\frac{1}{x^{-1}}+7\)
(v) √5x² + √3x + √2
(vi) \(m^{2}-\sqrt[3]{m}+7 m-10\)
விடை:
(i) பல்லுறுப்புக் கோவை அல்ல (X இன் ஓர் அடுக்கு ஒரு குறை எண்)
(ii) பல்லுறுப்புக் கோவை
(iii) பல்லுறுப்புக் கோவை அல்ல (X இன் ஓர் அடுக்கு ஒரு குறை எண்)
(iv) பல்லுறுப்புக் கோவை
(v) பல்லுறுப்புக் கோவை
(vi) பல்லுறுப்புக் கோவை அல்ல (m இன் ஓர் அடுக்கு ஒரு பின்ன எண்)

கேள்வி 2.
பின்வரும் ஒவ்வொரு பல்லுறுப்புக்கோவையிலும் x² மற்றும் x இன் கெழுக்களைக் காண்க.
(i) 4 + \(\frac{2}{5}\)x²– 3x
(ii) \(6-2 x^{2}+3 x^{3}-\sqrt{7 x}\)
(iii) ρx² – x + 2
(iv) \(\sqrt{3} x^{2}+\sqrt{2} x+0.5\)
(v) x² – \(\frac{7}{2}\)x + 8
விடை:
(i) \(\frac{2}{5}\) , -3
(ii) -2,-√7
(iii) ρ,-1
(iv) √3, √2
(v) 1,\(\frac{-7}{2}\)

கேள்வி 3.
பின்வரும் பல்லுறுப்புக் கோவைகளின் படியைக் காண்க.
(i) \(1-\sqrt{2 y^{2}}+y^{7}\)
(ii) \(\frac{x^{3}-x^{4}+6 x^{6}}{x^{2}}\)
(iii) x³ (x² + x)
(iv) 3x⁴ + 9x² + 27x⁶
(v) \(2 \sqrt{5} \mathrm{P}^{4}-\frac{8 \mathrm{P}^{3}}{\sqrt{3}}+\frac{2 \mathrm{P}^{2}}{7}\)
விடை:
(i) 7
(ii) 4
(iii) 5
(iv) 6
(v) 4

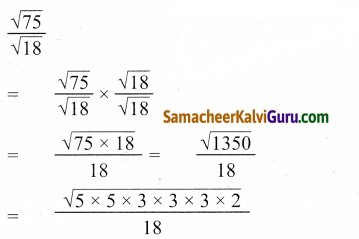
கேள்வி 4.
பின்வரும் பல்லுறுப்புக் கோவைகளைத் திட்ட வடிவில் மாற்றி எழுதுக.
(i) x – 9 + √7x³ + 6x²
(i) √2x² – \(\frac{7}{2}\)x⁴ + x – 5x³
(i) 7x³ – \(\frac{6}{5}\)x² + 4x – 1
(iv) y² + √5y³ – 11 – \(\frac{7}{3}\) y + 9y⁴
விடை:
(i) √7x³ + 6x² + x – 9
(ii) \(\frac{7}{2}\)x⁴ + 5x³ – √2x² – x
(iii) 7x³ – \(\frac{6}{5}\)x² + 4x – 1
(iv) 9y⁴ + √5y³ + y² – \(\frac{7}{3}\)y – 11

கேள்வி 5.
கீழ்க்காணும் பல்லுறுப்புக் கோவைகளைக் கூட்டி வரும் பல்லுறுப்புக் கோவையின் படியைக் காண்க.
(i) P(x) = 6x² – 7x + 2 q(x) = 6x³ – 7x + 15
(ii) h(x) =7x³ – 6x + 1 f(x) = 7x² + 17x -9
(iii) f (x) =16x⁴ + – 5x² + 9 g(x)= – 6x³ + 7x – 15
விடை:
(i) P(x) + q(x)
= 6x² -7x + 2 + 6x³ – 7x + 15
= 6x³ + 6x² – 7x – 7x + 2 + 15
= 6x³ + 6x² – 14x + 17
பல்லுறுப்புக் கோவையின் படி 3

(ii) h (x) + f (x) =7x³ – 6x + 1 + 7x² + 17x – 9
= 7x³ +7x² – 6x + 17x + 1 – 9
= 7x³ +7x² + 11x – 8
பல்லுறுப்புக் கோவையின் படி 3

(iii) f (x) + g(x) |
= 16x⁴ – 5x² + 9 + (-6x³ + 7x – 15)
= 16x⁴ – 6x³ – 5x² + 7x + 9 – 15
= 16x⁴ – 6x³ – 5x² + 7x – 6
பல்லுறுப்புக் கோவையின் படி 4

கேள்வி 6.
பின்வரும் பல்லுறுப்புக் கோவைகளைக் கழிக்க மேலும் கழித்து வரும் பல்லுறுப்புக் கோவையின் படியைக் காண்க.
(i) P(x)=7x² + 6x + 1 q(x) = 6x – 9
(ii) f (y) =16y² – 7y + 2 g(y)=7y + y³
(iii) h (z) = z⁵ – 6z⁴ + z f(z) = 6z² + 10z – 7
விடை:
(i) P(x) – q(x) =7x² + 6x – 1 – (6x – 9)
= 7x² + 6x – 1 – 6x + 9
= 7x² + 6x – 6x – 1 + 9
= 7x² + 8
பல்லுறுப்புக் கோவையின் படி 2

(ii) f (y) – g(y) = 6y² – 7y + 2 – (7y + y³)
= 6y² – 7y + 2 – 7y – y³
= -y³ + 6y² – 7y – 7y + 2
= y³ – 6y² + 7y + 7y – 2
= y³ – 6y² + 14y – 2
பல்லுறுப்புக் கோவையின் படி 3

(iii) h(z) – f (z)
= z⁵ – 6z⁴ + z – (6z² + 10z – 7)
= z⁵ – 6z⁴ + z – 6z² -10z + 7
= z⁵ – 6z⁴ – 6z² – 10z + z + 7
= z⁵ – 6z⁴ – 6z² – 9z + 7
பல்லுறுப்புக் கோவையின் படி 5

கேள்வி 7.
2x³ + 6x² + 8 – 5x உடன் எந்த பல்லுறுப்புக் கோவையைக் கூட்ட 3x³ – 2x² + 6x + 15 கிடைக்கும்?
விடை:
3x³ – 2x² + 6x + 15 கிடைக்க 2x³ + 6x² – 5x + 8 உடன் A ஐக் கூட்டுக.
2x³ + 6x² – 5x + 8 + A = 3x³ – 2x² + 6x + 15
A = 3x³ – 2x² + 6x + 15 – (2x³ + 6x² – 5x + 8)
A = 3x³ – 2x² + 6x + 15 – 2x³ – 6x² + 5x – 8
A = 3x³ – 2x³ – 2x² – 6x² + 6x + 5x + 15 – 8
A = x³ – 8x² + 11x + 7

கேள்வி 8.
2x⁴ + 4x² – 3x+7 இலிருந்து எந்தப் பல்லுறுப்புக் கோவையைக் கழிக்க 3x³ – x² + 2x + 1 கிடைக்கும்?
விடை:
3x³ – x² + 2x + 1 கிடைக்க 2x⁴ + 4x² – 3x + 7 இலிருந்து B ஐக் கழிக்க
2x⁴ + 4x² – 3x + 7 – B = 3x³ – x² + 2x + 1
2x⁴ + 4x² – 3x + 7 + x² – 2x – 1 – 3x³ = B
2x⁴ + 4x² + x² – 3x – 2x + 7 – 1 – 3x³ = B
2x⁴ – 3x³ + 5x² – 5x + 6 = B
B = 2x⁴ – 3x³ + 5x² – 5x + 6

கேள்வி 9.
பின்வரும் பல்லுறுப்புக் கோவைகளைப் பெருக்குக. பெருக்கி வரும் பல்லுறுப்புக் கோவையின் படியைக் காண்க.
(i) p(x) = x² – 9 q(x) = 6x² + 7x – 2
(ii) f (x) = 7x + 2 g(x) =15x – 9
(iii) h(x) = 6x² – 7x + 1 f (x) = 5x – 7
விடை:
(i) p(x) × q(x) = x² – 9 × (6x² + 7x – 2)
= x² (6x² + 7x – 2) -9 (6x² + 7x – 2)
= 6x⁴ + 7x³ – 2x² – 54x² – 63x + 18
= 6x⁴ + 7x³ – 56x² – 63x + 18
பல்லுறுப்புக் கோவையின் படி 4

(ii) f (x) × g(x) = (7x + 2) × (15x – 9)
= 7x(15x – 9) + 2(15x – 9)
=105x² – 63x + 30x – 18
= 105x – 33x – 18
பல்லுறுப்புக் கோவையின் படி 2

(iii) h(x) × f (x) = (6x² -7x + 1) × (5x – 7)
= (6x² – 7x + 1)5x – 7(6x² – 7x + 1)
= 30x³ – 35x² + 5x – 42x² + 49x – 7
= 30x³ – 35x² – 42x² + 5x + 49x – 7
= 30x³ – 77x² + 54x – 7
பல்லுறுப்புக் கோவையின் படி 3

கேள்வி 10.
ஒரு இனிப்பின் விலை ரூ. (x+y).அமீர் (x+y) இனிப்புகளை வாங்கினார். எனில் அவர் கொடுத்த மொத்தத் தொகையை X மற்றும் களில் காண்க. மேலும் x = 10, y = 5 எனில் அமீர் கொடுத்த தொகை எவ்வளவு?
விடை:
ஒரு இனிப்பின் விலை = ரூ (x + y)
அமீர் வாங்கிய இனிப்புகள் = (x + y)
அவர் கொடுத்த மொத்த தொகை
= ரூ (x + y) × (x + y)
= ரூ(x + y)²
x = 10, y = 5 எனில் அமீர் கொடுத்த மொத்த தொகை
= ரூ(x + y)²
= ரூ(10 + 5)²
= ரூ(15)²
= ரூ 225.

கேள்வி 11.
ஒருசெவ்வகத்தின் நீளம் (3X + 2) அலகுகள்மற்றும் அதன் அகலம் (3X – 2) அலகுகள் எனில் x ஐப் பொருத்து அதன் பரப்பளவைக் காண்க.மற்றும் X = 20 எனில் அதன் பரப்பளவைக் காண்க
விடை:
செவ்வகத்தின் நீளம் = (3x + 2) அலகுகள்
செவ்வகத்தின் அகலம் =(3x – 2) அலகுகள்
செவ்வகத்தின் பரப்பளவு = l × b ச.அலகுகள்
= (3x + 2)(3x – 2) ச.அலகுகள்
= (3x)² -(2)² ச.அலகுகள்
= 9x² – 4 ச.அலகுகள்

x = 20 அலகுகள் எனில்
பரப்பளவு = 9x² – 4 ச.அலகுகள்
= 9 × (20)² – 4 ச.அலகுகள்
= 9 × 400 – 4 ச.அலகுகள் சம்
= 3600 – 4 ச.அலகுகள்

கேள்வி 12.
p(x) என்பது 1 படி ஐக் கொண்ட ஒரு பல்லுறுப்புக் கோவை மற்றும் q(x) என்பது படி 2 ஐக் கொண்ட ஒரு பல்லுறுப்புக் கோவை எனில் p(x)xq(x) என்பது எவ்வகைப் பல்லுறுப்புக் கோவை?
விடை:
P(x) = 5x என்க
q(x) = x² +3
P(x) x q(x) = 5x (x² +3)
= 10x³ +15x
பல்லுறுப்புக் கோவையின் படி 3

Tamilnadu State Board New Syllabus Samacheer Kalvi 10th Maths Guide Pdf Chapter 8 புள்ளியியலும் நிகழ்தகவும் Ex 8.5 Textbook Questions and Answers, Notes.

TN Board 10th Maths Solutions Chapter 8 புள்ளியியலும் நிகழ்தகவும் Ex 8.5

கேள்வி 1.
கீழே கொடுக்கப்பட்டவைகளில் எது பரவல் அளவைகள் இல்லை?
அ) வீச்சு
ஆ) திட்டவிலக்கம்
இ) கூட்டுச் சராசரி
ஈ) விலக்க வர்க்கச் சராசரி
விடை :
இ) கூட்டுச் சராசரி

கேள்வி 2.
8,8,8,8,8,…… 8 ஆகிய தரவின் வீச்சு
அ) 0
ஆ) 1
இ) 8
ஈ) 3
விடை :
அ) 0
தீர்வு :
வீச்சு = L – S = 8 – 8 = 0

கேள்வி 3.
சராசரியிலிருந்து கிடைக்கப் பெற்ற தரவுப் புள்ளிகளுடைய விலக்கங்களின் கூடுதலானது
அ) எப்பொழுதும் மிகை எண்
ஆ) எப்பொழுதும் குறை எண்
இ) பூச்சியம்
ஈ) பூச்சியமற்ற முழுக்கள்
விடை :
இ) பூச்சியம்
தீர்வு :
Σ(x-\(\bar{x}\)) = 0

கேள்வி 4.
100 தரவு புள்ளிகளின் சராசரி 40 மற்றும் திட்டவிலக்கம் 3 எனில் விலக்கங்களின் வர்க்கக் கூடுதலானது
அ) 40000
ஆ) 160900
இ) 160000
ஈ) 30000
விடை :
ஆ) 160900
தீர்வு :
n = 100 \(\bar{x}\) = 40 σ = 3
σ² = \(\frac{\sum x^{2}}{n}-(\bar{x})^{2}\)
9 = \(\frac{\sum}{100}(40)\)
\(\) = 9 + 1600 = 1609
Σx² = 160900

கேள்வி 5.
முதல் 20 இயல் எண்களின் விலக்கவர்க்கச் சராசரியானது
அ) 32.25
ஆ) 44.25
இ) 33.25
ஈ) 30
விடை :
இ) 33.25
தீர்வு :
σ = \(\frac{n^{2}-1}{12}=\frac{20^{2}-1}{12}=\frac{400-1}{12}=\frac{399}{12}\) = 33.25

கேள்வி 6.
ஒரு தரவின் திட்டவிலக்கமானது 3. ஒவ்வொரு மதிப்பையும் 5 ஆல் பெருக்கினால் கிடைக்கும் புதிய தரவின் விலக்க வர்க்கச் சராசரியானது
அ) 3
ஆ) 15
இ) 5
ஈ) 225
விடை :
ஈ) 225
தீர்வு :
σ = 3
புதிய திட்டவிலக்கம் = 3 x 5 = 15
σ² = 15² = 225

கேள்வி 7.
x, y, z ஆகியவற்றின் திட்டவிலக்கம் P எனில் 3x+5, 3y+5, 3z+5 ஆகியவற்றின் திட்டவிலக்கமானது
அ) 3p+5
ஆ) 3p
இ) p+5
ஈ) 9p+15
விடை :
ஆ) 3p
தீர்வு:
x, y, z உடன் 5 ஜ கூட்டினால் திட்டவிலக்கம் மாறாது. மற்றும் 3 ஆல் பெருக்கினால் புதியதிட்டவிலக்கமும் 3 ஆல் பெருக்கல்
புதிய திட்டவிலக்கம் σ is 3p

கேள்வி 8.
ஒரு தரவின் சராசரி மற்றும் மாறுபாட்டுக்கெழு முறையே 4மற்றும் 87.5% எனில் திட்டவிலக்கமானது
அ) 3.5
ஆ) 3
இ) 4.5
ஈ) 2.5
விடை :
அ) 3.5
தீர்வு :
σ = \(\frac{\mathrm{C.V} \times \bar{x}}{100}=\frac{87.5 \times 4}{100}\) = 3.5

கேள்வி 9.
கொடுக்கப்பட்டவைகளில் எது தவறானது?
அ) P(A) > 1
ஆ) 0 ≤ P(A) ≤ 1
இ) P(Φ) = 0
ஈ) P(A) + P(A) = 1
விடை :
அ) P(A) > 1

கேள்வி 10.
p சிவப்பு 4 நீல , I பச்சை நிறக் கூழாங்கற்கள் உள்ள ஒரு குடுவையில் இருந்து ஒரு சிவப்பு கூழாங்கல் எடுப்பதற்கான நிகழ்தகவானது
அ) \(\frac{q}{p+q+r}\)
ஆ) \(\frac{p}{p+q+r}\)
இ) \(\frac{p+q}{p+q+r}\)
ஈ) \(\frac{p+r}{p+q+r}\)
விடை :
ஆ) \(\frac{p}{p+q+r}\)
தீர்வு :
n(s) = p+q+r
சிவப்பு கூழாங்கள் எடுப்பதற்கான நிகழ்தகவு = \(\frac{p}{p+q+r}\)

கேள்வி 11.
ஒரு புத்தகத்திலிருந்து சமவாய்ப்பு முறையில் ஒரு பக்கம் தேர்ந்தெடுக்கப்படுகிறது. அந்தப்பக்க எண்ணின் ஒன்றாம் இடமதிப்பானது 7 ஐ விடக் குறைவாக இருப்பதற்கான நிகழ்தகவானது
அ) \(\frac{3}{10}\)
ஆ) \(\frac{7}{10}\)
இ) \(\frac{3}{9}\)
ஈ) \(\frac{7}{9}\)
விடை :
ஆ) \(\frac{7}{10}\)
தீர்வு :
S = ஒன்றாம் இடமதிப்பு = { 0, 1, 9} n(S) = 10
ஒன்றாம் இடமதிப்பு 7 ஐ விட குறைவாக இருக்க நிகழ்தகவு = \(\frac{7}{10}\)

கேள்வி 12.
ஒரு நபருக்கு வேலை கிடைப்பதற்கான நிகழ்தகவானது வேலை கிடைக்காமல் இருப்பதற்கான நிகழ்தகவு 2/3 எனில் ன் மதிப்பானது
அ) 2
ஆ) 1
இ) 3
ஈ) 1.5
விடை :
ஆ) 1
தீர்வு :
A ஆனது வேலை கிடைப்பதற்கான நிகழ்ச்சி என்க =1
\(\frac{x}{3}+\frac{2}{3}\) = 1 ⇒ x + 2 = 3 = x = 3 – 2 = 1

கேள்வி 13.
கமலம் , குலுக்கல் போட்டியில் கலந்து கொண்டாள். அங்கு மொத்தம் 135 சீட்டுகர்
விற்கப்பட்டன. சமலம் வெற்றி பெறுவதற்கான வாய்ப்பு 1/9 எனில், கமலம் வாங்கிய சீட்டுகளின் எண்ணிக்கை அ) 5
ஆ) 10
இ) 15
ஈ) 20
விடை :
இ) 15
தீர்வு :
n(s) = 135 P(A) = \(\frac{1}{9}\)
\(\frac{n(A)}{n(S)}=\frac{1}{9} \quad \Rightarrow \frac{n(A)}{135}=\frac{1}{9}\)
n(A) = \(\frac{135}{9}\) =15

கேள்வி 14.
ஆங்கில எழுத்துக்கள் (a, b,…. z} யிலிருந்து ஓர் எழுத்து சமவாய்ப்பு முறையில் தேர்வு செய்யப்படுகிறது. அந்த எழுத்து : க்கு முந்தைய எழுத்துகளில் ஒன்றாக இருப்பதற்கான நிகழ்தகவு
அ) \(\frac{12}{13}\)
ஆ) \(\frac{1}{13}\)
இ) \(\frac{23}{26}\)
ஈ) \(\frac{3}{26}\)
விடை :
இ) \(\frac{23}{26}\)
தீர்வு :
n(S) = 26
x க்கு முந்தைய எழுத்துக்கள் தேர்ந்தெடுக்க நிகழ்தகவு = \(\frac{23}{26}\)

கேள்வி 15.
ஒரு பணப்பையில் ₹ 2000 நோட்டுகள் 10ம் 1500 நோட்டுகள் 15 ம் ₹200 நோட்டுகள் 25 ம் உள்ளன. ஒரு நோட்டு சமவாய்ப்பு முறையில் எடுக்கப்படுகின்றது. எனில், அந்த நோட்டு ₹500 நோட்டாகவோ அல்லது ₹ 200 நோட்டாகவோ இருப்பதற்கான நிகழ்தகவு என்ன?
அ) \(\frac{1}{5}\)
ஆ) \(\frac{3}{10}\)
இ) \(\frac{2}{3}\)
ஈ) \(\frac{4}{5}\)
விடை :
ஈ) \(\frac{4}{5}\)
தீர்வு :
n(S) = 10 + 15 + 25 = 50
₹500 அல்லது ₹ 200 நோட்டாக இருப்பதற்கான நிகழ்தகவு = \(\frac{15}{50}+\frac{25}{50}=\frac{40}{50}=\frac{4}{5}\)

Tamilnadu State Board New Syllabus Samacheer Kalvi 10th Maths Guide Pdf Chapter 8 புள்ளியியலும் நிகழ்தகவும் Ex 8.3 Textbook Questions and Answers, Notes.

TN Board 10th Maths Solutions Chapter 8 புள்ளியியலும் நிகழ்தகவும் Ex 8.3

கேள்வி 1.
மூன்று நாணயங்கள் சுண்டப்படும் பொழுது கிடைக்கும் கூறுவெளியை மர வரை படத்தைப் பயன்படுத்தி எழதுக.
தீர்வு :
ஒரு நாணயத்தை சுண்டும் பொழுது, கூறுவெளி = தலை (H) ,பூ (T).

மரவரைபடத்திலிருந்து கூறுவெளி :
S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}

கேள்வி 2.
ஒருபையிலுள்ள 1 முதல் வேரை எண்கள் குறிக்கப்பட்ட 6 பந்துகளிலிருந்து, இரண்டு பந்துகள் எடுப்பதற்கான கூறுவெளியை மரவரைப்படம் மூலமாகக் குறிப்பிடுக.
தீர்வு :

S = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6)
(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6)
(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6)
(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6)
(5,1), (5, 2), (5,3), (5, 4), (5, 5), (5, 6)
(6,1), (6,2), (6,3), (6, 4), (6,5), (6, 6)} என எழுதலாம்.

கேள்வி 3.
ஒரு சமவாய்ப்புச் சோதனையில் ஒரு நிகழ்ச்சி A என்க. இங்கு P(A) : P ( \(\overline{\mathrm{A}}\) ) = 17.15 மற்றும் n (S) = 640 எனில் (i) P (\(\overline{\mathrm{A}}\) )
(ii) n (A) ஐக் காண்க
தீர்வு :
P (A) : P (\(\overline{\mathrm{A}}\) ) = 17: 15 மற்றும் n (S) = 640
∴ P(A) = 17 x மற்றும் P (\(\overline{\mathrm{A}}\)) = 15 x என்க
P(A) + P (\(\overline{\mathrm{A}}\)) = 1
17 x + 15 x = 1
32 x = 1

விடை :
P(A) = \(\frac{15}{32}\) n(A) = 340

கேள்வி 4.
ஒரு நாணயம் மூன்று முறை சுண்டப்படுகிறது. இரண்டு அடுத்தடுத்த பூக்கள் கிடைப்பதற்கான நிகழ்தகவு என்ன?
தீர்வு :
ஒரு நாணயம் மூன்று முறை சுண்டப்படும் போது S = {HHH, HTH, HHT, THH, TTH, THT, HTT, TTT}
n (S) = 8
ஆனது இரண்டு அடுத்தடுத்து பூக்கள் கிடைப்பதற்கான நிகழ்ச்சி என்க
A = {TTH, HTT, TTT}
n (A) = 3
P(A) = \(\frac{n(\mathrm{~A})}{n(\mathrm{~S})}=\frac{3}{8}\)
விடை :
இரண்டு அடுத்தடுத்த பூக்கள் கிடைப்பதற்கான நிகழ்தகவு = \(\frac{3}{8}\)

கேள்வி 5.
ஒரு பொதுவிழாவில் 1 முதல் 100 வரை எண்களிட்ட அட்டைகள் ஒரு பெட்டியில் வைக்கப்பட்டுள்ளன. விளையாடும் ஒவ்வொருவரும் ஒரு அட்டையைச் சமவாய்ப்பு முறையில் எடுக்கிறார்கள். எடுத்த அட்டை திரும்ப வைக்கப்படவில்லை. தேர்ந்தெடுக்கப்பட்ட அட்டையில் எண் 500 ஐ விட அதிகமாக உள்ள வர்க்க எண் இருந்தால், அவர் வெற்றிக்கான பரிசைப் பெறுவர். (i) முதலில் விளையாடுபவர் பரிசு பெற (ii) முதலாமவர் வெற்றி பெற்ற பிறகு, இரண்டாவதாக விளையாடுபவர் வெற்றி பெற ஆகிய நிகழ்ச்சிகளுக்கான நிகழ்தகவுகளைக் காண்க.
தீர்வு :
n (S) = 1000
(i) A ஆனது 500 ஐ விட அதிகமாக உள்ள வர்க்க எண் தேர்ந்தெடுப்பதற்கான நிகழ்ச்சி என்க
(i) A = {23³, 24², 25², 26², 27², 28², 29², 30²,31²}
A = {529, 576, 625, 676,729, 784, 841, 900, 961}
∴ n (A) = 9
p(A) = n(A) = \(\frac { 9 }{ 1000 }\) |

(ii) எடுத்த அட்டை திரும்ப வைக்கப்படவில்லை .
∴ n(S) = 999
Bஆனது இரண்டாவதாக விளையாடபவர் வெற்றி பெறுவதற்கான நிகழ்ச்சி, முதலாமவர் வெற்றிபெற்ற பிறகு என்க.
n(B) = 8
∴ P(A) = \(\frac{n(A)}{n(S)}=\frac{8}{999}\)
விடை :
முதலில் விளையாடுபவர் பரிசு பெற நிகழ்தகவு = \(\frac { 9 }{ 1000 }\)
இரண்டாவது விளையாடுபவர் வெற்றி பெற நிகழ்தகவு = \(\frac { 8 }{ 5 }\) + 32

கேள்வி 6.
ஒரு பையில் 12 நீலநிறப்பந்துகளும் X சிவப்பு நிறப்பந்துகளும் உள்ளன. சமவாய்ப்பு முறையில் ஒரு பந்து தேர்ந்தெடுக்கப்படுகிறது. (i) அது சிவப்பு நிறப்பந்தாக இருப்பதற்கான நிகழ்தகவைக் காண்க (ii) 8 புதிய சிவப்பு நிறப்பந்துகள் அப்பையில் வைத்த பின்னர், ஒரு சிவப்பு நிறப்பந்தை தேர்ந்தெடுப்பதற்கான நிகழ்தகவானது (i) – யில் பெறப்பட்ட நிகழ்தகவைப் போல இருமடங்கு எனில் x ன் மதிப்பைக் காண்க?
தீர்வு :
ஒரு பையில் 12 நீலப்பந்துகள் மற்றும் x சிவப்புபந்துகள் உள்ளன.
∴ n (S) = 12 + x
(i) x என்பது சிவப்பு நிறப்பந்து எடுப்பதற்கான நிகழ்ச்சி என்க
n (R) = x
P(R) = \(\frac{\mathrm{n}(\mathrm{R})}{\mathrm{n}(\mathrm{S})}=\frac{x}{12+x}\)

(ii) 8 புதிய சிவப்பு நிறப்பந்துகள் பையில் வைக்கப்பட்ட பிறகு. \
∴ n (S) = 20 +x
p(R₁) = \(\frac{x+8}{20+x}\)
கொடுக்கப்பட்டுள்ளது p(R₁) = 2p(R₂)
\(\frac{x+8}{20+x}=2\left(\frac{x}{12+x}\right)\)
(12+x ) (12 + x) (x + 8) = 2x (20 +x)
12x + x2 + 8x + 96 = 40x + 2x²
2x² – x² + 40x – 20x – 96 = 0
x² + 20x – 96 = 0
(x + 24) (x – 4) = 0
x + 24 = 0 (அ) x – 4 = 0
x ≠ – 24, x = 4
விடை :
x ன் மதிப்பு = 4
(i) சிவப்பு நிறப்பந்து கிடைப்பதற்கான நிகழ்தகவு P(R) = \(\frac{4}{16}=\frac{1}{4}\)

கேள்வி 7.
இரண்டு சீரான பகடைகள் முறையாக ஒரே நேரத்தில் உருட்டுப்படுகின்றன.
(i) இரண்டு பகடைகளிலும் ஒரே முகமதிப்பு கிடைக்க,
(ii) முகமதிப்புகளின் பெருக்கற்பலன் பகா எண்ணாகக் கிடைக்க,
(iii) முகமதிப்புகளின் கூடுதல் பகா எண்ணாகக் கிடைக்க
(iv) முகமதிப்புகளின் கூடுதல் 1 ஆக இருக்க ஆகிய நிகழ்ச்சிகளின் நிகழ்தகவுகளைக் காண்க.
தீர்வு :
இரண்டு பகடைகள் உருட்டும் போது
S = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6)
(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6)
(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6)
(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6)
(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)
(6,1), (6, 2), (6,3), (6, 4), (6, 5), (6, 6)}
n (S) = 36

(i) A ஆனது இரண்டு பகடைகளிலும் ஒரே முகமதிப்பு கிடைக்கும் நிகழ்ச்சி என்க
A = {(1, 1) (2, 2) (3, 3) (4, 4) (5, 5) (6, 6)}
n (A) = 6
p(A) = \(\frac{n(A)}{n(S)}=\frac{6}{36}=\frac{1}{6}\)

(ii) B ஆனது பெருக்கற்பலன் பகாஎண்ணாகக் கிடைப்பதற்கான நிகழ்ச்சி என்க.
B = {(1, 2) (1, 3) (1, 5) (2, 1) (3, 1) (5, 1)}
n(B) = 6
P(B) = \(\frac{n(B)}{n(S)}=\frac{6}{36}=\frac{1}{6}\)

(iii) C ஆனது முகமதிப்புகளின் கூடுதல் பகா எண்ணாகக் கிடைப்பதற்கான நிகழ்ச்சி என்க.
C = {(1, 1) (1, 2) (1, 4) (1, 6) (2, 1) (2, 3) (2, 5) (3, 2) (3, 4) (4, 1) (4, 3) (5, 2) (5, 6) (6, 1) (6, 5)}
n (C) = 15

(iv) D ஆனது முகமதிப்புகளின் கூடுதல் 1 கிடைப்பதற்கான நிகழ்ச்சி என்க.
∴ D என்பது ஒரு இயலா நிகழ்ச்சி எனவே D = { }
∴ P (D) = 0

கேள்வி 8.
மூன்று சீரான நாணயங்கள் முறையாக ஒரே நேரத்தில் சுண்டப்படுகின்றன. (i) அனைத்தும் தலையாக கிடைக்க (ii) குறைந்தபட்சம் ஒரு பூ கிடைக்க (iii) அதிகபட்சம் ஒரு தலை கிடைக்க (iv) அதிகபட்சம் இரண்டு பூக்கள் கிடைக்க ஆகியவற்றிற்கான நிகழ்தகவுகளைக் காண்க.
தீர்வு :
மூன்று நாணயங்கள் சுண்டப்படுகின்றன
S= {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}
n (S) = 8
(i) A ஆனது அனைத்து தலையும் கிடைக்கும் நிகழ்ச்சி என்க
A = {HHH} n (H) = 1
P(A) = \(\frac{\mathrm{n}(\mathrm{A})}{\mathrm{n}(\mathrm{S})}=\frac{1}{8}\)

(ii) B ஆனது குறைந்தபட்சம் ஒரு பூகிடைப்பதற்கான நிகழ்ச்சி என்க.
B = {HHT, HTH, THH, HTT, THT, TTH, TTT} |
n (B) = 7
p(B) = \(\frac{n(B)}{n(S)}=\frac{7}{8}\)

(iii) C ஆனது அதிகபட்சம் ஒரு தலை கிடைக்கும் நிகழ்ச்சி என்க.
C = {HTT, THT,TTH, TTT}
n (C) = 4
P(C) = \(\frac{n(C)}{n(S)}=\frac{4}{8}=\frac{1}{2}\)

(iv) D ஆனது அதிகபட்சம் இரண்டு பூக்கள் கிடைக்கும் நிகழ்ச்சி என்க.
D = {HHH, HHT, HTH, THH, TTH, THT, HTT}
∴ n (D) = 7
P(D) = \(\frac{n(D)}{n(S)}=\frac{7}{8}\)

கேள்வி 9.
ஒரு பையில் 5 சிவப்பு நிறப்பந்துகளும் 6 வெள்ளை நிறப்பந்துகளும், 7 பச்சை நிறப்பந்துகளும், 8 கருப்பு நிறப்பந்துகளும் உள்ளன. சமவாய்ப்பு முறையில் பையிலிருந்து ஒரு பந்து எடுக்கப்படுகிறது. அந்த பந்து (i) வெள்ளை (ii) கருப்பு அல்லது சிவப்பு (iii) வெள்ளையாக இல்லாமல் (iv) வெள்ளையாகவும், கருப்பாகவும் இல்லாமல் இருப்பதற்கான நிகழ்தகவுகளைக் காண்க.
தீர்வு :
ஒரு பையில் உள்ள பந்துகள் = 5 சிவப்பு
பந்துகள், 6 வெள்ளை பந்துகள், 7 பச்சை
பந்துகள் மற்றும் 8 கருப்பு பந்துகள்.
∴ n (S) = 5 + 6 + 7 + 8 = 26

(i) A ஆனது வெள்ளை நிறப்பந்து கிடைப்பதற்கான நிகழ்ச்சி என்க
n (A) = 6
p(A) = \(\frac{n(A)}{n(S)}=\frac{6}{26}=\frac{3}{13}\)

(ii) B ஆனது கருப்பு அல்லது சிவப்பு நிறப்பந்து கிடைப்பதற்கான நிகழ்ச்சி என்க
n (B) = 8 + 5 = 13
p(B) = \(\frac{\mathrm{n}(\mathrm{B})}{\mathrm{n}(\mathrm{S})}=\frac{13}{26}=\frac{1}{2}\)

(iii) C ஆனது வெள்ளையாகவும் இல்லாமல் கிடைப்பதற்கான நிகழ்ச்சி என்க
n (C) = 26 – 6 = 20
P(C) = \(\frac{\mathrm{n}(\mathrm{C})}{\mathrm{n}(\mathrm{S})}=\frac{20}{26}=\frac{10}{13}\)

(iv) D ஆனது வெள்ளையாகவும் கருப்பாகவும் இல்லாமல் இருப்பதற்கான நிகழ்ச்சி என்க
n (D) = 5 + 7 = 12
p(D) = \(\frac{n(D)}{n(S)}=\frac{12}{36}=\frac{6}{13}\)

கேள்வி 10.
ஒரு பெட்டியில் 20 குறைபாடில்லாத விளக்குகளும் ஒரு சில குறைபாடுடைய விளக்குகளும் உள்ளன. பெட்டியிலிருந்து சமவாய்ப்பு முறையில் தேர்ந்தெடுக்கப்படும் ஒரு விளக்கானது குறைபாடுடையதாக இருப்பதற்கான வாய்ப்பு 3/8 எனில், குறைபாடுடைய விளக்குகளின் எண்ணிக்கையைக் காண்க.
தீர்வு :
குறைபாடுடைய விளக்குகளின் எண்ணிக்கை x என்க
குறைபாடில்லாத விளக்குகள் = 20
∴ n (S) = 20 +x
A ஆனது குறைபாடுடைய விளக்குகள் தேர்ந்தெடுப்பதற்கான நிகழ்ச்சி என்க

8x = 3 (20 + x)
8x = 60 + 3x
8x – 3x = 60
5x = 60 ⇒ x = \(\frac{60}{5}\) = 12
∴ x = 12
விடை :
குறைபாடுடைய விளக்குகளின் எண்ணிக்கை = 12.

கேள்வி 11.
நன்கு கலைத்து அடுக்கப்பட்ட 52 சீட்டுகள் கொண்ட ஒரு சீட்டுக்கட்டில், டைமண்ட் சீட்டுகளிலிருந்து இராசா மற்றும் இராணி சீட்டுகளும், ஹார்ட் சீட்டுகளிலிருந்து. இராணி மற்றும் மந்திரி சீட்டுகளும் , ஸ்பேடு சீட்டுகளிலிருந்து, மந்திரி மற்றும் இராசா சீட்டுகளும் நீக்கப்படுகிறது. மீதமுள்ள சீட்டுகளிலிருந்து, ஒரு சீட்டு சமவாய்ப்பு முறையில் எடுக்கப்படுகிறது. அந்தச் சீட்டானது (i) க்ளாவர் ஆக (ii) சிவப்பு இராணியாக (iii) கருப்பு இராசாவாக இருப்பதற்கான நிகழ்தகவுகளைக் காண்க.
தீர்வு :
52 சீட்டுகள் உள்ள சீட்டுகட்டிலிருந்து
டைமண்டில் – இராசா மற்றும் இராணி சீட்டு
ஹார்ட் – இராணி மற்றும் மந்திரி சீட்டு
ஸ்பேடு – மந்திரி மற்றும் இராசா சீட்டுகள் நீக்கப்படுகிறது
∴ n (S) = 52 – 6 = 46

(i) A ஆனது க்ளாவர் சீட்டாக கிடைப்பதற்கான நிகழ்ச்சி என்க
∴ n (A) = 13
p(A) = \(\frac{n(A)}{n(S)}=\frac{13}{46}\)

(ii) B ஆனது சிவப்பு இராணியாக கிடைப்பதற்கான நிகழ்ச்சி என்க
∴ n (B) = 0
P(B) = \(\frac{\mathrm{n}(\mathrm{B})}{\mathrm{n}(\mathrm{S})}=\frac{0}{46}\) = 0

(iii) C ஆனது கருப்பு இராசாவாக கிடைப்பதற்கான நிகழ்ச்சி என்க
∴ n (C) = 1
P(C) = \(\frac{n(C)}{n(S)}=\frac{1}{46}\)

கேள்வி 12.
மாணவர்கள் விளையாடும் ஒரு விளையாட்டில் அவர்களால் எறியப்படும் கல்லானது வட்டப்பரிதிக்குள் விழுந்தால் அதை வெற்றியாகவும் வட்டப்பரிதிக்கு வெளியே செவ்வகத்திற்குள் விழுந்தால் அதைத் தோல்வியாகவும் கருதப்படுகிறது. விளையாட்டில் வெற்றி கொள்வதற்கான நிகழ்தகவு என்ன ? (π = 3.14)
தீர்வு :

செவ்வகத்தின் பரப்பு = 3 x 4 = 12 அடி.
∴ n (S) = 12)
A ஆனது விளையாட்டில் வெற்றி கொள்வதற்கான நிகழ்ச்சி என்க.
எனவே A என்பது வட்டப்பரிதிக்குள் கல் விழும் பரப்பாகும் = πr²
= 3.14 x 1² = 3.14
P(A) = \(\frac{\mathrm{n}(\mathrm{A})}{\mathrm{n}(\mathrm{S})}=\frac{3.14}{12}=\frac{314}{1200}=\frac{157}{600}\)
விடை :
157 வெற்றி பெறுவதற்கான நிகழ்தகவு = \(\frac{157}{600}\)

கேள்வி 13.
இரண்டு நுகர்வோர்கள், பிரியா மற்றும் அமுதன் ஒரு குறிப்பிட்ட அங்காடிக்கு, குறிப்பிட்ட வாரத்தில் (திங்கள் முதல் சனி வரை ) செல்கிறார்கள். அவர்கள் அங்காடிக்குச் சமவாய்ப்பு முறையில் ஒவ்வொரு நாளும் செல்கிறார்கள். இருவரும் அங்காடிக்கு,
(1) ஒரே நாளில்
(2) வெவ்வெறு நாட்களில்
(3) அடுத்தடுத்த நாட்களில் செல்வதற்கான நிகழ்தகவுகளைக் காண்க.
தீர்வு :
பிரியாவும் அமுதனும் அங்காடிக்கு ஒரு குறிப்பிட்ட வாரத்தில் செல்கிறார்கள்.
S = {(தி, செ) (தி, செ) (தி, பு) (தி. வி) (தி, வெ) (தி, ச)
(செ.தி) (செ.செ) (செ.பு) (செ.வி) ( செ.வெ) (செ.ச)
(பு, தி) (பு. செ) (பு, பு) (பு.வி) (பு. வெ) (பு, ச)
(வி. தி) (வி. செ) (வி,பு) (வி, வி) (வி, வெ) (வி, ச)
(வெ, தி) (வெ. செ) (வெ. பு) (வெ.வி) (வெ.வி) (வெ, ச)
(ச, தி) (ச. செ) (ச. பு) (ச. வி) (ச, வெ) (ச, ச)}
n (S) = 36
(i) A ஆனது ஒரே நாள் கிடைக்கும் நிகழ்ச்சி என்க
A = {(தி,தி) (செ. செ) (ப.பு) (வி,வி) (வெ.வெ) (ச,ச)}
∴ n(A) = 6
P(A) = \(\frac{n(A)}{n(S)}=\frac{6}{36}=\frac{1}{6}\)

(ii) B ஆனது வெவ்வெறு நாட்கள் கிடைக்கும் நிகழ்ச்சி என்க.
எனவே B என்பது A ன் நிரப்புநிகழ்ச்சி ஆகும்.
∴ n (B) = 36 – 6 = 30
P(B) = \(\frac{n(B)}{n(S)}=\frac{30}{36}=\frac{5}{6}\)

(iii) C ஆனது அடுத்தடுத்த நாட்கள் கிடைக்கும் நிகழ்ச்சி என்க.
C = {(தி. செ) (செ. பு) (பு.வி) (வி, வெ) (வெ.ச)}
∴ n (C) = 5
P(C) = \(\frac{\mathrm{n}(\mathrm{C})}{\mathrm{n}(\mathrm{S})}=\frac{5}{6}\)

கேள்வி 14.
ஒரு விளையாட்டிற்கான, நுழைவுக் கட்டணம் ₹150. விளையாட்டில் ஒரு நாணயம் மூன்று முறை சுண்டப்டுகிறது. தனா ஒரு நுழைவுச்சீட்டு வாங்கினாள், அவ்விளையாட்டில் ஒன்று அல்லது இரண்டு தலைகள் விழுந்தால் அவள் செலுத்திய நுழைவுக் கட்டணம் திரும்பக் கிடைத்துவிடும். மூன்று தலைகள் கிடைத்தால் அவளது நுழைவுக்கட்டணம் இரண்டு மடங்காகக் கிடைக்கும். இல்லையென்றால் அவளுக்கு எந்தக் கட்டணமும் திரும்பக் கிடைக்காது. இவ்வாறெனில் (i) இரண்டு மடங்காக (ii) நுழைவுக் கட்டணம் திரும்பப்பெற (iii) நுழைவுக் கட்டணத்தை இழப்பதற்கு ஆகிய நிகழ்ச்சிகளுக்கான நிகழ்தகவுகளைக் காண்க.
தீர்வு :
ஒரு நாணயம் மூன்று முறை சுண்டப்படுகிறது. S = {HHH, HHT, HTH, THH, TTH, THT, HTT, TTT}
n (S) = 8
(i) A ஆனது நுழைவுக்கட்டணம் இரண்டு மடங்காக கிடைப்பதற்கான நிகழ்ச்சி என்க அதாவது மூன்று தலைகள் கிடைப்பதற்கான நிகழ்ச்சி.
∴ A = {HHH}
∴ n (A) = 1
P(A) = \(\frac{n(A)}{n(S)}=\frac{1}{8}\)

ii) B ஆனது நுழைவுக்கட்டணம் நுழைவுக் கட்டணம் திரும்பப் பெற கிடைக்கும் நிகழ்ச்சி என்க
B = {HTT, THT, HTT, HHT, THH, HTH}
∴ n (B) = 6
p(B) = \(\frac{n(B)}{n(S)}=\frac{6}{8}=\frac{3}{4}\)

iii) Cஆனது நுழைவுக்கட்டணத்தை இழப்பதற்கான நிகழ்ச்சி என்க
அதாவது மூன்று பூக்கள் கிடைப்பதற்கான நிகழ்ச்சி
C = {TTT}|
∴ n (C) = 1
P(C) = \(\frac{\mathrm{n}(\mathrm{C})}{\mathrm{n}(\mathrm{S})}=\frac{1}{8}\)

Tamilnadu State Board New Syllabus Samacheer Kalvi 10th Maths Guide Pdf Chapter 8 புள்ளியியலும் நிகழ்தகவும் Ex 8.2 Textbook Questions and Answers, Notes.

TN Board 10th Maths Solutions Chapter 8 புள்ளியியலும் நிகழ்தகவும் Ex 8.2

கேள்வி 1.
ஒரு தரவின் திட்டவிலக்கம் மற்றும் சராசரி அகியன முறையே 6.5 மற்றும் 12.5 எனில் மாறுபாட்டுக் கெழுவைக் காண்க.
தீர்வு :
திட்டவிலக்கம் σ = 6.5 சராசரி \(\overline{\mathrm{x}}\) = 12.5
மாறுபாட்டுக்கெழு C.V = \(\frac{\sigma}{\bar{x}}\) x 100
= \(\frac{6.5}{12.5}\) x 100
விடை :
மாறுபாட்டுக்கெழு = 52 %

கேள்வி 2.
ஒரு தரவின் திட்டவிலக்கம் மற்றும் மாறுபாட்டுக்கெழு ஆகியன முறையே 1.2 மற்றும் 25.6 எனில் அதன் சராசரியைக் காண்க.
தீர்வு :
σ = 12.5
C.V = 25.6
C.V = \(\frac{1.2}{\bar{x}}\) x 100
\(\bar{x}=\frac{1.2}{25.6} \times 100\)
\(\bar{x}\) = 4.96
விடை :
\(\bar{x}\) = 4.69

கேள்வி 3.
ஒரு தரவின் சராசரி மற்றும் மாறுபாட்டுக்கெழு முறையே 15 மற்றும் 48 எனில் அதன் திட்டவிலக்கத்தைக் காண்க.
தீர்வு :
\(\bar{x}\) = 15
C.V = 48
C.V= \(\frac{s}{x}\) = x 100
σ = \(\frac{48 \times 15}{100}\) = 7.2
விடை :
திட்டவிலக்கம் = 7.2

கேள்வி 4.
n = 5, \(\bar{x}\) = 6, Σx² = 765, எனில் மாறுபாட்டுக் கெழுவைக் காண்க.
தீர்வு :
n = 5
\(\bar{x}\) = 6, Σx² = 765

= 1.8028 x 100 = 180.28%
விடை :
மாறுபாட்டுக்கெழு = 180.28%

கேள்வி 5.
24, 26, 33, 37, 29, 31 ஆகியவற்றின் மாறுபாட்டுக்கெழுவைக் காண்க
தீர்வு :
ஏறுவரிசையில் எழுத 24, 26, 29, 31, 33, 37.
\(\bar{x}=\frac{24+26+29+31+33+37}{6}=\frac{180}{6}\) = 30
\(\bar{x}\) = 30

σ = \(\frac{\Sigma \mathrm{d}_{\mathrm{i}}^{2}}{\mathrm{n}}\)
= \(=\sqrt{\frac{112}{6}}=\sqrt{18.67}\)
= 4.32
C.V = \(\frac{1.2}{\bar{x}}\) x 100
= \(\frac{4.32}{30}\) x 100 = 14.4
விடை :
மாறுபாட்டுக்கெழு = 14.4%.

கேள்வி 6.
8மாணவர்கள் ஒருநாளில் வீட்டுப்பாடத்தை முடிப்பதற்கு எடுத்துக் கொள்ளும் கால அளவுகள் (நிமிடங்களில்) பின்வருமாறு கொடுக்கப்பட்டுள்ளது. 38, 40, 47, 44, 46, 43, 49, 53 இத்தரவின் மாறுபாட்டுக் கெழுவைக் காண்க. தீர்வு :
ஏறுவரிசையில் எழுத 38,40, 43, 44,46,47,49, 53


= 0.1007 x 100 = 10.07 %
விடை :
மாறுபாட்டுக்கெழு = 10.07%

கேள்வி 7.
சத்யா மற்றும் வித்யா இருவரும் 5 பாடங்களில் பெற்ற மொத்த மதிப்பெண்கள் முறையே
460 மற்றும் 480 ஆகும். மேலும் அதன் திட்ட விலக்கங்கள் முறையே 4.6 மற்றும் 2.4 எனில், யாருடைய செயல்திறன் மிகுந்த நிலைத்தன்மை கொண்டது?
தீர்வு :
n = 5

விடை :
வித்யாவின் மாறுபாட்டுக்கெழு சத்யாவின் மாறுபாட்டுக் கெழுவைவிட குறைவாக உள்ளது.
எனவே வித்யா செயல்திறன் மிகுந்த நிலைத்தன்மை உடையது.

கேள்வி 8.
ஒரு வகுப்பில் உள்ள 40 மாணவர்கள், கணிதம், அறிவியல் மற்றும் சமூக அறிவியல் ஆகிய மூன்று பாடங்களில் பெற்ற மதிப்பெண்களின் சராசரி மற்றும் திட்டவிலக்கம் கீழே கொடுக்கப்பட்டுள்ளன.

இந்த மூன்று பாடங்களில் எது அதிக நிலைத்தன்மை கொண்டது மற்றும் எது குறைந்த நிலைத்தன்மை கொண்டது?
தீர்வு :

விடை :
அதிக நிலைத்தன்மை கொண்டது அறிவியல்
குறைந்த நிலைத்தன்மை கொண்டது சமூக அறிவியல்.

Tamilnadu State Board New Syllabus Samacheer Kalvi 9th Maths Guide Pdf Chapter 2 மெய்யெண்கள் Ex 2.9 Textbook Questions and Answers, Notes.

TN Board 9th Maths Solutions Chapter 2 மெய்யெண்கள் Ex 2.9

பலவுள் தெரிவு வினாக்கள் :
கேள்வி 1.
n என்பது ஓர் இயல் எண் எனில் √n என்பது
(1) எப்போதும் ஓர் இயல் எண்.
(2) எப்போதும் ஒரு விகிதமுறா எண்.
(3) எப்போதும் ஒரு விகிதமுறு எண்
(4) ஒரு விகிதமுறு அல்லது விகிதமுறா எண்
விடை :
(4) ஒரு விகிதமுறு அல்லது விகிதமுறா எண்

கேள்வி 2.
பின்வனவற்றுள் எது உண்மையல்ல?
(1) ஒவ்வொரு விகிதமுறு எண்ணும் மெய்யெண்.
(2) ஒவ்வொரு முழுக்களும் விகிதமுறு எண்.
(3) ஒவ்வொரு மெய்யெண்ணும் விகிதமுறா எண்.
(4) ஒவ்வோர் இயல் எண்ணும் ஒரு முழு எண்.
விடை:
(3) ஒவ்வொரு மெய்யெண்ணும் விகிதமுறா எண்.

கேள்வி 3.
இரு விகிதமுறா எண்களின் கூடுதல் பற்றிய கீழ்க்காணும் கூற்றுகளில் எது உண்மை ?
(1) எப்போதும் ஒரு விகிதமுறா எண்.
(2) ஒருவிகிதமுறு அல்லது விகிதமுறா எண்ணாக இருக்கலாம்.
(3) எப்போதும் ஒரு விகிதமுறு எண்.
(4) எப்போதும் ஒரு முழுக்களாகும்.
விடை:
(2) ஒரு விகிதமுறு அல்லது விகிதமுறா எண்ணாக இருக்கலாம்.

கேள்வி 4.
பின்வனவற்றுள் எது முடிவுறு தசமத் தீர்வு?
(1) \(\frac{5}{64}\)
(2) \(\frac{8}{9}\)
(3) \(\frac{14}{15}\)
(4) \(\frac{1}{12}\)
விடை :
(1) \(\frac{5}{64}\)

கேள்வி 5.
பின்வனவற்றுள் எது விகிதமுறா எண்?
(1) \(\sqrt{25}\)
(2) \(\sqrt{\frac{9}{4}}\)
(3) \(\frac{7}{11}\)
(4) π
விடை:
(4) π

கேள்வி 6.
2 மற்றும் 2.5 என்ற எண்களுக்கிடையே உள்ள ஒரு விகிதமுறா எண்
(1) \(\sqrt{11}\)
(2) √5
(3) \(\sqrt{2.5}\)
(4) √8
விடை:
(2) √5

கேள்வி 7.
\(\frac{1}{3}\) ஐ எந்த மிகச் சிறிய விகிதமுறு எண்ணால் பெருக்கினால் அதன் தசம விரிவு ஓர் இலக்கத்தோடு முடிவுறு தசம விரிவாக அமையும்?
(1) \(\frac{1}{10}\)
(2) \(\frac{3}{10}\)
(3) 3
(4) 30
விடை:
(2) \(\frac{3}{10}\)

கேள்வி 8.
\(\frac{1}{7}\) = \(0 . \overline{142857}\) எனில் \(\frac{5}{7}\) இன் மதிப்பு என்ன?
(1) \(0 . \overline{142857}\)
(2) \(0 . \overline{714285}\)
(3) \(0 . \overline{571428}\)
(4) 0.714285
விடை :
(2) \(0 . \overline{714285}\)

கேள்வி 9.
கீழ்க்கண்டவற்றுள் பொருந்தாததைக் காண்க.
(1) \(\sqrt{32} \times \sqrt{2}\)
(2) \(\frac{\sqrt{27}}{\sqrt{3}}\)
(3) \(\sqrt{72} \times \sqrt{8}\)
(4) \(\frac{\sqrt{54}}{\sqrt{18}}\)
விடை:
(4) \(\frac{\sqrt{54}}{\sqrt{18}}\)

கேள்வி 10.
\(0 . \overline{34}+0.3 \overline{4}\) =
(1) \(0.6 \overline{87}\)
(2) \(0 . \overline{68}\)
(3) \(0.6 \overline{8}\)
(4) \(0.68 \overline{7}\)
விடை:
(1) \(0.6 \overline{87}\)

கேள்வி 11.
கீழ்க்காணும் கூற்றுகளில் எது தவறு?
(1) 25 இன் வர்க்க மூலம் 5 அல்லது – 5
(2) \(-\sqrt{25}=-5\)
(3) \(\sqrt{25}=5\)
(4) \(\sqrt{25}=\pm 5\)
விடை :
(4) \(\sqrt{25}=\pm 5\)

கேள்வி 12.
கீழ்க்காண்பவற்றுள் எது விகிதமுறு எண் அல்ல?
(1) \(\sqrt{\frac{8}{18}}\)
(2) \(\frac{7}{3}\)
(3) \(\sqrt{0.01}\)
(4) \(\sqrt{13}\)
விடை:
(4) \(\sqrt{13}\)

கேள்வி 13.
\(\sqrt{27}+\sqrt{12}=\)
(1) \(\sqrt{39}\)
(2) 5√6
(3) 5√3
(4) 3√5
விடை:
(3) 5√3

கேள்வி 14.
\(\sqrt{80}=\mathrm{k} \sqrt{5}\) எனில் k = ?
(1) 2
(2) 4
(3) 8
(4) 16
விடை :
(2) 4

கேள்வி 15.
\(4 \sqrt{7} \times 2 \sqrt{3}=\)
(1) \(6 \sqrt{10}\)
(2) \(8 \sqrt{21}\)
(3) \(8 \sqrt{10}\)
(4) \(6 \sqrt{21}\)
விடை:
(2) \(8 \sqrt{21}\)

கேள்வி 16.
\(\frac{2 \sqrt{3}}{3 \sqrt{2}}\) இன் பகுதியை விகிதமுறு எண்ணாக மாற்றிய பின் சுருங்கிய வடிவம்
(1) \(\frac{\sqrt{2}}{3}\)
(2) \(\frac{\sqrt{3}}{2}\)
(3) \(\frac{\sqrt{6}}{3}\)
(4) \(\frac{2}{3}\)
விடை:
(3) \(\frac{\sqrt{6}}{3}\)

கேள்வி 17.
(2√5 – √2)² இன் சுருங்கிய வடிவம்
(1) 4√5 + 2√2
(2) \(22-4 \sqrt{10}\)
(3) \(8-4 \sqrt{10}\)
(4) \(2 \sqrt{10}-2\)
விடை :
(2) \(22-4 \sqrt{10}\)

கேள்வி 18.
\((0.000729)^{\frac{-3}{4}} \times(0.09)^{\frac{-3}{4}}\) = ……………………
(1) \(\frac{10^{3}}{3^{3}}\)
(2) \(\frac{10^{5}}{3^{5}}\)
(3) \(\frac{10^{2}}{3^{2}}\)
(4) \(\frac{10^{6}}{3^{6}}\)
விடை:
(4) \(\frac{10^{6}}{3^{6}}\)

கேள்வி 19.
If \(\sqrt{9^{\mathrm{X}}}=\sqrt[3]{9^{2}}\) எனில் x = ?
(1) \(\frac{2}{3}\)
(2) \(\frac{4}{3}\)
(3) \(\frac{1}{3}\)
(4) \(\frac{5}{3}\)
விடை:
(2) \(\frac{4}{3}\)

கேள்வி 20.
ஒரு செவ்வக வடிவ வீட்டு மனையின் நீளம் மற்றும் அகலங்கள் முறையே 5 × 10⁵ மற்றும் 4 x 10⁴ மீட்டர் எனில், அதன் பரப்பளவு என்ன?
(1) 9 × 10¹ மீ²
(2) 9 × 10⁹ மீ²
(3) 2 × 10¹⁰ மீ²
(4) 20 × 10²⁰ மீ²
விடை:
(3) 2 × 10¹⁰ மீ²

Tamilnadu State Board New Syllabus Samacheer Kalvi 9th Maths Guide Pdf Chapter 2 மெய்யெண்கள் Ex 2.8 Textbook Questions and Answers, Notes.

TN Board 9th Maths Solutions Chapter 2 மெய்யெண்கள் Ex 2.8

கேள்வி 1.
கீழ்க்காணும் எண்களை அறிவியல் குறியீட்டு வடிவில் எழுதுக.
(i) 569430000000
(ii) 2000.57
(iii) 0.0000006000
(iv) 0.0009000002
விடை:
(i) 5.6943 × 10¹¹
(ii)2.00057 × 10³
iii) 6.0 × 10^-7
iv) 9.000002 × 10^-4

கேள்வி 2.
கீழ்க்காணும் எண்களைத் தசம வடிவில் எழுதுக.
(i) 3.459 × 10⁶
(ii) 5.678 × 10⁴
(iii) 1.00005 × 10^-5
(iv) 2.530009 × 10^-7
விடை:
(i) 3.459 × 10⁶
= 3.459 × 1000000
= 3459000

(ii) 5.678 × 10⁴
= 5.678 × 10000
= 56780

(iii) 1.00005 ×10^-5
= 0.0000100005

(iv) 2.530009 ×10^-7
0.0000002530009

கேள்வி 3.
கீழ்க்காண்பவற்றைச் சுருக்கி அறிவியல் குறியீட்டு வடிவில் எழுதுக.
(i) (300000)² × (20000)⁴
விடை:
(300000)² × (20000)⁴
= (3 × 10⁵)² × (2 × 10⁴)⁴
= 3² × 10¹⁰ × 2⁴ × 10¹⁶
= 3² × 2⁴ × 10¹⁰ × 10¹⁶
= 9 × 16 × 10²⁶
= 144 × 10²⁶
= 1.44 × 10²⁸

(ii) (0.000001)¹¹ ÷ (0.005)³
விடை:
(0.000001)¹¹ ÷ (0.005)³
= (1 × 10^-6)¹¹ ÷ (5 × 10^-3)³
= 10^-66 ÷ (5 × 10^-3)³

= 0.008 × 10^-57
= 8 × 10^-3 × 10^-57
= 8 × 10^-60

(iii){(0.00003)⁶ × (0.00005)⁴} ÷ {(0.009)³ × (0.05)²}
விடை:
(0.00003)⁶ × (0.00005)⁴ ÷ (0.009)³ × (0.05)²
(3 × 10^-5)⁶ × (5 × 10^-5)⁴ = (9 × 10^-3)³ × (5 × 10^-2)².

25 × 10^{-50 + 13}
25 × 10^-37
2.5 × 10^-36

கேள்வி 4.
கீழ்க்காணும் தகவலை அறிவியல் குறியீட்டில் எழுதுக.
(i) உலக மக்கள் தொகை சுமார் 7000,000,000
விடை:
7 × 10⁹

(ii) ஓர் ஒளி ஆண்டு என்பது 9460528400000000 கி.மீ தூரத்தைக் குறிக்கிறது.
விடை:
9.4605284 × 10¹⁵ கி.மீ

(iii) ஓர் எலக்ட்ரானின் நிறை 0.00000000000000000000000000000091093822 கி.கி
விடை:
9.1093822 × 10^-31கி.கி

கேள்வி 5.
சுருக்குக.
(i) (2.75 × 10⁷) + (1.23 × 10⁸)
விடை :
(2.75 × 10⁷) + (1.23 × 10⁸)
= 0.275 × 10⁸ + 1.23 × 10⁸
= (0.275 + 1.23) × 10⁸
= 1.505 × 10⁸

(ii) (1.598 × 10¹⁷) – (4.58 × 10¹⁵)
விடை:
(1.598 × 10¹⁷) – (4.58 × 10¹⁵)
= 1.598 × 10¹⁷ – 0.0458 × 10¹⁷
= (1.598 – 0.0458) × 10¹⁷
= 1.5522 × 10¹⁷

(iii) (1.02 × 10¹⁰) × (1.20 × 10^-3)
விடை:
(1.02 × 10¹⁰) × (1.20 × 10^-3)
= 1.02 × 1.20 × 10¹⁰ × 10^-3
= 1.224 × 10⁷

(iv) (8.41 × 10⁴) ÷ (4.3 × 10⁵)
விடை:
(8.41 × 10⁴) ÷ (4.3 × 10⁵)
\(=\frac{8.41 \times 10^{4}}{4.3 \times 10^{5}}\)
= 1.9558 × 10^{4 – 5}
= 1.9558 × 10^-1

Tamilnadu State Board New Syllabus Samacheer Kalvi 9th Maths Guide Pdf Chapter 2 மெய்யெண்கள் Ex 2.7 Textbook Questions and Answers, Notes.

TN Board 9th Maths Solutions Chapter 2 மெய்யெண்கள் Ex 2.7

கேள்வி 1.
பகுதியை விகிதப்படுத்துக.
(i) \(\frac{1}{\sqrt{\mathbf{5 0}}}\)
விடை:
= \(\frac{1}{\sqrt{\mathbf{5 0}}}\)
\(=\frac{1}{\sqrt{50}} \times \frac{\sqrt{50}}{\sqrt{50}}=\frac{\sqrt{50}}{50}\)
\(=\frac{5 \sqrt{2}}{50}\)
\(=\frac{\sqrt{2}}{10}\)

(ii) \(\frac{5}{3 \sqrt{5}}\)
விடை:
= \(\frac{5}{3 \sqrt{5}}\)

(iii) \(\frac{\sqrt{75}}{\sqrt{18}}\)
விடை:

(iv) \(\frac{3 \sqrt{5}}{\sqrt{6}}\)
விடை :
= \(\frac{3 \sqrt{5}}{\sqrt{6}}\)
\(=\frac{3 \sqrt{5}}{\sqrt{6}} \times \frac{\sqrt{6}}{\sqrt{6}}\)
\(=\frac{3 \sqrt{30}}{6}\)
\(=\frac{\sqrt{30}}{2}\)

கேள்வி 2.
பகுதியை விகிதப்படுத்திச் சுருக்குக.
(i) \(\frac{\sqrt{48}+\sqrt{32}}{\sqrt{27}-\sqrt{18}}\)
விடை:

(ii) \(\frac{5 \sqrt{3}+\sqrt{2}}{\sqrt{3}+\sqrt{2}}\)
விடை:

(iii) \(\frac{2 \sqrt{6}-\sqrt{5}}{3 \sqrt{5}-2 \sqrt{6}}\)
விடை:

(iv) \(\frac{\sqrt{5}}{\sqrt{6}+2}-\frac{\sqrt{5}}{\sqrt{6}-2}\)
விடை:
\(\frac{\sqrt{5}}{\sqrt{6}+2}-\frac{\sqrt{5}}{\sqrt{6}-2}\)

கேள்வி 3.
\(\frac{\sqrt{7}-2}{\sqrt{7}+2}=a \sqrt{7}+b\) எனில், a மற்றும் b இன் மதிப்புகளைக் காண்க.
விடை:
\(\frac{\sqrt{7}-2}{\sqrt{7}+2}=a \sqrt{7}+b\)

கேள்வி 4.
x = √5+2 எனில்,x² + \(\frac{1}{\mathbf{x}^{2}}\) இன் மதிப்பு காண்க.
விடை:
x = √5 +2
\(\frac{1}{\mathrm{x}}\) = √5 – 2
x² + \(\frac{1}{\mathbf{x}^{2}}\) = (√5 + 2)² + (√5 – 2)²
=(5 + 4 + 4√5) + (5 + 4 – 4√5)
= 9 + 4√5 + 9 – 4√5 =18

கேள்வி 5.
√2 = 1.414 எனில், \(\frac{8-5 \sqrt{2}}{3-2 \sqrt{2}}\) இன் மதிப்பை
3 தசம இடத்திருத்தமாகக் காணவும்.
விடை :
\(\frac{8-5 \sqrt{2}}{3-2 \sqrt{2}}\)

= 5.414

Tamilnadu State Board New Syllabus Samacheer Kalvi 9th Maths Guide Pdf Chapter 2 மெய்யெண்கள் Ex 2.6 Textbook Questions and Answers, Notes.

TN Board 9th Maths Solutions Chapter 2 மெய்யெண்கள் Ex 2.6

கேள்வி 1.
முறுடுகளின் கூட்டல் மற்றும் கழித்தல் பண்புகளைப் பயன்படுத்திச் சுருக்குக.
(i) 5√3 + 18√3 – 2√3
விடை :
5√3 + 18√3 – 2√3
= (5 + 18 – 2) √3
= 21√3

ii) \(4 \sqrt[3]{5}+2 \sqrt[3]{5}-3 \sqrt[3]{5}\)
விடை :
\(4 \sqrt[3]{5}+2 \sqrt[3]{5}-3 \sqrt[3]{5}\)
= \((4+2-3) \sqrt[3]{5}\)
= \(3 \sqrt[3]{5}\)

iii) \(3 \sqrt{75}+5 \sqrt{48}-\sqrt{243}\)
விடை:

\(3 \sqrt{75}+5 \sqrt{48}-\sqrt{243}\)
\(3 \sqrt{3 \times 5 \times 5}+5 \sqrt{2 \times 2 \times 2 \times 2 \times 3}-\sqrt{3 \times 3 \times 3 \times 3 \times 3}\)
= 3 × 5√3 + 5 × 2 × 2√3 – 3 × 3√3
= 15√3 + 20√3 – 9√3
= (15 + 20- 9) √3
= 26√3

iv) \(5 \sqrt[3]{40}+2 \sqrt[3]{625}-3 \sqrt[3]{320}\)
விடை:
\(5 \sqrt[3]{40}+2 \sqrt[3]{625}-3 \sqrt[3]{320}\)


= \(10 \sqrt[3]{5}+10 \sqrt[3]{5}-12 \sqrt[3]{5}\)
= \((10+10-12) \sqrt[3]{5}\)
\(=8 \sqrt[3]{5}\)

கேள்வி 2.
முறுடுகளின் பெருக்கல் மற்றும் வகுத்தல் பண்புகளைப் பயன்படுத்திச் சுருக்குக.
(i) √3 × √5 × √2
விடை :
√3 × √5 × √2
= \(=\sqrt{3 \times 5 \times 2}\)
= \(=\sqrt{30}\)

(ii) \(\sqrt{35} \div \sqrt{7}\)
விடை:
\(\sqrt{35} \div \sqrt{7}\)
\(=\frac{\sqrt{35}}{\sqrt{7}}=\sqrt{\frac{35}{7}}\)
= √5

(iii) \(\sqrt[3]{27} \times \sqrt[3]{8} \times \sqrt[3]{125}\)
விடை:

\(\sqrt[3]{27} \times \sqrt[3]{8} \times \sqrt[3]{125}\)
= 3 × 2 × 5
= 30

iv) \((7 \sqrt{a}-5 \sqrt{b})(7 \sqrt{a}+5 \sqrt{b})\)
விடை:
\((7 \sqrt{a}-5 \sqrt{b})(7 \sqrt{a}+5 \sqrt{b})\)
\(=(7 \sqrt{a})^{2}-(5 \sqrt{b})^{2}\)
= 49a – 25b

(v) \(\left[\sqrt{\frac{225}{729}}-\sqrt{\frac{25}{144}}\right] \div \sqrt{\frac{16}{81}}\)
விடை:
\(\left[\sqrt{\frac{225}{729}}-\sqrt{\frac{25}{144}}\right] \div \sqrt{\frac{16}{81}}\)

கேள்வி 3.
√2 = 1.414, √3 = 1.732, √5 = 2.236, √10 = 3.162 எனில், கீழ்க்காண்பவற்றின் மதிப்புகளை மூன்று தசம இடத்திருத்தமாகக் காண்க.

(i) \(\sqrt{40}-\sqrt{20}\)
விடை:
\(\sqrt{40}-\sqrt{20}\)
\(=\sqrt{2 \times 2 \times 2 \times 5}-\sqrt{2 \times 2 \times 5}\)
\(=2 \sqrt{10}-2 \sqrt{5}\)
2 × 3.162 – 2 × 2.236
6.324 – 4.472
= 1.852

(ii) \(\sqrt{300}+\sqrt{90}-\sqrt{8}\)
விடை :
\(\sqrt{300}+\sqrt{90}-\sqrt{8}\)

= 10 × 1.732 + 3 × 3.162 – 2 × 1.414
= 17.320 + 9.486 – 2.828
= 26.806 – 2.828
= 23.978

கேள்வி 4.
முறுடுகளை இறங்குவரிசையில் அமைக்க.
(i) \(\sqrt[3]{5}, \sqrt[9]{4}, \sqrt[6]{3}\)
விடை :
(i) \(\sqrt[3]{5}, \sqrt[9]{4}, \sqrt[6]{3}\)
3, 6, 9ன் மீ.பொ.ம.

3, 6, 9ன் மீ.பொ.ம. = 3 × 1 × 2 × 3 = 18

ii) \(\sqrt[2]{\sqrt[3]{5}}, \sqrt[3]{\sqrt[4]{7}}, \sqrt{\sqrt{3}}\)
விடை:
\(\sqrt[2]{\sqrt[3]{5}}, \sqrt[3]{\sqrt[4]{7}}, \sqrt{\sqrt{3}}\)
\(\sqrt[6]{5}, \sqrt[12]{7}, \sqrt[4]{3}\)
4, 6, 12 ன் மீ.பொ.ம.

4, 6, 12ன் மீ.பொ.ம. = 2 × 2 × 1 × 3 × 3 = 36

கேள்வி 5.
(i) இரு முறுடுகளின் கூட்டல்
(ii) இரு முறுடுகளின் வேறுபாடு
(iii) இரு முறுடுகளின் பெருக்கல்
(iv) இரு முறுடுகளின் ஈவு
ஆகிய நிகழ்வுகளில் உம்மால் ஒரு முழுமையான முறுடைப் பெற இயலுமா? ஒவ்வொரு விடையையும் ஓர் எடுத்துக்காட்டு கொண்டு விவரிக்க.
விடை:
i) ஆம்.
\(\frac{1}{2} \sqrt{2}+\frac{1}{2} \sqrt{2}\)
\(=\left(\frac{1}{2}+\frac{1}{2}\right) \sqrt{2}\)
= √2

(ii) ஆம்.
3√5 – 2√5 = √5

(iii) ஆம்.
√2 x √3 = √6

(iv) ஆம்.
\(\sqrt[3]{4} \div \sqrt[3]{2}=\sqrt[3]{\frac{4}{2}}\)
\(=\sqrt[3]{2}\)

கேள்வி 6.
(i) இரு முறுடுகளின் கூட்டல்
(ii) இரு முறுடுகளின் வேறுபாடு
(iii) இரு முறுடுகளின் பெருக்கல்
(iv) இரு முறுடுகளின் ஈவு
ஆகிய நிகழ்வுகளில் உம்மால் ஒரு விகிதமுறு எண்ணைப் பெற இயலுமா? ஒவ்வொரு விடையையும் ஓர் எடுத்துக்காட்டுகொண்டு விவரிக்க.
விடை:
(i) ஆம்.
= \(=\frac{3+\sqrt{2}}{1}+\frac{5-\sqrt{2}}{1}\)
\(=\frac{3+\sqrt{2}+5-\sqrt{2}}{1}\)
\(=\frac{8}{1}\)

(ii) ஆம்.
= 12 + √3 -3 – √3
= (12 – 3) + √3 – √3
= 9

iii) ஆம்.
√2 x 3√2 = 6

(iv) ஆம்.
\(\sqrt[3]{27} \div \sqrt[3]{64}=\frac{\sqrt[3]{27}}{\sqrt[3]{64}}\)
\(\frac{3}{4}\)