Samacheer Kalvi 10th Maths Guide Chapter 8 புள்ளியியலும் நிகழ்தகவும் Ex 8.3

Tamilnadu State Board New Syllabus Samacheer Kalvi 10th Maths Guide Pdf Chapter 8 புள்ளியியலும் நிகழ்தகவும் Ex 8.3 Textbook Questions and Answers, Notes.

TN Board 10th Maths Solutions Chapter 8 புள்ளியியலும் நிகழ்தகவும் Ex 8.3

கேள்வி 1.
மூன்று நாணயங்கள் சுண்டப்படும் பொழுது கிடைக்கும் கூறுவெளியை மர வரை படத்தைப் பயன்படுத்தி எழதுக.
தீர்வு :
ஒரு நாணயத்தை சுண்டும் பொழுது, கூறுவெளி = தலை (H) ,பூ (T).

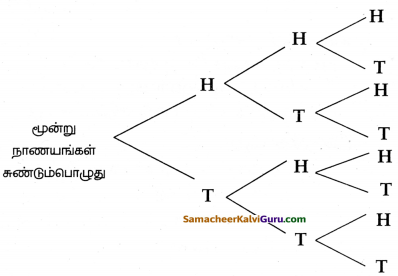
மரவரைபடத்திலிருந்து கூறுவெளி :
S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}

கேள்வி 2.
ஒருபையிலுள்ள 1 முதல் வேரை எண்கள் குறிக்கப்பட்ட 6 பந்துகளிலிருந்து, இரண்டு பந்துகள் எடுப்பதற்கான கூறுவெளியை மரவரைப்படம் மூலமாகக் குறிப்பிடுக.
தீர்வு :

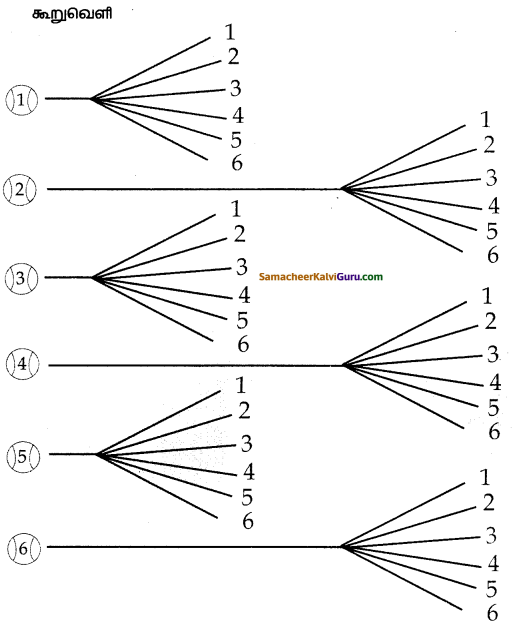
S = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6)
(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6)
(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6)
(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6)
(5,1), (5, 2), (5,3), (5, 4), (5, 5), (5, 6)
(6,1), (6,2), (6,3), (6, 4), (6,5), (6, 6)} என எழுதலாம்.

கேள்வி 3.
ஒரு சமவாய்ப்புச் சோதனையில் ஒரு நிகழ்ச்சி A என்க. இங்கு P(A) : P ( \(\overline{\mathrm{A}}\) ) = 17.15 மற்றும் n (S) = 640 எனில் (i) P (\(\overline{\mathrm{A}}\) )
(ii) n (A) ஐக் காண்க
தீர்வு :
P (A) : P (\(\overline{\mathrm{A}}\) ) = 17: 15 மற்றும் n (S) = 640
∴ P(A) = 17 x மற்றும் P (\(\overline{\mathrm{A}}\)) = 15 x என்க
P(A) + P (\(\overline{\mathrm{A}}\)) = 1
17 x + 15 x = 1
32 x = 1

விடை :
P(A) = \(\frac{15}{32}\) n(A) = 340

கேள்வி 4.
ஒரு நாணயம் மூன்று முறை சுண்டப்படுகிறது. இரண்டு அடுத்தடுத்த பூக்கள் கிடைப்பதற்கான நிகழ்தகவு என்ன?
தீர்வு :
ஒரு நாணயம் மூன்று முறை சுண்டப்படும் போது S = {HHH, HTH, HHT, THH, TTH, THT, HTT, TTT}
n (S) = 8
ஆனது இரண்டு அடுத்தடுத்து பூக்கள் கிடைப்பதற்கான நிகழ்ச்சி என்க
A = {TTH, HTT, TTT}
n (A) = 3
P(A) = \(\frac{n(\mathrm{~A})}{n(\mathrm{~S})}=\frac{3}{8}\)
விடை :
இரண்டு அடுத்தடுத்த பூக்கள் கிடைப்பதற்கான நிகழ்தகவு = \(\frac{3}{8}\)

கேள்வி 5.
ஒரு பொதுவிழாவில் 1 முதல் 100 வரை எண்களிட்ட அட்டைகள் ஒரு பெட்டியில் வைக்கப்பட்டுள்ளன. விளையாடும் ஒவ்வொருவரும் ஒரு அட்டையைச் சமவாய்ப்பு முறையில் எடுக்கிறார்கள். எடுத்த அட்டை திரும்ப வைக்கப்படவில்லை. தேர்ந்தெடுக்கப்பட்ட அட்டையில் எண் 500 ஐ விட அதிகமாக உள்ள வர்க்க எண் இருந்தால், அவர் வெற்றிக்கான பரிசைப் பெறுவர். (i) முதலில் விளையாடுபவர் பரிசு பெற (ii) முதலாமவர் வெற்றி பெற்ற பிறகு, இரண்டாவதாக விளையாடுபவர் வெற்றி பெற ஆகிய நிகழ்ச்சிகளுக்கான நிகழ்தகவுகளைக் காண்க.
தீர்வு :
n (S) = 1000
(i) A ஆனது 500 ஐ விட அதிகமாக உள்ள வர்க்க எண் தேர்ந்தெடுப்பதற்கான நிகழ்ச்சி என்க
(i) A = {23³, 24², 25², 26², 27², 28², 29², 30²,31²}
A = {529, 576, 625, 676,729, 784, 841, 900, 961}
∴ n (A) = 9
p(A) = n(A) = \(\frac { 9 }{ 1000 }\) |

(ii) எடுத்த அட்டை திரும்ப வைக்கப்படவில்லை .
∴ n(S) = 999
Bஆனது இரண்டாவதாக விளையாடபவர் வெற்றி பெறுவதற்கான நிகழ்ச்சி, முதலாமவர் வெற்றிபெற்ற பிறகு என்க.
n(B) = 8
∴ P(A) = \(\frac{n(A)}{n(S)}=\frac{8}{999}\)
விடை :
முதலில் விளையாடுபவர் பரிசு பெற நிகழ்தகவு = \(\frac { 9 }{ 1000 }\)
இரண்டாவது விளையாடுபவர் வெற்றி பெற நிகழ்தகவு = \(\frac { 8 }{ 5 }\) + 32

கேள்வி 6.
ஒரு பையில் 12 நீலநிறப்பந்துகளும் X சிவப்பு நிறப்பந்துகளும் உள்ளன. சமவாய்ப்பு முறையில் ஒரு பந்து தேர்ந்தெடுக்கப்படுகிறது. (i) அது சிவப்பு நிறப்பந்தாக இருப்பதற்கான நிகழ்தகவைக் காண்க (ii) 8 புதிய சிவப்பு நிறப்பந்துகள் அப்பையில் வைத்த பின்னர், ஒரு சிவப்பு நிறப்பந்தை தேர்ந்தெடுப்பதற்கான நிகழ்தகவானது (i) – யில் பெறப்பட்ட நிகழ்தகவைப் போல இருமடங்கு எனில் x ன் மதிப்பைக் காண்க?
தீர்வு :
ஒரு பையில் 12 நீலப்பந்துகள் மற்றும் x சிவப்புபந்துகள் உள்ளன.
∴ n (S) = 12 + x
(i) x என்பது சிவப்பு நிறப்பந்து எடுப்பதற்கான நிகழ்ச்சி என்க
n (R) = x
P(R) = \(\frac{\mathrm{n}(\mathrm{R})}{\mathrm{n}(\mathrm{S})}=\frac{x}{12+x}\)

(ii) 8 புதிய சிவப்பு நிறப்பந்துகள் பையில் வைக்கப்பட்ட பிறகு. \
∴ n (S) = 20 +x
p(R₁) = \(\frac{x+8}{20+x}\)
கொடுக்கப்பட்டுள்ளது p(R₁) = 2p(R₂)
\(\frac{x+8}{20+x}=2\left(\frac{x}{12+x}\right)\)
(12+x ) (12 + x) (x + 8) = 2x (20 +x)
12x + x2 + 8x + 96 = 40x + 2x²
2x² – x² + 40x – 20x – 96 = 0
x² + 20x – 96 = 0
(x + 24) (x – 4) = 0
x + 24 = 0 (அ) x – 4 = 0
x ≠ – 24, x = 4
விடை :
x ன் மதிப்பு = 4
(i) சிவப்பு நிறப்பந்து கிடைப்பதற்கான நிகழ்தகவு P(R) = \(\frac{4}{16}=\frac{1}{4}\)

கேள்வி 7.
இரண்டு சீரான பகடைகள் முறையாக ஒரே நேரத்தில் உருட்டுப்படுகின்றன.
(i) இரண்டு பகடைகளிலும் ஒரே முகமதிப்பு கிடைக்க,
(ii) முகமதிப்புகளின் பெருக்கற்பலன் பகா எண்ணாகக் கிடைக்க,
(iii) முகமதிப்புகளின் கூடுதல் பகா எண்ணாகக் கிடைக்க
(iv) முகமதிப்புகளின் கூடுதல் 1 ஆக இருக்க ஆகிய நிகழ்ச்சிகளின் நிகழ்தகவுகளைக் காண்க.
தீர்வு :
இரண்டு பகடைகள் உருட்டும் போது
S = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6)
(2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6)
(3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6)
(4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6)
(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)
(6,1), (6, 2), (6,3), (6, 4), (6, 5), (6, 6)}
n (S) = 36

(i) A ஆனது இரண்டு பகடைகளிலும் ஒரே முகமதிப்பு கிடைக்கும் நிகழ்ச்சி என்க
A = {(1, 1) (2, 2) (3, 3) (4, 4) (5, 5) (6, 6)}
n (A) = 6
p(A) = \(\frac{n(A)}{n(S)}=\frac{6}{36}=\frac{1}{6}\)

(ii) B ஆனது பெருக்கற்பலன் பகாஎண்ணாகக் கிடைப்பதற்கான நிகழ்ச்சி என்க.
B = {(1, 2) (1, 3) (1, 5) (2, 1) (3, 1) (5, 1)}
n(B) = 6
P(B) = \(\frac{n(B)}{n(S)}=\frac{6}{36}=\frac{1}{6}\)

(iii) C ஆனது முகமதிப்புகளின் கூடுதல் பகா எண்ணாகக் கிடைப்பதற்கான நிகழ்ச்சி என்க.
C = {(1, 1) (1, 2) (1, 4) (1, 6) (2, 1) (2, 3) (2, 5) (3, 2) (3, 4) (4, 1) (4, 3) (5, 2) (5, 6) (6, 1) (6, 5)}
n (C) = 15

(iv) D ஆனது முகமதிப்புகளின் கூடுதல் 1 கிடைப்பதற்கான நிகழ்ச்சி என்க.
∴ D என்பது ஒரு இயலா நிகழ்ச்சி எனவே D = { }
∴ P (D) = 0

கேள்வி 8.
மூன்று சீரான நாணயங்கள் முறையாக ஒரே நேரத்தில் சுண்டப்படுகின்றன. (i) அனைத்தும் தலையாக கிடைக்க (ii) குறைந்தபட்சம் ஒரு பூ கிடைக்க (iii) அதிகபட்சம் ஒரு தலை கிடைக்க (iv) அதிகபட்சம் இரண்டு பூக்கள் கிடைக்க ஆகியவற்றிற்கான நிகழ்தகவுகளைக் காண்க.
தீர்வு :
மூன்று நாணயங்கள் சுண்டப்படுகின்றன
S= {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}
n (S) = 8
(i) A ஆனது அனைத்து தலையும் கிடைக்கும் நிகழ்ச்சி என்க
A = {HHH} n (H) = 1
P(A) = \(\frac{\mathrm{n}(\mathrm{A})}{\mathrm{n}(\mathrm{S})}=\frac{1}{8}\)

(ii) B ஆனது குறைந்தபட்சம் ஒரு பூகிடைப்பதற்கான நிகழ்ச்சி என்க.
B = {HHT, HTH, THH, HTT, THT, TTH, TTT} |
n (B) = 7
p(B) = \(\frac{n(B)}{n(S)}=\frac{7}{8}\)

(iii) C ஆனது அதிகபட்சம் ஒரு தலை கிடைக்கும் நிகழ்ச்சி என்க.
C = {HTT, THT,TTH, TTT}
n (C) = 4
P(C) = \(\frac{n(C)}{n(S)}=\frac{4}{8}=\frac{1}{2}\)

(iv) D ஆனது அதிகபட்சம் இரண்டு பூக்கள் கிடைக்கும் நிகழ்ச்சி என்க.
D = {HHH, HHT, HTH, THH, TTH, THT, HTT}
∴ n (D) = 7
P(D) = \(\frac{n(D)}{n(S)}=\frac{7}{8}\)

கேள்வி 9.
ஒரு பையில் 5 சிவப்பு நிறப்பந்துகளும் 6 வெள்ளை நிறப்பந்துகளும், 7 பச்சை நிறப்பந்துகளும், 8 கருப்பு நிறப்பந்துகளும் உள்ளன. சமவாய்ப்பு முறையில் பையிலிருந்து ஒரு பந்து எடுக்கப்படுகிறது. அந்த பந்து (i) வெள்ளை (ii) கருப்பு அல்லது சிவப்பு (iii) வெள்ளையாக இல்லாமல் (iv) வெள்ளையாகவும், கருப்பாகவும் இல்லாமல் இருப்பதற்கான நிகழ்தகவுகளைக் காண்க.
தீர்வு :
ஒரு பையில் உள்ள பந்துகள் = 5 சிவப்பு
பந்துகள், 6 வெள்ளை பந்துகள், 7 பச்சை
பந்துகள் மற்றும் 8 கருப்பு பந்துகள்.
∴ n (S) = 5 + 6 + 7 + 8 = 26

(i) A ஆனது வெள்ளை நிறப்பந்து கிடைப்பதற்கான நிகழ்ச்சி என்க
n (A) = 6
p(A) = \(\frac{n(A)}{n(S)}=\frac{6}{26}=\frac{3}{13}\)

(ii) B ஆனது கருப்பு அல்லது சிவப்பு நிறப்பந்து கிடைப்பதற்கான நிகழ்ச்சி என்க
n (B) = 8 + 5 = 13
p(B) = \(\frac{\mathrm{n}(\mathrm{B})}{\mathrm{n}(\mathrm{S})}=\frac{13}{26}=\frac{1}{2}\)

(iii) C ஆனது வெள்ளையாகவும் இல்லாமல் கிடைப்பதற்கான நிகழ்ச்சி என்க
n (C) = 26 – 6 = 20
P(C) = \(\frac{\mathrm{n}(\mathrm{C})}{\mathrm{n}(\mathrm{S})}=\frac{20}{26}=\frac{10}{13}\)

(iv) D ஆனது வெள்ளையாகவும் கருப்பாகவும் இல்லாமல் இருப்பதற்கான நிகழ்ச்சி என்க
n (D) = 5 + 7 = 12
p(D) = \(\frac{n(D)}{n(S)}=\frac{12}{36}=\frac{6}{13}\)

கேள்வி 10.
ஒரு பெட்டியில் 20 குறைபாடில்லாத விளக்குகளும் ஒரு சில குறைபாடுடைய விளக்குகளும் உள்ளன. பெட்டியிலிருந்து சமவாய்ப்பு முறையில் தேர்ந்தெடுக்கப்படும் ஒரு விளக்கானது குறைபாடுடையதாக இருப்பதற்கான வாய்ப்பு 3/8 எனில், குறைபாடுடைய விளக்குகளின் எண்ணிக்கையைக் காண்க.
தீர்வு :
குறைபாடுடைய விளக்குகளின் எண்ணிக்கை x என்க
குறைபாடில்லாத விளக்குகள் = 20
∴ n (S) = 20 +x
A ஆனது குறைபாடுடைய விளக்குகள் தேர்ந்தெடுப்பதற்கான நிகழ்ச்சி என்க

8x = 3 (20 + x)
8x = 60 + 3x
8x – 3x = 60
5x = 60 ⇒ x = \(\frac{60}{5}\) = 12
∴ x = 12
விடை :
குறைபாடுடைய விளக்குகளின் எண்ணிக்கை = 12.

கேள்வி 11.
நன்கு கலைத்து அடுக்கப்பட்ட 52 சீட்டுகள் கொண்ட ஒரு சீட்டுக்கட்டில், டைமண்ட் சீட்டுகளிலிருந்து இராசா மற்றும் இராணி சீட்டுகளும், ஹார்ட் சீட்டுகளிலிருந்து. இராணி மற்றும் மந்திரி சீட்டுகளும் , ஸ்பேடு சீட்டுகளிலிருந்து, மந்திரி மற்றும் இராசா சீட்டுகளும் நீக்கப்படுகிறது. மீதமுள்ள சீட்டுகளிலிருந்து, ஒரு சீட்டு சமவாய்ப்பு முறையில் எடுக்கப்படுகிறது. அந்தச் சீட்டானது (i) க்ளாவர் ஆக (ii) சிவப்பு இராணியாக (iii) கருப்பு இராசாவாக இருப்பதற்கான நிகழ்தகவுகளைக் காண்க.
தீர்வு :
52 சீட்டுகள் உள்ள சீட்டுகட்டிலிருந்து
டைமண்டில் – இராசா மற்றும் இராணி சீட்டு
ஹார்ட் – இராணி மற்றும் மந்திரி சீட்டு
ஸ்பேடு – மந்திரி மற்றும் இராசா சீட்டுகள் நீக்கப்படுகிறது
∴ n (S) = 52 – 6 = 46

(i) A ஆனது க்ளாவர் சீட்டாக கிடைப்பதற்கான நிகழ்ச்சி என்க
∴ n (A) = 13
p(A) = \(\frac{n(A)}{n(S)}=\frac{13}{46}\)

(ii) B ஆனது சிவப்பு இராணியாக கிடைப்பதற்கான நிகழ்ச்சி என்க
∴ n (B) = 0
P(B) = \(\frac{\mathrm{n}(\mathrm{B})}{\mathrm{n}(\mathrm{S})}=\frac{0}{46}\) = 0

(iii) C ஆனது கருப்பு இராசாவாக கிடைப்பதற்கான நிகழ்ச்சி என்க
∴ n (C) = 1
P(C) = \(\frac{n(C)}{n(S)}=\frac{1}{46}\)

கேள்வி 12.
மாணவர்கள் விளையாடும் ஒரு விளையாட்டில் அவர்களால் எறியப்படும் கல்லானது வட்டப்பரிதிக்குள் விழுந்தால் அதை வெற்றியாகவும் வட்டப்பரிதிக்கு வெளியே செவ்வகத்திற்குள் விழுந்தால் அதைத் தோல்வியாகவும் கருதப்படுகிறது. விளையாட்டில் வெற்றி கொள்வதற்கான நிகழ்தகவு என்ன ? (π = 3.14)
தீர்வு :

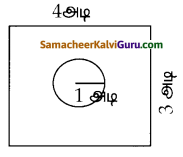
செவ்வகத்தின் பரப்பு = 3 x 4 = 12 அடி.
∴ n (S) = 12)
A ஆனது விளையாட்டில் வெற்றி கொள்வதற்கான நிகழ்ச்சி என்க.
எனவே A என்பது வட்டப்பரிதிக்குள் கல் விழும் பரப்பாகும் = πr²
= 3.14 x 1² = 3.14
P(A) = \(\frac{\mathrm{n}(\mathrm{A})}{\mathrm{n}(\mathrm{S})}=\frac{3.14}{12}=\frac{314}{1200}=\frac{157}{600}\)
விடை :
157 வெற்றி பெறுவதற்கான நிகழ்தகவு = \(\frac{157}{600}\)

கேள்வி 13.
இரண்டு நுகர்வோர்கள், பிரியா மற்றும் அமுதன் ஒரு குறிப்பிட்ட அங்காடிக்கு, குறிப்பிட்ட வாரத்தில் (திங்கள் முதல் சனி வரை ) செல்கிறார்கள். அவர்கள் அங்காடிக்குச் சமவாய்ப்பு முறையில் ஒவ்வொரு நாளும் செல்கிறார்கள். இருவரும் அங்காடிக்கு,
(1) ஒரே நாளில்
(2) வெவ்வெறு நாட்களில்
(3) அடுத்தடுத்த நாட்களில் செல்வதற்கான நிகழ்தகவுகளைக் காண்க.
தீர்வு :
பிரியாவும் அமுதனும் அங்காடிக்கு ஒரு குறிப்பிட்ட வாரத்தில் செல்கிறார்கள்.
S = {(தி, செ) (தி, செ) (தி, பு) (தி. வி) (தி, வெ) (தி, ச)
(செ.தி) (செ.செ) (செ.பு) (செ.வி) ( செ.வெ) (செ.ச)
(பு, தி) (பு. செ) (பு, பு) (பு.வி) (பு. வெ) (பு, ச)
(வி. தி) (வி. செ) (வி,பு) (வி, வி) (வி, வெ) (வி, ச)
(வெ, தி) (வெ. செ) (வெ. பு) (வெ.வி) (வெ.வி) (வெ, ச)
(ச, தி) (ச. செ) (ச. பு) (ச. வி) (ச, வெ) (ச, ச)}
n (S) = 36
(i) A ஆனது ஒரே நாள் கிடைக்கும் நிகழ்ச்சி என்க
A = {(தி,தி) (செ. செ) (ப.பு) (வி,வி) (வெ.வெ) (ச,ச)}
∴ n(A) = 6
P(A) = \(\frac{n(A)}{n(S)}=\frac{6}{36}=\frac{1}{6}\)

(ii) B ஆனது வெவ்வெறு நாட்கள் கிடைக்கும் நிகழ்ச்சி என்க.
எனவே B என்பது A ன் நிரப்புநிகழ்ச்சி ஆகும்.
∴ n (B) = 36 – 6 = 30
P(B) = \(\frac{n(B)}{n(S)}=\frac{30}{36}=\frac{5}{6}\)

(iii) C ஆனது அடுத்தடுத்த நாட்கள் கிடைக்கும் நிகழ்ச்சி என்க.
C = {(தி. செ) (செ. பு) (பு.வி) (வி, வெ) (வெ.ச)}
∴ n (C) = 5
P(C) = \(\frac{\mathrm{n}(\mathrm{C})}{\mathrm{n}(\mathrm{S})}=\frac{5}{6}\)

கேள்வி 14.
ஒரு விளையாட்டிற்கான, நுழைவுக் கட்டணம் ₹150. விளையாட்டில் ஒரு நாணயம் மூன்று முறை சுண்டப்டுகிறது. தனா ஒரு நுழைவுச்சீட்டு வாங்கினாள், அவ்விளையாட்டில் ஒன்று அல்லது இரண்டு தலைகள் விழுந்தால் அவள் செலுத்திய நுழைவுக் கட்டணம் திரும்பக் கிடைத்துவிடும். மூன்று தலைகள் கிடைத்தால் அவளது நுழைவுக்கட்டணம் இரண்டு மடங்காகக் கிடைக்கும். இல்லையென்றால் அவளுக்கு எந்தக் கட்டணமும் திரும்பக் கிடைக்காது. இவ்வாறெனில் (i) இரண்டு மடங்காக (ii) நுழைவுக் கட்டணம் திரும்பப்பெற (iii) நுழைவுக் கட்டணத்தை இழப்பதற்கு ஆகிய நிகழ்ச்சிகளுக்கான நிகழ்தகவுகளைக் காண்க.
தீர்வு :
ஒரு நாணயம் மூன்று முறை சுண்டப்படுகிறது. S = {HHH, HHT, HTH, THH, TTH, THT, HTT, TTT}
n (S) = 8
(i) A ஆனது நுழைவுக்கட்டணம் இரண்டு மடங்காக கிடைப்பதற்கான நிகழ்ச்சி என்க அதாவது மூன்று தலைகள் கிடைப்பதற்கான நிகழ்ச்சி.
∴ A = {HHH}
∴ n (A) = 1
P(A) = \(\frac{n(A)}{n(S)}=\frac{1}{8}\)

ii) B ஆனது நுழைவுக்கட்டணம் நுழைவுக் கட்டணம் திரும்பப் பெற கிடைக்கும் நிகழ்ச்சி என்க
B = {HTT, THT, HTT, HHT, THH, HTH}
∴ n (B) = 6
p(B) = \(\frac{n(B)}{n(S)}=\frac{6}{8}=\frac{3}{4}\)

iii) Cஆனது நுழைவுக்கட்டணத்தை இழப்பதற்கான நிகழ்ச்சி என்க
அதாவது மூன்று பூக்கள் கிடைப்பதற்கான நிகழ்ச்சி
C = {TTT}|
∴ n (C) = 1
P(C) = \(\frac{\mathrm{n}(\mathrm{C})}{\mathrm{n}(\mathrm{S})}=\frac{1}{8}\)