Samacheer Kalvi 10th Maths Guide Chapter 8 புள்ளியியலும் நிகழ்தகவும் Ex 8.1

Tamilnadu State Board New Syllabus Samacheer Kalvi 10th Maths Guide Pdf Chapter 8 புள்ளியியலும் நிகழ்தகவும் Ex 8.1 Textbook Questions and Answers, Notes.

TN Board 10th Maths Solutions Chapter 8 புள்ளியியலும் நிகழ்தகவும் Ex 8.1

கேள்வி 1.
கீழ்காணும் தரவுகளுக்கு வீச்சு மற்றும் வீச்சுக் கெழுவைக் காண்க
(i) 63,89,98,125,79,108,117,68
தீர்வு :
கொடுக்கப்பட்ட தரவுகளை ஏறுவரிசையில் எழுத,
63,68,79,89,98,108,117,125
மிகப்பெரிய மதிப்பு L = 125
மிகச்சிறிய மதிப்பு S = 63
வீச்சு = L – S = 125 – 63 = 62
வீச்சுக்கெழு = \(\frac{\mathrm{L}-\mathrm{S}}{\mathrm{L}+\mathrm{S}}\)
= \(\frac{125-63}{125+63}=\frac{62}{188}\) = 0.33
விடை :
வீச்சு = 62
வீச்சுக்கெழு = 0.33

(ii) 43.5,13.6,18.9,38.4,61.4,29.8
தீர்வு :
ஏறுவரிசையில் கொடுக்கப்பட்ட தரவுகளை எழத 13.6,18.9,29.8,38.4,43.5,61.4
மிகப்பெரிய மதிப்பு L = 61.4,
மிகச்சிறிய மதிப்பு S= 13.6
வீச்சு = L-S
61.4 – 13.6 = 47.8
வீச்சுக்கெழு = \(\)
= \(\frac{\mathrm{L}-\mathrm{S}}{\mathrm{L}+\mathrm{S}}\)
= \(\frac{61.4-13.6}{61.4+13.6}\)
\(\frac{47.8}{75}\) = 0.64
விடை :
வீச்சு = 47.8 வீச்சுக்கெழு = 0.64

கேள்வி 2.
ஒரு தரவின் வீச்சு மற்றும் மிகச்சிறிய மதிப்பு ஆகியன முறையே 36.8 மற்றும் 13.4 எனில் மிகப்பெரிய மதிப்பைக் காண்க?
தீர்வு :
வீச்சு R = 36.8
மிகச்சிறிய மதிப்பு S = 13.4
R = L – S
36.8= L – 13.4
L = 36.8 + 13.4 = 50.2
விடை :
மிகப்பெரிய மதிப்பு = 50.2

கேள்வி 3.
கொடுக்கப்பட்ட தரவின் வீச்சைக் காண்க

தீர்வு :
மிகப்பெரிய மதிப்பு L = 650
மிகச்சிறிய மதிப்பு S =400
வீச்சு R = L-S
= 650 – 450 = 250
விடை :
R = 250.

கேள்வி 4.
ஓர் ஆசிரியர் மாணவர்களை அவர்களின் செய்முறைப் பதிவேட்டின் 80 பக்கங்களை நிறைவு செய்து வருமாறு கூறினார். எட்டு மாணவர்கள் முறையே 32,35,37,30,33,36,3537 பக்கங்கள் மட்டுமே நிறைவு செய்திருந்தனர். மாணவர்கள் நிறைவு செய்யாதப் பக்கங்களின் திட்டவிலக்கத்தைக் காண்க.
(i) தீர்வு :
ஊகச் சராசரி முறை :
நிறைவு செய்யாத பக்கங்கள் முறையே
60-32, 60-35, 60-37, 60 – 30, 60 – 33, 60-36, 60 – 35, 60 – 37
ஊகச் சராசரி A = 25 n = 8
= 28, 25, 23, 30, 27, 24, 25, 23

திட்டவிலக்கம் :


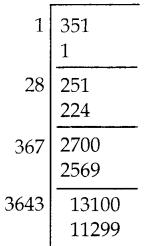
விடை :
நிறைவு செய்யாத
பக்கங்களின் திட்டவிலக்கம் = 2.34

கேள்வி 5.
10 ஊழியர்களின் ஊதியம் கீழே கொடுக்கப்பட்டுள்ளது. ஊதியங்களின் விலக்கவர்க்கச் சராசரி மற்றும் திட்டவிலக்கம் காண்க :
₹310, ₹290, ₹320, ₹280, ₹300, ₹290, ₹320, ₹310, 1280
சராசரி முறை :

விலக்க வர்க்கச் சராசரி
σ² = \(\)
= \(\frac{2000}{9}\)
= 222.22
திட்டவிலக்கம் = σ = \(\sqrt{\frac{\Sigma \mathrm{d}_{\mathrm{i}}^{2}}{\mathrm{n}}}\)
= \(\sqrt{222.22}\) = 14.91
விடை :
விலக்க வர்க்கச் சராசரி = 222.22
திட்டவிலக்கம் = 14.91

கேள்வி 6.
ஒரு சுவர் கடிகாரம் 1 மணிக்கு 1 முறையும், 2 மணிக்கு 2 முறையும், 3 மணிக்கு 3 முறையும் ஒலி எழுப்புகிறது எனில் ஒரு நாளில் அக்கடிகாரம் எவ்வளவு முறை ஒலி எழுப்பும்? மேலும் கடிகாரம் எழுப்பும் ஒலி எண்ணிக்கைகளின் திட்டவிலக்கம் காண்க.
தீர்வு :
ஒரு நாளில் கடிகாரம் எழுப்பும் ஒலி எண்ணிக்கை.
= 2 (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12).
= \(2\left[\frac{n(n+1)}{2}\right]\)
\(2\left(\frac{12 \times 13}{2}\right)\)
= 2 x 78 = 156
திட்ட விலக்கம் :
முதல் n இயல் எண்களின் திட்டவிலக்கம் = \(2 \sqrt{\frac{n^{2}-1}{12}}\)
\(\sigma=\sqrt{\frac{n^{2}-1}{12}}\)


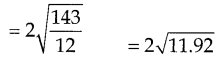
விடை :
திட்ட விலக்கம் = 6.9

கேள்வி 7.
முதல் 21 இயல் எண்களின் திட்ட விலக்கத்தைக் காண்க.
தீர்வு :

விடை :
முதல் 21 இயல் எண்க ளின் திட்டவிலக்கம் = 6.05

கேள்வி 8.
ஒரு தரவின் திட்டவிலக்கம் 4.5 ஆகும். அதில் இருக்கும் தரவுப்புள்ளி ஒவ்வொன்றிலும் 5 ஐ கழிக்க கிடைக்கும் புதிய தரவின் திட்டவிலக்கம் காண்க.
தீர்வு :
σ = 4.5
ஒவ்வொன்றிலும் 5 ஐ கழிக்க, திட்ட விலக்கம் மாறாது .
∴ புதிய திட்டவிலக்கம் 4.5
விடை : புதிய திட்டவிலக்கம் σ = 4.5

கேள்வி 9.
ஒரு தரவின் திட்டவிலக்கம் 3.6 ஆகும். அதன் ஒவ்வொரு புள்ளியையும் 3 ஆல் வகுக்கும் கோது கிடைக்கும் புதிய தரவின் திட்டவிலக்கம் மற்றும் விலக்க வர்க்கச் சராசரியைக் காண்க.
தீர்வு :
σ = 3.6
ஒவ்வொரு புள்ளியையும் 3 ஆல் வகுக்க, கிடைக்கும் புதிய திட்டவிலக்கமும் 3 ஆல் வகுபடும்.
புதிய திட்டவிலக்கம் σ = \(\frac{3.6}{3}\) = 1.2
∴ புதிய விலக்கவர்க்க சராசரி σ² = (1.2)²
= 1.44
விடை :
திட்ட விலக்கம் = 1.2
புதிய விலக்கவர்க்க சராசரி = 1.44

கேள்வி 10.
ஒரு வாரத்தில் ஐந்து மாவட்டங்களில் வெவ்வேறு இடங்களில் பெய்த மழையின் அளவானது
பதிவு செய்யப்பட்டு கீழே கொடுக்கப்பட்டுள்ளது கொடுக்கப்பட்ட மழையளவின் தரவிற்கு திட்டவிலக்கம் காண்க. \

தீர்வு :
ஊகச் சராசரி முறை A = 60

விடை :
திட்ட விலக்கம் ≅ 7.76

கேள்வி 11.
வைரஸ் காய்ச்சலைப் பற்றிய கருத்துக் கணிப்பில், பாதிக்கப்பட்ட மக்களின் எண்ணிக்கை கீழே கொடுக்கப்பட்டுள்ளது. இத்தரவின் திட்டவிலக்கம் காண்க.

வயது (வருடங்க ளில்) 0 – 10/10 -20 20 – 30/30 – 40 40 – 50 50 – 60 60 – 70 பாதிக்கப்பட்ட மக்களின்
தீர்வு :
ஊகச் சராசரி முறை A = 35

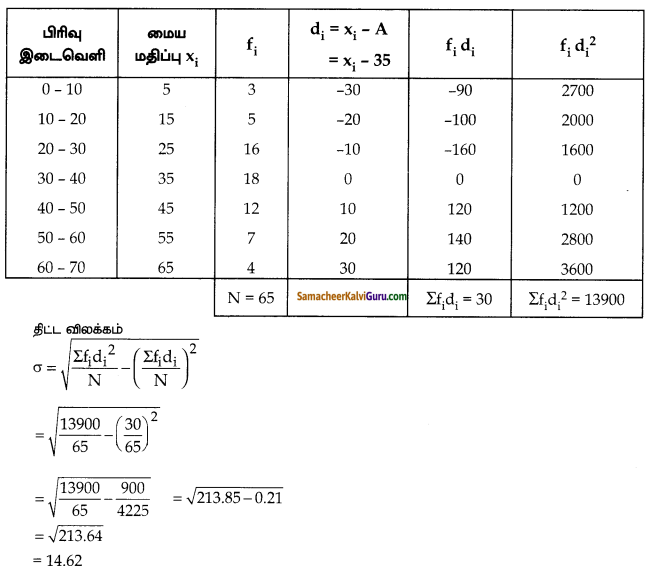
விடை :
σ ≅ 14.6

கேள்வி 12.
ஒரு தொழிற்சாலையில் தயாரிக்கப்பட்ட தட்டுகளின் விட்ட அளவுகள் (செ.மீ)ல் கீழே கொடுக்கப்பட்டுள்ளன. இதன் திட்டவிலக்கம் காண்க.

தீர்வு :
படி விலக்க முறை
A = 30.5
C = 4
d_i = \(\frac{x_{\mathrm{i}}-30.5}{4}\)

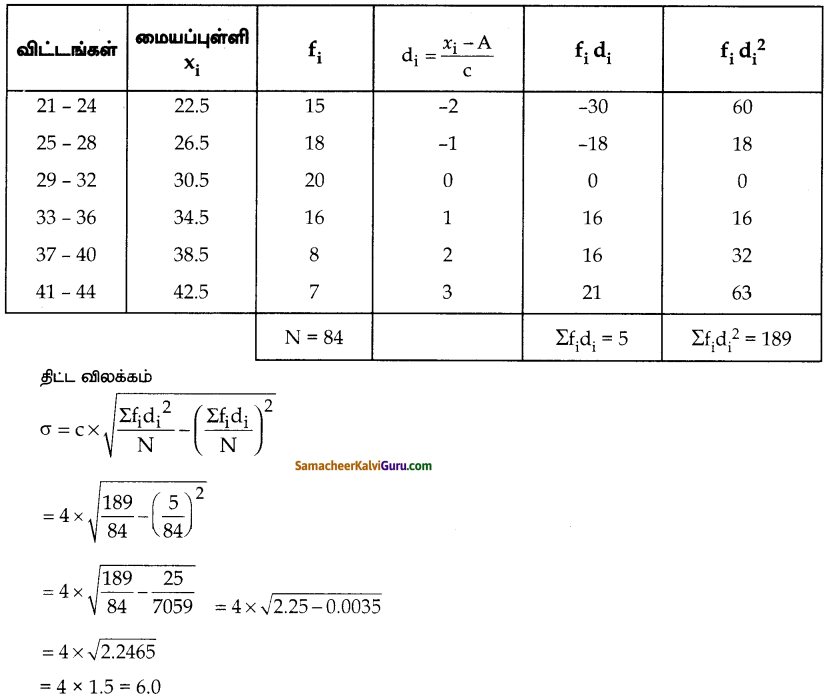
விடை :
S.D σ ≅ 6

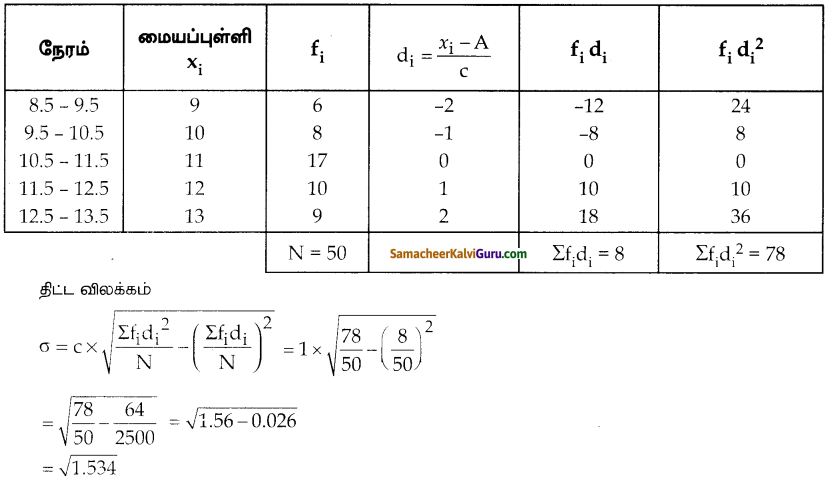
கேள்வி 13.
50 மாணவர்கள் 100 மீட்டர் தூரத்தை கடக்க எடுத்துக்கொண்ட கால அளவுகள் கீழே கொடுக்கப்பட்டுள்ளன. அவற்றின் திட்டவிலக்கம் காண்க.

தீர்வு :
படிவிலக்க முறை
A = 11
C = 1
d_i = \(\frac{x_{1}-A}{c}=\frac{x_{i}-11}{1}\)

விடை :
S.D σ ≅ 1.24

கேள்வி 14.
100 மாணவர்கள் கொண்ட ஒரு குழுவில், அவர்கள் எடுத்த மதிப்பெண்களின் சராசரி மற்றும்
திட்ட விலக்கமானது முறையே 60 மற்றும் 15 ஆகும். பின்னர் 45 மற்றும் 72 என்ற இரு மதிப்பெண்களுக்குப் பதிலாக முறையே 40 மற்றும் 27 என்று தவறாகப் பதிவு செய்யப்பட்டது தெரிய வந்தது. அவற்றைச் சரி செய்தால் கிடைக்கப்பெறும் புதிய தரவின் சராசரியும் திட்ட விலக்கமும் காண்க.
தீர்வு :
n = 100
\(\bar{x}\) = 60
σ = 15
சரியான மதிப்புகள் 45 மற்றும் 72 தவறான மதிப்புகள் 40 மற்றும் 27
\(\bar{x}=\frac{\Sigma x}{n}\) ⇒ n x \(\bar{x}\)
∴ தவறான கூடுதல் = 100 x 60 = 600
திருத்தப்பட்ட கூடுதல் = தவறான கூடுதல் – தவறான மதிப்புகள் + சரியான மதிப்புகள்
= 6000 – 40 – 27 + 45 + 72
= 6050

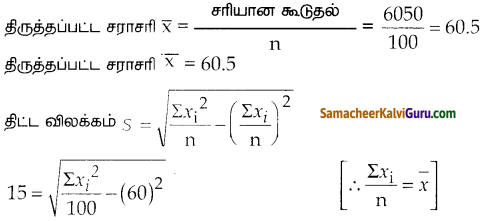
15² = \(\frac{\Sigma x_{\mathrm{i}}^{2}}{100}\) – 60²
\(\frac{\Sigma x_{\mathrm{i}}^{2}}{100}\) = 15² + 60² = 225 + 3600 = 3825
\(\Sigma x_{i}^{2}\)ன் திருத்தப்பட்ட மதிப்பு
= 3825 x 100 = 382500
\(\Sigma x_{i}^{2}\)ன் திருத்தப்பட்ட மதிப்பு
= 382500 – (40)² – (27)² + 45² + 72² \
= 382500 – 1600 – 729 + 2025 + 5184
= 382500 – 2329 + 7209
= 387380
திருத்தப்பட்ட திட்டவிலக்கம்

விடை :
திருத்தப்பட்ட சராசரி = 60.5,
திருத்தப்பட்ட திட்டவிலக்கம் σ ≅ 14.6

கேள்வி 15.
ஏழு தரவுப் புள்ளிகளின் சராசரி மற்றும் விலக்கச் சராசரி வர்க்கச் சராசரி முறையே 8,16 ஆகும். அதில் ஜந்து தரவுப் புள்ளிகள் 2,4, 10, 12 மற்றும் 14 எனில் மீதம் உள்ள இரு தரவுப் புள்ளிகளைக் கண்டறிக. 310, 290, 320, 280, 300, 290, 320, 310, 280
தீர்வு :
இரு தரவுப் புள்ளிகள் p மற்றும் ஏ என்க.
\(\overline{\mathrm{X}}\) = 8 மற்றும் σ² = 16, n = 7
ஐந்து தரவுப் புள்ளிகள் முறையே 2, 4, 10, 12 மற்றும் 14.

xi	Xi2
2	4
4	16
10	100
12	144
14	196
P	p2
q	q2

Σx = 42 + p + q
\(\overline{\mathrm{X}}\) = 82
\(\sum x_{1}^{2}\) = 460 + p +q
\(\frac{\Sigma x}{n}\) = 8
\(\frac{42+p+q}{7}\) = 8
42 + p +q = 56
p + q = 56 – 42 = 14
p + q = 14 —–(1)
திட்ட விலக்கம்

460 + p² + q² = 560
p² + q² = 560 – 460 = 100
(p + q)² – 2pq = 100
14² – 2pq = 100 196 – 2pq = 100
2pq = 96
pq= 48 –(2)
(1) மற்றும் (2) ஐ தீர்க்க
(2) லிருந்து ⇒ q = \(\frac{48}{\mathrm{P}}\) (i) ல் பிரதியிட
(1) = p + \(\frac{48}{\mathrm{P}}\) = 14
\(\frac{p^{2}+48}{p}\) = 14 ⇒ p² + 48 = 14p
p² – 14p + 48 = 0
(p – 8) (p – 6) = 0
p – 8 = 0 (அல்ல து) p – 6 = 0
∴ p = 8 p = 6.
p = 8, எனில் q = \(\frac{48}{8}\) = 6
p = 6, எனில் q = \(\frac{48}{6}\) = 8
விடை :
இரு தரவுப்புள்ளிகள் 6 மற்றும் 8.