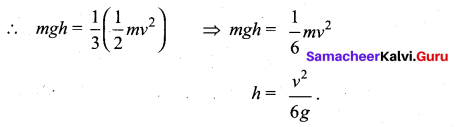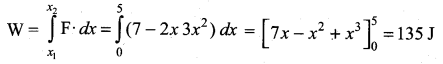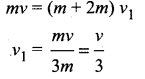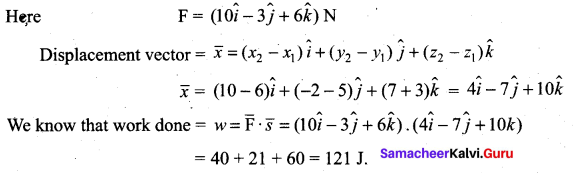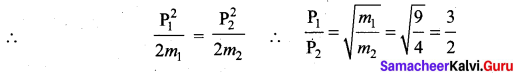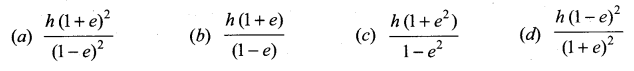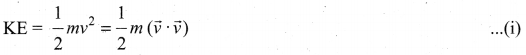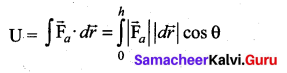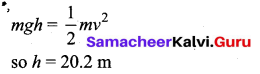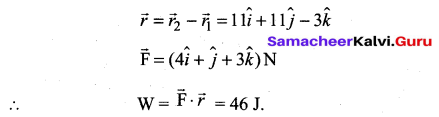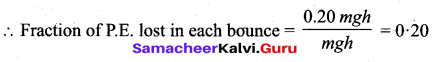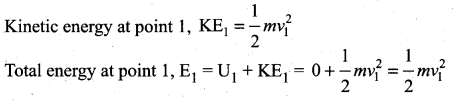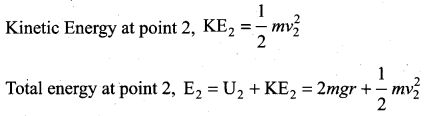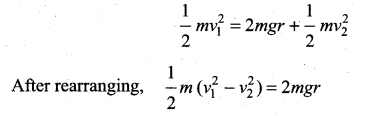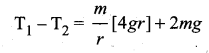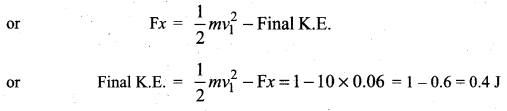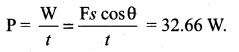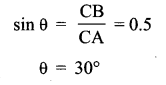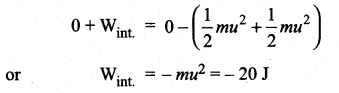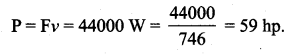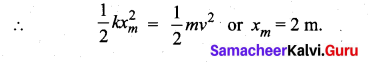You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 8 Vector Algebra – I Ex 8.2
11th Maths Exercise 8.2 Question 1.
Verify whether the following ratios are direction cosines of some vector or not.
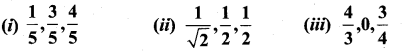
Solution:

11th Maths Vector Algebra Solutions Question 2.
Find the direction cosines of a vectors whose direction ratios are
(i) 1, 2, 3
(ii) 3, -1, 3
(iii) 0, 0, 7
Solution:
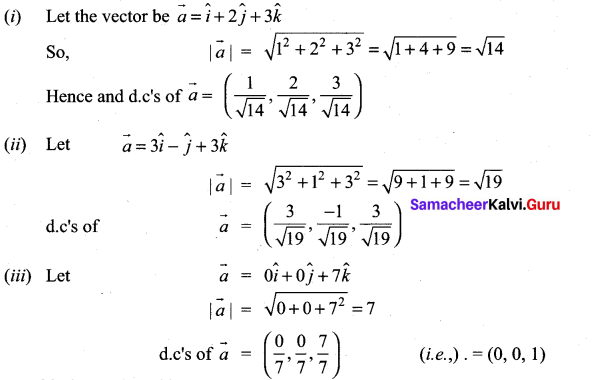
11th Maths Exercise 8.2 Answers Question 3.
Find the direction cosines and direction ratios for the following vectors
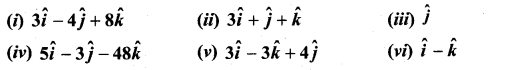
Solution:


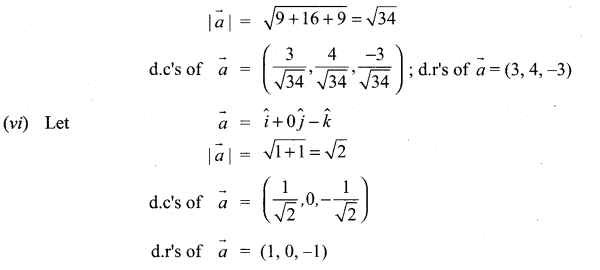
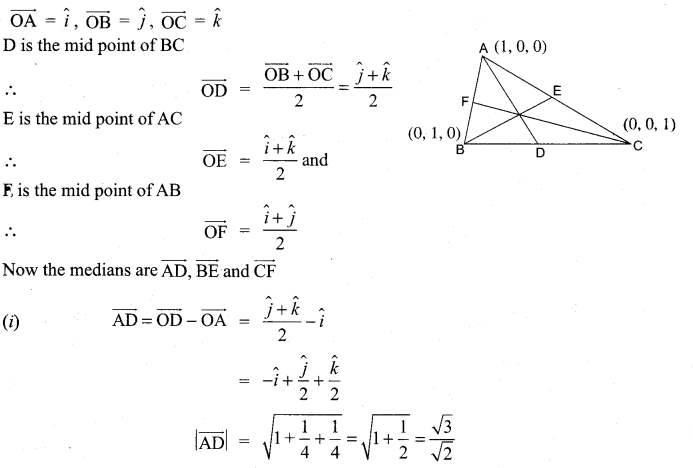
11th Maths Vector Algebra Exercise 8.2 Question 4.
A triangle is formed by joining the points (1, 0, 0), (0, 1, 0) and (0, 0, 1). Find the direction cosines of the medians.
Solution:
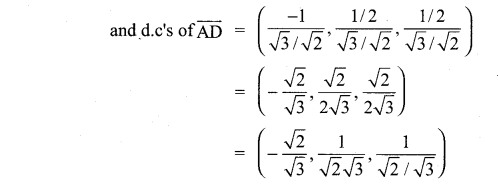

11th Maths 8.2 Question 5.
If \(\frac{1}{2}, \frac{1}{\sqrt{2}}\), a are the direction cosines of some vector, then find a.
Solution:
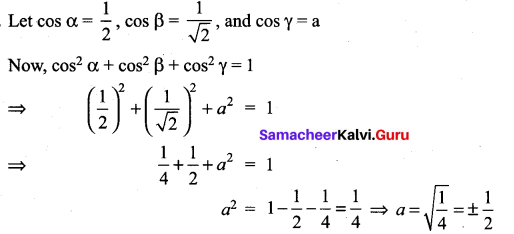
Class 11th Maths Exercise 8.2 Solution Question 6.
If (a, a + b, a + b + c) is one set of direction ratios of the line joining (1, 0, 0) and (0, 1, 0), then find a set of values of a, b, c.
Solution:
Let A be the point (1, 0, 0) and B be the point (0, 1, 0) (i.e.,) \(\overrightarrow{\mathrm{OA}}=\hat{i}\) and \(\overrightarrow{\mathrm{OB}}=\hat{j}\)
Then \(\overrightarrow{\mathrm{AB}}=\overrightarrow{\mathrm{OB}}-\overrightarrow{\mathrm{OA}}=\hat{j}-\hat{i}=-\hat{i}+\hat{j}\)
= (-1, 1, 0)
= (a, a + b, a + b + c)
⇒ a = -1, a + b = 1 and a + b + c = 0
Now a = -1 ⇒ -1 + b = 1 ;a + b + c = 0
⇒ b = 2; -1 + 2 + c = 0 ⇒ c + 1 = 0
⇒ c = -1
∴ a = -1; b = 2; c = -1.
Note: If we taken \(\overrightarrow{\mathrm{BA}}\) then we get a = 1, b = -2 and c = 1.
Class 11 Maths Chapter 8 Exercise 8.2 Solutions Question 7.
Show that the vectors \(2 \hat{i}-\hat{j}+\hat{k}, 3 \hat{i}-4 \hat{j}-4 \hat{k}, \hat{i}-3 \hat{j}-5 \hat{k}\) form a right angled triangle.
Sol:

⇒ The given vectors form the sides of a right angled triangle.
11th Maths Guide Question 8.
Find the value of k for which the vectors \(\vec{a}=3 \hat{i}+2 \hat{j}+9 \hat{k}\) and \(\vec{b}=\hat{i}+\lambda \hat{j}+3 \hat{k}\) are parallel.
Solution:
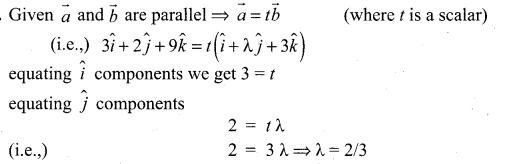
Samacheer Guru 11th Maths Question 9.
Show that the following vectors are coplanar.
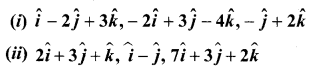
Solution:
Let the given three vectors be \(\vec{a}\), \(\vec{b}\) and \(\vec{c}\). When we are able to write one vector as a linear combination of the other two vectors, then the given vectors are called coplanar vectors.
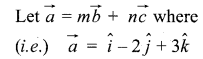



We are able to write \(\vec{a}\) as a linear combination of \(\vec{b}\) and \(\vec{c}\)
∴ The vectors \(\vec{a}\), \(\vec{b}\), \(\vec{c}\) are coplanar
11th Samacheer Maths Solutions Question 10.
Show that the points whose position vectors ![]() and
and ![]() are coplanar
are coplanar
Solution:
Let the given points be A, B, C and D. To prove that the points A, B, C, D are coplanar, we have to prove that the vectors \(\overrightarrow{\mathrm{AB}}, \overrightarrow{\mathrm{AC}}\) and \(\overrightarrow{\mathrm{AC}}\) are coplanar
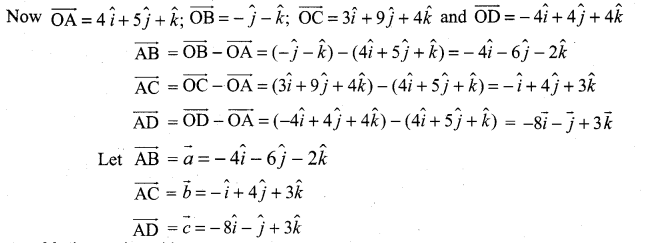

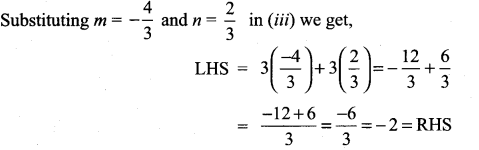
∴ we are able to write one vector as a linear combination of the other two vectors ⇒ the given vectors \(\vec{a}\), \(\vec{b}\), \(\vec{c}\) are coplanar.
(i.e.,) the given points A, B, C, D are coplanar.
Samacheer Kalvi 11th Guide Maths Question 11.
If \(\vec{a}=2 \hat{i}+3 \hat{j}-4 \hat{k}\), \(\vec{b}=3 \hat{i}-4 \hat{j}-5 \hat{k}\) and \(\vec{c}=-3 \hat{i}+2 \hat{j}+3 \hat{k}\), find the magnitude and direction cosines of
(i) \(\vec{a}+\vec{b}+\vec{c}\)
(ii) \(3 \vec{a}-2 \vec{b}+5 \vec{c}\)
Solution:
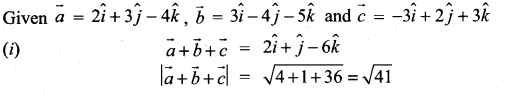
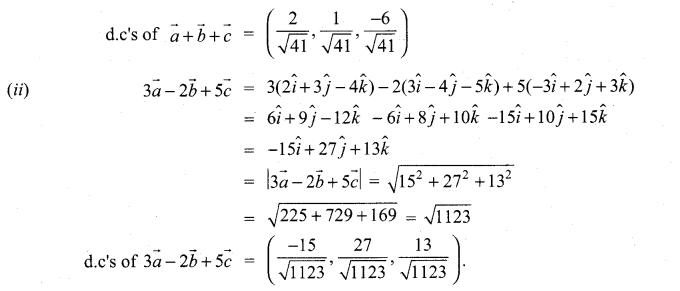 >
>
Samacheer Kalvi 11th Maths Question 12.
The position vectors of the vertices of a triangle are ![]() and
and ![]() . Find the perimeter of the triangle
. Find the perimeter of the triangle
Solution:
Let A, B, C be the vertices of the triangle ABC,

11 Samacheer Maths Solutions Question 13.
Find the unit vector parallel to ![]() and
and ![]()
Solution:
![]()

12th Maths Exercise 8.2 Samacheer Kalvi Question 14.
The position vector \(\vec{a}\), \(\vec{b}\), \(\vec{c}\) three points satisfy the relation \(2 \vec{a}-7 \vec{b}+5 \vec{c}=\overrightarrow{0}\). Are these points collinear?
Solution:

10th Maths Exercise 8.2 Samacheer Kalvi Question 15.
The position vectors of the point P, Q, R, S are ![]() and
and ![]() respectively. Prove that the line PQ and RS are parallel.
respectively. Prove that the line PQ and RS are parallel.
Solution:

Ex 8.2 Class 11 Question 16.
Find the value or values of m for which \(m(\hat{i}+\hat{j}+\hat{k})\) is a unit vector
Solution:
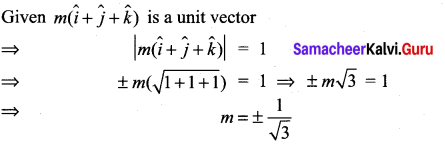
11th Maths 8th Chapter Question 17.
Show that the points A(1, 1, 1), B(1, 2, 3) and C(2, -1, 1) are vertices of an isosceles triangle.
Solution:

Samacheer Kalvi 11th Maths Solutions Chapter 8 Vector Algebra – I Ex 8.2 Additional Problems
Samacheer Kalvi Maths Guide 11th Question 1.
Show that the points whose position vectors given by
![]()
![]()
Solution:
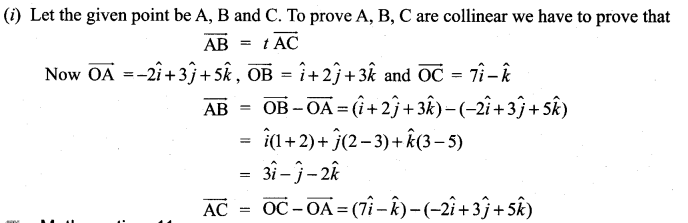
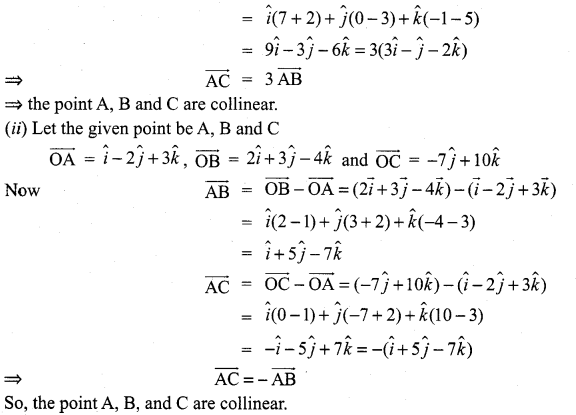
Samacheer Kalvi.Guru 11th Maths Question 2.
Find the unit vectors parallel to the sum of \(3 \hat{i}-5 \hat{j}+8 \hat{k}\) and \(-2 \hat{j}-2 \hat{k}\)
Solution:
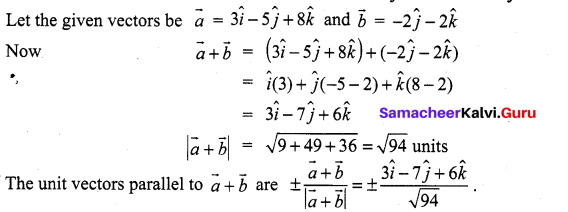
Maths Guide 11th Question 3.
The vertices of a triangle have position vectors ![]() Prove that the triangle is equilateral.
Prove that the triangle is equilateral.
Solution:


Maths Solutions Class 11 Samacheer Kalvi Question 4.
Prove that the points ![]() form an equilateral triangle.
form an equilateral triangle.
Solution:

Samacheer Kalvi 11th Maths Solution Book Question 5.
Examine whether the vectors ![]() are coplanar
are coplanar
Solution:
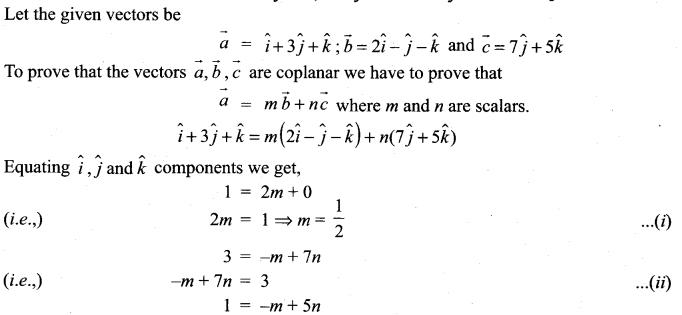
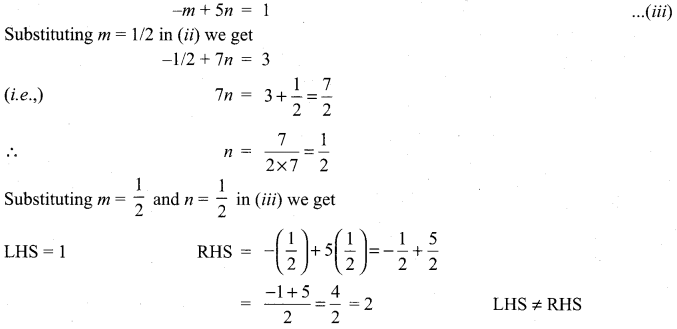
⇒ We are not able to write one vector as a linear combination of the other two vectors
⇒ the given vectors are not coplanar.
















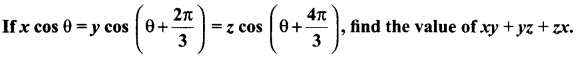
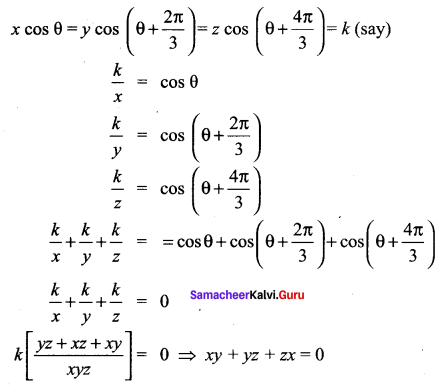





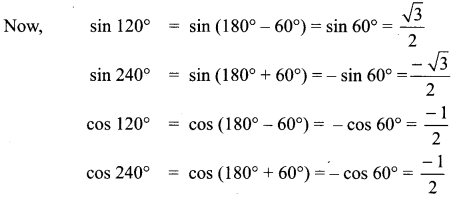
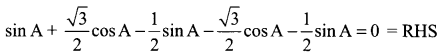
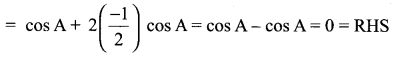
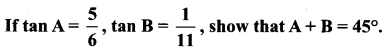


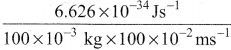


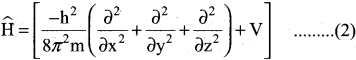

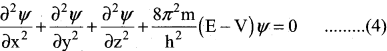
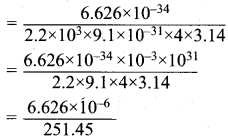
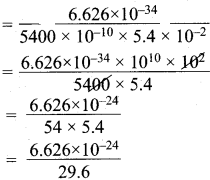

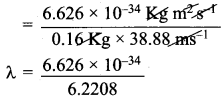
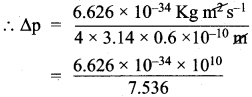
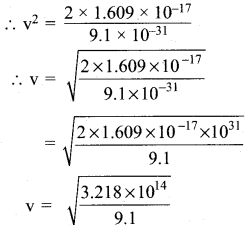
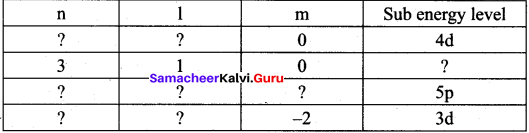
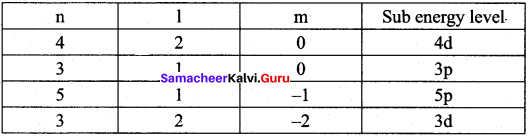
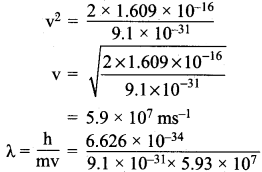
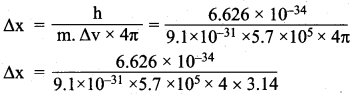






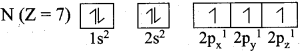
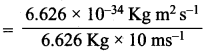
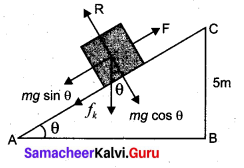
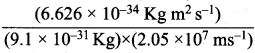 =355 x 10-4m.
=355 x 10-4m.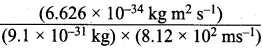
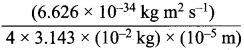 = 5.27 x 10-28mv
= 5.27 x 10-28mv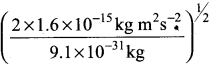 = 5.93 x 107m-1
= 5.93 x 107m-1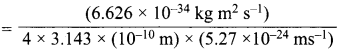 = 0.1 kg.
= 0.1 kg.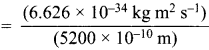
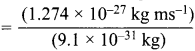 = 1.4 x 103 ms-1
= 1.4 x 103 ms-1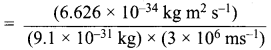
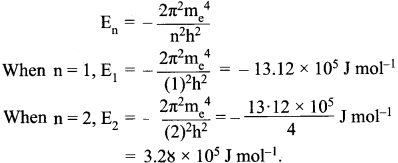
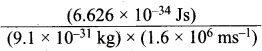





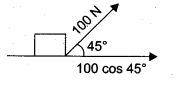
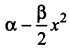 , then force experienced by the particle is
, then force experienced by the particle is



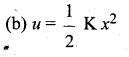
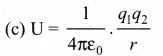





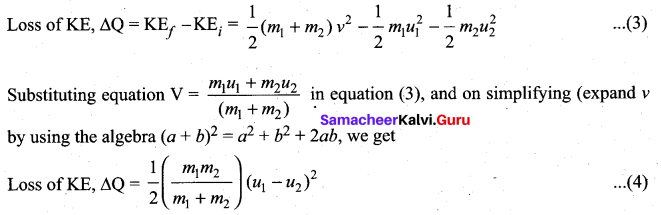

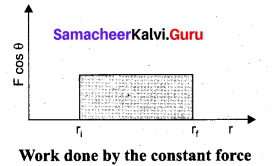

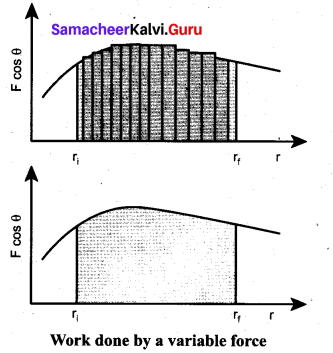
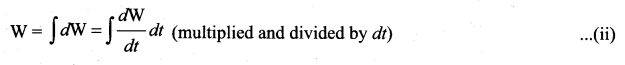
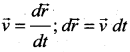 . Right hand side of the equation (i) can be written as dt
. Right hand side of the equation (i) can be written as dt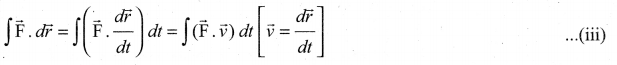
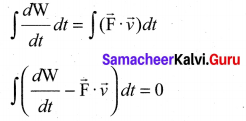
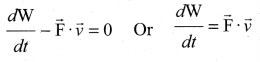
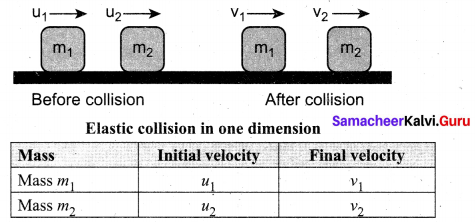


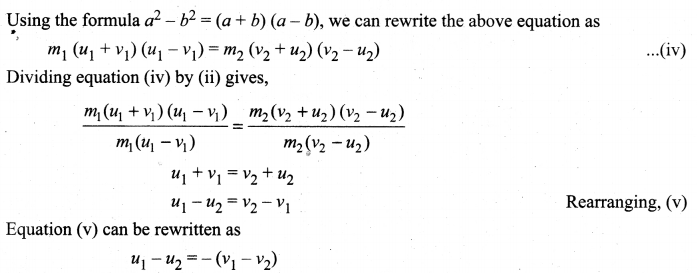
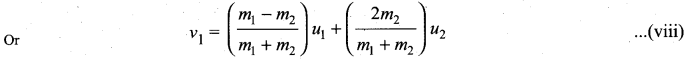
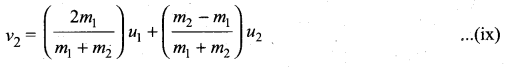
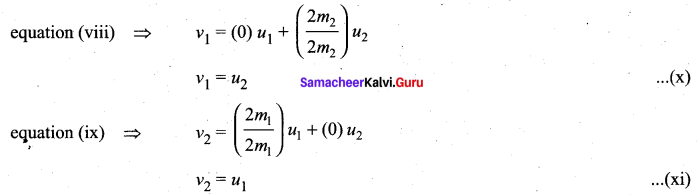
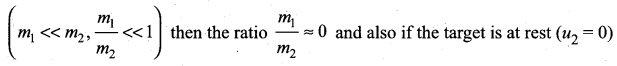
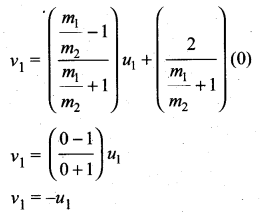
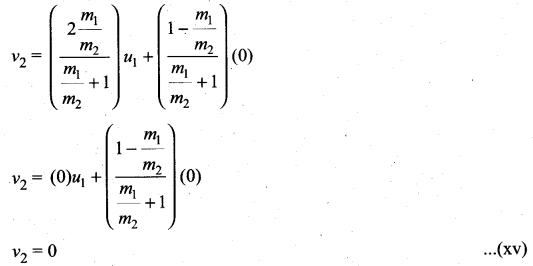

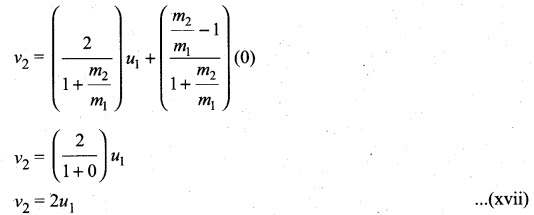


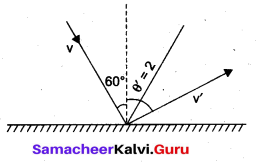


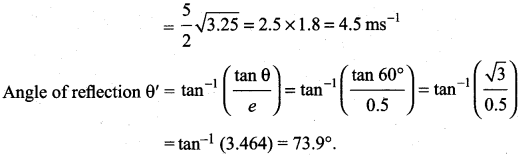
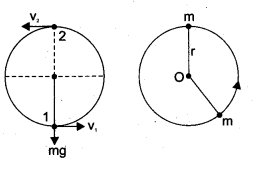
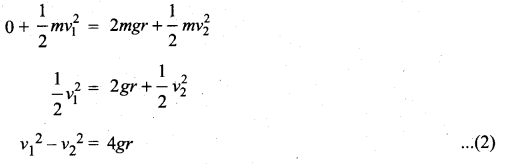

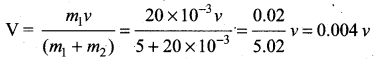


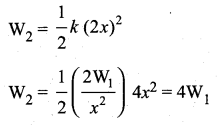
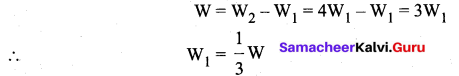
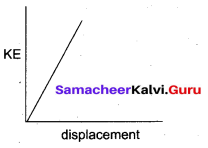





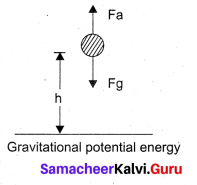
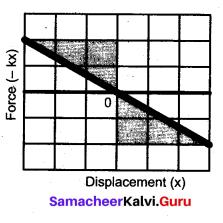
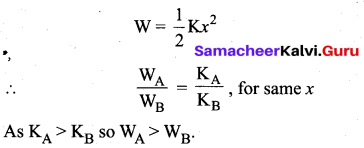
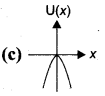
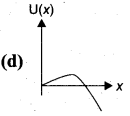
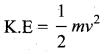 . The loss in K.E will be the gain in potential energy
. The loss in K.E will be the gain in potential energy