Category: Class 11

Students can find the most related topics which helps them to analyse the concepts if they practice according to the chapter-wise page. It is necessary for the students to practice more Questions and Answers for Tamilnadu State Board Solutions of 11th Commerce are given in the pdf format in chapter 33 Indirect Taxation Questions and Answers so that students can prepare in both online and offline modes. So, Download Samacheer Kalvi 11th Commerce Book Solutions Questions and Answers, Notes Pdf, to score good marks.

Samacheer Kalvi 11th Commerce Solutions Chapter 33 Indirect Taxation

Get the Questions and Answers, in Tamilnadu State Board 11th Commerce Solutions for Chapter 33 Indirect Taxation. Learn the concepts of 11th Commerce Chapter-Wise by referring to the Tamilnadu State Board Solutions for Chapter 33 Indirect Taxation Questions and Answers. Hence we suggest the students to Download Samacheer Kalvi 11th Commerce Book Solutions Questions and Answers pdf to enhance your knowledge.

Samacheer Kalvi 11th Commerce Indirect Taxation Textbook Exercise Questions and Answers

I. Choose the Correct Answer

Question 1.
Who is the chairman of the GST council?
(a) RBI Governor
(b) Finance Minister
(c) Prime Minister
(d) President of India
Answer:
(b) Finance Minister

Question 2.
GST Stands for …………….
(a) Goods and Supply Tax
(b) Government sales Tax
(c) Goods and Services Tax
(d) General Sales Tax
Answer:
(c) Goods and Services Tax

Question 3.
What kind of Tax the GST is?
(a) Direct Tax
(b) Indirect Tax
(c) Dependence on the Type of Goods and Services
(d) All Business Organisations
Answer:
(b) Indirect Tax

Question 4.
What is IGST?
(a) Integrated Goods and Service Tax
(b) India Goods and Service Tax
(c) Initial Goods and Service Tax
(d) All the above
Answer:
(a) Integrated Goods and Service Tax

Question 5.
In India GST became effective from?
(a) 1^st April, 2017
(b) 1^st January, 2017
(c) 1^st July, 2017
(d) 1^st March, 2017
Answer:
(d) 1^st March, 2017

II. Very Short Answer Questions

Question 1.
Define Indirect tax.
Answer:
Indirect Tax is levied on the goods and services. It is collected from the buyers by the sellers and paid by the sellers to the Government. Since it is indirectly imposed on the buyers it is called indirect tax.

Question 2.
List out any four types of indirect taxes levied in India.
Answer:

1. CGST
2. SGST
3. UGST
4. IGST

Question 3.
What do you mean by Goods and Services Taxes?
Answer:
Goods and Services Tax (GST) is the tax imposed on the supply (consumption) of goods and services. It is a destination based consumption tax and collected on those value added items at each stage of the supply chain.

Question 4.
Write a note on SGST.
Answer:
SGST – State Goods and Services Tax – is imposed and collected by the State Governments under State GST Act. (Tamil Nadu GST Act 2017 passed by Tamil Nadu Govt.)

Question 5.
What is CGST?
Answer:
CGST – Central Goods and Services Tax – is imposed and collected by the Central Government on all supply of goods within a state (intra – state) under CGST Act 2017.

III. Short Answer Questions

Question 1.
Write any two differences between direct taxes and indirect taxes?
Answer:

Basis	Direct Taxes	Indirect Taxes
1. Meaning	If a tax levied on the income or wealth of a person is paid by that person (or his office) directly to the Government, it is called direct tax.	If tax is levied on the goods or services of a person is collected from he buyers by another person (seller) and paid by him to the Government it is called indirect tax.
2. Incidence and Impact	Falls on the same person. Imposed on the income of a person and paid by the same person.	Falls on different persons. Imposed on the sellers but collected from the consumers and paid by sellers.

Question 2.
What are the objectives of GST?
Answer:

1. To create a common market with uniform tax rate in India. (One Nation, One Tax, One Market)
2. To eliminate the cascading effect of taxes, GST allows set-off of prior taxes for the same transactions as input tax credit.
3. To boost Indian exports, the GST already collected on the inputs will be refunded and thus there will be no tax on all exports.
4. To increase the tax base by bringing more number of tax payers and increase tax revenue.
5. To simplify tax return procedures through common forms and avoidance of visiting tax departments.
6. To provide online facilities for payment of taxes and submission of forms.

Question 3.
Briefly explain the functions of GST council.
Answer:

1. The GST Council will oversee the implementation of the GST. But the Central Board of Excise and Customs is responsible for administration of the CGST and IGST Acts.
2. The Council makes recommendations on rate of GST, apportionment of IGST, exemptions, model GST laws, etc.
3. The Minister of State in the Finance Ministry and all Finance Ministers of the State Governments shall be its members.
4. All decisions of the Council can be passed only with Atb of the total votes. Each state has one vote, irrespective of its size or population.

Question 4.
Explain IGST with an example.
Answer:
IGST – Inter-State Goods and Services Tax is imposed and collected by the Central Government and the revenue is shared with States under IGST Act 2017.

Question 5.
Write any three demerits of UGST.
Answer:

1. Several Economists says that GST in India would impact negatively on the real estate market. It would add up to 8 percent to the cost of new homes and reduce demand by about 12 percent.
2. Another criticism is that CGST, SGST are nothing but new names for Central Excise/ Service Tax, VAT and CST. Hence, there is no major reduction in the number of tax layers.
3. A number of retail products currently have only four percent tax on them. After GST, garments and clothes could become more expensive.

IV. Long Answer Questions

Question 1.
Distinguish between direct taxes and indirect taxes.
Answer:

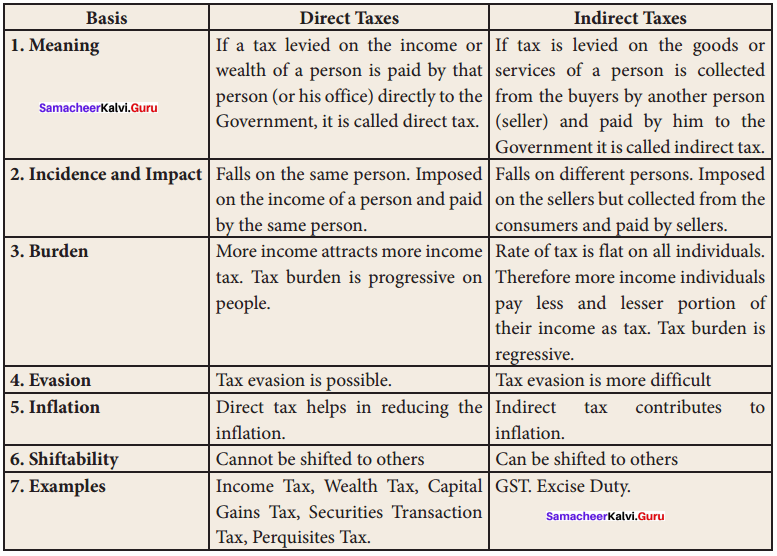
Question 2.
Discuss the different kinds of GST.
Answer:
GST is of three kinds: CGST, SGST/UGST, and IGST.
1. CGST – Central Goods and Services Tax – imposed and collected by the Central Government on all supply of goods within a state (intra-state) under CGST Act 2017.

2. SGST – State Goods and Services Tax – imposed and collected by the State Governments under State GST Act. (Tamil Nadu GST Act 2017 passed by Tamil Nadu Govt.)

3. UGST – Union Territory Goods and Services Tax – imposed and collected by the five Union Territory Administrations in India under UGST Act 2017.

4. IGST – Inter-State Goods and Services Tax – imposed and collected by the Central Government and the revenue shared with States under IGST Act 2017.

5. IGST on exports – All exports are treated as Inter-State supply under GST. Since exports are zero rated, GST is not imposed on all goods and services exported from India. Any input credit paid already on exports will be refunded.

Question 3.
Elucidate the merits of GST.
Answer:
A. To the Society and country:

1. Unified common national market will attract more foreign investment. GST has integrated the economy of all States and Union Territories.
2. It brings parity in taxation among imported goods and Indian manufactured goods. All imported goods will be charged with IGST which will be more or less equivalent to the total of CGST and SGST levied on manufactured goods. Removal of several taxes will make the price of Indian products more competitive at world market.
3. It will boost manufacturing, export, GDP leading to economic growth through increase in economic activity.
4. Creation of more employment opportunities which will result in poverty eradication.
5. It will bring more tax compliance (more tax payers) and increase revenue to the Governments.
6. It is transparent and will improve India’s ranking in the Ease of Doing Business in the world.
7. Uniform rates of tax will reduce tax evasion and rate arbitrage between States.

B. To Business Community:

1. Simpler Tax System with fewer exemptions. 17 taxes were abolished and one tax exists today.
2. Input tax credit will reduce cascading effect of taxes. Reduction in average tax burden will encourage manufacturers and help “Make in India” campaign and make India as a manufacturing hub.
3. Common procedures, common classification of goods and services and timelines will lend greater certainty to taxation system.
4. GSTN facility will reduce multiple record keeping, lesser investment in manpower and resources and improve efficiency.
5. All interactions will be through common GSTN portal and will ensure corruption free administration
6. Uniform prices throughout the country. Expansion of business to all states is made easy.

C. To Consumers:

1. Input tax credit allowed will lower the prices to the consumers.
2. All small retailers will get exemption and purchases from them will cost less for the consumers.

Question 4.
Compare CGST, SGST and IGST.
Answer:

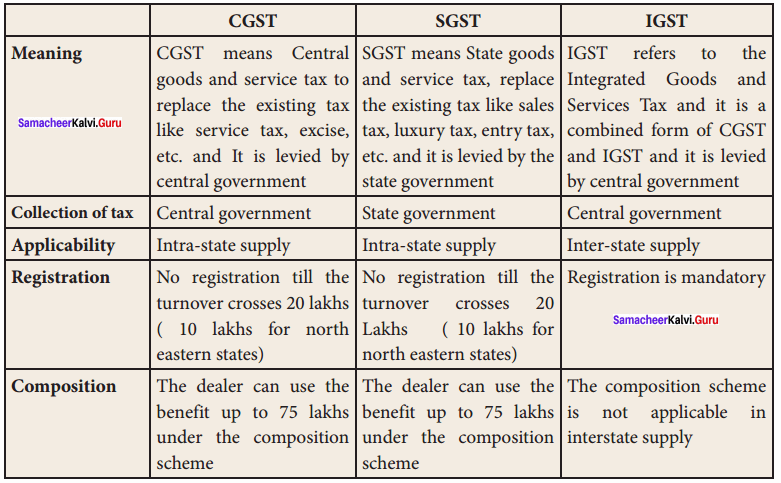
Share this Tamilnadu State Board Solutions for 11th Commerce Chapter 33 Indirect Taxation Questions and Answers with your friends to help them to overcome the issues in exams. Keep visiting this site Tamilnadu State Board Solutions frequently to get the latest information on different subjects. Clarify your doubts by posting the comments and get the answers in an easy manner.

Students can find the most related topics which helps them to analyse the concepts if they practice according to the chapter-wise page. It is necessary for the students to practice more Questions and Answers for Tamilnadu State Board Solutions of 11th Commerce are given in the pdf format in chapter 32 Direct Taxes Questions and Answers so that students can prepare in both online and offline modes. So, Download Samacheer Kalvi 11th Commerce Book Solutions Questions and Answers, Notes Pdf, to score good marks.

Samacheer Kalvi 11th Commerce Solutions Chapter 32 Direct Taxes

Get the Questions and Answers, in Tamilnadu State Board 11th Commerce Solutions for Chapter 32 Direct Taxes. Learn the concepts of 11th Commerce Chapter-Wise by referring to the Tamilnadu State Board Solutions for Chapter 32 Direct Taxes Questions and Answers. Hence we suggest the students to Download Samacheer Kalvi 11th Commerce Book Solutions Questions and Answers pdf to enhance your knowledge.

Samacheer Kalvi 11th Commerce Direct Taxes Textbook Exercise Questions and Answers

I. Choose the Correct Answer

Question 1.
Income Tax is ……………
(a) a business tax
(b) a direct tax
(c) an indirect tax
(d) none of these
Answer:
(b) a direct tax

Question 2.
Period of assessment year is ……………
(a) 1^st April to 31^st March
(b) 1^st March to 28^st Feb
(c) 1^st July to 30^st June
(d) 1^st Jan to 31^st Dec
Answer:
(a) 1^st April to 31^st March

Question 3.
The year in which income is earned is known as ……………
(a) Assessment Year
(b) Previous Year
(c) Light Year
(d) Calendar Year
Answer:
(b) Previous Year

Question 4.
The aggregate income under five heads is termed as ……………
(a) Gross Total Income
(b) Total Income
(c) Salary Income
(d) Business Income
Answer:
(b) Total Income

Question 5.
Agricultural income earned in India is ……………
(a) Fully Taxable
(b) Fully Exempted
(c) Not Considered for Income
(d) None of the above
Answer:
(b) Fully Exempted

II. Very Short Answer Questions

Question 1.
What is Income tax?
Answer:
Income tax is a direct tax under which tax is calculated on the income, gains or profits earned by a person such as individuals and. other artificial entities (a partnership firm, company, etc.).

Question 2.
What is meant by previous year?
Answer:
The year in which income is earned is called previous year. It is also normally consisting of a period of 12 months commencing on 1^st April every year and ending on 31^st March of the following year. It is also called as financial year immediately following the assessment year.

Question 3.
Define the term person?
Answer:
The term ‘person’ has been defined under the Income tax Act. It includes individual, Hindu, Undivided Family, Firm, Company, local authority, Association of person or body of Individual or any other artificial juridical persons.

Question 4.
Define the term assessee?
Answer:
Assessee means a person by whom any tax or any other sum of money is payable under this Act. It includes every person in respect of whom any proceeding has been taken for the assessment of his income or assessment of fringe benefits.

Question 5.
What is an assessment year?
Answer:
The term has been defined under section 2(9). The year in which tax is paid is called the assessment year. It normally consists of a period of 12 months commencing on 1^st April every year and ending on 31^st March of the following year.

III. Short Answer Questions

Question 1.
What is Gross Total Income?
Answer:
Income from the five heads, namely – Salaries, House Property, Profits and Gains of Business or Profession, Capital Gains, and Other Sources – is computed separately according to the provisions given in the Act. Income computed under these heads shall be aggregated after adjusting past and present losses and the total so arrived at is known as ‘Gross Total Income’.

Question 2.
List out the five heads of income.
Answer:
The five heads of income are:

1. Income from‘Salaries’ [Sections 15 – 17];
2. Income from ‘House Property’ [Sections 22 – 27];
3. Income from ‘Profits and Gains of Business or Profession’ [Sections 28 – 44];
4. Income from ‘Capital Gains’ [Sections 45 – 55]; and
5. Income from‘Other Sources’ [Sections 56 – 59].

Question 3.
Write a note on Agricultural Income.
Answer:
Any rent or revenue derived from land which is situated in India and is used for agriculture purposes. Agricultural income is fully exempted from tax u/s 10(1) and as such does not form part of total income.

Question 4.
What do you mean by Total Income.
Answer:
Out of Gross Total Income, Income Tax Act 1961 allows certain deductions under section 80. After allowing these deductions the figure which we arrive at is called ‘Total Income’ and on this figure tax liability is computed at the prescribed rates.

1. Gross Total Income ****
2. Less: Deductions (Sec. 80C to 80U) ****
3. Total Income (T.I.) ****

Question 5.
Write short notes on:

1. Direct Tax
2. Indirect Tax

Answer:
1. Direct Tax:
If a tax levied on the income or wealth of a person and is paid by that person (or his office) directly to the Government, , it is called direct tax, example Income – Tax, Wealth Tax, Capital Gains Tax, Securities Transaction Tax, Fringe Benefits Tax (from 2005), Banking Cash Transaction Tax (for Rs,50,000 and above – from 2005), etc. In India all direct taxes are levied and administered by Central Board of Direct Taxes.

2. Indirect Tax:
If tax is levied on the goods or services of a person (seller). It is collected from, the buyers and is paid by seller to the Government. It is called indirect tax example GST.

IV. Long Answer Questions

Question 1.
Elucidate any five features of Income Tax.
Features of Income Tax in India:
1. Levied as Per the Constitution Income tax is levied in India by virtue of entry No. 82 of list I (Union List) of Seventh Schedule to the Article 246 of the Constitution of India.

2. Levied by Central Government Income tax is charged by the Central Government on all incomes other than agricultural income. However, the power to charge income tax on agricultural income has been vested with the State Government as per entry 46 of list II, i.e., State List.

3. Direct Tax Income tax is direct tax. It is because the liability to deposit and ultimate burden are on same person. The person earning income is liable to pay income tax out of his own pocket and cannot pass on the burden of tax to another person.

4. Annual Tax Income tax is an annual tax because it is the income of a particular year which is chargeable to tax.

5. Tax on Person It is a tax on income earned by a person. The term ‘person’ has been defined under the Income tax Act. It includes individual, Hindu Undivided Family, Firm, Company, local authority, Association of person or body of Individual or any other artificial juridical persons. The persons who are covered under Income tax Act are called ‘assessees’.

Question 2.
Define Tax. Explain the term direct tax and indirect tax with an example.
Answer:
Tax is a compulsory contribution to state revenue by the Government. It is levied on the income or profits from business of individuals and institutions. It may be added to the price of goods, services or transactions. Tax is the basic source of revenue to the Government. This revenue is utilised for the expenses of civil administration, internal and external security, building infrastructure, etc.

There are two types of taxes – direct taxes and indirect, taxes.

1. Direct Tax:
If a tax levied on the income or wealth of a person and is paid by that person (or his office) directly to the Government, it is called direct tax, e.g., Income – Tax, Wealth Tax, Capital Gains Tax, Securities Transaction Tax, Fringe Benefits Tax (from 2005), Banking Cash Transaction Tax (for Rs.50,000 and above – from 2005), etc. In India all direct taxes are levied and administered by Central Board of Direct Taxes.

2. Indirect Tax:
If tax is levied on the goods or services of a person (seller). It is collected from the buyers and is paid by seller to the Government. It is called indirect tax. example GST.

Question 3.
List out any ten kinds of incomes chargeable under the head income tax.
Answer:

1. Profits and gains of business or profession.
2. Dividend
3. Voluntary contribution received by a charitable / religious trust or university/education institution or hospital/electoral trust[ w.e.f. 01.04.2010]
4. Value of perquisite or profit in lieu of salary taxable u/s 17 and social allowance or benefit specifically granted either to meet personal expenses or for performance Of duties of an office or an employment of profit.
5. Export incentives, like duty drawback, cash compensatory support, sale of licenses, etc.
6. Interest, salary, bonus, commission or remuneration earned by a partner of a firm from such firm.
7. Capital gain chargeable u/s 45.
8. Profits and gains from the business of banking carried on by a co – operative society with its members.
9. Winning from lotteries, crossword puzzles, races including horse races, card games and other games of any sort or from gambling or betting of any form or nature whatsoever.
10. Deemed income u/s 41 or 59.

Question 4.
Discuss the various kinds of assesses.
Answer:
Assessee means a person by whom any tax or any other sum of money is payable under this Act. It includes every person in respect of whom any proceeding has been taken for the assessment of his income or assessment of fringe benefits. The term ‘person’ includes the following:

1. an individual
2. a Hindu Undivided Family (HUE)
3. a company
4. a firm
5. an Association Of Persons or a Body Of Individual, whether incorporated or not
6. a local authority, and
7. every artificial juridical person example an idol or deity.

Share this Tamilnadu State Board Solutions for 11th Commerce Chapter 32 Direct Taxes Questions and Answers with your friends to help them to overcome the issues in exams. Keep visiting this site Tamilnadu State Board Solutions frequently to get the latest information on different subjects. Clarify your doubts by posting the comments and get the answers in an easy manner.

Students can find the most related topics which helps them to analyse the concepts if they practice according to the chapter-wise page. It is necessary for the students to practice more Questions and Answers for Tamilnadu State Board Solutions of 11th Commerce are given in the pdf format in chapter 31 Discharge and Breach of a Contract Questions and Answers so that students can prepare in both online and offline modes. So, Download Samacheer Kalvi 11th Commerce Book Solutions Questions and Answers, Notes Pdf, to score good marks.

Samacheer Kalvi 11th Commerce Solutions Chapter 31 Discharge and Breach of a Contract

Get the Questions and Answers, in Tamilnadu State Board 11th Commerce Solutions for Chapter 31 Discharge and Breach of a Contract. Learn the concepts of 11th Commerce Chapter-Wise by referring to the Tamilnadu State Board Solutions for Chapter 31 Discharge and Breach of a Contract Questions and Answers. Hence we suggest the students to Download Samacheer Kalvi 11th Commerce Book Solutions Questions and Answers pdf to enhance your knowledge.

Samacheer Kalvi 11th Commerce Discharge and Breach of a Contract Textbook Exercise Questions and Answers

I. Choose the Correct Answer

Question 1.
On the valid performance of the contractual obligation by the parties, the contract ……………….
(a) Is discharged
(b) Becomes enforceable
(c) Becomes void
(d) None of these
Answer:
(a) Is discharged

Question 2.
An agreement to do an act impossible in itself under Section 56 is ……………….
(a) Void
(b) Valid
(c) Voidable
(d) Unenforceable
Answer:
(a) Void

Question 3.
Any agreement which becomes impossible to perform under various circumstances.
(a) Voidable
(b) Void
(c) Valid
(d) None of these
Answer:
(b) Void

Question 4.
Discharge by mutual agreement may involve ……………….
(a) Novation
(b) Rescission
(c) Alteration
(d) All of the above
Answer:
(d) All of the above

Question 5.
The compensation given for breach of contract is ……………….
(a) Damage
(b) Remuneration
(c) Money
(d) Cheque
Answer:
(a) Damage

II. Very Short Answer Questions

Question 1.
What are the kinds of consent?
Answer:
The consent may be of the following types:

1. Express
2. Implied

Question 2.
What are the types of Impossibility of Performance?
Answer:
There are two types of impossibility of performance, such as –

1. Impossibility existing at the time of agreement.
2. Impossibility arising subsequent to the formation of contract.

Question 3.
What is Quantum merit?
Answer:
The meaning of the phrase quantum merit is ‘as much as earned’.

III. Short Answer Questions

Question 1.
What are the different modes of discharge by implied consent?
Answer:
Different modes of discharge by implied consent are:

1. Novation
2. Alteration
3. Recession
4. Remission
5. Accord and Satisfaction
6. Waiver
7. Merger

Question 2.
Define discharge by Performance.
Answer:
Performance implies carrying out the obligation of the contract. Performance must be completed according to the real intentions of the agreement. Performance must be done according to time and manner prescribed.

Question 3.
What are reasons for impossibility arising after the formation of contract?
Answer:
Impossibility arising subsequent to the formation of a contract or supervening impossibility may be:

1. By some event beyond the control of the parties; or
2. By some act either of the promisor or of the promisee.

Question 4.
What are the various rules regarding damages?
Answer:
Generally in the following cases, the court grants specific performance:

1. When the act agreed to be done is such that compensation in money for its non – performance is not sufficient.
2. When it is probable that compensation in money cannot be received for the non – performance of the act agreed to be done.
3. When there is no standard for ascertaining the actual damage caused by the non – performance of the act agreed to be done.

IV. Long Answer Questions

Question 1.
Explain the ways of discharge of Contract?
Answer:
Different modes of discharge of contract have been provided under different sections of the Act:
1. Discharge by Performance : Performance implies carrying out the obligation of the contract. Performance must be completed according to the real intentions of the agreement. Performance must be done according to time and manner prescribed. Performance of contract may be of two types namely:

• Actual performance
• Attempted performance

2. By Agreement on Consent : Agreement between the parties comes to an end by mutually agreeing for it. Any contract is created by an agreement, hence in the same way, it can be discharged by an agreement. The consent may be of the following types:

• Express consent
• Implied consent

3. By Impossibility of Performance : A contract may be discharged if its performance becomes impossible. There are two types of impossibility of performance, such as –

• Impossibility existing at the time of agreement.
• Impossibility arising subsequent to the formation of contract.

4. By Lapse of Time : According to the Limitation Act, 1963 a contract must be performed within a specified time. If it is not performed within this specified time limit and against which if no action is taken by the promisee in the Court of Law within specified time, then the promisee is deprived of his remedy at law. In such cases, the contract is discharged.

5. By Operation of Law : A contract can be discharged by the operation of law. The operation of law by which contract can be discharged are as follows:

• By Death
• By Merger
• By Insolvency
• Unauthorized Alteration of the Terms of a Contract
• Rights and liabilities vesting in the same person

Question 2.
Write about the various remedies for breach of contract.
Answer:
There are various types of remedies for the injured parties listed as follows:

1. Recission of Contract – In case of breach of contract by one party, then the other parties may rescind the contract and thereby the party is absolved from his all obligations under the contract.

2. Claim for Specific Performance – In some specific cases if the damages are not the adequate remedy, then the court can direct the party in breach for the specific performance of the contract. In such case, the promise is carried out as per terms and conditions of the contract.

3. Claim for Injunction – Injunction is an order passed by a competent Court restraining a person from doing some act. Injunction can be defined as a mode of securing the specific performance of the negative terms of a contract.

4. Claim for Quantum Merit – The claim for quantum merit may arise if a contract performed by one party has become discharged by breach of the other party. The meaning of the phrase quantum merit is as much as earned’.

5. Claim for Damages – The claim for quantum merit may arise if a contract performed by one party has become discharged by breach of the other party. The meaning of the phrase quantum merit is as much as earned.

Question 3.
Discuss the different types of damages awarded to the injured party.
Answer:
Damages are a monetary compensation awarded by the court to the injured party for the loss or injury suffered by him. As per contract, one party can claim damages if other party breach the contract. The main purpose of awarding the damages is to make good the loss suffered by him. It is known as doctrine of restitution. The Section 73 of the Indian Contract Act, 1872 deals with the compensation for loss or damages caused by a party for breach of contract. There are mainly four types of damages, such as

1. Ordinary damages
2. Special damages
3. Vindictive or exemplary damages; and
4. Nominal damages

Share this Tamilnadu State Board Solutions for 11th Commerce Chapter 31 Discharge and Breach of a Contract Questions and Answers with your friends to help them to overcome the issues in exams. Keep visiting this site Tamilnadu State Board Solutions frequently to get the latest information on different subjects. Clarify your doubts by posting the comments and get the answers in an easy manner.

Students can find the most related topics which helps them to analyse the concepts if they practice according to the chapter-wise page. It is necessary for the students to practice more Questions and Answers for Tamilnadu State Board Solutions of 11th Commerce are given in the pdf format in chapter 30 Performance of Contract Questions and Answers so that students can prepare in both online and offline modes. So, Download Samacheer Kalvi 11th Commerce Book Solutions Questions and Answers, Notes Pdf, to score good marks.

Samacheer Kalvi 11th Commerce Solutions Chapter 30 Performance of Contract

Get the Questions and Answers, in Tamilnadu State Board 11th Commerce Solutions for Chapter 30 Performance of Contract. Learn the concepts of 11th Commerce Chapter-Wise by referring to the Tamilnadu State Board Solutions for Chapter 30 Performance of Contract Questions and Answers. Hence we suggest the students to Download Samacheer Kalvi 11th Commerce Book Solutions Questions and Answers pdf to enhance your knowledge.

Samacheer Kalvi 11th Commerce Performance of Contract Textbook Exercise Questions and Answers

I. Choose the Correct Answer

Question 1.
On the valid performance of the contractual obligations by the parties, the contract ………………..
(a) Is discharged
(b) Become enforceable
(c) Becomes void
(d) Becomes legal
Answer:
(a) Is discharged

Question 2.
Which of the following persons can perform the contract?
(a) Promisor alone
(b) Legal representatives of promisor
(c) Agent of the promisor
(d) All the above
Answer:
(d) All the above

Question 3.
A, B, C jointly promised to pay Rs.50,000 to D. Before performance of the contract, C dies. Here, the contract ………………..
(a) Becomes void on C’s death
(b) Should be performed by A and B along with C’s legal representatives.
(c) Should be performed by A and B alone.
(d) Should be renewed between A, B and D.
Answer:
(b) Should be performed by A and B along with C’s legal representatives.

Question 4.
Which of these parties cannot demand performance of promise?
(a) Promisee
(b) Any of the Joint Promisees
(c) On the death of a Promisee, his Legal Representative.
(d) Stranger to the Contract
Answer:
(d) Stranger to the Contract

Question 5.
A person is said to be a third person if he is not a ………………..
(a) promisor
(b) promise
(c) agent
(d) Legal Representative
Answer:
(c) agent

II. Very Short Answer Questions

Question 1.
State the ways of Performing a Contract.
Answer:
There are mainly two ways of performing a contract such as:

1. Actual Performance
2. Attempted Performance

Question 2.
Who is a Legal Representative?
Answer:
Legal representative can demand Exception performance. Contrary intention appears from the contract. Contract is of a personal nature.

Question 3.
Who is an agent?
Answer:
According to Para 2 of Section 40, the promisor may employ a competent person such as agent to perform the promise, if the contract is not formed on personal condition.

Question 4.
Define Reciprocal Promise.
Answer:
Promises which form consideration or part of consideration for each other are called ‘reciprocal promise’.

Question 5.
By whom must contracts be performed?
Answer:

1. Promisor himself
2. Agent
3. Representations
4. Third person
5. Joint Promisors

III. Short Answer Questions

Question 1.
What is a Valid tender?
Answer:
A valid tender of performance is considered to be the performance of a promise.

Question 2.
Who can execute and Perform a Contract?
Answer:
Promisor himself – Under Para 1 to Section 40, it is laid down that where it appears from the nature of the contract, the intention of the parties that any promise contained in it must be performed by the promisor himself or by his legal representatives or by any other competent person employed by him.

Question 3.
Who can demand performance?
Answer:

1. Promisee – only a promisee can demand performance and not a stranger demand performance of the contract.
2. Legal Representative – legal representative can demand Exception performance. Contrary intention appears from the contract. Contract is of a personal nature.
3. Third party – Exception to “stranger to a contract”.

Question 4.
Write a note on the benefits of Reciprocal Promise.
Answer:
Promises which form consideration or part of consideration for each other are called ‘reciprocal promise’. For example X promises to sell his house to Y for Rs.5,00,000. The promises are reciprocal. X is the promisor to give the house and a promise to receive Rs.5,00,000. Y is the promise to receive the house and a promisor to pay Rs. 5,00,000.

Question 5.
Who is a Joint Promisors?
Answer:
Joint Promisors:
(a) Devolution of Joint Liabilities (Section 42)
Section 42 of Indian Contract Act lays down that “When two or more persons have made a joint promise, then unless a contrary intention appears in the contract, all such persons, during their joint lives and after the death of the last survivor, representatives of all, jointly must fulfil the promise”

(b) Devolution of Joint Rights (Section 45)
“When a person has made a promise to two or more persons jointly, then unless there is a contract to the contrary, the right to claim performance rests as between him and them, with them during their joint lives and after the death of them with representatives of such deceased person jointly with survivors, and after the death of last survivor, with the representatives of all jointly”.

IV. Long Answer Questions

Question 1.
Explain rules relating to place of performance of promise.
Answer:
Time and place of Performance of Promise:
It is only the promisee for whom the contract is performed. Only the promisee can demand the performance of the promise under a contract.

For Example:
X promises Y to pay Z ₹ 10,000/-. X does not pay the sum to Z. Here Z cannot bind X for the payment. It is only promisee Y who can enforce the promise against the promisor X. Of course, there are certain special cases, where a third party can enforce a promise though he is not a party to the contract For example in respect of trust, marriage settlement etc. In case of death of promisee, the representative appointed by him can ask for the performance of the promise under a contract.

Question 2.
Elucidate the provision regarding time as factor in performance.
Answer:
1. Under Section 46, performance within a reasonable time:
According to Section 46, a promisor is to perform his promise within a reasonable time. On the other hand, reasonable time will depend upon the circumstance of the case, the usage of trade or on the intention of the parties entering into the contract.
Example : A has given an order of supply of books in July which should be performed within 4 to 5 days of the month of July.

2. Under Section 47, specified time and place for performance:
If the promise is to be performed on a certain day, the promisor may undertake to perform it without application of the promisee. According to the Section 47, In such a case the promisor may perform the promise at any time during the usual hours of business on such day and at the place at which the promise ought to be performed.

Question 3.
How do you think appropriation of payments takes place?
Answer:
Appropriation means application of payments – The question of appropriation of payments arises when a debtor owes several debts to the same creditor and makes a payment that is not sufficient to discharge the whole indebtedness.

Appropriation of Payments : Sometimes, a debtor owes several distinct debts to the same creditor and he makes a payment which is insufficient to satisfy all the debts. In such a case, a question arises as to which particular debt the payment is to be appropriated. Section 59 to 61 of the Act lay down following rules as to appropriation of payments which provide an answer to this question.

Share this Tamilnadu State Board Solutions for 11th Commerce Chapter 30 Performance of Contract Questions and Answers with your friends to help them to overcome the issues in exams. Keep visiting this site Tamilnadu State Board Solutions frequently to get the latest information on different subjects. Clarify your doubts by posting the comments and get the answers in an easy manner.

Students can find the most related topics which helps them to analyse the concepts if they practice according to the chapter-wise page. It is necessary for the students to practice more Questions and Answers for Tamilnadu State Board Solutions of 11th Commerce are given in the pdf format in chapter 28 Balance of Trade and Balance of Payments Questions and Answers so that students can prepare in both online and offline modes. So, Download Samacheer Kalvi 11th Commerce Book Solutions Questions and Answers, Notes Pdf, to score good marks.

Samacheer Kalvi 11th Commerce Solutions Chapter 28 Balance of Trade and Balance of Payments

Get the Questions and Answers, in Tamilnadu State Board 11th Commerce Solutions for Chapter 28 Balance of Trade and Balance of Payments. Learn the concepts of 11th Commerce Chapter-Wise by referring to the Tamilnadu State Board Solutions for Chapter 28 Balance of Trade and Balance of Payments Questions and Answers. Hence we suggest the students to Download Samacheer Kalvi 11th Commerce Book Solutions Questions and Answers pdf to enhance your knowledge.

Samacheer Kalvi 11th Commerce Balance of Trade and Balance of Payments Textbook Exercise Questions and Answers

I. Choose the Correct Answer

Question 1.
The Statement which discloses a record of transactions between the residents of one country and residents of foreign country …………….
(a) Balance of Payment
(b) Balance of Trade
(c) Statement of Receipts and Payments
(d) Accounting Statement
Answer:
(a) Balance of Payment

Question 2.
The Balance of Payments councils consists of …………….
(a) Current Account
(b) Capital Account
(c) Receipts and Payments Account
(d) Both Current Account and Capital Account
Answer:
(d) Both Current Account and Capital Account

Question 3.
Foreign capital long – term loan and foreign currency reserve are recorded under …………….
(a) Official Capital
(b) Private Capital
(c) Banking Capital
(d) Both Private and Official Capital
Answer:
(b) Private Capital

Question 4.
The term official capital includes …………….
(a) RBI holdings of foreign currencies
(b) Special Drawing Rights held by the Government
(c) Both A and B
(d) Foreign Investment
Answer:
(c) Both A and B

Question 5.
Balance of payments surplus indicates …………….
(a) Exports are more than the Imports
(b) Imports are more than Exports
(c) Exports and Imports are at Equilibrium
(d) Exports and Imports are above Equilibrium
Answer:
(a) Exports are more than the Imports

II. Very Short Answer Questions

Question 1.
What do you mean by Balance of payments?
Answer:
Balance of payment refers to a systematic record of all economic transactions between the residents of one country and the residents of foreign countries during a particular period of time.

Question 2.
What do you mean by Balance of trade?
Answer:
Balance of trade denotes the difference between the value of import and the value of export during a year.

Question 3.
Define Balance of payments.
Answer:
According to International Monetary Fund, “The balance of payments for given period is a systematic records of all economic transactions taken place during the period between residents of the reporting countries.”

Question 4.
What is the composition of private capital?
Answer:
Private capital consists of foreign investments, long term loan and foreign currency deposits.

Question 5.
Mention the components of banking capital.
Answer:
Banking capital includes movement into external financial asset and liabilities commercial and co – operative banks authorized to dealing in foreign exchange.

Question 6.
Mention the components of official capital.
Answer:
It includes RBI’s holdings of foreign currency and special drawing rights (SDR) held by the Government.

III. Short Answer Questions

Question 1.
Why is Balance of payment prepared?
Answer:
Balance of payment help in framing monetary, fiscal and trade policies of country. Government keenly observes balance of payment position of its important trade partners in making policy decisions. It reveals whether a country produces enough economic output to pay for its growth.

Question 2.
What does Balance of payment disclose?
Answer:
A Balance of Payment surplus indicates that country’s exports are more than its imports and its government and residents are savers. A Balance of Payment deficit points to the fact that country’s import is more than the export. This situations forces the country to borrow from other countries to pay for its imports.

Question 3.
What are the credit items shown in currents accounts?
Answer:
A. Goods Export(visible)
B. Invisible Exports

1. Transport service sold abroad
2. Banking service sold abroad
3. Insurance service sold abroad
4. Income received on loan and investment made in foreign countries
5. Expenses incurred by foreign tourists in India

Question 4.
State the components of capital account.
Answer:
Capital account consists of three components

1. Private Capital
2. Banking Capital
3. Official Capital

IV. Long Answer Questions

Question 1.
Write down the structure of capital account.
Answer:
Capital account consists of three components

1. Private Capital
2. Banking Capital
3. Official Capital

1. Private Capital : Private capital consists of foreign investments, long term loan and foreign currency deposits.
2. Banking Capital : Banking capital includes movement into external financial asset and liabilities commercial and co – operative banks authorized to dealing in foreign exchange.
3. Official Capital : It includes RBI’s holdings of foreign currency and special drawing rights (SDR) held by the Government.

Question 2.
Distinguish balance of payment and balance of trade.
Answer:

Question 3.
Highlight the features of balance of trade.
Answer:

1. Balance of trade is statement showing the net effect of export and import of a country.
2. It records only transactions,relating to merchandise, i.e. goods transactions.
3. It does not record capital transactions.
4. It is part of current account of BOP.
5. It may be at favorable or unfavourable or in equilibrium state.
6. It is not true indicator of economic prosperity or economic relations of country. Unfavourable balance of trade can be converted into favorable balance of payment.

For Future Learning

Question a.
Impact of Balance of Payments and Trade.
Answer:
Global village is also a term to express the constituting relationship between economics and other social sciences throughout the world making it a part of our popular culture before it actually happened.

Question b.
Necessary for Global Village concept.
Answer:
The current account, capital account and financial account together make up the overall balance of payments, which accounts for all of the international inflows and outflows for a given Nation. The current account, as mentioned, capture the balance of trade meaning the purchases and sale of goods and services.

For Own Thinking

Question a.
Balance of Payment is key to economic development.
Answer:
Yes, it is correct.

Question b.
Importance of BOP and BOT.
Answer:
BOP:

1. It presents the international financial positions of the country.
2. It helps the government in taking decisions on monetary and fiscal policies on the one hand and on external trade and payments issued on the other.

BOT:

1. It is the difference between a country’s import and export over a period of time.
2. It is the largest component of the balance of payments for all nations.

Share this Tamilnadu State Board Solutions for 11th Commerce Chapter 28 Balance of Trade and Balance of Payments Questions and Answers with your friends to help them to overcome the issues in exams. Keep visiting this site Tamilnadu State Board Solutions frequently to get the latest information on different subjects. Clarify your doubts by posting the comments and get the answers in an easy manner.

Students can find the most related topics which helps them to analyse the concepts if they practice according to the chapter-wise page. It is necessary for the students to practice more Questions and Answers for Tamilnadu State Board Solutions of 11th Commerce are given in the pdf format in chapter 29 Elements of Contract Questions and Answers so that students can prepare in both online and offline modes. So, Download Samacheer Kalvi 11th Commerce Book Solutions Questions and Answers, Notes Pdf, to score good marks.

Samacheer Kalvi 11th Commerce Solutions Chapter 29 Elements of Contract

Get the Questions and Answers, in Tamilnadu State Board 11th Commerce Solutions for Chapter 29 Elements of Contract. Learn the concepts of 11th Commerce Chapter-Wise by referring to the Tamilnadu State Board Solutions for Chapter 29 Elements of Contract Questions and Answers. Hence we suggest the students to Download Samacheer Kalvi 11th Commerce Book Solutions Questions and Answers pdf to enhance your knowledge.

Samacheer Kalvi 11th Commerce Elements of Contract Textbook Exercise Questions and Answers

I. Choose the Correct Answer

Question 1.
An agreement enforceable by law is a ………………
(a) Enforceable acceptance
(b) Accepted offer
(c) Approved promise
(d) Contract
Answer:
(d) Contract

Question 2.
Every promise and every set of promises, forming the consideration for each other, is an ………………
(a) Agreement
(b) Contract
(c) Offer
(d) Acceptance
Answer:
(a) Agreement

Question 3.
Void agreement signifies ………………
(a) Agreement illegal in nature
(b) Agreement not enforceable by law
(c) Agreement violating legal procedure
(d) Agreement against public policy
Answer:
(b) Agreement not enforceable by law

Question 4.
Acceptance to be valid must ………………
(a) Be absolute
(b) Be unqualified
(c) Both be absolute & unqualified
(d) Be conditional
Answer:
(c) Both be absolute & unqualified

Question 5.
A contract with or by a minor is a ………………
(a) Valid contract
(b) Void contract
(c) Voidable contract
(d) Voidable at the option of either party
Answer:
(b) Void contract

II. Very Short Answer Questions

Question 1.
What is law?
Answer:
Law means a ‘set of rules’ which governs our behaviour and relating in a civilized society.

Question 2.
Why should one know law?
Answer:
One to should know the law to which he is subjected to because ignorance of law is no excuse.

Question 3.
Can a minor enter into a Contract?
Answer:
No, a minor cannot enter into contract.

Question 4.
Who can enter into a Contract?
Answer:
The Indian contract Act specifies that every person is competent to contract provided he is of the age of majority according to the Law which he is subject to and who is of sound mind.

Question 5.
Define Contract.
Answer:
Contract 2(h) An agreement enforceable by Law is a Contract.

III. Short Answer Questions

Question 1.
Define Offer.
Answer:
Offer (i.e. Proposal) [section 2(a)]: When one person signifies to another his willingness to do or to abstain from doing anything, with a view to obtaining the assent of that other person either to such act or abstinence, he is said to make a proposal.

Question 2.
What do you mean by Agreement?
Answer:
An “agreement” means ‘a promise or a set of promises’ forming consideration for each other. A promise arises when a proposal is accepted. By implication, an agreement is an accepted proposal. In other words, an agreement consists of an ‘offer’ and its ‘acceptance’.
Agreement = offer / Proposal + Acceptance

Question 3.
Define a Voidable Contract.
Answer:
An agreement which is enforceable by law at’the option of one or more parties but not at the option of the other- or others is a voidable contract. This is the result of coercion, undue influence, fraud and misrepresentation.

Question 4.
What do you mean by Revocation?
Answer:
The Revocation mean the withdrawal of an offer power of attorney.

Question 5.
Who is a promisor, promisee?
Answer:

1. A promisor – Contract law – a person who makes a promise.
2. A promisee – Contract law – a person to whom a promise is made.

IV. Long Answer Questions

Question 1.
Explain the essentials of a Valid Contract
Answer:
1. Offer and Acceptance : There must be two parties to an agreement namely one party making the offer and the other party accepting it.

2. Legal Relationship : The parties must have the intention to create legal relationship between them. An agreement of Social or domestic nature is not at all a contract.

3. Lawful Consideration (quid pro quo) : As per Contract Act under Sec.2(d) Consideration means something in return. A contract without consideration becomes invalid.

4. Lawful Object (Section 23) : The object of agreement should be lawful and legal. It must not be immoral, illegal or opposed to public policy.

5. Free Consent (Section 13 & 14) : Consent of the parties must be free and genuine. Consent means agreeing upon same thing in the same sense at the same time i.e. there should be consensus – ad – idem. Consent is said to be free when it is not caused by coercion, undue influence, fraud, misrepresentation or mistake.

6. Capacity of Parties (Section 11) : The parties to a contract must have capacity (legalability) to make valid contract.

7. Certainty of Terms (Section 29) : The agreement should be clear to the parities of the agreement. The agreement must be precise.

8. Possibility of Performance (Section 56) : The terms of the agreement should be capable of performance. An agreement to do an act, impossible in itself cannot be enforced.

9. Not declared Void : The agreement should be such that it should be capable of being enforced by law. Certain agreements have been expressly declared illegal or void by the law.

10. Necessary Legal Formalities : A contract may be oral or in writing. Where a particular type of contract is required by law to be in writing and registered, it must comply with necessary formalities as to writing, registration and attestation.

Question 2.
Difference between Contract and Agreement.
Answer:

Question 3.
Explain the classification of Contract on the basis of the Validity.
Answer:
1. Valid Contract : An agreement which fulfils all the essentials prescribed by law on the basis of its creation. For example S offers to sell his car for Rs.2,00,000 to T. T agrees to buy it. It is a Valid Contract.

2. Void Contract 2(j) : A contract which ceases to be enforceable by law. A contract which does not satisfy any of the essential elements of a valid contract is said to be Void.

3. Voidable Contract 2(i) : An agreement which is enforceable by law at the option of one or more parties but not at the option of the other or others is a voidable contract.

4. Illegal Contract : It is a contract which is forbidden by law. All illegal agreements are Void but all void agreements or contracts are not necessarily illegal. Contract that is immoral or opposed to public policy are illegal in nature.

5. Unenforceable Contract : Where a contract is unenforceable because of some technical defect i.e. absence in writing barred by imitation etc. If the parties perform the contract it will be valid, but the court will not compel them if they do not.

Question 4.
Explain the classification of Contract on the basis of the Formation.
Answer:
1. Express Contract : A contract made by word spoken or written. According to Section. 9, in so for as the proposal or acceptance of any promise is made in words, the promise is said to be express. For example P says to Q ‘will you buy my bicycle for Rs. 1,000?” Q says to P “Yes”.

2. Implied Contract : The implied contract is one, which is not expressly written but understood by the conduct of parties. Where the proposal or acceptance of any promise is made otherwise than in words, the promise is said to be implied. For example A gets into a public bus, there is an implied contract that he will pay the bus fare.

3. Quasi Contract : It is a contract created by law. Actually, there is no contract. It is based on the principle that “a person shall not be allowed to enrich himself unjustly at the expense of the other”. In other words it is an obligation of one party to another imposed by law independent of an agreement between the parties.

4. Tacit Contract : A contract is said to be tacit when it has to be inferred from the conduct of the parties. For example obtaining cash through automatic teller machine, sale by fall of.hammer of an auction sale.

Question 5.
Explain the classification of Contract on the basis of the Performance.
Answer:
1. Executed Contract : A contract in which both the parties have fulfilled their obligations under the contract. For example X contracts to buy a car from Y by paying cash, Y instantly delivers his car.

2. Executory Contract : A contract in which both the parties are yet to fulfil their obligations, it is said to be an executory contract. For example A agrees to buy B’s cycle by promising to pay cash on 15th June. B agrees to deliver the cycle on 20th June.

3. Unilateral Contract : A unilateral contract is a one sided contract in which only one party has performed his promise or obligation, the other party has to perform his promise or obligation.

For example X promises to pay Y a sum of Rs. 10,000 for the goods to be delivered by Y. X paid the money and Y is yet to deliver the goods.

4. Bilateral Contract : A contract in which both the parties commit to perform their respective promises is called a bilateral contract. For example R offers to sell his fiat car to S for Rs. 10,00,000 on acceptance of R’s offer by S, there is a promise by R to Sell the car and there is a promise by S to purchase the car, there are two promises.

For Future Learning

Question 1.
After studying this chapter any one can enter into Valid Contract and can also identify the essentials present in the contract.
Answer:
Anyone can enter into the valid contract but he must attain the age of majority. He should be sound mind.

Question 2.
After understanding this chapter entering into Offer and giving Acceptance becomes easier.
Answer:
Offer – Proposal
Acceptance – Proposal is accepted

Question 3.
After going through this chapter the value of consideration and the requirement for return payment can be understood better.
Answer:
Consideration means something in return.

Question 4.
After reviewing this chapter the parties who are allowed to enter and the parties who are not allowed to enter into a contract can be clearly demarcated.
Answer:
Major can enter into contract with sound mind. Minor cannot enter into contract with unsound mind.

Question 5.
After analysing this chapter an obligation imposed by law – Quasi Contracts are better understood and distinguished from other contracts.
Answer:
It is an obligation of one party to another imposed by law independent of an agreement between the parties.

Share this Tamilnadu State Board Solutions for 11th Commerce Chapter 29 Elements of Contract Questions and Answers with your friends to help them to overcome the issues in exams. Keep visiting this site Tamilnadu State Board Solutions frequently to get the latest information on different subjects. Clarify your doubts by posting the comments and get the answers in an easy manner.