Enhance your subject knowledge with Tamilnadu State Board for Chapter 2 Quantum Mechanical Model of Atom and learn all the underlying concepts easily. Make sure to Download Samacheer Kalvi 11th Chemistry Book Solutions, Notes Pdf Chapter 2 Quantum Mechanical Model of Atom Questions and Answers PDF on a day to day basis and score well in your exams. Are given after enormous research by people having high subject knowledge. You can rely on them and prepare any topic of Chemistry as per your convenience easily.
Tamilnadu Samacheer Kalvi 11th Chemistry Solutions Chapter 2 Quantum Mechanical Model of Atom
Students looking for Chapter 2 Quantum Mechanical Model of Atom Concepts can find them all in one place from our Tamilnadu State Board Solutions. Simply click on the links available to prepare the corresponding topics of Chemistry easily. Samacheer Kalvi 11th Chemistry Chapter wise Questions and Answers are given to you after sample research and as per the latest edition textbooks. Clarify all your queries and solve different questions to be familiar with the kind of questions appearing in the exam. Thus, you can increase your speed and accuracy in the final exam.
Samacheer Kalvi 11th Chemistry Chapter 2 Quantum Mechanical Model of Atom Textual Evaluation Solved
I. Choose the correct answer
Quantum Mechanical Model Of Atom Class 11 Book Back Answers Question 1.
Electronic configuration of species M2+ is 1s2 2s2 2p63s2 3p6 3d6 and its atomic weight is 56. The number of neutrons in the nucleus of species M is ………..
(a) 26
(b) 22
(c) 30
(d) 24
Answer:
(c) 30
Solution:
M2+ : 1s2 2s2 2p63s2 3p6 3d6
M : 1s2 2s2 2p63s2 3p6 3d8
Atomic number = 26
Mass number = 56
No. of neutrons = 56 – 26 = 30.
11th Chemistry Quantum Mechanical Model Of Atom Question 2.
The energy of light of wavelength 45 nm is
(a) 6.67 x 1015 J
(b) 6.67 x 1011 J
(c) 4.42 .x 1018 J
(d) 4.42 x 10-15 J
Answer:
(c) 4.42 .x 1018 J
Solution:
E = hv = hc / λ
\(\frac{6.626 \times 10^{-34} \mathrm{J} \mathrm{s} \times 3 \times 10^{8} \mathrm{ms}^{-1}}{45 \times 10^{-9} \mathrm{m}}\) = 4.42 .x 1018 J.
11th Chemistry Chapter 2 Book Back Answers Question 3.
The energies E1 and E2 of two radiations are 25 eV and 50 eV respectively. The relation between their wavelengths i.e. λ1 and λ2 will be …………
(a) \(\frac{\lambda_{1}}{\lambda_{2}}=1\)
(b) λ1 = 2 λ2
(c) λ1 = \(\sqrt{25 \times 50} \lambda_{2}\)
(d) 2 λ1 = λ2
Answer:
(b) λ1 = 2 λ2
Solution:
\(\frac{E l}{E 2}\) = \(\frac{25eV}{50eV}\) = \(\frac{1}{2}\)
\(\frac{\mathrm{hc}}{\lambda_{1}} \times \frac{\lambda_{2}}{\mathrm{hc}}\) = \(\frac{1}{2}\)
2λ2 = λ1.
Samacheer Kalvi Guru 11th Chemistry Question 4.
Splitting of spectral lines in an electric field is called …………….
(a) Zeeman effect
(b) Shielding effect
(c) Compton effect
(d) Stark effect
Answer:
(d) Stark effect
Solution:
Splitting of spectral lines in magnetic field is called Zeeman effect and splitting of spectral lines in electric field, is called Stark effect.
Samacheerkalvi.Guru 11th Chemistry Question 5.
Based on equation E = -2.178 x 1018 J \(\left(\frac{z^{2}}{n^{2}}\right)\) certain conclusions are written. Which of them is not correct ? (NEET)
(a) Equation can be used to calculate the change in energy when the electron changes orbit
(b) For n = 1, the electron has a more negative energy than it does for n = 6 which means that the electron is more loosely bound in the smallest allowed orbit
(c) The negative sign in equation simply means that the energy of electron bound to the nucleus is lower than it would be if the electrons were at the infinite distance from the nucleus.
(d) Larger the value of n, the larger is the orbit radius.
Answer:
(b) For n = 1, the electron has a more negative energy than it does for n = 6 which means that the electron is more loosely bound in the smallest allowed orbit
Solution:
Correct statement:
For n = 6, the electron has more negative energy than it does for n = 6 which means that the electron is strongly bound in the smallest allowed orbit.
11th Chemistry Samacheer Kalvi Question 6.
According to the Bohr Theory, which of the following transitions in the hydrogen atom will give rise to the least energetic photon?
(a) n = 6 to n = 1
(b) n = 5 to n = 4
(c) n = 5 to n = 3
(d) n = 6 to n = 5
Answer:
(d) n = 6 to n = 5
Solution:
n = 6 to n = 5
E6 = -13.6 / 62 ; E5 = – 13.6 / 52
E6 – E5 = (-13.6 / 62) – (-13.6 / 52)
= 0.166 eV atom-1
E5 – E4 = (-13.6 / 52) – (-13.6 / 42)
= 0.306 eV atom-1
Samacheer Kalvi.Guru 11th Chemistry Question 7.
Assertion : The spectrum of He+ is expected to be similar to that of hydrogen
Reason : He+ is also one electron system,
(a) If both assertion and reason are true and reason is the correct explanation of assertion.
(b) If both assertion and reason are true but reason is not the correct explanation of assertion.
(c) If assertion is true but reason is false
(d) If both assertion and reason are false
Answer:
(a) If both assertion and reason are true and reason is the correct explanation of assertion.
Samacheer Kalvi Guru 11 Chemistry Question 8.
Which of the following pairs of d-orbitals will have electron density along the axes ? (NEET Phase – II)
(a) dz2, dxz
(b) dxz, dyz
(c) dz2, \(d_{x^{2}-y^{2}}\)
(d) dxy, \(d_{x^{2}-y^{2}}\)
Answer:
(c) dz2, \(d_{x^{2}-y^{2}}\)
Samacheer Kalvi 11th Chemistry Question 9.
Two electrons occupying the same orbital are distinguished by …………
(a) azimuthal quantum number
(b) spin quantum number
(c) magnetic quantum number
(d) orbital quantum number
Answer:
(b) spin quantum number
Solution:
Spin quantum number For the first electron ms = +\(\frac {1}{2}\)
For the second electron ms = –\(\frac {1}{2}\).
Quantum Mechanical Model Of Atom Question 10.
The electronic configuration of Eu (atomic no. 63) Gd (atomic no. 64) and Tb (atomic no. 65) are (NEET – Phase II)
(a) [Xe] 4f7 5d1 6s2, [Xe] 4f7 5d1 6s2 and [Xe] 4f8 5d1 6s2
(b) [Xe] 4f7, 6s2, [Xe] 4f7 5d1 6s2 and [Xe] 4f9 6s2
(c) [Xe] 4f7 , 6s2, [Xe] 4f8 6s2 and [Xe] 4f8 5d1 6s2
(d) [Xe] 4f8 5d1 6s2[Xe] 4f7 5d1 6s2 and [Xe] 4f9 6s2
Answer:
(b) [Xe] 4f7, 6s2, [Xe] 4f7 5d1 6s2 and [Xe] 4f9 6s2
Solution:
Eu : [Xe] 4f7, 5d0, 6s2
Gd : [Xe] 4f7, 5d1, 6s2
Tb : [Xe] 4f9, 5d0,6s2
Chemistry Class 11 Samacheer Kalvi Question 11.
The maximum number of electrons in a sub shell is given by the expression …………..
(a) 2n2
(b) 21 + 1
(c) 41 + 2
(d) none of these
Answer:
(c) 41 + 2
Solution:
2 (21 + 1) = 41 + 2.
11th Chemistry 2nd Lesson Question 12.
For d-electron, the orbital angular momentum is ………….
(a) \(\frac{\sqrt{2} h}{2 \pi}\)
(b) \(\frac{\sqrt{2 \mathrm{h}}}{2 \pi}\)
(c) \(\sqrt{2 \times 4}\)
(d) \(\frac{\sqrt{6} h}{2 \pi}\)
Answer:
(d) \(\frac{\sqrt{6} h}{2 \pi}\)
Solution:
Orbital angular momentum
= \(\sqrt{(1(1+1)}) \mathrm{h} / 2 \pi\)
For d orbital = \(\sqrt{(2 × 3)} \mathrm{h} / 2 \pi\) = \(\sqrt{6} \mathrm{h} / 2 \pi\).
Quantum Mechanical Model Of Atom Class 11 Question 13.
What is the maximum numbers of electrons that can be associated with the following set of quantum numbers ? n = 3,l = 1 and m = -1
(a) 4
(b) 6
(c) 2
(d) 10
Answer:
(c) 2
Solution:
n = 3; l = 1; m = -1 either 3px or 3py
Samacheer Kalvi Guru Chemistry Question 14.
Assertion: Number of radial and angular nodes for 3p orbital are l, l respectively. Reason: Number of radial and angular nodes depends only on principal quantum number.
(a) both assertion and reason are true and reason is the correct explanation of assertion.
(b) both assertion and reason are true but reason is not the correct explanation of assertion.
(c) assertion is true but reason is false
(d) both assertion and reason are false
Answer:
(c) assertion is true but reason is false
Solution:
No. of radial node = n- l – 1
No. of angular node = l for 3p orbital
No. of angular node = l =1
No. of radial node = n- l – 1 = 3 – 1 – 1 = 1.
Question 15.
The total number of orbitals associated with the principal quantum number n = 3 is ………..
(a) 9
(b) 8
(c) 5
(d) 7
Answer:
(a) 9
Solution:
n = 3; l = 0; m1 = 0 – one s orbital n = 3; l = 1; m1 = -1, 0, 1 – three p orbitals n = 3; l = 2; m1 = -2, -1, 0, 1, 2 – five d orbitals, overall nine orbitals are possible.
Question 16.
If n = 6, the correct sequence for filling of electrons will be, …………
(a) ns → (n – 2) f → (n – 1)d → np
(b) ns → (n – 1) d → (n – 2) f → np
(c) ns → (n – 2) f → np → (n – 1) d
(d) none of these are correct
Answer:
(a) ns → (n – 2)f → (n – l)d → np
Solution:
n = 6 According Aufbau principle,
6s → 4f → 5d → 6p
ns → (n – 1)f → (n – 2)d → np.
Question 17.
Consider the following sets of quantum numbers:

Which of the following sets of quantum number is not possible ?
(a) (i), (ii), (iii) and (iv)
(b) (ii), (iv) and (v)
(c) (z) and (iii)
(d) (ii), (iii) and (iv)
Answer:
(b) (ii), (iv) and (v)
Solution:
(ii) l can have the values from 0 to n – 1 n = 2; possible l values are 0, 1 hence l = 2 is not possible.
(iv) for l = 0; m = -1 not possible
(v) for n = 3 l = 4 and m = 3 not possible.
Question 18.
How many electrons in an atom with atomic number 105 can have (n + 1) = 8 ?
(a) 30
(6) 17
(c) 15
(d) unpredictable
Answer:
(b) 17
Solution:
n + 1 = 8
Electronic configuration of atom with atomic number 105 is [Rn] 5f14 6d3 7s2
| Orbital | (n+1) | No. of electrons |
| 5f | 5 + 3 = 8 | 14 |
| 6d | 6 + 2 = 8 | 3 |
| 7s | 7 + 0 = 0 | 2 |
| No. of electrons = 14 + 3 = 17 | ||
Question 19.
Electron density in the yz plane of 3 dx2-y2 orbital is …………….
(a) zero
(b) 0.50
(c) 0.75
(d) 0.90
Answer:
(a) zero
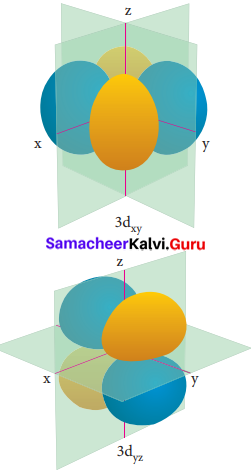
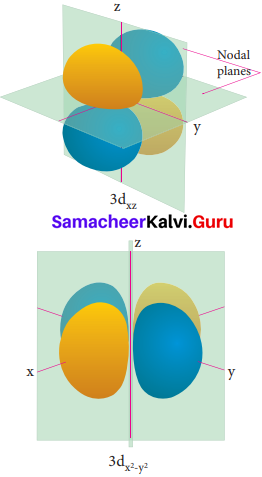
Question 20.
If uncertainty in position and momentum are equal, then minimum uncertainty in velocity is ……….
(a) \(\frac{1}{m} \sqrt{\frac{h}{\pi}}\)
(b) \(\sqrt{\frac{\mathrm{h}}{\pi}}\)
(c) \(\frac{1}{2 m} \sqrt{\frac{h}{\pi}}\)
(d) \(\frac{\mathrm{h}}{4 \pi}\)
Answer:
(c) \(\frac{1}{2 m} \sqrt{\frac{h}{\pi}}\)
Solution:

Question 21.
A macroscopic particle of mass 100 g and moving at a velocity of 100 cm s-1d will have a de Broglie wavelength of ………….
(a) 6.6 x 10-29 cm
(b) 6.6 x 10-30 cm
(c) 6.6 x 10-31 cm
(d) 6.6 x 10-32 cm
Answer:
(c) 6.6 x 10-31 cm
Solution:
m = 100 g = 100 x 10-3 kg
v = 100 cm s-1 = 100 x 10-2 m s-1
λ = \(\frac{h}{mv}\) =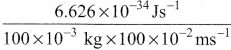
= 6.626 x 10-31 ms-1
= 6.626 x 10-31 cm s-1
Question 22.
The ratio of de Broglie wavelengths of a deuterium atom to that of an a – particle, when the velocity of the former is five times greater than that of later, is ……………
(a) 4
(b) 0.2
(c) 2.5
(d) 0.4
Answer:
(d) 0.4
Question 23.
The energy of an electron in the 3rd orbit of hydrogen atom is -E. The energy of an electron in the first orbit will be ……………..
(a) – 3E
(b) – E /3
(c) – E / 9
(d) – 9E
Answer:
(c) – E / 9
Solution:
En = \(\frac{-13.6}{n^{2}}\) eV atom-1
E1 = \(\frac{-13.6}{1^{2}}\)13.6 = \(\frac{-13.6}{9}\)
Given that,
E3 = – E
\(\frac{-13.6}{9}\) = -E
13.6 = – 9E = E1 = – 9E
E1 = – 9E
Question 24.
Time independent Schnodinger wave equation is ………….

Answer:
(a) \(\widehat{\mathrm{H}} \psi=\mathrm{E} \psi\).
Question 25.
Which of the following does not represent the mathematical expression for the Heisenberg uncertainty principle?
(a) ∆E.∆p ≥ h/4π
(b) ∆E.∆v ≥ h/4πm
(c) ∆E.∆t ≥ h/4π
(d) ∆E.∆x ≥ h/4π
Answer:
(d) ∆E.∆x ≥ h/4π.
II. Write brief answer to the following questions
Question 26.
Which quantum number reveal information about the shape, energy, orientation and size of orbitals?
Answer:
Magnetic quantum number reveal information about the shape, energy, orientation and size of orbitals.
Question 27.
How many orbitals are possible for n =4?
Answer:
If n = 4, the possible number of orbitals are calculated as follows –
n = 4, main shell = N
If n = 4, l values are 0, 1, 2, 3
If l = 0, 4s orbital = 1 orbital
If l = 1, m = -1,0, +1 = 3 orbitals
If l = 2, m = -2,-1,0, +1,+2 = 5 orbitals
If l = 3, m = -3,-2,-1,0, +1,+2,+3 = 7 orbitals
∴ Total number of orbitals = 16 orbitals
Question 28.
How many radial nodes for 2s, 4p, 5d and 4f orbitals exhibit? How many angular nodes?
Answer:
Formula for total number of nodes = n – 1
1. For 2s orbital: Number of radial nodes =1.
2. For 4p orbital: Number of radial nodes = n – l – 1. = 4 – 1 – 1 = 2
Number of angular nodes = l
∴ Number of angular nodes = 1
So, 4p orbital has 2 radial nodes and 1 angular node.
3. For 5d orbital:
Total number of nodes = n – 1 = 5 – 1 = 4 nodes
Number of radial nodes = n – l – 1 = 5 – 2 – 1 = 2 radial nodes.
Number of angular nodes = l = 2
∴ 5d orbital have 2 radial nodes and 2 angular nodes.
4. For 4f orbital:
Total number of nodes = n – 1 = 4 – 1 = 3 nodes
Number of radial nodes = n – 7 – 1 = 4 – 3 – 1 = 0 node.
Number of angular nodes = l = 3 nodes
∴ 4f orbital have 0 radial node and 3 angular nodes.
Question 29.
The stabilization of a half filled d-orbital is more pronounced than that of the p-orbital why?
Answer:
The exactly half filled orbitals have greater stability. The reason for their stability are –
- symmetry
- exchange energy.
(1) Symmetry:
The half filled orbitals are more symmetrical than partially filled orbitals and this symmetry leads to greater stability.
(2) Exchange energy:
The electrons with same spin in the different orbitals of the same sub shell can exchange their position. Each such exchange release energy and this is known as exchange energy. Greater the number of exchanges, greater the exchange energy and hence greater the stability. In d-orbital, 10 exchanges are possible but in p-orbital 6 exchanges are possible. So, d – orbital with 5 unpaired electrons (10 exchanges)n i.e. half filled is more stable than p – orbital with 3 unpaired electrons (6 exchanges).
Question 30.
Consider the following electronic arrangements for the d5 configuration.
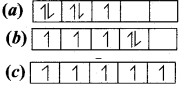
(1) Which of these represents the ground state
(2) Which configuration has the maximum exchange energy.
Answer:
(1) ![]() – This represents the ground state.
– This represents the ground state.
(2) ![]() – This represents the maximum exchange energy.
– This represents the maximum exchange energy.
Question 31.
State and explain Pauli’s exclusion principle.
Answer:
Pauli’s exclusion principle states that “No two electrons in an atom can have the same set of values of all four quantum numbers”.
Illustration: H(Z = 1) 1s1.
One electron is present in hydrogen atom, the four quantum numbers are n = 1, l = 0, m = 0 and s = + \(\frac {1}{2}\). For helium Z = 2. He: 1s2. In this one electron has the quantum number same as that of hydrogen, n = 1,l = 0, m = 0 and s = +½ For other electron, fourth quantum number is different, i.e. n = 1, l = 0, m = 0 and s = – ½.
Question 32.
Define orbital? What are the n and l values for 3px and 4 dx2-y2 electron?
Answer:
(i) Orbital is a three dimensional space which the probability of finding the electron is maximum.

Question 33.
Explain briefly the time independent Schrodinger wave equation?
Answer:
The time independent Schrodinger equation can be expressed as
\(\widehat{\mathrm{H}}\) Ψ = EΨ ……………(1)
Where \(\widehat{\mathrm{H}}\) is called Hamiltonian operator.
Ψ is the wave function.
E is the energy of the system.
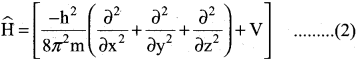
Since Ψ is a function of position coordinates of the particle and is denoted by Ψ (x, y, z)
∴ Equation (1) can be written as,

Multiply the equation (3) by \(\widehat{\mathrm{H}}\) and rearranging
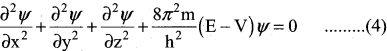
The above equation (4) Schrodinger wave equation does not contain time as a variable and is referred to as time independent Schrodinger wave equation.
Question 34.
Calculate the uncertainty in position of an electron, if ∆v = 0.1% and n = 2.2 x 106 ms-1.
Answer:
Mass of an electron = m = 9.1 x 10-31 kg.
∆v = Uncertainty in velocity = \(\frac {0.1}{100}\) x 2.2 x 103 ms-1 .
∆v = 0.22 x 104 = 2.2 x 103 ms-1
∆x . ∆v . m = \(\frac {h}{4π}\)
∆x = \(\frac {h}{∆v . m x 4π}\)
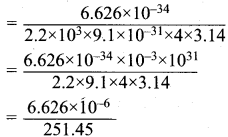
= 0.02635 x 10-6
∆x = 2.635 x 10-8
Uncertainty in position = 2.635 x 10-8.
Question 35.
Determine the values of all the four quantum numbers of the 8th electron in O – atom and 15th electron in Cl atom and the last electron in chromium.
Answer:
(1) O (Z = 8) 1s2 2s2 2px2 2py1 2pz1
Four quantum numbers for 2px1 electron in oxygen atom:
n = principal quantum number = 2
l = azimuthal quantum number =1
m = magnetic quantum number =+1
s = spin quantum number = +\(\frac {1}{2}\)
(2) Cl (Z = 17) 1s2 2s2 2p6 3s2 3px2 3py2 3pz1
Four quantum numbers for 15th electron in chlorine atom:
n = 3, l = 1, m = 0, s = + ½
(3) Cr (Z = 24) 1s2 2s2 2p2 3s2 3p2 3d2 4s1
n = 3, l = 2, m = +2, s = + ½
Question 36.
The quantum mechanical treatment of the hydrogen atom gives the energy value:
En = \(\frac{-13.6}{n^{2}}\) eV atom-1
- use this expression to find ∆E between n = 3 and n = 4
- Calculate the wavelength corresponding to the above transition.
Answer:
(1) When n = 3
E3 = \(\frac{-13.6}{3^{2}}\) = \(\frac {-13.6}{9}\) = – 1.511 eV atom-1
When n = 4 E4 = \(\frac{-13.6}{4^{2}}\) = – 0.85 eV atom-1
∆E = E4 – E3 = – 0.85 – (-1.511) = + 0.661 eV atom
∆E = E3 – E4
= – 1.511 – (-0.85)
= – 0.661 eV atom-1
(2) Wave length = λ
∆E = \(\frac {hc}{ λ}\)
λ = \(\frac {hc}{∆E}\)
h = Planck’s constant = 6.626 x 10-34 Js-1
c = 3 x 108 m/s
λ = \(\frac{6.626 \times 10^{-34} \times 3 \times 10^{8}}{0.661}\)
= 10.02 x 10-34 x 3 x 108
= 30 x 10-26
λ = 3 x 10-25 m.
Question 37.
How fast must a 54 g tennis ball travel in order to have a de Broglie wavelength that is equal to that of a photon of green light 5400 Å?
Answer:
m = mass of tennis ball = 54 g = 5.4 x 10-2 kg.
λ = de Broglie wavelength = 5400 Å. = 5400 x 10-10 m.
V = velocity of the ball = ?
λ = \(\frac {h}{mV}\)
V = \(\frac {h}{λ.m}\)
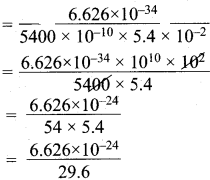
= 0.2238 x 10-24
= 2.238 x 10-25 m.
Question 38.
For each of the following, give the sub level designation, the allowable m values and the number of orbitals.
- n = 4, l = 2,
- n = 5, l = 3
- n = 7, l = 0
Answer:
1. n = 4, l = 2
If l = 2, ‘m’ values are -2, -1, 0, +1, +2
So, 5 orbitals such as dxy,dyz,dxz,\(d_{x^{2}-y^{2}}\) and dz
2. n = 5 , l = 3
If l = 3, ‘m’ values are -3, -2, -1, 0, +1, +2, +3
So, 7 orbitals such as f z, fxz, fyz, fxyz, fz(x2 y2)’ ^x(x2-3y2)’ ^y(3×2 ??y
3. n = 7 , l = 0
If l = 0, ‘m’ values are 0. Only one value.
So, 1 orbital such as 7s orbital.
Question 39.
Give the electronic configuration of Mn2+ and Cr3+
Answer:
1. Mn (Z = 25)
Mn → Mn2+ + 2e–
Mn2+ electronic configuration is 1s 1s2 2s2 2p6 3s2 3p6 3d5
2. Cr (Z = 24)
Cr → Cr3+ + 3e–
Cr3+ electronic configuration is Is2 2s2 2p6 3s23p6 3d3
Question 40.
Describe the Aufbau principle.
Answer:
In the ground state of the atoms, the orbitals are filled in the order of their increasing energies. That is the electrons first occupy the lowest energy orbital available to them. Once the lower energy orbitals are completely filled, then the electrons enter the next higher energy orbitals.
The order of filling of various orbitals as per Aufbau principle is –
1 s < 2s < 2p < 3s < 3p < 4s < 3d < 4p < 5s < 4d ………..
For e.g., K (Z =19)
The electronic configuration is 1s2 2s2 2p6 3s2 3p6 4s1.
After filling 4s orbital only we have to fill up 3d orbital.
Question 41.
A n atom of an element contains 35 electrons and 45 neutrons. Deduce
- the number of protons
- the electronic configuration for the element
- All the four quantum numbers for the last electron
Answer:
An element X contains 35 electrons, 45 neutrons
- The number of protons must be equal to the number of electrons. So the number of protons = 35.
- Number of electrons = 35. So the electronic configuration is 1s2 2s2 2p6 3s2 3p6 4s2 3d10 4p5.
- The last electron i.e. 5th electron in 4p orbital has the following quantum numbers. n = 4, l = 1, m =+1, s = + \(\frac {1}{2}\)
Question 42.
Show that the circumference of the Bohr orbit for the hydrogen atom is an integral multiple of the de Broglie wave length associated with the electron revolving around the nucleus.
Answer:
In order for the electron wave to exist in phase, the circumference of the orbit should be an integral multiple of the wavelength of the electron wave. Otherwise, the electron wave is out of phase.
mvr = nh / 2π, 2πr = nλ,
where mvr = angular momentum
where 2πr = circumference of the orbit
n = 3, n = 4
Question 43.
Calculate the energy required for the process.
He+(g) → He2+(g) + e–
The ionization energy for the H atom in its ground state is – 13.6 eV atom-1.
Answer:
The ionization energy for the H atom in its ground state =-13.6 eV atom-1.
Ionization energy = \(\frac{13.6 z^{2}}{n^{2}}\) eV
Z = atomic number
n = principal quantum number or shell number
For He, n = 1, z = 2
IE = \(\frac{-13.6 \times 2^{2}}{1^{2}}\)eV.
Question 44.
An ion with mass number 37 possesses unit negative charge. If the ion contains 11.1% more neutrons than electrons. Find the symbol of the ion.
Answer:
Let the number of electrons in an ion = x
number of neutrons = n = x + \(\frac{11.1}{100}\) eV = 1.111 x
(As the number of neutrons are 11.1% more than the number of electrons)
In the neutral of atom, number of electron.
e– = x – 1 (as the ion carries -1 charge)
Similarly number of protons = P = x – 1 Number of protons + number of neutrons = mass number = 37
(x – 1) + 1.111 x = 37 .
2.111 x = 37 +1
2.111 x = 38
x = \(\frac{38}{2.111}\) = 18.009 = 18
∴ Number of protons = atomic number – 1 = 18-1 = 17
∴ The symbol of the ion = \(_{17}^{37} \mathrm{Cl}\).
Question 45.
The Li2+ ion is a hydrogen like ion that can be described by the Bohr model. Calculate the Bohr radius of the third orbit and calculate the energy of an electron in 4th orbit.
Answer:
Li2+ hydrogen like ion.
Bohr radius of the third orbit = r3 = ?
r3 = \(\frac{(0.529) n^{2}}{Z}\) A
Where n = shell number, Z = atomic number.
r3 = \(\frac{(0.529) 3^{2}}{3}\) A [∴for lithium Z = 3, n = 3]
= \(\frac{0.529 x 9}{3}\)
r3 = l.587Å
En = \(\frac{(-13.6) Z^{2}}{n^{2}}\) eV atom-1.
E4 = Energy of the fourth orbit = ?
E4 = \(\frac{(-13.6) \times 3^{2}}{4^{2}}\) = \(\frac{-13.6 \times 9}{16}\) = -7.65 eV atom-1
E4 = – 7.65 eV atom-1
Question 46.
Protons can be accelerated in particle accelerators. Calculate the wavelength (in Å)of such accelerated proton moving at 2.85 × 108 ms-1 (the mass of proton is 1.673 x 10-27 Kg).
Answer:
m = mass of the proton = 1.673 x 10-27 Kg
v = velocity of the proton = 2.85 x 108 ms-1
λ = \(\frac{h}{mv}\)
h = Planck’s constant = 6.626 x 1034 Kg m2 s-1

Wavelength of proton = λ = 1.389 x 10-15 m.
Question 47.
What is the de Broglie wavelength (in cm) of a 160g cricket ball travelling at 140 Km hr-1.
Answer:
m = mass of the cricket ball = 160g = 0.16 kg.
v = velocity of the cricket ball =140 Km h-1
= \(\frac {140 x 5}{18}\) = 38.88 ms-1
de Broglie equation = λ = \(\frac{h}{mv}\)
h = Planck’s constant = 6.626 x 10-34 kg m2 s-1
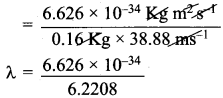
λ = 1.065 x 10-34m
Wave length in cm = 1.065 x 10-34 x 100
= 1.065 x 10-32 cm.
Question 48.
Suppose that the uncertainty in determining the position of an electron in an orbit is 0.6 A. What is the uncertainty in its momentum?.
Answer:
∆x = uncertainty in position of an electron = 0.6 Å = 0.6 x 10-10 m.
∆p = uncertainty in momentum = ?
Heisenberg’s uncertainty principle states that,
∆x.∆p ≥ \(\frac{h}{4π}\)
∆p = \(\frac{h}{4π.∆x}\)
h = Planck’s constant = 6.626 x 10-34 kg m2 s-1
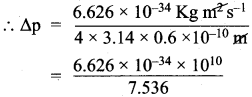
Uncertainty in momentum = 0.8792 x 10-24 kg ms-1 (or) = 8.792 x 10-25 kg ms-1
Question 49.
Show that if the measurement of the uncertainty in .the location of the particle is equal to its de Broglie wavelength, the minimum uncertainty in its velocity is equal to its velocity /4π
Answer:
If, uncertainty in position = ∆x = λ , the value of uncertainty in velocity = \(\frac{v}{4π}\)
Heisenberg’s principle states that
∆x.∆v. m = \(\frac{h}{4π}\) …………(1)
de Broglie equation states that
λ = \(\frac{h}{mv}\) ………….(2)
∴ h = λ .m.v …………(3)
∆x = \(\frac{h}{∆v.4π}\) ………….(4)
Substituting the value of h in equation (4)
∆x = \(\frac{λ x m. v}{∆v.4π.m}\)
if ∆x = λ
∆v = ![]() = \(\frac{v}{4π}\)
= \(\frac{v}{4π}\)
Question 50.
What is the de Broglie wave length of an electron, which is accelerated from the rest, through a potential difference of 100V?
Answer:
Potential difference = V = 100 V
Potential energy = eV = 1.609 x 10-19c x 100V
\(\frac{v}{4π}\) m v2 = 1.609 x 10-19 x 100
\(\frac{v}{4π}\) m v2 = 1.609 x 10-19 J
v2 = \(\frac{2 \times 1.609 \times 10^{-17}}{m}\)
m = mass of electron = 9.1 x 10-31 Kg
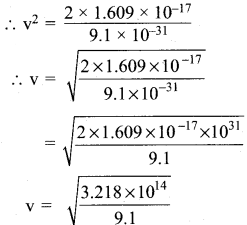
v = 5.93 x 106 m/s
λ = \(\frac{h}{mv}\) where h = 6.62 x 10-34 JS
= \(\frac{6.62 \times 10^{-34}}{9.1 \times 10^{-31} \times 5.93 \times 10^{6}}\)
= 1.2x 10-10m
A= 1.2 Å.
Question 51.
Identify the missing quantum numbers and the sub energy level
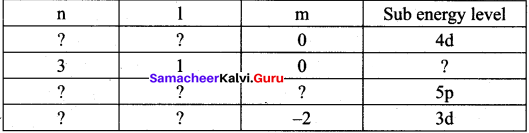
Answer:
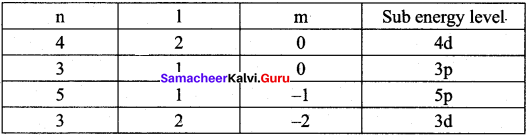
Samacheer Kalvi 11th Chemistry Quantum Mechanical Model of Atom In-Text Questions – Evaluate Yourself
Question 1.
Calculate the de Broglie wavelength of an electron that has been accelerated from rest through a potential difference of 1 k eV.
Answer:
λ = \(\frac{h}{mv}\)
Potential difference of an electron = V = 1 keV.
Potential energy = \(\frac{1}{2}\) mv2 = eV
e = charge of an electron = 1.609 x 10-19c
l k V = 1000 V
:. Potential energy = 1.609 x 10-19 x 1000 = 1.609 x 10-19
\(\frac{1}{2}\) mv2 = 1.609 x 10-16V
m = 9.1 x 10-31 kg
λ = \(\frac{h}{mv}\)
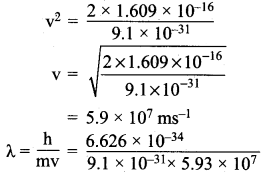
= 1.2 x 10-11 m
λ = 1.2 x 10-11 m.
Question 2.
Calculate the uncertainty in the position of an electron, if the uncertainty in its velocity is 5.7 x 10 s ms-1.
Answer:
Uncertainty in velocity = Av = 5.7 x 105 ms-1
Mass of an electron = m = 9.1 x 10-31 kg.
Uncertainty in position = ∆x = ?
∆x.m.∆v = \(\frac{h}{4π}\)
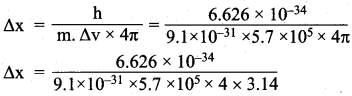
= 1 x 10-10m.
Uncertainty in position = 1 x 10-10 m.
Question 3.
How many orbitals are possible in the 4th energy level? (n = 4)
Answer:
n = 4
Number of orbitals in 4th energy level = ?
When n = 4, l = 0,1,2,3
If l = 0 orbital = 4s =1
If l = 1 orbital = 4px, 4py, 4pz = 2
If l = 2 orbital = \(4 \mathrm{d}_{\mathrm{xy}}, 4 \mathrm{d}_{\mathrm{yz}}, 4 \mathrm{d}_{\mathrm{zx}}, 4 \mathrm{d}_{\mathrm{x}} 2_{\mathrm{y}}, 2,4 \mathrm{d}_{\mathrm{z}^{2}}\) = 5
If l = 3 orbital = -3,-2, -1, 0, +1, +2, +3 = 7
Number of orbitals in 4th energy level = 16.
Question 4.
Calculate the total number of angular nodes and radial nodes present in 3d and 4f orbitals.
Answer:
Number of angular nodes in 3d orbital = ?
Number of radial nodes in 3d orbital = ?
Number of angular nodes = l
Number of radial nodes = n – l – 1
1. For 3d orbital:
Number of angular nodes = 2 because l = 2
Number of radial nodes = 3 – 2 -1 = 0
Total number of nodes in 3d orbital = 2
2. For 4f orbital:
Number of angular nodes = 3 because l = 3
Number of radial nodes = n – l – l =4 – 3 – 1 = 0
Total number of nodes in 4f orbital = 3.
Question 5.
Energy of an electron in hydrogen atom in ground state is -13.6 eV. What is the energy of the electron in the second excited state?
Answer:
Energy of an electron in ground state = -13.6 eV.
∴ Energy of an electron in the second excited state = E2.
n = 2
E2 = \(\frac{-13.6 \mathrm{eV}}{\mathrm{n}^{2}}\) = \(\frac{-13.6}{2^{2}}\) = \(\frac{-13.6}{4}\) = -3.4 eV.
Question 6.
How many unpaired electrons are present in the ground state of Fe3+ (z = 26), Mn2+ (z = 25) and argon (z=18)?
Answer:
![]()
1s2 2s2 2p6 3s2 3p6 3d6 4s2 for Fe atom.
1s2 2s2 2p6 3s2 3p6 3d6 3d5 for Fe3+ ion.
So, it contain 5 unpaired electrons.
Mn (Z = 25). Electronic configuration is 1s2 2s2 2p6 3s2 3p6 3d6 3d5
Mn → Mn2+ + 2e–
Number of unpaired electrons in Mn2+ = 5
Ar (Z = 18). Electronic configuration is 1s2 2s2 2p6 3s2 3p6.
All orbitals are completely filled. So, no unpaired electrons in it.
Question 7.
Explain the meaning of the symbol 4f2. Write all the four quantum numbers for these electrons.
Answer:
4f2 : It means that the element has 2 electrons in outermost 4f shell.
Quantum number values are, ![]()
n = principal quantum number = 4
l = azimuthal quantum number = 3
m = magnetic quantum number = – 3, -2
s = spin quantum number = +\(\frac {1}{2}\) – \(\frac {1}{2}\).
Question 8.
Which has the stable electronic configuration? Ni2+ or Fe3+
Answer:
Ni (Z = 28). 1s2 2s2 2p6 3s2 3p64s23d8
Ni2+ electronic configuration = Is2 2s22p6 3s2 3p6 3d8
Fe (Z = 26). 1s2 2s2 2p6 3s2 3p6 4s2 3d6
Fe3+ Is2 2s2 2p6 3s23p6 3d5
If d orbital is half filled, according to Aufbau principle, it is more stable. So Fe3+ is more stable than Ni2+.
Samacheer Kalvi 11th Chemistry Solutions Quantum Mechanical Model of Atom Additional Questions Solved
I. Choose the correct answer
Question 1.
Which of the following experiment proves the presence of an electron in an atom?
(a) Rutherford’s α-ray scattering experiment
(b) Davisson and Germer experiment
(c) J.J. Thomson cathode ray experiment
(d) G.R Thomson gold foil experiment
Answer:
(c) J.J. Thomson cathode ray experiment.
Question 2.
Consider the following statements regarding Rutherford’s α-ray scattering experiment.
i. Most of the α-particles were deflected through a small angle.
ii. Some of α-particles passed through the foil.
iii. Very few α-particles were reflected back by 180°.
Which of the above statements is/are not correct.
(a) i and ii
(b) ii and iii
(c) i and iii
(d) i ii and iii
Answer:
(a) i and ii.
Question 3.
Considering Bohr’s model which of the following statements is correct?
(a) The energies of electrons are continuously reduced in the form of radiation.
(b) The electron is revolving around the nucleus in a dynamic orbital.
(c) Electrons can revolve only in those orbits in which the angular momentum (mvr) of the electron must be equal to an integral multiple of h/2 π.
(d) In an atom, electrons are embedded like seeds in watermelon.
Answer:
(c) Electrons can revolve only in those orbits in which the angular momentum (mvr) of the electron must be equal to an integral multiple of h/2π.
Question 4.
The energy of an electron of hydrogen atom in 2nd main shell is equal to
(a) – 13.6 eV atom-1
(b) – 6.8 eV atom-1
(c) – 0.34 eV atom-1
(d) – 3.4 eV atom-1
Answer:
(d) -3.4 eV atom-1
Hints:
Energy of an electron in 2nd main shell = \(\frac{(-13.6) Z^{2}}{n^{2}}\); Z = 1, n = 2
E = \(\frac{-13.6}{2^{2}}\) = \(\frac{-13.6}{4}\) = -3.4 atom-1.
Question 5.
The energy of an electron of Li2+ in the 3rd main shell is …………..
(a) – 1.51 eV atom-1
(b) – 6.8 eV atom-1
(c) + 1.51 eV atom-1
(d) – 3.4 eV atom-1
Answer:
(a) -1.51 eV atom-1
Hints:
E = \(\frac{(-13.6) Z^{2}}{n^{2}}\) eV atom-1
Li2+= H atom. So Z = 1, n = 3.
E = \(\frac{(-13.6) 1^{2}}{3^{2}}\) = \(\frac{-13.6}{9}\) = -1.51 eV atom-1
Question 6.
The energy of an electron of hydrogen atom in main shell in terms of U mold is
(a) – 1312.8 k J mol-1
(b) – 82.05 k J mol-1
(c) – 328.2 kJ mol-1
(d) – 656.4 k J mol-1
Answer:
(b) – 82.05 k J mol-1
Hints:
E = \(\frac{(-13.6) Z^{2}}{n^{2}}\) kJ mol-1 , Z = 1, n = 4
∴ E = \(\frac{-1312.8}{16}\) = -82.50 kJ mol-1
Question 7.
The Bohr’s radius of Li2 0f21d orbit is
(a) 0.529 Å
(b) 0.0753 Å
(c) 0.7053 Å
(d) 0.0529 Å
Answer:
(c) 0.7053 Å
Hints:
rn = \(\frac{(0.529) Z^{2}}{n^{2}}\)Å, n = 2, Z = 3(for Li2+)
r = \(\frac{(0.529) 3^{2}}{2^{2}}\) = \(\frac{0.529 x 4}{3}\) = 0.7053 Å.
Question 8.
The formula used to calculate the Boh’s radius is ………..
(a) rn = \(\frac{(-13.6) Z^{2}}{n^{2}}\) eV atom-1
(b) rn = \(\frac{(0.529) Z^{2}}{n^{2}}\) A
(c) rn= \(\frac{(-1312.8) Z^{2}}{n^{2}}\) kJ mol-1
(d) rn = \(\frac{(+1312.8) Z^{2}}{n^{2}}\) kJ mol-1
Answer:
(b) rn = \(\frac{(0.529) Z^{2}}{n^{2}}\) A.
Question 9.
Who proposed the dual nature of light to all forms of matter?
(a) John Dalton
(b) Neils Bohr
(c) Albert Einstein
(d) J.J. Thomson
Answer:
(c) Albert Einstein
Question 10.
dc Brogue equation is ………..
(a) E = h γ
(b) E = mc2
(c) γ = \(\frac{\mathrm{E}_{2}-\mathrm{E}_{1}}{\mathrm{h}}\)
(d) λ = \(\frac{h}{mv}\)
Answer:
(d) λ = \(\frac{h}{mv}\).
Question 11.
The crystal used in Davison and Germer experiment is …………….
(a) nickel
(b) zinc suiphide
(c) gold foil
(d) NaCl
Answer:
(a) nickel.
Question 12.
Which one of the following is the time independent Schrodinger wave equation?

Answer:
![]()
Question 13.
Match the list-I and list-II correctly using the code given below the list.
List – I
A. Principal quantum number
B. Azimuthal quantum number
C. Magnetic quantum number
D. Spin quantum number
List – II
1. represents the directional orientation of orbital
2. represents the spin of the electron
3. represents the main shell
4. represents the sub shell

Answer:
![]()
Question 14.
The maximum number of electrons that can be accommodated in N shell is …………..
(a) 8
(b) 18
(c) 32
(d) 36
Answer:
(c) 32
Hints:
Number of electrons in the main shell = 2n2 n = 4, for N shell.
∴ Maximum number of electrons in N shell = 2(4)2 = 32.
Question 15.
The maximum number of electrons that can be accommodated in f orbital is ………….
(a) 10
(b) 14
(c) 16
(d) 6
Answer:
(6) 14
Hints:
forbital – l = 3.
Maximum number of electrons in sub shell = 2(2l + 1)
∴ For ‘f’ orbital, the maximum number of electrons = 2(2 x 3 + l) = 14.
Question 16.
When l = 0, the number of electrons that can be accommodated in the sub shell is ……………..
(a) 0
(b) 2
(c) 6
(d) 8
Answer:
(b) 2
Hints:
If l = 0, number of electrons = (2l + 1)
= 2 (2 x 0 + 1) = 2.
Question 17.
Which one of the quantum number is used to calculate the angular momentum of an atom?
(a) n
(b) m
(c) l
(d) s
Answer:
(c) l
Question 18.
What is the formula used to calculate the angular momentum?
(a) \(\sqrt{l^{(l+1)}} \frac{h}{2 \pi}\)
(b) \(\frac{\mathrm{mvr}}{2 \pi}\)
(c) \(\frac{mvr}{2}\)
(d) m . ∆v
Answer:
(a) \(\sqrt{l^{(l+1)}} \frac{h}{2 \pi}\).
Question 19.
Which of the following provides the experimental justification of magnetic quantum number?
(a) Zeeman effect
(b) Stark effect
(c) Uncertainty principle
(d) Quantum condition
Answer:
(a) Zeeman effect.
Question 20.
What are the values of n, l, m and s for 3px electron?
(a) 3, 2, 1, 0
(b) 3, 1,-l, +½
(c) 3, 2, +1, -½
(d) 3, 0, 0, +½]
Answer:
(b) 3, 1, -1, +½
Hint:
3px electron ; n = 3 (main shell)
for px orbitaI, l = 1, m = -1, s = \(\frac {1}{2}\).
Question 21.
Identify the quantum number for \(4 d_{x^{2}-y^{2}}\) electron.
(a) 4, 2, -2, +½
(b) 4, 0, 0, +½
(c) 4, 3, 2, +½
(d) 4, 3, 2, -½
Answer:
(a) 4, 2, -2, +½.
Question 22.
How many orbitals are possible in 3rd energy level?
(a) 16
(6) 9
(c) 3
(d) 27
Answer:
(b) 9
Hints:
3rd energy level Number of orbitals = ?
n = 3 main shell = m
l = 0, 1,2 m = 0, -1,0, +1
Total = 9 orbitals.
Question 23.
The region where the probability density function of electron reduces to zero is called
(a) orbit
(b) orbital
(c) nodal surface
(d) sub shell
Answer:
(c) nodal surface.
Question 24.
Consider the following statements.
(i) The region where the probability density of electron is zero, called nodal surface.
(ii) The probability of finding the electron is independent of the direction of the nucleus.
(iii) The number of radial nodes is equal to n + l + 1 Which of the above statements is/are correct?
(a) (i) and (iii)
(b) (i) and (ii)
(c) (iii) only
(d) (ii) and (iii)
Answer:
(b) (i) and (ii).
Question 25.
Match the list-I and list-II correctly using the code given below the list.
List-I
A. s – orbital
B. p – orbital
C. d – orbital
D. f – orbital
List-II
1. complex three-dimensional shape
2. symmetrical sphere
3. dumb-bell shape
4. clover leaf shape

Answer:
![]()
Question 26.
Which one of the following is the correct increasing order of effective nuclear charge felt by an electron?
(a) s>p>d>f
(b) s<p<d<f
(c) s>p>f>d
(d) f<p<d<s
Answer:
(a) s>p>d>f.
Question 27.
The value of n, l, m and s of 8th electron in an oxygen atom are respectively
(a) 1, 0, 0, + ½
(b) 2, 1, +1, – ½
(c) 2, 1, -1, – ½
(d) 2, 1, 0, +½
Answer:
(a) 2, 1, +1, – ½.
Question 28.
The number of impaired electrons in carbon atom in the gaseous state is
(a) 0
(b) 1
(c) 2
(d) 3
Answer:
(c) 2
Question 29.
Which of the following is not used in writing electronic configuration of an atom?
(a) Aufbau principle
(b) Hund’s rule
(c) Pauli’s exclusion principle
(d) Heisenberg’s uncertainty principle
Answer:
(d) Heisenberg’s uncertainty principle.
Question 30.
Which of the following is the expected configuration of Cr (Z = 24)?
(a) 1s2 2s2 2p6 3s2 3p6 3d4 4s2
(b) 1s2 2s2 2p6 3s2 3p6 3d5 4s1
(c) 1s2 2s2 2p6 3s2 3p6 3d6
(d) 1s2 2s2 2p6 3s2 3p6 3d5 4s3
Answer:
(a) 1s2 2s2 2p6 3s2 3p6 3d4 4s2
Question 31.
Which of the following is the actual configuration of Cr (Z = 24)?
(a) 1s2 2s2 2p6 3s2 3p6 3d4 4s2
(b) 1s2 2s2 2p6 3s2 3p6 3d5 4s1
(c) 1s2 2s2 2p6 3s2 3p6 3d6
(d) 1s2 2s2 2p6 3s2 3p6 3d5 4s3
Answer:
(b) 1s2 2s2 2p6 3s2 3p6 3d5 4s1
Question 32.
Assertion (A) : Cr with electronic configuration [Ar] 3d5 4s1 is more stable than [Ar] 3d4 4s1.
Reason(R ): Half filled orbitals have been found to have extra stability than partially filled orbitals.
(a) A and R are correct and R is the correct explanation of A.
(b) A and R are correct but R is not the correct the explanation of A.
(c) A is correct but R is wrong.
(d) A is wrong but R is correct.
Answer:
(a) A and R are correct and R is the correct explanation of A.
Question 33.
Assertion (A): Copper (Z = 29) with electronic configuration [Ar] 4s1 3d10 is more stable than [Ar] 4s1 3d10.
Reason(R): Copper with [Ar] 4s2 3d9 is more stable due to symmetrical distribution and exchange energies of d electrons.
(a) A and R are correct and R is the correct explanation of A.
(b) A and R are correct but R is not the correct explanation of A.
(c) A is correct but R is wrong.
(d) A is wrong but R is correct.
Answer:
(a) A and R are correct and R is the correct explanation of A.
Question 34.
In a sodium atom (atomic number = 11 and mass number = 23) and the number of neutrons is …………..
(a) equal to the number of protons
(b) less than the number of protons
(c) greater than the number of protons
(d) none of these
Answer:
(c) greater than the number of protons.
Question 35.
The idea of stationary orbits was first given by …………
(a) Rutherford
(b) J.J. Thomson
(c) Nails Bohr
(d) Max Planck
Answer:
(c) Niels Bohr.
Question 36.
de Broglie equation is ……………
(a) λ = \(\frac {h}{mv}\)
(b) λ = \(\frac {hv}{m}\)
(c) λ = \(\frac {mv}{h}\)
(d) λ = hmv
Answer:
(a) λ = \(\frac {h}{mv}\).
Question 37.
The orbital with n = 3 and l = 2 is …………..
(a) 3s
(b) 3p
(c) 3d
(d) 3J
Answer:
(c) 3d
Question 38.
The outermost electronic configuration of manganese (at. no. = 25) is …………
(a) 3d5 4s2
(b) 3d6 4s1
(c) 3d7 4s0
(d) 3d6 4s2
Answer:
(a) 3d5 4s2
Question 39.
The maximum number of electrons in a sub-shell is given by the equation
(a) n2
(b) 2 n2
(c) 2 l – l
(d) 2 l + 1
Answer:
(d) 2 l + 1
Question 40.
Which of the following statements is correct for an electron that has the quantum numbers n = 4 and m = -2.
(a) The electron may be in 2 p orbital
(b) The electron may be in 4 d orbital
(c) The electron is in the second main shell
(d) The electron must have spin quantum number as +\(\frac {1}{2}\).
Answer:
(b) The electron may be in 4d orbital.
Samacheer Kalvi 11th Chemistry Quantum Mechanical Model of Atom 2 – Marks Questions
Question 1.
Write a note about J.J. Thomson’s atomic model.
Answer:
- J.J. Thomson’s cathode ray experiment revealed that atoms consist of negatively charged particles called electrons.
- He proposed that atom is a positively charged sphere in which the electrons are embedded like the seeds in the watermelon.
Question 2.
Explain about theory of electromagnetic radiation.
Answer:
- The theory of electromagnetic radiation states that a moving charged particle should continuously loose its energy in the form of radiation.
- O Therefore, the moving electron in an atom should continuously loose its energy and finally collide with nucleus resulting in the collapse of the atom.
Question 3.
Explain how matter has dual character?
Answer:
- Albert Einstein proposed that light has dual nature, i.e. like photons behave both like a particle and as a wave.
- Louis de Broglie extended this concept and proposed that all forms of matter showed dual character.
- He combined the following two equations of energy of which one represents wave character (hυ) and the other represents the particle nature (mc2).
Question 4.
Explain about the significance of de Broglie equation.
Answer:
- X = \(\frac {h}{mv}\). This equation implies that a moving particle can be considered as a wave and a wave can exhibit the properties of a particle.
- For a particle with high linear momentum (mv) the wavelength will be so small and cannot be observed.
- For a microscopic particle such as an electron, the mass is of the order of 10-31 kg, hence the wavelength is much larger than the size of atom and it becomes significant.
- For the electron, the de Broglie wavelength is significant and measurable while for the iron ball it is too small to measure, hence it becomes insignificant.
Question 5.
How many electrons can be accommodated in the main shell l, m and n?
Answer:

Question 6.
How many electrons that can be accommodated in the sub shell s, p, d, f ?
Answer:

Question 7.
What are quantum numbers?
Answer:
- The electron in an atom can be characterized by a set of four quantum numbers, namely principal quantum number (n), azimuthal quantum number (l), magnetic quantum number (m) and spin quantum number (s).
- When Schrodinger equation is solved for a wave function T, the solution contains the first three quantum numbers n, l
- and m.
- The fourth quantum number arises due to the spinning of the electron about its own axis.
Question 8.
How many orbitals are possible in the 3rd energy level?
Answer:
n = 3, main shell is m.
Total number of orbitals in 3rd energy level = ?

Total number of orbitals = 9.
Question 9.
What are Ψ and Ψ2 ?
Answer:
- Ψ itself has no physical meaning but it represents an atomic orbital.
- Ψ2 is related to the probability of finding the electrons within a given volume of space.
Question 10.
What is meant by nodal surface?
Answer:
- The. region where there is probability density function reduces to zero is called nodal surface or a radial node.
- For ns orbital, (n-1) nodes are found in it.
Question 11.
Mention the shape of s, p, d orbitals.
Answer:
- Shape of s – orbital – sphere
- Shape of p – orbital – dumb bell
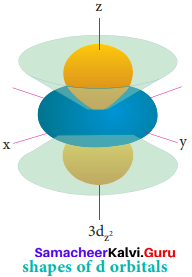
- Shape of d – orbital – clover leaf
Question 12.
Calculate the total number of angular nodes and radial nodes present in 4p and 4d orbitals.
Answer:
1. For 4p orbital:
Number of angular nodes = l
For 4p orbital 7 = l
Number of angular nodes = l
Number of radial nodes = n – l – 1 = 4 -1 -1 = 2
Total number of nodes = n -1 = 4 – 1 = 3
1 angular node and 2 radial nodes.
2. For 4d orbital:
Number of angular nodes = l
For 4d orbital l = 2
Number of angular nodes = 2
Number of radial nodes = n – l – 1 = 4 – 2 – 1 = 1
Total number of nodes = n – l = 4 – l = 3
1 radial nodes and 2 angular node.
Question 13.
Write the equation to calculate the energy of nth orbit.
Answer:
En = \(\frac{(-1312.8) Z^{2}}{n^{2}}\) kJ mol-1
Where Z = atomic number, n = principal quantum number.
Question 14.
what are degenerate orbitals?
Answer:
- Three different orientations in space that are possible for a p-orbital. All the three p-orbitals, namely px, py and pz have same energies and are called degenerate orbitals.
- In the presence of magnetic or electric field, the degeneracy is lost.
Question 15.
Energy of an electron in hydrogen atom in ground state is -13.6 eV. What is the energy of the electron in the third excited state?
Answer:
E1 = – 13.6 eV
E3 = \(\frac{-13.6}{n^{2}}\) Where n = 3
E3 = \(\frac{-13.6}{9}\) = 1.511 eV
Energy of the electron in the third excited state = 1.511 eV.
Question 16.
The energies of the same orbital decreases with an increase in the atomic number. Justify this statement.
Answer:
The energy of the 2s orbital of hydrogen atom is greater than that of 2s orbital of lithium and that of lithium is greater than that of sodium and so on because H (Z =1), Li (Z = 3) and Na (Z = 11). When atomic number increases, the energies of the same orbital decreases. E2s(H) > E2s(Li) > E2s(Na) > E2s(K) ………….
Question 17.
State Hund’s rule of maximum multiplicity.
Answer:
It states that electron pairing in the degenerate orbitals does not take place until all the available orbitals contain one electron each.
Question 18.
How many unpaired electrons are present in the ground state of –
1. Cr3+ (Z = 24)
2. Ne (Z = 10)
Answer:
1. Cr3+ (Z = 24) 1s2 2s2 2p6 3s2 3p6 3d5 4s1
Cr3+ – 1s2 2s2 2p6 3s2 3p6 3d4.
It contains 4 unpaired electrons.
2. Ne (Z = 10) 1s22s22p6. No unpaired electrons in it.
Question 19.
What is meant by electronic configuration? Write the electronic configuration of N (Z = 7).
Answer:
The distribution of electrons into various orbitals of an atom is called its electronic configuration.
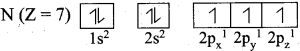
Question 20.
Which is the actual configuration of Cr (Z = 24) Why?
Answer:
Cr (Z = 24) 1s22s22p6.
The reason for this is, Cr with 3d5 configuration is half filled and it will be more stable. Chromium has [Ar] 3d5 4s1 and not [Ar] 3d4 4s2 due to the symmetrical distribution and exchange energies of d electrons.
Question 21.
What is the actual configuration of copper (Z = 29)? Explain about its stability.
Answer:
Copper (Z = 29)
Expected configuration : 1s2 2s2 2p6 3s2 3p6 3d9 4s2
Actual configuration : 1s2 2s2 2p6 3s2 3p6 3d10 4s1
The reason is that fully filled orbitals have been found to have extra stability. Copper has the electronic configuration [Ar] 3d10 4s1 and not [Ar] 3d9 4s2 due the symmetrical distribution and exchange energies of d electrons. Symmetry leads to stability. The full filled configuration have symmetrical distribution of electrons and hence they are more stable than unsymmetrical configuration.
Samacheer Kalvi 11th Chemistry Quantum Mechanical Model of Atom 3 – Mark Questions
Question 1.
What are the conclusions of Rutherford’s α – rays scattering experiment?
Answer:
- Rutherford bombarded a thin gold foil with a stream of fast moving α – particles.
- It was observed that most of the a-particles passed through the foil.
- Some of them were deflected through a small angle.
- Very few α- particles were reflected back by 180°.
- Based on these observations, he proposed that in an atom, there is a tiny positively charged nucleus and the electrons are moving around the nucleus with high speed.
Question 2.
What are the limitations of Bohr’s atom model?
Answer:
- The Bohr’s atom model is applicable only to species having one electron such as hydrogen, Li2+ etc and not applicable to multi – electron atoms.
- It was unable to explain the splitting of spectral lines in the presence of magnetic field (Zeeman effect) or an electric field (Stark effect).
- Bohr’s theory was unable to explain why the electron is restricted to revolve around the nucleus in a fixed orbit in which the angular momentum of the electron is equal to nh / 2π.
Question 3.
Illustrate the significance of de Broglie equation with an iron ball and an electron.
- 6.626 kg iron ball moving with 10 ms-1.
- An electron moving at 72.73 ms-1.
Answer:
1. λiron ball = \(\frac{h}{mv}\)
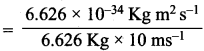
= 1 x 10-35m
2. λiron ball = \(\frac{h}{mv}\)
![]()
= \(\frac{6.626}{662.6}\) x 10-3m = 1 x 105m
For an electron, the de Broglie wavelength is significant and measurable while for iron ball it is too small to measure, hence it becomes insignificant.
Question 4.
Explain Davisson and Germer experiment.
Answer:
- The wave nature of electron was experimentally confirmed by Davisson and Germer.
- They allowed the accelerated beam of electrons to fall on a nickel crystal and recorded the diffraction pattern.
- The resultant diffraction pattern is similar to the X – ray diffraction pattern.
- The finding of wave nature of electron leads to the development of various experimental ’ techniques such as electron microscope, low energy electron diffraction etc.
Question 5.
Bohr radius of 1st orbit of hydrogen atom is 0.529 Å. Assuming that the position of an electron in this orbit is determined with the accuracy of 0.5% of the radius, calculate the uncertainty in the velocity of the electron in hydrogen atom.
Answer:
Uncertainty in position = ∆x
= \(\frac{0.5}{100}\) x 0.529 Å
= \(\frac{0.5}{100}\) x 10-10 x 0.529 m
∆x = 2.645 x 10-13 m
From Heisenberg’s uncertainty principle,
∆x.∆p ≥ \(\frac{h}{4π}\)
∆x.m.∆p ≥ \(\frac{h}{4π}\)
∆v ≥ \(\frac{h}{∆x.m.4π}\)
∆v = ![]()
∆v = 2.189 x 108m.
Question 6.
Write a note about principal quantum number.
Answer:
- The principal quantum number represents the energy level in which electron revolves around the nucleus and is denoted by the symbol ‘n’.
- The ‘n’ can have the values 1, 2, 3,… n = 1 represents K shell; n=2 represents L shell and n = 3, 4, 5 represent the M, N, O shells, respectively.
- The maximum number of electrons that can be accommodated in a given shell is 2n2.
- ‘n’ gives the energy of the electron,
En = \(\frac{(-1312.8) Z^{2}}{n^{2}}\) KJ mol-1 and the distance of the electron from the nucleus is given by rn = \(\frac{(-0.529) n^{2}}{Z}\) A.
Question 7.
Explain about azimuthal quantum number.
Answer:
- It is represented by the letter 7′ and can take integral values from zero to n – 1, where n is the principal quantum number.
- Each l value represents a subshell (orbital). l = 0, 1, 2, 3 and 4 represents the s, p, d, f and g orbitals respectively.
- The maximum number of electrons that can be accommodated in a given subshell (orbital) is 2(2l + 1).
It is used to calculate the orbital angular momentum using the expression Angular momentum = \(\sqrt{l(l+1)} \frac{h}{2 \pi}\).
Question 8.
Draw the shapes of 1s, 2s and 3s orbitals
Answer:
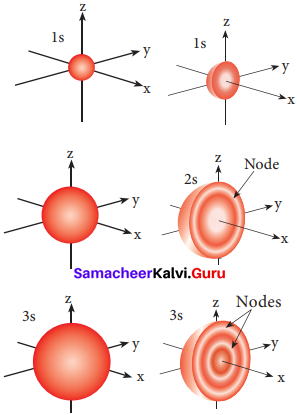
Question 9.
Explain how effective nuclear charge is related with stability of the orbital.
Answer:
- In a multi-electron atom, in addition to the electrostatic attractive force between the electron and nucleus, there exists a repulsive force among the electrons.
- These two forces are operating in the opposite direction. This results in the decrease in the nuclear force of attraction on electron.
- The net charge experienced by the electron is called effective nuclear charge.
- The effective nuclear charge depends on the shape of the orbitals and it decreases with increase in azimuthal quantum number l.
- The order of the effective nuclear charge felt by a electron in an orbital within the given shell is s > p > d > f.
- Greater the effective nuclear charge, greater is the stability of the orbital. Hence, within a given energy level, the energy of the orbitals are in the following order s < p < d < f.
Question 10.
Calculate the wavelength of an electron moving with a velocity of 2.05 x 107 ms-1.
Answer:
According to de Broglie’s equation, λ = \(\frac {h}{mv}\)
Mass of electron (m) = 9.1 x 10-31 kg
Velocity of electron (υ) = 2.05 x 107 ms-1
Planck’s constant (h) = 6.626 x 10-34 kg m2 s-1
λ = 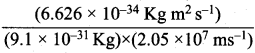 =355 x 10-4m.
=355 x 10-4m.
Question 11.
The mass of an electron is 9.1 x 10-31 kg. If its kinetic energy is 3.0 x 10-25 J, calculate its wavelength.
Answer:
Step I.
Calculation of the velocity of electron
Kinetic energy = 1 / 2 mυ2 = 3.0 x 10-25 kg m2 s-2
υ2![]() = 65.9 x 104 m2 s-2
= 65.9 x 104 m2 s-2
υ = (65.9 x 104 m s-2) = 8.12 x 102 ms-1
Step II.
Calculation of wavelength of the electron
According to de Broglie’s equation,
λ = \(\frac {h}{mv}\) = 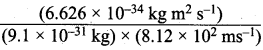
= 0.08967 x l0-5 m = 8967 x 10-10 m = 8967 Å (∴1Å = 10-10m).
Question 12.
From the following sets of quantum numbers, state which are possible. Explain why the others are not possible.
- n = 0, l = 0, ml = 0, ms = + \(\frac {1}{2}\)
- n = 1, l = 0, ml = 0, ms = – \(\frac {1}{2}\)
- n = 1, l = 1, ml = 0, ms = + \(\frac {1}{2}\)
- n = 1, l = 0, ml = +1, ms= +\(\frac {1}{2}\)
- n = 3, l = 3, ml = -3, ms = + \(\frac {1}{2}\)
- n = 3, l = 1, ml = 0, ms = +\(\frac {1}{2}\)
Answer:
- The set of quantum numbers is not possible because the minimum value of n can be 1 and not zero.
- The set of quantum numbers is possible.
- The set of quantum numbers is not possible because, for n = 1,1 cannot be equal to 1. It can have 0 value.
- The set of quantum numbers is not possible because for l = 0, ml; cannot be +1. It must be zero.
- The set of quantum numbers is not possible because, for n = 3, l = 3.
- The set of quantum numbers is possible.
Question 13.
How many electrons in an atom may have the following quantum numbers?
(a) n = 4; ms = – ½
(b) n = 3, l = 0.
Answer:
(a) For n = 4
1 Total number of electrons = 2n2 = 2 x 16 = 32
Half out of these will have ms = – \(\frac {1}{2}\)
Total electrons with ms (-½) = 16.
(b) For n = 3
l = 0; m1 = 0, ms = + ½ – ½ (two e–).
Question 14.
Show that the circumference of the Bohr orbit for the hydrogen atom is an integral multiple of the de Broglie wavelength associated with the electron revolving around the orbit.
Answer:
According to Bohr’s theory,
mυr = \(\frac {nh}{2π}\) (n = 1,2,3, …… so on)
or 2πr = \(\frac {nh}{mυ}\) or mυ = \(\frac {nh}{2πr}\) ………..(i)
According to de Brogue equation,
λ = \(\frac {h}{mυ}\) or mυ = \(\frac {h}{λ}\) ……….(ii)
Comparing (i) and (ii),
\(\frac {nh}{2πr}\) = \(\frac {h}{λ}\) or 2πr = nλ
Thus, the circumference (2πr) of the Bohr orbit for hydrogen atom is an into the de Broglie wave length.
Question 15.
An ion with mass number 56 contains 3 units of positive charge and 30.4% more neutrons than electrons. Assign symbol to the ion.
Answer:
Let the no. of electrons in the ion = x
the no. of the protons = x + 3 (as the ion has three units positive charge)
and the no. of neutrons = x + \(\frac {30.4x }{100}\) = x + 0.304 x
Now, mass number of ion = Number of protons + Number of neutrons
= (x + 3) + (x + 0.304 x)
∴ 56 = (x + 3) + (x + 0.304 x) or 2.304 x = 56 – 3 = 53
x = \(\frac {53}{2.304}\) = 23
Atomic number of the ion (or element) = 23 + 3 = 26
The element with atomic number 26 is iron (Fe) and the corresponding ion is Fe3+.
Question 16.
The uncertainty in the position of a moving bullet of mass 10 g is 10 s m. Calculate the uncertainty in its velocity?
Answer:
According to uncertainty principle,
∆x.m∆υ = \(\frac {h}{4π}\) or ∆υ = \(\frac {h}{4πm∆x}\);
h = 6.626 x 1o-34 kg m2 s-1; m = 10 g = 10-2 kg
∆x = 10-5m; ∆v = 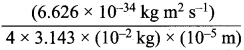 = 5.27 x 10-28mv
= 5.27 x 10-28mv
= 1.6 x 10-15 kg m2 s-15
Or
\(\frac {1}{2}\) mv2 = 1.6 x 10-15kg m2s-2
v = 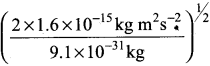 = 5.93 x 107m-1
= 5.93 x 107m-1
Question 17.
The uncertainty in the position and velocity of a particle are 10-10 m and 5.27 × 10-24 ms-1 respectively. Calculate the mass of the particle.
Answer:
According to uncertainty principle.
∆x. m∆υ = \(\frac {h}{4π}\)
or
m = \(\frac {h}{4π∆x.∆υ}\);
h = 6.626 x 10-34 kg m2 s-1
∆x = 10-10 m; ∆x = 5.27 x 10-24ms-1
m 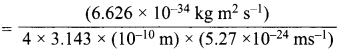 = 0.1 kg.
= 0.1 kg.
Question 18.
With what velocity must an electron travel so that its momentum Is equal to that of a photon of wave length = 5200 A?
Answer:
According to de Brogue equation, λ = \(\frac {h}{mv}\)
Momentum of electron, mv = \(\frac {h}{λ}\) 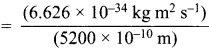
= 1.274 x 10-27 kg ms-1 ………(i)
The momentum of electron can also be calculated as = mv = (9.1 x 10-31kg) x v ………(ii)
Comparing (i) and (ii)
(9.1 X 10-31kg) v = (1.274 x 10-27 kg ms-1)
v 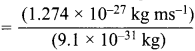 = 1.4 x 103 ms-1
= 1.4 x 103 ms-1
Question 19.
Using Aufbau principle, write the ground state electronic configuration of following atoms.
- Boron (Z = 5)
- Neon (Z = 10)
- Aluminium (Z = 13)
- Chlorine (Z = 17)
- Calcium (Z = 20)
- Rubidium (Z = 37)
Answer:
- Boron (Z = 5) ; 1s2 2s2 2p1
- Neon (Z = 10) ; 1s2 2s2 2p6
- Aluminium (Z = 13) ; 1s2 2s2 2p6 3s2 3p1
- Chlorine(Z = 17) ; 1s2 2s2 2p6 3s2 3p5
- Calcium (Z = 20) ; 1s2 2s2 2p6 3s2 3p6 4s2
- Rubidium (Z = 37) ; 1s2 2s22p6 3s2 3p63d10 4s2 4p6 5s1
Question 20.
Calculate the de Broglie wavelength of an electron moving with 1 % of the speed of light?
Answer:
According to de Brogue equation, A = \(\frac {h}{mv}\)
Mass of electron = 9.1 x 10-31 kg; Planck’s constant 6.626 x 10-34 kg m2 s-1
Velocity of electron = 1% of speed of light = 3.0 x 108 x 0.01 = 3 106 ms-1
Wavelength of electron (λ) = \(\frac {h}{mv}\) 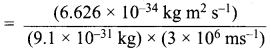
= 2.43 x 10-10m.
Question 21.
What is the wavelength for the electron accelerated by 1.0 X i0 volts?
Answer:
Step I.
Calculation of the velocity of electron
Energy (kinetic energy) of electron = 1.0 x 104 volts.
= 1.0 x 104 x 1.6 x 10-19 J = 1.6 x 10-15J.
Step II.
Calculation of wavelength of the electron
According to de Broglie equation,
λ = \(\frac {h}{mυ}\); λ ![]()
= 1.22 x 10-11m .
Question 22.
In a hydrogen atom, the energy of an electron in first Bohr’s orbit is 13.12 x 105 J mol-1. What is the energy required for its excitation to Bohr’s second orbit?
Answer:
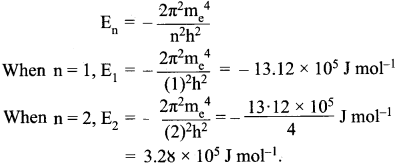
The energy required for the excitation is:
∆E = E2 – E1 = (-3.28 x l05) – (- 13.12 x 105) = 9.84 x 105 J mol-1
Question 23.
Dual behavior of matter proposed by de Broglie led to the discovery of electron microscope often used for the highly magnified images of biological molecules and other type of material. If the velocity of the electron in this microscope is 1.6 x 106 ms-1, calculate de Broglie wavelength associated with this electron.
Answer:
λ = \(\frac {h}{mυ}\); λ = 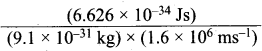
= 0.455 x 10-34 + 25 m = 0.455 nm = 455 pm.
Question 24.
An element with mass number 81 contains 31.7% more neutrons as compared to protons. Assign the symbol to the element.
Answer:
An element can be identified by its atomic number only. Let us find the atomic number.
Let the number of protons = x
∴ Number of neutrons = x + \(\frac {x × 31.7}{100}\) = (x + 0.317 x)
Now, Mass no. of element = No. of protons + No. of neutrons
81 = x + x + 0.317 x = 2.317 x
Or
x = \(\frac {81}{2.317}\) = 35
∴ No. of protons = 35, No. of neutrons = 81 – 35 = 46
Atomic number of element (Z) = Number of protons = 35
The element with atomic number (Z) 35 is bromine 8135Br.
Question 25.
The electron energy in hydrogen atom is given by En = (- 2.18 × 10-18) / n2 J. Calculate the energy required to remove an electron completely from the n = 2 orbit. What is the longest wavelength of light in cm that can be used to cause this transition?
Answer:
Step I.
Calculation of energy required
The energy required is the difference in the energy when the electron jumps from orbit with
n = ∞ to orbit with n = 2.
The energy required (∆E) = E∞ – E2
= 0 – \(\left(-\frac{2.18 \times 10^{-18}}{4} \mathrm{J}\right)\) = 5.45 x 10-19 J.
Step II.
Calculation of the longest wavelength of light in cm used to cause the transition
∆E = hv = hc / λ.
λ = \(\frac {hc}{∆E}\) = ![]() n= 3.644 x 10-7
n= 3.644 x 10-7
m = 3.644 x 10-7 x 102 = 3.645 x 10-5 cm.
Samacheer Kalvi 11th Chemistry Quantum Mechanical Model of Atom 5-Mark Questions
Question 1.
Describe about Bohr atom model.
Answer:
Assumptions of Bohr atom model.
1. The energies of electrons are quarantined
2. The electron is revolving around the nucleus in a certain fixed circular path called the stationary orbit.
3. Electron can revolve only in those orbits in which the angular momentum (mvr) of the electron must be equal to an integral multiple of h/2π
mvr = \(\frac {nh}{2π}\) where n = 1,2,3,…etc.,
4. As long as an electron revolves in a fixed stationary orbit, it doesn’t lose its energy. But if an electron jumps from a higher energy state (E2) to a lower energy state (E1), the excess energy is emitted as radiation. The frequency of the emitted radiation is E2 – E1= hv.
∴ v = \(\frac{\mathrm{E}_{2}-\mathrm{E}_{1}}{\mathrm{h}}\)
Conversely, when suitable energy is supplied to an electron, it will jump from lower energy orbit to a higher energy orbit.
5. Bohr’s postulates are applied to a hydrogen like atom (H, He+ and Li2+ etc..) the radius of the nth orbit and the energy of the electron revolving in the th orbit were derived.
rn = \(\frac{(0.529) n^{2}}{Z}\) A(0.529) n2
En = \(\frac{(-1 3.6) Z^{2}}{n}\) eV atom-1
En = \(\frac{(1312.8) Z^{2}}{n}\) kJ mol-1
Question 2.
Derive de Brogue equation and give its significance.
Answer:
1. Louis de Brogue extended the concept of dual nature of light to all forms of matter. To quantify this relation, he derived an equation for the wavelength of a matter-wave.
2. He combined the following two equations of the energy of which one represents wave character (hu) and the other represents the particle nature (mc2).
Planck’s quantum hypothesis:
E = hv ……….(1)
Einsteins mass-energy relationship:
E = mc2 ………(2)
From (1) and (2)
hv = mc2
hc/λ = mc2
∴ λ = \(\frac{h}{mc}\) ………(3)
The equation (3) represents the wavelength of photons whose momentum is given by mc. (Photons have zero rest mass).
3. For a particle of matter with mass m and moving with a velocity y, the equation (3) can be written as λ = \(\frac{h}{mc}\) ………(4)
4. This is valid only when the particle travels at speed much less than the speed of Light.
5. This equation implies that a moving particle can be considered as a wave and a wave can exhibit the properties of a particle (i.e momentum).
6. Significance of de Brogue equation:
For a particle with high linear momentum, the wavelength will be too small and cannot be observed. For a microscopic particle such as an electron, the mass is 9.1 x 10-31 kg. Hence the wavelength is much larger than the size of atom and it becomes significant.
Question 3.
What are the main features of the quantum mechanical model of an atom.
Answer:
1. The energy of electrons in an atom is quarantined.
2. The existence of quarantined electronic energy levels is a direct result of the wave-like properties of electrons. The solutions of the Schrodinger wave equation gives the allowed energy levels (orbits).
3. According to Heisenberg’s uncertainty principle, the exact position and momentum of an electron cannot be determined with absolute accuracy. As a consequence, quantum mechanics introduced the concept of orbital. Orbital is a three-dimensional space in which the probability of finding the electron is maximum.
4. The solution of the Schrodinger wave equation for the allowed energies of an atom gives the wave function Ψ, which represents an atomic orbital. The wave nature of the electron present in an orbital can be well defined by the wave function Ψ.
5. The wave function Ψ itself has no physical meaning. However, the probability of finding the electron in a small volume dx, dy, dz around a point (x,y,z) is proportional to |Ψ (x,y,z)|2 dx dy dz |Ψ (x,y,z)|2 is known as probability density and is always positive.
Question 4.
Explain about –
(1) Magnetic quantum number
(2) Spin quantum number
Answer:
(1) Magnetic quantum number:
- It is denoted by the letter ml. It takes integral values ranging from – l to +l through 0.
i.e. if l = 1; m = -1, 0 and +1. - The Zeeman Effect (the splitting of spectral lines in a magnetic field) provides the experimental justification for this quantum number.
- The magnitude of the angular momentum is determined by the quantum number l while its direction is given by magnetic quantum number.
(2) Spin quantum number:
- The spin quantum number represents the spin of the electron and is denoted by the letter ‘ms‘.
- The electron in an atom revolves not only around the nucleus but also spins. It is usual to write this as electron spins about its own axis either in a clockwise direction or in anti-clockwise direction.
- Corresponding to the clockwise and anti-clockwise spinning of the electron, maximum two values are possible for this quantum number.
- The values of ‘ms‘ is equal to –\(\frac {1}{2}\) and +\(\frac {1}{2}\).
Question 5.
Explain about the shape of orbitals.
Answer:
Orbital: The solution to Schrodinger equation gives the permitted energy values called eigen values and the wave functions corresponding to the eigen values are called atomic orbitals.
Shape of orbital:
s – orbital:
For Is orbital, l = 0, m = 0, f(θ) = 1√2 and g(φ) = 1/√2π. Therefore, the angular distribution function is equal to 1/√2π. i.e. it is independent of the angle θ and φ. Hence, the probability of finding the electron is independent of the direction from the nucleus. So, the shape of the s orbital is spherical.

p – orbital:
For p orbitals l = 1 and the corresponding m values are -1, 0 and +1. The three different m values indicates that there are three different orientations possible for p orbitals. These orbitals are designated as px, py and pz. The shape of p orbitals are dumb bell shape.
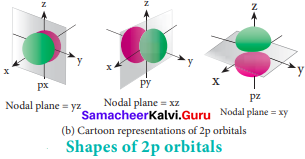
d – orbital:
For ‘d’ orbital 1 = 2 and the corresponding m values are -2, -1, 0, +l,+2. The shape of the d orbital looks like a clover leaf. The five m values give rise to five d orbitals namely dxy, dyz, dzx, dx2-y2 and dz2 The 3d orbitals contain two nodal planes.



f – orbital
For f orbital, 1 = 3 and the m values are -3, -2,-1, 0, +1, +2, +3 corresponding to seven f orbitals, \(\mathrm{f}_{\mathrm{z}^{3}}, \mathrm{f}_{\mathrm{xz}^{2}}, \mathrm{f}_{\mathrm{yz}^{2}}, \mathrm{f}_{\mathrm{xyz}}, \mathrm{f}_{\mathrm{z}\left(\mathrm{x}^{2}-\mathrm{y}^{2}\right)}, \mathrm{f}_{\mathrm{x}\left(\mathrm{x}^{2}-3 \mathrm{y}^{2}\right)}, \mathrm{f}_{\mathrm{y}\left(3 \mathrm{x}^{2}-\mathrm{y}^{2}\right)}\). They contain 3 nodal planes.
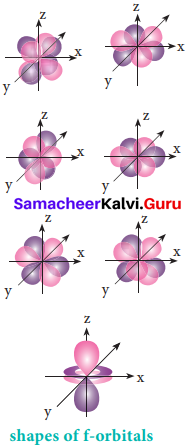
Question 6.
What is exchange energy? How it is related with stability of atoms? Explain with suitable examples.
Answer:
1. If two or more electrons with the same spin are present in degenerate orbitals, there is a possibility for exchanging their positions. During exchange process, the energy is released and the released energy is called exchange energy.
2. If more number of exchanges are possible, more exchange energy is released. More number of exchanges are possible only in the case of half filled and fully filled configurations.
3. For example, in chromium, the electronic configuration is [Ar]3d5 4s1. The 3d orbital is half filled and there are ten possible exchanges.
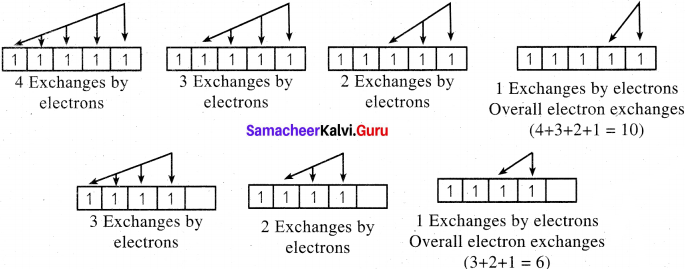
4. On the other hand only six exchanges are possible for [Ar] 3d4 4s2 configuration.
5. Hence, exchange energy for the half filled configuration is more This increases the stability of half filled 3d orbitals.
We as a team believe the information prevailing regarding the Samacheer Kalvi Solutions for 11th Chemistry Chapter 2 Quantum Mechanical Model of Atom has been helpful in clearing your doubts to the fullest. For any other help do leave us your suggestions and we will look into them. Stay in touch to get the latest updates on Tamilnadu State Board Solutions for different subjects in the blink of an eye.