Prasanna

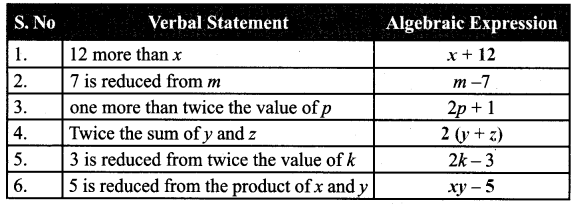
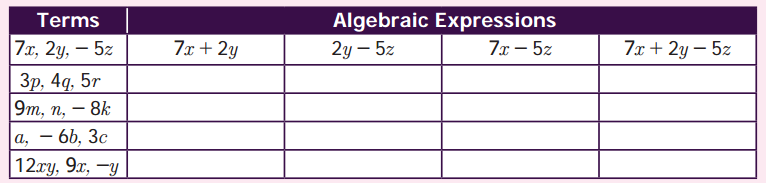
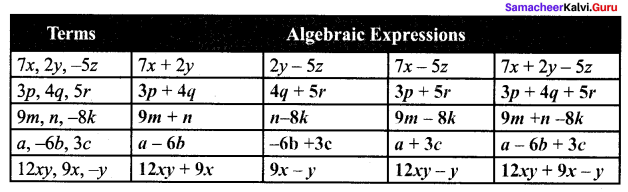
You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 3 Chapter 2 Integers Ex 2.2

Miscellaneous Practice Problems

Question 1.
Write two different real life situations that represent the integer -3.
Solution:
(i) A sapling planted at a depth of 3m
(ii) Sheela lost ₹ 3 on selling an apple.

Question 2.
Mark the following numbers on a number line
(i) All integers which are greater than -7 but less than 7.
(ii) The opposite of 3.
(iii) 5 units to the left of -1
Solution:
(i) All integers which are greater than -7 but less than 7.

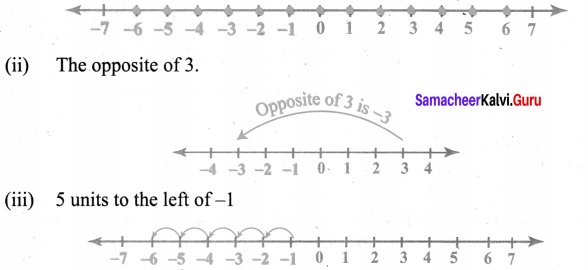
-6 is placed 5 units to the left of-1.

Question 3.
Construct a number line that shows the depth of 10 feet from the ground level and its opposite.
Solution:

Question 4.
Identify the integers and mark on the number line that are at a distance of 8 units from -6.
Solution:

Question 5.
Answer the following questions from the number line given below

(i) Which integer is greater : G or K ? Why?
(ii) Find the integer that represents C.
(iii) How many integers are there between G and H?
(iv) Find the pairs of letters which are opposite of a number.
(v) Say True or False: 6 units to the left of D is -6. ‘
Solution:
(i) K is greater. K represents -1 and G represents -3. Because it is to the right of G in the negative side of the number line.
(ii) C represents -4
(iii) G represents -3 and H represents 4.
∴ -2, -1, 0, 1, 2, 3 are the 6 numbers between G and H.
(iv) (C, H) and (E, J) are opposite pairs.
(v) False. 6 units to the left of D is 0. Because D represents +6 on the number line

Question 6.
If G is 3 and C is -1, what numbers are A and K on the number line?

Solution:
Given G is 3 and C is -1,
∴ The number line becomes

A represents -3 and K represents 7

Question 7.
Find the integers that are 4 units to the left of 0 and 2 units to the right of -3
Solution:

4 units to the left of 0 is -4.2 units to the right of -3 is -1.

Challenge Problems

Question 8.
Is there the smallest and the largest number in the set of integers? Give reason.
Solution:
No, we cannot find the smallest (-) and largest (+) number in the set of integers, as the numbers on the number line extends on both the sides without end.

Question 9.
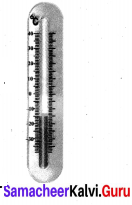
Look at the Celsius Thermometer and answer the following questions:
i) What is the temperature that is shown in the thermometer?
ii) Where will you mark the temperature 5°C below 0° C in the Thermometer?
iii) What will be the temperature, if 10°C is reduced from the temperature shown in the thermometer.
iv) Mark the opposite of 15°C in the Thermometer.

Solution:
(i) Temperature shown in the Thermometer is -10°
(ii) 5°C below 0°C is at -5°C.
(iii) Thermometer shows – 10°C if 10QC is reduced that means -10°C – (10°C) gives ^20°C.
(iv) Opposite of 15°C is -15°C

Question 10.
P, Q, R and S are four different integers on a number line. From the following clues, find these integers and write them in ascending order.
i) S is the least of the given integers.
ii) R is the smallest positive integer.
iii) The integers P and S are at the same distance from 0.
iv) Q is 2 units to the left of integer R.
Solution:
According to the clues, plotting the points on a number line, we get

As S is the least of the given integers, it is placed at the left most end.
Since R is the smallest positive integer, it is placed next to the right of 0.
As Q is 2 units to the left of R it is placed as the left next number of 0.
P and S are at the some distance from 0. P is placed opposite to S.
∴ Ascending order : S < Q < 0 < R < P.

Question 11.
Assuming that the home to be the starting point, mark the following places in order on the number line as per instructions given below and write their corresponding integers.

Places : Home, School, Library, Playground, Park, Departmental Store, Bus Stand, Railway station, Post office, Electricity Board.
Instructions:
i) Bus Stand is 3 units to the right of Home.
ii) Library is 2 units to the left of Home.
iii) Departmental Store is 6 unit to the left of Home
iv) Post office is 1 unit to the right of the library.
v) Park is 1 unit right of Departmental Store.
vi) Railway Station is 3 units left of Post Office.
vii) Bus Stand is 8 units to the right of Railway Station.
viii) School is next to the right hf Bus Stand.
ix) Playground and Library are opposite to each other.
x) Electricity Board and Departmental Store are at equal distance from Home.
Solution:

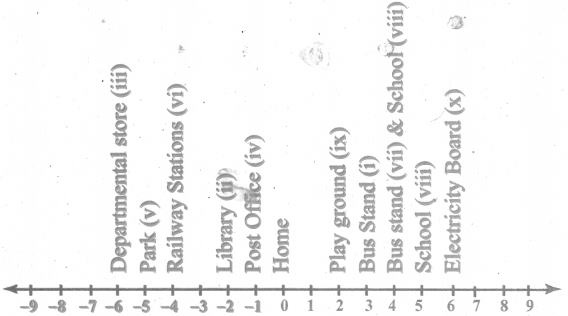
Question 12.
Complete the table using the following hints:

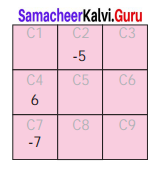
C1 : the first non-negative integer.
C3 : the opposite to the second negative integer.
C5 : the additive identity in whole numbers.
C6 : the successor of the integer in C2.
C8 : the predecessor of the integer in C7
C9 : the opposite to the integer in C5.
Solution:
C1 : First non negative integer is 0
C3 : Second negative integer is -2 its opposite is 2
C5 : 0 is the additive identity in whole numbers
C6 : C2 has -5. Its successor is -A
C8 : Integer in C7 is -7. Predecessor of-7 is -8
C9 : C5 has 0. Opposite of 0 is 0.

Question 13.
The following bar graph shows the profit (+) and loss (-) of a small scale company (in crores) between the years 2011 to 2017.

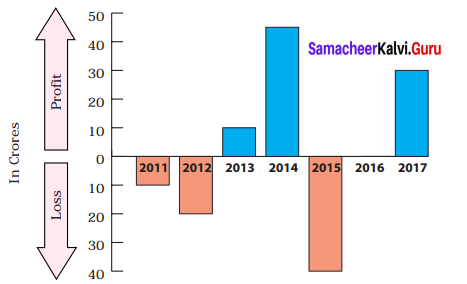
i) Write the integer that represents a profit or a loss for the company in 2014?
ii) Denote by an integer on the profit or loss in 2016.
iii) Denote by integers on the loss for the company in 2011 and 2012
iv) Say True or False: The loss is minimum in 2012.
v) Fill in: The amount of loss in 2011 is _____ as profit in 2013.
Solution:
(i) Profit ₹ 45 crores. ∴ Ans : + 45
(ii) In 2016 neither profit nor loss happened. ∴ Ans : 0
(iii) In 2011 loss is 10 crores and in 2012 loss is 20 crores. ∴ Ans : -10 and-20.
(iv) False. In 2011 the company’s loss is minimum.
(v) The same. Because in 2013 the profit is 10 crores and in 2011 the loss is 10 crores.

You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 3 Chapter 4 Geometry Additional Questions

Question 1.
List any three letters having same mirror image as the object or letters?
Solution:
A, O and T

Question 2.
In the word SYMMETRY which letters do not have identical mirror images?
Solution:
S, E and R

Question 3.
Is Indian National flag symmetrical ?
Solution:
Yes, Horizontal

Question 4.
In the word ‘FIGURE’ mention the symmetrical letters.
Solution:
I, U and E

Question 5.
Are the number of symmetrical lines equal in rectangle and square?
Solution:
No, not equal.

Question 6.
Find the number of lines of symmetry in

i) The number of lines of symmetry
ii) The number of lines of symmetry
Solution:
i) The number of lines of symmetry for this figure are 2.

ii) The number of lines of symmetry for this figure are 2.

Question 7.
Give the reflection of the letter M as shown in the figure.

Solution:

Question 8.
Find the number of lines of symmetry of the following.

Solution:

Question 9.
Are human faces symmetrical ?
Solution:
Yes

Question 10.
List some symmetrical objects from your home?
Solution:
Wall clock, dining table top, bucket, photo frame etc.

You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 2 Chapter 2 Measurements Additional Questions

Question 1.
Convert into indicated units: 200 mg into g.
Solution:
200 mg = \(200.0 \times \frac{1}{1000}\) = 0.2 g

Question 2.
(a) What are the universally accepted basic metric units?
(b) A cow gives 10 litres of milk in the morning and 8 litres in the evening. Find the total milk it gives for a week in ml?
Solution:
(a) Universally accepted basic metric units are:
Length in metre, Weight in gram and Capacity (Volume) in litre.
(b) Litres of milk the cow gives in the morning = 10 l.
Litres of milk the cow gives in the evening = 8 l.
Total milk per day = 10 + 8 = 18 l
Total milk for a week = 18 × 7 l = 126 l = 126 × 1000 ml = 126000 ml.
Total milk the cow gives for a week = 1,26,000 ml.

Question 3.
A box contains 20 kg 280 g of sugar. After transferring into a smaller box of 2 kg 720 g 7 times find the remaining sugar left in the big box in cg.
Solution:
Total sugar in the box = 20 kg 280 g.
Measurement of smaller box = 2 kg 720 g.
7 times the smaller box = 2 kg 720 g × 7 = 19 kg 040 g.
Remaining sugar = 20 kg 280 g – 19 kg 40 g = 1 kg 240 g = 1240 g. = 1240 × 100 cg = 124000 eg.
Sugar left in the box = 1,24,000 eg.

Question 4.
Sneha needs 1 m 20 cm of cloth for her blouse. If she bought 20 such cloths find the total cloth she bought in cm?
Solution:
For one blouse the cloth needed = 1 m 20 cm
Cloth needed for 20 blouse = 1 m 20 cm × 20
= 20 m 400 cm
= 20 × 100 + 400 cm
= 2000 + 400 cm
= 2400 cm.
Total cloth bought = 2400 cm.

Question 5.
Can you add 2 m 20 cm and 4 kg 80 g? Why?
Solution:
No, we can’t. To add or subtract, the measures should be in the same unit.

Question 6.
If you serve a cup of coffee measuring 150 ml each for 200 people find the volume of coffee needed in litres?
Solution:
For one cup of coffee it needs 150 ml.
For 200 people it needs 150 × 200 ml = 30000 ml = 30000 × \(\frac{1}{1000}\) l = 30 l
Coffee needed = 30 l.

Question 7.
A lorry full of fertiliser is bought to the garden having 120 coconut trees. If the lorry contain 1920 kg, then find the measure of fertiliser each coconut tree can have?
Solution:
Total measure of fertiliser = 1920 kg.
Number of coconut tress = 120
For one tree = \(\frac{1920}{120}\) kg = 16 kg.
One tree can have 16 kg of fertiliser

Question 8.
Convert 7 kg 250 g in to mg, g and cg?
Solution:
7 kg 250 g.
(i) 7 kg 250 g = 7 × 1000 + 250 g. = 7000 + 250 = 7250 g.
(ii) 7 kg 250 g = 7250 g. = 7250 × 1000 mg = 72,50,000 mg.
(iii) 7 kg 250 g = 7250 g. = 7250 × 100 cg = 7,25,000 cg.

Question 9.
Convert 20 m 20 cm into cm, m and km.
Solution:
20 m 20 cm.
(i) 20 m 20 cm = 20 × 100 + 20 cm = 2000 + 20 cm = 2020 cm
(ii) 20 m 20 cm = 2020 cm = 2020 × \(\frac{1}{100}\) m = 20.20 m
(iii) 20 m 20 cm = 20.20 m = 20.20 × \(\frac{1}{1000}\) km = 0.02020 km

Question 10.
Convert 85 l 720 ml into ml, l and kl?
Solution:
85 l 720 ml
(i) 85 l 720 ml = 85 × 1000 + 720 ml = 85000 + 720 ml = 85,720
(ii) 85 l 720 ml = 85 l + 720 × \(\frac{1}{1000}\) l = 85 l + 0.720 l = 85.72 l.
(iii) 85 l 720 ml = 85.72 l = 85.72 × \(\frac{1}{1000}\) kl = 0.08572 kl.

Question 11.
Which is greater 0.007 g, 0.7 kg or 70 mg?
Solution:
0.007 g = 0.007 × 1000 mg = 7 mg
0.7 kg = 0.7 × 10,00,000 mg = 7,00,000 mg
70 mg = 70 mg
∴ 0.7 kg is greater.

Question 12.
A bus leaves for Kanchipuram from Chennai at 4.30 p.m. It takes 1 hr 25 min. to reach there. At what time will it reach at Kanchipuram?
Solution:
Starting time from Chennai = 4 : 30 pm.
Duration of travel = 01 hr : 25 min
Arrival at Kanchipuram = 5 : 55 pm
The bus will reach Kanchipuram at 5 : 55 pm.

Question 13.
The duration of a film show is 3 hrs 15 min. It starts at 6 : 30 p.m. When will it end?
Solution:
The film starts at = 6 : 30 pm.
Duration of the film show = 3 hr : 15 min
The show end at = 9 : 45 p.m.

Question 14.
A train arrive Chennai Central at 11 : 55 am. It reached Chennai 1 hr 25 min late. What is the scheduled arrival time of the train at Chennai?
Solution:
The train arrived Chennai at 11 : 55 am = 11 : 55 hours
The train is late by = 1 hour 25 min
Scheduled Time = 10 : 30 hours
The scheduled arrival time = 10.30 a.m

Question 15.
Raju visited a fashion show. He stayed there for 2 hr 30 min and came back to home. If he reached in the fashion show at 8 : 45 pm. When did he leave for his home?
Solution:
Raju reached the fashion show at 8 : 45 p.m
He stayed there for 2 hr : 30 min
He will leave the show at 10 : 75 min
= 10 hr 75 min
= 10 hrs (60 + 15) min
= 10 hrs + 1 hr 15 min
= 11 hrs 15 min
Raju will leave the show at 11 : 15 p.m

Question 16.
Mammalia travelled 4 hrs 45 min by bus and 4 hrs 45 min by train. Calculate the time she spent in travelling?
Solution:
Time travelled by bus = 4 hrs 45 min
Time travelled by train = 4 hrs 45 min
Total time she travelled = 8 hrs 90 min
= 8 hrs (60 + 30) min 8 hrs + 1 hr 30 min
Total time she travelled = 9 hr 30 min

Question 17.
David left home at 4 : 30 p.m to meet his friend. He came back after 3 hr 25 min At what time did he came back?
Solution:
Time at which David left home = 4 : 30 p.m.
Time he spent outside = 3 hr : 25 min
Time at which he came back = 7 : 55 p.m

Question 18.
Malar reached her school at 7 : 30 a.m. and left for home at 12 : 45 p.m. How long did she stay in school?
Solution:
Malar left for home at 12 : 45 p.m. = 12 : 45 hrs
She reached school at = 7 : 30 hrs
She stayed at school for = 5 : 15 hrs

Question 19.
Mathi’s date of birth was 25.07.2000. What is her age on 29.08.2017?
Solution:
Convert the given date in YY MM DD format
Age = 2017.08.29
Date of birth = 2000 .07 .25
Age = 17. 01. 04
She is 17 years one month 04 days old.

Question 20.
Find whether 2000,2018 and 2012 are leap years or not.
Solution:
2000 is a leap year (divisible by 400)
2018 is a not leap year (not divisible by 4)
2012 is a leap year (divisible by 4)

Question 21.
Find the railway time for 12 : 05 a.m, 4 : 20 pm
Solution:
12 : 05 am is 00 : 05 hrs
4 : 20 p.m. is (12 + 4) : 20 hrs = 16 : 20 hrs

You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 3 Chapter 2 Integers Ex 2.1

Question 1.
Fill in the blanks.
(i) The potable water available at 100m below the ground level is denoted as ______ m.
Hint: Below ground level – negative; ground level – 0; above ground level – positive.
(ii) A swimmer dives to a depth of 7 feet from the ground into the swimming pool. The integer that represents this, is ______ feet.
Hint: Below ground level – negative numbers.
(iii) -46 is to the _____ of -35 on the number line.
Hint: -46 <-35
(iv) There are _____ integers from -5 to +5 (both inclusive).

(v) ______ is an integer which is neither positive nor negative.

Solutions:
(i) -100
(ii) -7
(iii) Left
(iv) 11
(v) 0

Question 2.
Say True or False.
(i) Each of the integers -18, 6, -12, 0 is greater than -20.
(ii) -1 is to the right of 0.
(iii) -10 and 10 are at equal distance from 1.
(iv) All negative integers are greater than zero.
(v) All whole numbers are integers.
Solution:
(i) True
(ii) False
(iii) False
(iv) False
(v) True

Question 3.
Mark the numbers 4, -3, 6, -1 and -5 on the number line.
Solution:

Question 4.
On the number line, which number is
i) 4 units to the right of-7?
ii) 5 units to the left of 3?
Solution:

(i) – 3 is 4 units to the right of -7
(ii) – 2 is 5 units to the left of 3

Question 5.
Find the opposite of the following numbers.
(i) 44
(ii) -19
(iii) 0
(iv) -312
(v) 789
Solution:
(i) Opposite of 44 is – 44
(ii) Opposite of-19 is + 19 or 19
(iii) Opposite of 0 is 0
(iv) Opposite of-312 is + 312 or 312
(v) Opposite of 789 is – 789.

Question 6.
If 15 km east of a place is denoted as + 15 km, what is the integer that represents 15 km west of it?
Solution:
Opposite of east is west.
∴ If 15 km east is + 15 km, then 15 km west is – 15 km.

Question 7.
From the following number lines, identify the correct and the wrong representations with reason?

Solution:
(i) This representation is wrong. Because the numbers are not continuously marked as -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6,
(ii) This is the correct representation of Integers
(iii) The representation is wrong. – 2 is misplaced in the number line.
(iv) This representation is correct as the numbers are marked at equal intervals in the correct order.
(v) Here negative integers are marked wrongly to the left of 0

Question 8.
Write all the integers between the given numbers.
(a) 7 and 10
(b) -5 and 4
(c) -3 and 3
(d) -5 and 0
Solution:

Question 9.
Put the appropriate signs as <, > or = in the box?

Solution:
(i) We know that -7 is to the left of 8.
(ii) -8 is to the left of -7,
(iii) -1000 is to the left of -999,
(iv) -111 and-111 coincides in the number line.
(v) 0 is to the right of -200,

Question 10.
Arrange the following integers in ascending order.
i) -11, 12, -13, 14, -15, 16, -17, 18, -19, -20
ii) -28, 6, -5, -40, 8, 0, 12, -1, 4, 22
iii) -100, 10, -1000, 100,0, -1, 1000, 1, -10
Solution:
(i) -11, 12, -13, 14, -15, 16, -17, 18, -19, -20

• First separating the positive integers 12, 14, 16, 18 and the negative integers -11,-13,-15,-17,-19,-20.
• Then arranging the positive integers in ascending order we get 12, 14, 16, 18 and negative integers in ascending order as -20, -19, -17, -15, -13, -11 4
• Now the ascending order : -20, -19, -17, -15, -13, -11, 12, 14, 16, 18.

(ii) -28, 6, -5, -40, 8, 0, 12, -1, 4, 22

• Positive integers are 6, 8, 12, 4, 22 Negative integers are -28, -5, -40, -1
• Arranging the positive integers in ascending order we get 4, 6, 8, 12, 22 and the negative integers in ascending order -40, -28, -5, -1
• The number 0 is neither positive nor negative and stand in the middle.
• In ascending order : -40, -28, -5, -1, 0, 4, 6, 8,12, 22

(iii) -100, 10, -1000, 100, 0, -1, 1000, 1, -10

• Separating positive integers 10, 100, 1000, 1 and negative integers -100, -1000, -1, -10.
• Now the positive integers in ascending order 1,10,100,1000 and the negative integers in ascending order. -1000, -100, -10, -1
• Also ‘0’ stand in the middle as its is neither positive nor negative.
• ∴ The numbers in ascending order: -1000, -100, -10, -1, 0, 1, 10, 100, 1000.

Question 11.
Arrange the following integers in descending order.
i) 14, 27, 15, -14, -9, 0, 11, -17
ii) -99, -120, 65, -46, 78, 400, -600
iii) 111, -222, 333, -444, 555, -666, 7777, -888
Solution:
(i) 14, 27, 15, -14, -9, 0,11, -17

• Separating the positive integers 14, 27, 15, 11 and negative integers -14, -9, -17
• Arranging in descending order we get the positive integers 27,15,14,11 and the negative integers -9, -14, -17.
• ‘0’ is neither positive nor negative and so it stand in middle.
• ∴ The numbers in descending order : 27, 15, 14, 11, 0, -9, -14, -17

(ii) -99, -120, 65, -46, 78, 400, -600

• Separating the positive integers 65, 78, 400 and negative integers -99, -120, -46, -600
• Arranging the positive integers in descending order as 400, 78, 65 and the negative integers in descending order -46, -99, -120, -600.
• The numbers in descending order : 400, 78, 65, -46, -99, -120, -600.

(iii) 111, -222, 333, -444, 555, -666, 7777, -888

• Separating the positive integers 111, 333, 555, 7777 and negative integers -222, -444, -666, -888
• Arranging the positive integers in descending order as 7777, 555, 333, 111 and negative integers in descending order as -222, -444, -666, -888
• The numbers in descending order : 7777, 555, 333, 111, -222, -444, -666, -888

Objective Type Questions

Question 12.
There are _______ positive integers from – 5 to 6.
(a) 5
(b) 6
(c) 7
(d) 11
Solution:
(b) 6
Hint:

Question 13.
The opposite of 20 units to the left of 0 is
(a) 20
(b) 0
(c) -20
(d) 40
Solution:
(a) 20
Hint:

Question 14.
One unit to the right of -7 is
(a) +1
(b) -8
(c) -7
(d) -6
Solution:
(d) -6
Hint:

Question 15.
3 units to the left of 1 is
(a) -4
(b) -3
(c) -2
(d) 3
Solution:
(c) -2
Hint:

Question 16.
The number which determines marking the position of any number to its opposite on a number line is?
(a) -1
(b) 0
(c) 1
(d) 10
Solution:
(b) 0
Hint:

You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 3 Chapter 1 Fractions Intext Questions

(Try These Textbook Page No. 2)

Question 1.
If all the three cakes are divided among the total participants of the function what would be each one’s share? Discuss.
Solution:
Total participants of the function = 9
Total number of cakes = 3
∴ Each cake should be divided into 3 equal parts.
∴ Total number of equal parts of cake = 9
∴ Each one’s share may be \(\frac{1}{9}\) of total cakes or \(\frac{1}{3}\) of a cake.

Question 2.
Observe the following and represent the shaded parts as fraction.

Solution:
(i) Total number of equal parts = 8
Shaded Parts = 3
Fraction representing the shaded parts = \(\frac{3}{8}\)

(ii) Total number of equal parts = 15
Shaded parts = 5
∴ Fraction representing the shaded parts = \(\frac{5}{15}\)

(iii) Total number of equal parts = 9
Shaded parts = 3
∴ Fraction representing the shaded parts = \(\frac{3}{9}\)

(iv) Total number of equal parts = 9
Shaded parts = 5
Fraction representing the shaded parts = \(\frac{5}{9}\)

Question 3.
Look at the following beakers, express the quantity of water as fraction and arrange them in ascending order:

Solution:
Quantity of water in the first beaker = 1 full
Quantity of water in the second beaker = \(\frac{1}{4}\)
Quantity of water in the third beaker = \(\frac{3}{4}\)
Quantity of water in the fourth beaker = \(\frac{1}{2}\)
Ascending order \(\frac{1}{4}\) < \(\frac{1}{2}\) < \(\frac{3}{4}\) < 1

Question 4.
Write the fraction of shaded part in the following.

Solution:
(i) Total number of equal parts = 3
Shaded parts = 2
Fraction representing the shaded portion = \(\frac{2}{3}\)

(ii) Total number of equal parts = 4
Shaded parts = 3
Fraction representing the shaded parts = \(\frac{3}{4}\)

(iii) Total number of equal parts = 5
Shaded parts = 4
Fraction representing the shaded parts = \(\frac{4}{5}\)

Question 5.
Write the fraction that represents the dots In the triangle.

Solution:
Total number of dots = 24
Number of dots in the triangle = 6
∴ Fraction represents the dots in the triangle = \(\frac{6}{24}\)

Question 6.
Find the fractions of the shaded and unshaded portions in the following.

Solution:
(a) Total number of equal parts = 8
Shaded parts = 2
∴ Fraction representing shaded parts = \(\frac{2}{8}\)

(b) Total number of equal parts = 8
Unshaded parts = 6
∴ Fraction of unshaded portion = \(\frac{6}{8}\)

(Activity Textbook Page No. 3)

Take a rectangular paper. Fold it into two equal parts. Shade one part, write the fraction. Again fold it into two halves. Write the fraction for the shaded part. Continue this process 5 times and write the fraction of the shaded part. Establish the equivalent fractions of \(\frac{1}{2}\) in the folded paper to your friends.

Solution:
First time = \(\frac{1}{2}\)
Second time = \(\frac{2}{4}\)
Third time = \(\frac{4}{8}\)
Fourth time = \(\frac{8}{16}\)
Fifth time = \(\frac{16}{32}\)

(Try These Textbook Page No. 4)

Question 1.
Find the unknown in the following equivalent fractions.

Solution:

(Try These Textbook Page No. 7)

Question 1.
Shade the rectangle for the given pair of fractions and say which is greater among them.

Solution:

Question 2.
Which is greater \(\frac{3}{8}\) or \(\frac{3}{5}\) ?
Solution:
LCM of the denominators 8 and 5 is 40.
Finding the equivalent fractions.

Question 3.
Arrange the fractions in ascending order : \(\frac{3}{5}, \frac{9}{10}, \frac{11}{15}\)
Solution:

Question 4.
Arrange the fractions in descending order : \(\frac{9}{20}, \frac{3}{4}, \frac{7}{12}\)
Solution:

(Try These Textbook Page No. 9)

(i) \(\frac{2}{3}+\frac{5}{7}\)
Solution:
By cross multiplication technique

(ii) \(\frac{3}{5}-\frac{3}{8}\)
Solution:
By cross multiplication technique

(Activity Textbook Page No. 10)

Question 1.
Using the given fractions \(\frac{1}{5}, \frac{1}{6}, \frac{1}{10}, \frac{1}{15}, \frac{2}{15}, \frac{4}{15}, \frac{1}{30}, \frac{7}{30} \text { and } \frac{9}{30}\) fill in the missing ones in the given 3 × 3 square in such a way that the addition of fractions through rows, columns and diagonals give the same total \(\frac{1}{2}\)

Solution:

(Try These Textbook Page No. 10)

Question 1.
Complete the following table. The first one is done for you.

(Try These Textbook Page No. 11)

Question 1.
(i) Are 5\(\frac{2}{3}\) and 5\(\frac{4}{6}\) equal?
Solution:

(ii) \(\frac{3}{2} \neq 3 \frac{1}{2}\) why?
Solution:

Question 2.
Convert 3\(\frac{1}{3}\) into improper fraction.
Solution:

Question 3.
Convert \(\frac{45}{7}\) into mixed fraction.
Solution:

(Try These Textbook Page No. 13)

Question 1.
Find the sum of 5\(\frac{4}{9}\) and 3\(\frac{1}{6}\).
Solution:

Question 2.
Subtract 7\(\frac{1}{6}\) and 12\(\frac{3}{8}\)
Solution:

Question 3.
Subtract the sum of 6\(\frac{1}{6}\) and 3\(\frac{1}{5}\) from the sum of 9\(\frac{2}{3}\) and 2\(\frac{1}{2}\).
Solution:

(Try These Textbook Page No. 15)

Question 1.
2\(\frac{1}{4}\) × 3 is not equal to 6\(\frac{1}{4}\). Why?
Solution:

Question 2.
Simplify : 35 × \(\frac{3}{7}\).
Solution:

Question 3.
Find the value of \(\frac{1}{5}\) of 15.
Solution:
\(\frac{1}{5}\) of 15 = \(\frac{1}{5}\) × 15 = \(\frac{15}{5}\) = 3

Question 4.
Find the value of \(\frac{1}{3}\) of \(\frac{3}{4}\)
Solution:

Question 5.
Multiply 7\(\frac{3}{4}\) by 5\(\frac{1}{2}\).
Solution:

(Activity Textbook Page No. 15)

Take a paper. Fold it into 4 parts vertically of equal width. Shade one part of it with red. Then, fold it into 3 parts horizontally of equal width. Shade two parts of it with blue. Now, you count the number of shaded grids which have both the colours. (Hint: The total number of grids is the product of \(\frac{2}{3}\) and \(\frac{1}{4}\))
Solution:
Activity to be done by the students themselves

(Try These Textbook Page No. 17)

Question 1.
(i) How many 6s are there in 18?
Solution:
Number of 6s in 18 are \(\frac{18}{6}\) = 3

(ii) How many \(\frac{1}{4}\)s are there in 5?
Solution:
Number of \(\frac{1}{4}\) s in 5 are 5 ÷ \(\frac{1}{4}\) = 5 × \(\frac{4}{1}\) = 20

(iii) \(\frac{1}{3}\) ÷ 5 = ?
Solution:
\(\frac{1}{3}\) ÷ 5 = \(\frac{1}{3} \times \frac{1}{5}\) = \(\frac{1}{15}\)

(Try These Textbook Page No. 18)

Question (i)
Find the value of 5 ÷ 2\(\frac{1}{2}\).
Solution:

Question (ii)
Simplify: \(1 \frac{1}{2} \div \frac{1}{2}\)
Solution:

Question (iii)
Divide 8 \(\frac{1}{2}\) by 4\(\frac{1}{4}\).
Solution:

You can Download Samacheer Kalvi 6th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 6th Maths Solutions Term 3 Chapter 5 Information Processing Intext Questions

Exercise 5.1

Try These (Text book Page No. 74)

Question 1.
Find the 10th term of the Fibonacci sequence
Solution:
We have the Fibonacci sequence 1, 1, 2, 3, 5, 8, 13, 21, 34, 55,….
The 10th term is 55.

Question 2.
If the 11^th term of the Fibonacci sequence is 89 and 13^th term is 233 then, what is the 12^th term?
Solution:
Given 11^th term of the Fibonacci sequence is 89 and 13^th term of is 233
We know that a number in Fibonacci sequence is got by adding the previous two consecutive numbers.
11^th term + 12^th term = 13^th term
89 +12^th term =233
∴ 12^th term = 233 – 89 = 144
∴ 12^th term in Fibonacci sequence = 144.

Try this (Text book Page No.75)

Question 1.
Are two consecutive Fibonacci numbers relatively prime?
Solution:
GCD of two consecutive numbers in Fibonacci sequence is 1.
∴ They are relatively prime.

Try These (Text book Page No. 78)

Question 1.
The teacher should give oral instructions to the students to draw the geometrical figure already drawn by him / her.
i) Draw a square. In the middle of the square, draw a circle in such a way that the circle does not touch any side of the square. Divide the circle into four equal parts. Shade the bottom right part of the circle. Ask the students to show that figure drawn by them.
ii) Draw a triangle on a piece of paper. Make it crazy looking by adding some features. Give instructions to your friend to draw it exactly the same.

Solution:
i) The figure will be as drawn below.
ii) The instructions may be:

1. Draw a square of side 3 cm.
2. Draw an equilateral triangle of side 2 cm inside the square without touching the sides of the square.
3. Draw a small circle at the middle of the triangle.
4. Draw two eyes above the circle.
5. Draw a mouth below the circle.
6. Draw two legs at the base of the triangle.
7. Draw hands to the other to sides of the triangle stretching inside the square. Draw two ears above the hands.

Question 2.
Suppose your friend wants to come to your house from his/her house. Give clear instructions in order, to reach your house.
Solution:
Activity to be done by the students themselves

Students can Download Maths Chapter 3 Algebra Additional Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 3 Algebra Additional Questions

Additional Questions and Answers

Exercise 3.1

Question 1.
Write any three expressions each having 4 terms:
Solution:
(i) 2x³ – 3x² + 3xy + 8
(ii) 7x³ + 9y² – 2xy² – 6
(iii) 9x² – 2x + 3xy – 1

Question 2.
Identify the co-efficients of the terms of the following expressions
(i) 2x – 2y
(ii) x + y +3
Solution:
(i) 2x – 2y
The co-efficient of x in 2x is 2
The co-efficient of y in – 2y is – 2

(ii) x + y + 3
The co-efficient of x is 1
The co-efficient ofy is 1
The constant term is 3

Question 3.
Group the like terms together from the following: 6x, 6, -5x, – 5, 1, x, 6y, y, 7y, 16x, 3
Solution:
We have 6x, -5x, x, 16x are like terms
6y, y, 7y, are like terms
6, – 5, 1, 3 are like terms

Question 4.
Give the algebraic expressions for the following cases:
(i) One half of the sum of a and b.
(ii) Numbers p and q both squared and added
Solution:
(i) \(\frac{1}{2}\) (a + b)
(ii) p² + q²

Exercise 3.2

Question 1.
If A = 2a² – 4b – 1 ; B = 5a² + 3b – 8 and C = 2a² – 9b + 3 then find the value of A – B + C.
Solution:
Given A = 2a² – 4b – 1 ; B = 5a² + 3b – 8 ; C = 2a² – 9b + 3
A – B + C = (2a² – 4b – 1) – (5a² + 3b – 8) + (2a² – 9b + 3)
= 2a² – 4b – 1 + (-5a² – 3b + 8) + 2a² – 9b + 3
= 2a² – 4b – 1 – 5a² – 3b + 8 + 2a² – 9b + 3
= 2a² – 5a² + 2a² – 4b – 3b – 9b – 1 + 8 + 3
= (2 – 5 + 2) a² + (-4 – 3 – 9) 6 + (-1 + 8 + 3)
= -a² – 16b + 10

Question 2.
How much 2x³ – 2x² + 3x + 5 is greater than 2x³ + 7x² – 2x + 7?
Solution:
The required expression can be obtained as follows.
= 2x³ – 2x² + 3x + 5 – (2x³ + 7x² – 2x + 7)
= 2x³ – 2x² + 3x + 5 + (-2x³ – 7x² + 2x – 7)
= 2x³– 2x² + 3x + 5 – 2x³ – 7x² + 2x – 7
= (2 – 2) x³ + (-2 – 7) x² + (3 + 2) x + (5 – 7)
= 0x³ + (-9x²) + 5x – 2 = -9x² + 5x – 2
∴ 2x³ – 2x² + 3x + 5 is greater than 2x³ + 7x² – 2x + 7 by -9x² + 5x – 2

Question 3.
What should be added to 2b² – a² to get b² – 2a²
Solution:
The required expression is obtained by subtracting 2b² – a² from b² – 2a²
b² – 2a² – (2b² – a²) = b² – 2a² + (-2b² + a²)
= b² – 2a² – 2b² + a²
= (1 – 2) b² + (-2 + 1) a² = -b² – a²
So -b² – a² must be added

Exercise 3.3

Question 1.
Length of one side of an equilateral triangle is 3x – 4 units. Find the perimeter.
Solution:
Equilateral triangle has three sides equal.
Perimeter = Sum of three sides
= (3x – 4) + (3x – 4) + (3x – 4) = 3x – 4 + 3x – 4 + 3x – 4
= (3 + 3 + 3)x + [(-4) + (-4) + (-4)] = 9x + (-12) = 9x – 12
∴ Perimeter = 9x – 12 units.

Question 2.
Find the perimeter of a square whose side is y – 2 units.
Solution:
Perimeter = (y – 2) + (y – 2) + (y – 2) + (y – 2)
= y – 2 + y – 2 + y – 2 + y – 2 = 4y – 8
Perimeter of the square = 4y – 8 units.

Question 3.
Simplify 3x – 5 – x + 9 if x = 3
Solution:
3x – 5 – x + 9 = 3(3) – 5 – 3 + 9
= 9 – 5 – 3 + 9 = 18 – 8 = 10

Students can Download Maths Chapter 3 Algebra Ex 3.4 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 3 Algebra Ex 3.4

Miscellaneous Practice Problems

Question 1.
Subtract – 3ab – 8 from 3ab – 8. Also subtract 3ab + 8 from -3ab – 8.
Solution:
Subtracting -3ab – 8 from 3ab + 8
= 3ab + 8 – (-3ab – 8) = 3ab + 8 + (3ab + 8)
= 3ab + 8 + 3ab + 8 = (3 + 3) ab + (8 + 8)
= 6ab + 16
Also subtracting 3 ab + 8 from – 3ab – 8
= – 3ab – 8 – (3ab + 8) = – 3ab – 8 + (-3ab – 8) = – 3ab – 8 – 3 ab – 8
= [(-3) + (- 3)] ab + [(-8) + (-8)] = – 6ab + (- 16)
= -6ab – 16

Question 2.
Find the perimeter of a triangle whose sides are x + 3y, 2x + y, x – y.
Solution:
Perimeter of a triangle = Sum of three sides
= (x + 3y) + (2x + y) + (x – y)
= x + 3y + 2x + y + x – y
= (1 + 2 + 1)x + (3 + 1 + (-1))y = 4x + 3y
∴ Perimeter of the triangle = 4x + 3y

Question 3.
Thrice a number when increased by 5 gives 44. Find the number.
Solution:
Let the required number be x.
Thrice the number = 3x.
Thrice the number increased by 4 = 3x + 5
Given 3x + 5 = 44
3x + 5 – 5 = 44 – 5
3x = 39
\(\frac{3 x}{3}=\frac{39}{3}\)
x = 13
∴ The required number = 13

Question 4.
How much smaller is 2ab + 4b – c than 5ab – 3b + 2c.
Solution:
To find the answer we have to find the difference.
Here greater number 5ab – 3ab + 2c.
∴ Difference = 5ab – 3b + 2c – (2ab + 4b – c) = 5ab – 3b + 2c + (- 2ab -4b + c)
= 5ab – 3b + 2c – 2ab – 4b + c
= (5 – 2) ab + (-3 – 4) b + (2 + 1) c = 3ab + (-7)b + 3c
= 3ab – 7b + 3c
It is 3ab – 7b + 3c smaller.

Question 5.
Six times a number subtracted from 40 gives – 8. Find the number.
Solution:
Let the required number be x. Six times the number = 6x.
Given 40 – 6x = – 8
-6x + 40 – 40 = -8 – 40
– 6x = – 48
\(\frac{-6 x}{-6}=\frac{-48}{-6}\)
x = 8
∴ The required number is 8.

Challenge Problems

Question 6.
From the sum of 5x + 7y -12 and 3x – 5y + 2, subtract the sum of 2x – 7y – 1 and – 6x + 3y + 9.
Solution:
Sum of 5x + 7y – 12 and 3x – 5y + 2 .
= 5x + 7y- 12 + 3x – 5y + 2 = (5 + 3) x + (7 – 5) y + ((- 12) + 2)
= 8x + 2y – 10.
Again Sum of 2x – 7y – 1 and – 6x + 3y + 9
= 2x – 7y – 1 + (- 6x + 3y + 9) = 2x – 7y – 1 – 6x + 3y + 9
= (2 – 6) x + (- 7 + 3) y + (- 1 + 9)
= – 4x – 4y + 8
Now 8x + 2y – 10 – (-4x – 4y + 8)
= 8x + 2y – 10 + (4x + 4y – 8)
= 8x + 2y – 10 + 4x + 4y – 8
= (8 + 4) x + (2 + 4) y + ((- 10) + (- 8))
= 12x + 6y – 18

Question 7.
Find the expression to be added with 5a – 3b – 2c to get a – 4b – 2c?
Solution:
To get the required expression we must subtract 5a – 3b + 2c from a – 4b – 2c.
∴ a – 4b – 2c – (5a – 3b + 2c) = a – 4b – 2c + (- 5a + 3b – 2c)
= a – 4b – 2c – 5a + 3b -2c
= (1 – 5) a + (- 4 + 3) b + (- 2 – 2) c
= – 4a – b – 4c.
∴ -4a – b – 4c must be added.

Question 8.
What should be subtracted from 2m + 8n + 10 to get – 3m + 7n + 16?
Solution:
To get the expression we have to subtract – 3m + 7n + 16 from 2m + 8n + 10.
(2m + 8n + 10) – (-3m + 7n + 16) = 2m + 8n + 10 + 3m – 7n – 16
= (2 + 3) m + (8 – 7) n + (10 – 16)
= 5m + n – 6

Question 9.
Give an algebraic equation for the following statement:
“The difference between the area and perimeter of a rectangle is 20”.
Solution:
Let the length of a rectangle = l and breadth = b then Area = lb; Perimeter = 2(1 + b)
Area – Perimeter = 20
∴ lb – 2(l + b)

Question 10.
Add : 2a + b + 3c and a + \(\frac{1}{3}\)b + \(\frac{2}{5}\)c
Solution:

Students can Download Maths Chapter 3 Algebra Intext Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 3 Algebra Intext Questions

Exercise 3.1

Try These (Text Book Page No. 51)

Question 1.
Identify the variable and constants among the following terms.
a, 11 – 3x, xy, -89, -m, -n, 5, 5ab, -5 3y, 8pqr, 18, -9t, -1, -8
Solution:
Variable : a, -3x, xy, -m, -n, 5ab, 3y, -9t, 8pqr
Constants : 11, -89, 5, -5, 18, -1, -8

Question 2.
Complete the following table.

Solution:

Try this (Text book Page No. 53)

Question 1.
Can we use the operations multiplication and division to combine terms?
Solution:
No, We can use addition and subtraction to combine terms.
If we use multiplication or division to combine then it become a single term.
Eg : xy, \(\frac{x}{y}\) are monomials.

Try This (Text book Page No. 54)

Question 1.
Complete the following table by forming expressions using the terms given. One is done for you.

Solution:

Try this (Text book Page No. 56)

Question 1.
Identify the like terms among the following and group them.
7xy, 19x, 1, 5y, x, 3yx, 15, -13y, 6x, 12xy, -5, 16y, -9x, 15xy, 23, 45y, -8y, 23x, -y, 11
Solution:
7xy, 3yx, 12xy, 15xy, are like terms
19x, x, 6x,-9x, 23x, are like terms
5y, -13y, 16y, 45y, -8y, -y, are like terms
1, 15, -5, 23, 11, are like terms.

Try This (Text book Page No. 57)

Question 1.
Try to find the value of the following expressions if p = 5 and q = 6.
(i) p + q
(ii) q – p
(iii) 2p + 2 > q
(iv) pq – p – q
(v) 5pq – 1
Solution:
(i) Given p = 5; q = 6
p + q = 5 + 6 = 11
(ii) q – p = 6 – 5 = 1
(iii) 2p + 2 > q = 2(5) + 3(6) = 10 + 18 = 28
(iv) pq – p – q = (5) (6) – 5 – 6 = 30 – 5 – 6 = 25 – 6 = 19

Exercise 3.2

Try These (Text book Page No. 59)

Question 1.
Add the terms
(i) 3p, 14p
(ii) m, 12m, 21m
(iii) 11abc, 5abc
(iv) 12y, -y
(v) 4x, 2x, -7x.
Solution:
(i) 3p + 14p = 17p
(ii) m + 12m + 21m = (1 + 12 + 21 )m
= 34 m
(iii) 11abc + 5abc = (11 + 5) abc
= 16 abc
(iv) 12y + (-y) = (12 + (-1))y
= (12 – 1 )y
= 11y
(v) 4x + 2x + (-7x) = (4 + 2+(-7))x
= (6 + (-7))x
= -1x

Ty this (Text Book Page No. 60)

Question 1.
3x; + (y – x) = 3x + y – x, but 3x – (y – x) ≠ 3x – y – x. why ?
Solution:
In the first case
LHS = 3x + (y – x) = 3x + y – x = 3x – x + y = (3 – 1)x + y
= 2x + y
RHS = 3x + y – x = 2x + y
LHS = RHS ⇒ 3x + (y – x) = 3x + y – x
But in the second case
LHS = 3x – (y – x) = 3x – y + x
= (3 + 1)x – y = 4x – y
RHS = 3x – y – x = 3x – x – y
LHS ≠ RHS
∴ 3x – (y – x) ≠ 3x – y – x

Try this (Page No. 1)

Question 1.
What will you get if twice a number is subtracted from thrice the same number?
Solution:
Let the unknown number be x.
Twice the number = 2x.
Thrice the number = 3x.
Twice the number is subtracted from thrice the number = 3x – 2x = (3 – 2)x = x

Exercise 3.3

Try These (Text book Page No. 65)

Question 1.
Try to construct algebraic equations for the following verbal statements.

Question 1.
One third of a number plus 6 to 10.
Solution:
\(\frac{1}{3}\) + 6 = 10

Question 2.
The sum of five times of x and 3 is 28
Solution:
5 (x + 3) = 28

Question 3.
Taking away 8 from y gives 11
Solution:
y – 8 = 11

Question 4.
Perimeter of a square with side a is 16 cm.
Solution:
4 × a = 16

Question 5.
Venkat’s mother’s age is 7 years more than 3 times venkat’s age. His mother’s age is 43 years.
Solution:
3x + 7 = 43, where x is venkat’s age.

Try this (Text book Page No. 65)

Question 1.
Why should we subtract 5 and not some other number ? why don’t we add 5 on both sides? Discuss.
Solution:
Given x + 5 = 12
(i) Our aim is to find the value of x. Which means we have to eliminate the other values from LHS. Since 5 is given with x it should be subtracted.
(ii) If we add 5 on both sides we cannot eliminate the numbers from LHS and we get x + 10.

Try this (Text book Page No. 66)

Question 1.
If the dogs, cats and parrots represents unknown find them. Substitute each of the values so obtained in the equations and verify the answers.
Solution:
(i) 1 dog + 1 dog + 1 dog = 24
3 dog = 24

(ii) 1 dog + 1 cat + 1 cat = 14
1 dog + 2cat = 14
8 + 2cat = 14
2cat = 14 – 8
2 cat = 6
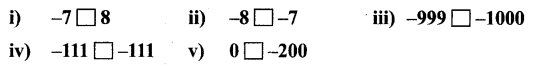
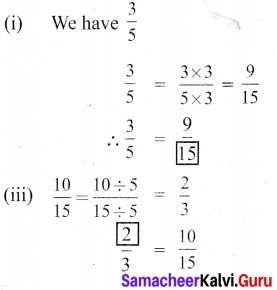
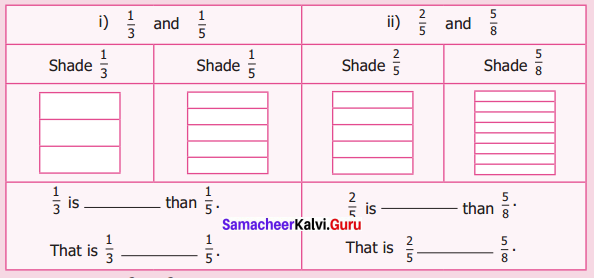
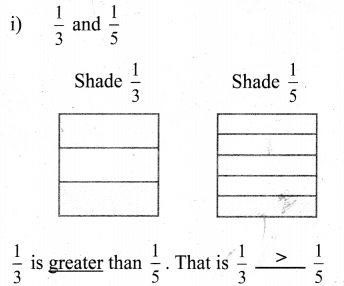
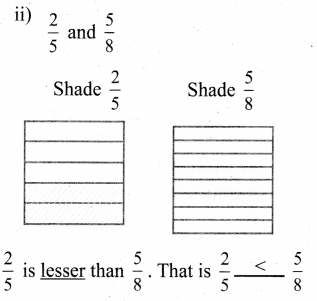
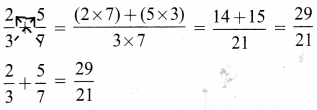
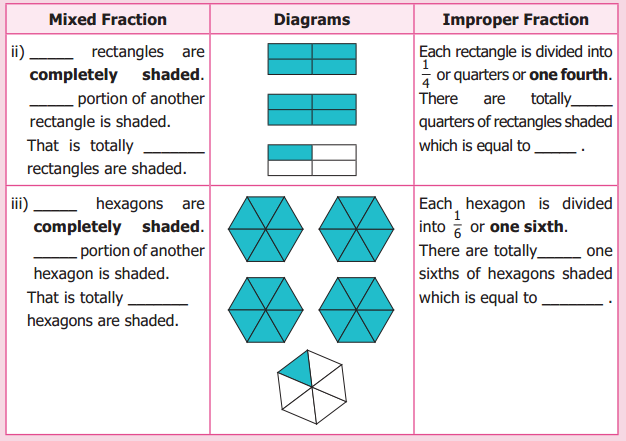
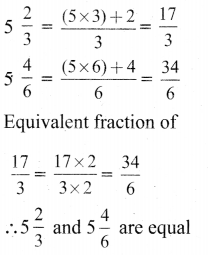
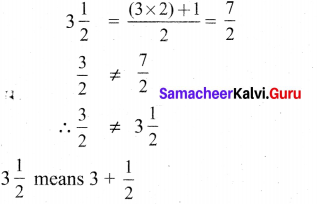
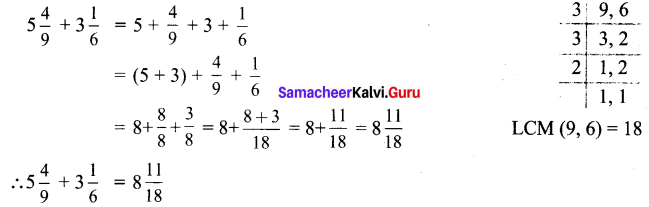
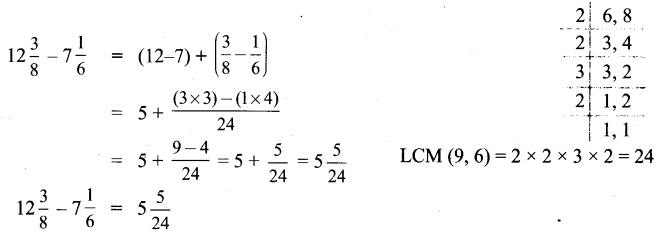
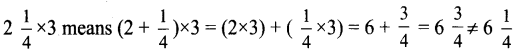
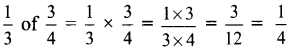
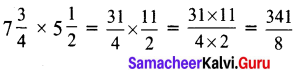
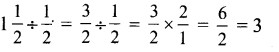
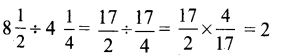
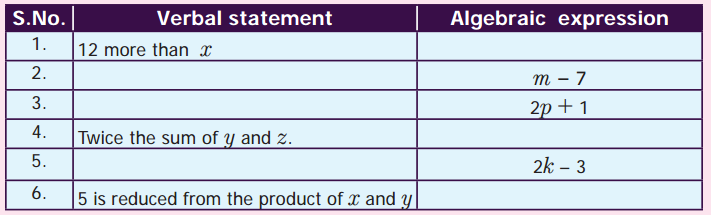
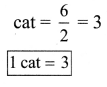ditional Questions 63″ width=”107″ height=”87″ />

(iii) 1 dog + 1 cat – 1 parrot = 9
8 + 3 – 1 parrot = 9
8 + 3 – 9 = 1 parrot
11 – 9 = 1 parrot
2 = 1 parrot
1 parrot = 2

(iv) 1 dog + 1 cat + 1 parrot = ?
8 + 3 + 2 = 13
Verification:
(i) 8 + 8 + 8 = 24
(ii) 8 + 3 + 3 = 14
(iii) 8+ 3 – 2 = 9
(iv) 8 + 3 + 2 = 13

Try These (Text book Page No. 68)

Question 1.
Kandhan and kaviya are friends. Both of them are having some pen. Kandhan: If you give me one pen then, we will have equal number of pens. Will you? Kaviya: But, if you give me one of your pens, then mine will become twice as yours. Will you?
Construct algebraic equations for this situation, can you guess and find the actual number of pens, they have?
Solution:
Let the number of pens initially Kandhan and Kaviya had be x and y respectively.

Students can Download Maths Chapter 3 Algebra Ex 3.3 Questions and Answers, Notes Pdf, Samacheer Kalvi 7th Maths Book Solutions Guide Pdf helps you to revise the complete Tamilnadu State Board New Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 7th Maths Solutions Term 1 Chapter 3 Algebra Ex 3.3

Question 1.
Fill in the blanks.
(i) An expressions equated to another expression is called _______.
(ii) If a = 5, the value of 2a + 5 is _______.
(iii) The sum of twice and four times of the variable x is ______.
Solution:
(i) an equation
(ii) 15
(iii) 6x

Question 2:
Say True or False
(i) Every algebraic expression is an equation.
(ii) The expression 7x + 1 cannot be reduced without knowing the value of x.
(iii) To add two like terms, its coefficients can be added.
Solution:
(i) False
(ii) True
(iii) True

Question 3.
Solve (i) x + 5 = 8
(ii) p – 3 = 1
(iii) 2x = 30
(iv) \(\frac{m}{6}\) = 5
(v) 7x + 10 = 80
Solution:
(i) Given x + 5 = 8 ; Subtracting 5 on both the sides
x + 5 – 5 = 8 – 5
x = 3

(ii) Given p – 3 = 7 ; Adding 3 on both the sides,
p – 3 + 3 = 7 + 3
p = 10

(iii) Given 2x = 30 ; Dividing both the sides by 2,
\(\frac{2 x}{2}=\frac{30}{2}\)
x = 15

(iv) Given \(\frac{m}{6}\) = 5 ; Multiplying both the sides by 6,
\(\frac{m}{6}\) × 6 = 5 × 6
m = 30

(v) Given 7x + 10 = 80 ; Subtracting 10 from both the sides,
7x + 10 – 10 = 80 – 10
7x = 70
Dividing both sides by 7,
\(\frac{7 x}{7}=\frac{70}{7}\)
x = 10

Question 4.
What should be added to 3x + 6y to get 5x + 8y?
Solution:
To get the expression we should subtract 3x + 6y from 5x + 8y
5x + 8y – (3x + 6y) = 5x + 8y + (-3x – 6y)
= 5x + 8y – 3x – 6y = (5 – 3) x + (8 – 6) y
= 2x + 2y
So 2x + 2y should be added.

Question 5.
Nine added to thrice a whole number gives 45. Find the number
Solution:
Let the whole number required be x.
Thrice the whole number = 3x
Nine added to it = 3x + 9
Given 3x + 9 = 45
3x + 9 – 9 = 45 – 9 [Subtracting 9 on both sides]
3x = 36
\(\frac{3 x}{3}=\frac{36}{3}\)
x = 12
∴ The required whole number is 12

Question 6.
Find the two consecutive odd numbers whose sum is 200
Solution:
Let the two consecutive odd numbers be x and x + 2
∴ Their sum = 200
x + (x + 2) = 200
x + x + 2 = 200
2x + 2 = 200
2x + 2 – 2 = 200 – 2 [∵ Subtracting 2 from both sides]
2x = 198
\(\frac{2 x}{2}=\frac{198}{2}\) [Dividing both sides by 2]
x = 99
The numbers will be 99 and 99 + 2.
∴ The numbers will be 99 and 101.

Question 7.
The taxi charges in a city comprise of a fixed charge of ₹ 100 for 5 kms and ₹ 16 per km for ever additional km. If the amount paid at the end of the trip was ₹ 740, find the distance traveled.
Solution:
Let the distance travelled by taxi be ‘x’ km
For the first 5 km the charge = ₹ 100
For additional kms the charge = ₹ 16(x – 5)
∴ For x kms the charge = 100 + 16(x – 5)
Amount paid = ₹ 740
∴ 100 + 16 (x – 5) = 740
100 + 16 (x – 5) – 100 = 740- 100
16 (x – 5) = 640
\(\frac{16(x-5)}{16}=\frac{640}{16}\)
x – 5 = 40
x – 5 + 5 = 45 + 5
x = 45
x = 45 km
∴ Total distance travelled = 45 km

Objective Type Questions

Question 8.
The generalization of the number pattern 3, 6, 9, 12, …………. is
(i) n
(ii) 2n
(iii) 3n
(iv) 4n
Solution:
(iii) 3n

Question 9.
The solution of 3x + 5 = x + 9 is t
(i) 2
(ii) 3
(iii) 5
(iv)4
Solution:
(i) 2
Hint: 3x + 5 = x + 9 ⇒ 3x – x = 9 – 5 ⇒ 2x = 4 ⇒ x = 2

Question 10.
The equation y + 1 = 0 is true only when y is
(i) 0
(ii) -1
(iii) 1
(iv) – 2
Solution:
(ii) -1