Prasanna

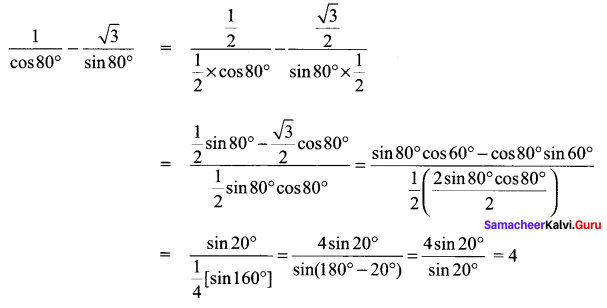
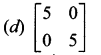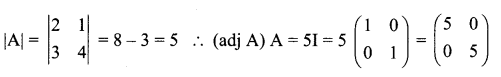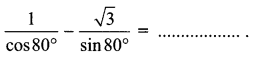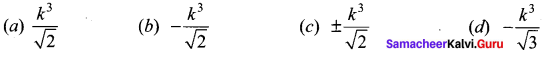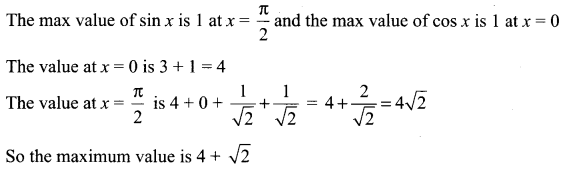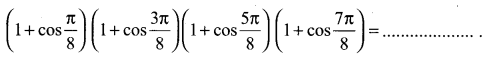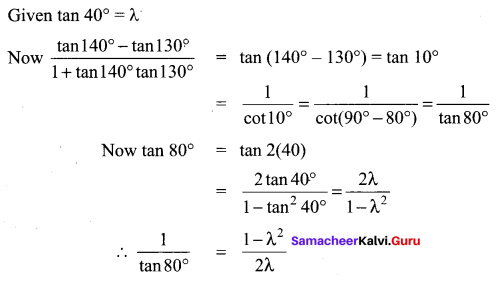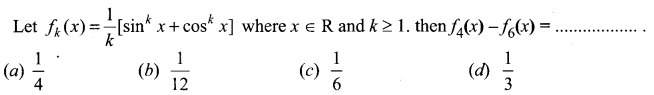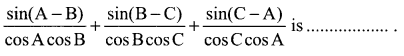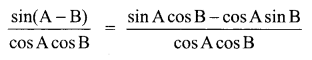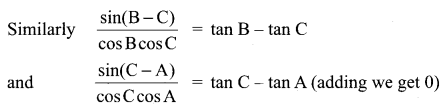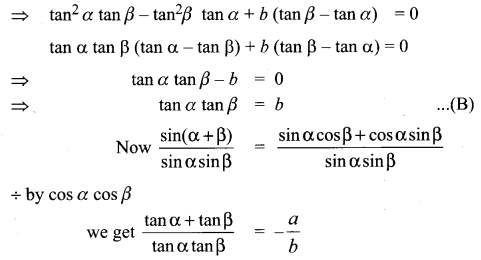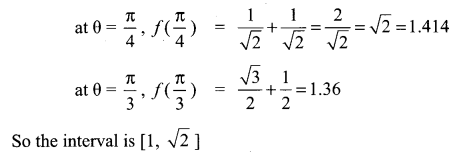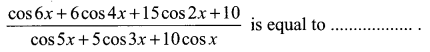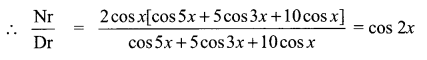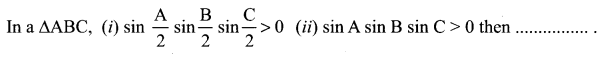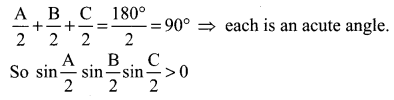You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 2 Complex Numbers Ex 2.7

Question 1.
Write in polar form of the following complex numbers.
(i) 2 + i2√3
(ii) 3 – i√3
(iii) -2 – i2
(iv) \(\frac{i-1}{\cos \frac{\pi}{3}+i \sin \frac{\pi}{3}}\)
Solution:

Question 2.
Find the rectangular form of the following complex numbers.

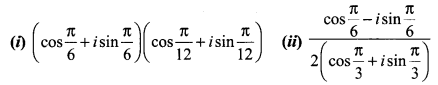
Solution:

Question 3.

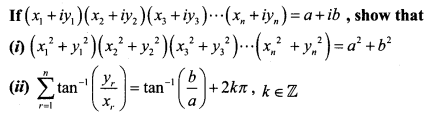
Solution:
(i) (x₁ + iy₁) (x₂ + iy₂) (x₃ + iy₃) …….. (x_n + iy_n) = a + ib …… (1)
Taking modulus on both sides,
|(x₁ + iy₁) (x₂ + iy₂) (x₃ + iy₃) …….. (x_n + iy_n)| = |a + ib|
|x₁ + iy₁| |x₂ + iy₂| |x₃ + iy₃| ….. |x_n + iy_n| = |a + ib|

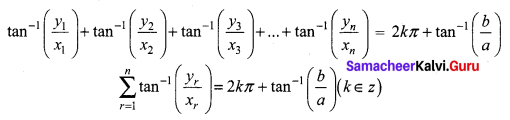
Question 4.
If \(\frac{1+z}{1-z}\) = cos 2θ + i sin 2θ, show that z = i tan θ.
Solution:

Question 5.
If cos α + cos β + cos γ = sin α + sin β + sin γ = 0, then show that
(i) cos 3α + cos 3β + cos 3γ = 3 cos (α + β + γ)
(ii) sin 3α + sin 3β + sin 3γ = 3 sin (α + β + γ)
Solution:
Let a = cos α + i sin α = e^iα
b = cos β + i sin β = e^iβ
c = cos γ + i sin γ = e^iγ
a + b + c = (cos α + cos β + cos γ) + i (sin α + sin β + sin γ)
⇒ a + b + c = 0 + i 0
⇒ a + b + c = 0
If a + b + c = 0 then a³ + b³ + c³ = 3abc

(cos 3α + i sin 3α + cos 3β + i sin 3β + cos 3γ + i sin 3γ) = 3 [cos (α + β + γ) + i sin (α + β + γ)]
(cos 3α + cos 3β + cos 3γ) + i (sin 3α + sin 3β + sin 3γ) = 3 cos (α + β + γ) + i 3sin(α + β + γ)
Equating real and Imaginary parts
(i) cos 3α + cos 3β + cos 3γ = 3 cos (α + β + γ)
(ii) sin 3α + sin 3β + sin 3γ = 3 sin (α + β + γ)

Question 6.
If z = x + iy and arg \(\left(\frac{z-i}{z+2}\right)=\frac{\pi}{4}\), then show that x² + y² + 3x – 3y + 2 = 0.
Solution:
arg \(\left(\frac{z-i}{z+2}\right)=\frac{\pi}{4}\)
We have arg (\(\frac{z_{1}}{z_{2}}\)) = arg(z₁) – arg(z₂)
arg (z – i) – arg (z + 2) = \(\frac{\pi}{4}\)
Let z = x + iy
arg (x + iy – i) – arg (x + iy + 2) = \(\frac{\pi}{4}\)
arg(x + i(y – 1)) – arg(x + 2 + iy) = \(\frac{\pi}{4}\)

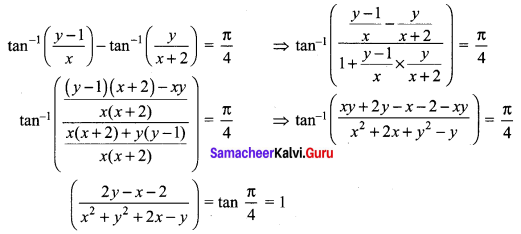
2y – x – 2 = x² + y² + 2x – y
x² + y² + 3x – 3y + 2 = 0
Hence proved.

Samacheer Kalvi 12th Maths Solutions Chapter 2 Complex Numbers Ex 2.7 Additional Problems

Question 1.
Write the following complex numbers in the polar form:

Solution:

Question 2.
Find the modulus and principal argument of (1 + i) and hence express it in the polar form.
Solution:

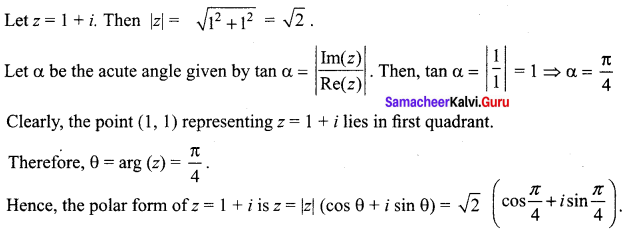
Question 3.
Express the following complex numbers in the polar form.

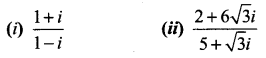
Solution:

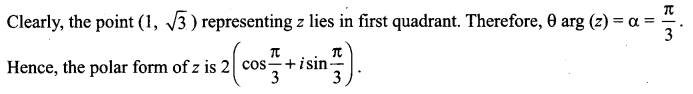
Question 4.
Express the following complex numbers in the polar form: \(2+2 \sqrt{3} i\)
Solution:

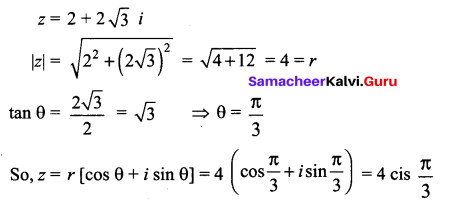
Question 5.
Express the following complex numbers in the polar form: \(-1+i \sqrt{3}\)
Solution:

Question 6.
Express the following complex numbers in the polar form: -1 – i
Solution:

Question 7.
Express the following complex numbers in the polar form: 1 – i
Solution:

You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 2 Complex Numbers Ex 2.6

Question 1.
If z = x + iy is a complex number such that \(\left|\frac{z-4 i}{z+4 i}\right|=1\). show that the locus of z is real axis.
Solution:
\(\left|\frac{z-4 i}{z+4 i}\right|=1\)
⇒ |z – 4i| = |z + 4i|
let z = x + iy
⇒ |x + iy – 4i| = |x + iy + 4i|
⇒ |x + i(y – 4)| = |x +(y + 4)|
⇒ \(\sqrt{x^{2}+(y-4)^{2}}=\sqrt{x^{2}+(y+4)^{2}}\)
Squaring on both sides, we get
x² + y² – 8y + 16 = x² + y² + 16 + 8y
⇒ -16y = 0
⇒ y = 0 in two equation of real axis.

Question 2.
If z = x + iy is a complex number such that Im \(\left(\frac{2 z+1}{i z+1}\right)=0\) show that the locus of z is 2x² + 2y² + x – 2y = 0.
Solution:
Let z = x + iy

2x² + 2y² + x – 2y = 0.
Hence proved.

Question 3.
Obtain the Cartesian form of the locus of z = x + iy in each of the following cases:
(i) [Re(iz)]² = 3
(ii) Im[(1 – i)z + 1] = 0
(iii) |z + i| = |z – 1|
(iv) \(\bar{z}=z^{-1}\)
Solution:
(i) z = x + iy
[Re(iz)]² = 3
⇒ [Re[i(x + iy]]² = 3
⇒ [Re(ix – y)]² = 3
⇒ (-y)² = 3
⇒ y² = 3

(ii) Im[(1 – i)z + 1] = 0
⇒ Im [(1 – i)(z + iy) + 1] = 0
⇒ Im[x + iy – ix + y + 1] = 0
⇒ Im[(x + y + 1) + i(y – x)] = 0
Considering only the imaginary part
y – x = 0 ⇒ x = y

(iii) |z + i| = |z – 1|
⇒ |x + iy + i| = | x + iy – 1|
⇒ |x + i(y + 1)| = |(x – 1) + iy|
Squaring on both sides
|x + i(y + 1)|² = |(x – 1) + iy|²
⇒ x² + (y + 1)² = (x – 1)² + y²
⇒ x² + y² + 2y + 1 = x² – 2x + 1 + y²
⇒ 2y + 2x = 0
⇒ x + y = 0

(iv) \(\bar{z}=z^{-1}\)
⇒ \(\bar{z}=\frac{1}{z}\)
⇒ \(z \bar{z}=1\)
⇒ |z|² = 1
⇒ |x + iy|² = 1
⇒ x² + y² = 1

Question 4.
Show that the following equations represent a circle, and, find its centre and radius.
(i) |z – 2 – i| = 3
(ii) |2z + 2 – 4i| = 2
(iii) |3z – 6 + 12i| = 8
Solution:
(i) Let z = x + iy
|z – 2 – i| = 3
⇒ |x + iy – 2 – i| = 3
⇒ |(x – 2) + i(y – 1)| = 3
⇒ \(\sqrt{(x-2)^{2}+(y-1)^{2}}=3\)
Squaring on both sides
(x – 2)² + (y – 1)² = 9
⇒ x² – 4x + 4 + y² – 2y + 1 – 9 = 0
⇒ x² + y² – 4x – 2y – 4 = 0 represents a circle
2g = -4 ⇒ g = -2
2f = -2 ⇒ f = -1
c = -4
(a) Centre (-g, -f) = (2, 1) = 2 + i
(b) Radius = \(\sqrt{g^{2}+f^{2}-c}=\sqrt{4+1+4}=3\)
Aliter: |z – (2 + i)| = 3
Centre = 2 + i
radius = 3

(ii) |2(x + iy) + 2 – 4i| = 2
⇒ |2x + i2y + 2 – 4i| =2
⇒ |(2x + 2) + i(2y – 4)| = 2
⇒ |2(x + 1) + 2i(y – 2)| = 2
⇒ |(x + 1) + i(y – 2)| = 1
⇒ \(\sqrt{(x+1)^{2}(y-2)^{2}}=1\)
Squaring on both sides,
x² + 2x + 1 + y² + 4 – 4y – 1 = 0
⇒ x² + y² + 2x – 4y + 4 = 0 represents a circle
2g = 2 ⇒ g = 1
2f = -4 ⇒ f = -2
c = 4
(a) Centre (-g, -f) = (-1, 2) = -1 + 2i
(b) Radius = \(\sqrt{g^{2}+f^{2}-c}=\sqrt{1+4-4}=1\)
Aliter: 2|(z + 1 – 2i)| = 2
|z – (-1 + 2i)| = 1
Centre = -1 + 2i
radius = 1

(iii) |3(x + iy) – 6 + 12i| = 8
⇒ |3x + i3y – 6 + 12i| = 8
⇒ |3(x – 2) + i3 (y + 4)| = 8
⇒ 3|(x – 2) + i (y + 4)| = 8
⇒ \(3 \sqrt{(x-2)^{2}+(y+4)^{2}}=8\)
Squaring on both sides,
9[(x – 2)² + (y + 4)²] = 64
⇒ x² – 4x + 4 + y² + 8y + 16 = \(\frac{64}{9}\)
⇒ x² + y² – 4x + 8y + 20 – \(\frac{64}{9}\) = 0
x² + y² – 4x + 8y + \(\frac{116}{9}\) = 0 represents a circle.
2g = -4 ⇒ g = -2
2f = 8 ⇒ f = 4
c = \(\frac{116}{9}\)
(a) Centre (-g, -f) = (2, -4) = 2 – 4i
(b) Radius = \(=\sqrt{g^{2}+f^{2}-c}=\sqrt{4+16-\frac{116}{9}}=\sqrt{\frac{180-116}{9}}=\frac{8}{3}\)
Aliter:
|z – 2 + 4i| = \(\frac{8}{3}\)
⇒ |z – (2 – 4i)| = \(\frac{8}{3}\)
Centre = 2 – 4i, Radius = \(\frac{8}{3}\)

Question 5.
Obtain the Cartesian equation for the locus of z = x + iy in each of the following cases.
(i) |z – 4| = 16
(ii) |z – 4|² – |z – 1|² = 16
Solution:
(i) z = x + iy
|z – 4| = 16
⇒ |x + iy – 4| = 16
⇒ |(x – 4) + iy| = 16
⇒ \(\sqrt{(x-4)^{2}+y^{2}}=16\)
Squaring on both sides
(x – 4)² + y² = 256
⇒ x² – 8x + 16 + y² – 256 = 0
⇒ x² + y² – 8x – 240 = 0 represents the equation of circle

(ii) |x + iy – 4|² – |x + iy – 1|² = 16
⇒ |(x – 4) + iy|² – |(x – 1) + iy|² = 16
⇒ [(x – 4)² + y²] – [(x – 1)² + y²] = 16
⇒ (x² – 8x + 16 + y²) – (x² – 2x + 1 + y²) = 16
⇒ x² + y² – 8x + 16 – x² + 2x – 1 – y² = 16
⇒ -6x + 15 = 16
⇒ 6x + 1 = 0

Samacheer Kalvi 12th Maths Solutions Chapter 2 Complex Numbers Ex 2.6 Additional Problems

Question 1.
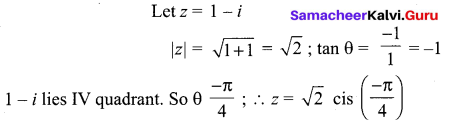
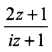If the imaginary part of is -2, then show that the locus of the point representing z in the argand plane is a straight line.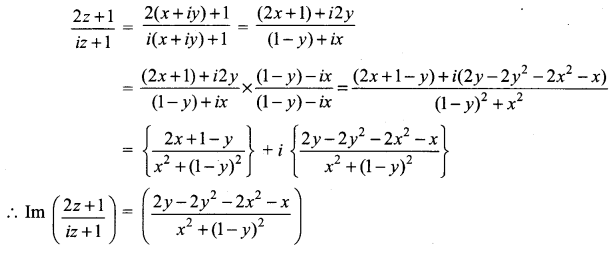
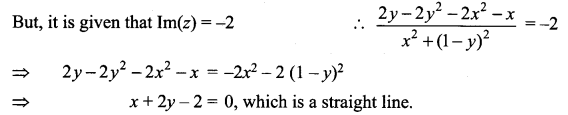
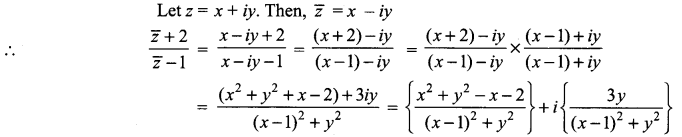
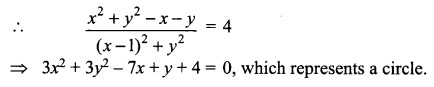
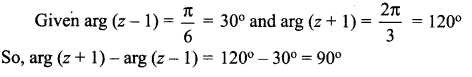
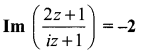
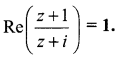
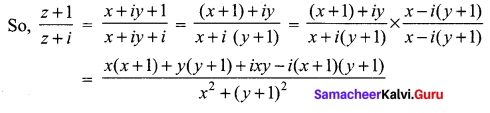
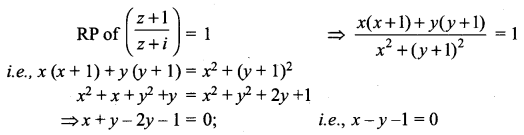
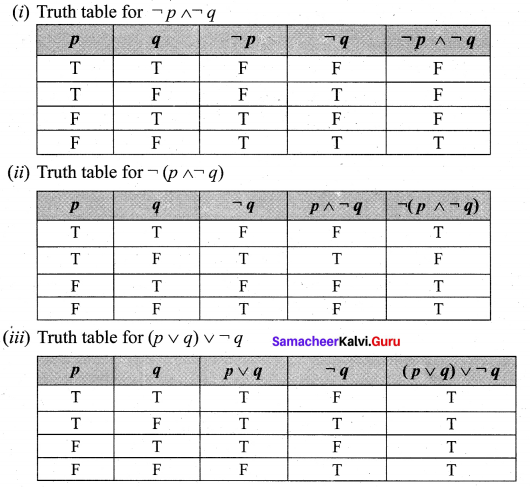
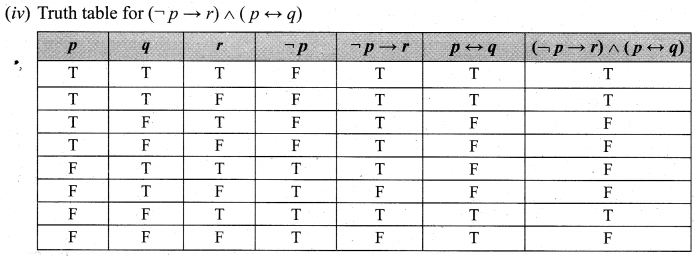
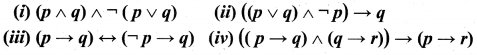
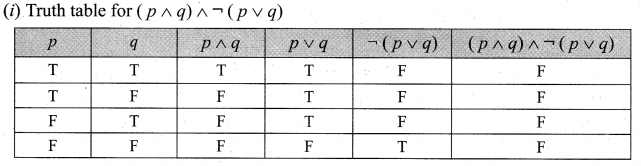
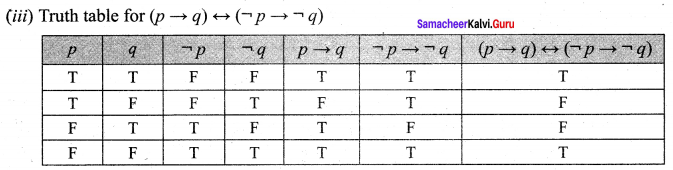
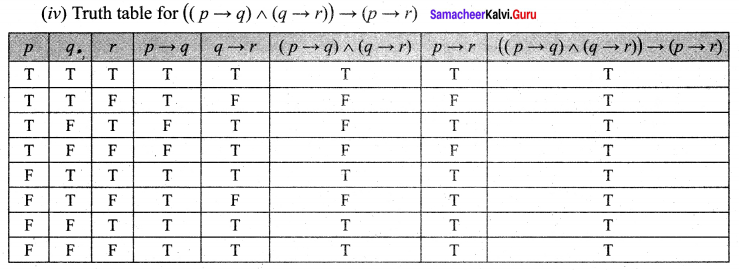
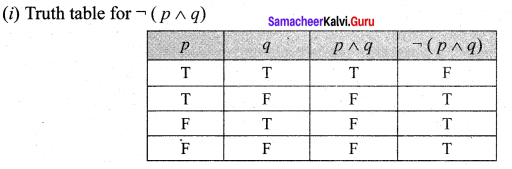
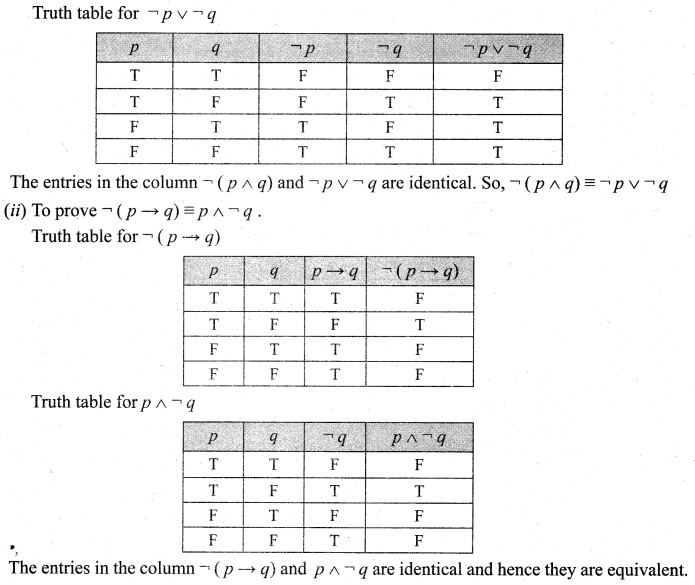
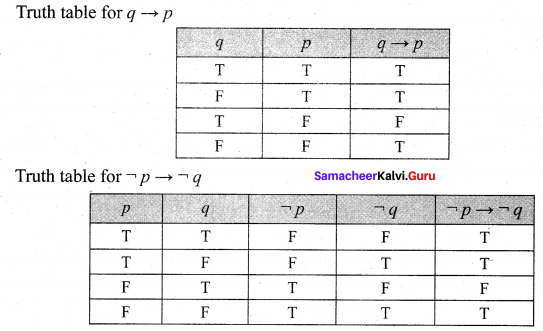
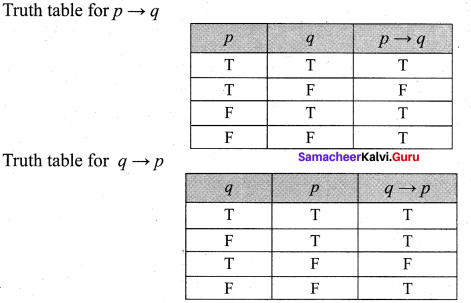
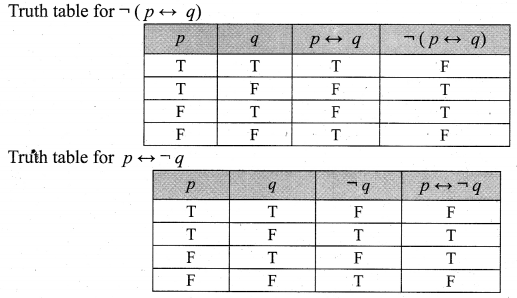
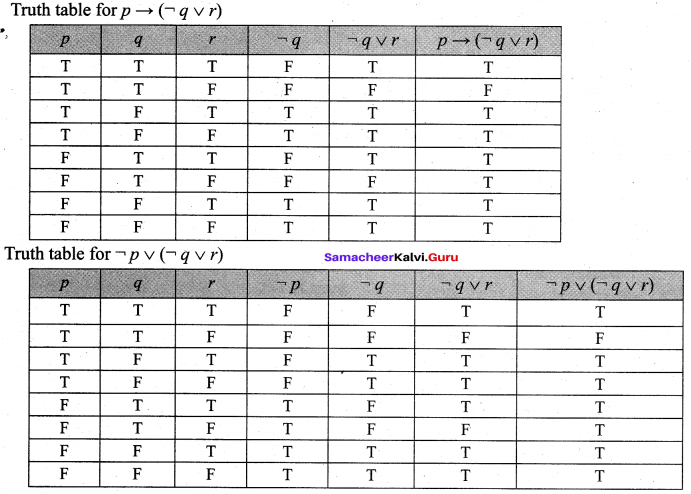
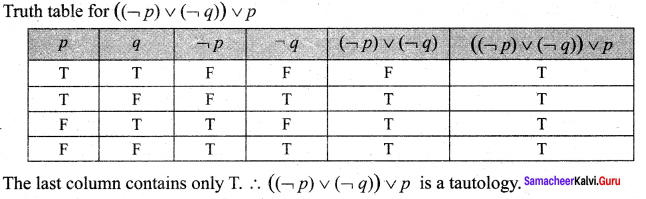
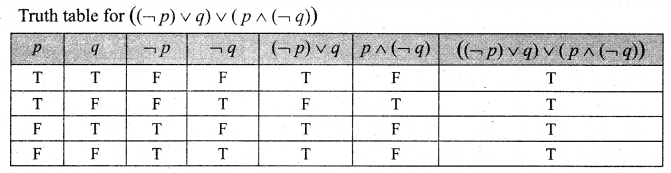
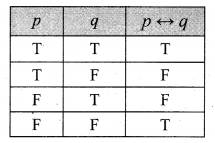
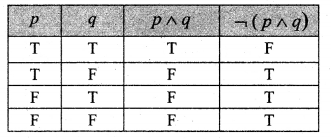
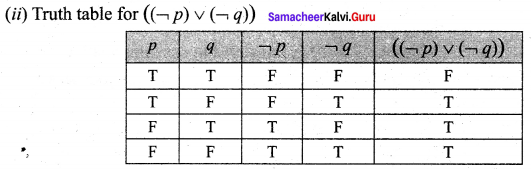
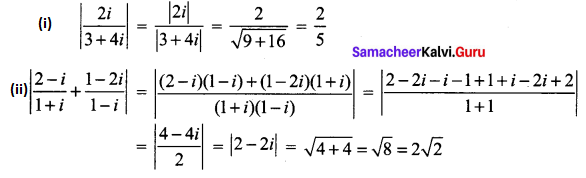
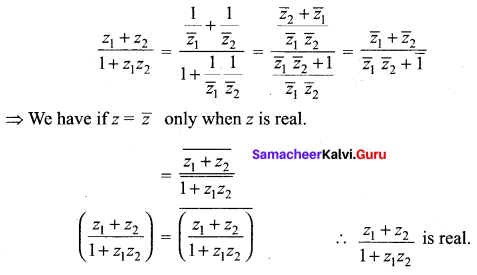
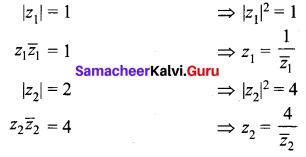
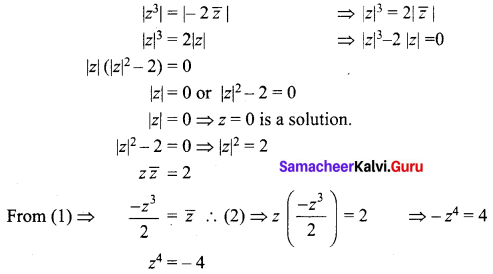
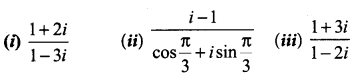
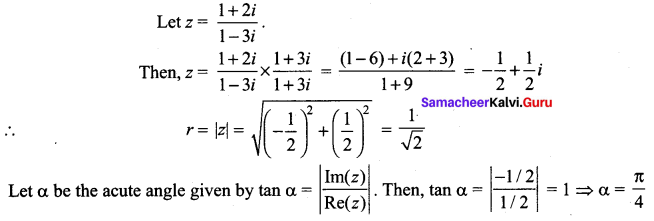
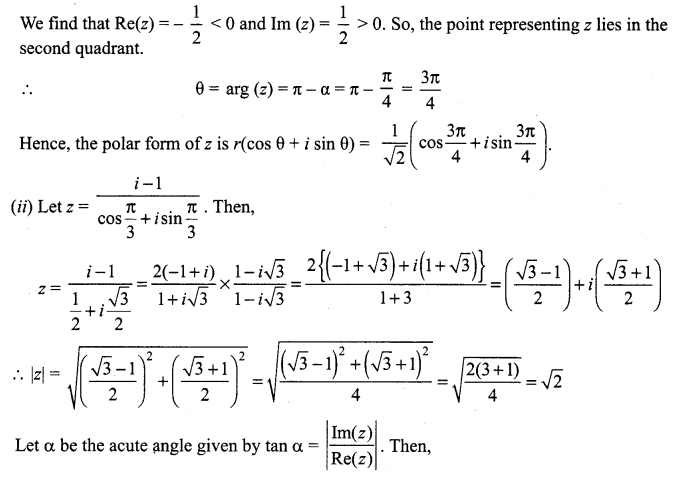
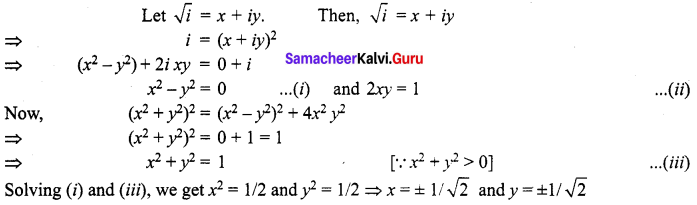
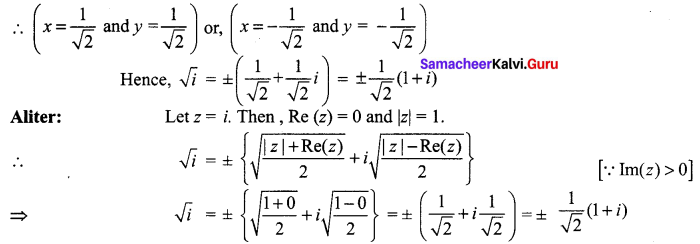
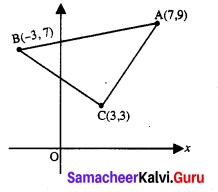
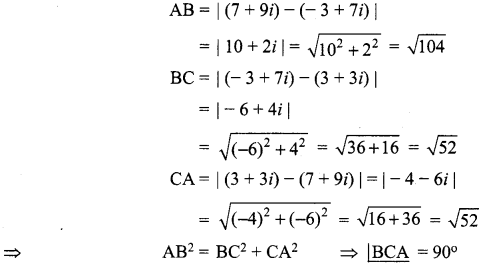
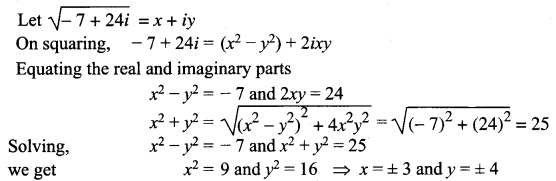
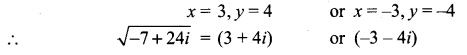
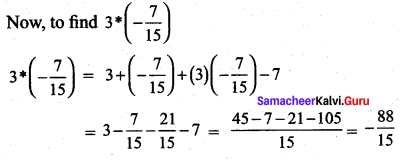
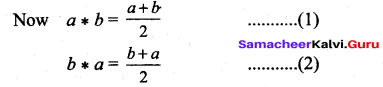
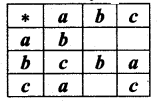
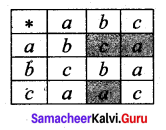
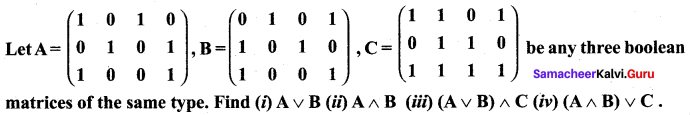
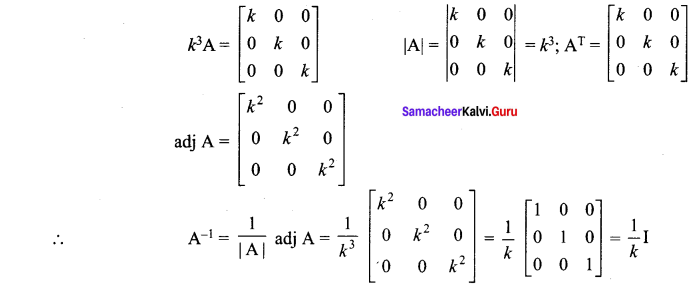
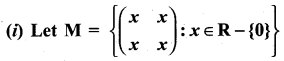Solution:
Let z = x + iy. Then,


Hence, the locus of z is a straight line

Question 2.
If the real part of is 4, then show that locus of the point representing z in the complex plane is a circle.
Solution:

It is given that the real part of is 4.

Question 3.

Solution:

Question 4.
If arg (z – 1) = \(\frac{\pi}{6}\) and arg (z + 1) = 2 \(\frac{\pi}{3}\) , then prove that |z| = 1.
Solution:

Question 5.
P represents the variable complex number z. Find the locus of P, if
Solution:

Question 6.
P represents the variable complex number z. Find the locus of P, if
Solution:
Let z = x + iy

You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 12 Discrete Mathematics Ex 12.2

Question 1.
Let p : Jupiter is a planet and q : India is an island be any two simple statements. Give verbal sentence describing each of the following statements.

Solution:
(i) \(\neg p\) : Jupiter is not a planet
(ii) \(p \wedge \neg q\) : Jupiter is not a planet and India is not an island
(iii) \(\neg p \vee q\) : Jupiter is not a planet or India is an island.
(iv) \(p \rightarrow \neg q\) : If Jupiter is a planet then India is not an island
(v) \(p \leftrightarrow q\) : If Jupiter is a planet if and only if India is an island

Question 2.
Write each of the following sentences in symbolic form using statement variables p and q.
(i) 19 is not a prime number and all the angles of a triangle are equal.
(ii) 19 is a prime number or all the angles of a triangle are not equal
(iii) 19 is a prime number and all the angles of a triangle are equal
(iv) 19 is not a prime number
Solution:
p : 19 is a prime number
q : All the angles of a triangle are equal

Question 3.
Determine the truth value of each of the following statements
(i) If 6 + 2 = 5 , then the milk is white.
(ii) China is in Europe or \(\sqrt{3}\) is an integer
(iii) It is not true that 5 + 5 = 9 or Earth is a planet
(iv) 11 is a prime number and all the sides of a rectangle are equal
Solution:

Question 4.
Which one of the following sentences is a proposition?
(i) 4 + 7 = 12
(ii) What are you doing?
(iii) 3ⁿ ≤ 81, n ∈ N
(iv) Peacock is our national bird
(v) How tall this mountain is!
Solution:
(i) is a proposition
(ii) not a proposition
(iii) is a proposition
(iv) is a proposition
(v) not a proposition

Question 5.
Write the converse, inverse, and contrapositive of each of the following implication.
(i) If x and y are numbers such that x = y, then x² = y²
(ii) If a quadrilateral is a square then it is a rectangle
Solution:
(i) Converse: If x and y are numbers such that x² = y² then x = y.
Inverse: If x and y are numbers such that x ≠ y then x² ≠ y².
Contrapositive : If x and v are numbers such that x² ≠ y² then x ≠ y.

(ii) Converse: If a quadrilateral is a rectangle then it is a square.
Inverse: If a quadrilateral is not a square then it is not a rectangle.
Contrapositive : If a quadrilateral is not a rectangle then it is not a square.

Question 6.
Construct the truth table for the following statements.

Solution:

Question 7.
Verify whether the following compound propositions are tautologies or contradictions or contingency

Solution:

In the above Truth table the last column entries are ‘F’. So the given propositions is a contradiction.

In the above truth table the last column entries are ‘T’. So the given propositions is a tautology.

In the above truth table the entries in the last column are a combination of’ T ‘ and ‘ F ‘. So the given statement is neither propositions is neither tautology nor a contradiction. It is a contingency.

The last column entires are ‘T’. So the given proposition is a tautology.

Question 8.

Solution:

Question 9.

Solution:

The entries in the column corresponding to q ➝ p and \(\neg p \rightarrow \neg q\) are identical and hence they are equivalent.

Question 10.
Show that p ➝ q and q ➝ p are not equivalent
Solution:

The entries in the column corresponding to p ➝ q and q ➝ p are not identical, hence they are not equivalent.

Question 11.

Solution:

Question 12.
Check whether the statement p ➝ (q ➝ p) is a tautology or a contradiction without using the truth table.
Solution:

Question 13.
Using truth table check whether the statements are logically equivalent.
Solution:

Question 14.
without using truth table
Solution:

Question 15.

Solution:

The entries in the column corresponding to are identical.
Hence they are equivalent.

Samacheer Kalvi 12th Maths Solutions Chapter 12 Discrete Mathematics Ex 12.2 Additional Problems

Question 1.
Show that is a tautology.
Solution:

Question 2.
Show that is a contradiction.
Solution:

Question 3.
Use the truth table to determine whether the statement is a tautology.
Solution:

The last column contains only T. ∴ The given statement is a tautology.

Question 4.
Show that
Solution:
(i) Truth table for p \(\leftrightarrow\) q

Question 5.
Show that .
Solution:


The last columns of statements (i) and (ii) are identical.

You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 2 Complex Numbers Ex 2.5

Question 1.
Find the modulus of the following complex numbers.
(i) \(\frac{2 i}{3+4 i}\)
(ii) \(\frac{2-i}{1+i}+\frac{1-2 i}{1-i}\)
(iii) (1 – i)¹⁰
(iv) 2i(3 – 4i) (4 – 3i)
Solution:

(iii) |(1 – i)¹⁰| = (|1 – i|)¹⁰
= \((\sqrt{1+1})^{10}=(\sqrt{2})^{10}=2^{5}=32\)
(iv) |2i(3 – 4i) (4 – 3i)|
= |2i| |3 – 4i| |4 – 3i|
= \(2 \sqrt{9+16} \sqrt{16+9}\)
= 2 × 5 × 5
= 50

Question 2.
For any two complex numbers z₁ and z₂, such that |z₁| = |z₂| = 1 and z₁ z₂ ≠ -1, then show that \(\frac{z_{1}+z_{2}}{1+z_{1} z_{2}}\) is a real number.
Solution:
|z₁|² = 1
⇒ \(z_{1} \bar{z}_{1}=1\)
⇒ \(z_{1}=\frac{1}{\bar{z}_{1}}\)
Similarly \(z_{2}=\frac{1}{\bar{z}_{2}}\)

Question 3.
Which one of the points 10 – 8i, 11 + 6i is closest to 1 + i.
Solution:
A (1 + i), B (10 – 8i), C (11 + 6i)
|AB| = |(10 – 8i) – (1 + i)|
= |10 – 8i – 1 – i|
= |9 – 9i|
= \(\sqrt{81+81}\)
= \(\sqrt{162}\)
= 9(1.414)
= 12.726
CA = |(11 + 6i) – (1 + i)|
= |11 + 6i – 1 – i|
= |10 + 5i|
= \(\sqrt{100+25}\)
= \(\sqrt{125}\)
C (11 + 6i) is closest to the point A (1 + i)

Question 4.
If |z| = 3, show that 7 ≤ |z + 6 – 8i| ≤ 13.
Solution:
|z| = 3, To find the lower bound and upper bound we have
||z₁| – |z₂|| ≤ |z₁ + z₂| ≤ |z₁| + |z₂|
||z| – |6 – 8i|| ≤ |z + 6 – 8i| ≤ |z| + |6 – 8i|
|3 – \(\sqrt{36+64}\)| ≤ |z + 6 – 8i| ≤ 3 + \(\sqrt{36+64}\)
|3 – 10| ≤ |z + 6 – 8i| ≤ 3 + 10
7 ≤ |z + 6 – 8i| ≤ 13

Question 5.
If |z| = 1, show that 2 ≤ |z² – 3| ≤ 4.
Solution:
|z| = 1 ⇒ |z|² = 1
||z₁| – |z₂|| ≤ |z₁ + z₂| ≤ |z₁| + |z₂|
||z|² – |-3|| ≤ |z² – 3| ≤ |z|² + |-3|
|1 – 3| ≤ |z² – 3| ≤ 1 + 3
2 ≤ |z² – 3| ≤ 4

Question 6.
If \(\left|z-\frac{2}{z}\right|\) = 2, show that the greatest and least value of |z| are √3 + 1 and √3 – 1 respectively.
Solution:
\(\left|z-\frac{2}{z}\right|\) = 2
We know that

The minimum value of |z| is |1 – √3| = √3 – 1
The greatest value of |z| is √3 + 1

Question 7.
If z₁, z₂ and z₃ are three complex numbers such that |z₁| = 1, |z₂| = 2, |z₃| = 3 and |z₁ + z₂ + z₃| = 1, show that |9z₁ z₂ + 4z₁ z₃ + z₂ z₃| = 6.
Solution:

Question 8.
If the area of the triangle formed by the vertices z, iz, and z + iz is 50 square units, find the value of |z|.
Solution:
The given vertices are z, iz, z + iz ⇒ z, iz are ⊥r to each other.
Area of triangle = \(\frac { 1 }{ 2 }\) bh = 50
⇒ \(\frac { 1 }{ 2 }\) |z| |iz| = 50
⇒ \(\frac { 1 }{ 2 }\) |z| |z| = 50
⇒ |z|² = 100
⇒ |z| = 10

Question 9.
Show that the equation z³ + 2\(\bar{z}\) = 0 has five solutions.
Solution:
Given that z³ + 2\(\bar{z}\) = 0
z³ = -2 \(\bar{z}\) ……. (1)
Taking modulus on both sides,

z has four non-zero solution.
Hence including zero solution. There are five solutions.

Question 10.
Find the square roots of
(i) 4 + 3i
(ii) -6 + 8i
(iii) -5 – 12i
Solution:
(i) z = 4 + 3i
|z| = |4 + 3i| = \(\sqrt{16+9}\) = 5

Samacheer Kalvi 12th Maths Solutions Chapter 2 Complex Numbers Ex 2.5 Additional Problems

Question 1.
Find the modulus and argument of the following complex numbers and convert them in polar form.

Solution:
(i)

Question 2.
Find the square roots of – 15 – 8i
Solution:

On solving (i) and (iii), we get
x² = 1 and y² = 16 => x = ± 1 and y = ±4 From (ii), we observe that 2xy is negative. So, x and y are of opposite signs.

Question 3.
Find the square roots of i.
Solution:

From (ii) we observe that we find that 2xy is positive. So, x and y are of same sign.

Question 4.
Find the modulus or the absolute value of
Solution:

Question 5.
Find the modulus and argument of the following complex numbers:

Solution:

Question 6.
Show that the points representing the complex numbers 7 + 9i, – 3 + 7i, 3 + 3i form a right angled triangle on the Argand diagram.
Solution:
Let A, B and C represent the complex numbers
7 + 9i, – 3 + 7i and 3 + 3i in the Argand diagram respectively.


Hence ∆ABC is a right angled isosceles triangle.

Question 7.
Find the square root of (- 7 + 24i).
Solution:

You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 12 Discrete Mathematics Ex 12.1

Question 1.
Determine whether * is a binary operation on the sets given below
(i) a * b = a.|b| on R ,
(ii) a * b = min (a, b) on A = {1, 2, 3, 4, 5}
(iii) (a * b) = \(a \sqrt{b}\) is binary on R.
Solution:
(i) Yes.
Reason: a, b ∈ R. So, |b| ∈ R when b ∈ R
Now multiplication is binary on R
So a|b| ∈ R when a,be R.
(Le.) a * b ∈ R.
* is a binary operation on R.

(ii) Yes.
Reason: a, b ∈ R and minimum of (a, b) is either a or b but a, b ∈ R.
So, min (a, b) ∈ R.
(Le.) a * b ∈ R.
* is a binary operation on R.

(iii) a* b = \(a \sqrt{b}\) where a, b ∈ R.
No. * is not a binary operation on R.
Reason: a, b ∈ R.
⇒ b can be -ve number also and square root of a negative number is not real.
So \(\sqrt{b}\) ∉ R even when b ∈ R.
So \(\sqrt{b}\) ∉ R. ie., a * b ∉ R.
* is not a binary operation on R.

Question 2.

Solution:
No. * is not a binary operation on Z.
Reason: Since m, n ∈ Z.
So, m, n can be negative also.
Now, if n is negative (Le.) say n = -k where k is +ve.

Similarly, when m is negative then n^m ∉ Z.
∴ m * n ∉ Z. ⇒ * is not a binary operation on Z.

Question 3.
Let * be defined on R by (a * b) = a + b + ab – 1 .Is * binary on R ? If so, find \(3 *\left(\frac{-7}{15}\right)\)
Solution:
a * b = a + b + ab – 7.
Now when a, b ∈ R, then ab ∈ R also a + b ∈ R.
So, a + b + ab ∈ R.
We know – 7 ∈ R.
So, a + b + ab – 7 ∈ R.
(ie.) a * b ∈ R.
So, * is a binary operation on R.

Question 4.
Let A= {a+ \(\sqrt{5}\)b: a, b ∈ Z}. Check whether the usual multiplication is a binary operation on A.
Solution:
Let A = a + \(\sqrt{5}\) b and B = c + \(\sqrt{5}\)d, where a, b, c, d ∈ M.
Now A * B ={a + \(\sqrt{5}\)b)(c + \(\sqrt{5}\)d)
= ac + \(\sqrt{5}\)ad + \(\sqrt{5}\)bc + \(\sqrt{5}\)b\(\sqrt{5}\)d
= (ac + 5bd) + \(\sqrt{5}\)(ad+ bc) ∈ A
Where a, b, c, d ∈ Z
So * is a binary operation.

Question 5.
(i) Define an operation * on Q as follows: a * b = \(\left(\frac{a+b}{2}\right)\); a, b ∈ Q. Examine the closure,
commutative, and associative properties satisfied by * on Q.
(ii) Define an operation * on Q as follows: a*b = \(\left(\frac{a+b}{2}\right)\); a, b ∈ Q. Examine the existence of identity and the existence of inverse for the operation * on Q.
Solution:
(i) 1. Closure property:
Let a,b ∈ Q.

So, closure property is satisfied.

2. Commutative property:
Let a, b ∈ Q.

(1) = (2) ⇒ Now a * b = b * a
⇒ Commutative property is satisfied.

3. Associative property:
Let a,b,c G Q. ^
To prove associative property we have to prove that a * (b * c) = (a * b) * c
LHS: a * (b * c)


(i.e.) the identity Clement e = a which is not possible.
So, the identity element does not exist and so inverse does not exist.

Question 6.
Fill In the following table so that the binary operation * on A = {a, b, c} is commutative.

Solution:
Given that the binary operation * is Commutative.
To find a * b :
a * b = b * a (∵ * is a Commutative)
Here b * a = c. So a * b = c
To find a *c:

a * c = c * a (∵ * is a Commutative)
c * a = a. (Given)
So a * c = a
To find c * b:
c * b = b * c
Here b * c = a.
So c * b = a

Question 7.
Consider the binary operation * defined on the set A = [a, b, c, d] by the following table:

– Is it commutative and associative?
Solution:
From the table
b * c = b
c * b = d
So, the binary operation is not commutative.
To check whether the given operation is associative.
Let a, b, c ∈ A.
To prove the associative property we have to prove that a * (b * c) = (a * b) * c
From the table,
LHS: b * c = b
So, a * (b * c) = a * b = c ……. (1)
RHS: a * b = c
So, (a * b) * c = c * c = a …… (2)
(1) ≠ (2). So, a * (b * c) ≠ (a * b) * c
∴ The binary operation is not associative.

Question 8.

Solution:

Question 9.
and Let * be the matrix multiplication. Determine whether M is closed under * . If so, examine the commutative and associative properties satisfied by * on M .

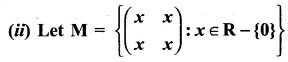and let * be the matrix multiplication. Determine whether M is closed under *. If so, examine the existence of identity, existence of inverse properties for the operation * on M.
Solution:



So, inverse property is satisfied.

Question 10.
(i) Let A be Q\{1). Define * on A by x * y = x + y – xy. Is * binary on A ? If so, examine the commutative and associative properties satisfied by * on A.
(ii) Let A be Q\{1}. Define *on A by x * y = x + y – xy. Is * binary on A ? If so, examine the existence of identity, existence of inverse properties for the operation * on A.
Solution:
(i) Let a,b ∈ A (i.e.) a ≠ ±1 , b ≠ 1
Now a * b = a + b – ab
If a + b – ab = 1 ⇒ a + b – ab – 1 = 0
(i.e.) a(1 – b) – 1(1 – b) = 0
(a – 1)(1 – b) = 0 ⇒ a = 1, b = 1
But a ≠ 1 , b ≠ 1
So (a – 1) (1 – 6) ≠ 1
(i.e.) a * b ∈ A. So * is a binary on A.

To verify the commutative property:

Let a, b ∈ A (i.e.) a ≠ 1 , b ≠ 1
Now a * b = a + b – ab
and b * a = b + a – ba
So a * b = b * a ⇒ * is commutative on A.

To verify the associative property:
Let a, b, c ∈ A (i.e.) a, b, c ≠ 1
To prove the associative property we have to prove that
a * (b * c) = (a * b) * c

LHS: b * c = b + c – bc = D(say)
So a * (b * c) = a * D = a + D – aD
= a + (b + c – bc) – a(b + c – bc)
= a + b + c – bc – ab – ac + abc
= a + b + c – ab – bc – ac + abc …… (1)

RHS: (a * b) = a + b – ab = K(say)
So (a * b) * c = K * c = K + c – Kc
= (a + b – ab) + c – (a + b – ab) c
= a + b – ab + c – ac – bc + abc
= a + b + c – ab – bc – ac + abc ….. (2)

(ii) To verify the identity property:
Let a ∈ A (a ≠ 1)
If possible let e ∈ A such that
a * e = e * a = a
To find e:
a * e = a
(i.e.) a + e – ae = a

So, e = (≠ 1) ∈ A
(i.e.) Identity property is verified.
To verify the inverse property:
Let a ∈ A (i.e. a ≠ 1)
If possible let a’ ∈ A such that
To find a’:
a * a’ = e
(i.e.) a + a’ – aa’ = 0
⇒ a'(1 – a) = – a

⇒ For every a ∈ A there is an inverse a’ ∈ A such that
a* a’ = a’ * a = e
⇒ Inverse property is verified.

Samacheer Kalvi 12th Maths Solutions Chapter 12 Discrete Mathematics Ex 12.1 Additional Problems

Question 1.
Show that the set G = {a + b\(\sqrt{2}\)/ a, b ∈ Q} is an infinite abelian group with respect to Binary operation addition. Satisfies closure, associative, identity and inverse properties.
Solution:
(i) Closure axiom :
Let x, y ∈ G. Then x = a + b\(\sqrt{2}\), y = c + d\(\sqrt{2}\); a, b, c, d ∈ Q.
x + y = (a + b\(\sqrt{2}\)) + (c + d\(\sqrt{2}\)) = (a + c) + (b + d) \(\sqrt{2}\) ∈ G,
Since (a + c) and (b + d) are rational numbers.
∴ G is closed with respect to addition.

(ii) Associative axiom : Since the elements of G are all real numbers, addition is associative.

(iii) Identity axiom : There exists 0 = 0 + 0 \(\sqrt{2}\) ∈ G
such that for all x = a + b\(\sqrt{2}\) ∈ G.
x + 0 = (a + b\(\sqrt{2}\) ) + (0 + 0\(\sqrt{2}\))
= a + b\(\sqrt{2}\) = x
Similarly, we have 0 + x = x. ∴ 0 is the identity element of G and satisfies the identity axiom.

(iv) Inverse axiom: For each x = a + b\(\sqrt{2}\) ∈ G,
there exists -x = (-a) + (-b) \(\sqrt{2}\) ∈ G
such that x + (-x) = (a + b\(\sqrt{2}\)) + ((-a) + (- b)\(\sqrt{2}\))
= (a + (-a)) + (b + (-b)) \(\sqrt{2}\) = 0
Similarly, we have (- x) + x = 0 .
∴ (- a) + (-b)\(\sqrt{2}\) is the inverse of a + b \(\sqrt{2}\) and satisfies the inverse axiom.

(v) Commutative axiom:
x + y = (a + c) + (b + d) \(\sqrt{2}\) = (c + a) + (d + b) \(\sqrt{2}\)
= (c + d\(\sqrt{2}\)) + (a + b\(\sqrt{2}\))
= y + x, for all x, y ∈ G.
∴ The commutative property is true.
∴ (G, +) is an abelian group. Since G is infinite, we see that (G, +) is an infinite abelian group.

Question 2.
Show that (Z₇ – { [0]}, .7) write to the binary operation multiplication modul07 satisfies closure, associative, identity and inverse properties.
Solution:
Let G = [[1], [2],… [6]]
The Cayley’s table is

From the table:
(i) all the elements of the composition table are the elements of G.
∴ The closure axiom is true.
(ii) multiplication modulo 7 is always associative.
(iii) the identity element is [1] ∈ G and satisfies the identity axiom.
(iv) the inverse of [1] is [1]; [2] is [4]; [3] is [5]; [4] is [2]; [5] is [3] and [6] is [6] and it satisfies the inverse axiom.

Question 3.
Show that the set G of all positive rationals with respect to composition * defined by ab
a* b = \(\frac{a b}{3}\) for all a, b ∈ G satisfies closure, associative, identity and inverse properties.
Solution:
Let G = Set of all positive rational number and * is defined by,

(i) Closure axiom: Let a, b ∈ G

∴ closure axiom is satisfied.

(ii) Associative axiom: Let a, b, c ∈ G.
To prove the associative property, we have to prove that

(1) = (2) ⇒ LHS = RHS i.e., associative axiom is satisfied.

(iii) Identity axiom: Let a ∈ G.
Let e be the identity element.
By the definition, a * e = a

e = 3 ∈ G ⇒ identity axiom is satisfied.

(iv) Inverse axiom: Let a ∈ G and a’ be the inverse of a * a’ = e = 3.

Question 4.
Show that the set G of all rational numbers except – 1 satisfies closure, associative, identity and inverse property with respect to the operation * given by a * b = a + b + ab for all a, b ∈ G
Solution:
G = [Q, -{-l}]
* is defined by a * b = a + b + ab
To prove G is an abelian group.

G₁: Closure axiom: Let a, b ∈ G.
i.e., a and b are rational numbers and a ≠ -1, b ≠ -1.
So, a * b = a + b + ab
If a + b + ab = – 1
⇒ a + b + ab + 1 = 0
i.e., (a + ab) + (b + 1) = 0
a (1 + b) + (b + 1) = 0
i.e., (a + 1)(1 + b) = 0
⇒ a = -1, b = -1
But a ≠ -1, b ≠ -1
⇒ a + b + ab ≠ -1
i.e., a + b + ab ∈ G ∀ a, b ∈ G
⇒ Closure axiom is verified.

G₂: Associative axiom: Let a, b, c ∈ G.
To prove G₂, we have to prove that,
a * {b * c) = (a * b) * c
LHS:
b * c = b + c + bc = D (say)
a * (b * c) = a * D = a + D + aD
= a + (b + c + bc) + a(b + c + bc)
= a + b + c + bc + ab + ac + abc
= a + b + c + ab + bc + ac + abc ……. (1)
RHS:
a * b = a + b + ab = E (say)
∴ (a * b) * c = E * c = E + c + Ec
= a + b + ab + c + (a + b + ab) c
= a + b + ab + c + ac + bc + abc ……. (2)
= a + b + c + ab +be+ ac + abc
(1) = (2) ⇒ Associative axiom is verified.

G₃: Identity axiom: Let a ∈ G. To prove G₃ we have to prove that there exists an element e ∈ G such that a * e = e * a = a.
To find e: a * e = a
i.e., a + e + ae = a
⇒ e(1 + a) = a – a = 0

So, e = 0 ∈ G ⇒ Identity axiom is verified.

G₄ : Inverse axiom: Let a ∈ G. To prove G₄, we have to prove that there exists an element a’ ∈ G such that a * a’ = a’ * a = e.
To find a’: a * a’ = e
i.e., a + a’ + aa’=: 0 {∵ e = 0}
⇒ a'(1 + a) = -a

Thus, inverse axiom is verified.

Question 5.
Show that the set { [1], [3], [4], [5], [9]} under multiplication modulo 11 satisfies closure, associative, identity and inverse properties.
Solution:
G = {[1], [3], [4], [5], [9]}
* is defined by multiplication modulo 11.
To prove G is an abelian group with respect to *
Since we are given a finite number of elements i.e., since the given set is finite, we can frame the multiplication table called Cayley’s table.
The Cayle’s table is as follows:

G₁: The elements in the above table are [1], [3], [4], [5] and [9] which are elements of G.
∴ closure axiom is verified.

G₂: Consider [3], [4], [5] which are elements of G.
{[3] * [4]} * [5] = [1] * [5] = [5] ……. (1)
[3] * {[4] * [5]} = [3] * [9] = [5] …… (2)
(1) = (2) ⇒ (a * b) * c = a * (b * c) i.e., associative axiom is verified.

G₃: The first row elements are the same as that of the given elements in the same order. ie., from the table, the identity element is [1] ∈ G. So identity axiom is verified.

G₅: From the table * is commutative i.e., the entries equidistant from the leading diagonal on either sides are equal ⇒ a * b = b * a

You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 2 Complex Numbers Ex 2.4

Question 1.
Write the following in the rectangular form:
(i) \(\overline{(5+9 i)+(2-4 i)}\)
(ii) \(\frac{10-5 i}{6+2 i}\)
(iii) \(\overline{3 i}+\frac{1}{2-i}\)
Solution:

Question 2.
If z = x + iy, find the following in rectangular form.
(i) Re(\(\frac{1}{z}\))
(ii) Re(i\(\bar{z}\))
(iii) Im(3z + 4\(\bar{z}\) – 4i)
Solution:
(i) Re(\(\frac{1}{z}\)) = Re(\(\frac{1}{x+i y} \times \frac{x-i y}{x-i y}\))
= Re(\(\frac{x-i y}{x^{2}+y^{2}}\))
= \(\frac{x}{x^{2}+y^{2}}\)
(ii) Re(i\(\bar{z}\)) = Re[i(\(\overline{x+i y}\))]
= Re(ix + y)
= y
(iii) Im(3z + 4\(\bar{z}\) – 4i)
= Im (3(x + iy) + 4(x – iy) – 4i)
= Im (3x + 3iy + 4x – 4iy – 4i)
= Im (3x + 4 + i (3y – 4y – 4)
= Im (3x + 4x + i(-y – 4))
= Im [7x + i(-y – 4)]
= -y – 4
= -(y + 4)

Question 3.
If z₁ = 2 – i and z₂ = -4 + 3i, find the inverse of z₁ z₂ and \(\frac{z_{1}}{z_{2}}\)
Solution:
z₁ = 2 – i, z₂ = -4 + 3i
(i) z₁ z₂ = (2 – i) (-4 + 3i)
= (-8 + 6i + 4i – 3 i²)
= (-8 + 10i + 3)
= (-5 + 10i)

Question 4.
The complex numbers u, v, and w are related by \(\frac{1}{u}=\frac{1}{v}+\frac{1}{w}\). If v = 3 – 4i and w = 4 + 3i, find u in rectangular form.
Solution:
v = 3 – 4i, w = 4 + 3i = i (3 – 4i)

Question 5.
Prove the following properties:
(i) z is real if and only if z = \(\bar{z}\)
(ii) Re(z) = \(\frac{z+\bar{z}}{2}\) and Im(z) = \(\frac{z-\bar{z}}{2 i}\)
Solution:
(i) z is real iff z = \(\bar{z}\)
Let z = x + iy
z = \(\bar{z}\)
⇒ x + iy = x – iy
⇒ 2iy = 0
⇒ y = 0
⇒ z is real.
z is real iff z = \(\bar{z}\)
(ii) \(\frac{z+\bar{z}}{2 i}=\frac{x+i y+x-i y}{2}=\frac{2 x}{2}=x\)
Real part of z = x
(iii) \(\frac{z-\bar{z}}{2 i}=\frac{(x+i y)-(x-i y)}{2 i}=\frac{x+i y-x+i y}{2 i}=\frac{2 i y}{2 i}=y\)
Im part of z = y.

Question 6.
Find the least value of the positive integer n for which (√3 + i)ⁿ
(i) real
(ii) purely imaginary
Solution:
(√3 + i)ⁿ
(√3 + i)²
= 3 – 1 + 2√3 i
= (2 + 2 √3 i)
(√3 + i)³ = (√3 + i)² (√3 + i)
= (2 + 2√3 i) (√3 + i)
= 2√3 + 2i + 6i – 2√3
(√3 + i) = 8i ⇒ purely Imaginary when n = 3
(√3 + i)⁴ = (√3 + i)³ (√3 + i)
= 8i (√3 + i)
= (-8 + 8√3 i)
(√3 + i)⁵ =(√3 + i)⁴ (√3 + i)
= (-8 + 8√3 i) (√3 + i)
= -8√3 – 8i + 24i – 8√3
= -16√3 + 16i
(√3 + i)⁶ = (√3 + i)⁵ (√3 + i)
= (√3 + i) (-16√3 + 16i)
= 16 (√3 + i) (-√3 + i)
= 16 (-3 + i√3 – i√3 – 1)
= -64 purely real when n = 6
Another Method:

Question 7.
Show that
(i) (2 + i√3)¹⁰ – (2 – i√3)¹⁰ is purely imaginary
(ii) \(\left(\frac{19-7 i}{9+i}\right)^{12}+\left(\frac{20-5 i}{7-6 i}\right)^{12}\)
Solution:
(i) (2 + i√3)¹⁰ – (2 – i√3)¹⁰

Samacheer Kalvi 12th Maths Solutions Chapter 2 Complex Numbers Ex 2.4 Additional Problems

Question 1.
Express the following in the standard form a + ib.

Solution:

Question 2.
Find the least positive integer n such that
Solution:

Question 3.
Find the real values of x and y for which the following equations are satisfied.

Solution:
(i) (1 – i)x + (1 + i)y = x – ix + y + iy
= (x + y) + i (y – x) = 1 – 3i (given)
So, equating their RP and IP we get,

Take real part, we get
i.e., 3x + (x – 2) + 6y – (1 – 3y) = 0
⇒ 3x + x – 2 + 6y – 1 + 3y = 0
4x + 9y = 3 …….. (1)
Take imaginary part, we get
3(x – 2) – x + 3 (1 – 3y) + 2y = 10
⇒ 3x – 6 – x + 3 – 9y + 2y = 10

Squaring on both sides, x² + 3x + 8 = 4 (x + 4)²
i.e., x² + 3x +8 = 4 (x² + 8x +16) ⇒ 4x² + 32x + 64 – x² – 3x – 8 = 0
3x² + 29x + 56 = 0
3x² + 21x + 8x + 56 = 0
(x + 7) (3x + 8) = 0

You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 12 Introduction to Probability Theory Ex 12.5

Choose the correct or most suitable answer from the given four alternatives:
Question 1.
Four persons are selected at random from a group of 3 men, 2 women and 4 children. The probability that exactly two of them are children is
(a) \(\frac{3}{4}\)
(b) \(\frac{10}{23}\)
(c) \(\frac{1}{2}\)
(d) \(\frac{10}{21}\)
Solution:
(d)
Hint:
Total no of person = 3 + 2 + 4 = 9
Selecting 4 from 9 can be done in 9 C₄ ways

Question 2.
A number is selected from the set {1, 2, 3, ….., 20}. The probability that the selected number is divisible by 3 or 4 is ……………
(a) \(\frac{2}{5}\)
(b) \(\frac{1}{8}\)
(c) \(\frac{1}{2}\)
(d) \(\frac{2}{3}\)
Solution:
(c)
Hint:
n(S) = 20
A = {3, 6, 9, 12, 15, 18} ⇒ n(A) = 6
B = {4, 8, 12, 16, 20} ⇒ n(B) = 5
A ∩ B = {12} ⇒ n(A ∩ B) = 1
so P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= \(\frac{6}{20}+\frac{5}{20}-\frac{1}{20}=\frac{10}{20}=\frac{1}{2}\)

Question 3.
A, B and C try to hit a target simultaneously but independently. Their respective probabilities of hitting the target are \(\frac{3}{4}, \frac{1}{2}, \frac{5}{8}\). The probability that the target is hit by A or B but not by C

Solution:
(a)
Hint:
P(A) = \(\frac{3}{4}\) P(A’) = 1/4
P(B) = 1/2 P(B’) = 1/2
P(C) = 5/8 P(C’) = 3/8
Probability of hitting the target = 1

Question 4.
If A and B are any two events, then the probability that exactly one of them occur is …………
(a) P(A ∪ \(\overline{B}\)) + P(\(\overline{A}\) ∪ B)
(b) P(A ∩ \(\overline{B}\)) + P(\(\overline{A}\) ∩ B)
(c) P(A) + P(B) – P(A ∩ B)
(d) P(A) + P(B) + 2P(A ∩ B)
Solution:
(b)
Hint:

Question 5.
Let A and B be two events such that P(\(\overline{A \cup B}\)) = \(\frac{1}{6}\), P(A ∩ B) = \(\frac{1}{4}\) and P(\(\overline{A}\)) = \(\frac{1}{4}\).
Then the events A and B are …………………
(a) Equally likely but not independent
(b) Independent but not equally likely
(c) Independent and equally likely
(d) Mutually inclusive and dependent
Solution:
(b)
Hint:

So P(A). P(B) = \(\frac{3}{4} \times \frac{1}{3}=\frac{1}{4}\)
P(A ∩ B) = P(A). P(B)
⇒ A and B are independent and not equally likely

Question 6.
Two items are chosen from a lot containing twelve items of which four are defective, then the probability that at least one of the item is defective
when two items are chosen at random probability of atleast one of them is defective ………….

Solution:
(a)
Hint:
Total number = 12
Defective = 4
∴ good ones = 12 – 4 = 8
when two items are chosen at random probability of atleast one of them is defective
= P(one defective or 2 defectives) = P(GD or DD)
= P(G) P(D) + P(D) P(D)

Question 7.
A man has 3 fifty rupee notes, 4 hundred rupees notes and 6 five hundred rupees notes in his pocket. If 2 notes are taken at random, what are the odds in favour of both notes being of hundred rupee denomination?
(a) 1 : 12
(b) 12 : 1
(c) 13 : 1
(d) 1 : 13
Solution:
(d)
Hint:

The odds in favour done of P is P : 1 – P
(i.e.,) \(\frac{1}{13}: \frac{12}{13}\) = 1 : 12

Question 8.
A letter is taken at random from the letters of the word ‘ASSISTANT’ and another letter is taken at random from the letters of the word ‘STATISTICS’. The probability that the selected letters are the same is ………….

Solution:
(d)
Hint:

Question 9.
A matrix is chosen at random from a set of all matrices of order 2, with elements 0 or 1 only. The probability that the determinant of the matrix chosen is not zero will be

Solution:
(b)
Hint: Then given elements are 0 and So each term of a matrix can be filled (Using or 1) is 2 ways.
The No. of elements is a 2 × 2 matrix = 2 × 2 = 4. So the possible ways of filling the elements of a 2 × 2 matrix is 2⁴ = 16 (i.e.,) n(S) = 16
Let A be the event of getting a 2 × 2 matrix for which the determinant value is non zero.

Question 10.
A bag contains 5 white and 3 black balls. Five balls are drawn successively without replacement. The probability that they are alternately of different colours is …………..

Solution:
(c)
Hint:

Question 11.
If A and B are two events such that A ⊂ B and P(B) ≠ 0, then which of the following is correct?
(a) P(A/B) = \(\frac{\mathrm{P}(\mathrm{A})}{\mathrm{P}(\mathrm{B})}\)
(b) P(A/B) < P(A) (c) P(A/B) ≥ P(A) (d) P(A/B) > P(B)
Solution:
(c)
Hint:

Question 12.
A bag contains 6 green, 2 white, and 7 black balls. If two balls are drawn simultaneously then the probability that both are different colours is ………..

Solution:
(a)
Hint:

Question 13.
If X and Y be two events such that P(X/Y) = \(\frac{1}{2}\), P(Y/X) = \(\frac{1}{3}\) and P(X ∩ Y) = \(\frac{1}{6}\) then P(X ∪ Y) is …………
(a) \(\frac{1}{3}\)
(b) \(\frac{2}{5}\)
(c) \(\frac{1}{6}\)
(d) \(\frac{2}{3}\)
Solution:
(d)
Hint:

Question 14.
An um contains 5 red and 5 black balls. A balls is drawn at random, its colour is noted and is returned to the um. Moreover, 2 additional balls of the colour drawn are put in the um and then a ball is drawn at random. The probability that the second ball drawn is red will be …………

Solution:
(b)
Hint:

Question 15.
A number x is chosen at random from the first 100 natural numbers. Let A be the event of numbers which satisfies \(\frac{(x-10)(x-50)}{x-30}\) ≥ 0, then P(A) is …………….
(a) 0.20
(b) 0.51
(c) 0.71
(d) 0.70
Solution:
(c)
Hint:

Question 16.
If two events A and B are independent such that P(A) = 0.35 and P(A ∪ B) = 0.6, then P(B) is …………..

Solution:
(a)
Hint:
Given A and B are independent
P(A ∩ B) = P(A) + P(B)
⇒ Now P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
(i.e.,) Now P(A ∪ B) = P(A) + P(B) – P(A).P(B)
0.6 = 0.35 + P(B) – (0.35) P(B)
⇒ P(B) = (1 – 0.35) = 0.6 – 0.35
0.65 P(B) = 0.25
∴ P(B) = \(\frac{0.25}{0.65}=\frac{25}{65}=\frac{5}{13}\)

Question 17.
If two event A and B are such that P(\(\overline{A}\)) and P(A ∩ \(\overline{B}\)) = 1/2, then P(A ∩ B) is ………….

Solution:
(d)
Hint:

Question 18.
If A and B are two events such that P(A) = 0.4, P(B) = 0.8 and P(B/A) = 0.6, then P(\(\overline{A}\) ∩ B) is …………..
(a) 0.96
(b) 0.24
(c) 0.56
(d) 0.66
Solution:
(c)
Hint:
P(B/A) = 0.6 ⇒ \(\frac{P(A \cap B)}{P(A)}\) = 0.6
⇒ P(B/A) = 0.6 × P(A) = 0.6 × 0.4 = 0.24
Now P(\(\overline{A}\) ∩ B) = P(B) – P(A ∩ B)
= 0.8 – 0.24 = 0.56

Question 19.
There are three events A, B, and C of which one and only one can happen. If the odds are 7 to 4 against A and 5 to 3 against B, then odds against C is ……………
(a) 23 : 65
(b) 65 : 23
(c) 23 : 88
(d) 88 : 23
Solution:
(b)
Hint: If the probability of an event is P then the odds against its occurrence are 1 – P to P.
Selecting 1 from the 4 number 1, 2, 3,4, can be done in 4 ways
Here for the event A we are given that = \(\frac{1-\mathrm{P}}{\mathrm{P}}=\frac{7}{4}\)
⇒ 4 – 4P = 7P
⇒ 11 P = 4 ⇒ P = \(\frac{4}{11}\) ⇒ P(A) = \(\frac{4}{11}\) for the event B we are given
\(\frac{1-\mathrm{P}}{\mathrm{P}}=\frac{5}{3}\) ⇒ 5P = 3 – 3P
⇒ 8P = 3 ⇒ P = 3/8
P(B) = \(\frac{3}{8}\)
Now we are given P(A) + P(B) + P(C) = 1
P(C) = 1 – P(A) – P(B)
P(C) = 1 – \(\frac{4}{11}-\frac{3}{8}\)

Question 20.
If a and b are chosen randomly from the set {1, 2, 3, 4} with replacement, then the probability of the real roots of the equation x² + ax + b = 0 is

Solution:
(c)
Hint:
x² + ax + b = 0 ⇒ x = \(\frac{-a \pm \sqrt{a^{2}-4 b}}{2}\)
Given that the roots are real ⇒ a² – 4b ≥ 0 or a² > 4b
When a = 1, b = 1 or 2 or 3 or 4 a² – 4b < 0
When a = 2, b = 1 a² – 4b = 0
When a = 3, b = 1 or 2 for which a² – 4b ≥ 0
When a = 4, b = 1 or 2, 3 or 4 for which a² – 4b ≥ 0
So, Selecting from the 4 number 4² = 16 ways.
(i.e.,) n(s) = 16
n(A) = (2 or 3 or 4) = 3
n(B) = (1 or 2 or 3 or 4) = 4
P(A) + P(B) = \(\frac{3}{16}+\frac{4}{16}=\frac{7}{16}\)

Question 21.
It is given that the events A and B are such that P(A) = \(\frac{1}{4}\), P(A/B) = \(\frac{1}{2}\) and P(B/ A) = \(\frac{2}{3}\) then P(B) is ……………

Solution:
(b)
Hint:

Question 22.
In a certain college 4% of the boys and 1% of the girls are taller than 1.8 meter. Further 60% of the students are girls. If a student is selected at random and is taller than 1.8 meters, then the probability that the students is a girls is ………….

Solution:
(b)
Hint:

Question 23.
Ten coins are tossed. The probability of getting at least 8 heads is …………….

Solution:
(d)
Hint:
When 10 coins are tossed, No. of element in sample space
n(S) = 2¹⁰ = 1024
Probability of getting atleast 8 heads

Question 24.
The probability of two events A and B are 0.3 and 0.6 respectively. The probability that both A and B occur simultaneously is 0.18. The probability that neither A nor B occurs is …………….
(a) 0.1
(b) 0.72
(c) 0.42
(d) 0.28
Solution:
(d)
Hint:
P(A) = 0.3, P(B) = 0.6
P(A ∩ B) = 0.18
So P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
= 0.3 + 0.6 – 0.18
= 0.9 – 0.18 = 0.72
P(A’ ∩ B’) = P[(A ∪ B)’] = 1 – P(A ∪B)
= 1 – 0.72 = 0.28

Question 25.
If m is a number such that m≤ 5, then the probability that quadratic equation 2x² + 2mx + m + 1 = 0 has real roots is ………….

Solution:
(c)
Hint:
2x² + 2mx + m + 1 = 0


roots are real ⇒ m² – 2m – 2 ≥ 0
Here m ≤ 5 ⇒ n(S) = 5
When m= 1,m² – 2m – 2
When m = 2, m² – 2m- 2
When m = 3, m² – 2m – 2
When m = 4, m² – 2n- 2
When m = 5, m² – 2m – 2
⇒ n{A) = 3 and so P(A) = \(\frac{3}{5}\)

You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 2 Complex Numbers Ex 2.3

Question 1.
If z₁ = 1 – 3i, z₂ = -4i, and z₃ = 5, show that
(i) (z₁ + z₂) + z₃ = z₁ + (z₂ + z₃)
(ii) (z₁ z₂) z₃ = z₁ (z₂ z₃)
Solution:
(i) z₁ = 1 – 3i, z₂ = -4i, z₃ = 5
(z₁ + z₂) + z₃
= (1 – 3i – 4i) + 5
= (1 – 7i) + 5
= 6 – 7i …… (1)
z₁ + (z₂ + z₃)
= (1 – 3i) + (-4i + 5)
= 6 – 7i ……. (2)
from (1) & (2) we get
∴ (z₁ + z₂) + z₃ = z₁ + (z₂ + z₃)

(ii) (z₁ z₂) z₃ = [(1 – 3i) (-4i]5
= [-4i + 12 i²]5
= [-12 – 4i] 5
= -60 – 20i ……. (1)
z₁ (z₂ z₃) = (1 – 3i)[(-4i)(5)]
= (-20i + 60 i²)
= -20i – 60 ……. (2)
from (1) & (2) we get
∴ (z₁ z₂)(z₃) = z₁ (z₂ z₃)

Question 2.
If z₁ = 3, z₂ = -7i, and z₃ = 5 + 4i, show that
(i) z₁ (z₂ + z₃) = z₁ z₂ + z₁ z₃
(ii) (z₁ z₂) z₃ = z₁ z₃ + z₂ z₃
Solution:
(i) z₁ = 3, z₂ = -7i, z₃ = 5 + 4i
z₁ (z₂ + z₃) = 3 (-7i + 5 + 4i)
= 3 (5 – 3i)
= 15 – 9i …… (1)
z₁ z₂ + z₁ z₃ = 3 (-7i) + 3 (5 + 4i)
= -21i + 15 + 12i
= 15 – 9i …… (2)
from (1) & (2), we get
∴ z₁ (z₂ + z₃) = z₁ z₂ + z₁ z₃

(ii) (z₁ + z₂) z₃ = (3 – 7i) (5 + 4i)
= 15 + 12i – 35i – 28 i²
= 15 – 23i + 28
= 43 – 23i ……. (1)
z₁ z₃ + z₂ z₃ = 3(5 + 4i) – 7i(5 + 4i)
= 15 + 12i – 35i – 28 i²
= 15 – 23i + 28
= 43 – 23i ….. (2)
from (1) & (2), we get
∴ (z₁ + z₂) z₃ = z₁ z₃ + z₂ z₃

Question 3.
If z₁ = 2 + 5i, z₂ = -3 – 4i, and z₃ = 1 + i, find the additive and multiplicative inverse of z₁, z₂, and z₃.
Solution:
z₁ = 2 + 5i
(а) Additive inverse of z₁ = -z₁ = -(2 + 5i) = -2 – 5i
(b) Multiplicative inverse of
\(z_{1}=\frac{1}{z_{1}}=\frac{1}{2+5 i} \times \frac{2-5 i}{2-5 i}=\frac{(2-5 i)}{4+25}=\frac{2-5 i}{29}\)

z₂ = -3 – 4i
(a) Additive inverse of z₂ = -z₂ = -(-3 – 4i) = 3 + 4i
(b) Multiplicative inverse of
\(z_{2}=\frac{1}{z_{2}} \frac{1}{-3-4 i} \times \frac{-3+4 i}{-3+4 i}=\frac{-3+4 i}{9+16}=\frac{-3+4 i}{25}\)

z₃ = 1 + i
(а) Additive inverse of z₃ = -z₃ = -(1 + i) = -1 – i
(b) Multiplicative inverse of
\(z_{3}=\frac{1}{z_{3}} \frac{1}{1+i} \times \frac{1-i}{1-i}=\frac{1-i}{2}\)

Samacheer Kalvi 12th Maths Solutions Chapter 2 Complex Numbers Ex 2.3 Additional Problems

Question 1.
If z₁ = 4 – 7i, z₂ = 2 + 3i and z₃ = 1 + i show that.
(i) z₁ + (z₂ + z₃) = (Z₁ + z₂) + Z₃
(ii) (Z₁ z₂) z₃ = Z₁ (z₂ z₃)
Solution:
(i) Z₁ + (z₂ + z₁₃) = 4 – 7i + (2 + 3i + 1 + i) = 4 – 7i + (3 + 4i) = 7 – 3i
(z₁ + z₂) + z₃ = (4 – 7i + 2 + 3i) + (1 + i) = (6 – 4i) + (1 + i)
= 7 – 3i …(2)
From (1) and (2) we get, z₁ + (z₂ + z₃) = (z₁ + z₂) + z₃

(ii) (z₁z₂) z₃ = (4 – 7i) + (2 + 3i) (1 + i) = (8 + 12i – 14 i + 21) (1 + i)
= (29 – 2i)(1 + i) = 29 + 29i – 2i + 2
= 31 + 27i ….(1)
Z₁ (z₂z₃) = (4 – 7i) [(2 + 3i) (1 + i)] = 4 – 7i [2 + 2i + 3i – 3]
= 4 – 7i[5i – 1] = 20i – 4 + 35 + 7i
= 31 + 27i …(2)
From (1) and (2) we get, (Z₁Z₂) z₃ = z₁ (z₂z₃)

Question 2.
Given z₁ = 1 + i, z₂ = 4 – 3i and z₃ = 2 + 5i verify that.
Z₁(Z₂ Z₃) = Z₁ Z₂ – z₁z₃
Solution:
Z₁ = 1 + i,
z₂ = 4 – 3i,
z₃ = 2 + 5i
Z₁ (z₂ – z₃) = 1 + i[(4 – 3i) – (2 + 5i)] = 1 + i[2 – 8i] = 2 – 8i + 2i + 8
= 10 – 6i …(1)
Z₁ z₂ = (1 + i) (4 – 3i) = 4 – 3i + 4i + 3 = 7 + i
Z₁Z₃= (1 + i) (2 + 5i) = 2 + 5i + 2i – 5 = 7i – 3
Z₁Z₂ – Z₁ z₃ = 7 + i – (7i – 3) = 7 + i – 7i + 3
= 10 – 6i …(2)
From (1) and (2) we get, Z₁ (z₂ – z₃) = z₁ z₂ – z₁ z₃

Question 3.
Given z₁ = 4 – 7i and z₂ = 5 + 6i find the additive and multiplicative inverse of z₁ + z₂ and Z₁ – Z₂.
Solution:
Z₁ = 4 – 7i, z₂ = 5 + 6i
Z₁ + z₂ = 4 – 7i + 5 + 6i = 9 + i
Additive inverse of z₁ + z₂ = – (z₁ + z₂) = – (9 – i) = i – 9

You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 1 Applications of Matrices and Determinants Ex 1.8

Choose the correct or the most suitable answer from the given four alternatives.

Question 1.
If |adj(adj A)| = |A|⁹, then the order of the square matrix A is _______
(a) 3
(b) 4
(c) 2
(d) 5
Answer:
(b) 4

Question 2.
If A is a 3 × 3 non-singular matrix such that AA^T = A^TA and B = A^-1A^T, then BB^T = ______
(a) A
(b) B
(c) I₃
(d) B^T
Answer:
(c) I₃

Question 3.

Answer:

Question 4.

Answer:

Question 5.

Answer:

Question 6.
If A = \(\left[\begin{array}{ll}{2} & {0} \\ {1} & {5}\end{array}\right]\) and B = \(\left[\begin{array}{ll}{1} & {4} \\ {2} & {0}\end{array}\right]\) then |adj(AB)| = _______
(a) -40
(b) -80
(c) -60
(d) -20
Answer:
(b) -80
Hint:

Question 7.
If P = \(\left[\begin{array}{ccc}{1} & {x} & {0} \\ {1} & {3} & {0} \\ {2} & {4} & {-2}\end{array}\right]\) is the adjoint of 3 × 3 matrix A and |A| = 4, then x is ______
(a) 15
(b) 12
(c) 14
(d) 11
Answer:
(d) 11
Hint: Given |A| = 4 and P is the adjoint matrix of A
|P| = 4² = 16
⇒ -2 (3 – x) = 16
⇒ -6 + 2x = 16
⇒ 2x = 22
⇒ x = 11

Question 8.

Answer:

Question 9.
If A, B and C are invertible matrices of some order, then which one of the following is not true?
(a) adj A =|A| A^-1
(b) adj(AB) = (adj A) (adj B)
(c) det A^-1 = (det A)^-1
(d) (ABC)^-1 = C^-1B^-1A^-1
Answer:
(b) adj(AB) = (adj A) (adj B)

Question 10.

Answer:

Question 11.
If A^T A^-1 is symmetric, then A² = _______
(a) A^-1
(b) (A^T)²
(c) A^T
(d) (A^-1)²
Answer:
(b) (A^T)²

Question 12.
If A is a non-singular matrix such that \(A^{-1}=\left[\begin{array}{rr}{5} & {3} \\ {-2} & {-1}\end{array}\right]\), then (A^T)^-1 = _______

Answer:

Question 13.

Answer:

Question 14.

Answer:

Question 15.

Answer:

Question 16.

Answer:

Question 17.

Answer:

Question 18.

Answer:

Question 19.

Answer:

Question 20.
Which of the following is/are correct?
(i) Adjoint of a symmetric matrix is also a symmetric matrix
(ii) Adjoint of a diagonal matrix is also a diagonal matrix.
(iii) If A is a square matrix of order n and λ, is a scalar, then adj(λA) = λⁿ adj(A).
(iv) A(adj A) = (adj A)A = |A| I
(a) Only (i)
(b) (ii) and (iii)
(c) (iii) and (iv)
(d) (i), (ii) and (iv)
Answer:
(d) (i), (ii) and (iv)

Question 21.
If ρ(A) = ρ([A|B]), then the system AX = B of linear equations is ______
(a) consistent and has a unique solution
(b) consistent
(c) consistent and has infinitely many solution
(d) inconsistent
Answer:
(b) consistent

Question 22.
If 0 ≤ θ ≤ π, the system of equations x + (sin θ)y – (cos θ)z = 0, (cos θ)x – y + z = 0, (sin θ)x + y – z = 0 has a non-trivial solution then θ is ______
(a) \(\frac{2 \pi}{3}\)
(b) \(\frac{3 \pi}{4}\)
(c) \(\frac{5 \pi}{4}\)
(d) \(\frac{\pi}{4}\)
Answer:
(d) \(\frac{\pi}{4}\)

Question 23.
The augmented matrix of a system of linear equations is \(\left[\begin{array}{cccc}{1} & {2} & {7} & {3} \\ {0} & {1} & {4} & {6} \\ {0} & {0} & {\lambda-7} & {\mu+5}\end{array}\right]\). The system has infinitely many solutions if _____
(a) λ = 7, μ ≠ 5
(b) λ = -7, μ = 5
(c) λ ≠ 7, μ ≠ -5
(d) λ = 7, μ = -5
Answer:
(d) λ = 7, μ = -5

Question 24.

Answer:

Question 25.

Answer:

Samacheer Kalvi 12th Maths Solutions Chapter 1 Applications of Matrices and Determinants Ex 1.8 Additional Problems

Question 1.

(a) m < n (b) m > n
(c) m = n
(d) None of these
Solution:
(c) m = n
Hint:
A = [a_ij]_m×n is a square matrix if number of rows is equal to that of columns, i.e., m = n.

Question 2.
Matrices A and B will be inverse of each other only if ……..
(a) AB = BA
(b) AB = BA = O
(c) AB = O, BA = I
(d) AB = BA = I
Solution:
(d) AB = BA = I
Hint:
By the definition of invertible matrices two matrices A and B are inverse of each other if AB = BA = I.

Question 3.
If A is an invertible matrix of order 2 then det (A^-1) is equal to

Solution:

Hint.

Question 4.


Solution:
(d) \(\frac{1}{-3}\left(\begin{array}{ll}{1} & {0} \\ {0} & {1}\end{array}\right)\)

Question 5.


Solution:
(d) Inverse does not exist

Question 6.
Given ρ(A, B) = ρ(A) = number of unknowns, then the system has …….
(a) unique solution
(b) no solution
(c) inconsistent
(d) infinitely many solution
Solution:
(a) unique solution

Question 7.
Given ρ(A, B) ≠ ρ(A) then the system has
(a) no solution
(b) unique solution
(c) infinitely many solution
(d) None
Solution:
(a) no solution

Question 8.
Given ρ(A, B) = ρ(A) < number of unknowns, then the system has …….
(a) unique solution
(b) no solution
(c) 3 solutions
(d) infinitely many solution
Solution:
(d) infinitely many solution

Question 9.

(a) 1
(b) 2
(c) 3
(d) None of these
Solution:
(a) 1

Question 10.

(a) 1
(b) 0
(c) 4
(d) any real number
Solution:
(d) any real number

Question 11.
If A = [2 0 1], then the rank of AA^T is ………
(a) 1
(b) 2
(c) 3
(d) 0
Solution:
(a) 1
Hint.

Question 12.
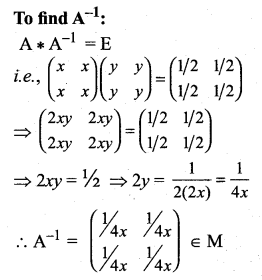
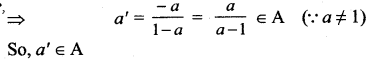
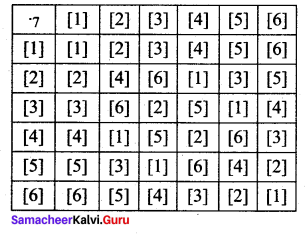
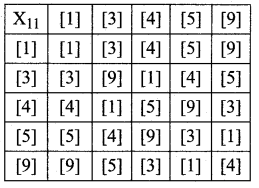
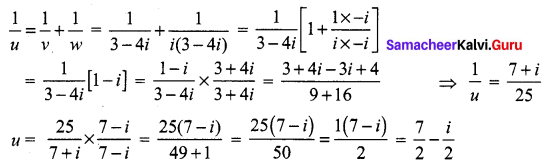
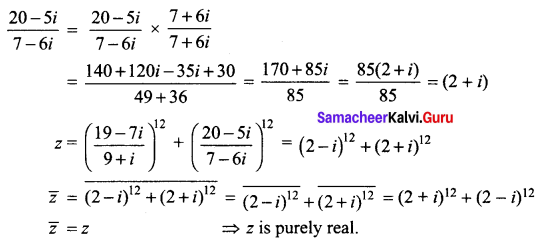
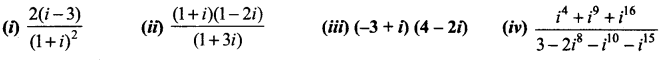
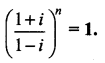
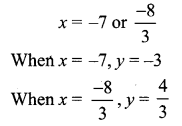
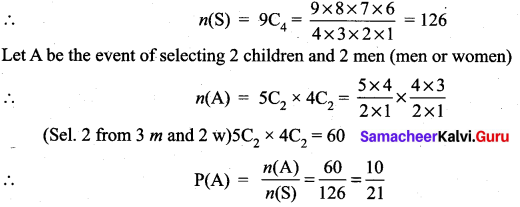
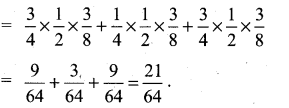
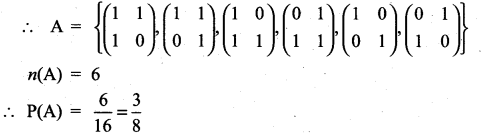
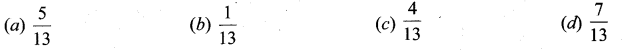
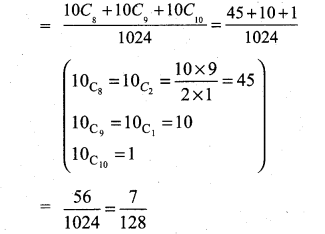
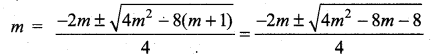
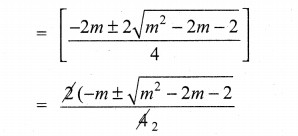
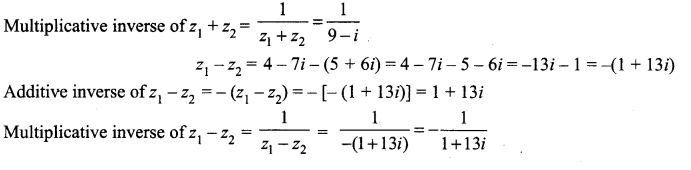
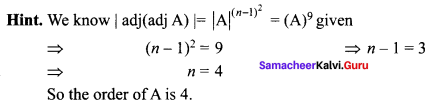
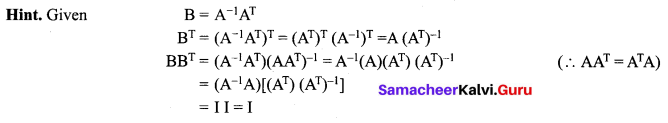
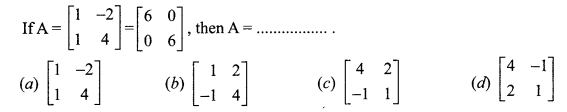
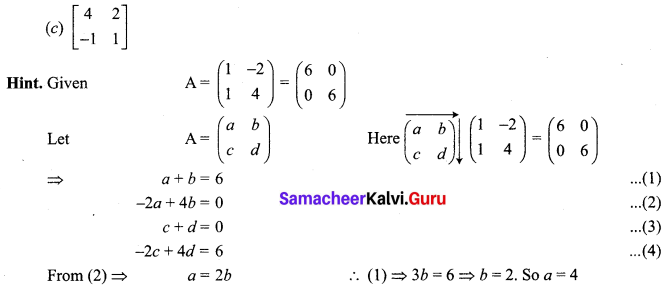
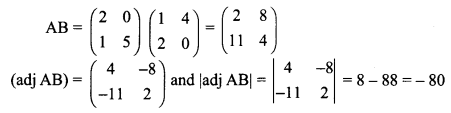
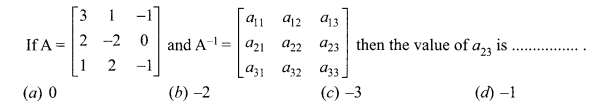
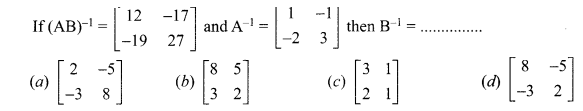
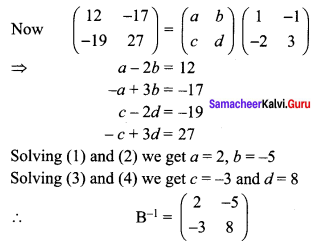
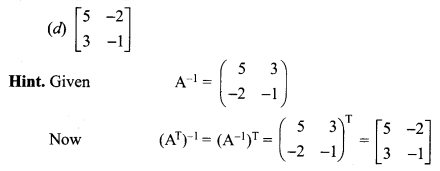
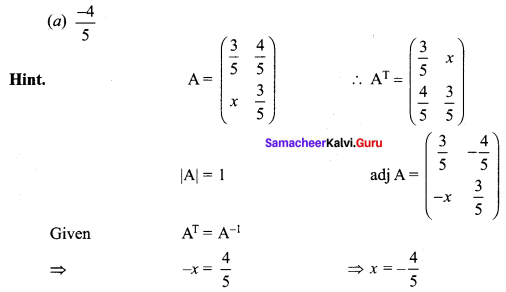
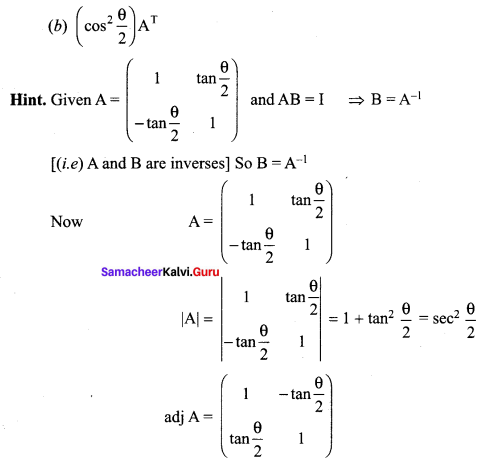
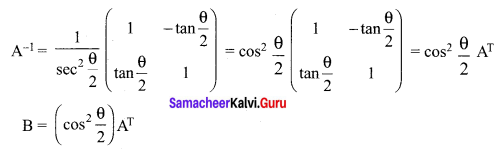
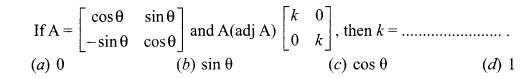
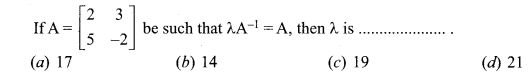
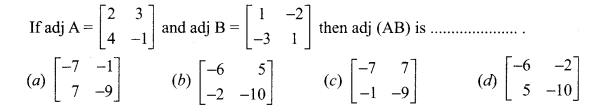
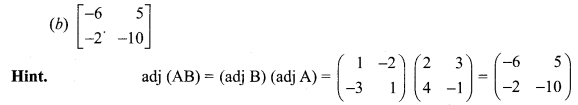
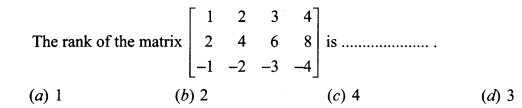
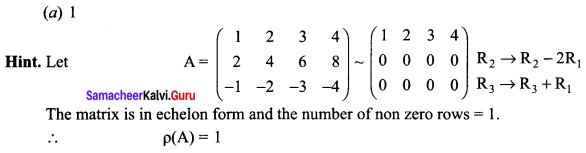
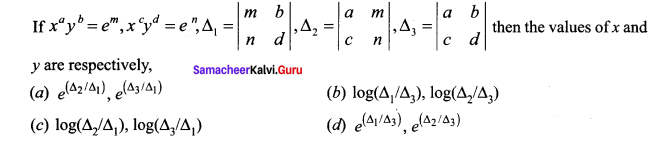
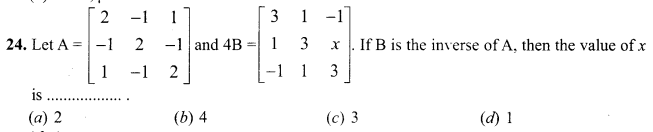
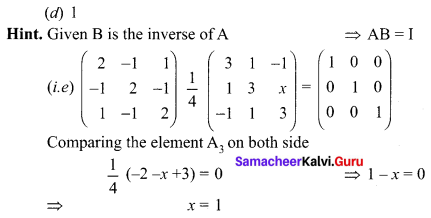
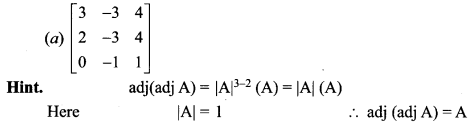
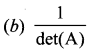
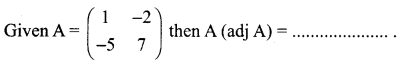
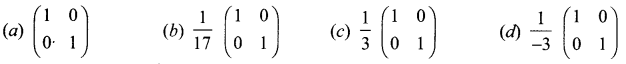
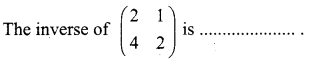
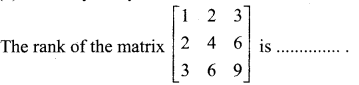
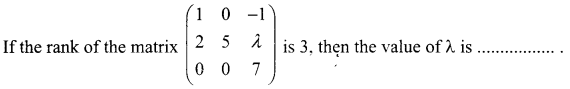
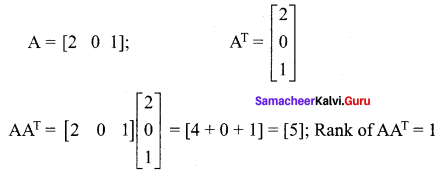
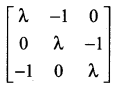If the rank of the matrix is 2, then λ is ……
(a) 1
(b) 2
(c) 3
(d) any real number
Solution:
(a) 1
Hint.
Since the rank of the given matrix is 2, the value of 3^rd order determinant is zero.

Question 13.
If A is a scalar matrix with scalar k ≠ 0, of order 3, then A^-1 is …….

Solution:
\(\frac{1}{k} \mathrm{I}\)
Hint:

Question 14.


Solution:

Hint:
(adj A)(A) = |A|I

Question 15.
If A is a square matrix of order n, then |adj A| is …….
(a) |A|²
(b) |A|ⁿ
(c) |A|^{n – 1}
(d) |A|
Solution:
(c) |A|^{n – 1}
Hint:
When A is square matrix of order 3, then |adj A| = |A|² = |A|^{3 – 1} ∴ When A is a square matrix of order n, |adj A| = |A|^{n – 1}

Question 16.
If A is a matrix of order 3, then det (kA)
(a) k³(det A)
(b) k²(det A)
(c) k(det A)
(d) det (A)
Solution:
(a) k³(det A)
Hint:
A is a matrix of order 3. ∴ det (kA) = k³ (det A)

Question 17.
If I is the unit matrix of order n, where k ± 0 is a constant, then adj(kI) = …….
(a) kⁿ(adj I)
(b) k(adj I)
(c) k²(adj I)
(d) k^{n – 1} (adj I)
Solution:
(d) k^{n – 1} (adj I)
Hint:
When I is a unit matrix of order 3, then adj (kI) = k² (adj I)
∴ When I is a unit matrix of order n, then adj (kI) = k^{n – 1} (adj I)

Question 18.
In a system of 3 linear non-homogeneous equations with three unknowns, if ∆ = 0 and ∆x = 0, ∆y ≠ 0 and ∆z = 0, then the system has …..
(a) unique solution
(b) two solutions
(c) infinitely many solutions
(d) no solution
Solution:
(d) no solution
Hint:
When ∆ = 0 ∆x, ∆z = 0 but ∆y ≠ 0 ⇒ that the system is inconsistent.
∴ There is no solution.

You can Download Samacheer Kalvi 11th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 11th Maths Solutions Chapter 3 Trigonometry Ex 3.12

Choose the correct answer or most suitable answer:

Question 1.

(a) \(\sqrt{2}\)
(b) \(\sqrt{3}\)
(c) 2
(d) 4
Solution:
(d) 4
Hint:

Question 2.
If cos 28° + sin 28° = k³, then cos 17° is equal to …….

Solution:
(a) \(\frac{k^{3}}{\sqrt{2}}\)
Hint:

Question 3.

(a) 4 + \(\sqrt{2}\)
(b) 3 + \(\sqrt{2}\)
(c) 9
(d) 4
Solution:
(a) 4 + \(\sqrt{2}\)
Hint:

Question 4.

Solution:
(a) \(\frac{1}{8}\)
Hint:

Question 5.

Solution:
(c) 2 cos θ
Hint:

Here θ is in II Quadrant

Question 6.

Solution:
(d) \(\text { (d) } \frac{1-\lambda^{2}}{2 \lambda}\)
Hint:

Question 7.
cos 1° + cos 2° + cos 3° + …. + cos 179° = …….
(a) 0
(b) 1
(c) -1
(d) 89
Solution:
(a) 0
Hint:
LHS = (cos 10 + cos 179°)+(cos 2° ÷ cos 178°)+ ….. +cos(89° + cos 91°)+cos 90°
cos 179° = cos (180° – 1) = – cos 1°
cos 178° = cos(180° – 2)= – cos 2°
So (cos 1°- cos 1°)+(cos 2° – cos 2°) + (cos 89° – cos 89°) + cos 90°
= 0 + 0 …. + 0 + 0 = 0.

Question 8.

Solution:
(b) \(\frac{1}{12}\)
Hint:

Question 9.
Which of the following is not true?

Solution:
(d) sec θ = \(\frac{1}{4}\)
Hint:
sec θ = \(\frac{1}{4}\) ⇒ cos θ = 4, which is not true.

Question 10.
cos 2θ cos 2ϕ+ sin² (θ – ϕ) – sin² (θ + ϕ) is equal to …….
(a) sin 2(θ + ϕ)
(b) cos 2(θ + ϕ)
(c) sin 2(θ – ϕ)
(d) cos 2(θ – ϕ)
Solution:
(b) cos 2(θ + ϕ)
Hint.
Given cos 2θ . cos 2ϕ + sin² (θ – ϕ) – sin² (θ + ϕ)
= cos 2θ cos 2ϕ + sin (θ – ϕ + θ + ϕ) sin (θ – ϕ – θ – ϕ)
= cos 2θ cos 2ϕ + sin 2θ sin(-2ϕ)
= cos 2θ cos 2ϕ – sin 2θ sin(2ϕ)
= cos (2θ + 2ϕ) = cos 2(θ + ϕ)

Question 11.

(a) sin A + sin B + sin C
(b) 1
(c) 0
(d) cos A + cos B + cos C
Solution:
(c) 0
Hint:

= tan A – tan B

Question 12.
cos pθ + cos qθ = 0 and if p ≠ q, then 0 is equal to (n is any integer) …….

Solution:
(b) \(\frac{\pi(2 n+1)}{p \pm q}\)
Hint:
cos pθ + cos qθ = 0

Question 13.
If tan α and tan β are the roots x² + ax + b = 0, then \(\frac{\sin (\alpha+\beta)}{\sin \alpha \sin \beta}\) is equal to …….
Solution:
(b) \(\frac{a}{b}\)
Hint:
tan² x + a tan x + b = 0
α and β are the roots of the equation
⇒ tan² α + a tan α + b = 0 ….. (1)
tan² β + a tan β + b = 0 …… (2)
(1) – (2) => tan² α – tan² β + a (tan α – tan β) = 0
(tan α – tan β) (tan α + tan β) + a (tan α – tan β) = 0
⇒ tan α + tan β = – a …. (A)
(1) × tan β – (2) × tan α

Question 14.
In a triangle ABC, sin² A + sin² B + sin² C = 2, then the triangle is …….
(a) equilateral triangle
(b) isosceles triangle
(c) right triangle
(d) scalene triangle
Solution:
(c) right triangle
Hint.
On simplifying we get
sin² A + sin² B + sin² C = 2 + 2 cos A cos B cos C
= 2 (given)
⇒ cos A cos B cos C = 0
cos A (or) cos B (or) cos C = 0
⇒ A (or) B (or) C = π/2
⇒ ABC (is a right angled triangle).

Question 15.
If f(θ) = |sin θ| + |cos θ|, θ ∈ R, then f(θ) is in the interval …….
(a) [0, 2]
(b) [1, \(\sqrt{2}\)]
(c) [1, 2]
(d) [0, 1]
Solution:
(b) [1, \(\sqrt{2}\)]
Hint:

Question 16.

Solution:
Nr: cos 6x + cos 4x + 5 cos 4x + 5 cos 2x + 10 cos 2x + 10
= 2 cos 5x cos x+5(2 cos 3x cos x)+ 10(2 cos²x)
= 2 cos x [cos 5x + 5 cos 3x + 10 cos x]

Question 17.
The triangle of maximum area with constant perimeter 12m
(a) is an equilateral triangle with side 4m
(b) is an isosceles triangle with sides 2m, 5m, 5m
(c) is a triangle with sides 3m, 4m, 5m
(d) does not exists
Solution:
(a) is an equilateral triangle with side 4m
Hint.
A triangle will have a max area (with a given perimeter) when it is an equilateral triangle.

Question 18.
A wheel is spinning at 2 radians/second. How many seconds will it take to make 10 complete rotations?
(a) 10π seconds
(b) 20π seconds
(c) 5π seconds
(d) 15π seconds
Solution:
(a) 10π seconds
Hint.
1 rotation makes 2π^c
Distance travelled in 1 second = 2 radians
So time taken to complete 10 rotations = 6 × 2π = 20 π^c
\(=\frac{20 \pi}{2}=10 \pi\) seconds

Question 19.
If sin α + cos α = b, then sin 2α is equal to ……..

Solution:
(b) b² – 1, if b > \(\sqrt{2}\)
Hint:
sin α + cos β = b
(sin α + cos β)² = b²
sin² α + cos² α + 2 sin α cos α = b²
sin² α = b² – 1

Question 20.

(a) Both (i) and (ii) are true
(b) Only (i) is true
(c) Only (ii) is true
(d) Neither (i) nor (ii) is true
Solution:
(a) Both (i) and (ii) are true
Hint.
When A + B + C = 180°

When A + B + C = 180° each angle will be lesser than 180°
So sin A, sin B, sin C > 0
⇒ sin A sin B sin C > 0
So both (i) and (ii) are true