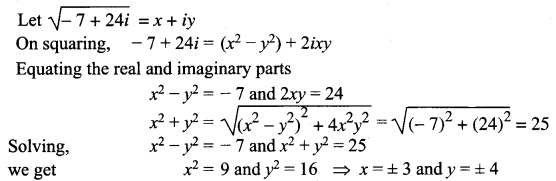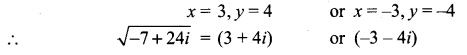You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.
Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 2 Complex Numbers Ex 2.5
Question 1.
Find the modulus of the following complex numbers.
(i) \(\frac{2 i}{3+4 i}\)
(ii) \(\frac{2-i}{1+i}+\frac{1-2 i}{1-i}\)
(iii) (1 – i)10
(iv) 2i(3 – 4i) (4 – 3i)
Solution:
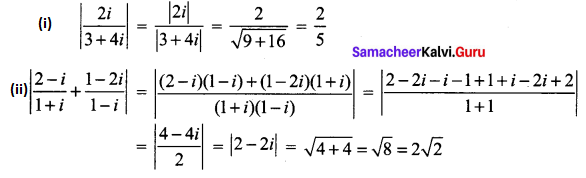
(iii) |(1 – i)10| = (|1 – i|)10
= \((\sqrt{1+1})^{10}=(\sqrt{2})^{10}=2^{5}=32\)
(iv) |2i(3 – 4i) (4 – 3i)|
= |2i| |3 – 4i| |4 – 3i|
= \(2 \sqrt{9+16} \sqrt{16+9}\)
= 2 × 5 × 5
= 50
![]()
Question 2.
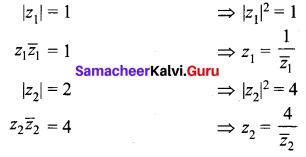
For any two complex numbers z1 and z2, such that |z1| = |z2| = 1 and z1 z2 ≠ -1, then show that \(\frac{z_{1}+z_{2}}{1+z_{1} z_{2}}\) is a real number.
Solution:
|z1|2 = 1
⇒ \(z_{1} \bar{z}_{1}=1\)
⇒ \(z_{1}=\frac{1}{\bar{z}_{1}}\)
Similarly \(z_{2}=\frac{1}{\bar{z}_{2}}\)
Question 3.
Which one of the points 10 – 8i, 11 + 6i is closest to 1 + i.
Solution:
A (1 + i), B (10 – 8i), C (11 + 6i)
|AB| = |(10 – 8i) – (1 + i)|
= |10 – 8i – 1 – i|
= |9 – 9i|
= \(\sqrt{81+81}\)
= \(\sqrt{162}\)
= 9(1.414)
= 12.726
CA = |(11 + 6i) – (1 + i)|
= |11 + 6i – 1 – i|
= |10 + 5i|
= \(\sqrt{100+25}\)
= \(\sqrt{125}\)
C (11 + 6i) is closest to the point A (1 + i)
Question 4.
If |z| = 3, show that 7 ≤ |z + 6 – 8i| ≤ 13.
Solution:
|z| = 3, To find the lower bound and upper bound we have
||z1| – |z2|| ≤ |z1 + z2| ≤ |z1| + |z2|
||z| – |6 – 8i|| ≤ |z + 6 – 8i| ≤ |z| + |6 – 8i|
|3 – \(\sqrt{36+64}\)| ≤ |z + 6 – 8i| ≤ 3 + \(\sqrt{36+64}\)
|3 – 10| ≤ |z + 6 – 8i| ≤ 3 + 10
7 ≤ |z + 6 – 8i| ≤ 13
Question 5.
If |z| = 1, show that 2 ≤ |z2 – 3| ≤ 4.
Solution:
|z| = 1 ⇒ |z|2 = 1
||z1| – |z2|| ≤ |z1 + z2| ≤ |z1| + |z2|
||z|2 – |-3|| ≤ |z2 – 3| ≤ |z|2 + |-3|
|1 – 3| ≤ |z2 – 3| ≤ 1 + 3
2 ≤ |z2 – 3| ≤ 4
![]()
Question 6.
If \(\left|z-\frac{2}{z}\right|\) = 2, show that the greatest and least value of |z| are √3 + 1 and √3 – 1 respectively.
Solution:
\(\left|z-\frac{2}{z}\right|\) = 2
We know that

The minimum value of |z| is |1 – √3| = √3 – 1
The greatest value of |z| is √3 + 1
Question 7.
If z1, z2 and z3 are three complex numbers such that |z1| = 1, |z2| = 2, |z3| = 3 and |z1 + z2 + z3| = 1, show that |9z1 z2 + 4z1 z3 + z2 z3| = 6.
Solution:

Question 8.
If the area of the triangle formed by the vertices z, iz, and z + iz is 50 square units, find the value of |z|.
Solution:
The given vertices are z, iz, z + iz ⇒ z, iz are ⊥r to each other.
Area of triangle = \(\frac { 1 }{ 2 }\) bh = 50
⇒ \(\frac { 1 }{ 2 }\) |z| |iz| = 50
⇒ \(\frac { 1 }{ 2 }\) |z| |z| = 50
⇒ |z|2 = 100
⇒ |z| = 10
Question 9.
Show that the equation z3 + 2\(\bar{z}\) = 0 has five solutions.
Solution:
Given that z3 + 2\(\bar{z}\) = 0
z3 = -2 \(\bar{z}\) ……. (1)
Taking modulus on both sides,
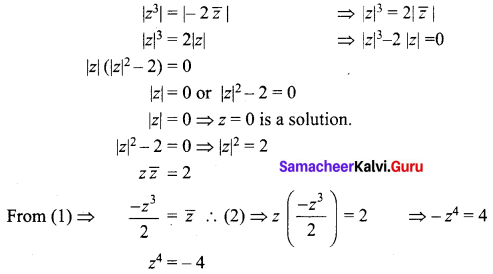
z has four non-zero solution.
Hence including zero solution. There are five solutions.
![]()
Question 10.
Find the square roots of
(i) 4 + 3i
(ii) -6 + 8i
(iii) -5 – 12i
Solution:
(i) z = 4 + 3i
|z| = |4 + 3i| = \(\sqrt{16+9}\) = 5


Samacheer Kalvi 12th Maths Solutions Chapter 2 Complex Numbers Ex 2.5 Additional Problems
Question 1.
Find the modulus and argument of the following complex numbers and convert them in polar form.
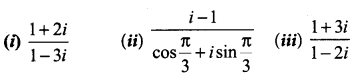
Solution:
(i)
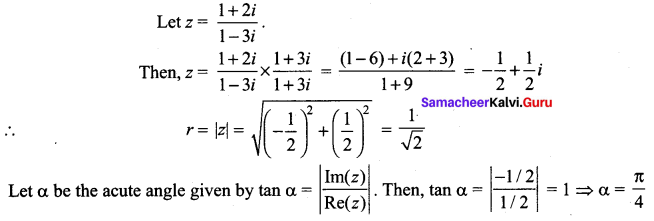
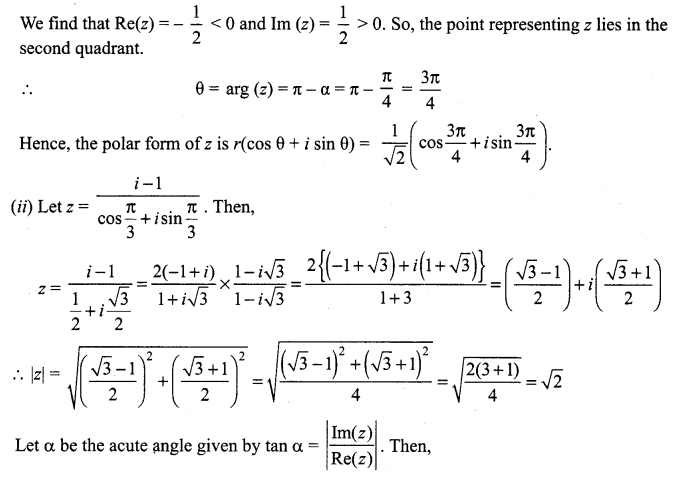


Question 2.
Find the square roots of – 15 – 8i
Solution:

On solving (i) and (iii), we get
x2 = 1 and y2 = 16 => x = ± 1 and y = ±4 From (ii), we observe that 2xy is negative. So, x and y are of opposite signs.
![]()
Question 3.
Find the square roots of i.
Solution:
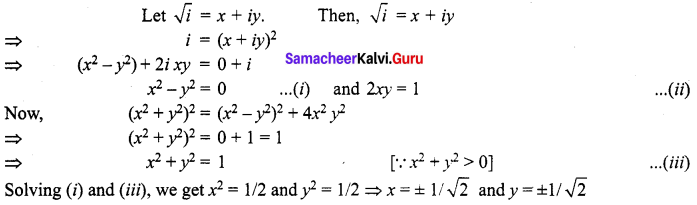
From (ii) we observe that we find that 2xy is positive. So, x and y are of same sign.
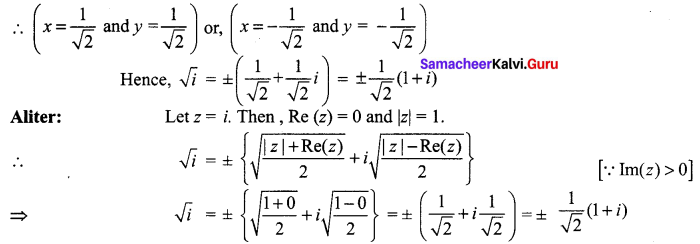
Question 4.
Find the modulus or the absolute value of ![]()
Solution:

Question 5.
Find the modulus and argument of the following complex numbers:
![]()
Solution:



Question 6.
Show that the points representing the complex numbers 7 + 9i, – 3 + 7i, 3 + 3i form a right angled triangle on the Argand diagram.
Solution:
Let A, B and C represent the complex numbers
7 + 9i, – 3 + 7i and 3 + 3i in the Argand diagram respectively.
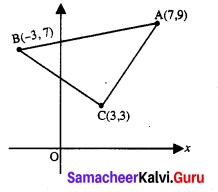
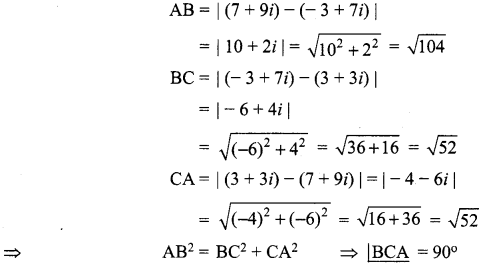
Hence ∆ABC is a right angled isosceles triangle.
![]()
Question 7.
Find the square root of (- 7 + 24i).
Solution: