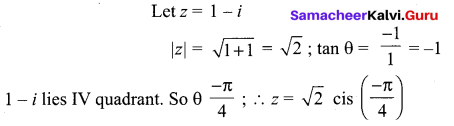Samacheer Kalvi 12th Maths Solutions Chapter 2 Complex Numbers Ex 2.7

You can Download Samacheer Kalvi 12th Maths Book Solutions Guide Pdf, Tamilnadu State Board help you to revise the complete Syllabus and score more marks in your examinations.

Tamilnadu Samacheer Kalvi 12th Maths Solutions Chapter 2 Complex Numbers Ex 2.7

Question 1.
Write in polar form of the following complex numbers.
(i) 2 + i2√3
(ii) 3 – i√3
(iii) -2 – i2
(iv) \(\frac{i-1}{\cos \frac{\pi}{3}+i \sin \frac{\pi}{3}}\)
Solution:

Question 2.
Find the rectangular form of the following complex numbers.

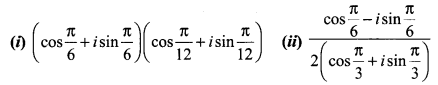
Solution:

Question 3.

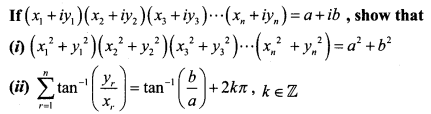
Solution:
(i) (x₁ + iy₁) (x₂ + iy₂) (x₃ + iy₃) …….. (x_n + iy_n) = a + ib …… (1)
Taking modulus on both sides,
|(x₁ + iy₁) (x₂ + iy₂) (x₃ + iy₃) …….. (x_n + iy_n)| = |a + ib|
|x₁ + iy₁| |x₂ + iy₂| |x₃ + iy₃| ….. |x_n + iy_n| = |a + ib|

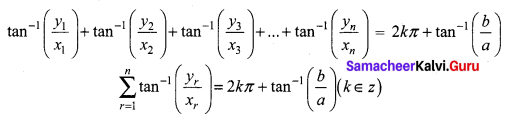
Question 4.
If \(\frac{1+z}{1-z}\) = cos 2θ + i sin 2θ, show that z = i tan θ.
Solution:

Question 5.
If cos α + cos β + cos γ = sin α + sin β + sin γ = 0, then show that
(i) cos 3α + cos 3β + cos 3γ = 3 cos (α + β + γ)
(ii) sin 3α + sin 3β + sin 3γ = 3 sin (α + β + γ)
Solution:
Let a = cos α + i sin α = e^iα
b = cos β + i sin β = e^iβ
c = cos γ + i sin γ = e^iγ
a + b + c = (cos α + cos β + cos γ) + i (sin α + sin β + sin γ)
⇒ a + b + c = 0 + i 0
⇒ a + b + c = 0
If a + b + c = 0 then a³ + b³ + c³ = 3abc

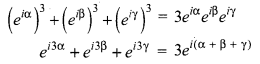
(cos 3α + i sin 3α + cos 3β + i sin 3β + cos 3γ + i sin 3γ) = 3 [cos (α + β + γ) + i sin (α + β + γ)]
(cos 3α + cos 3β + cos 3γ) + i (sin 3α + sin 3β + sin 3γ) = 3 cos (α + β + γ) + i 3sin(α + β + γ)
Equating real and Imaginary parts
(i) cos 3α + cos 3β + cos 3γ = 3 cos (α + β + γ)
(ii) sin 3α + sin 3β + sin 3γ = 3 sin (α + β + γ)

Question 6.
If z = x + iy and arg \(\left(\frac{z-i}{z+2}\right)=\frac{\pi}{4}\), then show that x² + y² + 3x – 3y + 2 = 0.
Solution:
arg \(\left(\frac{z-i}{z+2}\right)=\frac{\pi}{4}\)
We have arg (\(\frac{z_{1}}{z_{2}}\)) = arg(z₁) – arg(z₂)
arg (z – i) – arg (z + 2) = \(\frac{\pi}{4}\)
Let z = x + iy
arg (x + iy – i) – arg (x + iy + 2) = \(\frac{\pi}{4}\)
arg(x + i(y – 1)) – arg(x + 2 + iy) = \(\frac{\pi}{4}\)

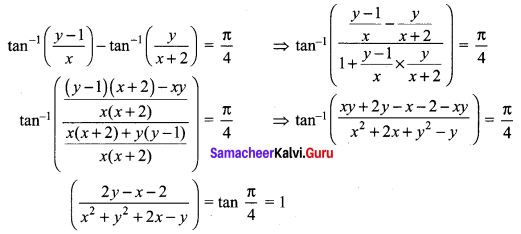
2y – x – 2 = x² + y² + 2x – y
x² + y² + 3x – 3y + 2 = 0
Hence proved.

Samacheer Kalvi 12th Maths Solutions Chapter 2 Complex Numbers Ex 2.7 Additional Problems

Question 1.
Write the following complex numbers in the polar form:

Solution:

Question 2.
Find the modulus and principal argument of (1 + i) and hence express it in the polar form.
Solution:

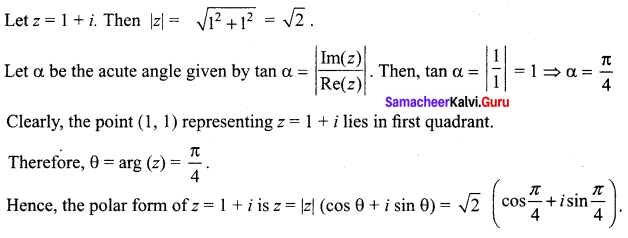
Question 3.
Express the following complex numbers in the polar form.

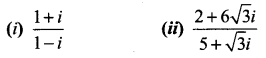
Solution:

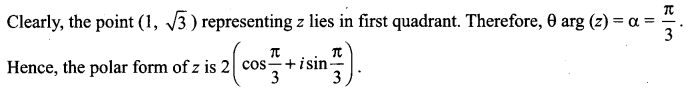
Question 4.
Express the following complex numbers in the polar form: \(2+2 \sqrt{3} i\)
Solution:

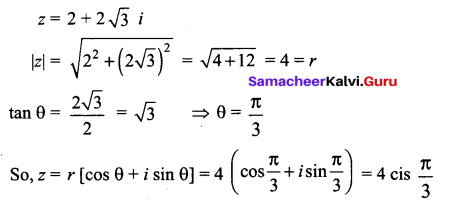
Question 5.
Express the following complex numbers in the polar form: \(-1+i \sqrt{3}\)
Solution:

Question 6.
Express the following complex numbers in the polar form: -1 – i
Solution:

Question 7.
Express the following complex numbers in the polar form: 1 – i
Solution: